② 中国石油大学(北京)地质地球物理综合研究中心, 北京 102249;
③ 中国石油塔里木油田分公司勘探开发研究院, 新疆库尔勒 841000;
④ 中国石化石油勘探开发研究院, 北京 100083;
⑤ 中国石油大港油田井下作业公司, 天津 300283
② Laboratory for Integration of Geology and Geophysics, China University of Petroleum(Beijing), Beijing 102249, China;
③ Research Institute of Exploration and Development, Tarim Oilfield Company, PetroChina, Korla, Xinjiang 841000, China;
④ Research Institute of Petroleum Exploration and Production, SINOPEC, Beijing 100083, China;
⑤ Downhole Operation, Dagang Oilfield Company, PetroChina, Tianjin 300283, China
就世界范围而言,古喀斯特储层并不多见,但却可以蕴藏大量的油气资源[1-3]。奥陶系碳酸盐岩储层一直是中国西部塔里木盆地油气勘探、开发的重要领域[4]。奥陶系储层埋深普遍大于5000m,其原生孔隙已经基本消失,基质孔隙度普遍低于2%,储集空间多由次生的不均匀分布的孔、洞、缝组成(图 1a),常表现为不同尺度的缝洞组合储集体[5-7]。储层分布受原始沉积相带的控制作用相对较小,空间分布变化大,具有很强的非均质性(图 1b、图 1c),难以准确刻画。这类储层的地震波速度和密度明显低于致密基质,当其规模达到地震可识别的尺度时会在叠后地震剖面上形成显著的强反射[8-9]。由速度、密度、泊松比和拉梅系数等在低频模型约束下反演的弹性属性可以评价次生碳酸盐岩储层的分布和品质(流体性质),但反演结果会随初始模型的不同而差别较大。在反演过程中初始模型是对地下物性参数的初始猜测,要求最终反演结果能准确模拟实际地质现象[10],因此初始模型的精度决定了弹性参数反演精度。

|
图 1 次生碳酸盐岩储层特征与地震响应 (a)岩心照片;(b)野外露头;(c)地震响应(绿线为碳酸盐岩顶界面) |
人们一般基于地震解释的地质层位,利用有限实际测井数据按照某种数学方法(如反距离加权、克里金插值等)内插、外推,从而获得全区的初始模型,其依赖于测井资料的精度和分布特征。对于沉积相带变化剧烈的地区,当井资料较少或分布不均时上述方法会引起地质假象[11],不能刻画强非均质储层。Cerney等[12]引入地震速度信息构建初始模型,但限于地震速度的精度难以获得高分辨率、高精度的初始模型。近年来,业界逐渐利用多种地震参数控制或改善低频模型和反演质量[13-21],但是这些参数存在品质不高、与井数据相关性低的问题。如,传统的全叠加数据常受AVO效应的影响而精度不高。
传统的碎屑岩储层的“相控建模”技术主要依据沉积相带的分布规律确定沉积物、弹性参数以及模型的空间分布特征[22],方法虽然较成熟,但是难以准确地描述次生碳酸盐岩储层的极强非均质特征。常规碳酸盐岩储层的“岩溶相控”[23-24]建模技术,依据碳酸盐岩出露遭受风化,特别是表层受水流影响形成“岩溶带”、深层相对致密的特征建立稳定的区域模型,虽然能较好地建立风化壳型碳酸盐岩储层模型,但并不适用于埋藏岩溶型碳酸盐岩储层建模。碳酸盐岩储层相控建模技术[8]基于钻、测井信息,通过融合与优化多种地震属性信息构建储层模型,但求取均方根振幅、分频、波阻抗等基础属性的过程复杂,且只能得到定性/半定量结果,不能直接用于反演。
为此,本文综合地质、地震和测井资料,建立了基于地震约束建模的反演方法,并刻画了塔中地区ZG8井区深层碳酸盐岩储层。
1 地震约束建模的反演方法本文提出一种基于振幅约束建模的地震反演方法。首先基于线性反演去除资料的AVO效应获得纯纵波数据,然后结合测井信息计算相对波阻抗,并进一步转化为绝对波阻抗属性定量质控波阻抗反演质量。文中采用的建模方法本质上属于确定性建模范畴[25],流程包括纯纵波数据提取、相对阻抗计算、振幅约束低频建模、波阻抗反演等(图 2)。

|
图 2 基于地震约束建模的波阻抗反演方法流程 |
即便道集完全平直,地下岩性或流体差异产生的AVO效应也会降低叠加资料分辨能力和精度。塔里木盆地碳酸盐岩储层埋深普遍大于5000m,极易将全叠加资料的AVO效应造成的调谐现象错误地解释为片状反射型储层[8],因此必须采用去除AVO效应的纯纵波数据进行解释,计算公式为[26-27]
| $ \begin{array}{l} {R_{{\rm{PP}}}}(\theta ) \approx \frac{1}{2}{R_{\rm{P}}}{\sec ^2}\theta - 8\frac{{{\beta ^2}{{\sin }^2}\theta }}{{{\alpha ^2}}}{R_{\rm{S}}} - \\ \left( {\frac{1}{2}{{\tan }^2}\theta - 2\frac{{{\beta ^2}}}{{{\alpha ^2}}}{{\sin }^2}\theta } \right){R_{\rm{D}}} \end{array} $ | (1) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{R_{\rm{P}}} = \frac{1}{2}\left( {\frac{{\Delta \rho }}{\rho } + \frac{{\Delta \alpha }}{\alpha }} \right)}\\ {{R_{\rm{S}}} \approx \frac{1}{2}\left( {\frac{{\Delta \rho }}{\rho } + \frac{{\Delta \beta }}{\beta }} \right)}\\ {{R_{\rm{D}}} \approx \frac{{\Delta \rho }}{\rho }} \end{array}} \right. $ | (2) |
式中:
对于非线性方程(式(1))的求解,常规线性反演方法假设β/α为常数,将式(1)转换为线性方程组,这种做法运算简便,效率高,但反演的RS、RD、β/α存在较大误差[26]。若采用完全非线性求解算法同时求解RP、RS、RD、β/α等4个未知数,计算效率较低,容易陷入局部寻优,且同样严重依赖于初始模型[26]。实际上,由于RP低阶项与β/α不相关且低阶项系数值较大,β/α近似误差主要影响RS和RRD,而不影响RP[26-27],因此可以高效、准确地线性反演RP。
实际计算中,假设叠前资料品质较好,将叠前道集SPP(θ)直接视为RPP(θ),令纵横波速度比为2,在道集数大于3的情况下,可求得准确的纯纵波数据SP
| $ \begin{array}{l} {S_{{\rm{PP}}}}(\theta ) \approx \frac{1}{2}{S_{\rm{P}}}{\sec ^2}\theta - 8\frac{{{\beta ^2}{{\sin }^2}\theta }}{{{\alpha ^2}}}{S_{\rm{S}}} - \\ \left( {\frac{1}{2}{{\tan }^2}\theta - 2\frac{{{\beta ^2}}}{{{\alpha ^2}}}{{\sin }^2}\theta } \right){S_{\rm{D}}} \end{array} $ | (3) |
式中SP、SS、SD分别为纯纵波、纯横波和纯密度数据。此时由于没有去除零相位地震子波,所得的SP为真正的纵波剖面,其值不受纵横波速度比精度影响[26-27],且消除了AVO效应的影响,较全叠加资料具有更高的分辨率和精度[26-27]。
1.2 相对阻抗计算由传统的储层插值建模方法得到的储层分布不能在空间上完全解释层位,因此不适合塔里木盆地次生碳酸盐岩储层预测。如何有效利用纯纵波振幅的空间信息和钻、测井资料的纵向分辨率是次生碳酸盐岩储层建模的关键。为此,本文引入颜色反演方法[28]求取纯纵波资料对应的相对阻抗(RI),即
| $ {\rm{RI}} = OS $ | (4) |
式中:S为地震道;O为操作因子。通过拟合测井资料的声波阻抗频谱指数关系,然后提取井旁道地震谱的指数关系,两者相除可得操作因子谱,再做-90°相位移动即得操作因子O[28]。与传统带限反演方法(如90°相位旋转、道积分、递归反演等)不同,颜色反演的操作因子包含子波因素,可建立地质体和振幅间的联系,并且其操作过程较稀疏脉冲反演类方法简便,人为因素少。
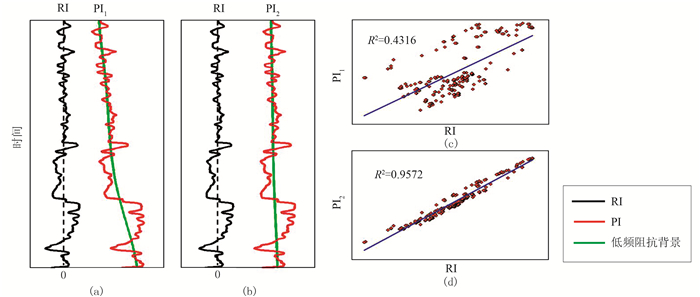
1.3 振幅约束建立低频模型虽然RI同样含有储层非均质性信息,并且可评价储层性质,但其中的相对正、负数值无法直接建立低频模型,必须转换为绝对阻抗信息PI。理论上,PI是RI与低频背景之和(图 3)。低频背景随着地质条件的不同而发生变化,通常随着埋深和压实作用增大而逐渐增大(图 3a),导致RI与PI相关性变差,拟合优度R变小(图 3c)。对于沉积环境稳定、地质体变化不大的情况,低频背景相对稳定(图 3b),PI与RI相关性很强,R较大(图 3d)。塔里木盆地奥陶系碳酸盐岩地层埋深较大,基质孔隙度很小,具有十分稳定的高阻抗碳酸盐岩背景,正好适合阻抗转换运算。依据PI与RI的关系,对纵波阻抗低频背景十分稳定的区域,可建立RI与PI的线性转化关系
|
图 3 在不同低频背景下RI与PI的对比(据文献[9]修改) (a)正常压实情况下RI与PI1的关系;(b)塔里木盆地深层碳酸盐岩内部RI与PI2的关系;(c)RI与PI1交会图;(d)RI与PI2交会图 |
| $ {\rm{PI = }}{a} \times {\rm{RI + }}b $ | (5) |
式中a与b为线性相关常数。
1.4 地震波阻抗反演获得低频模型后,基于得到的纯纵波资料,即可利用确定性反演方法(本文选用约束稀疏脉冲波阻抗反演)获得波阻抗参数。
2 应用效果对比塔中地区深层次生碳酸盐岩储层一般位于岩溶高地或岩溶斜坡等古地貌环境,集中分布于古水流系统或断裂附近。图 4为过ZG12—TZ35—ZG21—ZG23—ZG8井测线数据。由图可见:纯纵波数据在碳酸盐岩顶界面附近的反射很清晰(图 4b蓝色箭头处),特别是对于碳酸盐岩内部储层(T03s界面以下)的响应更明显,因此利用纯纵波资料分析属性和预测储层的精度更高;通过颜色反演进一步去掉了子波因素,储层的非均质特征更清晰(图 4c蓝圈处),有助于提高建模和反演精度。

|
图 4 过ZG12—TZ35—ZG21—ZG23—ZG8井测线数据 (a)叠加数据;(b)纯纵波数据;(c)颜色反演的相对阻抗 T03l与To3l-1分别为鹰山组1段顶、底界面,To3s为碳酸盐岩顶界面。蓝色箭头指示AVO效应去除前、后同相轴的变化,蓝圈对应碳酸盐岩内部非均质储层(强反射)位置。ZG8、ZG23、ZG21和ZG12井均钻遇了碳酸盐岩储层,TZ35井在碳酸盐岩层段未揭示储层 |
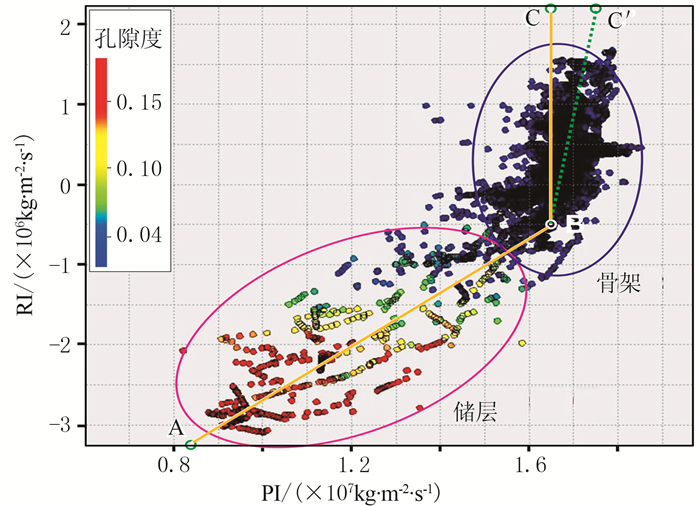
图 5为ZG8井区测井PI—颜色反演RI交会图。由图可见,碳酸盐岩基质落在PI>1.55×107 kg·m-2·s-1的范围(图 5蓝圈处),优质储层落在PI < 1.55×107kg·m-2·s-1的范围。实际上,碳酸盐岩基质速度大,次生储集空间的速度相对较小,两者产生的强烈阻抗差会在地震剖面上形成强反射,这是传统叠后储层预测的依据。
|
图 5 ZG8井区测井PI—颜色反演RI交会图 RI与PI呈分段线性相关关系:PI=3.556RI+1.828×107(AB段);PI=0.129RI+1.656×107(BC′段) |
颜色反演获得的RI受控于地震振幅,而子波旁瓣常常导致所有反演结果在低阻储层周围出现高阻阴影,故常在塔里木盆地深层碳酸盐岩储层地震反演中令基质段纵波阻抗数值基本不变,以避免子波旁瓣对反演的影响。对于碳酸盐岩顶界面T03s以下、RI>-5×106kg·m-2·s-1(图 5中BC′段)的区域,令PI均为1.65×107kg·m-2·s-1(图 5中的BC段)。
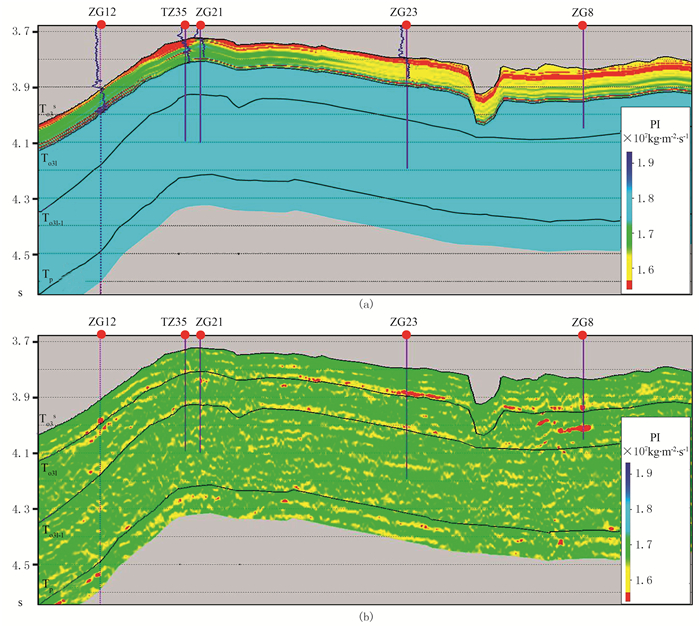
2.1 低频模型对比图 6为过ZG12—TZ35—ZG21—ZG23—ZG8井测线的纵波阻抗低频模型。由图可见:①传统插值建模结果在浅层受井分布的影响呈大面积条带状干扰,且受测井曲线深度限制,无深部有效信息(图 6a)。②振幅约束建模阻抗模型充分利用地震数据的空间信息,结合高分辨率测井资料,可定量、清楚地表征强非均质碳酸盐岩储层(T03s界面以下)的分布规律(图 6b黄色和红色区域)。另外,由于阻抗模型计算过程(式(4)、式(5))对碳酸盐岩背景区域采用统一为常数的均一处理,可以降低阻抗反演过程的子波旁瓣效应,提高反演精度。
|
图 6 过ZG12—TZ35—ZG21—ZG23—ZG8井测线的纵波阻抗低频模型 (a)传统插值建模;(b)振幅约束建模。井旁曲线为声波阻抗曲线,ZG8井无测量数据 |
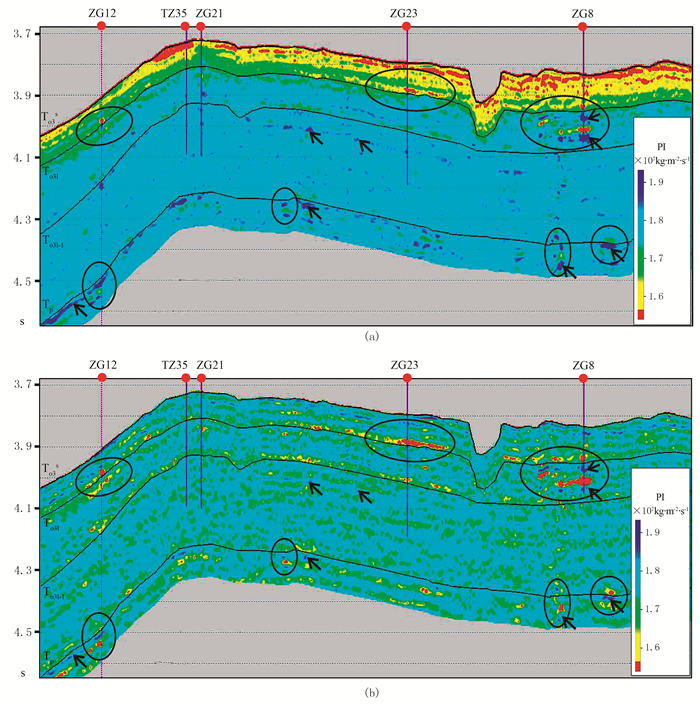
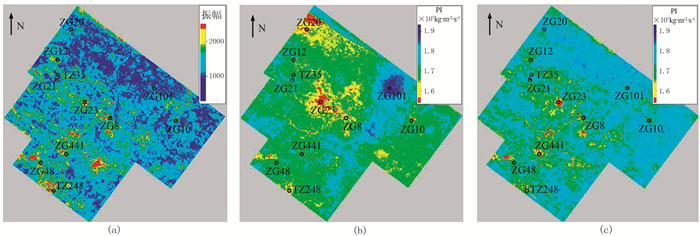
基于得到的纯纵波数据,分别采用传统插值建模和地震约束建模产生的初始模型进行约束稀疏脉冲波阻抗反演(图 7)。可见:①传统插值建模反演结果在浅层仍然存在明显的条带效应,难以准确反映相对均质模型背景上的储层变化(图 7a黑圈处);依据数据末尾的数值外推,仅获得相对均一的深部结果(图 7a)。因此传统插值建模反演结果可能对浅层(T03s-T03l)的波阻抗值估计过大,而对深层(T03l以下)的波阻抗值估计过小。②振幅约束建模反演结果不仅准确地反映了储层的空间分布特征,而且降低了子波旁瓣效应(图 7b黑色箭头处)。图 8为鹰山组1段均方根振幅平面分布。由图可见:传统插值建模反演结果受井点影响较大,平面分布存在显著的“牛眼”特征(图 8b),与纯纵波信息(图 8a)不一致;振幅约束建模反演结果较好地反映了储层的空间非均质特征(图 8c)。
|
图 7 过ZG12—TZ35—ZG21—ZG23—ZG8井测线的纵波阻抗反演结果 (a)传统插值建模反演;(b)振幅约束建模反演 |
|
图 8 鹰山组1段(T03l-T03l-1)均方根振幅平面分布 (a)纯纵波;(b)传统插值建模反演;(c)振幅约束建模反演 |
基于塔里木盆地深层碳酸盐岩储层的发育特征和弹性参数特点,本文构建了碳酸盐岩相对阻抗与绝对阻抗计算关系,并结合纯纵波资料建立了基于地震约束建模的地震反演方法,提高了ZG8井区碳酸盐岩储层刻画精度。对于强非均质储层描述,基于纯纵波振幅约束建模的反演方法可以避免传统插值建模方法受井资料影响大的局限,克服了常规融合层速度等建模方法精度不高的缺陷,准确反演了强非均质储层的分布规律,特别适合描述中国西部塔里木盆地的次生碳酸盐岩储层。
| [1] |
刘坤岩, 马丽娟, 邬兴威, 等. 塔河奥陶系薄层状孔洞储集体定量预测方法研究[J]. 地球物理学进展, 2017, 32(4): 1614-1620. LIU Kunyan, MA Lijuan, WU Xingwei, et al. Quantitative predication of flaggy reservoir of Ordovician formation in Tahe oilfield[J]. Progress in Geophy-sics, 2017, 32(4): 1614-1620. |
| [2] |
李鹏飞, 崔德育, 田浩男, 等. 塔里木盆地塔北地区X区块断溶体刻画方法与效果[J]. 石油地球物理勘探, 2017, 52(增刊1): 189-194. LI Pengfei, CUI Deyu, TIAN Haonan, et al. Fault-karst carbonate reservoir description with GeoEast interpretation sub-system in the Tabei Area, Tarim Basin[J]. Oil Geophysical Prospecting, 2017, 52(S1): 189-194. |
| [3] |
徐红霞, 沈春光, 李斌, 等. 多属性分析技术在碳酸盐岩断溶体预测中的应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 158-163. XU Hongxia, SHEN Chunguang, LI Bin, et al. Fault-karst carbonate reservoir prediction with comprehensive multi-attribute analysis[J]. Oil Geophysical Prospecting, 2017, 52(S2): 158-163. |
| [4] |
杨子川, 刘军, 陈黎, 等. 顺南地区奥陶系碳酸盐岩储层地震识别与评价[J]. 石油物探, 2017, 56(2): 280-287. YANG Zichuan, LIU Jun, CHEN Li, et al. Seismic identification and evaluation of Ordovician carbonate reservoir in Shunnan area[J]. Geophysical Prospecting for Petroleum, 2017, 56(2): 280-287. DOI:10.3969/j.issn.1000-1441.2017.02.015 |
| [5] |
Yang P, Sun Z D, Liu Y L, et al. Origin and architecture of fractured-cavernous carbonate reservoirs and their influences on seismic amplitudes[J]. The Lea-ding Edge, 2012, 31(2): 140-150. DOI:10.1190/1.3686911 |
| [6] |
Loucks R G. Paleocave carbonate reservoirs:origins, burial-depth modifications, spatial complexity, and reservoir implications[J]. AAPG Bulletin, 1999, 83(11): 1795-1834. |
| [7] |
Sun Z D, Wang H Y, Liu Z S, et al. The theory and application of DEM-Gassmann rock physics model for complex carbonate reservoirs[J]. The Leading Edge, 2012, 31(2): 152-158. DOI:10.1190/1.3686912 |
| [8] |
张远银, 孙赞东, 唐志远, 等. 基于AVO反演的溶蚀孔洞型碳酸盐岩储层预测[J]. 石油地球物理勘探, 2013, 48(1): 109-113. ZHANG Yuanyin, SUN Zandong, TANG Zhiyuan, et al. Caved carbonate reservoir prediction based on AVO inversion[J]. Oil Geophysical Prospecting, 2013, 48(1): 109-113. |
| [9] |
Zhang Y Y, Sun Z D, Yang H J, et al. Pre-stack inversion for caved carbonate reservoir prediction:A case study from Tarim Basin, China[J]. Petroleum Science, 2011, 8(4): 415-421. DOI:10.1007/s12182-011-0159-4 |
| [10] |
Zhang Y Y, Sun Z D, Han J F, et al. Fluid mapping in deeply buried Ordovician paleokarst reservoirs in Ta-rim Basin, western China[J]. Geofluids, 2016, 16(3): 421-433. DOI:10.1111/gfl.12160 |
| [11] |
刘立峰, 孙赞东, 杨海军, 等. 塔中地区碳酸盐岩储集相控建模技术及应用[J]. 石油学报, 2010, 31(31): 952-958. LIU Lifeng, SUN Zandong, YANG Haijun, et al. Modeling of facies-controlled carbonate reservoirs in the Tazhong area and its application[J]. Acta Petrolei Sinica, 2010, 31(6): 952-958. |
| [12] |
Cerney B, Bartel D C. Uncertainties in low-frequency acoustic impedance models[J]. The Leading Edge, 2007, 26(1): 74-87. |
| [13] |
Pedersen-Tatalovic R, Uldall A, Jacobsen N L. Event-based low-frequency impedance modeling using well logs and seismic attributes[J]. The Leading Edge, 2008, 27(5): 592-603. DOI:10.1190/1.2919576 |
| [14] |
Grant S R.The impact of low frequency models on reservoir property predictions[C].Extended Abstracts of 75th EAGE Conference & Exhibition, London, England, 2013, doi: 10.3997/2214-4609.20130335.
|
| [15] |
Zou Z, Ling Y, Wang Y J, et al.Low-frequency impe-dance modeling based on well logs and seismic attri-butes[C].Extended Abstracts of 75th EAGE Conference & Exhibition, London, England, 2013, doi: 10.3997/2214-4609.20130949.
|
| [16] |
Hampson D P.Simultaneous inversion of pre-stack seismic data[C].SEG Technical Program Expanded Abstracts, 2005, 24, doi: 10.1190/1.2148008.
|
| [17] |
Huck A, Quiquerez G, de G P.Improving seismic in-version through detailed low frequency model building[C].Extended Abstracts of 72nd EAGE Conference & Exhibition, Barcelona, Spain, 2010, doi: 10.3997/2214-4609.201400776.
|
| [18] |
Xi X Y, Ling Y, Zou Z, et al.The applicaion of a low-frequency model constrained by seismic velocity to acoustic impedance inversion[C].SEG Technical Program Expanded Abstracts, 2013, 32, doi: 10.1190/segam2013-0310.1.
|
| [19] |
Liu Z P, Liu J Q. Seismic-controlled nonlinear extra-polation of well parameters using neural networks[J]. Geophysics, 1998, 63(6): 2035-2041. DOI:10.1190/1.1444496 |
| [20] |
Nivlet P.Low-frequency constrain in a priori model building for stratigraphic inversion[C].SEG Technical Program Expanded Abstracts, 2004, 23, doi: 10.1190/1.1839678.
|
| [21] |
Kumar N, Negi S S.Low-frequency modeling and its impact on seismic inversion data[C].9th Biennial International Conference & Exposition on Petroleum Geophysics, Hyderabad, India.2012, doi: 10.1190/1.2148016.
|
| [22] |
Damsleth E, Tjolsen C B, More H. A two-stage stochastic model applied to a North Sea reservoir[J]. Journal of Petroleum Technology, 1992. DOI:10.2118/20605-pa |
| [23] |
杨辉廷, 江同文, 颜其彬, 等. 缝洞型碳酸盐岩储层三维地质建模方法初探[J]. 大庆石油地质与开发, 2004, 23(4): 11-12, 16. YANG Huiting, JIANG Tongwen, YAN Qibin, et al. Establishment of 3D geology models of fracture-cavern carbonate reservoir[J]. Petroleum Geology and Oilfield Development in Daging, 2004, 23(4): 11-12, 16. DOI:10.3969/j.issn.1000-3754.2004.04.004 |
| [24] |
霍春亮, 古莉, 赵春明, 等. 基于地震、测井和地质综合一体化的储层精细建模[J]. 石油学报, 2007, 28(6): 66-71. HUO Chunliang, GU Li, ZHAO Chunming, et al. Integrated reservoir geological modeling based on seismic, log and geological data[J]. Acta Petrolei Sinica, 2007, 28(6): 66-71. |
| [25] |
董少群, 曾联波, 徐超辉, 等. 储层裂缝随机建模方法研究进展[J]. 石油地球物理勘探, 2018, 53(3): 625-641. DONG Shaoqun, ZENG Lianbo, XU Chaohui, et al. Some progress in reservoir fracture stochastic mode-ling research[J]. Oil Geophysical Prospecting, 2018, 53(3): 625-641. |
| [26] |
Zhang Y Y, Sun Z D, Fan C Y.An iterative AVO inversion workflow for S-wave improvement[C].Extended Abstracts of 75th EAGE Conference & Exhibition, London, England, 2013, doi: 10.3997/1365-2397.2014014.
|
| [27] |
Han J F, Sun Z D, Zhang X C, et al.Integrated identification for complex reservoir based on pure P-wave data and post-stack data[C].SEG Technical Program Expanded Abstracts, 2013, 32, doi: 10.1190/segam2013-1287.1.
|
| [28] |
Lancaster S, Whitcombe D.Fast track 'coloured' inversion[C].SEG Technical Program Expanded Abstracts, 2000, 19, doi: 10.1190/1.1815711.
|



 张远银 北京市海淀区北四环中路奥运大厦中国地质调查局油气资源调查中心油气地质室, 100083。Email:
张远银 北京市海淀区北四环中路奥运大厦中国地质调查局油气资源调查中心油气地质室, 100083。Email: