② 中联煤层气有限责任公司, 北京 100011;
③ 中海石油(中国)有限公司非常规油气分公司, 北京 100011;
④ 中国科学院大学, 北京 100049;
⑤ 中海油研究总院, 北京 100028
② China United Coalbed Methane Corporation Ltd., Beijing 100011, China;
③ Unconventional Oil & Gas Branch, CNOOC, Beijing 100011, China;
④ University of Chinese Academy of Sciences, Beijing 100049, China;
⑤ ResearchInstitute, CNOOC, Beijing 100028, China
对于“亮点”型气层,可以利用地震数据的高振幅异常进行识别[1];对于振幅差异不明显的储层,则需要利用地震数据的其他特征,如弹性参数进行识别。泊松比在AVO理论出现的伊始就被用于指示含气储层,并广泛应用于碎屑岩储层的预测[2]。Connolly[3]提出弹性阻抗的概念,并证明了利用不同角度弹性阻抗的差异可以指示含气层的存在;Gray[4]利用拉梅参数探测油气储层,并建立了反射系数与拉梅参数之间的关系;Russell等[5]基于孔隙弹性介质理论,从Gassmann方程中推导出流体项;Sena等[6]在页岩储层的研究中发现杨氏模量和泊松比可以作为有利储层的指示参数。
叠前地震反演是基于地震资料获取此类参数的有效途径[7],但是地震数据的反演通常是一个病态问题,为了得到合理稳定的解,需要对问题进行正则化,稀疏正则化是目前解决地震反演问题常用方法之一[8]。L0范数正则化虽然有较好的稀疏性,但求解L0范数稀疏最优化是公认的难度较大的问题,需要采用贪婪迭代的策略进行求解[9];匹配追踪算法是一种经典的贪婪算法,Nguyen[10]利用匹配追踪算法分解地震信号、反演反射系数;张繁昌等[11]基于匹配追踪算法提取地震数据的时频谱特征识别三角洲砂岩层的尖灭线;刘晓晶等[12]利用基于正交匹配追踪算法的叠前AVO反演方法实现了块化反演。虽然匹配追踪算法在地震反演领域应用广泛,但缺点是空间分辨率低及横向连续性差。为此,Zhang等[13-14]提出了利用基追踪算法开展地震反演,该方法不仅有较好的横向连续性,而且计算效率高。基追踪可以得到块化的反演结果,Theune等[15]认为块化反演结果的分辨率更高,对地层的解释能力更强。为了进一步提高基追踪反演的横向连续性,Zhang等[16]提出了基于空间正则化的多道基追踪反演方法。
致密气储层是一种非常规储层,通常具有低孔、低渗的特征,常用的储层预测方法难以对其进行有效识别[17-18]。本文借鉴页岩气勘探的成功经验,利用杨氏模量和泊松比表征致密砂岩储层含油气特征,并从Zoeppritz方程的近似公式出发推导出以杨氏模量和泊松比表示的地震反射系数公式。基于该方程开展叠前稀疏层基追踪反演,为了提高反演结果的稳定性和横向连续性,在基追踪的目标函数中加入模型约束项。利用谱投影梯度法算法进行求解,得到稳定的反演结果。模型实验证明了方法的有效性和稳定性。实际工区数据应用不仅得到了稳定连续的反演结果,同时块化反演结果为储层边界的确定提供了数据基础。
1 方法原理叠前地震反演是进行弹性参数预测常用的方法之一,其基础是地震反射系数方程。由于Zoeppritz方程形式复杂,很少直接用于地震反演。Gray[4]提出了利用体积模量和剪切模量表示的反射系数近似公式
| $ \begin{array}{*{20}{c}} {{R_{{\rm{PP}}}}\left( \theta \right) = \left( {\frac{1}{4} - \frac{1}{3}{\gamma ^2}} \right){{\sec }^2}\theta \frac{{\Delta K}}{K} + {\gamma ^2}\left( {\frac{1}{3}{{\sec }^2}\theta - } \right.}\\ {\left. {2{{\sin }^2}\theta } \right)\frac{{\Delta \mu }}{\mu } + \left( {\frac{1}{2} - \frac{1}{4}{{\sec }^2}\theta } \right)\frac{{\Delta \rho }}{\rho }} \end{array} $ | (1) |
式中:RPP(θ)表示入射角θ对应的反射系数;K、ΔK、μ、Δμ、ρ、Δρ分别表示界面两侧介质的体积模量、剪切模量及密度的均值和差值;γ为横、纵波速度比。
根据岩石物理理论,体积模量K、剪切模量μ与杨氏模量E、泊松比σ之间的关系可表示为
| $ K = \frac{E}{{3\left( {1 - 2\sigma } \right)}} $ | (2) |
| $ \mu = \frac{E}{{2\left( {1 + \sigma } \right)}} $ | (3) |
对式(2)和式(3)两边进行差分运算,可得
| $ \frac{{\Delta K}}{K} = \frac{{\Delta E}}{E} + \frac{{2\sigma }}{{1 - 2\sigma }}\frac{{\Delta \sigma }}{\sigma } $ | (4) |
| $ \frac{{\Delta \mu }}{\mu } = \frac{{\Delta E}}{E} - \frac{\sigma }{{1 + \sigma }}\frac{{\Delta \sigma }}{\sigma } $ | (5) |
将式(4)和式(5)代入式(1),整理得到用杨氏模量、泊松比和密度的相对变化率表示的地震反射系数近似方程
| $ {R_{{\rm{pp}}}}\left( \theta \right) = A\left( \theta \right)\frac{{\Delta E}}{E} + B\left( \theta \right)\frac{{\Delta \sigma }}{\sigma } + C\left( \theta \right)\frac{{\Delta \rho }}{\rho } $ | (6) |
式中:E、σ和ΔE、Δσ分别表示界面两侧杨氏模量和泊松比的平均值和差值;
利用式(6)进行叠前数据反演,可以在地震尺度上估计杨氏模量和泊松比,据此进行有利储层的预测和评价。
2 反演方法根据褶积理论,地震信号可以表示为子波与反射系数的褶积形式。在有噪条件下,三者的关系可以表示为
| $ d = WR + e $ | (7) |
式中:d表示地震数据;W表示子波;e表示噪声。
以地层为研究对象,进行反射系数奇偶分解有利于得到更加清晰的地层边界。地层顶、底界面的反射系数可以表示为奇、偶反射系数对的线性组合[19]
| $ R = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\left[ {{a_{i,j}}{R_{\rm{e}}}\left( {i,j,\Delta t} \right) + {b_{i,j}}{R_{\rm{o}}}\left( {i,j,\Delta t} \right)} \right]} } $ | (8) |
式中Ro(i, j, Δt)和Re(i, j, Δt)分别为奇、偶系数对,表达式如下
| $ {R_{\rm{e}}}\left( {i,j,\Delta t} \right) = \delta \left( {t - i\Delta t} \right) + \delta \left( {t - i\Delta t + j\Delta t} \right) $ | (9) |
| $ {R_{\rm{o}}}\left( {i,j,\Delta t} \right) = \delta \left( {t - i\Delta t} \right) + \delta \left( {t - i\Delta t + j\Delta t} \right) $ | (10) |
式中:Δt表示地震数据采样间隔;i、j表示反射点位置。
式(8)可以表示为矩阵形式
| $ R = \left[ {\begin{array}{*{20}{l}} {{R_{\rm{e}}}}&{{R_{\rm{o}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} a\\ b \end{array}} \right] $ | (11) |
根据式(11)可将式(8)表示为
| $ \left[ {\begin{array}{*{20}{c}} {{r_E}}\\ {{r_\sigma }}\\ {{r_\rho }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_{\rm{e}}}}&{{R_{\rm{o}}}}&0&0&0&0\\ 0&0&{{R_{\rm{e}}}}&{{R_{\rm{o}}}}&0&0\\ 0&0&0&0&{{R_{\rm{e}}}}&{{R_{\rm{o}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{a_{{\rm{e}}E}}}\\ {{b_{{\rm{o}}E}}}\\ {{a_{{\rm{e}}\sigma }}}\\ {{b_{{\rm{o}}\sigma }}}\\ {{a_{{\rm{e}}\rho }}}\\ {{b_{{\rm{o}}\rho }}} \end{array}} \right] = \mathit{\boldsymbol{Dm}} $ | (12) |
式中rE、rσ、rρ分别表示杨氏模量、泊松比和密度的相对变化率。
将式(12)代入式(7),可以得到
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{WDm}} + \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{Gm}} + \mathit{\boldsymbol{e}} $ | (13) |
式中W表示具体的子波矩阵。
为了得到稀疏性较强的反演结果,基于基追踪理论建立反演算法[20-23]。常规的基追踪反演目标函数由L2模的误差项和L1模的约束项组成
| $ \left\{ {\begin{array}{*{20}{l}} {F\left( \mathit{\boldsymbol{m}} \right) = \left\| {\mathit{\boldsymbol{Gm}} - \mathit{\boldsymbol{d}}} \right\|_2^2 + \lambda {{\left\| \mathit{\boldsymbol{m}} \right\|}_1}}\\ {\mathit{\boldsymbol{G}} = \mathit{\boldsymbol{WD}}} \end{array}} \right. $ | (14) |
式中λ表示权重系数。
L1模约束无法提供合理的低频信息[24],且逐道的基追踪反演结果缺乏横向连续性,需要结合测井资料建立低频模型对式(14)进行约束,目标函数变为
| $ \left\{ \begin{array}{l} F\left( \mathit{\boldsymbol{m}} \right) = \left\| {\mathit{\boldsymbol{Gm}} - \mathit{\boldsymbol{d}}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{m}} \right\|_1} + \mathit{\boldsymbol{Y}}\\ \mathit{\boldsymbol{Y}} = {\lambda _E}{\left( {\mathit{\boldsymbol{C}}{r_E} - {\mathit{\boldsymbol{\zeta }}_E}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{C}}{r_E} - {\mathit{\boldsymbol{\zeta }}_E}} \right) + {\lambda _\sigma }{\left( {\mathit{\boldsymbol{C}}{r_\sigma} - {\mathit{\boldsymbol{\zeta }}_\sigma }} \right)^{\rm{T}}} \times \\ \;\;\;\left( {\mathit{\boldsymbol{C}}{r_\sigma } - {\mathit{\boldsymbol{\zeta }}_\sigma }} \right) + {\lambda _\rho }{\left( {\mathit{\boldsymbol{C}}{r_\rho } - {\mathit{\boldsymbol{\zeta }}_\rho }} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{C}}{r_\rho } - {\mathit{\boldsymbol{\zeta }}_\rho }} \right) \end{array} \right. $ | (15) |
式中:积分矩阵
由于低频信息来自实际工区的测井资料,因此最终的反演结果更多包含了工区内的真实背景信息,反演的结果则更加合理,并且模型约束能够有效地改善反演结果横向的连续性。
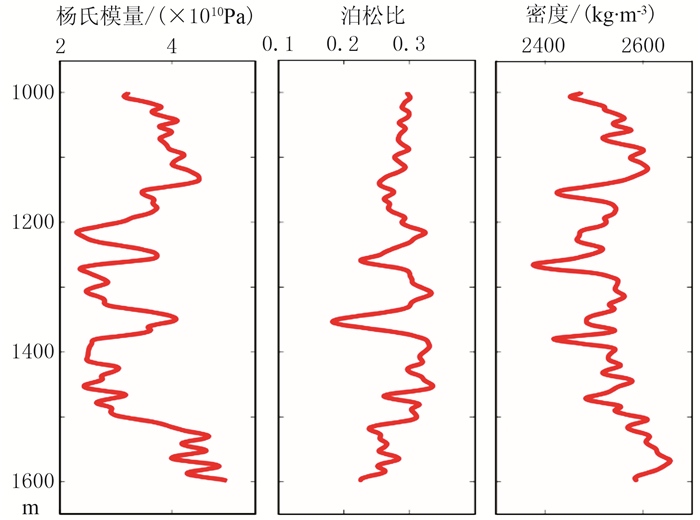
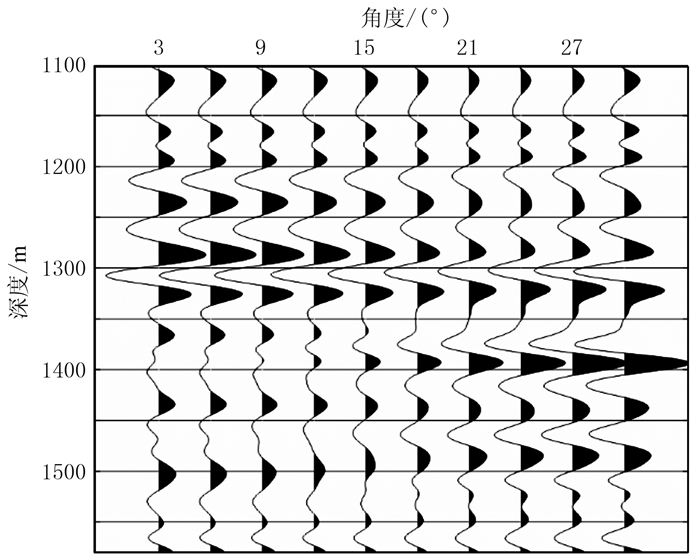
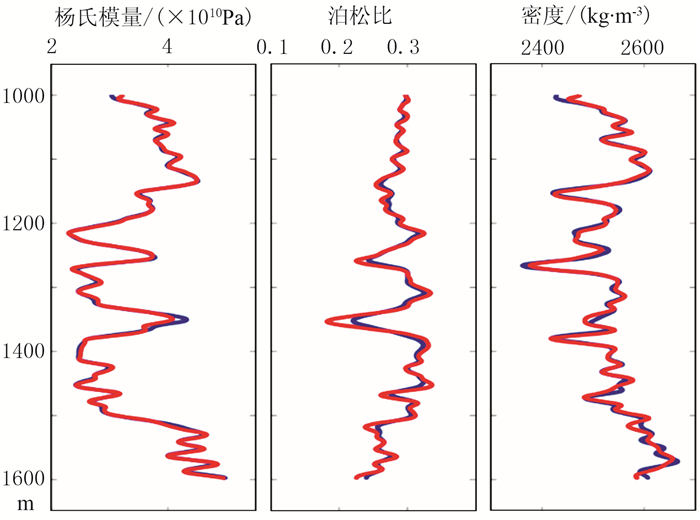
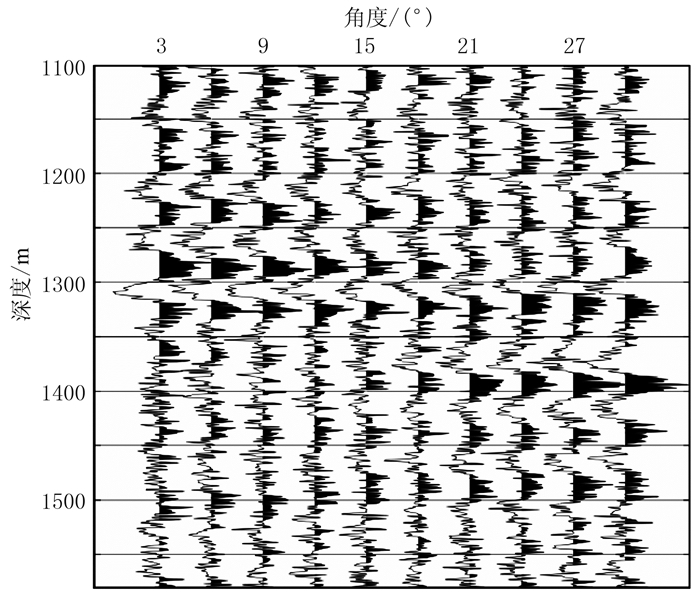
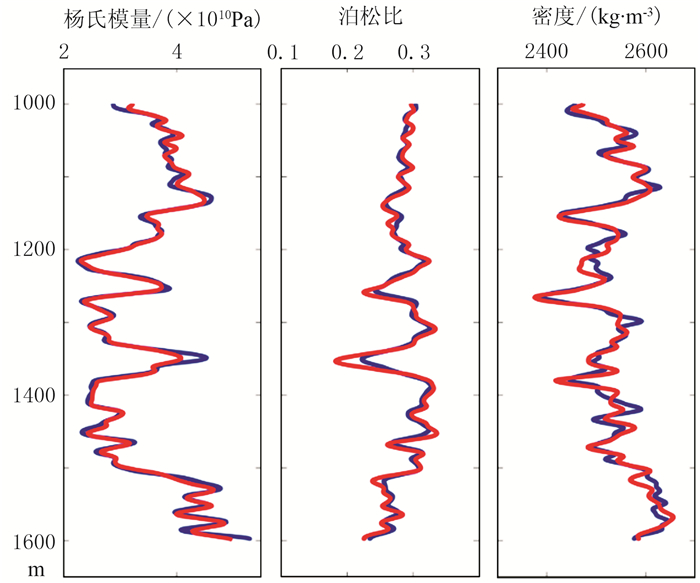
3 模型试算为了检验本文反演方法的正确性,根据实际工区测井数据建立了一维模型进行试验。图 1为根据工区测井数据建立的杨氏模量、泊松比和密度模型曲线。将模型曲线代入Zoeppritz方程,利用30Hz雷克子波进行褶积得到合成地震道集,作为输入的地震数据(图 2),进行叠前地震反演。得到的反演结果如图 3所示,可以看出,模型数据与反演结果基本吻合。为了进一步检验方法的抗噪性,在合成地震道集中加入信噪比为2的高斯白噪声(图 4),反演结果如图 5所示。可以看出,反演结果的精度较图 3有所下降,但是仍然比较准确,证明反演方法具有一定的抗噪性。
|
图 1 根据工区测井数据建立的杨氏模量(左)、泊松比(中)和密度(右)模型曲线 |
|
图 2 合成地震记录 |
|
图 3 图 2数据反演结果 图中红色曲线和蓝色曲线分别是模型曲线和反演结果 |
|
图 4 含噪合成地震记录 |
|
图 5 对应图 4数据的反演结果 |
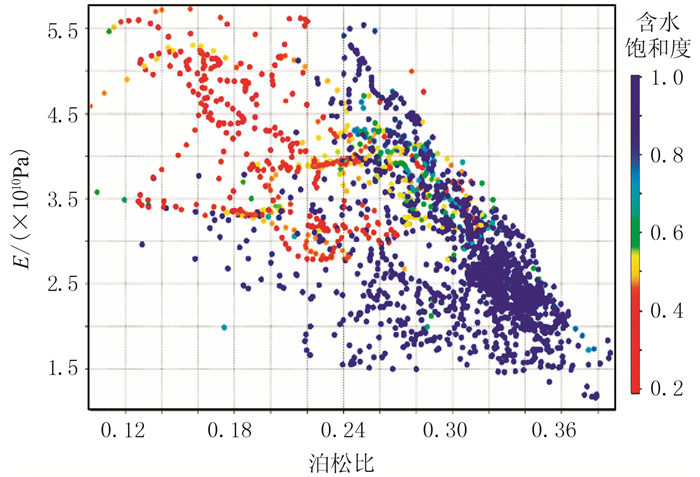
为了检验本文提出方法的实际应用效果,在中国M油田开展方法的实际应用。工区发育石盒子组含气致密砂岩储层,目的层埋深约1000~1500m。首先利用工区内A井的测井数据计算得到杨氏模量和泊松比曲线,进行岩石物理交会分析(图 6)。可以看出,含气储层具有较高的杨氏模量值和较低的泊松比,对这两种弹性参数进行反演可以为含气储层的预测提供数据支持。
|
图 6 测井数据交会分析 |
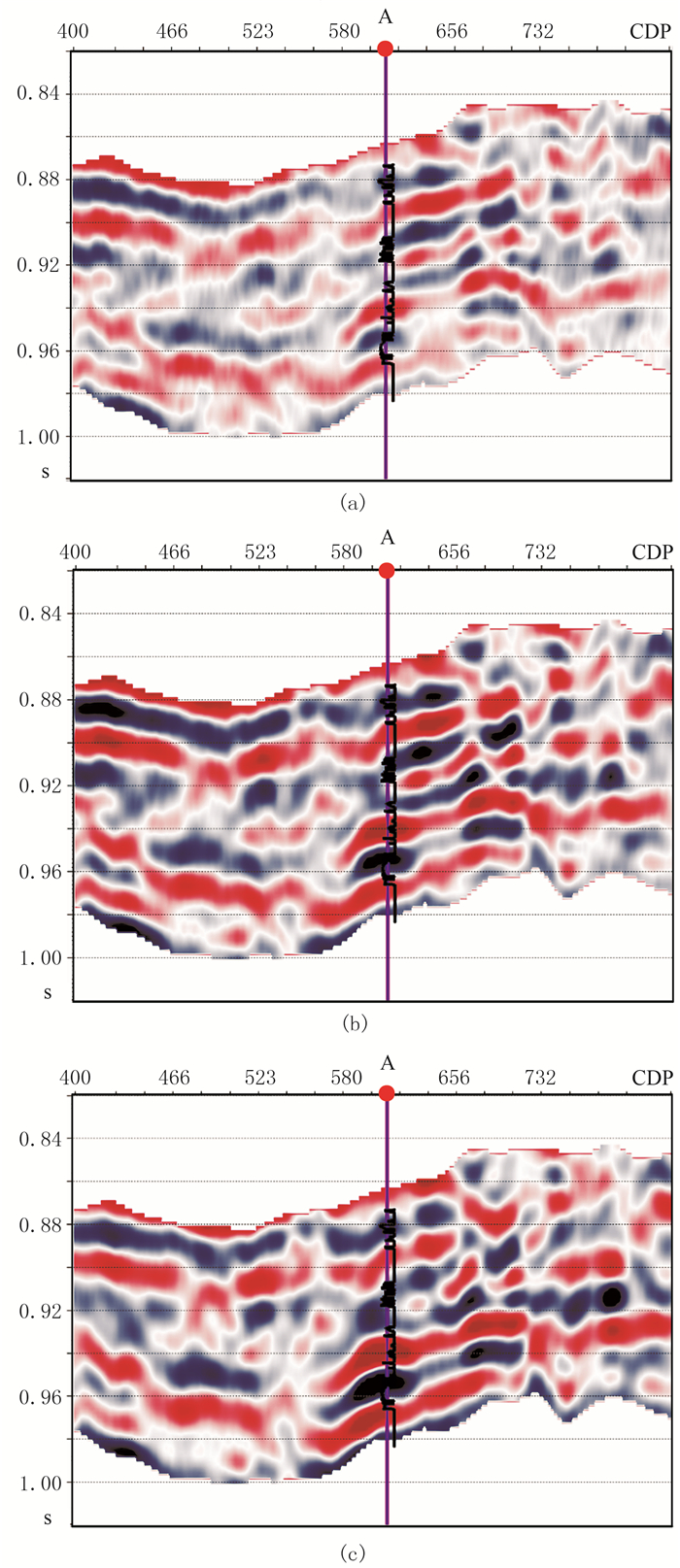
将处理后的地震道集转换到角度域,并进行分角度叠加,得到小角度(1°~13°)叠加道集、中角度道集(14°~26°)和大角度道集(27°~39°)(图 7)。分别利用常规叠前反演方法和本文方法进行叠前地震反演,得到的杨氏模量和泊松比如图 8所示。由图可见,在井旁道的0.89、0.91、0.93和0.96s处有四套储层,显示出杨氏模量高值异常和泊松比低异常。对比可以发现,图 8中两种弹性参数的异常位置与测井曲线(含水饱和度)吻合度更高,显示的储层边界更加清楚,横向展布更加合理。
|
图 7 部分角度叠加地震剖面 (a)小角度;(b)中角度;(c)大角度 |

|
图 8 常规方法(上)与本文方法(下)反演结果对比 (a)杨氏模量;(b)泊松比 |
杨氏模量和泊松比可以表征岩石的脆性,对于致密砂岩油气藏的评价和描述非常有利。本文提出了一种基于模型约束的叠前基追踪反演方法,可以从地震数据直接反演得到杨氏模量和泊松比,用来指示致密砂岩油气藏。模型数据测试表明,该方法在低信噪比的情况下仍可以得到高质量的反演结果;实际数据计算结果证明了利用本文方法可以在生产中得到准确、稳定的杨氏模量和泊松比反演结果,为致密砂岩气藏的评价提供可靠的数据支持。
| [1] |
Backus M M, Chen R L. Flat spot exploration[J]. Geophysical Prospecting, 1975, 23(3): 533-577. DOI:10.1111/j.1365-2478.1975.tb01547.x |
| [2] |
Shuey R T. A simplification of the Zoeppritz equa-tions[J]. Geophysics, 1985, 50(4): 609-614. DOI:10.1190/1.1441936 |
| [3] |
Connolly P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. DOI:10.1190/1.1438307 |
| [4] |
Gray D.Bridging the gap: Using AVO to detect changes in fundamental elastic constants[C].SEG Technical Program Expanded Abstracts, 1999, 18: 852-855.
|
| [5] |
Russell B H, Hedlin K, Hilterman F J, et al. Fluid-property discrimination with AVO:A Biot-Gassmann perspective[J]. Geophysics, 2003, 68(1): 29-39. DOI:10.1190/1.1543192 |
| [6] |
Sena A, Castillo G, Chesser K, et al. Seismic reservoir characterization in resource shale plays:stress analysis and sweet spot discrimination[J]. The Leading Edge, 2011, 30(7): 758-764. DOI:10.1190/1.3609090 |
| [7] |
李蒙, 刘震, 刘敏珠, 等. 小入射角叠加地震数据波阻抗反演方法[J]. 石油地球物理勘探, 2018, 53(6): 1291-1298. LI Meng, LIU Zhen, LIU Minzhu, et al. Impedance inversion based on small-angle stacking seismic data[J]. Oil Geophysical Prospecting, 2018, 53(6): 1291-1298. |
| [8] |
Debeye H W J, Riel P V. Lp-norm deconvolution[J]. Geophysical Prospecting, 1990, 38(4): 381-403. DOI:10.1111/j.1365-2478.1990.tb01852.x |
| [9] |
Amaldi E, Kann V. On the approximability of minimizing nonzero variables or unsatisfied relations in linear systems[J]. Theoretical Computer Science, 1998, 209(1): 237-260. |
| [10] |
Nguyen T H.High Resolution Seismic Reflectivity Inversion[D].University of Houston, Houston, 2008.
|
| [11] |
张繁昌, 李传辉, 印兴耀. 三角洲砂岩尖灭线的地震匹配追踪瞬时谱识别方法[J]. 石油地球物理勘探, 2012, 47(1): 82-88. ZHANG Fanchang, LI Chuanhui, YIN Xingyao. Delta fringe line recognition based on seismic matching pursuit instantaneous spectral characteristics[J]. Oil Geo-physical Prospecting, 2012, 47(1): 82-88. |
| [12] |
刘晓晶, 印兴耀, 吴国忱, 等. 基于正交匹配追踪算法的叠前地震反演方法[J]. 石油地球物理勘探, 2015, 56(5): 925-935. LIU Xiaojing, YIN Xingyao, WU Guochen, et al. Pre-stack seismic inversion based on orthogonal matching pursuit algorithm[J]. Oil Geophysical Prospecting, 2015, 56(5): 925-935. |
| [13] |
Zhang R, Castagna J. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition[J]. Geophysics, 2011, 76(6): R147-R158. DOI:10.1190/geo2011-0103.1 |
| [14] |
Zhang R, Sen M K, Srinivasan S. A prestack basis pursuit seismic inversion[J]. Geophysics, 2013, 78(1): R1--R11. |
| [15] |
Theune U, Jensås I Ø, Eidsvik J. Analysis of prior models for a blocky inversion of seismic AVA data[J]. Geophysics, 2010, 75(3): C25-C35. DOI:10.1190/1.3427538 |
| [16] |
Zhang R, Sen M K, Srinivasan S. Multi-trace basis pursuit inversion with spatial regularization[J]. Journal of Geophysics and Engineering, 2013, 10(3): 1-6. |
| [17] |
王海龙, 曲永强, 张巧凤, 等. 松辽盆地深层沙河子组致密砂岩储层预测[J]. 石油地球物理勘探, 2017, 52(增刊2): 129-134. WANG Hailong, QU Yongqiang, ZHANG Qiaofeng, et al. Tight-sand reservoir prediction in the deep Shahezi formation, Songliao Basin[J]. Oil Geophysical Prospecting, 2017, 52(S2): 129-134. |
| [18] |
牛聪, 张益明, 王迪, 等. LA地区盒8段优质储层的特征与分布预测[J]. 石油地球物理勘探, 2017, 52(3): 591-598. NIU Cong, ZHANG Yiming, WANG Di, et al. Prediction of high-quality reservoir characteristics and distribution in the area LA[J]. Oil Geophysical Prospecting, 2017, 52(3): 591-598. |
| [19] |
Bork J, and Wood L.Seismic interpretation of sonic logs[C].SEG Technical Program Expanded Abstracts, 2001, 20: 510-513.
|
| [20] |
Santosa F, Symes W W. Linear inversion of band-limited reflection seismograms[J]. SIAM Journal on Scientific and Statistical Computing, 1986, 7(4): 1307-1330. DOI:10.1137/0907087 |
| [21] |
Tibshirani R. Regression shrinkage and selection via the Lasso[J]. Journal of the Royal Statistical Society:Series B (Methodological), 1996, 58(1): 267-288. DOI:10.1111/j.2517-6161.1996.tb02080.x |
| [22] |
Donoho D L. For most large underdetermined systems of linear equations the minimal L1-norm solution is also the sparsest solution[J]. Communications on Pure and Applied Mathematics, 2006, 59(6): 797-829. DOI:10.1002/cpa.20132 |
| [23] |
Candès E J, Romberg J K, Tao T. Stable signal reco-very from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathema-tics, 2006, 59(8): 1207-1223. DOI:10.1002/cpa.20124 |
| [24] |
Pérez D, Velis D, Sacchi M. High-resolution prestack seismic inversion using a hybrid FISTA least-squares strategy[J]. Geophysics, 2013, 78(5): R185-R195. DOI:10.1190/geo2013-0077.1 |
| [25] |
Birgin E G. Inexact spectral projected gradient methods on convex sets[J]. SIMA Journal of Numerical Analysis, 2003, 23(4): 539-559. DOI:10.1093/imanum/23.4.539 |



 李超 北京市朝阳区太阳宫南街6号院, 100028。Email:
李超 北京市朝阳区太阳宫南街6号院, 100028。Email: