② 中海石油(中国)有限公司湛江分公司, 广东湛江 524057
② Zhanjiang Branch, CNOOC, Zhanjiang, Guangdong 524057, China
目前油气勘探正由构造向构造-岩性复合型或者隐蔽型油气藏转变。统计资料表明,全球隐蔽型油气藏的储量占比达到35%[1]。其中,具有Ⅱ类AVO异常特征的“暗点”型油气藏具有良好的勘探前景。Brown[2-3]认为“亮点”型与“暗点”型油藏在数量上是相当的,但目前发现的“暗点”油气藏数量或许还不及前者的千分之一,因此“暗点”型油气藏的勘探潜力非常巨大。
莺歌海盆地“暗点”型油气藏难以识别主要是因为:①相比浅层,深层地震资料信噪比低、分辨率更低、保真性差,难以满足识别需求;②“暗点”型油气藏振幅特征与背景泥岩接近,呈弱反射,而弱振幅地震反射多解性强,存在不确定性;③“暗点”型油气藏缺乏针对性的储层和流体预测技术,而岩性预测和流体识别是“暗点”型油气藏评价的关键。
基于叠前地震资料的储层和流体识别技术始于20世纪80年代。Ostrander[4]首次通过AVO技术预测储层流体含量,奠定了流体识别基础。随后Smith等[5]提出流体因子的概念,利用纵、横波的加权差预测储层流体。Gidlow等[6]和Fatti等[7]进一步将其表示成纵、横波阻抗反射系数的加权差预测储层流体。Goodway等[8]将流体识别从反射系数扩展到了阻抗域,其中拉梅系数与密度的乘积属性是阻抗域应用最广的流体识别因子,当岩石骨架性质相对稳定,结合拉梅系数交会分析,对含气砂岩和含水砂岩有更好的识别能力。Quakenbush等[9]研究泊松阻抗属性,通过旋转纵、横波阻抗交会图的轴以达到最佳区分任意两岩性流体类型的目的。但当岩石具有较低的泊松比、很高的密度时,泊松阻抗就不再适用。陈学华等[10]发现时频域中低频阴影可以很好地用于油气检测。
Russell等[11]以Biot-Gassmann理论为基础,研究了多孔介质中弹性模量参数与孔隙流体的关系,利用纵波与横波速度提出了Russell流体因子(测井序列中有横波速度时可以直接利用;无横波速度测井资料时,可由孔隙度、泥质含量、含水饱和度与矿物模量等利用经验公式或者等效理论模型进行估算)。Russell流体因子除了与流体弹性效应有关外,还与干岩石骨架模量、矿物基质模量以及孔隙度等岩石固体参数的综合影响有关。对固结成熟、孔隙度变化不大的储层,Russell流体因子具有较高的流体指示敏感性。印兴耀等[12]基于Russell多孔流体饱和弹性介质的Zoeppritz方程的近似式,提出直接从弹性波阻抗数据体中提取流体因子进行流体识别的方法,减少了间接计算的累积误差。此后,由于Russell流体因子具有良好的应用性,很多学者开展了Russell流体因子的估算方法研究。针对深层储层无法有效获取大角度入射信息的情况,印兴耀等[13]提出两项弹性阻抗反演与Russell流体因子直接估算方法,可以提高深层储层流体识别的可靠性。孙瑞莹等[14]提出基于随机地震反演的Russell流体因子直接估算方法,对于判识储层含流体特征具有较好的指示作用。邓炜等[15]基于等效介质理论,实现了基于弹性阻抗的等效流体体积模量直接反演,提高了流体识别准确度。
此外,多位学者提出了杨氏模量、泊松比直接反演方法以及含气饱和度预测方法,为流体识别和预测提供了新的手段[16-19]。
一般来说,常规的流体因子(弹性模量、泊松阻抗、LMR流体因子、Russell流体因子等)均具有一定的流体识别的能力,但每种流体因子都只是在某些特定的地质条件下应用效果良好[20]。“暗点”型油气藏一般具有Ⅱ类AVO异常,常规的AVO属性(如P×G属性)无法进行有效刻画,而目前针对性的敏感指示因子构建方面的研究很少。莺歌海盆地勘探揭示,中深层“暗点”型目标油气勘探潜力巨大,传统流体因子在浅层“亮点”型目标的识别与评价中应用效果好,而在中深层“暗点”型油气藏识别和预测中无能为力。为了解决“暗点”型油气藏识别的难题,本文综合多方面信息,从Zoeppritz方程Fatti近似式出发,构建新的“暗点”识别因子,达到预测“暗点”型油气藏目的。
1 算法原理和理论模型实验 1.1 “暗点”油气藏指示因子理论推导Fatti等[7]于1994年重新推导Aki-Richards近似式的表示形式,给出了包含纵波阻抗相对变化量的近似式,即
| $ \begin{array}{l} R(\theta ) = \frac{1}{2}\left( {1 + {{\tan }^2}\theta } \right)\frac{{\Delta {I_{\rm{P}}}}}{{{I_{\rm{P}}}}} - 4{\left( {\frac{{{V_{\rm{S}}}}}{{{V_{\rm{P}}}}}} \right)^2}\frac{{\Delta {I_{\rm{S}}}}}{{{I_{\rm{S}}}}}{\sin ^2}\theta - \\ \left[ {\frac{1}{2}{{\tan }^2}\theta - 2{{\left( {\frac{{{V_{\rm{S}}}}}{{{V_{\rm{P}}}}}} \right)}^2}{{\sin }^2}\theta } \right]\frac{{\Delta \rho }}{\rho } \end{array} $ | (1) |
式中:
在小角度入射情况下,考虑到密度项的权重系数较小,且密度项本身的变化也很小,因此两项近似即可满足小角度的近似精度,此时的反射系数近似公式可以表示为
| $ R(\theta ) = \frac{1}{2}\frac{{\Delta {I_{\rm{P}}}}}{{{I_{\rm{P}}}}}{\sec ^2}\theta - 4{\left( {\frac{{{V_{\rm{S}}}}}{{{V_{\rm{P}}}}}} \right)^2}\frac{{\Delta {I_{\rm{S}}}}}{{{I_{\rm{S}}}}}{\sin ^2}\theta $ | (2) |
合并角度同类项后,进一步可表示为
| $ R(\theta ) = \frac{{\Delta {I_{\rm{P}}}}}{{2{I_{\rm{P}}}}} - 4{\left( {\frac{{{V_{\rm{S}}}}}{{{V_{\rm{P}}}}}} \right)^2}\frac{{\Delta {I_{\rm{S}}}}}{{{I_{\rm{S}}}}}{\sin ^2}\theta + \frac{{\Delta {I_{\rm{P}}}}}{{2{I_{\rm{P}}}}}{\tan ^2}\theta $ | (3) |
式中
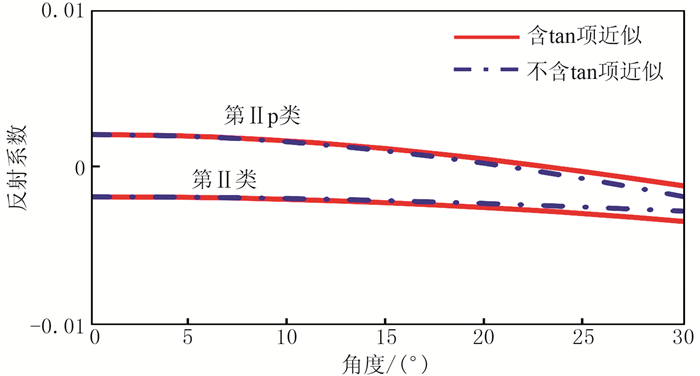
|
图 1 不同近似条件下Ⅱ类AVO误差对比 |
本文主要利用“暗点”型储层截距较小的特点,将梯度与截距的比值定义为“暗点”型油气藏指示因子,这样就可以放大Ⅱ类AVO异常的差异,实现对Ⅱ类AVO异常识别与评价的目的。根据式(3),“暗点”型油气藏指示因子可以表示为
| $ {F_{\rm{g}}} = \frac{{ - 4{{\left( {\frac{{{V_{\rm{s}}}}}{{{V_{\rm{P}}}}}} \right)}^2}\frac{{\Delta {I_{\rm{S}}}}}{{{I_{\rm{S}}}}}}}{{\frac{{\Delta {I_{\rm{P}}}}}{{{I_{\rm{P}}}}}}} $ | (4) |
相对于纵、横波阻抗的变化数量级,纵横波速度比近似为常数,可进一步简化为
| $ {F_{\rm{g}}} \approx - c\left( {\frac{{{I_{\rm{P}}}}}{{{I_{\rm{S}}}}}} \right)\frac{{\Delta {I_{\rm{S}}}}}{{\Delta {I_{\rm{P}}}}} $ | (5) |
其中常数
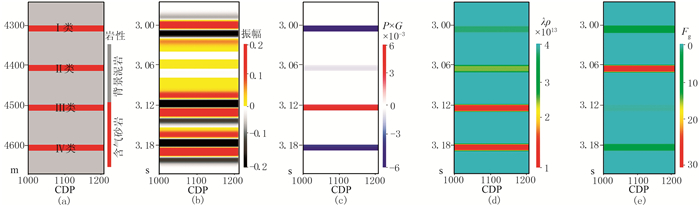
为了验证Fg的有效性与可靠性,分别设计包含Ⅰ~Ⅳ类AVO异常的含气砂岩模型(图 2a),模型参数具体见表 1,含气砂岩从上至下分别表现为Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类AVO异常响应特征。在叠后地震剖面(图 2b)上,相对于Ⅰ、Ⅲ、Ⅳ类AVO异常,Ⅱ类AVO异常振幅响应与背景泥岩较接近,很难有效识别;通过传统AVO属性(P×G)解释也很难判断“暗点”型储层位置(图 2c),其更适用于截距和梯度都大的Ⅲ类、Ⅳ类AVO异常“亮点”型储层识别;对于流体因子λρ(拉梅系数与密度的乘积)而言,其对Ⅲ类、Ⅳ类AVO异常的流体识别效果明显,但对于Ⅱ类AVO异常的“暗点”型储层识别效果并不突出(图 2d);利用本文构建的Fg可以较好识别Ⅱ类AVO异常“暗点”的响应特征(图 2e)。
|
图 2 不同AVO类型属性对比 (a)砂岩模型;(b)模拟叠后地震剖面;(c)P×G;(d)λρ;(e)Fg |
|
|
表 1 不同AVO类型模型参数及AVO属性 |
根据前文“暗点”型指示因子的理论推导,Fg可表示为纵、横波阻抗均值及其差值的关系式,其中纵、横波阻抗通常可以利用叠前同时反演获得。在进行叠前同时反演之前,对Ⅱ类AVO叠前道集的保护尤为关键,其质量直接影响着“暗点”型储层纵、横波阻抗反演结果。而在勘探开发的实际应用中,叠前地震道集质量通常较差,动校正道集不平往往是一个重要原因,尤其对于具有极性反转特征的“暗点”道集,由于参考道表现为弱振幅的地震反射特征,容易受随机噪声的影响,“暗点”道集的动校正存在一定的不确定性。
为了有效解决这一问题,本文在常规速度分析动校正的基础上,利用绝对值互相关道集拉平的方法,可以有效实现对Ⅱ类AVO异常“暗点”道集的保护。绝对值互相关道集拉平方法,即计算每个地震道与参考道在给定时窗内的最大绝对值互相关系数Coefmax(τshift)及所对应的初步时移量τshift,具体表达式为
| $ {\mathop{\rm Coef}\nolimits} (\tau ) = \int_{{t_1}}^{{t_2}} | R(t)| * |f(t + \tau )|{\rm{d}}t $ | (6) |
式中:“*”代表互相关运算;R(t)表示选择信噪比较高叠前道集通过部分叠加形成的参考道;f(t)表示实际地震道;t1、t2分别为滑动时窗的起点、终点时间。根据上式计算的地震道集的时移量,设立最大校正时移量和最小绝对值相关系数门槛值,剔除异常时移量得到校正时移量场,并应用于整个地震数据体实现道集拉平。
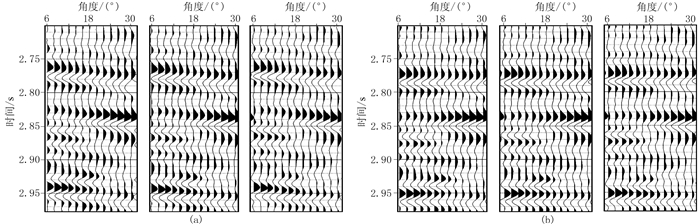
为了取得较好的拉平效果,通常先应用大时窗进行初步拉平,再应用小时窗进行精细处理。图 3为动校正拉伸处理前、后的地震反射特征,由于Ⅱ类AVO异常极性反转导致部分叠加道振幅较弱,虽然容易受随机噪声影响,但利用绝对值互相关道集拉平可以有效拉平“暗点”型道集,拉平前、后道集的波形特征未发生改变,保证相位反转的地震道集与低信噪比区域道集处理前、后的相位一致,为后续叠前同时反演提供更可靠的部分叠加数据体。
|
图 3 动校正拉伸处理前(a)、后(b)的地震反射特征对比 |
莺歌海盆地乐东区中深层油气勘探揭示,储层为低孔、低渗型,相比泥岩表现为高纵波速度、高横波速度、低密度特征,在叠后地震剖面上表现为强波峰反射。
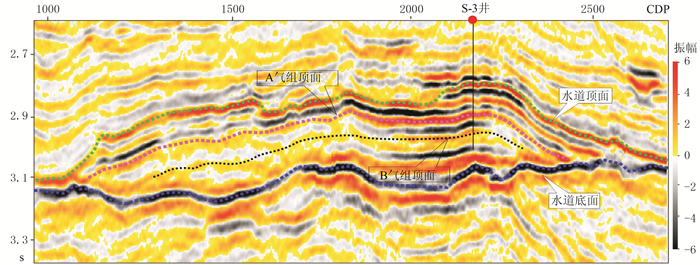
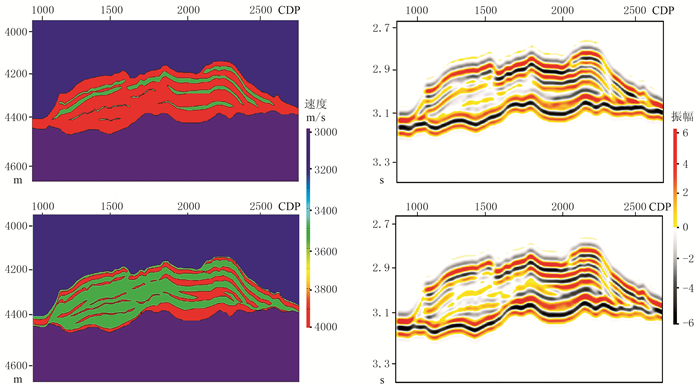
研究区岩性油气储层为黄流组二段河道砂体,埋深为4000~4500m。地震资料显示(图 4),振幅能量纵、横向变化大(水道高部位波峰为强振幅,低部位波峰为弱振幅),地震振幅的快速变化给储层评价带来很大挑战,S-3井位于该水道高部位,钻遇了上百米含气砂岩,水道低部位是否具有发育有利砂岩储层成为制约该区油气勘探的关键问题。为进一步分析纵、横向振幅能量变化大的原因以及水道的地层组合特征,根据已钻井砂、泥岩参数统计,分别建立不同厚度砂—泥岩组合的地质模型,并进行地震正演模拟。表 2为本区已钻遇三口井的纵波、横波速度及密度参数,数值大小显示,三口井的砂、泥岩的速度、密度变化规律一致。本次模拟选取过S-3井的地震剖面,根据S-3井的参数,设定富砂、富泥等多种情况进行模拟。模拟结果(图 5)表明,不论是富砂模型,还是富泥模型,A气组顶面低部位振幅都会减弱,与实际地震剖面特征比较接近,说明两种地层组合都有可能。
|
图 4 乐东区黄流组水道地震剖面 |
|
|
表 2 乐东区黄流组砂、泥岩参数统计 |
|
图 5 乐东区黄流组水道地震正演模拟 左为地质模型,右为正演地震剖面;上为富砂型,下为富泥型。红色为砂岩储层,绿色为泥岩夹层 |
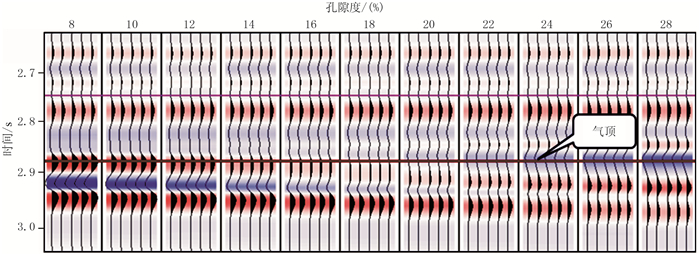
通过对S-3井水道砂体进行变孔隙度正演模拟(图 6)发现,当孔隙度较低时,砂体顶界面表现为波峰“亮点”反射;随着孔隙度增加,波峰“亮点”振幅逐渐减弱,逐渐向“暗点”型转变,因此对于深层砂岩储层,物性变好也会导致弱振幅的“暗点”反射特征。
|
图 6 S-3井含气砂岩变孔隙度正演模拟 |
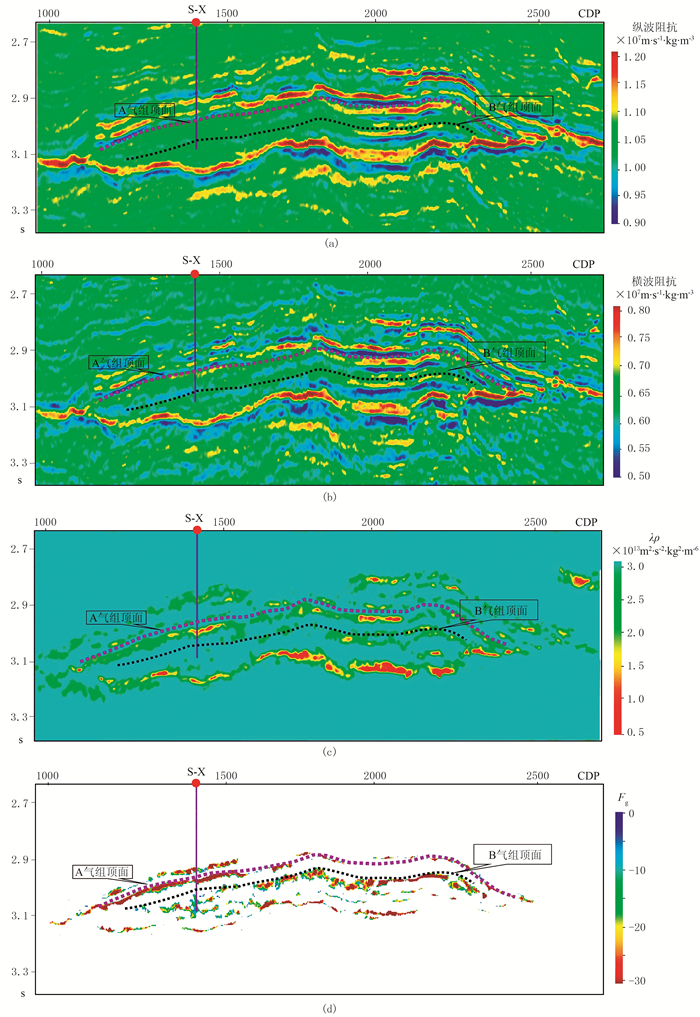
乐东区黄流组水道地震正演模拟结果表明,“暗点”和泥岩具有相似的地震响应,即弱振幅反射,因此,利用叠后纯波地震资料无法有效区分砂、泥岩展布。为此,尝试开展Fg提取与分析。首先,利用部分叠加资料和多井子波标定进行叠前同时反演,获得纵、横波阻抗、密度等反演数据体,可见水道低部位A气组顶面表现为中等纵、横波阻抗特征,利用纵、横波阻抗难以预测该阻抗特征是砂岩还是泥岩(图 7a、图 7b);由于该区埋深大,气、水岩石物理特征差异较小,λρ对该“暗点”型储层的识别也基本失效(图 7c);Fg属性在低部位A气组顶面具有明显异常(图 7d),并且在B气组高部位也具有明显异常,推测该水道低部位弱振幅处发育“暗点”型砂岩,含气概率较高。
|
图 7 过S地区黄流组水道叠前反演结果及指示因子分析 (a)纵波阻抗;(b)横波阻抗;(c)λρ;(d)Fg |
根据Fg研究成果,在水道低部位部署S-X井,结果在A气组钻遇细砂岩56m,孔隙度为12%,为该水道所有钻遇砂岩中物性最好。这证实了该技术方法的有效性,较好地解决了弱振幅“暗点”型目标评价难的问题,有效指导了该区深层“暗点”型油气藏预测工作。
3 结论(1) 利用“暗点”型储层AVO截距相对较小的特点,构建了只与纵、横波阻抗有关的“暗点”型油气藏指示因子,提高了“暗点”型油气藏识别的敏感性,数值模拟证实了该指示因子对“暗点”型目标较好的检测能力。
(2) 在实际资料流体研究中,结合叠前反演结果提取“暗点”型指示因子,较好地解决了莺歌海盆地乐东区“暗点”型目标预测难题,为该区深层复杂地质情况的岩性预测和流体识别提供了一种新的思路和方法。
本文所述方法仍具有一定局限性,它不适用于“亮点”型目标,新构建的指示因子是基于“暗点”型油气藏的特定条件所推导的,适用于具有Ⅱ类AVO异常的“暗点”型目标储层和流体识别。其次,道集质量也十分重要,对Ⅱ类AVO叠前道集的保护尤为关键,其质量好坏直接影响着本文指示因子的识别精度。
| [1] |
郝芳, 邹华耀, 方勇, 等. 隐蔽油气藏研究的难点与前沿[J]. 地学前缘, 2005, 12(4): 481-488. HAO Fang, ZOU Huayao, FANG Yong, et al. The difficulties and frontiers of subtle oil/gas reservoir research[J]. Earth Science Frontiers, 2005, 12(4): 481-488. DOI:10.3321/j.issn:1005-2321.2005.04.017 |
| [2] |
Brown A R. Dim spots:opportunity for future hydrocarbon discoveries[J]. The Leading Edge, 2012, 31(6): 682-683. DOI:10.1190/tle31060682.1 |
| [3] |
Brown A R. The challenge of dim spots[J]. Inerpretation, 2013, 1(1): 6-7. DOI:10.1190/INT2013-0052-PS.1 |
| [4] |
Ostrander W J. Plane-wave reflection coefficients for gas sands at normal angles of incidence[J]. Geophy-sics, 1984, 49(10): 1637-1648. |
| [5] |
Smith G C, Gidlow P M. Weighted stacking for rock property estimation and detection of gas[J]. Geophy-sical Prospecting, 1987, 35(9): 993-1014. DOI:10.1111/j.1365-2478.1987.tb00856.x |
| [6] |
Gidlow P M, Smith G C, Vail P J.Hydrocarbon detection using fluid factor traces, a case study: How useful is AVO analysis?[C].SEG/EAEG Summer Research, 1992, 78-89.
|
| [7] |
Fatti J, Smith G, Vail P, et al. Detection of gas in sandstone reservoirs using AVO analysis:a 3-D seismic case history using the geostack technique[J]. Geo-physics, 1994, 59(9): 1362-1376. |
| [8] |
Goodway B, Chen T, Downton J.Improved AVO fluid detection and lithology discrimination using Lame petrophysical parameters[C].SEG Technical Program Expanded Abstracts, 1997, 16: 183-186.
|
| [9] |
Quakenbush M, Shang B, Tuttle C. Poisson impedance[J]. The Leading Edge, 2006, 25(2): 128-138. DOI:10.1190/1.2172301 |
| [10] |
陈学华, 贺振华, 黄德济, 等. 时频域油气储层低频阴影检测[J]. 地球物理学报, 2009, 52(1): 215-221. CHEN Xuehua, HE Zhenhua, HUANG Deji, et al. Low frequency shadow detection of gas reservoirs in time-frequency domain[J]. Chinese Journal of Geophysics, 2009, 52(1): 215-221. |
| [11] |
Russell B H, Hedlin K, Hilterman F J. Fluid-property discrimination with AVO:A Biot-Gassmann perspective[J]. Geophysics, 2003, 68(1): 29-39. DOI:10.1190/1.1543192 |
| [12] |
印兴耀, 张世鑫, 张繁昌, 等. 利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别[J]. 石油地球物理勘探, 2010, 45(3): 373-380. YIN Xingyao, ZHANG Shixin, ZHANG Fanchang, et al. Utilizing Russell approximation based elastic wave impedance inversion to conduct reservoir description and fluid identification[J]. Oil Geophysical Prospecting, 2010, 45(3): 373-380. |
| [13] |
印兴耀, 张世鑫, 张峰. 针对深层流体识别的两项弹性阻抗反演与Russell流体因子直接估算方法研究[J]. 地球物理学报, 2013, 56(7): 2378-2390. YIN Xingyao, ZHANG Shixin, ZHANG Feng. Two-term elastic impedence inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification[J]. Chinese Journal of Geophysics, 2013, 56(7): 2378-2390. |
| [14] |
孙瑞莹, 印兴耀, 王保丽, 等. 基于随机地震反演的Russell流体因子直接估算方法[J]. 地球物理学报, 2016, 59(3): 1143-1150. SUN Ruiying, YIN Xingyao, WANG Baoli, et al. A direct estimation method for the Russell fluid factor based on stochastic seismic inversion[J]. Chinese Journal of Geophysics, 2016, 59(3): 1143-1150. |
| [15] |
邓炜, 印兴耀, 宗兆云. 等效流体体积模量直接反演的流体识别方法[J]. 石油地球物理勘探, 2017, 52(2): 315-325. DENG Wei, YIN Xingyao, ZONG Zhaoyun. Fluid identification based on direct inversion of equivalent fluid bulk modulus[J]. Oil Geophysical Prospecting, 2017, 52(2): 315-325. |
| [16] |
张瑞, 文晓涛, 杨吉鑫, 等. 杨氏模量和泊松比反射系数近似方程及地震叠前反演[J]. 石油地球物理勘探, 2019, 54(1): 145-153. ZHANG Rui, WEN Xiaotao, YANG Jixin, et al. Two-term reflection coefficient equation with Young's modulus and Poisson ration and its prestack inversion[J]. Oil Geophysical Prospecting, 2019, 54(1): 145-153. |
| [17] |
方圆, 张丰麒, 李玉凤. 基于YPD-Zoeppritz方程的杨氏模量和泊松比直接反演方法[J]. 石油物探, 2019, 58(2): 272-284. FANG Yuan, ZHANG Fengqi, LI Yufeng. Direct inversion of Young's modulus and Poisson's ratio based on the YPD-Zoeppritz equation[J]. Geophysical Prospecting for Petroleum, 2019, 58(2): 272-284. DOI:10.3969/j.issn.1000-1441.2019.02.013 |
| [18] |
周家雄, 李芳, 马光克, 等. 利用密度差值识别和预测莺歌海盆地高温高压气藏[J]. 石油物探, 2014, 53(5): 609-616. ZHOU Jiaxiong, LI Fang, MA Guangke, et al. High-tempreature and high pressure gas detection and prediction method by density difference in Yinggehai Basin[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 609-616. DOI:10.3969/j.issn.1000-1441.2014.05.015 |
| [19] |
罗鑫, 陈学华, 张杰, 等. 基于依赖频率AVO反演的高含气饱和度储层预测方法[J]. 石油地球物理勘探, 2019, 54(2): 356-364. LUO Xin, CHEN Xuehua, ZHANG Jie, et al. High gas-saturation reservoir prediction based on frequency-dependent AVO inversion[J]. Oil Geophysical Prospecting, 2019, 54(2): 356-364. |
| [20] |
桂金咏, 高建虎, 李胜军, 等. 面向实际储层的流体因子优选方法[J]. 石油地球物理勘探, 2015, 50(1): 129-135. GUI Jinyong, GAO Jianhu, LI Shengjun, et al. Reservoir-oriented fluid factor optimization method[J]. Oil Geophysical Prospecting, 2015, 50(1): 129-135. |



 李芳 广东省湛江市坡头区22号信箱中海石油(中国)有限公司湛江分公司, 524057。Email:
李芳 广东省湛江市坡头区22号信箱中海石油(中国)有限公司湛江分公司, 524057。Email: