② 中国石油天然气股份有限公司勘探开发研究院西北分院, 甘肃兰州 730020;
③ 中国石油化工股份有限公司石油勘探开发研究院, 北京 100083
② Northwest Branch, Research Institute of Petroleum Exploration and Development, CNPC, Lanzhou, Gansu 730020, China;
③ Research Institute of Petroleum Exploration and Production, SINOPEC, Beijing 100083, China
面对复杂勘探目标,高精度成像方法已成为油气勘探的关键技术。近年来,地震偏移成像普遍存在两大难点:①陡倾构造成像;②潜山结构复杂,资料信噪比较低,成像质量较差。因此,需要找到一种高效且灵活的高精度成像方法克服上述难点。目前,业界常用的Kirchhoff偏移成像效率很高,但面对复杂勘探目标时易出现焦散现象[1-3]及多路径问题[4-7]。高斯束偏移由于无射线追踪角度限制,适合陡倾构造成像;同时采用复值初始束参数动力学射线追踪,避免了焦散点附近的振幅奇异现象,且不同方向的局部平面波映射成像过程相互独立,可以对多次波波至成像。总体来说,高斯束偏移不仅具有接近波动方程偏移的精度,而且具有Kirchhoff偏移灵活、高效的特点。
高斯束偏移起源于电磁学,在20世纪80年代初期引入地球物理学领域,并取得了飞速发展[8-12]。Hill[13]基于高斯束表征的格林函数推导了叠后深度偏移公式,奠定了高斯束偏移的理论基础。为了适应陆地和海底正交电缆观测系统,Nowack等[14]、Gray[15]改进了Hill的局部倾斜叠加以适应共炮点和共检波点道集。针对高程剧烈变化的复杂地表条件,Gray[15]提出了具有局部高程静校正的保幅延拓高斯束偏移方法。此外,考虑到介质的复杂性,出现了弹性波高斯束偏移[16-17]和各向异性高斯束偏移[18-22]。随着对勘探精度的要求逐步提高,常规的高斯束偏移难以满足高精度成像的需求,相继出现许多新方法及优化算法。一方面,基于逆时偏移波场延拓的高斯束逆时偏移[23-26]极大地提高了复杂构造的成像精度,利于层位及断层解释;另一方面,基于振幅保真[27-31]及最小二乘[32-33]理论的高斯束偏移在保幅成像及提高成像分辨率方面取得重大突破,极大提高了AVA分析及AVO反演精度。黄建平等[34]通过改进倾斜叠加推出了一种非倾斜叠加的精确束偏移方法。张瑞等[35]结合高斯束传播过程的反射张角信息的计算,发展了高精度高斯束叠前深度偏移,并在复杂海洋模型中取得了较好的应用效果。Yang等[36]在考虑菲涅耳带因素的基础上优化了传统高斯束偏移方法,提高了稀疏数据的成像精度。
控制束偏移是一种改进的高斯束偏移方法,增强了低信噪比资料的处理效果。Vinje等[37]提出了各向同性介质的控制束偏移方法,并用于裂缝基底、盐丘底边界、低覆盖次数及宽方位角数据等成像。Zhou等[38]将各向同性控制束偏移推广到各向异性介质中,发展了一种各向异性高保真度控制束偏移方法。Casasanta等[39-40]实现了基于共炮检距、共炮点(共检波点)道集的PS转换波高斯束偏移,并推广到TTI介质,用实际算例证明了对非规则数据的适应性。黄建平等[41]在τ-p域内设定阈值,适当地切除不同信噪比的实际数据进行控制束偏移,但这种阈值仅仅是根据有效信号和干扰信号在τ-p域中的能量分布特征设定的,并没有考虑相干性差异。
本文在传统高斯束偏移的基础上,根据有效信号和干扰信号在τ-p域中的相干性差异,发展了一种基于相似系数阈值滤波的数据驱动控制束偏移方法。采用数据驱动策略,在高斯束偏移成像过程中,先计算τ-p道集的相似系数,再通过设定相似系数阈值控制干扰信号,从而降低偏移剖面中的随机噪声;同时给出了角度域共成像点道集(ADCIGs)的提取方法。层状模型、Marmousi模型及实际资料处理结果验证了本文方法的合理性。
1 局部道集相干性分析 1.1 局部倾斜叠加为了偏移某一特定反射同相轴,需要首先测量其射线参数。测量射线参数的一种经典方法是“局部倾斜叠加”,也称“线性局部τ-p变换”[42]。根据文献[13]可知,二维频率域局部倾斜叠加表达式为
| $ \begin{array}{l} D\left( {{\mathit{\boldsymbol{x}}_L},{p_L},\omega } \right) = {\left| {\frac{\omega }{{{\omega _{\rm{r}}}}}} \right|^{\frac{3}{2}}}\int {{\rm{d}}{\mathit{\boldsymbol{x}}_{\rm{g}}}{P_{{\rm{up}}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{g}}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega } \right)} \times \\ \;\;\;\;\exp \left[ { - {\rm{i}}\omega {p_L}\left( {{\mathit{\boldsymbol{x}}_{\rm{g}}} - {\mathit{\boldsymbol{x}}_L}} \right) - \left| {\frac{\omega }{{{\omega _{\rm{r}}}}}} \right|\frac{{{{\left( {{\mathit{\boldsymbol{x}}_{\rm{g}}} - {\mathit{\boldsymbol{x}}_L}} \right)}^2}}}{{2w_0^2}}} \right] \end{array} $ | (1) |
式中:Pup为高斯窗内的局部地震记录;w0为高斯窗宽度;xs和xg分别为炮点、检波点位置;pL为束中心位置xL的水平慢度(射线参数);ωr为参考频率。利用式(1)可以将束中心附近的地震记录进行加窗局部倾斜叠加、平面波分解,然后通过高斯束将平面波分量反传至地下局部成像区域成像,这也是高斯束偏移的基本思想。
1.2 相干分析考虑到实际地震资料中通常存在背景噪声及随机噪声等干扰信号,通过对含噪地震记录进行局部倾斜叠加发现,τ-p坐标图板上的峰值在局部地震记录中表现为地下某一特定反射段的相干同相轴,而一些相对较弱的能量团可能是一些背景和随机噪声等干扰信号。为了降低随机噪声对偏移结果的影响,根据有效信号和干扰信号在τ-p域中的相干性差异,本文利用τ-p域相似系数阈值滤波提高偏移剖面的信噪比。
相干体技术不仅能检测地震同相轴的不连续性,也可识别断层、特殊岩性体以及河道等,在地震解释中具有重要作用[43]。目前,相干体算法主要分为基于相关的、相似系数的以及本征结构分析的三类[44-46],本文采用基于相似系数的算法推导τ-p道集的相似系数计算公式。相似系数为归一化的输出能量与输入能量的比值[47]
| $ S = \frac{{\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {\sum\limits_{j = 1}^J {{f_{i,j}}} } \right)}^2}} }}{{\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^J {f_{i,j}^2} } }} $ | (2) |
式中fi, j为第i(i=1,…,N)样点、第j(j=1,…,J)道的振幅,其中N为短时窗内的样点数,J为总道数。由式(2)可见,输出道能量为输入道能量的简单合成或求和。在传统高斯束偏移方法中,相干分析的步骤为:
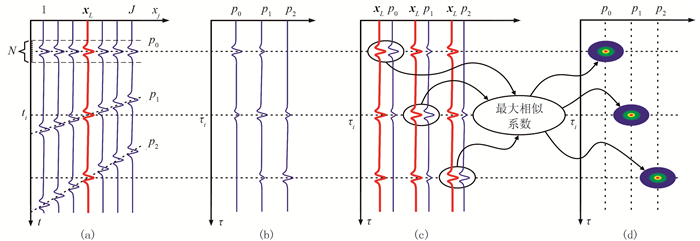
(1) 选择束中心位置xL的地震道作为参考道(图 1a);
|
图 1 局部地震记录相干性分析 (a)局部地震记录;(b)τ-p道集;(c)相干性分析;(d)相似系数 |
(2) 对局部地震记录进行倾斜叠加,对于任意时刻ti,依次按照不同斜率(水平慢度)p0、p1、p2等对局部地震记录叠加,对所有时刻重复上述步骤,得到τ-p道集(图 1b);
(3) 对τ-p道集进行相干性分析(图 1c)得到对应的相似系数(图 1d)。
根据式(2)可以得到τ-p道集的相似系数
| $ S\left( {\tau ,{\mathit{\boldsymbol{x}}_L},{p_{{\mathit{\boldsymbol{x}}_L}}}} \right) = \frac{{\sum\limits_{i = 1}^N {\left[ {\sum\limits_{j = 1}^J {u\left( {\tau + i\Delta t - {p_{Lx}}\Delta x,{x_j}} \right)} } \right]} }}{{N\sum\limits_{i - 1}^N {\sum\limits_{j = 1}^J {{u^2}\left( {\tau + i\Delta t - {p_{Lx}}\Delta x,{x_j}} \right)} } }} $ | (3) |
式中:u为高斯束内的地震记录;xj为高斯窗内第j道的笛卡尔坐标;τ为走时;Δt和Δx分别为时间采样间隔和空间采样间隔。
不同时刻、斜率对应不同的相似系数,不同斜率对应不同出射方向的高斯束。对于某一时刻,与最大相似系数对应的斜率即为高斯束在该束中心的主要出射方向(优势出射方向),较小相似系数可能对应随机噪声的出射方向(图 1d)。因此,若要在偏移结果中压制随机噪声,需要计算高斯束的优势出射方向,即找到最大相似系数对应的τ-p道集。为此,本文提出了τ-p域相似系数阈值滤波方法,即应用相似系数阈值滤波公式
| $ W\left( {{\tau _i},{\mathit{\boldsymbol{x}}_L},{p_j}} \right) = \left\{ {\begin{array}{*{20}{l}} 1&{S \ge T}\\ 0&{其他} \end{array}} \right. $ | (4) |
对τ-p道集滤波。式中T为相似系数阈值参数,范围为0~1。式(4)可以理解为扫描不同时刻、不同斜率的相似系数并保留满足阈值条件的τ-p道集。
2 数据驱动控制束偏移 2.1 基本原理及实现过程叠前高斯束偏移通过高斯束构建炮、检点在地下成像点处的格林函数,然后由格林函数构建上、下行波场,最后利用上、下行波场的互相关得到偏移结果。基于频率域互相关成像条件的二维叠前高斯束偏移公式为[48]
| $ \begin{array}{l} I\left( {{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = \frac{{\Delta L}}{{4{{\rm{ \mathsf{ π} }}^2}\sqrt {2{\rm{ \mathsf{ π} }}} {w_0}}}\sum\limits_{{\mathit{\boldsymbol{x}}_L}} {\int {{\rm{d}}\omega \int {\frac{{{\rm{d}}{p_{{\rm{s}}x}}}}{{{p_{{\rm{s}}z}}}}} \int {\frac{{{\rm{d}}{p_{Lx}}}}{{{p_{Lz}}}}} } } \times \\ \;\;\;\;\;\;\;\;\;{\rm{i}}\omega \frac{{\cos {\theta _{\rm{s}}}}}{{{v_{\rm{s}}}}}A_{\rm{s}}^*\exp \left( { - {\rm{i}}\omega T_{\rm{s}}^*} \right)\frac{{\cos {\theta _L}}}{{{v_L}}} \times \\ \;\;\;\;\;\;\;\;\;A_L^*\exp \left( { - {\rm{i}}\omega T_L^*} \right)D\left( {{\mathit{\boldsymbol{x}}_L},{p_L},\omega } \right) \end{array} $ | (5) |
式中:vs和vL分别为xs和xL处的速度;ΔL为束中心采样间隔;θs和θL分别为炮点和xL处的高斯束出射角;psx、psz和pLx、pLz分别为炮点和xL处射线参数的水平、垂直分量;Ts、As和TL、AL分别为炮点和xL处的复值走时、振幅;上标“*”表示取复共轭。
式(5)表示先对频率、炮点出射的高斯束以及束中心出射的高斯束进行三重积分,然后再对不同束中心对应的三重积分求和的过程。考虑到高斯束的振幅和走时均为复数,令
| $ \left\{ {\begin{array}{*{20}{l}} {{T_{{\rm{Re}}}} = {\rm{Re}}\left( {T_{\rm{s}}^* + T_{\rm{g}}^*} \right)}\\ {{A_{{\rm{Re}}}} = {\rm{Re}}\left( {A_{\rm{s}}^*A_{\rm{g}}^*} \right)}\\ {{T_{{\rm{Im}}}} = {\rm{Im}}\left( {T_{\rm{s}}^* + T_{\rm{g}}^*} \right)}\\ {{A_{{\rm{Im}}}} = {\rm{Im}}\left( {A_{\rm{s}}^*A_{\rm{g}}^*} \right)} \end{array}} \right. $ | (6) |
式中Tg、Ag分别为检波点的复值走时、振幅。直接求解式(5)存在不同频率求和的巨大计算量,因此通过改变积分次序,并且应用傅里叶反变换和希尔伯特变换,得到式(5)对应的时间域表达式[49]
| $ \begin{array}{l} I\left( {{\mathit{\boldsymbol{x}}_0},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = \frac{{\Delta L{\omega _{\rm{r}}}}}{{4{{\rm{ \mathsf{ π} }}^2}\sqrt {2{\rm{ \mathsf{ π} }}} {w_0}}}\sum\limits_{{\mathit{\boldsymbol{x}}_L}} {\int {\frac{{{\rm{d}}{p_{{\rm{s}}x}}}}{{{p_{{\rm{s}}z}}}}} } \int {\frac{{{\rm{d}}{p_{Lx}}}}{{{p_{Lz}}}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\cos {\theta _{\rm{s}}}}}{{{v_{\rm{s}}}}}\frac{{\cos {\theta _L}}}{{{v_L}}}\left[ {{A_{{\rm{Re}}}}\bar D\left( {{\mathit{\boldsymbol{x}}_L},{p_L},{T_{{\rm{Re}}}},{T_{{\rm{Im}}}}} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{A_{{\rm{Im}}}}{{\bar D}_{\rm{H}}}\left( {{\mathit{\boldsymbol{x}}_L},{p_L},{T_{{\rm{Re}}}},{T_{{\rm{Im}}}}} \right)} \right] \end{array} $ | (7) |
式中:D表示D的反傅里叶变换;下标“H”表示希尔伯特变换。
根据文献[50]可知:在成像过程中首先评估TIm的范围;然后对TRe和TIm离散采样,并计算D和DH的离散样板表;最后根据地下成像点的旅行时信息与离散样板表进行匹配成像。该过程可以理解为一个数据驱动过程,即从地震记录中提取每一个样点的采集“属性特征”(炮、检点坐标,炮检距以及方位角等)和旅行时,然后找到这些特定数据点指向的成像点。
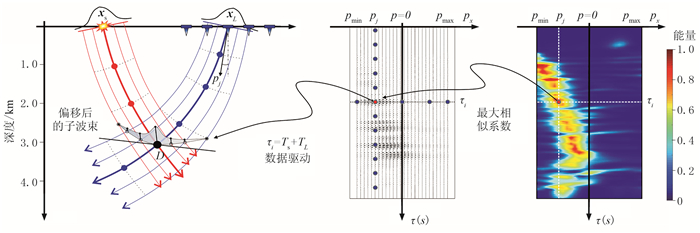
对含噪地震记录而言,在一定程度上噪声会影响样点信息的正确提取,从而影响最终的成像结果。为了压制噪声干扰,可以应用式(4)对离散样板表滤波处理,去除τ-p道集中的部分干扰能量,提高偏移剖面中同相轴的连续性。基于相干性分析的数据驱动控制束偏移过程概括为(图 2):①计算τ-p道集对应的相似系数并选取最大相似系数对应的τ-p道集;②分别计算来自炮、检点的中心射线以及旁轴射线;③组合两组旁轴射线以计算两个“胖射线”相交区域内所有点的走时和振幅;④根据走时关系和选取的τ-p道集中的能量得到偏移后的子波束,叠加所有偏移后的子波束得到最终的成像结果。图 3为数据驱动控制束偏移流程图。
|
图 2 基于相似系数阈值滤波的数据驱动控制束偏移过程 |
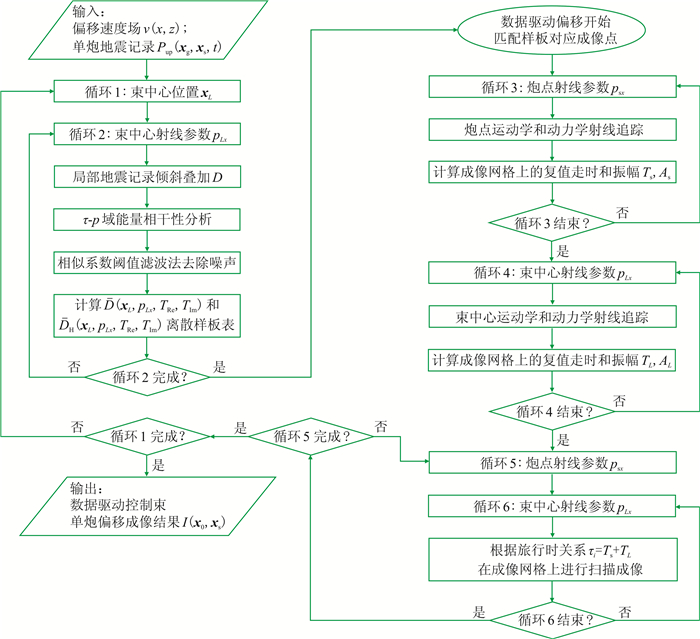
|
图 3 数据驱动控制束偏移流程图 |
在传统意义上,受地下照明强度的影响,互相关成像条件并不保幅,如在照明不充分的区域成像振幅会很弱。然而,Xu等[51]和Zhang等[48]证明,若将基于互相关成像条件的偏移结果转换到角度域,得到的ADCIGs包含与角度相关的反射系数信息,即互相关成像条件在角度域是保幅的。此外,ADCIGs还可用于迭代速度建模、AVA分析及AVO反演,因此本文给出了数据驱动控制束偏移的ADCIGs提取策略。
在波动方程偏移中,ADCIGs的提取方法主要基于空移成像条件和时移成像条件[52-54]。首先提取局部炮检距道集(L-ODCIGs)和时移成像道集(TSCIGs),分别代表波场在空间、时间方向的聚焦性。然后根据角度映射关系将L-ODCIGs和TSCIGs转换成ADCIGs。与波动方程偏移不同,由于高斯束在偏移过程中包含地下射线的传播角度信息,因此可以直接提取ADCIGs,无需复杂的映射变换,因此非常方便且高效。
基于有效邻域波场近似理论可知,中心射线附近一点R(xR, zR)处的复值走时满足(图 4)
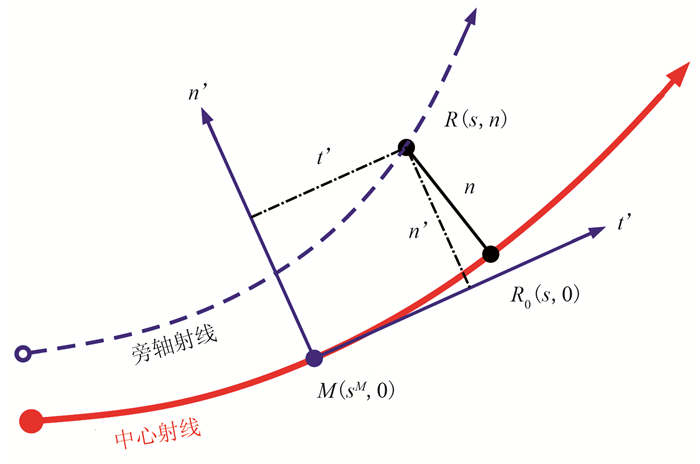
|
图 4 中心射线和旁轴射线传播示意图 R0为R点在中心射线上的投影点 |
| $ \tau \left( R \right) \approx {\tau ^M} + \frac{{s - {s^M}}}{{{v^M}}} - \frac{1}{2}\frac{{v_{,s}^M{{\left( {s - {s^M}} \right)}^2}}}{{{{\left( {{v^M}} \right)}^2}}} + \frac{1}{2}{\mathit{\Gamma }^M}{n^2} $ | (8) |
式中:(s, n)为射线中心坐标;vM和v, sM分别为M(xM, zM)点的速度及其沿射线方向的导数;ΓM=P(M)/Q(M),P和Q为M点的动力学射线参数。引入射线附近局部笛卡尔坐标系(t’, n’),坐标原点为M,则式(8)在笛卡尔坐标系转化为
| $ \tau \left( R \right) \approx {\tau ^M} + \frac{{{\mathit{\boldsymbol{l}}^{\rm{T}}}\mathit{\boldsymbol{x}}}}{{{v^M}}} + \frac{1}{2}{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{Wx}} $ | (9) |
其中
| $ \mathit{\boldsymbol{x}} = \left[ {\begin{array}{*{20}{l}} {x - {x^M}}\\ {z - {z^M}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{l}} = \left[ {\begin{array}{*{20}{l}} {\cos {\theta ^M}}\\ {\sin {\theta ^M}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{W}} = {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{A\sigma }} $ |
而
| $ \mathit{\boldsymbol{A}} = {\left( {{v^M}} \right)^{ - 2}}\left[ {\begin{array}{*{20}{c}} {{{\left( {{v^M}} \right)}^2}{\mathit{\Gamma }^M}}&{ - v_{,n}^M}\\ { - v_{,n}^M}&{ - v_{,s}^M} \end{array}} \right] $ | (10) |
其中
| $ {v_{,n}} = {v_{,x}}\cos {\theta ^M} - {v_{,z}}\sin {\theta ^M} $ |
| $ {v_{,s}} = {v_{,x}}\sin {\theta ^M} + {v_{,z}}\cos {\theta ^M} $ |
式中:θM为中心射线在M点的传播角度;σ为旋转矩阵;v, x和v, z分别为速度沿x和z方向的导数。根据式(9),旁轴射线上一点R的实值走时为
| $ \begin{array}{*{20}{l}} {\tau \left( R \right) = \tau \left( M \right) + \left[ {p_x^M\left( {{x^R} - {x^M}} \right) + p_z^M\left( {{z^R} - {z^M}} \right)} \right] + }\\ {\;\;\;\;\;\;\;\;\frac{1}{2}\left[ {\begin{array}{*{20}{l}} {{x^R} - {x^M}}\\ {{z^R} - {z^M}} \end{array}} \right] \cdot {\rm{Re}}\left( {\bf{W}} \right) \cdot \left[ {\begin{array}{*{20}{c}} {{x^R} - {x^M}}&{{z^R} - {z^M}} \end{array}} \right]} \end{array} $ | (11) |
式中pxM和pzM分别为M点的水平慢度和垂直慢度。
式(11)分别对x、z求导,可得[55]
| $ \begin{array}{*{20}{c}} {p_x^R = p_x^M + {\rm{Re}}\left( {{W_{11}}} \right)\left( {{x^R} - {x^M}} \right) + }\\ {{\rm{Re}}\left( {{W_{12}}} \right)\left( {{z^R} - {z^M}} \right)} \end{array} $ | (12) |
| $ \begin{array}{*{20}{c}} {p_z^R = p_z^M + {\rm Re}\left( {{W_{21}}} \right)\left( {{x^R} - {x^M}} \right) + }\\ {{\rm Re}\left( {{W_{22}}} \right)\left( {{z^R} - {z^M}} \right)} \end{array} $ | (13) |
则旁轴射线上R点的传播角度为
| $ \alpha = \left\{ {\begin{array}{*{20}{c}} { - {\rm{ \mathsf{ π} }} + \arctan \left( {\frac{{p_x^R}}{{p_z^R}}} \right)}&{p_x^R < 0,p_z^R < 0}\\ {{\rm{ \mathsf{ π} }} + \arctan \left( {\frac{{p_x^R}}{{p_z^R}}} \right)}&{p_x^R > 0,p_z^R < 0}\\ {\arctan \left( {\frac{{p_x^R}}{{p_z^R}}} \right)}&{其他} \end{array}} \right. $ | (14) |
如图 5所示,v为垂直于反射界面的倾角矢量,γ为偏移倾角。αs和αg分别为来自炮、检点射线的单位方向矢量,αs和αg分别为炮、检点射线在成像点处的传播角度,可由式(14)得到。为了提取ADCIGs,仅仅需要计算成像点处的偏移张角θ,然后根据θ将对应的成像振幅放在ADCIGs的对应位置。根据简单的角度关系,成像点处的偏移张角可以表示为

|
图 5 局部角度域示意图 |
| $ \theta = \frac{1}{2}\left( {{\alpha _{\rm{s}}} + {\alpha _{\rm{g}}}} \right) $ | (15) |
在编程实现算法的基础上,利用层状模型、Marmousi模型及实际资料验证本文方法的合理性。
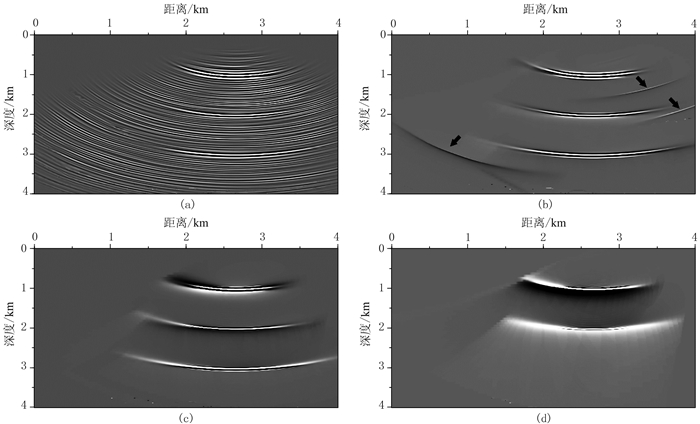
3.1 层状模型为了验证本文方法的正确性,建立了简单层状模型(图 6a)进行正演模拟,可见低信噪比单炮记录的同相轴变得模糊并混叠在背景噪声中(图 6c)。在偏移处理前,先选取第15个束中心处高斯束窗内(图 6b蓝色矩形框)的地震记录进行局部道集相干性分析(图 7)。可见:①随机噪声在τ-p道集中能量较弱(图 7c、图 7e),即使在标准τ-p道集中能量也不能很好地聚焦(图 7e红色箭头),这主要是由于对局部道集施加的高斯窗显著降低了τ-p道集的水平分辨率所致;然而利用控制束方法可不同程度地压制随机噪声(图 7f~图 7h红色箭头)。②采用相似系数阈值滤波方法处理τ-p道集,当选取合适的阈值参数时可不同程度地压制随机噪声(图 7f~图 7h红色椭圆),但过大的阈值参数也可能损害有效信号(蓝色椭圆),不能使有效信号成像。图 8为第15个束中心处高斯束及控制束偏移结果。由图可见:常规高斯束偏移结果(图 8a)存在明显的偏移噪声,控制束偏移结果(图 8b~图 8d)中噪声得到明显压制,信噪比显著提高;控制束偏移的阈值较小时(T=0.2)噪声压制不彻底(图 8b黑色箭头),但过大的阈值(T=0.8)也可能损害有效信号(图 8d)。因此选取合适的阈值参数(T=0.5)才能得到较理想的控制束偏移剖面(图 8c)。
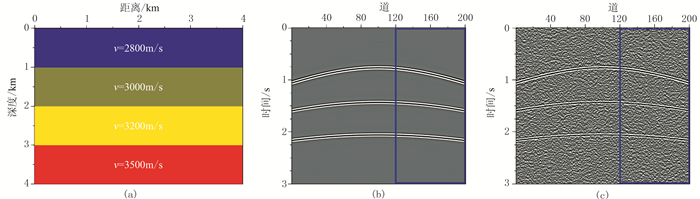
|
图 6 层状模型及正演模拟地震记录 (a)层状模型;(b)无噪单炮记录;(c)低信噪比单炮记录模型共四层,纵、横向范围均为4km。正演模拟采用声波交错网格高阶有限差分法,震源为主频20Hz的Ricker子波,采用中间激发两边接收,炮点位于2km处,单炮记录共有201道,道间距为20m,总记录长度为3s,采样率为4ms。使用Seismic Unix软件包中的suaddnoise命令模拟噪声 |
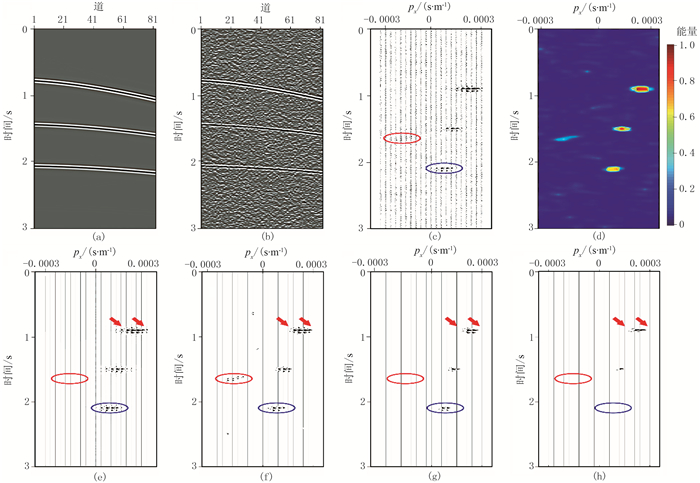
|
图 7 第15个束中心处局部道集相干性分析 (a)图 6b蓝色矩形框内局部道集;(b)图 6c蓝色矩形框内局部道集;(c)图 7b生成的τ-p道集;(d)相似系数;(e)图 7a生成的标准τ-p道集;(f)相似系数阈值(T=0.2)滤波后的τ-p道集;(g)相似系数阈值(T=0.5)滤波后的τ-p道集;(h)相似系数阈值(T=0.8)滤波后的τ-p道集 |
表 1为二维层状模型偏移计算效率对比。由表可见,控制束方法虽然在τ-p道集滤波过程增加了一定的计算量,但并不会明显降低计算效率,因此控制束偏移和高斯束偏移的计算效率相当,但对于低信噪比数据而言,前者具有更大优势。
|
|
表 1 二维层状模型偏移计算效率对比 |
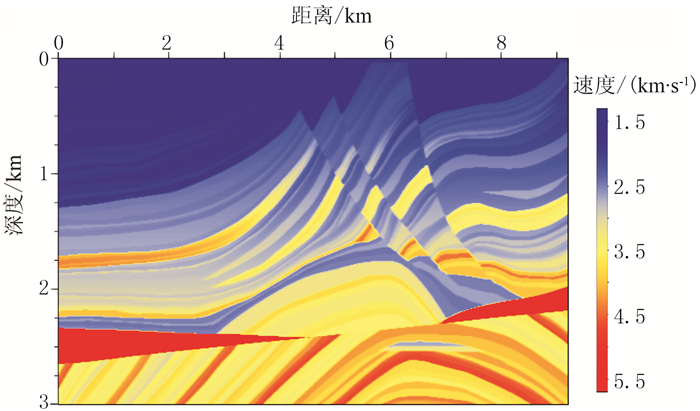
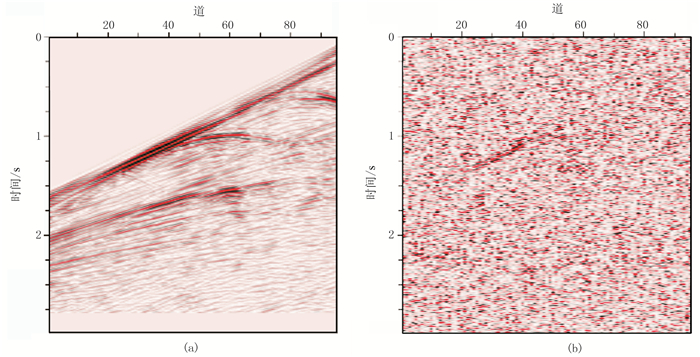
为了进一步验证本文方法的有效性,对Marmo-usi模型进行测试(图 9),该模型不仅包含尖灭、背斜和侵入体等典型地质构造,而且浅部还存在多期复杂断裂系统,横向速度变化剧烈,是测试深度偏移成像方法的经典模型。对第100炮无噪地震记录(图 10a)通过Seismic Unix软件包中的suaddnoise命令加入随机噪声,得到低信噪比炮记录(图 10b)。无噪地震记录的反射同相轴较清晰(图 10a),低信噪比记录的同相轴模糊并混叠在背景噪声中(图 10b)。
|
图 9 Marmousi模型 网格数为737×750,水平和深度方向采样间隔分别为12.5、4m。共240炮数据,右边放炮、左边接收,每炮96道,道间距为25m,最小和最大炮检距分别为200、2575m,每道750个采样点,采样间隔为4ms |
|
图 10 Marmousi模型第100炮地震记录 (a)无噪;(b)低信噪比 |
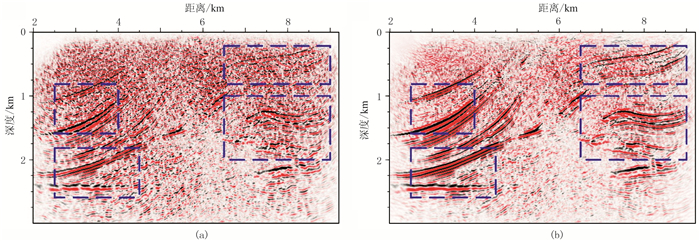
分别采用常规高斯束和控制束方法对低信噪比的炮集偏移处理。图 11为图 10b的常规高斯束和控制束偏移结果。由图可见:常规高斯束偏移结果存在明显的偏移噪声(图 11a);控制束偏移结果明显压制了噪声,同相轴连续性变好(图 11b)。图 12为图 11的局部放大。由图可见:由于偏移噪声的影响,常规高斯束偏移结果的同相轴模糊不清且连续性较差(图 12a);控制束偏移结果明显压制了噪声,提高了同相轴的连续性,成像效果明显改善(图 12b)。由此可见,控制束偏移方法在一定程度上提高了低信噪比数据的偏移成像质量。
|
图 11 图 10b的常规高斯束(a)和控制束(b)偏移结果 |
3.3 实际资料处理
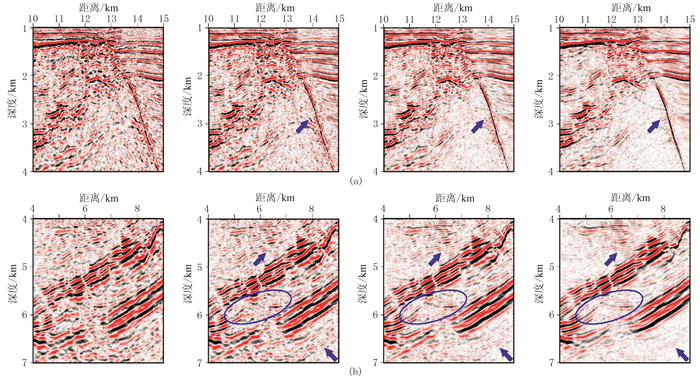
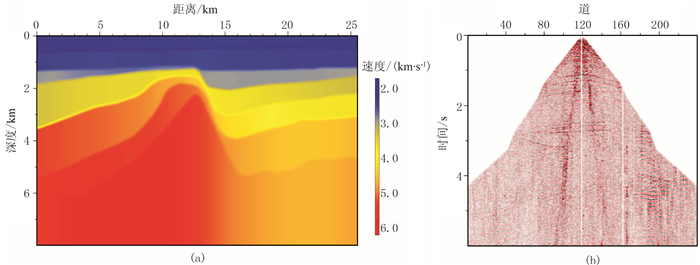
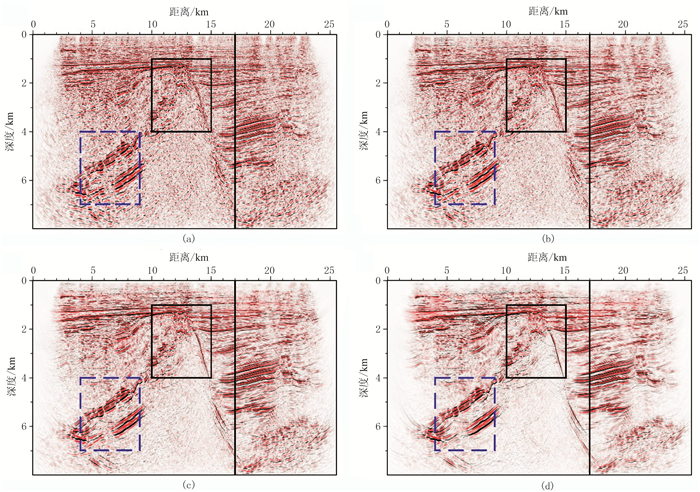
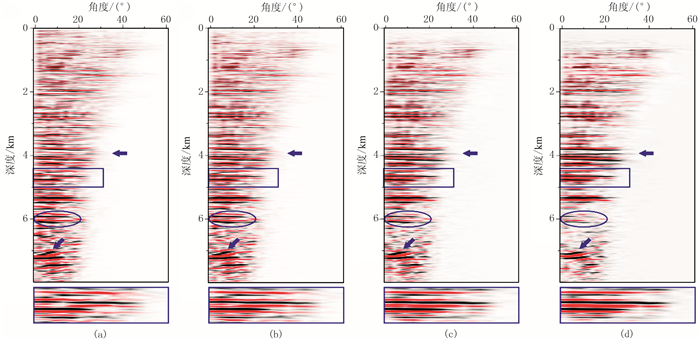
图 13为中国东部陆地A探区速度模型及第201炮记录。由图可知:模型中存在一个潜山披覆构造(图 13a);单炮记录中存在较明显的背景及随机噪声,资料信噪比较低,适合进行控制束偏移处理(图 13b)。图 14为常规高斯束偏移及不同相似系数阈值参数控制束偏移结果。由图可见,控制束偏移显著提高了成像剖面的信噪比(图 14b~图 14d)。图 15为图 14的局部放大。由图可见,控制束偏移剖面中潜山构造轮廓及其内部的弱同相轴更清晰(图 15蓝色箭头处),陡倾同相轴更连续(图 15蓝色椭圆区域),但也有可能损失相对振幅的可靠性。图 16为17km处的ADCIGs。由图可见,控制束偏移生成的角道集分辨率更高,同相轴更清晰(图 16b~图 16d蓝色箭头处和底部局部角道集放大),但相似系数阈值参数过大时会损失部分有效信息(图 16d蓝色椭圆处)。
|
图 13 中国东部陆地A探区速度模型(a)及第201炮记录(b) 速度场由传统射线层析方法构建,共炮道集已经过直达波切除、带通滤波等预处理 |
|
图 14 常规高斯束偏移及不同相似系数阈值参数控制束偏移结果 (a)常规高斯束;(b)控制束(T=0.1);(c)控制束(T=0.2);(d)控制束(T=0.3) |
|
图 16 17km处(图 14中黑线标记处)的ADCIGs (a)常规高斯束;(b)控制束(T=0.1);(c)控制束(T=0.2);(d)控制束(T=0.3) |
本文根据有效信号和干扰信号在τ-p域中的相干性差异,发展了一种基于相似系数阈值滤波的数据驱动控制束偏移方法。采用数据驱动策略,在高斯束偏移成像过程中计算τ-p道集的相似系数,通过τ-p域相似系数阈值滤波方法控制干扰信号,从而降低偏移剖面中的随机噪声,提高同相轴的连续性;同时给出了ADCIGs的提取方法,得到的高信噪比角度域共成像点道集更利于偏移速度分析。
模型测试及实际资料处理结果表明,对于低信噪比数据,控制束偏移剖面的信噪比明显高于常规高斯束偏移,但会损失相对振幅的可靠性。尽管控制束偏移在τ-p道集的滤波过程增加了一定的计算量,但与常规高斯束偏移方法的计算效率相当。
应该指出,在实际资料处理中,应根据资料特点采取相应的偏移方法,才能得到较可信的偏移结果。相似系数阈值参数选取十分关键,阈值较小时偏移噪声较强,但过大阈值也可能压制部分有效信息或产生偏移假象,选取合适的阈值参数才能得到较理想的偏移剖面。
在成文过程中,与美国德克萨斯州达拉斯大学的杨继东博士以及CGG石油服务公司的肖祥博士进行了有益的讨论,并得到中国石油大学(华东)地震波传播与成像(SWPI)课题组的支持与帮助,在此表示感谢!
| [1] |
Babich V M, Popov M M. Gaussian summation me-thod[J]. Radiophysics and Quantum Electronics, 1989, 32(12): 1063-1081. DOI:10.1007/BF01038632 |
| [2] |
Popov M M. A new method of computation of wave fields using Gaussian beams[J]. Wave Motion, 1982, 4(1): 85-97. DOI:10.1016/0165-2125(82)90016-6 |
| [3] |
Popov M M. Ray Theory and Gaussian Beam Method for Geophysicists[M]. EDUFBA, 2002.
|
| [4] |
Bleistein N. Hagedoorn told us how to do Kirchhoff migration and inversion[J]. The Leading Edge, 1999, 18(8): 918-927. DOI:10.1190/1.1438407 |
| [5] |
Hill N R. Prestack Gaussian-beam depth migration[J]. Geophysics, 2001, 66(4): 1240-1250. DOI:10.1190/1.1487071 |
| [6] |
Gray S H, Notfors C, Bleistein N.Imaging using multi-arrivals: Gaussian beams or multi-arrival Kirchhoff?[C].SEG Technical Program Expanded Abstracts, 2002, 21: 1117-1120.
|
| [7] |
Liu J, Palacharla G. Multiarrival Kirchhoff beam migration[J]. Geophysics, 2011, 76(5): WB109-WB118. DOI:10.1190/geo2010-0403.1 |
| [8] |
Kachalov A P, Popov M M. Application of the method of summation of Gaussian beams for calculation of high-frequency wave fields[J]. Soviet Physics Dok-lady, 1981, 26(1): 604-606. |
| [9] |
Červený V, Popov M M, Pšeněík I. Computation of wave fields in inhomogeneous media Gaussian beam approach[J]. Geophysical Journal International, 1982, 70(1): 109-128. DOI:10.1111/j.1365-246X.1982.tb06394.x |
| [10] |
Červený V. Synthetic body wave seismograms for la-terally varying layered structures by the Gaussian beam method[J]. Geophysical Journal of the Royal Astronomical Society, 2010. DOI:10.1111/j.1365-246X.1983.tb03322.x |
| [11] |
Červený V, Pšeněík I. Gaussian beams in two-dimensional elastic inhomogeneous media[J]. Geophysical Journal International, 1983, 72(2): 417-433. DOI:10.1111/j.1365-246X.1983.tb03793.x |
| [12] |
Červený V, Pšeněík I. Gaussian beams in elastic 2-D laterally varying layered structures[J]. Geophysical Journal of the Royal Astronomical Society, 1983. DOI:10.1111/j.1365-246x.1984.tb06472.x |
| [13] |
Hill N R. Gaussian beam migration[J]. Geophysics, 1990, 55(11): 1416-1428. DOI:10.1190/1.1442788 |
| [14] |
Nowack R L, Sen M K, Stoffa P L.Gaussian beam migration for sparse common-shot and common-receiver data[C].SEG Technical Program Expanded Abstracts, 2003, 22: 1114-1117.
|
| [15] |
Gray S H. Gaussian beam migration of common-shot records[J]. Geophysics, 2005, 70(4): S71-S77. DOI:10.1190/1.1988186 |
| [16] |
Casasanta L, Gray S H. Converted-wave beam migration with sparse sources or receivers[J]. Geophysical Prospecting, 2015, 63(3): 534-551. DOI:10.1111/1365-2478.12226 |
| [17] |
Yang J, Zhu H, Huang J, et al. 2D isotropic elastic Gaussian beam migration for common-shot multicomponent records[J]. Geophysics, 2017, 83(2): S127-S140. |
| [18] |
Alkhalifah T. Gaussian beam depth migration for anisotropic media[J]. Geophysics, 1995, 60(5): 1474-1484. DOI:10.1190/1.1443881 |
| [19] |
Zhu T, Gray S H, Wang D. Prestack Gaussian-beam depth migration in anisotropic media[J]. Geophysics, 2007, 72(3): S133-S138. DOI:10.1190/1.2711423 |
| [20] |
Protasov M I. 2-D Gaussian beam imaging of multicomponent seismic data in anisotropic media[J]. Geophysical Supplements to the Monthly Notices of the Royal Astronomical Society, 2015, 203(3): 2021-2031. DOI:10.1093/gji/ggv408 |
| [21] |
段鹏飞, 程玖兵, 陈爱萍, 等. TI介质局部角度域高斯束叠前深度偏移成像[J]. 地球物理学报, 2013, 56(12): 4206-4214. DUAN Pengfei, CHENG Jiubing, CHEN Aiping, et al. Local angle-domain Gaussian beam prestack depth migration in a TI medium[J]. Chinese Journal of Geophysics, 2013, 56(12): 4206-4214. DOI:10.6038/cjg20131223 |
| [22] |
李振春, 刘强, 韩文功, 等. VTI介质角度域转换波高斯束偏移成像方法研究[J]. 地球物理学报, 2018, 61(4): 1471-1481. LI Zhenchun, LIU Qiang, HAN Wengong, et al. Angle domain converted wave Gaussian beam migration in VTI media[J]. Chinese Journal of Geophysics, 2018, 61(4): 1471-1481. |
| [23] |
Popov M M, Semtchenok N M, Popov P M, et al. Depth migration by the Gaussian beam summation method[J]. Geophysics, 2010, 75(2): S81-S93. DOI:10.1190/1.3361651 |
| [24] |
黄建平, 张晴, 张凯, 等. 格林函数高斯束逆时偏移[J]. 石油地球物理勘探, 2014, 49(1): 101-106. HUANG Jianping, ZHANG Qing, ZHANG Kai, et al. Reverse time migration with Gaussian beams based on the Green function[J]. Oil Geophysical Prospecting, 2014, 49(1): 101-106. |
| [25] |
张凯, 段新意, 李振春, 等. 角度域各向异性高斯束逆时偏移[J]. 石油地球物理勘探, 2015, 50(5): 912-918. ZHANG Kai, DUAN Xinyi, LI Zhenchun, et al. Angle domain reverse time migration with Gaussian beams in anisotropic media[J]. Oil Geophysical Prospecting, 2015, 50(5): 912-918. |
| [26] |
Huang J, Yuan M, Zhang Q, et al. Reverse timemigration with elastodynamic Gaussian beams[J]. Journal of Earth Science, 2017, 28(4): 695-702. DOI:10.1007/s12583-015-0609-9 |
| [27] |
Gray S H, Bleistein N. True-amplitude Gaussian-beam migration[J]. Geophysics, 2009, 74(2): S11-S23. DOI:10.1190/1.3052116 |
| [28] |
李振春, 岳玉波, 郭朝斌, 等. 高斯波束共角度保幅深度偏移[J]. 石油地球物理勘探, 2010, 45(3): 360-365. LI Zhenchun, YUE Yubo, GUO Chaobin, et al. Gau-ssian beam common angle preserved-amplitude migration[J]. Oil Geophysical Prospecting, 2010, 45(3): 360-365. |
| [29] |
Protasov M I, Tcheverda V A. True amplitude elastic Gaussian beam imaging of multicomponent walkaway vertical seismic profiling data[J]. Geophysical Prospecting, 2012, 60(6): 1030-1042. DOI:10.1111/j.1365-2478.2012.01068.x |
| [30] |
岳玉波, 李振春, 钱忠平, 等. 复杂地表条件下保幅高斯束偏移[J]. 地球物理学报, 2012, 55(4): 1376-1383. YUE Yubo, LI Zhenchun, QIAN Zhongping, et al. Amplitude-preserved Gaussian beam migration under complex topographic conditions[J]. Chinese Journal of Geophysics, 2012, 55(4): 1376-1383. DOI:10.6038/j.issn.0001-5733.2012.04.033 |
| [31] |
黄建平, 杨继东, 李振春, 等. 基于有效邻域波场近似的起伏地表保幅高斯束偏移[J]. 地球物理学报, 2016, 59(6): 2245-2256. HUANG Jianping, YANG Jidong, LI Zhenchun, et al. An amplitude-preserved Gaussian beam migration based on wave field approximation in effective vicinity under irregular topographical conditions[J]. Chinese Journal of Geophysics, 2016, 59(6): 2245-2256. |
| [32] |
Hu H, Liu Y, Zheng Y, et al. Least-squares Gaussian beam migration[J]. Geophysics, 2016, 81(3): S87-S100. DOI:10.1190/geo2015-0328.1 |
| [33] |
Yuan M, Huang J, Liao W, et al. Least-squares Gau-ssian beam migration[J]. Journal of Geophysics and Engineering, 2017, 14(1): 184-196. DOI:10.1088/1742-2140/14/1/184 |
| [34] |
黄建平, 袁茂林, 李振春, 等. 双复杂条件下非倾斜叠加精确束偏移方法及应用Ⅰ——声波方程[J]. 地球物理学报, 2015, 58(1): 267-276. HUANG Jianping, YUAN Maolin, LI Zhenchun, et al. The accurate beam migration method without slant stack under dual-complexity conditions and its application (I):Acoustic equation[J]. Chinese Journal of Geophysics, 2015, 58(1): 267-276. |
| [35] |
张瑞, 黄建平, 崔超, 等. 莺歌海盆地二维剖面高斯束高精度叠前深度偏移[J]. 海洋地质与第四纪地质, 2017, 37(1): 168-175. ZHANG Rui, HUANG Jianping, CUI Chao, et al. High precision Gaussian beam pre-stack depth migration for Yinggehai basin 2D seismic profiles[J]. Marine Geology and Quaternary Geology, 2017, 37(1): 168-175. |
| [36] |
Yang J, Zhu H. A practical data-driven optimization strategy for Gaussian beam migration[J]. Geophy-sics, 2017, 83(1): S81-S92. |
| [37] |
Vinje V, Roberts G A, Taylor R. Controlled beam migration:a versatile structural imaging tool[J]. First Break, 2008, 26(9): 109-113. |
| [38] |
Zhou B, Zhou J, Wang Z, et al.Anisotropic depth imaging with high fidelity controlled beam migration: A case study in Bohai, offshore China[C].SEG Technical Program Expanded Abstracts, 2011, 30: 217-221.
|
| [39] |
Casasanta L, Grion S.Converted-wave controlled-beam migration for vector-offset volumes[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [40] |
Casasanta L, Gray S, Grion S.Converted-wave con-trolled beam migration with sparse sources or recei-vers[C].Extended Abstracts of 75th EAGE Conference & Exhibition, 2013, doi: 10.3997/2214-4609.20130716.
|
| [41] |
黄建平, 吴建文, 杨继东, 等. 一种τ-p域二维控制束成像方法[J]. 石油地球物理勘探, 2016, 51(2): 342-349. HUANG Jianping, WU Jianwen, YANG Jidong, et al. A 2D control beam migration in the τ-p domain[J]. Oil Geophysical Prospecting, 2016, 51(2): 342-349. |
| [42] |
Robein E[法]著; 王克斌, 曹孟起, 王永明, 等译.地震资料叠前偏移成像——方法、原理和优缺点分析[M].北京: 石油工业出版社, 2012.
|
| [43] |
孙夕平, 杜世通. 相干体技术算法研究及其在地震资料解释中的应用[J]. 中国石油大学学报(自然科学版), 2003, 27(2): 32-35. SUN Xiping, DU Shitong. Study on coherent body algorithm and its application in seismic data interpretation[J]. Journal of China University of Petroleum(Edition of Natural Science), 2003, 27(2): 32-35. DOI:10.3321/j.issn:1000-5870.2003.02.009 |
| [44] |
Bahorich M, Farmer S. 3-D seismic discontinuity for faults and stratigraphic features:The coherence cube[J]. The Leading Edge, 1995, 14(10): 1053-1058. DOI:10.1190/1.1437077 |
| [45] |
Marfurt K J, Kirlin R L, Farmer S L, et al. 3-D seis-mic attributes using a semblance-based coherency al-gorithm[J]. Geophysics, 1998, 63(4): 1150-1165. DOI:10.1190/1.1444415 |
| [46] |
Marfurt K J, Sudhaker V, Gersztenkorn A, et al. Coherency calculations in the presence of structural dip[J]. Geophysics, 1999, 64(1): 104-111. DOI:10.1190/1.1444508 |
| [47] |
Neidell N S, Taner M T. Semblance and other cohe-rency measures for multichannel data[J]. Geophysics, 1971, 36(3): 482-497. DOI:10.1190/1.1440186 |
| [48] |
Zhang Y, Xu S, Bleistein N, et al. True-amplitude, angle-domain, common-image gathers from one-way wave-equation migrations[J]. Geophysics, 2007, 72(1): S49-S58. DOI:10.1190/1.2399371 |
| [49] |
高成, 孙建国, 齐鹏, 等. 2D共炮时间域高斯波束偏移[J]. 地球物理学报, 2015, 58(4): 1333-1340. GAO Cheng, SUN Jianguo, QI Peng, et al. 2-D Gau-ssian-beam migration of common-shot records in time domain[J]. Chinese Journal of Geophysics, 2015, 58(4): 1333-1340. |
| [50] |
Hale D.Migration by the Kirchhoff, Slant Stack, and Gaussian Beam Methods[R].Center for Wave Phenomena, Colorado School of Mines, 1992, CWP-126.
|
| [51] |
Xu S, Chauris H, Lambaré G, et al. Common-angle migration:A strategy for imaging complex media[J]. Geophysics, 2001, 66(6): 1877-1894. DOI:10.1190/1.1487131 |
| [52] |
Sava P C, Fomel S. Angle-domain common-image gathers by wavefield continuation methods[J]. Geophy-sics, 2003, 68(3): 1065-1074. |
| [53] |
Sava P, Fomel S.Coordinate-independent angle-gathers for wave equation migration[C].SEG Technical Program Expanded Abstracts, 2005, 24: 2052-2055.
|
| [54] |
Sava P, Fomel S. Time-shift imaging condition in seismic migration[J]. Geophysics, 2006, 71(6): S209-S217. DOI:10.1190/1.2338824 |
| [55] |
岳玉波.复杂介质高斯束偏移成像方法研究[D].山东青岛: 中国石油大学(华东), 2011.
|



 黄建平 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
黄建平 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: