② 中国地质大学(武汉)地球物理与空间信息学院, 湖北武汉 430074
② Institute of Geophysics and Geomatics, China University of Geosciences(Wuhan), Wuhan, Hubei 430074, China
全波形反演(Full-waveform Inversion)以波动方程作为数学模型模拟地震波的传播规律,能够更充分地利用地震数据信息,具有成像更准确、分辨率更高的特点[1-2]。Tarantola[1]首先提出了基于广义最小二乘的时间域全波形反演理论和方法,随后Pratt[3-4]将其推广到频率域内。相比于时间域,频率域全波形反演具有计算过程稳定、占用内存小、不存在累计误差、缓和局部极小、降低反演的非线性、易于处理衰减频散效应、易于并行计算等特点[5-10],近些年得到广泛发展与应用[11-12]。
在频率域计算中,选择合适的数值方法离散波动方程,处理区域边界、求解大型线性方程组是必要的。常见的数值离散方法包括有限差分法[13-14]、有限元法[15-16]、谱元法[17-18]等。当网格不够密集时,常规的有限差分(Ordinary Finite-difference,OFD)方法容易出现明显的数值频散现象,尽管通过加密离散网格可以在一定程度上压制频散,但是相应的计算量增大,所需时间和内存也会增加[19]。
针对以上问题,Yang等[20-21]引入了近似解析离散化(Nearly Analytic Discrete,NAD)方法,并应用于时间域地震波模拟,随后Lang等[8]将其引入到频率域正演模拟中,其基本思想是利用波场位移与其梯度值的联合近似得到位移的高阶偏导数,进而离散波动方程。相比于其他差分方法,NAD算子携带了更多的波场信息,特别是含有刻画波场变化特征的梯度信息。前人研究表明,针对较粗的离散网格,NAD方法在压制数值频散方面具有很好的效果[8],此外,与同阶差分格式相比,NAD数值格式计算量小,易于并行计算。然而现有的频率域四阶NAD(NAD4)方法对于计算效率的提升还很有限,需要考虑在此基础上构造更加有效的数值方法。
为提高全波形反演的计算效率,本文构造了频率域八阶NAD(NAD8)格式离散二维声波方程,采用完全匹配层吸收边界(Perfectly Matched Layer,PML)[22]条件。首先详细介绍了NAD8格式的具体离散过程;然后使用一类不精确旋转分块三角预处理算子(IRBTP)加速广义极小残量方法(GMRES)[23]求解离散后的大型稀疏线性方程组;通过数值频散分析以及波场模拟与六阶NAD(NAD6)、八阶OFD(OFD8)方法进行对比,结果表明NAD8方法在压制频散和提高计算效率等方面具有优势;最后,基于共轭梯度法[24],首次构造了基于NAD8方法的频率域全波形反演算法,对两种典型分层介质模型和经典Marmousi模型进行了反演试算,获得了高保真、高分辨率的成像结果,进而验证了所提方法的有效性和适用性。
1 方法原理归结起来,频率域NAD方法的离散过程可概括为以下几步:对频率域波动方程关于各个方向求偏导,并在计算区域的边界处施加吸收边界条件,进而得到偏微分方程组,采用NAD网格差分模板离散其中的高阶偏导数项,再按一定节点排序规则形成大型稀疏线性方程组。
假定地球为完全弹性介质时,可以用声波方程研究地震波的传播规律。常密度介质下的二维频率域声波方程为
| $ \begin{array}{l} \frac{{{\partial ^2}u\left( {x,z,\omega } \right)}}{{\partial {x^2}}} + \frac{{{\partial ^2}u\left( {x,z,\omega } \right)}}{{\partial {z^2}}} + \frac{{{\omega ^2}}}{{{c^2}}}u\left( {x,z,\omega } \right)\\ \;\;\;\;\;\;\; = - \frac{1}{{{c^2}}}s\left( {x,z,\omega } \right) \end{array} $ | (1) |
式中:u(x,z,ω)表示位移或者压力场;ω=2πf表示角频率;c为地震波波速;s表示震源项。
对式(1)两端分别关于x方向与z方向求偏导,有
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}} + \frac{{{\omega ^2}}}{{{c^2}}} = - \frac{1}{{{c^2}}}s\\ \frac{{{\partial ^2}{u_x}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u_x}}}{{\partial {z^2}}} + \frac{{{\omega ^2}}}{{{c^2}}}{u_x} = - \frac{1}{{{c^2}}}\frac{{\partial s}}{{\partial x}}\\ \frac{{{\partial ^2}{u_z}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u_z}}}{{\partial {z^2}}} + \frac{{{\omega ^2}}}{{{c^2}}}{u_z} = - \frac{1}{{{c^2}}}\frac{{\partial s}}{{\partial z}} \end{array} \right. $ | (2) |
不同于传统的差分方法,NAD方法同时求解
与时间域不同,在频率域施加PML边界条件的过程中,不需要进行反褶积计算,实现更方便、准确。首先引入复坐标控制衰减,以x方向为例,有
| $ \tilde x = x - \frac{{\rm{i}}}{\omega }\int_0^x {{d_x}} (s){\rm{d}}s $ | (3) |
将衰减函数取为
| $ {d_x}(x) = - \frac{{3\tilde v}}{{2L}}{\left( {\frac{l}{L}} \right)^2}\lg R $ | (4) |
式中:R表示离散后的理论边界反射系数;l表示PML层内节点到内部计算区域的横向距离(同理,z方向时表示纵向距离);L表示PML层厚度;
| $ \left\{ \begin{array}{l} \frac{1}{{t_x^2}}\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{1}{{t_z^2}}\frac{{{\partial ^2}u}}{{\partial {z^2}}} + \frac{{{\rm{i}}{{d'}_x}}}{{\omega t_x^3}}\frac{{\partial u}}{{\partial x}} + \frac{{{\rm{i}}{{d'}_z}}}{{\omega t_z^3}}\frac{{\partial u}}{{\partial z}} + \frac{{{\omega ^2}}}{{{c^2}}}u\\ \;\;\;\; = - \frac{1}{{{c^2}}}s\\ \frac{1}{{t_x^2}}\frac{{{\partial ^3}u}}{{\partial {x^3}}} + \frac{1}{{t_z^2}}\frac{{{\partial ^3}u}}{{\partial x\partial {z^2}}} + 3\frac{{{\rm{i}}{{d'}_x}}}{{\omega t_x^3}}\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\rm{i}}{{d'}_z}}}{{\omega t_z^3}}\frac{{{\partial ^2}u}}{{\partial x\partial z}} + \\ \;\;\;\;\;\;\;\;\left( {\frac{{ - 3d{'}_x^2}}{{{\omega ^2}t_x^4}} + \frac{{{\rm{i}}{{d''}_x}}}{{\omega t_x^3}} + \frac{{{\omega ^2}}}{{{c^2}}}} \right)\frac{{\partial u}}{{\partial x}} = - \frac{1}{{{c^2}}}\frac{{\partial s}}{{\partial x}}\\ \frac{1}{{t_z^2}}\frac{{{\partial ^3}u}}{{\partial {z^3}}} + \frac{1}{{t_x^2}}\frac{{{\partial ^3}u}}{{\partial {x^2}\partial z}} + 3\frac{{{\rm{i}}{{d'}_x}}}{{\omega t_x^3}}\frac{{{\partial ^2}u}}{{\partial {z^2}}} + \frac{{{\rm{i}}{{d'}_x}}}{{\omega t_x^3}}\frac{{{\partial ^2}u}}{{\partial x\partial z}} + \\ \;\;\;\;\;\;\;\frac{{ - 3d{'}_x^2}}{{{\omega ^2}t_x^4}} + \frac{{{\rm{i}}{{d''}_x}}}{{\omega t_x^3}} + \frac{{{\omega ^2}}}{{{c^2}}}\left( {\frac{{ - 3d{'}_x^2}}{{{\omega ^2}t_z^4}} + \frac{{{\rm{i}}{{d''}_x}}}{{\omega t_z^3}} + \frac{{{\omega ^2}}}{{{c^2}}}} \right)\frac{{\partial u}}{{\partial z}}\\ \;\;\; = - \frac{1}{{{c^2}}}\frac{{\partial s}}{{\partial z}} \end{array} \right. $ | (5) |
式中
| $ \left\{ {\begin{array}{*{20}{l}} {{t_x} = 1 - \frac{{\rm{i}}}{\omega }{d_x}}\\ {{t_z} = 1 - \frac{{\rm{i}}}{\omega }{d_z}} \end{array}} \right. $ | (6) |
与NAD4方法[19]不同,对于NAD8格式,任一点(i, j)的高阶偏导数需要由(i-2,j)、(i-1,j)、(i,j)、(i+1,j)、(i+2,j)五个点处的波场及其空间梯度的加权组合近似。求解微分方程中高阶偏导数的离散格式为
| $ \begin{array}{l} \frac{{{\partial ^2}{u_{i,j}}}}{{\partial {x^2}}} = \frac{1}{{54{h^2}}}\left( {7{u_{i + 2,j}} + 128{u_{i + 1,j}} - 270{u_{i,j}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {128{u_{i - 1,j}} + 7{u_{i - 2,j}}} \right) + \frac{1}{{36h}}\left( { - \frac{{\partial {u_{i + 2,j}}}}{{\partial x}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {32\frac{{\partial {u_{i + 1,j}}}}{{\partial x}} + 32\frac{{\partial {u_{i - 1,j}}}}{{\partial x}} + \frac{{\partial {u_{i - 2,j}}}}{{\partial x}}} \right) \end{array} $ | (7) |
| $ \begin{array}{l} \frac{{{\partial ^2}{u_{i,j}}}}{{\partial {z^2}}} = \frac{1}{{54{h^2}}}\left( {7{u_{i,j + 2}} + 128{u_{i,j + 1}} - 270{u_{i,j}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {128{u_{i,j - 1}} + 7{u_{i,j - 2}}} \right) + \frac{1}{{36h}}\left( { - \frac{{\partial {u_{i,j + 2}}}}{{\partial z}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {32\frac{{\partial {u_{i,j + 1}}}}{{\partial z}} + 32\frac{{\partial {u_{i,j - 1}}}}{{\partial z}} + \frac{{\partial {u_{i,j - 2}}}}{{\partial z}}} \right) \end{array} $ | (8) |
| $ \begin{array}{l} \frac{{{\partial ^3}{u_{i,j}}}}{{\partial {x^3}}} = \frac{1}{{144{h^3}}}\left( {31{u_{i + 2,j}} + 1408{u_{i + 1,j}} - 1408{u_{i - 1,j}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {31{u_{i - 2,j}}} \right) - \frac{1}{{24{h^2}}}\left( {\frac{{\partial {u_{i + 2,j}}}}{{\partial x}} + 64\frac{{\partial {u_{i + 1,j}}}}{{\partial x}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {360\frac{{\partial {u_{i,j}}}}{{\partial x}} + 64\frac{{\partial {u_{i - 1,j}}}}{{\partial x}} + \frac{{\partial {u_{i - 2,j}}}}{{\partial x}}} \right) \end{array} $ | (9) |
| $ \begin{array}{l} \frac{{{\partial ^3}{u_{i,j}}}}{{\partial {z^3}}} = \frac{1}{{144{h^3}}}\left( {31{u_{i,j + 2}} + 1408{u_{i,j + 1}} - 1408{u_{i,j - 1}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {31{u_{i,j - 2}}} \right) - \frac{1}{{24{h^2}}}\left( {\frac{{\partial {u_{i,j + 2}}}}{{\partial z}} + 64\frac{{\partial {u_{i,j + 1}}}}{{\partial z}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {360\frac{{\partial {u_{i,j}}}}{{\partial z}} + 64\frac{{\partial {u_{i,j - 1}}}}{{\partial z}} + \frac{{\partial {u_{i,j - 2}}}}{{\partial z}}} \right) \end{array} $ | (10) |
| $ \begin{array}{l} \frac{{{\partial ^2}{u_{i,j}}}}{{\partial x\partial z}} = \frac{1}{{216{h^2}}}\left( {7{u_{i + 2,j + 2}} - 7{u_{i - 2,j + 2}} + 128{u_{i + 1,j + 1}} - } \right.\\ \;\;\;\;\;\;\;\;\;128{u_{i - 1,j + 1}} - 128{u_{i + 1,j - 1}} + 128{u_{i - 1,j - 1}} - \\ \;\;\;\;\;\;\;\;\;\left. {7{u_{i + 2,j - 2}} + 7{u_{i - 2,j - 2}}} \right) + \\ \;\;\;\;\;\;\;\;\;\frac{1}{{144h}}\left( { - \frac{{\partial {u_{i + 2,j + 2}}}}{{\partial x}} - 32\frac{{\partial {u_{i + 1,j + 1}}}}{{\partial x}} + } \right.\\ \;\;\;\;\;\;\;\;\;32\frac{{\partial {u_{i - 1,j - 1}}}}{{\partial x}} + \frac{{\partial {u_{i - 2,j - 2}}}}{{\partial x}} - \frac{{\partial {u_{i - 2,j + 2}}}}{{\partial x}} - \\ \left. {\;\;\;\;\;\;\;\;\;32\frac{{\partial {u_{i - 1,j + 1}}}}{{\partial x}} + 32\frac{{\partial {u_{i + 1,j - 1}}}}{{\partial x}} + \frac{{\partial {u_{i + 2,j - 2}}}}{{\partial x}}} \right) + \\ \;\;\;\;\;\;\;\;\;\frac{1}{{144h}}\left( { - \frac{{\partial {u_{i + 2,j + 2}}}}{{\partial z}} - 32\frac{{\partial {u_{i + 1,j + 1}}}}{{\partial z}} + } \right.\\ \;\;\;\;\;\;\;\;\;32\frac{{\partial {u_{i - 1,j - 1}}}}{{\partial z}} + \frac{{\partial {u_{i - 2,j - 2}}}}{{\partial z}} + \frac{{\partial {u_{i - 2,j + 2}}}}{{\partial z}} + \\ \;\;\;\;\;\;\;\;\;\left. {32\frac{{\partial {u_{i - 1,j + 1}}}}{{\partial z}} - 32\frac{{\partial {u_{i + 1,j - 1}}}}{{\partial z}} - \frac{{\partial {u_{i + 2,j - 2}}}}{{\partial z}}} \right) \end{array} $ | (11) |
| $ \begin{array}{l} \frac{{{\partial ^3}{u_{i,j}}}}{{\partial x\partial {z^2}}} = \frac{1}{{864{h^3}}}\left( {31{u_{i + 2,j + 2}} - 31{u_{i - 2,j + 2}} + } \right.\\ \;\;\;\;\;\;\;\;1408{u_{i + 1,j + 1}} - 1408{u_{i - 1,j + 1}} - 62{u_{i + 2,j}} - \\ \;\;\;\;\;\;\;\;2816{u_{i + 1,j}} + 2816{u_{i - 1,j}} + 62{u_{i - 2,j}} + \\ \;\;\;\;\;\;\;\;31{u_{i + 2,j - 2}} + 1408{u_{i + 1,j - 1}} - 1408{u_{i - 1,j - 1}} - \\ \;\;\;\;\;\;\;\;\left. {31{u_{i - 2,j - 2}}} \right) + \frac{1}{{144{h^2}}}\left( {\frac{{ - \partial {u_{i + 2,j + 2}}}}{{\partial x}} - \frac{{\partial {u_{i - 2,j + 2}}}}{{\partial x}} - } \right.\\ \;\;\;\;\;\;\;\;64\frac{{\partial {u_{i + 1,j + 1}}}}{{\partial x}} - 64\frac{{\partial {u_{i - 1,j + 1}}}}{{\partial x}} + 2\frac{{\partial {u_{i + 2,j}}}}{{\partial x}} + \\ \;\;\;\;\;\;\;\;128\frac{{\partial {u_{i + 1,j}}}}{{\partial x}} + 128\frac{{\partial {u_{i - 1,j}}}}{{\partial x}} + 2\frac{{\partial {u_{i - 2,j}}}}{{\partial x}} - \\ \;\;\;\;\;\;\;\;64\frac{{\partial {u_{i + 1,j - 1}}}}{{\partial x}} - 64\frac{{\partial {u_{i - 1,j - 1}}}}{{\partial x}} - \frac{{\partial {u_{i + 2,j - 2}}}}{{\partial x}}\\ \;\;\;\;\;\;\;\;\left. {\frac{{\partial {u_{i - 2,j - 2}}}}{{\partial x}}} \right) + \frac{1}{{144{h^2}}}\left( {\frac{{ - \partial {u_{i + 2,j + 2}}}}{{\partial z}} + \frac{{\partial {u_{i - 2,j + 2}}}}{{\partial z}} - } \right.\\ \;\;\;\;\;\;\;\;64\frac{{\partial {u_{i + 1,j + 1}}}}{{\partial z}} + 64\frac{{\partial {u_{i - 1,j + 1}}}}{{\partial z}} + 64\frac{{\partial {u_{i + 1,j - 1}}}}{{\partial z}} - \\ \;\;\;\;\;\;\;\;\left. {64\frac{{\partial {u_{i - 1,j - 1}}}}{{\partial z}} + \frac{{\partial {u_{i + 2,j - 2}}}}{{\partial z}} - \frac{{\partial {u_{i - 2,j - 2}}}}{{\partial z}}} \right) \end{array} $ | (12) |
| $ \begin{array}{l} \frac{{{\partial ^3}{u_{i,j}}}}{{\partial {x^2}\partial z}} = \frac{1}{{864{h^3}}}\left( {31{u_{i + 2,j + 2}} - 62{u_{i,j + 2}} + 31{u_{i - 2,j + 2}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;1408{u_{i + 1,j + 1}} - 2816{u_{i,j + 1}} + 1408{u_{i - 1,j + 1}} - \\ \;\;\;\;\;\;\;\;\;\;1408{u_{i + 1,j - 1}} + 2816{u_{i,j - 1}} - 1408{u_{i - 1,j - 1}} - \\ \;\;\;\;\;\;\;\;\;\;\left. {31{u_{i + 2,j - 2}} + 62{u_{i,j - 2}} - 31{u_{i - 2,j - 2}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{{144{h^2}}}\left( {\frac{{ - \partial {u_{i + 2,j + 2}}}}{{\partial x}} + \frac{{\partial {u_{i - 2,j + 2}}}}{{\partial x}} - 64\frac{{\partial {u_{i + 1,j + 1}}}}{{\partial x}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;64\frac{{\partial {u_{i - 1,j + 1}}}}{{\partial x}} + 64\frac{{\partial {u_{i + 1,j - 1}}}}{{\partial x}} - 64\frac{{\partial {u_{i - 1,j - 1}}}}{{\partial x}} + \\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{{\partial {u_{i + 2,j - 2}}}}{{\partial x}} - \frac{{\partial {u_{i - 2,j - 2}}}}{{\partial x}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{{144{h^2}}}\left( {\frac{{ - \partial {u_{i + 2,j + 2}}}}{{\partial z}} + 2\frac{{\partial {u_{i,j + 2}}}}{{\partial z}} - \frac{{\partial {u_{i - 2,j + 2}}}}{{\partial z}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;64\frac{{\partial {u_{i + 1,j + 1}}}}{{\partial z}} + 128\frac{{\partial {u_{i,j + 1}}}}{{\partial z}} - 64\frac{{\partial {u_{i - 1,j + 1}}}}{{\partial z}} - \\ \;\;\;\;\;\;\;\;\;\;64\frac{{\partial {u_{i + 1,j - 1}}}}{{\partial z}} + 128\frac{{\partial {u_{i,j - 1}}}}{{\partial z}} - 64\frac{{\partial {u_{i - 1,j - 1}}}}{{\partial z}} - \\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{{\partial {u_{i + 2,j - 2}}}}{{\partial z}} + 2\frac{{\partial {u_{i,j - 2}}}}{{\partial z}} - \frac{{\partial {u_{i - 2,j - 2}}}}{{\partial z}}} \right) \end{array} $ | (13) |
式中h表示空间离散步长。将离散结果依次代入式(5),并写成统一线性方程形式
| $ \begin{array}{l} {\mathit{\boldsymbol{T}}_1}{{\mathit{\boldsymbol{\tilde u}}}_{i - 2,j - 2}} + {\mathit{\boldsymbol{T}}_3}{{\mathit{\boldsymbol{\tilde u}}}_{i,j - 2}} + {\mathit{\boldsymbol{T}}_5}{{\mathit{\boldsymbol{\tilde u}}}_{i + 2,j - 2}} + {\mathit{\boldsymbol{T}}_7}{{\mathit{\boldsymbol{\tilde u}}}_{i - 1,j - 1}} + \\ {\mathit{\boldsymbol{T}}_8}{{\mathit{\boldsymbol{\tilde u}}}_{i,j - 1}} + {\mathit{\boldsymbol{T}}_9}{{\mathit{\boldsymbol{\tilde u}}}_{i + 1,j - 1}} + {\mathit{\boldsymbol{T}}_{11}}{{\mathit{\boldsymbol{\tilde u}}}_{i - 2,j}} + {\mathit{\boldsymbol{T}}_{12}}{{\mathit{\boldsymbol{\tilde u}}}_{i - 1,j}} + {\mathit{\boldsymbol{T}}_{13}}{{\mathit{\boldsymbol{\tilde u}}}_{i,j}} + \\ {\mathit{\boldsymbol{T}}_{14}}{{\mathit{\boldsymbol{\tilde u}}}_{i + 1,j}} + {\mathit{\boldsymbol{T}}_{15}}{{\mathit{\boldsymbol{\tilde u}}}_{i + 2,j}} + {\mathit{\boldsymbol{T}}_{17}}{{\mathit{\boldsymbol{\tilde u}}}_{i - 1,j + 1}} + {\mathit{\boldsymbol{T}}_{18}}{{\mathit{\boldsymbol{\tilde u}}}_{i - 1,j + 2}} + \\ {\mathit{\boldsymbol{T}}_{19}}{{\mathit{\boldsymbol{\tilde u}}}_{i + 1,j + 1}} + {\mathit{\boldsymbol{T}}_{21}}{{\mathit{\boldsymbol{\tilde u}}}_{i - 2,j + 2}} + {\mathit{\boldsymbol{T}}_{23}}{{\mathit{\boldsymbol{\tilde u}}}_{i,j + 2}} + {\mathit{\boldsymbol{T}}_{25}}{{\mathit{\boldsymbol{\tilde u}}}_{i + 2,j + 2}} = \tilde b \end{array} $ | (14) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\alpha }}_3} = \left( {\frac{7}{{54t_z^2}},0,\frac{h}{{36t_z^2}}} \right)}\\ {{\mathit{\boldsymbol{\alpha }}_8} = \left( {\frac{{64}}{{27t_z^2}},0,\frac{{8h}}{{9t_z^2}}} \right)}\\ {{\mathit{\boldsymbol{\alpha }}_{11}} = \left( {\frac{7}{{54t_x^2}},\frac{h}{{36t_x^2}},0} \right)} \end{array}} \right. $ | (15a) |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\alpha }}_{12}} = \left( {\frac{{64}}{{27t_x^2}},\frac{{8h}}{{9t_x^2}},0} \right)\\ {\mathit{\boldsymbol{\alpha }}_{13}} = \left( { - \frac{5}{{t_x^2}} - \frac{5}{{t_z^2}} + \frac{{{\omega ^2}{h^2}}}{{{c^2}}},\frac{{{\rm{i}}{{d'}_x}{h^2}}}{{\omega t_x^3}},\frac{{{\rm{i}}{{d'}_z}{h^2}}}{{\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\alpha }}_{14}} = \left( {\frac{{64}}{{27t_x^2}},\frac{{ - 8h}}{{9t_x^2}},0} \right)\\ {\mathit{\boldsymbol{\alpha }}_{15}} = \left( {\frac{7}{{54t_x^2}},\frac{{ - h}}{{36t_x^2}},0} \right)\\ {\mathit{\boldsymbol{\alpha }}_{18}} = \left( {\frac{{64}}{{27t_z^2}},0,\frac{{ - 8h}}{{9t_z^2}}} \right)\\ {\mathit{\boldsymbol{\alpha }}_{23}} = \left( {\frac{7}{{54t_z^2}},0,\frac{{ - h}}{{36t_z^2}}} \right)\\ {\mathit{\boldsymbol{\alpha }}_{1,5,7,9,17,19,21,25}} = O\left( {1 \times 3} \right) \end{array} \right. $ | (15b) |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\beta }}_1} = \left( {\frac{{ - 31}}{{864t_z^2}} + \frac{{7{\rm{i}}{{d'}_z}h}}{{216\omega t_z^3}},\frac{{ - h}}{{144t_z^2}} + \frac{{{\rm{i}}{{d'}_z}{h^2}}}{{144\omega t_z^3}},} \right.\\ \;\;\;\;\;\;\;\left. {\frac{{ - h}}{{144t_z^2}} + \frac{{{\rm{i}}{{d'}_z}{h^2}}}{{144\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\beta }}_5} = \left( {\frac{{31}}{{864t_z^2}} - \frac{{7{\rm{i}}{{d'}_z}h}}{{216\omega t_z^3}},\frac{{ - h}}{{144t_z^2}} + \frac{{{\rm{i}}{{d'}_z}{h^2}}}{{144\omega t_z^3}},} \right.\\ \;\;\;\;\;\;\left. {\frac{h}{{144t_z^2}} - \frac{{{\rm{i}}{{d'}_z}{h^2}}}{{144\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\beta }}_7} = \left( {\frac{{ - 44}}{{27t_z^2}} - \frac{{16{\rm{i}}{{d'}_z}h}}{{27\omega t_z^3}},\frac{{ - 4h}}{{9t_z^2}} + \frac{{{\rm{2i}}{{d'}_z}{h^2}}}{{9\omega t_z^3}},} \right.\\ \;\;\;\;\;\;\left. {\frac{{ - 4h}}{{9t_z^2}} - \frac{{{\rm{2i}}{{d'}_z}{h^2}}}{{9\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\beta }}_9} = \left( {\frac{{44}}{{27t_z^2}} - \frac{{16{\rm{i}}{{d'}_z}h}}{{27\omega t_z^3}},\frac{{ - 4h}}{{9t_z^2}} + \frac{{{\rm{2i}}{{d'}_z}{h^2}}}{{9\omega t_z^3}},} \right.\\ \;\;\;\;\;\;\left. {\frac{{4h}}{{9t_z^2}} - \frac{{{\rm{2i}}{{d'}_z}{h^2}}}{{9\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\beta }}_{11}} = \left( {\frac{{ - 31}}{{144t_x^2}} + \frac{{31}}{{432t_z^2}} + \frac{{7{\rm{i}}{{d'}_x}h}}{{18\omega t_x^3}},} \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{{ - h}}{{24t_x^2}} + \frac{h}{{72t_z^2}} + \frac{{{\rm{i}}{{d'}_x}{h^2}}}{{12\omega t_x^3}},0} \right)\\ {\mathit{\boldsymbol{\beta }}_{12}} = \left( {\frac{{ - 88}}{{9t_x^2}} + \frac{{88}}{{27t_z^2}} + \frac{{64{\rm{i}}{{d'}_x}h}}{{9\omega t_x^3}},} \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{{ - 8h}}{{3t_x^2}} + \frac{8}{{9t_z^2}} + \frac{{8{\rm{i}}{{d'}_x}{h^2}}}{{3\omega t_x^3}},0} \right)\\ {\mathit{\boldsymbol{\beta }}_{13}} = \left( {\frac{{ - 15{\rm{i}}{{d'}_x}h}}{{\omega t_x^3}},\frac{{ - 15h}}{{t_x^2}} - \frac{{3d{'}_x^2{h^3}}}{{{\omega ^2}t_x^4}} + } \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{{{\rm{i}}{{d''}_x}{h^3}}}{{\omega t_x^3}} + \frac{{{\omega ^2}{h^3}}}{{{c^2}}},0} \right)\\ {\mathit{\boldsymbol{\beta }}_{14}} = \left( {\frac{{88}}{{9t_x^2}} - \frac{{88}}{{27t_z^2}} + \frac{{64{\rm{i}}{{d'}_x}h}}{{9\omega t_x^3}},} \right.\\ \;\;\;\;\;\;\;\left. {\frac{{ - 8h}}{{3t_x^2}} + \frac{{8h}}{{9t_z^2}} - \frac{{8{\rm{i}}{{d'}_x}{h^2}}}{{3\omega t_x^3}},0} \right) \end{array} \right. $ | (16a) |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\beta }}_{15}} = \left( {\frac{{31}}{{144t_x^2}} - \frac{{31}}{{432t_z^2}} + \frac{{7{\rm{i}}{{d'}_x}h}}{{18\omega t_x^3}},} \right.\\ \;\;\;\;\;\;\left. {\frac{{ - h}}{{24t_x^2}} + \frac{h}{{72t_z^2}} - \frac{{{\rm{i}}{{d'}_x}{h^2}}}{{12\omega t_x^3}},0} \right)\\ {\mathit{\boldsymbol{\beta }}_{17}} = \left( {\frac{{ - 44}}{{27t_z^2}} - \frac{{16{\rm{i}}{{d'}_z}h}}{{27\omega t_z^3}},\frac{{ - 4h}}{{9t_z^2}} - \frac{{2{\rm{i}}{{d'}_z}{h^2}}}{{9\omega t_z^3}},} \right.\\ \;\;\;\;\;\;\;\left. {\frac{{4h}}{{9t_z^2}} + \frac{{2{\rm{i}}{{d'}_z}{h^2}}}{{9\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\beta }}_{19}} = \left( {\frac{{44}}{{27t_z^2}} + \frac{{16{\rm{i}}{{d'}_z}h}}{{27\omega t_z^3}},\frac{{ - 4h}}{{9t_z^2}} - \frac{{2{\rm{i}}{{d'}_z}{h^2}}}{{9\omega t_z^3}},} \right.\\ \;\;\;\;\;\;\;\left. {\frac{{ - 4h}}{{9t_z^2}} - \frac{{2{\rm{i}}{{d'}_z}{h^2}}}{{9\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\beta }}_{21}} = \left( {\frac{{ - 31}}{{864t_z^2}} - \frac{{7{\rm{i}}{{d'}_z}h}}{{216\omega t_z^3}},\frac{{ - h}}{{144t_z^2}} - \frac{{{\rm{i}}{{d'}_z}{h^2}}}{{144\omega t_z^3}},} \right.\\ \;\;\;\;\;\;\;\left. {\frac{h}{{144t_z^2}} + \frac{{{\rm{i}}{{d'}_z}{h^2}}}{{144\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\beta }}_{25}} = \left( {\frac{{31}}{{864t_z^2}} + \frac{{7{\rm{i}}{{d'}_z}h}}{{216\omega t_z^3}},\frac{{ - h}}{{144t_z^2}} - \frac{{{\rm{i}}{{d'}_z}{h^2}}}{{144\omega t_z^3}},} \right.\\ \;\;\;\;\;\;\;\left. {\frac{{ - h}}{{144t_z^2}} - \frac{{{\rm{i}}{{d'}_z}{h^2}}}{{144\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\beta }}_{3,8,18,23}} = O\left( {1 \times 3} \right) \end{array} \right. $ | (16b) |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\gamma }}_1} = \left( {\frac{{ - 31}}{{864t_x^2}} + \frac{{7{\rm{i}}{{d'}_x}h}}{{216\omega t_x^3}},\frac{{ - h}}{{144t_x^2}} + \frac{{{\rm{i}}{{d'}_x}{h^2}}}{{144\omega t_x^3}},} \right.\\ \;\;\;\;\;\;\;\left. {\frac{{ - h}}{{144t_x^2}} + \frac{{{\rm{i}}{{d'}_x}{h^2}}}{{144\omega t_x^3}}} \right)\\ {\mathit{\boldsymbol{\gamma }}_3} = \left( {\frac{{ - 31}}{{144t_z^2}} + \frac{{31}}{{432t_x^2}} + \frac{{7{\rm{i}}{{d'}_z}h}}{{18\omega t_z^3}},0,} \right.\\ \;\;\;\;\;\;\left. {\frac{{ - h}}{{24t_z^2}} + \frac{h}{{72t_x^2}} + \frac{{{\rm{i}}{{d'}_z}{h^2}}}{{12\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\gamma }}_5} = \left( {\frac{{ - 31}}{{864t_x^2}} - \frac{{7{\rm{i}}{{d'}_x}h}}{{216\omega t_x^3}},\frac{h}{{144t_x^2}} + \frac{{{\rm{i}}{{d'}_x}{h^2}}}{{144\omega t_x^3}},} \right.\\ \;\;\;\;\;\;\;\left. {\frac{{ - h}}{{144t_x^2}} - \frac{{{\rm{i}}{{d'}_x}{h^2}}}{{144\omega t_x^3}}} \right)\\ {\mathit{\boldsymbol{\gamma }}_7} = \left( {\frac{{ - 44}}{{27t_x^2}} + \frac{{16{\rm{i}}{{d'}_x}h}}{{27\omega t_x^3}},\frac{{ - 4h}}{{9t_x^2}} + \frac{{2{\rm{i}}{{d'}_x}{h^2}}}{{9\omega t_x^3}},} \right.\\ \;\;\;\;\;\;\left. {\frac{{ - 4h}}{{9t_x^2}} + \frac{{2{\rm{i}}{{d'}_x}{h^2}}}{{9\omega t_x^3}}} \right)\\ {\mathit{\boldsymbol{\gamma }}_8} = \left( {\frac{{ - 88}}{{9t_z^2}} + \frac{{88}}{{27t_x^2}} + \frac{{64{\rm{i}}{{d'}_z}h}}{{9\omega t_z^3}},0,} \right.\\ \;\;\;\;\;\left. {\frac{{ - 8h}}{{3t_z^2}} + \frac{{8h}}{{9t_x^2}} + \frac{{8{\rm{i}}{{d'}_z}{h^2}}}{{3\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\gamma }}_9} = \left( {\frac{{ - 44}}{{27t_x^2}} - \frac{{16{\rm{i}}{{d'}_x}h}}{{27\omega t_x^3}},\frac{{4h}}{{9t_x^2}} + \frac{{2{\rm{i}}{{d'}_x}{h^2}}}{{9\omega t_x^3}},} \right.\\ \;\;\;\;\;\;\left. {\frac{{ - 4h}}{{9t_x^2}} - \frac{{2{\rm{i}}{{d'}_x}{h^2}}}{{9\omega t_x^3}}} \right) \end{array} \right. $ | (17a) |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\gamma }}_{13}} = \left( {\frac{{ - 15{\rm{i}}{{d'}_z}h}}{{\omega t_z^3}},0,\frac{{ - 15h}}{{t_z^2}} - \frac{{3d_z^{\prime 2}{h^3}}}{{{\omega ^2}t_z^4}} + } \right.\\ \;\;\;\;\;\;\;\left. {\frac{{{\rm{i}}d_z^{\prime \prime }{h^3}}}{{\omega t_z^3}} + \frac{{{\omega ^2}{h^3}}}{{{c^2}}}} \right)\\ {\mathit{\boldsymbol{\gamma }}_{17}} = \left( {\frac{{44}}{{27t_x^2}} - \frac{{16{\rm{i}}{{d'}_x}h}}{{27\omega t_x^3}},\frac{{4h}}{{9t_x^2}} - \frac{{2{\rm{i}}{{d'}_x}{h^2}}}{{9\omega t_x^3}},} \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{{ - 4h}}{{9t_x^2}} + \frac{{2{\rm{i}}{{d'}_x}{h^2}}}{{9\omega t_x^3}}} \right)\\ {\mathit{\boldsymbol{\gamma }}_{18}} = \left( {\frac{{88}}{{9t_z^2}} - \frac{{88}}{{27t_x^2}} + \frac{{64{\rm{i}}{{d'}_z}h}}{{9\omega t_z^3}},0,} \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{{ - 8h}}{{3t_z^2}} + \frac{{8h}}{{9t_x^2}} - \frac{{8{\rm{i}}{{d'}_z}{h^2}}}{{3\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\gamma }}_{19}} = \left( {\frac{{44}}{{27t_x^2}} + \frac{{16{\rm{i}}{{d'}_x}h}}{{27\omega t_x^3}},\frac{{ - 4h}}{{9t_x^2}} - \frac{{2{\rm{i}}{{d'}_x}{h^2}}}{{9\omega t_x^3}},} \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{{ - 4h}}{{9t_x^2}} + \frac{{2{\rm{i}}{{d'}_x}{h^2}}}{{9\omega t_x^3}}} \right)\\ {\mathit{\boldsymbol{\gamma }}_{21}} = \left( {\frac{{31}}{{864t_x^2}} - \frac{{7{\rm{i}}{{d'}_x}h}}{{216\omega t_x^3}},\frac{h}{{144t_x^2}} - \frac{{{\rm{i}}{{d'}_x}{h^2}}}{{144\omega t_x^3}},} \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{{ - h}}{{144t_x^2}} + \frac{{{\rm{i}}{{d'}_x}{h^2}}}{{144\omega t_x^3}}} \right)\\ {\mathit{\boldsymbol{\gamma }}_{23}} = \left( {\frac{{31}}{{144t_z^2}} - \frac{{31}}{{432t_x^2}} + \frac{{7{\rm{i}}{{d'}_z}h}}{{18\omega t_z^3}},0,} \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{{ - h}}{{24t_z^2}} + \frac{h}{{72t_x^2}} - \frac{{{\rm{i}}{{d'}_z}{h^2}}}{{12\omega t_z^3}}} \right)\\ {\mathit{\boldsymbol{\gamma }}_{25}} = \left( {\frac{{31}}{{864t_x^2}} + \frac{{7{\rm{i}}{{d'}_x}h}}{{216\omega t_x^3}},\frac{{ - h}}{{144t_x^2}} - \frac{{{\rm{i}}{{d'}_x}{h^2}}}{{144\omega t_x^3}},} \right.\\ \;\;\;\;\;\;\;\left. {\frac{{ - h}}{{144t_x^2}} - \frac{{{\rm{i}}{{d'}_x}{h^2}}}{{144\omega t_x^3}}} \right)\\ {\mathit{\boldsymbol{\gamma }}_{11,12,14,15}} = O\left( {1 \times 3} \right) \end{array} \right. $ | (17b) |
由式(14)的离散结果发现,NAD8差分格式共涉及周围17个节点,显然算子长度小于同阶精度的其他格式[25],具体差分模板如图 1所示。

|
图 1 NAD8差分网格模板 |
设nx和nz分别代表水平方向与垂直方向的网格点数,N=(nx-2)(nz-2)是整个正演问题的规模,离散后的波动方程可表示为
为快速有效求解离散后的大型稀疏线性方程组,本文采用一类不精确旋转分块三角(IRBT)预处理算子加速广义极小残量方法(GMRES)。该方法是一种专门用于非对称线性方程组求解的Krylov子空间方法,充分利用了系数矩阵T的稀疏结构,结合不精确预处理的思想,在迭代次数并未显著增加的前提下,可节省较多的运算时间与存储量,从而能明显提高计算效率[23]。
2 正演计算从数值频散分析和波场模拟两方面考查NAD8方法相对于NAD6和常规八阶有限差分方法的模拟效率。震源选取雷克(Ricker)子波,根据Fourier变换的性质,其频率域表达式[9]为
| $ F\left[ {w\left( t \right)} \right] = \frac{{\sqrt 2 A}}{{{\rm{ \mathsf{ π} }}{f_0}}}{\left( {\frac{f}{{{f_0}}}} \right)^2}\exp \left[ { - {{\left( {\frac{f}{{{f_0}}}} \right)}^2}} \right] $ | (18) |
式中:A表示振幅,波场模拟时统一设置为1;f0是主频。根据频谱分析[8],主要能量分布在0~3f0。定义网格频率(Gf)为每个波长包含的离散网格点数,以度量网格剖分的大小[26],其计算公式为
| $ {G_{\rm{f}}} = \frac{w}{h} = \frac{c}{{2.5{f_0}h}} $ | (19) |
式中w表示波长。从式(19)可以看出,对于同一计算区域,Gf越大,每个波长内网格点数目会越多,从而计算精度越高,但是相应地增大了计算量。
2.1 理论频散曲线分析首先从理论上论证各种数值方法在压制数值频散方面的能力。基本思想为:通过计算数值速度与实际波速的偏差考察各种离散方法的准确性,偏差越小说明频散越小。
为计算NAD方法的数值速度,首先引入均匀介质中的波动方程及其关于x、z方向的偏导
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}} + \frac{{{\omega ^2}}}{{{c^2}}}u = 0}\\ {\frac{{{\partial ^2}{u_x}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u_x}}}{{\partial {z^2}}} + \frac{{{\omega ^2}}}{{{c^2}}}{u_x} = 0}\\ {\frac{{{\partial ^2}{u_z}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u_z}}}{{\partial {z^2}}} + \frac{{{\omega ^2}}}{{{c^2}}}{u_z} = 0} \end{array}} \right. $ | (20) |
与式(5)的离散过程类似,通过NAD方法可将式(20)离散为矩阵形式
| $ \left( {\begin{array}{*{20}{c}} 1&{}&{}\\ {}&{\frac{1}{h}}&{}\\ {}&{}&{\frac{1}{h}} \end{array}} \right)\mathit{\boldsymbol{M}}\left( {\begin{array}{*{20}{c}} 1&{}&{}\\ {}&h&{}\\ {}&{}&h \end{array}} \right)\left( {\begin{array}{*{20}{c}} u\\ {{u_x}}\\ {{u_z}} \end{array}} \right) = - \frac{{{\omega ^2}{h^2}}}{{{c^2}}}\left( {\begin{array}{*{20}{c}} u\\ {{u_x}}\\ {{u_z}} \end{array}} \right) $ | (21) |
显然
| $ \left\{ \begin{array}{l} {m_{11}} = - 10 + \frac{{64}}{{27}}\left( {a + {a^{ - 1}} + b + {b^{ - 1}}} \right) + \\ \;\;\;\;\;\;\frac{7}{{54}}\left( {{a^2} + {a^{ - 2}} + {b^2} + {b^{ - 2}}} \right)\\ {m_{12}} = - \frac{8}{9}\left( {{a^{ - 1}} - a} \right) - \frac{1}{{36}}\left( {{a^{ - 2}} - {a^2}} \right)\\ {m_{13}} = - \frac{8}{9}\left( {{b^{ - 1}} - b} \right) - \frac{1}{{36}}\left( {{b^{ - 2}} - {b^2}} \right)\\ {m_{21}} = \frac{{176}}{{27}}\left( {{a^{ - 1}} - a} \right) + \frac{{44}}{{27}}\left( {{a^{ - 1}}{b^{ - 1}} - ab - } \right.\\ \;\;\;\;\;\;\;\;\left. {a{b^{ - 1}} + {a^{ - 1}}b} \right) \end{array} \right. $ | (22a) |
| $ \left\{ \begin{array}{l} {m_{22}} = - \frac{4}{9}\left( {{a^{ - 1}}{b^{ - 1}} + ab + a{b^{ - 1}} + {a^{ - 1}}b} \right) - \\ \;\;\;\;\;\;\;\;\frac{{16}}{9}\left( {{a^{ - 1}} + a} \right) - 15 - \frac{1}{{36}}\left( {{a^2} + {a^{ - 2}}} \right) - \\ \;\;\;\;\;\;\;\;\frac{1}{{144}}\left( {{a^{ - 2}}{b^{ - 2}} + {a^2}{b^2} + {a^2}{b^{ - 2}} + {a^{ - 2}}{b^2}} \right)\\ {m_{23}} = - \frac{4}{9}\left( {{a^{ - 1}}{b^{ - 1}} + ab - a{b^{ - 1}} - {a^{ - 1}}b} \right) - \\ \;\;\;\;\;\;\;\;\frac{1}{{144}}\left( {{a^{ - 2}}{b^{ - 2}} + {a^2}{b^2} - {a^2}{b^{ - 2}} - {a^{ - 2}}{b^2}} \right)\\ {m_{31}} = \frac{{176}}{{27}}\left( {{b^{ - 1}} - b} \right) + \frac{{44}}{{27}}\left( {{a^{ - 1}}{b^{ - 1}} - ab + a{b^{ - 1}} - } \right.\\ \;\;\;\;\;\;\;\;\left. {{a^{ - 1}}b} \right) + \frac{{31}}{{126}}\left( {{b^{ - 2}} - {b^2}} \right) + \frac{{31}}{{864}}\left( {{a^2}{b^{ - 2}} + } \right.\\ \;\;\;\;\;\;\;\;\left. {{a^2}{b^2} - {a^2}{b^{ - 2}} - {a^{ - 2}}{b^2}} \right)\\ {m_{32}} = - \frac{4}{9}\left( {{a^{ - 1}}{b^{ - 1}} + ab - a{b^{ - 1}} - {a^{ - 1}}b} \right) - \\ \;\;\;\;\;\;\;\;\frac{1}{{144}}\left( {{a^{ - 2}}{b^{ - 2}} + {a^2}{b^2} - {a^2}{b^{ - 2}} - {a^{ - 2}}{b^2}} \right)\\ {m_{33}} = - \frac{4}{9}\left( {{a^{ - 1}}{b^{ - 1}} + ab + a{b^{ - 1}} + {a^{ - 1}}b} \right) - \\ \;\;\;\;\;\;\;\;\frac{{16}}{9}\left( {{b^{ - 1}} + b} \right) - 15 - \frac{1}{{36}}\left( {{b^2} + {b^{ - 2}}} \right) - \\ \;\;\;\;\;\;\;\;\frac{1}{{144}}\left( {{a^{ - 2}}{b^{ - 2}} + {a^2}{b^2} + {a^2}{b^{ - 2}} + {a^{ - 2}}{b^2}} \right) \end{array} \right. $ | (22b) |
式中:a=exp(ikxh);b=exp(ikzh)。
数值速度cn与真实速度c之比

|
图 2 θ=0(a)和θ=π/6(b)时三种数值方法的频散曲线 |
以均匀介质模型(M1)和双层介质模型(M2),进一步讨论NAD8方法的计算精度与数值效率。
M1模型的速度v=4km/s;M2模型的速度v1=4km/s、v2=5km/s,界面位于z=4km处,其他参数设置如表 1所示。
|
|
表 1 M1和M2模型的基本参数 |
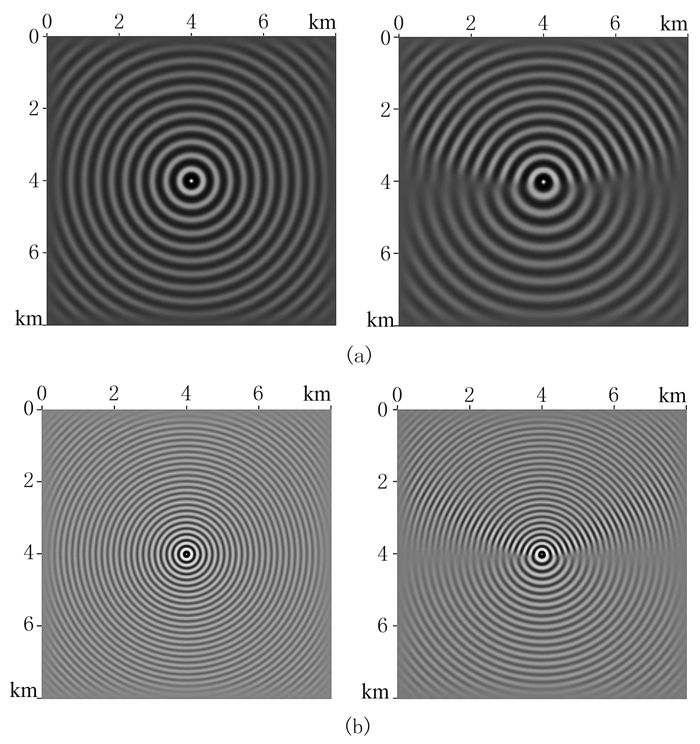
图 3为频率f=10和30Hz时,本文构造的NAD8方法针对以上两种模型得到的频率域单频波波场快照。图 4为NAD8、NAD6和OFD8三种方法模拟的t=0.5s时刻时间域波场快照。从图中可以看出,在相同网格规模的情况下,NAD8方法有效地压制了数值频散,而后两种方法则出现了明显的频散现象,OFD8方法频散最为严重,表明在相同网格频率下,NAD8方法较其他方法精度较高。根据Shannon采样定理[27],为了准确地刻画波场,网格频率至少大于2.0,而NAD8方法突破了这个极限,Gf最小值可到达1.98,这是因为NAD方法除了利用位移信息,还利用了波场梯度信息,大大提高了波场模拟精度,降低了对网格频率的要求。
|
图 3 由八阶NAD方法计算的M1(左)和M2(右)模型频率域单频波波场快照 (a)10Hz;(b)30Hz |

|
图 4 三种方法计算的M1(左)和M2(右)模型t=0.5s时刻的时间域波场快照 (a)NAD8;(b)NAD6;(c)OFD8 |
最后,针对以上两个模型,在不产生数字频散的情况下,统计三种方法运行时间(表 2,10次计算结果的平均),其中NAD8(Gf=1.98)用时最少,比NAD6方法(Gf=2.40)约省时12%,比OFD8方法(Gf=3.50)约省时25%。
|
|
表 2 不同方法简单模型波场模拟运行时间对比 |
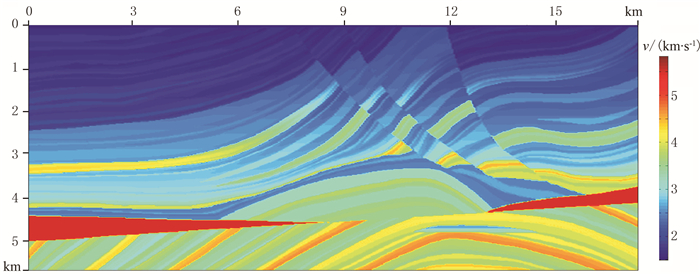
选取经典的Marmousi模型[28](图 5)检验NAD8方法的适用性。模型尺寸为17.25km×5.63km;网格间距h=18.75m,网格频率Gf=3.0;四周均为10层PML边界,震源位于(8.63km,0.38km),主频为20Hz。
|
图 5 Marmousi速度模型 |
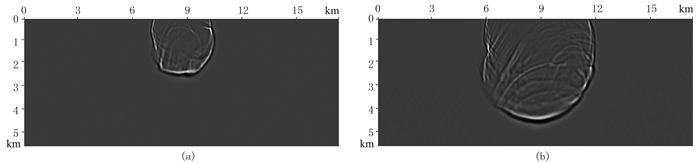
图 6为NAD8方法模拟的频率f=10Hz和15Hz时Marmousi模型的频率域单频波波场快照,图 7为t=1.00、1.67s时刻的时间域波场快照。可以看出,对于复杂的Marmousi模型,没有明显的频散,可见NAD8方法适用于复杂介质模型的正演模拟。

|
图 6 NAD8方法模拟的Marmousi模型单频波波场快照 (a)f=10Hz;(b)f=15Hz |
|
图 7 NAD8方法模拟的Marmousi模型时间域波场快照 (a)t=1.00s;(b)t=1.67s |
所谓反演即从初始模型出发,进行正演模拟,匹配计算波场与真实波场,然后不断修正模型,最终达到特定的精度。本文基于NAD8正演算法对经典模型进行反演,反演采用非线性共轭梯度法,其优势在于:与最速下降法相比,不用引入显著的正演计算量便可以得到更加准确、稳健的计算结果,与牛顿类方法相比,不用计算反演目标函数的二阶偏导数矩阵(Hessian矩阵),收敛性较强。将离散后的频率域声波方程(式(14))改写为
| $ \mathit{\boldsymbol{T}}\left( \omega \right)\mathit{\boldsymbol{u}}\left( \omega \right) = \mathit{\boldsymbol{s}}\left( \omega \right) $ | (23) |
式中:T表示系数矩阵;u表示波场项;s表示震源项,且三者都与角频率ω有关。合成波场与观测波场数据残差的L2范数可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {E\left( \mathit{\boldsymbol{m}} \right) = \frac{1}{2}\sum\limits_{i = 1}^{{n_{\rm{s}}}} {\sum\limits_{j = 1}^{{n_{\rm{r}}}} {{\rm{ \mathsf{ δ} }}{d_{ij}}{\rm{ \mathsf{ δ} }}d_{ij}^*} } }\\ {{\rm{ \mathsf{ δ} }}{d_{ij}} = {u_{ij}} - {d_{ij}}} \end{array}} \right. $ | (24) |
式中:m为模型参数;“*”表示复共轭;ns为炮数;nr为每炮接收点数。δdij表示第i炮的第j个检波点对应的模拟波场值u与观测波场d的残差。选择合适的方法求解E(m)的最小值是问题的关键,基于梯度算法,通过推导计算可得相邻步数之间的迭代基本格式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{m}}^{\left( {k + 1} \right)}} - {\mathit{\boldsymbol{m}}^{\left( k \right)}} = - {r^{\left( k \right)}}{\nabla _\mathit{\boldsymbol{m}}}{E^{\left( k \right)}}}\\ {{\nabla _\mathit{\boldsymbol{m}}}E = \frac{{\partial E}}{{\partial \mathit{\boldsymbol{m}}}} = Re\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}{\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{d}}^ * }} \right)} \end{array}} \right. $ | (25) |
式中:∇mE(k)表示第k步迭代的梯度场;r(k)表示第k步迭代的步长;Re(·)表示取实部;J表示Frechét矩阵,具体元素为
通过对波动方程关于模型参数求偏导,进而可导出
| $ {\nabla _\mathit{\boldsymbol{m}}}E = - {\mathop{\rm Re}\nolimits} \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}^{\rm{T}}}\frac{{\partial {\mathit{\boldsymbol{T}}^{\rm{T}}}}}{{\partial {m_1}}}\mathit{\boldsymbol{v}}}\\ {{\mathit{\boldsymbol{u}}^{\rm{T}}}\frac{{\partial {\mathit{\boldsymbol{T}}^{\rm{T}}}}}{{\partial {m_2}}}\mathit{\boldsymbol{v}}}\\ \vdots \\ {{\mathit{\boldsymbol{u}}^{\rm{T}}}\frac{{\partial {\mathit{\boldsymbol{T}}^{\rm{T}}}}}{{\partial {m_l}}}\mathit{\boldsymbol{v}}} \end{array}} \right) $ | (26) |
式中v表示残差反传波场。可见计算反演目标函数梯度时候,不需要计算矩阵J的具体表达式,整个问题只需计算TTv=δd*。复杂的矩阵计算可以变成简单的求解一次线性方程组的问题,大大降低了计算量。
通过以上过程计算出梯度之后,进而可以确定搜索方向。本文选用计算效率较高的抛物线拟合方法选择步长,即近似认为目标函数是关于步长的二次函数,确定一个试探步长r1,使其满足在目标函数的下降方向上,不断重复搜索步骤,直到目标函数不降反增,确定另一步长r2;结合初始步长r0,三点确定抛物线,求取极值点便为搜索步长。最后,反演频率的选择参照非等距频率选择策略[29],这样频率间距随着频率的增加变得越来越大,从而整体上越来越松散,但不损失反演结果的分辨率,使用更少的频率参与反演,可节省计算时间。
此外,定义标准化残差的概念来衡量反演误差的大小,即
| $ \kappa = \frac{{{{\left\| {\mathit{\boldsymbol{u}}\left( {{\mathit{\boldsymbol{m}}_k}} \right) - \mathit{\boldsymbol{u}}\left( {{\mathit{\boldsymbol{m}}_{\rm{t}}}} \right)} \right\|}_2}}}{{{{\left\| {\mathit{\boldsymbol{u}}\left( {{\mathit{\boldsymbol{m}}_0}} \right) - \mathit{\boldsymbol{u}}\left( {{\mathit{\boldsymbol{m}}_{\rm{t}}}} \right)} \right\|}_2}}} $ | (27) |
式中:mt表示真实模型;‖·‖2表示L2范数。显然给定某一频率,κ是一个随迭代步数变化的曲线,曲线越趋近于0表示反演结果越好。
3.2 简单模型反演基于NAD8方法的正演程序,依据上文所述的频率域反演原理,首先对两个简单的速度模型进行反演与分析。
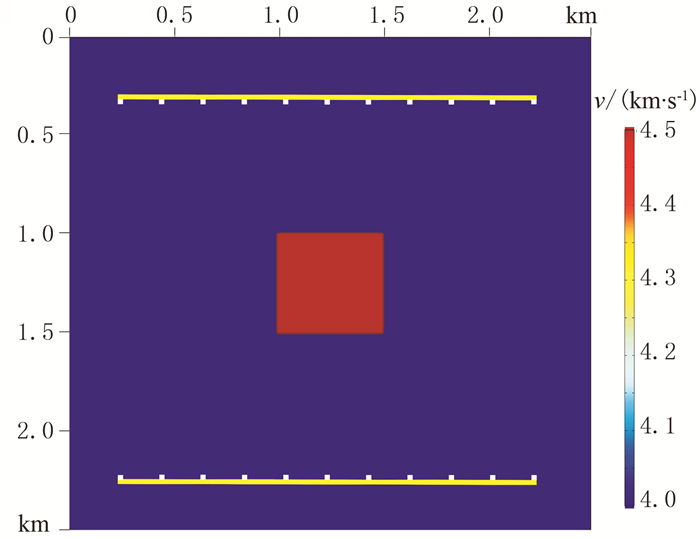
模型一(图 8)参数设置如下:模型尺寸为2.5km×2.5km,背景速度为4.0km/s,中央有一速度为4.5km/s、边长为0.5km的异常体,网格间距h=25m;将四周设置为10层PML边界,主频设置为10Hz,震源振幅为1.0×105(为了避免波场值太小而引起的机器出错),初始速度设置为4.0km/s。炮点与接收点布设两组,位于计算区域内。在频率域接收点的多少并不会增大反演的计算量,而震源数目的增多会使计算量成倍增大。为保证计算效率,需要选择适量的震源数目,而尽量多布设接收点,横向间距为一个网格距离。为了得到深部更高分辨率的成像结果,分别设置两排震源和接收器,设置震源数目为上、下各11个,共计22个,纵向上分别位于0.275km和2.225km处,横向上为0.25~2.25km,间距为0.2km。上、下接收点同时接收传播信号。
|
图 8 速度模型一及震源与接收点布设示意图 |
首先选取5个频率(1、7、13、19、25Hz),低频勾勒大致轮廓,高频细化内部结构,每个频率的最大迭代步数为30步,将反演过程记为S1,最终f=25Hz的反演结果如图 9a所示。可以看出反演的速度模型与理论模型整体轮廓基本一致,但是分辨率相对较低,特别在靠近速度异常体周边的数值与理论值差异较大。进一步加密震源,每行放置21个,即2×21个,增加反演频数到30个(1~30Hz,间隔1Hz),每个频率最大的迭代步数为50,将反演过程记为S2,最终f=30Hz的反演结果如图 9b所示。与图 9a相比,图 9b的分辨率明显提高,细节刻画更清晰,对异常体的刻画更准确。

|
图 9 模型一反演结果 (a)S1;(b)S2 |
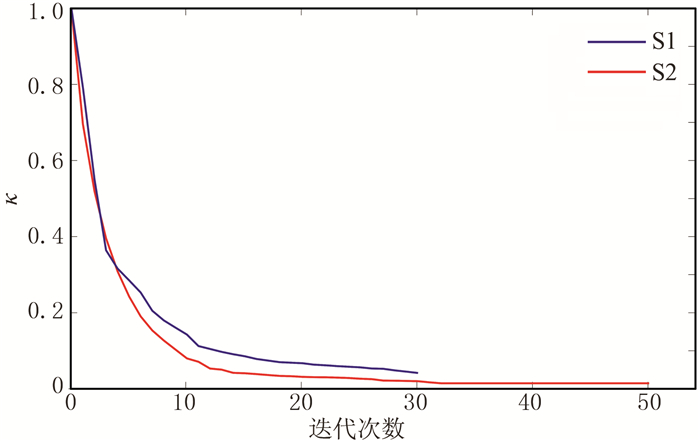
图 10中蓝色曲线是频率取25Hz时S1反演的误差曲线,可以看出,当步数到达最终30时,误差曲线还有下降趋势;红色曲线为频率取25Hz时S2反演的误差曲线,表现为前几步急剧下降,后期逐步平缓,停滞在小于0.1范围内且基本不再下降,1~30Hz中其他频率的误差曲线类似。
|
图 10 模型一反演误差曲线 |
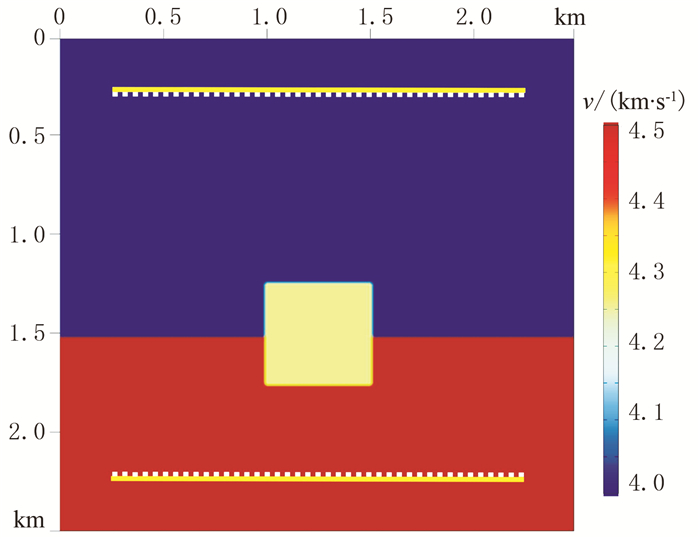
模型二(图 11)为双层模型,尺寸为2.5km×2.5km,上层速度为4.00km/s,下层速度为4.50km/s在分界面处有一速度为4.25km/s、边长为0.5km的异常体,网格间距为h=25m。将四周设置10层的PML边界,震源主频设为10Hz,震源振幅设置为1.0×105。反演的初始速度设置为4.00km/s。接收器尽可能多的放置,间距为一个网格距离,震源数目为上、下各布设41个,共计82个,纵向上分别位于0.275km和2.225km处,横向上从0.25km到2.25km,间距为0.05km。上、下接收点同时接收传播信号。
|
图 11 速度模型二及震源与接收器布设示意图 |
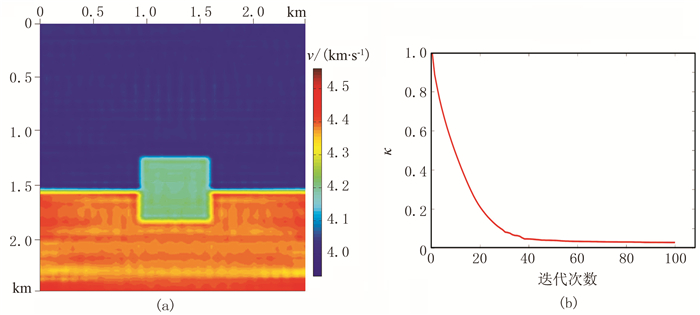
设置反演频数为30个(1~30Hz,间隔为1Hz),每个频点的最大迭代次数为100。图 12a为f=30Hz的反演结果,可以看出,整体分辨率较高,细节刻画清晰,特别是在速度分界面与异常体的形态反映较为真实,整体效果较为理想;图 12b为f=30Hz的反演误差曲线,开始时下降明显,40次后稳定在0.1以内,符合高精度反演的误差曲线形态。可见,本文的基于NAD8的频率域反演方法对于简单的模型一和模型二取得了较为理想的结果。
|
图 12 模型二反演结果(a)及反演误差曲线(b) |
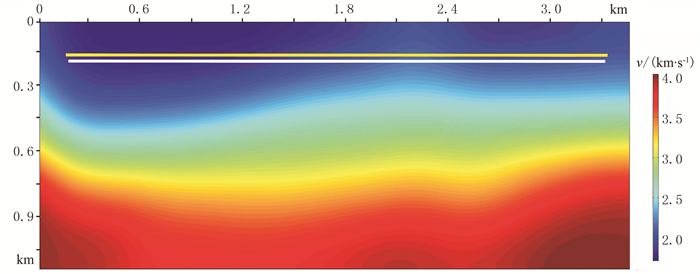
针对Marmousi模型(图 5)的反演,参数设置如下:网格间距h=15m,反演区域为3.47km×1.14km,PML层数为10,主频设置为10Hz,震源振幅设为1.0×105。初始模型(图 13)是对真实模型进行Gauss平滑后的结果,只具有大致的分层结构。震源布设44个,纵向上位于0.17km处,横向上从0.15km到3.35km,间距为0.075km。仅在地表放置一排。接收器排列与震源的间隔相同,纵向位置上位于0.15km处,横向上往外多扩了两个网格距离。
|
图 13 初始Marmousi速度模型及震源与接收点布设示意图 |
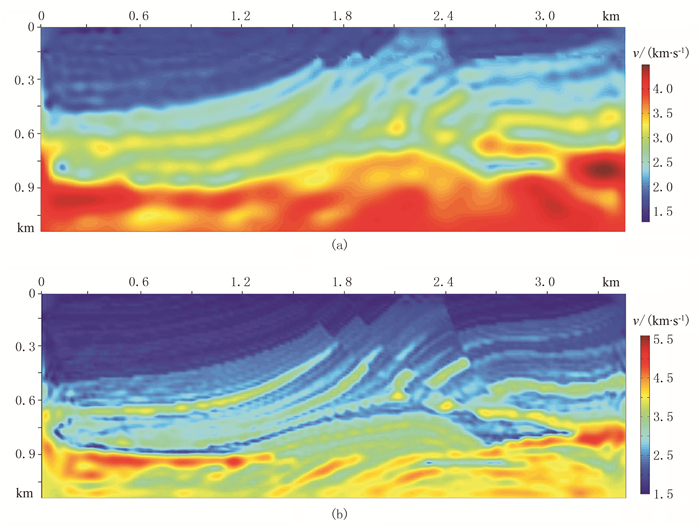
选择30个频点(1~30Hz,间隔为1Hz)、每个频点迭代200次进行反演,图 14为10和30Hz的反演结果。由图可以看出,10Hz低频反演结果基本给出了模型的大体轮廓,但是整体分辨率较低,出现了多处异常亮点,特别是深部高速异常体的精度较低。30Hz反演结果分辨率明显提高、细节更加清晰,特别是深部高速异常体的刻画更加精确。
|
图 14 Marmousi模型10(a)和30Hz(b)的速度反演结果 |
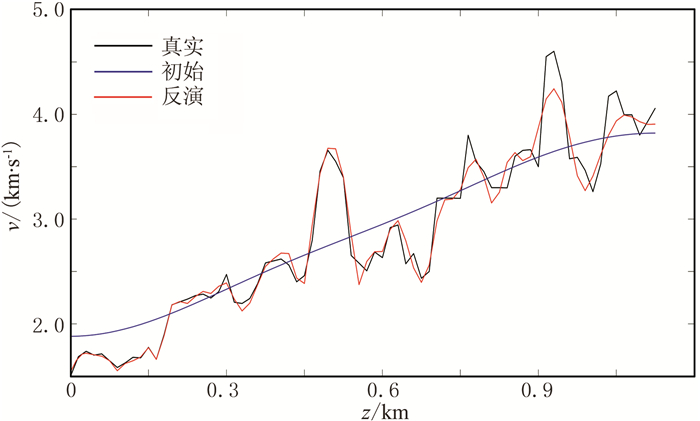
图 15是x=2.0km处、频率为30Hz的速度反演曲线与真实、初始速度曲线的对比,可以看出,整体的反演结果较为理想,特别是浅部低速体保真度较高,但是深层精度略有下降,导致反演速度与真实模型速度之差的L2范数略高(约为0.8),这是因为震源位于地表处,波传播到深层时振幅降低、误差累积,从而分辨率下降。
|
图 15 x=2.0km处反演曲线与真实模型、初始模型的对比 |
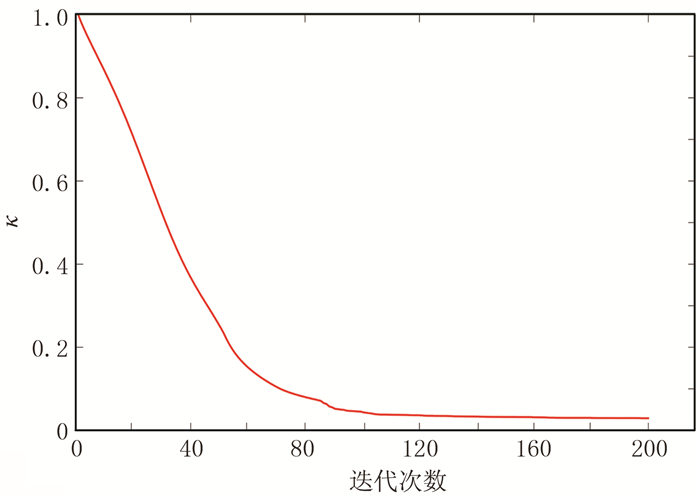
图 16为频率为30Hz的反演误差曲线,可以看出,整体上一开始下降明显,并逐渐稳定在0.1以内,反演效果较好,其他频率反演误差曲线基本相似。可见,基于NAD8的频率域全波形反演方法针对复杂模型依然适用,且分辨率、保真度都较高,效果良好。
|
图 16 Marmousi模型反演误差曲线 |
为进一步提高频率域全波形反演的计算效率,本文首次构造了频率域NAD8差分格式离散波动方程,给出了PML边界条件与频率域NAD方法相结合的正演算法,并详细推导总结了整个数值离散过程,得到了大型线性代数方程组,根据方程组系数矩阵的数学结构,采用一类不精确旋转分块三角预处理算子加速Krylov迭代方法,提高了正演计算效率。数值频散分析以及均匀介质和双层介质模型的波场模拟结果表明:①与OFD8方法、NAD6方法相比,NAD8方法计算精度最高,在压制频散方面效果最明显;②在有效压制频散的情况下,NAD8方法所需网格频率最小(Gf=1.98),突破了Shannon采样定理可达到的理论最小值(Gf=2.0),所用的计算时间最短,大约比NAD6方法(Gf=2.4)省时12%,比OFD8方法(Gf=3.5)省时25%。
对于两种典型的分层介质模型及经典Mar-mousi模型,本文基于NAD8格式的频率域全波形反演算法获得了较高分辨率和保真度的结果,结合反演误差曲线验证了方法的正确性和适用性。
| [1] |
Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [2] |
Mora P. Nonlinear two-dimensional elastic inversion of multi offset seismic data[J]. Geophysics, 1987, 52(9): 1211-1228. DOI:10.1190/1.1442384 |
| [3] |
Pratt R G. Frequency-domain elastic wave modeling by finite differences:A tool for crosshole seismic imaging[J]. Geophysics, 1990, 55(5): 626-632. DOI:10.1190/1.1442874 |
| [4] |
Pratt R G. Inverse theory applied to multi-source cross-hole tomography[J]. Geophysical Prospecting, 1990, 38(3): 311-329. DOI:10.1111/j.1365-2478.1990.tb01847.x |
| [5] |
Liu S L, Li X F, Wang W S, et al. A modified symplectic scheme for seismic wave modeling[J]. Journal of Applied Geophysics, 2017, 99: 28-36. |
| [6] |
Liu S L, Li X F, Wang W S, et al. A new kind of optimal second-order symplectic scheme for seismic wave simulations[J]. Science China:Earth Sciences, 2014, 57(4): 751-758. DOI:10.1007/s11430-013-4805-0 |
| [7] |
廖建平, 刘和秀, 戴世鑫, 等. 二维时间空间域和频率空间域声波全波形速度反演方法的对比研究[J]. 地球物理学进展, 2017, 32(5): 2029-2034. LIAO Jianping, LIU Hexiu, DAI Shixin, et al. Research on comparisons of 2D acoustic wave full waveform velocity inversion in time-space domain and frequency-space domain[J]. Progress in Geophysics, 2017, 32(5): 2029-2034. |
| [8] |
Lang C, Yang D H. A nearly analytic discrete method for solving the acoustic-wave equations in the frequency domain[J]. Geophysics, 2016, 82(1): T43-T57. |
| [9] |
张广智, 孙昌路, 潘新朋, 等. 快速共轭梯度法频率域声波全波形反演[J]. 石油地球物理勘探, 2016, 51(4): 730-737. ZHANG Guangzhi, SUN Changlu, PAN Xinpeng, et al. Acoustic full waveform inversion in the frequency domain based on fast conjugate gradient method[J]. Oil Geophysical Prospecting, 2016, 51(4): 730-737. |
| [10] |
王毓玮, 董良国, 黄超, 等. 降低弹性波全波形反演强烈非线性的分步反演策略[J]. 石油地球物理勘探, 2016, 51(2): 288-294. WANG Yuwei, DONG Liangguo, HUANG Chao, et al. A multi-step strategy for mitigating severe nonli-nearity in elastic full-waveform inversion[J]. Oil Geophysical Prospecting, 2016, 51(2): 288-294. |
| [11] |
Liu S L, Yang D H, Ma J. A modified symplectic PRK scheme for seismic wave modeling[J]. Computers and Geosciences, 2017, 99: 28-36. DOI:10.1016/j.cageo.2016.11.001 |
| [12] |
张文生, 庄源. 频率域声波方程全波形反演[J]. 数值计算与计算机应用, 2017, 38(3): 167-196. ZHANG Wensheng, ZHUANG Yuan. Full-waveform inversion based on the acoustic wave equation in the frequency[J]. Journal on Numerical Methods and Computer Applications, 2017, 38(3): 167-196. |
| [13] |
Alterman Z S. Finite difference solutions to geophysical problems[J]. Journal of Physics of the Earth, 1968, 16(Special): 113-128. DOI:10.4294/jpe1952.16.Special_113 |
| [14] |
姚振岸, 孙成禹, 唐杰, 等. 基于不同震源机制的黏弹各向异性微地震波场模拟[J]. 石油地球物理勘探, 2017, 52(1): 63-70. YAO Zhen'an, SUN Chengyu, TANG Jie, et al. Micro-seismic forward modeling in viscoelastic anisotropic media based on different focal mechanisms[J]. Oil Geo-physical Prospecting, 2017, 52(1): 63-70. |
| [15] |
Lysmer J, Drake L A. A finite element method for seismology[J]. Methods of Computational Physics, 1972, 11: 181-216. |
| [16] |
Liu S L, Li X F, Wang W S, et al. A mixed-grid finite element method with PML absorbing boundary conditions for seismic wave modeling[J]. Journal of Geophysics and Engineering, 2014, 11(5): 055009. DOI:10.1088/1742-2132/11/5/055009 |
| [17] |
Dan D K, Baysal E. Forward modeling by a Fourier method[J]. Geophysics, 1982, 47(10): 1402-1412. DOI:10.1190/1.1441288 |
| [18] |
Komatitsch D, Tsuboi S, Tromp J.The Spectral-element method in seismology//Seismic Earth: Array Analysis of Broadband Seismograms[M].American Geophysical Union, 2005, 205-227.
|
| [19] |
Yang D H, Wang L, Deng X Y. An explicit split-step algorithm of the implicit Adams method for solving 2D acoustic and elastic wave equations[J]. Geophysical Journal International, 2010, 180(1): 291-310. DOI:10.1111/j.1365-246X.2009.04407.x |
| [20] |
Yang D H, Teng J W, Zhang Z J, et al. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media[J]. Bulletin of the Seismological Society of America, 2003, 93(2): 882-890. DOI:10.1785/0120020125 |
| [21] |
Yang D H, Peng J M, Lu M, et al. Optimal nearly analytic discrete approximation to the scalar wave equation[J]. Bulletin of the Seismological Society of America, 2006, 96(3): 1114-1130. DOI:10.1785/0120050080 |
| [22] |
胡建林, 宋维琪, 张建坤, 等. 交错网格有限差分正演模拟的联合吸收边界[J]. 石油地球物理勘探, 2018, 53(5): 914-920. HU Jianlin, SONG Weiqi, ZHANG Jiankun, et al. Joint absorbing boundary in the staggered-grid finite difference forward modeling simulation[J]. Oil Geophysical Prospecting, 2018, 53(5): 914-920. |
| [23] |
Lang C, Ren Z R. Inexact rotated block triangular preconditioners for a class of block two-by-two matrices[J]. Journal of Engineering Mathematics, 2015, 93(1): 1-12. |
| [24] |
Liu S L, Suardi I, Yang D H, et al. Tele seismic tra-veltime tomography of northern Sumatra[J]. Geophy-sical Research Letters, 2018, 45(24): 13231-13239. DOI:10.1029/2018GL078610 |
| [25] |
Shin C, Sohn H. A frequency-space 2-D scalar wave extrapolator using extended 25-point finite-difference operator[J]. Geophysics, 2012, 63(1): 289-296. |
| [26] |
Liu Q H. The PSTD algorithm:A time-domain me-thod requiring only two cells per wavelength[J]. Microwave and Optical Technology Letters, 1997, 15(3): 158-165. DOI:10.1002/(SICI)1098-2760(19970620)15:3<158::AID-MOP11>3.0.CO;2-3 |
| [27] |
Jerri A J. The Shannon sampling theorem-Its various extensions and applications:A tutorial review[J]. Proceedings of the IEEE, 2005, 65(11): 1565-1596. |
| [28] |
Versteeg R. The Marmousi experience:Velocity model determination on a synthetic complex data set[J]. The Leading Edge, 1994, 13(9): 927-936. DOI:10.1190/1.1437051 |
| [29] |
Sirgue L, Pratt R G. Efficient waveform inversion and imaging:A strategy for selecting temporal frequencies[J]. Geophysics, 2004, 69(24): 231-248. |



 郎超, 北京市西城区百万庄大街26号中国地质科学院地质研究所, 100037。Email:
郎超, 北京市西城区百万庄大街26号中国地质科学院地质研究所, 100037。Email: