② 北京大学地球与空间科学学院, 北京 100871
② School of Earth and Space Sciences, Peking University, Beijing 100871, China
多次波是在地下经过多次向上、向下反射的地震波。多次波与一次反射波的相互混淆,导致地震资料处理和解释结果出现偏差。多次波分为地表多次波和层间多次波。地表多次波是指在地表和地下界面之间发生一次或多次向下散射的波;层间多次波的所有向下散射点均位于地下界面而非地表。当地下存在速度差异较大的地层界面时,层间多次波振幅可能高于一次反射波。一般情况下,层间多次波的动校正量、叠加速度、旅行时与一次波较为相似,因此预测和压制层间多次波比较困难。
地表多次波衰减的探讨和研究已有很多显著成果[1-6],然而关于层间多次波的研究进展却相对有限。Weglein等[2]基于逆散射级数给出了所有阶次层间多次波的理论计算公式;针对该算法计算成本较高的问题,金德刚等[7]改进了该一维层间多次波预测公式,提高了计算效率。Jakubowicz[8]和Keydar等[9]提出了利用一次反射波预测一阶层间多次波的方法。Berkhout等[10]将地表多次波迭代去除方法(SRME)推广到层间多次波,并提出了广义SRME方法;叶月明等[11]基于SRME模型给出了层间多次波的迭代数据驱动去除算法。黄饶等[12]基于点震源的球面波理论采用反射率法有效模拟了层间多次波。Ypma等[13]将一次波稀疏反演方法(EPSI方法)推广到层间多次波,并提出了广义EPSI方法。基于Marchenko自聚焦方法,da Costa Filho等[14]讨论了弹性介质中的层间多次波压制方法。Ikelle等[15-16]提出了虚同相轴概念,并将其运用于合成数据的层间多次波预测和压制。
除了上述有关层间多次波预测和压制的理论进展以外,很多学者也从实际资料处理以及方法实践应用的角度对层间多次波衰减方法进行了有益的讨论和改进。van Borselen[17]将基于迭代反馈模型的层间多次波衰减方法运用于实际海洋数据以改进多次波压制效果;Verschuur等[18]和Ypma等[13]将广义SRME和广义EPSI方法运用于北海实际海洋数据,在部分区域取得了一定效果;Brookes[19]将反馈迭代模型运用于三维实际地震资料,得益于计算性能的提升,该方法在墨西哥湾的海上三维地震资料和西非沙漠三维地震资料的层间多次波衰减中取得较好效果;An等[20]将虚同相轴方法成功运用于1.5维实际地震资料;叶月明等[21-22]将基于扩展SRME模型的迭代算法运用于叠后实际地震资料和海上地震资料。此外,谭军等[23]和李兴旺等[24]对于三维多次波射线追踪进行了有益的研究。
目前陆上实际资料层间多次波压制的技术需求较大,本文给出虚同相轴方法的基本公式和物理意义,讨论虚同相轴方法在陆上资料应用中的实际困难,结合中国西部地区深层石油天然气勘探开发的现状,提出虚同相轴在陆上资料应用的近似假设和实施方法。通过对合成地震数据和陆上地震资料的处理,验证近似虚同相轴方法对于陆上二维叠前数据的多次波的衰减效果及对于一次波能量的突显作用。
1 虚同相轴原理虚同相轴概念及其层间多次波预测方法由Ikelle[15]提出,这里虚同相轴是指在实际地震资料当中并不存在的同相轴。借助虚同相轴可以将多次波的向下散射点从产生层间多次波的真实界面转移至地表,从而预测出层间多次波。
假设d0为某一地下浅层界面的一次反射波,d′0为该界面之下不含d0的深部数据,d0*为该界面d0的一次反射超前波,其中*表示复共轭运算。这样,虚同相轴定义为一次反射超前波与不含该一次波的深部数据的褶积
| $ {d_{\rm{V}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{R}}}} \right) = \int {d_0^\prime } \left( {{\mathit{\boldsymbol{x}}_{\rm{s}}}, \mathit{\boldsymbol{x}}} \right)d_0^*\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{R}}}} \right){\rm{d}}\mathit{\boldsymbol{x}} $ | (1) |
式中xS和xR分别代表炮点和检波点位置。将虚同相轴与不含浅层界面一次反射波的原始数据进行褶积,即可预测出其产生的层间多次波
| $ {d_1}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{R}}}} \right) = \int {{d_{\rm{V}}}} \left( {{\mathit{\boldsymbol{x}}_{\rm{s}}}, \mathit{\boldsymbol{x}}} \right)d_0^\prime \left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{R}}}} \right){\rm{d}}\mathit{\boldsymbol{x}} $ | (2) |
图 1描述了虚同相轴的物理过程。当地震深层一次反射波与地震浅层一次反射超前波进行褶积运算时,两者重叠的路径导致其时间延迟相互“抵消”,不重叠的路径保留,得到右端的结果,称为虚同相轴(图 1a)。当这个虚同相轴与地震深层反射波进行褶积运算,两者重叠的路径其时间延迟同样被“抵消”,运算得到的路径为层间多次反射波(图 1b)。虚同相轴与原始数据褶积可以预测出与某浅层一次波相关的层间多次波,再通过自适应匹配并向深部逐层位重复即可预测所有层间多次波。该方法经后续改进后,具有较好的应用前景[25-27]。

|
图 1 虚同相轴原理示意图 (a)构建虚同相轴;(b)通过虚同相轴构建层间多次波 ✧表示炮点,▽形表示检波点,*表示褶积运算,检波点与炮点之间的连线表示两者的位置相同,地下射线路径分为实线和虚线两种,实线表示延迟波,虚线表示超前波 |
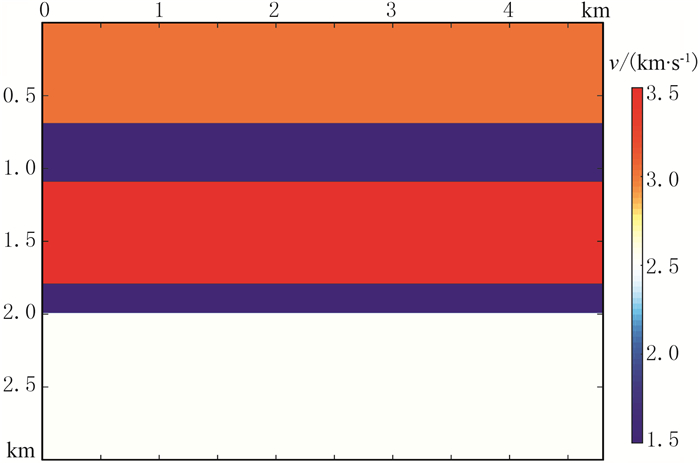
图 2为一简单的水平层状速度模型,密度为常数2000kg/m3。图 3a为有限差分方法正演的炮集记录,直达波已被切除。由于四周采用吸收边界,记录中不包含地表多次波。根据虚同相轴的基本定义,每次选取一个界面一次反射同相轴构建层间多次波,因此构建出来的层间多次波都与该层相关。例如,为了构建与第一个界面有关的层间多次波,在所有炮集记录中选取第一界面一次反射同相轴,将其与去掉该一次反射的原始数据做褶积,即可得到虚同相轴。将该虚同相轴再次与上述原始数据褶积,即可得到层间多次波预测模型。通过自适应相减即可得到去除了与第一界面有关的层间多次波的炮集记录。依此类推,分别选取其余界面的一次反射,重复上述过程,即可得到最终的层间多次波压制结果。
|
图 2 简单速度模型 |
|
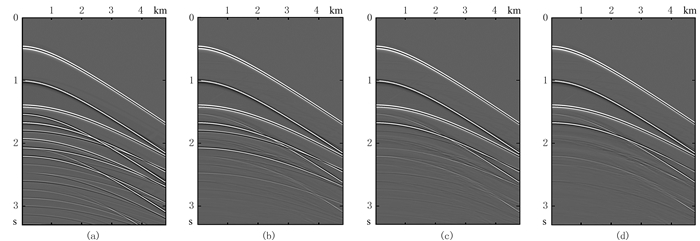
图 3 合成地震数据及层间多次波衰减结果 (a)原始炮集;(b)去除与第一界面相关的多次波后;(c)去除与第二界面相关的多次波后;(d)去除所有层间多次波后 |
本文合成和实际资料多次波压制中均采用L1范数匹配相减技术[28],该算法以最小化地震道信号绝对值和为目标。合成数据采用多道全局匹配算法,实际地震数据采用多道全局和局部匹配相结合的算法。图 3b为去除了与第一界面相关的层间多次波后的炮记录。为了预测和压制与剩余三个界面有关的层间多次波,可通过开时窗依次提取各界面的一次反射同相轴。图 3c为去除了与第二界面有关的层间多次波结果,图 3d为去除了所有层间多次波后的结果。可以看出,所有阶次的层间多次波均得到了有效压制,一次波也得到了完整保留。
上述合成数据的同相轴时差较大,交叉重叠现象较少。图 4为基于真实测井数据建立的地震速度模型,图 5a~图 5c为模拟的炮记录,不含地表多次波。应用该模型数据检验虚同相轴方法在较为复杂波场条件下对层间多次波的衰减能力。模型速度分层较多,且存在速度反转和密度反转,导致地震数据多次波较发育,无法用传统方法较好压制。选定波阻抗差异较大的一个分界面作为向下散射界面,构建虚同相轴和层间多次波,多次波衰减结果如图 5d~图 5f所示。

|
图 4 基于实际测井资料建立的速度模型 |
|
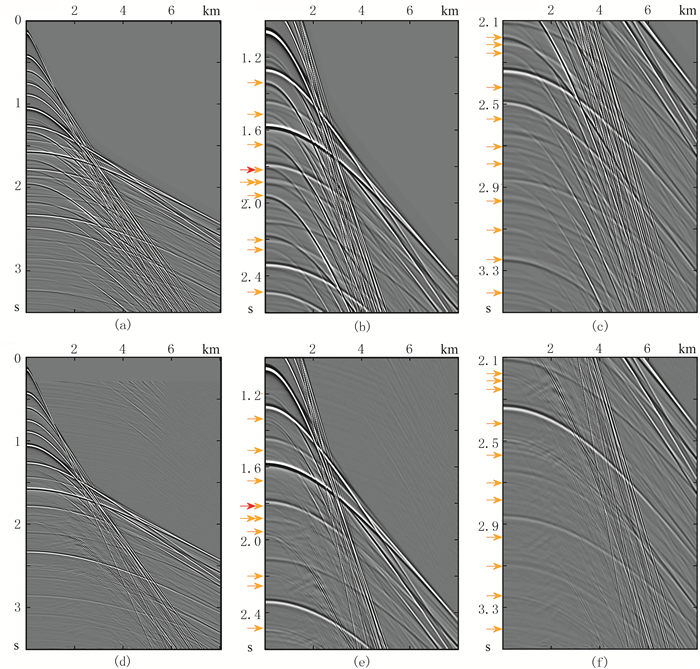
图 5 基于测井数据模型的合成地震数据及层间多次波衰减结果 (a)原始炮集;(b)图a的浅层局部记录;(c)图a的深层局部记录;(d)去除层间多次波后的炮集;(e)图d的浅层局部记录;(f)图d的深层局部记录。红箭头表示易受影响的一次波,黄箭头表示层间多次波的零炮检距理论旅行时 |
从衰减结果看,虚同相轴方法对于复杂波场条件下的层间多次波具有较好的预测和衰减能力:第一,在不需要局部时窗等复杂匹配算法的前提下,仅仅依靠全局时窗匹配即可对远炮检距、交叠现象严重的深层层间多次波、以及近炮检距振幅较强的层间多次波实现有效压制,突显深层一次波能量;第二,在多次波和一次波重合区域,多次波能被准确预测和压制,且一次波能量得到完整保留;第三,在一次波和多次波同相轴相交的区域,多次波依然能被准确预测和压制。此外,存在多次波残留的主要原因:一是由于为避免引入切除导致的预测误差,数据分割仅针对第一界面和第二界面对应的一次反射波;二是由于多次波预测模型的振幅与真实情况存在误差;三是由于部分多次波振幅与一次波较为接近。
2 陆上层间多次波衰减近似方法上文对虚同相轴方法的基本原理、基本公式、物理意义做了阐述,通过合成数据检验方法的正确性。对于实际地震数据,问题比理想情形复杂很多,在应用虚同相轴方法之前,需要做一定的近似和假设。首先讨论这些近似、假设的必要性,并给出虚同相轴算法在实际陆上数据中的具体应用方法。
在实际地震数据中,以下两种情况选取的真实一次波同相轴不符合虚同相轴方法的要求:①某一次波同相轴与其他一次波同相轴的时差十分接近以至于除了峰值外没有明显间隔,无法直接分离;②浅层部分地震波记录的不可靠导致关键的浅层数据无法应用于虚同相轴算法。
针对同相轴时差很近、不容易单独分离的问题,本文把与关键界面(即产生层间多次波的波阻抗界面)反射轴相邻的振幅较弱的同相轴同时选择,并将其作为向下散射的产生来源构建虚同相轴。对于由地表风化层质地松软且横向不连续、层位较多而导致的陆上资料浅部数据可靠性差的问题,本文通过依靠旅行时更长、信噪比更高的一次波构建的虚同相轴,替代浅层不可靠的信号。
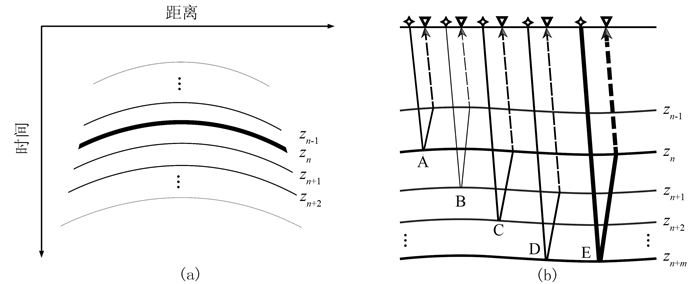
2.1 散射体近似方法对于同相轴时差很小、不容易单独分离的问题,可以把与关键界面反射轴相邻的振幅较弱的同相轴同时选择,并将其作为向下散射的产生来源构建虚同相轴,但需证明这种近似的合理性。如图 6a所示,假设在炮集存在一条能够产生层间多次波的向下散射界面(简称“关键界面”)的同相轴zn,由于其上、下界面zn-1~zn+2的反射轴时差较小且同相轴振幅相对较小,一并选取作为向下散射算子,记为关键向下散射体(简称“关键散射体”)。按照虚同相轴算法的定义,这种近似选取不影响那些向上反射全部发生在zn+3~zN界面的层间多次波,其中N代表层位数目。因此只需考虑是否会影响在zn-1~zn+2界面产生的一次或一次以上向上反射的层间多次波即可,涉及到的虚同相轴如图 6b所示。
|
图 6 适用于虚同相轴方法的向下散射界面近似选取示意图 (a)炮集记录的同相轴近似选取;(b)与炮集记录同相轴对应的5类典型 虚同相轴(同相轴粗细代表相对振幅大小)。✧表示炮点,▽形表示检波点 |
假设弱反射层zn-1、zn+1、zn+2的一次反射振幅均为RW,关键界面的一次反射振幅为RS,且RS≫RW,那么为了预测上面提到的在zn-1~zn+2界面有过至少一次向上反射的层间多次波而必须构建的虚同相轴可分为图 6b所示的A、B和C三类情况。A类表示在关键界面zn发生向上反射、在弱反射界面zn-1发生向下反射的虚同相轴,只有如图 6b最左侧所示的一种情况,涉及的界面用{zn,zn-1}标记。B类表示向下和向上反射均发生在弱反射层的虚同相轴,涉及的界面不仅有图 6b所示的{zn+1,zn-1},还包括{zn+2,zn-1}、{zn+2,zn+1};C类表示在弱反射层向上反射、在关键界面zn发生向下反射的多次波,虚同相轴构建不仅涉及图中所示的界面{zn+2,zn},还包括{zn+1,zn}。A、B和C代表的三类多次波振幅量级分别为RWRS、RW2和RWRS。由于RW≪RS,RW2≪RWRS,因此B类虚同相轴的振幅及其构建的层间多次波振幅远小于A和C类,因此由B类虚同相轴构建的层间多次波可被忽略。
进一步将A和C类虚同相轴与涉及关键散射体以下的强反射轴(例如zn+m)的虚同相轴进行振幅比较。假设界面zn+m (m>2)距离zn+2不远,且界面的一次反射振幅量级也为RS。定义D类虚同相轴表示在zn+m发生向上反射、在弱反射层发生向下反射的虚同相轴(如{zn+m,zn+2}、{zn+m,zn+1}、{zn+m,zn-1});定义E类虚同相轴表示在zn+m发生向上反射、在关键界面zn发生向下反射的虚同相轴{zn+m,zn}。那么D类虚同相轴的振幅量级为RWRS,与A和C类量级相当;E类虚同相轴的振幅量级为RS2。由于RW≪RS,RWRS≪RS2,因此当存在E类虚同相轴时,A、C和D类虚同相轴及其构建的层间多次波振幅远小于E类,可以被忽略。因此,当在时空域有旅行时十分相近的一组一次波反射轴,且当其中有且仅有一条较强反射轴时,这一组一次波同相轴对应的真实层位可以作为一个整体——关键散射体,产生向下散射。
上述定性结论表明,关键散射体产生的层间多次波近似地等价于将逐层依次计算关键界面产生的向下多次散射波之和。对于在时空域十分邻近、不便人工分离的弱同相轴,连同关键界面反射轴一起分离出来构建层间多次波模型具有明确的物理意义。从物理图像上看,这个过程等价于将强反射轴附近的厚度较小、波阻抗差异较小的各个层位视作一个关键散射体,并假定其内部不发生层间多次反射,或者认为其内部的多次散射波振幅远小于强反射轴产生的多次波,从而使这个整个散射体可以很好地近似成关键界面,并作为向下散射源产生层间多次波。
2.2 同相轴替代方法对于陆上地震资料,近地表风化层质地松软且横向不连续、层位较多,导致浅部数据可靠性差,浅部同相轴无论是从物理意义上还是从信噪比上都无法作为有效的向下散射算子。然而,浅部波阻抗差异较大的界面对于层间多次波的生成和预测具有重要意义。因此,十分有必要提出一种针对陆上浅层同相轴低信噪比数据的近似方法。下文将证明,由相对较深的反射波数据构建的虚同相轴和层间多次波,在一定的假设条件下可以完全替代基于浅层反射轴构建的多次波,从而在一定程度上缓解虚同相轴方法对浅层同相轴数据的依赖。这种用深层反射数据构建层间多次波的近似方式,忽略了由浅层界面产生的一阶层间多次波。
假设第一个界面的一次反射波数据可靠,那么对于图 7a中的层间多次波,其预测模型可以采用如图 7a所示的方式建立。然而,实际地震数据的浅层反射波数据未必可靠,如果第一个界面的一次反射波数据不可靠,那么还可以通过图 7b的方式建立预测模型。在该模型中,第二界面被看作关键界面,虚同相轴的构建需要用到相对可靠的第二和第三界面的反射信号,由此得到的层间多次波预测也更接近真实情况。进一步,如果前两个界面反射信号都不可靠,可以如图 7c所示通过第三界面反射信号预测该多次波。值得注意的是,对于所有向下散射都发生在浅层界面的多次波来说,对于这类多次波的预测模型没有替代方案。此近似方法成立的前提条件是:待预测的层间多次波至少有一个向下散射点所在的界面具有可靠的一次反射波同相轴。实际上,如果前提不成立,意味着对于那些无法形成有效连续反射信号的浅层界面引发较强层间多次波的可能性较小,因此前提假设的不满足意味着该层产生的层间多次波能量小到可以在一定程度上被忽略,因此该近似方法在提高虚同相轴方法的适用性的同时,不会显著影响结果的准确性。
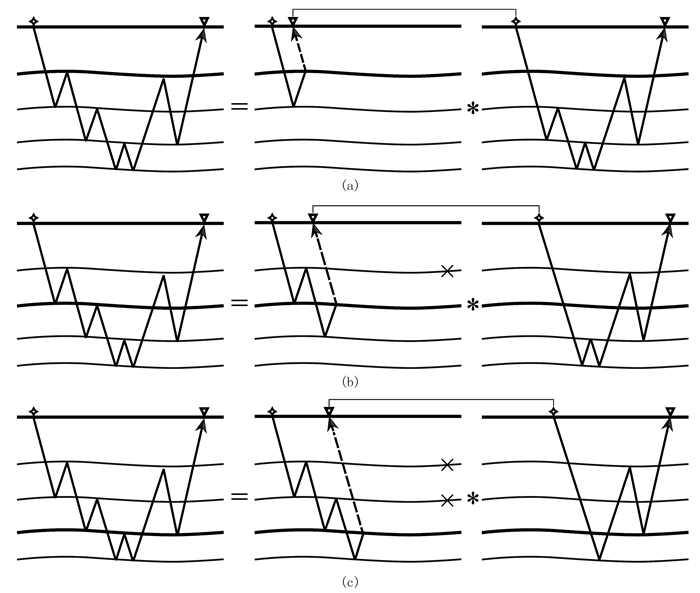
|
图 7 适用于虚同相轴方法的层间多次波等价构建示意图 (a)理想情况下的构建方式;(b)部分浅层数据信噪比较低时的等价构建方式;(c)大部分浅层数据信噪比较低时的等价构建方式 ✧表示炮点,▽表示检波点,“×”表示表示真实地下界面的一次反射波信噪比不高,不能用于构建虚同相轴 |
由上文得出,基于上覆分界面一次反射波构建的虚同相轴和预测模型一定可以被基于其下方的某个界面的预测结果所替代。因此,对于下行反射发生在不同深度界面的二阶及以上阶次的层间多次波,如果浅层反射信号不可靠,最佳策略是舍弃这些浅层同相轴,并依靠中深层信号得到理论上等价、信噪比不受近地表信号影响的层间多次波预测结果。
将上述近似方法应用于图 5所示的合成数据,得到了较好的多次波压制效果(图 8)。图 8a和图 8c给出了同时选取第一和第二界面反射波同相轴作为一个整体来构建虚同相轴时的压制结果。图 8b和图 8d给出了只选取第一个界面的一次反射同相轴构建虚同相轴时的多次波压制结果;与图 5e和图 5f对比,效果接近,从而验证近似方法的有效性。同相轴的分割选取方法是:通过时窗选出第一、第二条一次反射波同相轴,将其整体或其中单独一条同相轴作为向下散射界面,构建虚同相轴。由图可见,近似方法一定程度上降低了多次波压制精度,存在多次波残余情况。
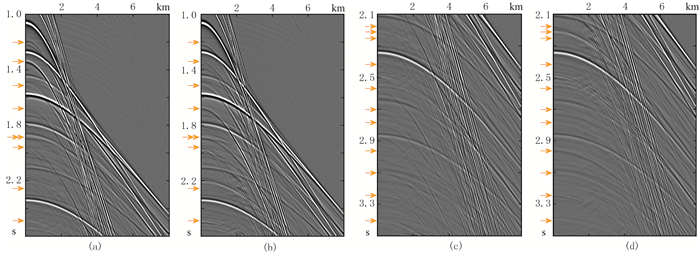
|
图 8 虚同相轴近似方法在复杂合成地震数据中的层间多次波衰减效果 (a)同时选取第一和第二界面一次反射同相轴作为整体构建虚同相轴的层间多次波压制结果(浅层局部);(b)只选取第一界面一次反射同相轴构建虚同相轴的层间多次波压制结果(浅层局部);(c)同时选取第一和第二界面一次反射同相轴作为整体构建虚同相轴的层间多次波压制结果(深层局部);(d)只选取第一界面反射同相轴构建虚同相轴的层间多次波深层局部压制结果红箭头表示易受影响的一次波,黄箭头表示层间多次波的零炮检距理论旅行时 |
注意到把两条同相轴作为一个整体来预测压制层间多次波的效果劣于使用一条同相轴。原因是:前者(图 8a和图 8c)违反了虚同相轴原理的假设(向下散射界面是真实存在的单一波阻抗分界面)。在理想状况下,应该分别将第一和第二条反射轴作为向下散射界面,进行多次波压制(图 5c和图 5f)。第二种近似方法则不违反假设。从整体上看,两种近似方法均对最终压制结果产生了较小的负面影响,能够较好地替代虚同相轴方法,有效压制层间多次波。
3 陆上层间多次波衰减实例本文将虚同相轴近似方法应用于实际二维叠前地震数据中,证明该近似方法在去除层间多次波、突显一次波同相轴方面的效果。实际数据来自中国西部,层间多次波较发育。
图 9为虚同相轴层间多次压制结果,可以看出,原始炮集记录中的多次波现象十分严重,振幅较强,旅行时与一次波接近。通过虚同相轴近似方法处理后,大部分多次波被衰减,少部分一次波受到影响,这主要是由于近似方法在理论上与理想情形的预测模型具有一定的误差,且其中一部分误差无法通过自适应匹配算法得到完全校正。
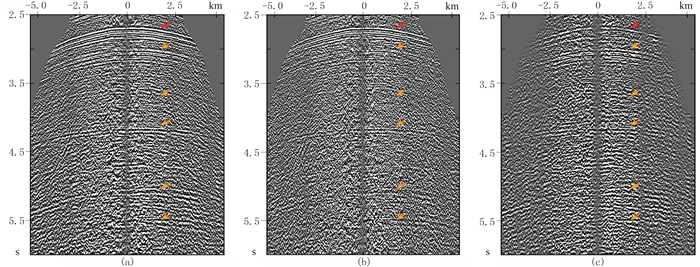
|
图 9 实际二维陆上叠前地震资料的虚同相轴近似方法层间多次波压制结果 (a)原始炮集;(b)多次波衰减结果;(c)预测的多次波。黄箭头表示多次波,红箭头表示易受影响的一次波 |
图 10为层间多次波压制前、后叠加剖面的对比,进一步证实了方法对多次波衰减的良好效果,证明虚同相轴近似方法对于存在一定倾角的地下构造环境中的多次波具有较好的识别、预测和衰减能力。

|
图 10 虚同相轴近似方法在实际二维陆上叠前地震资料中的应用结果 (a)原始叠加剖面;(b)多次波衰减结果;(c)多次波剖面。蓝箭头表示被去掉的多次波,红箭头表示易受影响的一次波 |
此外,实际地震层间多次波压制效果与合成数据结果存在差距,其主要原因包括:虚同相轴多次波模型与真实值相比存在误差;近似方法对多次波预测和压制精度存在一定的影响;实际资料比合成数据存在更多的与一次波旅行时较为接近的多次波,在对此类多次波进行压制时,无法完全避免伤害有效波。
4 结束语本文给出了虚同相轴的方法原理,并针对陆上数据实际情况提出了应用该算法的近似条件和具体步骤。通过合成地震数据和陆上地震资料的处理实例,表明虚同相轴近似方法对于预测和衰减层间多次波的显著效果。虚同相轴陆上近似应用方法适用于复杂条件下的叠前地震数据,能够衰减陆上层间多次波,突显一次波能量。在不显著降低多次波压制精度的情况下,该近似方法可以提高虚同相轴算法在复杂条件下实际地震数据中的适用性。
| [1] |
Berkhout A J, Verschuur D J. Estimation of multiple scattering by iterative inversion, Part Ⅰ:Theoretical considerations[J]. Geophysics, 1997, 62(5): 1586-1595. DOI:10.1190/1.1444261 |
| [2] |
Weglein A B, Gasparotto F A, Carvalho P M, et al. An inverse-scattering series method for attenuating multiples in seismic reflection data[J]. Geophysics, 1997, 62(6): 1975-1989. DOI:10.1190/1.1444298 |
| [3] |
van Groenestijn G J, Verschuur D J. Estimating primaries by sparse inversion and application to near-offset data reconstruction[J]. Geophysics, 2009, 74(3): A23-A28. DOI:10.1190/1.3111115 |
| [4] |
Lopez G A, Verschuur D J. Closed-loop surface-related multiple elimination and its application to simultaneous data reconstruction[J]. Geophysics, 2015, 80(6): V189-V199. DOI:10.1190/geo2015-0287.1 |
| [5] |
Verschuur D J, Berkhout A J. From removing to using multiples in closed-loop imaging[J]. The Leading Edge, 2015, 34(7): 744-759. DOI:10.1190/tle34070744.1 |
| [6] |
宋家文, Verschuur D J, 陈小宏. 多次波压制的研究现状与进展[J]. 地球物理学进展, 2014, 29(1): 240-247. SONG Jiawen, Verschuur D J, CHEN Xiaohong. Research status and progress in multiple elimination[J]. Progress in Geophysics, 2014, 29(1): 240-247. |
| [7] |
金德刚, 常旭, 刘伊克. 逆散射级数法预测层间多次波的算法改进及其策略[J]. 地球物理学报, 2008, 51(4): 1209-1217. JIN Degang, CHANG Xu, LIU Yike. Algorithm improvement and strategy of internal multiples prediction based on inverse scattering series method[J]. Chinese Journal of Geophysics, 2008, 51(4): 1209-1217. DOI:10.3321/j.issn:0001-5733.2008.04.032 |
| [8] |
Jakubowicz H.Wave equation prediction and removal of interbed multiples[C].SEG Technical Program Expanded Abstracts, 1998, 17: 1527-1530.
|
| [9] |
Keydar S, Lande E, Gurevich B, et al.Multiple prediction using wavefront characteristics of primary reflections[C].Extended Abstracts of 59th EAGE Confe-rence & Exhibition, 1997, A016.
|
| [10] |
Berkhout A J, Verschuur D J. Removal of internal multiples with the common-focus-point(CFP) approach Part 1:Explanation of the theory[J]. Geophysics, 2005, 70(3): V45-V60. DOI:10.1190/1.1925753 |
| [11] |
叶月明, 赵昌垒, 姚根顺, 等. 数据驱动型层间多次波预测方法研究[J]. 石油地球物理勘探, 2014, 49(2): 244-251. YE Yueming, ZHAO Changlei, YAO Genshun, et al. Study of data-driven interbed multiple prediction[J]. Oil Geophysical Prospecting, 2014, 49(2): 244-251. |
| [12] |
黄饶, 陈小宏, 李景叶. 层间多次波模拟与影响分析[J]. 地球物理学进展, 2009, 24(3): 981-987. HUANG Rao, CHEN Xiaohong, LI Jingye. Simulation and effect analysis of interbed multiples[J]. Progress in Geophysics, 2009, 24(3): 981-987. DOI:10.3969/j.issn.1004-2903.2009.03.022 |
| [13] |
Ypma F H C, Verschuur D J. Estimating primaries by sparse inversion, a generalized approach[J]. Geophy-sical Prospecting, 2013, 61(S1): 94-108. |
| [14] |
da Costa Filho C A, Meles G A, Curtis A. Elastic internal multiple analysis and attenuation using Mar-chenko and interferometric methods[J]. Geophysics, 2017, 82(2): Q1-Q12. DOI:10.1190/geo2016-0162.1 |
| [15] |
Ikelle L T. A construct of internal multiples from surface data only:the concept of virtual seismic events[J]. Geophysical Journal International, 2006, 164(2): 383-393. DOI:10.1111/j.1365-246X.2006.02857.x |
| [16] |
Ikelle L T, Erez I, Yang X. Scattering diagrams in seismic imaging:More insights into the construction of virtual events and internal multiples[J]. Journal of Applied Geophysics, 2009, 67(2): 150-170. DOI:10.1016/j.jappgeo.2008.10.009 |
| [17] |
van Borselen R.Data-driven interbed multiple remo-val: Strategies and examples[C].SEG Technical Program Expanded Abstracts, 2002, 21: 2106-2109.
|
| [18] |
Verschuur D J, Berkhout A J. Removal of internal multiples with the common-focus-point (CFP) app-roach:Part 2-Application strategies and data examples[J]. Geophysics, 2005, 70(3): V61-V72. DOI:10.1190/1.1925754 |
| [19] |
Brookes D. Case studies in 3D interbed multiple atte-nuation[J]. The Leading Edge, 2011, 30(8): 914-918. DOI:10.1190/1.3626499 |
| [20] |
An S, Hu T, Liu J, et al.Scheme of applying virtual event method for internal multiples on land seismic data[C].2017 CGS/SEG International Geophysical Conference, 2017, 391-394.
|
| [21] |
叶月明, 赵昌垒, 庄锡进, 等. 基于地震干涉法的叠后层间多次波衰减方法[J]. 石油地球物理勘探, 2014, 49(6): 1077-1082. YE Yueming, ZHAO Changlei, ZHUANG Xijin, et al. Poststack interbed multiple suppression based on seismic interferometry[J]. Oil Geophysical Prospecting, 2014, 49(6): 1077-1082. |
| [22] |
叶月明, 姚根顺, 赵昌垒, 等. 利用地震干涉法衰减海底相关层间多次波[J]. 石油地球物理勘探, 2015, 50(2): 225-231. YE Yueming, YAO Genshun, ZHAO Changlei, et al. Sea bottom peg-leg multiple suppression based on seismic interferometry[J]. Oil Geophysical Prospecting, 2015, 50(2): 225-231. |
| [23] |
谭军, 宋鹏, 李金山, 等. 基于同相轴追踪的三维地震资料多次波压制方法[J]. 石油地球物理勘探, 2017, 52(5): 894-905. TAN Jun, SONG Peng, LI Jinshan, et al. 3D multiple suppression based on event tracking[J]. Oil Geophy-sical Prospecting, 2017, 52(5): 894-905. |
| [24] |
李兴旺, 白超英, 李晓玲. 四面体单元剖分下三维各向异性TI介质中多次波射线追踪[J]. 石油地球物理勘探, 2017, 52(1): 48-55. LI Xingwang, BAI Chaoying, LI Xiaoling. Multiples raytracing in 3D anisotropic TI media with a tetrahe-dron cell model[J]. Oil Geophysical Prospecting, 2017, 52(1): 48-55. |
| [25] |
吴静, 吴志强, 胡天跃, 等. 基于构建虚同相轴压制地震层间多次波[J]. 地球物理学报, 2013, 56(3): 985-994. WU Jing, WU Zhiqiang, HU Tianyue, et al. Seismic internal multiple attenuation based on constructing virtual events[J]. Chinese Journal of Geophysics, 2013, 56(3): 985-994. |
| [26] |
Liu J, Hu T.Inversion based internal multiple atte-nuation study[C].2017 CGS/SEG International Geophysical Conference, 2017, 561-564.
|
| [27] |
Liu J, Hu T.Internal multiple attenuation by iterative construction of virtual events[C].Extended Abstracts of 79th EAGE Conference and Exhibition, 2017, B306.
|
| [28] |
Guitton A, Verschuur D J. Adaptive subtraction of multiples using the L1-norm[J]. Geophysical Prospecting, 2004, 52(1): 27-38. DOI:10.1046/j.1365-2478.2004.00401.x |



 胡天跃, 北京市海淀区颐和园路5号北京大学地球与空间科学学院, 100871。Email:
胡天跃, 北京市海淀区颐和园路5号北京大学地球与空间科学学院, 100871。Email: