② 有色资源与地质灾害探查湖南省重点实验室, 湖南长沙 410083;
③ 中南大学地球科学与信息物理学院, 湖南长沙 410083;
④ 南方科技大学地球与空间科学系, 广东深圳 518055
② Hunan Key Laboratory of Nonferrous Resources and Geological Hazards Exploration, Changsha, Hunan 410083, China;
③ School of Geosciences and Info-Physics, Central South University, Changsha, Hunan 410083, China;
④ Department of Earth and Space Sciences, Southern University of Sciences and Technology, Shen-zhen, Guangdong 518055, China
瑞雷面波在速度垂向不均匀介质中呈频散特性[1],因此近年来在地震工程、工程地质勘查和无损检测等领域得到了广泛的应用[2-3]。瑞雷面波勘探的流程主要包括数据采集、频散曲线提取[4-5]、频散曲线反演及解释等四个环节。频散曲线的反演方法主要有局部线性化和非线性全局优化[6]两大类。局部线性化反演方法中最具代表性的是最小二乘法[7],该方法对初始模型依赖较大,因此要求数据处理人员具有较丰富经验。常用的非线性全局优化方法包括遗传算法[8]、BP神经网络法[9]、模拟退火法[10]、粒子群算法(Particle Swarm Optimization,PSO)[11]和模式识别法[12]等,这类方法对初始模型的依赖较小,求解精度高,但针对复杂地层数据反演时易出现收敛速度慢、陷入局部极小值等问题,一定程度上影响了其实际应用效果。
粒子群算法作为一种全局优化算法,因收敛速度快、求解精度高等特点被广泛应用于瑞雷面波频散曲线的反演,但传统的粒子群算法存在易陷入局部最优、过于早熟等问题[13],因此对其进行了诸多改进。如惯性权重改进[14]、学习因子改进、粒子位置和速度改变[15]、加入混沌局部搜索[16]和混合遗传算法[17]等。
本文基于上述研究成果,设计了一种能同步提高全局和局部搜索能力的自适应混沌遗传粒子群算法(Adaptive Chaos Genetic Particle Swarm Optimization Algorithm,ACGPSO),该算法采用自适应惯性权重和混合遗传算法的交叉和变异操作以增强基本粒子群算法的全局搜索能力,约束全部粒子的行进速度,对最优粒子进行单维全分量的混沌局部搜索以增强其局部搜索能力。
瑞雷面波频散包括基阶和高阶频散曲线,目前瑞雷面波的反演主要还是采用基阶模式的频散曲线,这使得反演多解性问题非常突出。若在反演过程中加入高阶模式频散曲线,就可显著降低反演结果的多解性。另一方面,当地层中含有低速软夹层或高速硬夹层时,高阶模式的面波能量相对于基阶模式的面波在中—高频段渐渐占据主导优势[18-19],对于这类地层采用瑞雷波勘探时,必须将基阶与多阶瑞雷波频散曲线进行联合反演[20-21]才能获取准确的地下横波速度结构[22]。因此,在瑞雷面波频散曲线反演算法设计时须考虑进行基阶与高阶频散曲线联合反演,以进一步提高反演精度。
为了检验ACGPSO算法的准确性,利用两种测试函数对该算法进行测试,并将试算结果与遗传算法(GA)和PSO的结果进行对比。在此基础上对理论模型的无噪和含噪数据的基阶和多阶频散曲线进行反演,验证其有效性、稳定性和抗噪性;最后将该方法应用于实际数据反演,进一步验证其适用性。
1 粒子群算法的基本原理及其改进 1.1 粒子群算法的基本原理粒子群算法也称鸟群觅食算法,是由Kennedy等[23]开发的一种进化算法。在用户给定的d维搜索范围内,所有粒子通过跟踪其本身找到的最优解(pi)和整个种群当前找到的最优解(g)更新自己,完成迭代寻优。在对比适应度值寻找到这两个解后,通过下式更新自己的速度(vi)和位置(xi)
| $ \left\{\begin{array}{l}{v_{i, j}^{t+1}=w v_{i, j}^{t}+c_{1} r_{1}\left(p_{i, j}-x_{i, j}^{t}\right)+c_{2} r_{2}\left(g_{j}-x_{i, j}^{t}\right)} \\ {x_{i, j}^{t+1}=x_{i, j}^{t}+v_{i, j}^{t+1} \quad j=1, 2, \cdots, d}\end{array}\right. $ | (1) |
式中:t为当前迭代次数;xi, jt、vi, jt分别为当代第i个粒子的第j维的位置和速度;w为惯性权重;c1、c2为正的学习因子,它们决定了粒子本身经验信息和其他粒子的经验信息对粒子运行轨迹的影响,反映了粒子群之间的信息交流,本文均取1.49445;r1、r2为0~1之间均匀分布的随机数。
1.2 粒子群算法的改进本文对粒子群算法的改进主要体现在四个方面:①采用自适应惯性权重;②设置粒子节速度;③引入GA算法的交叉和变异操作;④对与历史最优解连续3次重复相同的g进行单维全分量的混沌局部搜索。采用此四项改进即可获得一种能同步提高全局和局部搜索能力的自适应混沌遗传粒子群算法(ACGPSO)。
1.2.1 自适应惯性权重在PSO算法的可调参数中,惯性权重w是最重要的参数,较大的w有利于提高算法的全局搜索能力,而较小的w会增强算法的局部搜索能力。基本的PSO算法采用的是固定权重法,即采用一个固定的w。在面对复杂问题时,由于难以预知一个适宜的w使得算法收敛到正确的解,因此固定权重法在处理实际问题时通常并不可取。为了平衡PSO算法的全局搜索能力和局部搜索能力,本文采用非线性的动态惯性权重系数,其表达式为[24]
| $ w=\left\{\begin{array}{ll}{w_{\min }+\frac{\left(w_{\max }-w_{\min }\right)\left(f-f_{\min }\right)}{f_{\mathrm{avg}}-f_{\min }}} & {f \leqslant f_{\mathrm{avg}}} \\ {w_{\max }} & {f>f_{\mathrm{avg}}}\end{array}\right. $ | (2) |
式中:wmax、wmin分别表示w的最大和最小值,本文取0.9和0.6;f为粒子当前目标函数值;favg、fmin分别为当前所有粒子的平均目标函数值和最小目标函数值。分析式(2)可知:当某粒子的目标函数值小于平均目标函数值时,对应惯性权重较小,从而保护了该粒子;反之,当某粒子目标函数值大于平均目标函数值时,对应的惯性权重较大,使该粒子向较好搜索区域靠拢。因此,该自适应惯性权重能根据当前粒子整体状况动态地给出不同粒子的惯性权重,全局性地改善算法的搜索能力。
1.2.2 设置节速度粒子在解空间中搜索的速度须得到控制,太大导致局部搜索能力不够,太小则收敛过慢。为使粒子具有合理的搜索速度,粒子的节速度设定为
| $ \begin{array}{c}{v_{\text {knot }}^{i}=\frac{b_{\mathrm{u}}^{i}-b_{1}^{i}}{\sum\limits_{j=1}^{d}\left(b_{\mathrm{u}}^{j}-b_{1}^{j}\right)} \sqrt{\sum\limits_{j=1}^{d} \frac{\left(b_{\mathrm{u}}^{j}-b_{1}^{j}\right)^{2}}{n_{\mathrm{pop}}}}} \\ {i=1, 2, \cdots, d}\end{array} $ | (3) |
式中:vknoti表示粒子第i维节速度;bui、bli分别为第i维对应的搜索范围的上、下边界;npop为粒子个数。当粒子速度超过一节速度时,其速度在该节速度内重新随机选取,但保留速度方向。可见节速度限定了粒子在一次迭代中能行走的最远距离。
1.2.3 交叉和变异操作PSO算法收敛速度快、过于早熟的缺陷缘于进化后期基因多样性的缺失。针对此现象本文引入遗传算法中的交叉和变异操作,使其能较好地弥补该缺陷。若某次迭代满足交叉概率Pc (本文取0.9),则选取指定数量的粒子放入杂交池内,池中粒子随机两两杂交,产生同样数目的子代,并用子代粒子替代父代粒子。针对交叉得到的变异概率小于预设阈值(本文取0.05)的子代,进行特定基因位置的突变。子代位置(xchild)和速度(vchild)分别为
| $ \left\{\begin{array}{l}{\boldsymbol{x}_{\text {child }}=q \boldsymbol{x}_{\text {parent1 }}+(1-q) \boldsymbol{x}_{\text {parent2} }} \\ {\boldsymbol{v}_{\text {child }}=\frac{\boldsymbol{v}_{\text {parent1}}+\boldsymbol{v}_{\text {parent2} }}{\left|\boldsymbol{v}_{\text {parent1 }}+\boldsymbol{v}_{\text {parent2} }\right|}\left|\boldsymbol{v}_{\text {parent1}}\right|}\end{array}\right. $ | (4) |
| $ \left\{\begin{array}{l}{x_{\text {child }}^{m}=x_{\text {child }}^{m}+r_{3}\left(b_{\mathfrak{u}}^{m}-b_{1}^{m}\right) \frac{t}{t_{\max }}} \\ {v_{\text {child }}^{m}=\left(1-r_{4}\right) v_{\text {child }}^{m}}\end{array}\right. $ | (5) |
式中:q是0~1之间均匀分布的随机数;xparent、vparent分别为父代的位置和速度;xchildm、vchildm分别为子代突变基因(维度)m对应的位置和速度;r3、r4为-1~1之间均匀分布的随机数;bum、blm分别为基因(维度)m对应的搜索范围的上、下边界;tmax为最大迭代次数。从式(5)可知,随着迭代次数的增多,变异幅度加大,这样就能有效克服基本粒子群算法在过早陷入局部最优解后停滞不前的缺点。
1.2.4 单维全分量的混沌局部搜索PSO算法本身具有记忆性,能随时将搜寻到的最优解记录在g中。如果当前种群最优解g已与历史最优解连续3次重复相同,就对第3次的g执行单维全分量混沌局部搜索,即从解向量的第1分量到第d分量,分别只对其中一个分量增加一个混沌扰动量,从而形成d个混沌解。计算这d个混沌解的目标函数值,并将其与g的目标函数值比较,选出最小目标函数值对应的解替换g,并将其作为本次迭代搜寻到的最优解。混沌解的具体公式为
| $ \left\{\begin{array}{ll}{g_{\text {new} i}^{j}=g^{j}+\alpha\left(b_{\mathfrak{u}}^{j}-b_1^{j}\right) s_{i}^{j}} \\ {s_{i}^{j}=\left\{\begin{array}{ll}{4 \sin \frac{2}{R_{i}}} & {j=i} \\ {0} & {j \neq 0}\end{array}\right.}\end{array}\right. $ | (6) |
式中:si为第i个混沌解gnewi的混沌系统扰动量;sij为si的第j个分量;Ri为si的0~1之间均匀分布的随机数;gnewij为混沌解的第j个分量;gj为当前最优解g的第j个分量;α为控制参数,本文取0.01。显然,混沌解受混沌系统扰动量和控制参数调控,在当前最优解附近做局部搜寻,一旦发现混沌解中最优的解优于当前最优解,即将其赋值给当前最优解。因此,单维全分量的混沌局部搜索有利于增强算法的局部搜索能力,提高求解精度。
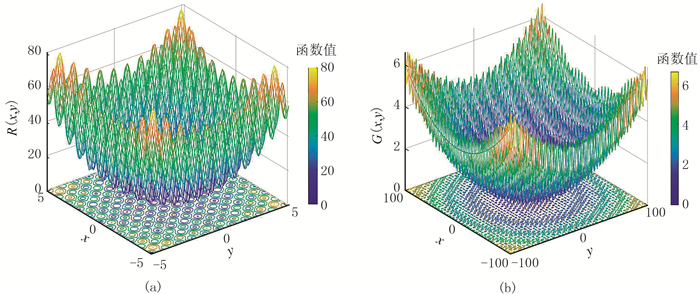
1.3 ACGPSO算法测试为了验证ACGPSO算法处理复杂问题的性能,选择Rastrigin函数和Griewank函数对其进行测试。Rastrigin函数由于有非常多的局部最小值点和局部最大值点,很容易使算法陷入局部最优,而得不到全局最优解,因此对模拟退火等进化算法具有很强的欺骗性。Griewank函数是典型的非线性多模态函数,具有广泛的搜索空间,通常被认为是优化算法很难处理的复杂多模态问题。利用上述两种函数对ACGPSO算法进行测试可验证算法的准确性。两者的二维表达式分别为[22]
| $ R(x, y)= 20+x^{2}+y^{2}-10[\cos (2 {\rm{ \mathsf{ π} }} x)+\\ ~~~~~~~~~\cos (2 {\rm{ \mathsf{ π} }} y)] \quad x, y \in[-5.12, 5.12] \\ G(x, y)=\frac{x^{2}+y^{2}}{4000}-\cos x \cos \frac{y}{\sqrt{2}}+1 \\ ~~~~~~~~~x, y \in[-100, 100] $ |
两函数均在(x, y)=(0, 0)处取得全局最小值0。图 1为两函数的曲面,从中可直观地看到它们有很多局部最优解。
|
图 1 Rastrigin函数(a)和Griewank函数(b)的曲面 |
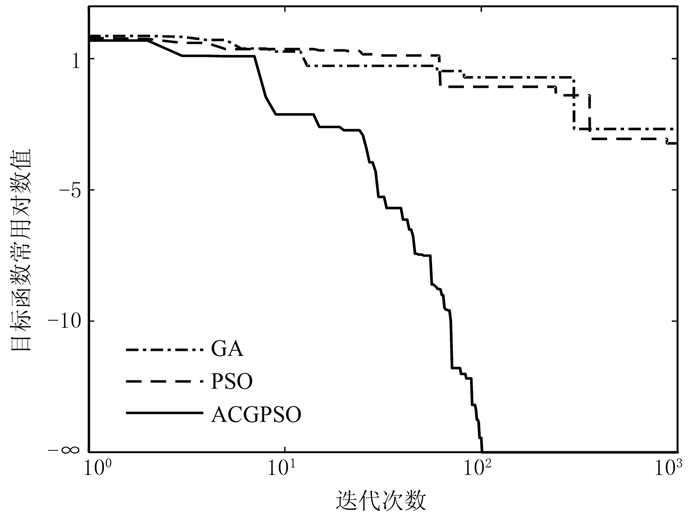
分别运用GA、PSO和ACGPSO算法对Rastri-gin函数和Griewank函数寻优求解,设定迭代次数为1000,种群数为40。三种算法均求取10次平均值作为该算法的最终值,最终计算结果(全文均保留小数点后两位)如表 1和图 2所示。
|
|
表 1 三种算法寻优结果对比 |
由表 1可知:GA和PSO两种算法在当前设置的搜索范围内未搜索到理论解,寻优能力过弱;而ACGPSO算法能100%收敛到测试函数的理论解,寻优结果明显优于另两种算法。就求解速度而言,ACGPSO算法略慢于PSO算法的主要原因是前者增加了交叉和变异操作及混沌局部搜索,但其速度快于GA算法。从图 2可见:GA和PSO两种算法迭代曲线下降缓慢,收敛不到理论解附近;而ACGPSO算法在1~100代目标函数值持续下降,迅速收敛,基本不存在GA和PSO算法出现的多代停滞进化的现象,100代后寻找到理论解。
|
图 2 三种算法对Rastrigin函数的寻优迭代对比 |
通过上述对比,证明综合改进后的ACGPSO算法克服了PSO算法疏于开发、易陷入局部最优解的缺陷,增强了其全局和局部搜索能力,提升了对全局最优解的收敛速度,且显著提高了最终解的精度。因此,在面对多参数、多极值的复杂问题时,ACG-PSO算法比常规PSO或GA算法具有更强寻优能力和更快收敛速度,这为瑞雷面波频散曲线的反演提供了很好的求解方案。
2 理论模型试算在完成Rastrigin和Griewank函数测试后,将ACGPSO算法应用于瑞雷面波理论模型频散曲线反演。采用实际工程勘查中常见的层状模型作为测试理论模型。模型A和B分别为四层含高速硬夹层、低速软夹层的地质模型,其参数及反演搜索范围如表 2所示。由于瑞雷面波频散曲线对于层厚和横波速度较敏感[7],因此选取这两个参数作为反演目标。为了减少初始模型对反演的影响,利用智能优化算法反演时通常设置较大的横波速度和层厚搜索范围。本次测试设定的搜索上、下限与理论参数值相差60%。为了充分验证ACGPSO算法的有效性和稳定性,反演均取10次的均值作为最终结果。反演迭代次数为80,粒子数是40。
|
|
表 2 模型参数及反演搜索范围 |
在瑞雷面波勘探中,通常从能量相对较强的基阶频散曲线中提取较准确的频散曲线,即仅利用基阶频散曲线作为反演对象。模型A提取5~100Hz频段基阶频散曲线,模型B提取5~70Hz频段基阶频散曲线进行反演。
反演采用如下目标函数
| $ P(M)=\sqrt{\sum\limits_{i=1}^{N} \frac{\left(V_{i}^{\mathrm{obs}}-V_{i}^{\mathrm{cal}}\right)^{2}}{N}} $ | (7) |
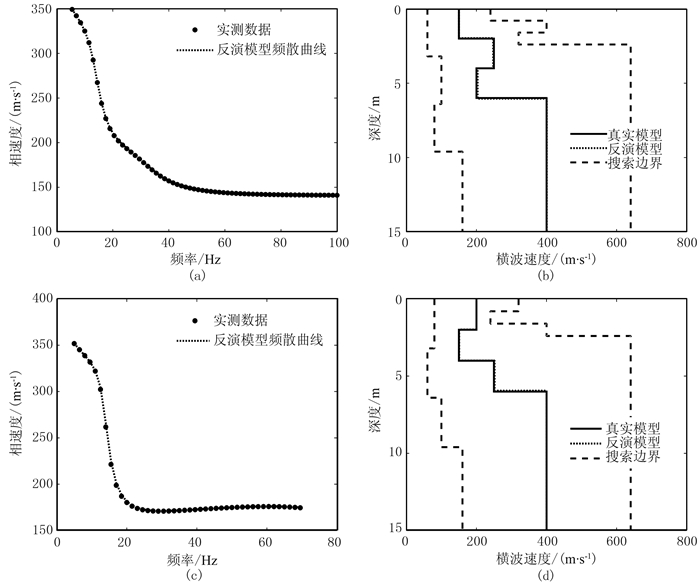
式中:M为某一反演模型;N为实测频散点个数;Vobs、Vcal分别为实测的与反演模型M的基阶频散曲线。采用该目标函数的ACGPSO算法反演结果如图 3和表 3所示。
|
图 3 模型A、B不含噪声数据的反演结果 (a)模型A频散曲线;(b)模型A反演的速度剖面;(c)模型B频散曲线;(d)模型B反演的速度剖面 |
|
|
表 3 不含噪与含噪数据反演结果统计表 |
从模型A和模型B计算得到的无噪声频散曲线的反演结果(图 3)可见:在预设的较大搜索范围内(图 3b和图 3d中短划线),ACGPSO算法能对理论模型的实测数据(图 3a和图 3c中圆点)进行有效反演,反演模型的频散曲线(图 3a和图 3c中虚线)与实测数据几乎完全拟合;各理论模型的参数(图 3b和图 3d中实线)也被很好地重建(图 3b和图 3d中虚线),平均相对误差分别仅为1.03%和0.70%,平均标准差分别为2.21和2.93。这些充分表明,ACGPSO算法能对理论模型的频散曲线进行有效而准确的反演。
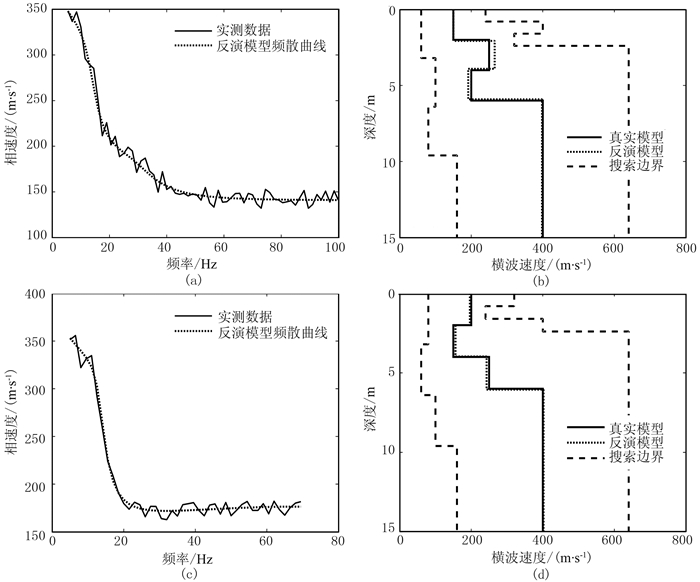
实际应用中瑞雷面波所提取的频散曲线中不可避免地含有一定的噪声,因此反演方法的抗噪能力是非常重要的。为了检验ACGPSO算法对含噪声频散曲线反演的能力,对模型A和模型B的频散曲线(图 3a和图 3c)加入10%的白噪声,反演结果见图 4和表 3所示。
|
图 4 模型A、B含噪声数据的反演结果 (a)模型A频散曲线;(b)模型A反演的速度剖面;(c)模型B频散曲线;(d)模型B反演的速度剖面 |
从图 4可看出:反演所得模型的频散曲线(图 4a和图 4c中虚线)能较好地拟合加噪后的频散曲线(图 4a和图 4c中实线);同时反演所得到的模型参数(图 4b和图 4d中虚线)与理论模型参数(图 4b和图 4d中实线)非常接近,平均相对误差分别为3.25%和2.23%,平均标准差分别为4.01和3.85。虽然加入噪声后的平均相对误差和平均标准差均有所增大,但反演结果依然具有可靠性和稳定性。因此,ACGPSO算法具有一定的抗噪性。以模型A为例,无论是对无噪还是对含噪数据反演,ACGPSO算法均能快速地在20代内收敛到最优解附近,随后的迭代曲线下降缓慢,直至趋于平缓,表明目标函数已收敛到最优解(图 5)。这说明ACGPSO算法反演频散曲线具有很好的收敛性。
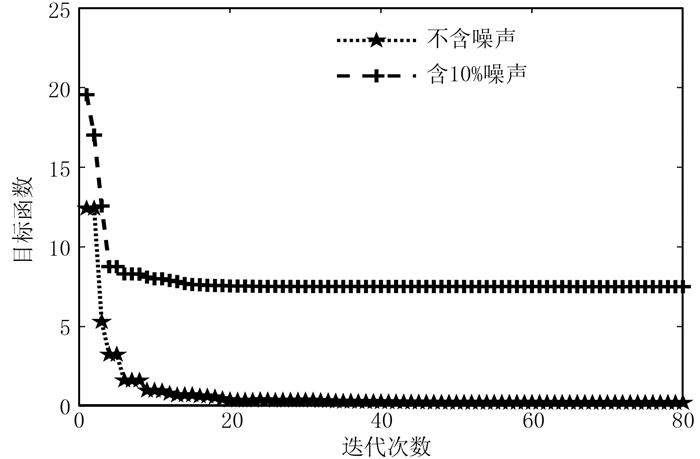
|
图 5 不含噪和含噪时模型A的目标函数变化曲线 |
对于类似模型A和模型B的含异常夹层的地层,在利用瑞雷面波法勘探时所获频散曲线常呈现呈现“之”字形回折现象[3, 25],该频散曲线随着频率增大,高阶模式的面波能量相对于基阶模式的面波渐渐占据主导优势。另外,通过对一些模型的测试可知,不同阶次的频散曲线对同一层的敏感度会有所不同,同阶次的频散曲线在不同层和不同频率上的敏感度也有所差异,这种情况下仅反演基阶频散曲线很难获取所有层的准确信息。因此在反演过程中加入高阶模式的频散曲线进行联合反演是非常有必要的。ACGPSO算法进行多阶频散曲线联合反演时的目标函数为[21]
| $ \mathit{\Phi } = \sum\limits_{i = 1}^m {\left\{ {{e_i}\left[ {\frac{1}{{{N_i}}}\sum\limits_{j = 1}^{{N_i}} {{{\left( {V_{i, j}^{{\rm{obs}}} - V_{i, j}^{{\rm{cal}}}} \right)}^2}} } \right]} \right\}} $ | (8) |
式中:i为频散曲线阶次;ei为第i阶权系数,依据各阶频散曲线数据质量确定,须满足e1+e2+… +em=1,因本文重点在于验证ACGPSO算法的适用性,为方便起见反演中均采用等值权重,即ei=1/m;Ni为第i阶频散曲线的频点个数;Vi, jobs、Vi, jcal分别为第i阶频散曲线在第j个频点上的实测相速度和反演模型的理论相速度。在模型A含噪实测数据中加入30~100Hz频段的二阶频散曲线和40~100Hz频段的三阶频散曲线;在模型B含噪实测数据中加入40~80Hz频段的二阶频散曲线和50~100Hz频段的三阶频散曲线。分别运用ACGPSO算法对其进行10次反演,反演结果取其均值,如图 6和表 4所示。
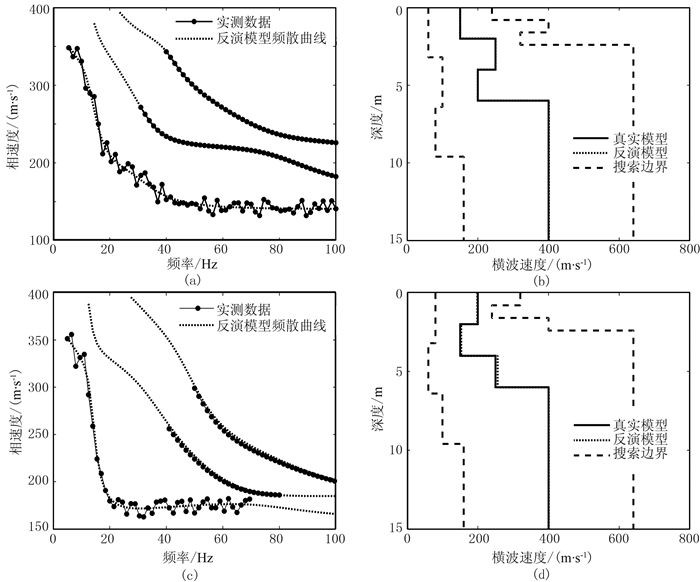
|
图 6 模型A和模型B多阶频散曲线联合反演结果 (a)模型A频散曲线;(b)模型A反演的速度剖面;(c)模型B频散曲线;(d)模型B反演的速度剖面 |
|
|
表 4 多阶频散曲线联合反演结果统计表 |
多阶频散曲线联合反演所得频散曲线(图 6a和图 6c中虚线)能与各阶实测频散曲线(图 6a和图 6c中点线)很好地拟合;反演模型参数(图 6b和图 6d中虚线)与理论模型参数(图 6b和图 6d中实线)的平均相对误差分别仅为0.22%和0.92%。平均标准差分别为1.42和2.79;与仅用基阶反演的结果相比,平均相对误差分别下降了3.03%和1.31%,平均标准差分别下降了2.59和1.06。特别是模型A中反演最差的高速层的相对误差和标准差分别由6.13%和15.16降至0.09%和1.62;模型B中反演最差的第三层的相对误差和标准差分别由2.92%和16.74降至2.43%和11.17。由此可见,运用多阶频散曲线联合反演能有效降低解的多解性,提高解的稳定性和精度;同时也证明ACGPSO算法不仅能应用于基阶频散曲线反演,也能应用于多阶频散曲线联合反演。
2.3 与PSO算法反演的对比为了证明ACGPSO算法在反演应用中优于PSO算法,现用PSO算法对模型A含噪数据进行多阶频散曲线的联合反演,反演的粒子数、迭代数和反演次数均与ACGPSO算法相同。将PSO算法与ACGPSO算法的最佳反演结果进行对比(图 7)。从图 7a可见:PSO算法收敛速度低于ACGPSO算法,最终的目标函数值也大于后者。从图 7b可见:ACGPSO算法反演得到的当前最佳模型在迭代前期能迅速向理论模型靠近,在后期能保持相对的稳定;而PSO算法反演得到的当前最佳模型不仅向理论模型靠近缓慢,还存在反复跳跃的不稳定性现象,因此所得最终反演结果比ACGPSO算法差。这充分说明在频散曲线反演中,ACGPSO算法比PSO算法具有更快的收敛速度、更强的稳定性和更高的反演精度。
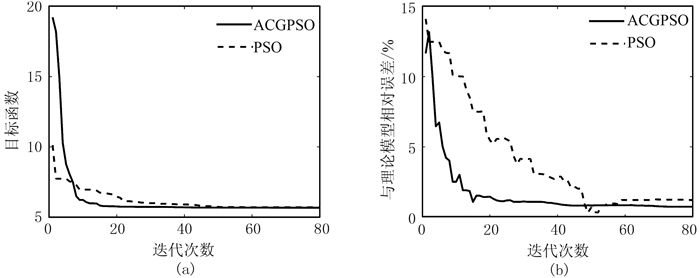
|
图 7 ACGPSO算法与PSO算法对比 (a)目标函数变化曲线;(b)当前最优模型与理论模型的相对误差变化曲线 |
对理论模型的基阶和多阶频散曲线的反演,验证了ACGPSO算法在频散曲线反演中的可行性。为了进一步验证ACGPSO算法的实用性,现对美国怀俄明M地区现场实测地震数据进行反演和分析。本次现场数据采集采用了48个8Hz垂直分量检波器,道间距为0.9m,最小炮检距为0.9m,选用锤击震源。采集所得地震记录如图 8a所示;图 8b为从炮集记录提取的频散能量图,通过采集能量最大点提取所需频散点。从图 8b中可见频散点分为两段:第1段为10~27Hz的基阶频散曲线;第2段为35~55Hz的高阶模式频散曲线。为了充分利用高阶频散信息,对该实测数据做两步法反演:①仅对第1段的频散曲线进行单纯的基阶频散曲线反演;②将第2段高阶频散点与第①步反演所得模型的理论频散曲线进行对比,确定其模态的归属,再对两段频散点做多阶频散曲线联合反演,将此结果作为最终反演结果。反演的初始模型数据取自测井资料,将该区划分为10个地层并设定搜索范围(表 5)。
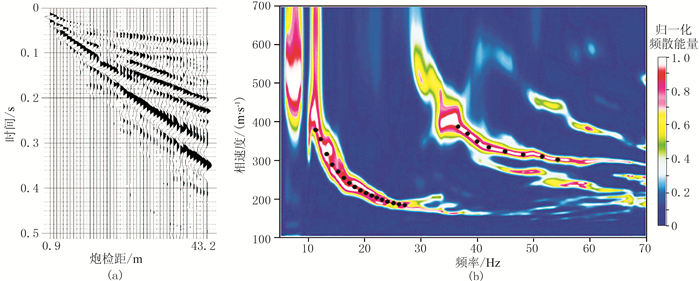
|
图 8 怀俄明地区实际地震数据与频散能量图 (a)实测地震记录;(b)频散能量图 |
|
|
表 5 怀俄明M地区反演搜索范围、密度和泊松比 |
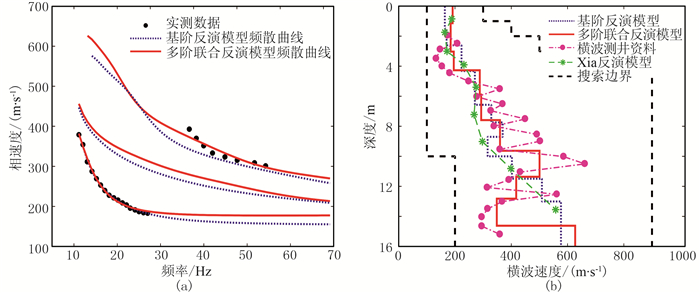
对最终反演结果(图 9)进行对比分析。图 9a为频散曲线对比图,其中虚线为仅用基阶面波频散曲线反演的模型频散曲线;第2段实测频散点归属于三阶的频散曲线;实线为采用多阶频散曲线反演得到的模型频散曲线,该频散曲线与实测数据提取的两段频散点都能较好地对应。在横波速度剖面(图 9b)中,多阶(实线)比仅用基阶(虚线)频散曲线反演得到的横波速度更接近于测井曲线(粉红点线)。与Xia等[26]的局部线性优化结果(绿星点线)相比,在深度为8m范围内两者基本一致,但在较大深度上更能体现测井速度的变化,特别是在12~15m段内,该反演模型准确地刻画出测井低速段。因此,ACGPSO算法中多阶联合反演相比于单纯基阶反演和局部线性化方法,能获取地下介质的更精准地质信息,这也充分证明ACGPSO算法在实际资料处理中具有较好的适用性。
|
图 9 怀俄明M地区频散曲线反演结果 (a)实测数据(圆点)、基阶(虚线)和多阶联合(实线)反演模型频散曲线;(b)横波速度剖面与测井资料 |
本文从四个方面改进了PSO算法的全局和局部搜索能力,提出了自适应混沌遗传粒子群算法(ACGPSO);采用两种测试函数检测了新算法的优化能力,并将其运用于瑞雷波频散曲线理论模型和实测数据的反演与分析中,取得了以下认识。
(1) ACGPSO算法对两种测试函数均能100%收敛到其理论解,比常规PSO算法和GA算法具有更高的寻优求解能力和收敛速度。
(2) ACGPSO算法对无噪和含噪的频散曲线反演均能取得很好效果,充分表明了该算法的有效性、稳定性和抗噪性,同时也证明基于ACGPSO算法的反演比PSO算法具有更快的收敛速度,更强的稳定性和更高的反演精度。
(3) 两步法反演可较好地判断高阶频散曲线对应的模态,以此进行的多模式联合反演更能反映地下地层真实情况,更具可信度及适用性。
感谢夏江海教授团队和中国地质大学(武汉)地球内部成像与探测实验室提供的实测数据。
| [1] |
夏江海. 高频面波方法[M]. 湖北武汉: 中国地质大学出版社, 2015. XIA Jianghai. High-frequency Surface-wave Methods[M]. Wuhan, Hubei: China University of Geosciences Press, 2015. |
| [2] |
Park C B, Mille R D, Xia J H. Multichannel analysis of surface wave[J]. Geophysics, 1999, 64(3): 800-808. DOI:10.1190/1.1444590 |
| [3] |
张碧星, 肖柏勋, 杨文杰, 等. 瑞利波勘探中"之"字型频散曲线的形成机理及反演研究[J]. 地球物理学报, 2000, 43(4): 557-567. ZHANG Bixing, XIAO Baixun, YANG Wenjie, et al. Mechanism of zigzag dispersion curve in Rayleigh exploration and its inversion study[J]. Chinese Journal of Geophysics, 2000, 43(4): 557-567. DOI:10.3321/j.issn:0001-5733.2000.04.017 |
| [4] |
姜福豪, 李培明, 张翊孟, 等. 多道面波频散分析在实际大炮数据中的应用[J]. 石油地球物理勘探, 2018, 53(1): 17-24, 46. JIANG Fuhao, LI Peiming, ZHANG Yimeng, et al. Frequency dispersion analysis of MASW in real seismic data[J]. Oil Geophysical Prospecting, 2018, 53(1): 17-24, 46. |
| [5] |
李子伟, 刘学伟. 空间假频对频率-波数域瑞利面波频散曲线反演的影响[J]. 石油地球物理勘探, 2013, 48(3): 395-402. LI Ziwei, LIU Xuewei. Effects of spatial aliasing on frequency-wavenumber domain inversion of Rayleigh-wave dispersion curve[J]. Oil Geophysical Prospecting, 2013, 48(3): 395-402. |
| [6] |
李庆春, 邵广周, 刘金兰, 等. 瑞雷面波勘探的过去、现在和未来[J]. 地球科学与环境学报, 2006, 28(3): 74-77. LI Qingchun, SHAO Guangzhou, LIU Jinlan, et al. Past, present and future of Rayleigh surface wave exploration[J]. Journal of Earth Sciences and Environment, 2006, 28(3): 74-77. DOI:10.3969/j.issn.1672-6561.2006.03.016 |
| [7] |
Xia J H, Miller R D, Park C B. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves[J]. Geophysics, 1999, 64(3): 691-700. DOI:10.1190/1.1444578 |
| [8] |
崔建文. 一种改进的全局优化算法及其在面波频散曲线反演中的应用[J]. 地球物理学报, 2004, 47(3): 521-527. CUI Jianwen. An improved global optimization me-thod and its application to the inversion of surface wave dispersion curve[J]. Chinese Journal of Geophysics, 2004, 47(3): 521-527. DOI:10.3321/j.issn:0001-5733.2004.03.024 |
| [9] |
曹旭, 熊章强, 张大洲. 基于BP神经网络的瑞雷面波智能优化反演[J]. 工程地球物理学报, 2015, 12(4): 514-519. CAO Xu, XIONG Zhangqiang, ZHANG Dazhou. The Rayleigh surface wave intelligent inversion based on the BP artificial neural network[J]. Chinese Journal of Engineering Geophysics, 2015, 12(4): 514-519. DOI:10.3969/j.issn.1672-7940.2015.04.017 |
| [10] |
Beaty K S, Schmitt D R, Sacchi M. Simulated annealing inversion of multimode Rayleigh wave dispersion curve for geological structure[J]. Geophysical Journal International, 2002, 151(2): 622-631. DOI:10.1046/j.1365-246X.2002.01809.x |
| [11] |
蔡伟, 宋先海, 袁士川, 等. 利用粒子群优化算法快速、稳定反演瑞雷波频散曲线[J]. 石油地球物理勘探, 2018, 53(1): 25-34. CAI Wei, SONG Xianhai, YUAN Shichuan, et al. Fast and stable Rayleigh-wave dispersion-curve inversion based on particle swarm optimization[J]. Oil Geophysical Prospecting, 2018, 53(1): 25-34. |
| [12] |
Song X, Gu H, Zhang X, et al. Pattern search algo-rithms for nonlinear inversion of high-frequency Rayleigh wave dispersion curve[J]. Computer & Geosciences, 2008, 34(6): 611-624. |
| [13] |
张鑫源, 胡晓敏, 林盈. 遗传算法和粒子群优化算法的性能对比分析[J]. 计算机科学与探索, 2014, 8(1): 90-102. ZHANG Xinyuan, HU Xiaomin, LIN Ying. Comparisons of genetic algorithm and particle swarm optimization[J]. Journal of Frontiers of Computer Science and Technology, 2014, 8(1): 90-102. |
| [14] |
Mahor A, Rangnekar S. Short term generation sche-duling of cascadedhydro electric system using novel selfadaptive inertia weight PSO[J]. International Journal of Electrical Power & Energy Systems, 2012, 34(1): 1-9. |
| [15] |
Bonyadi M R, Michalewicz Z. A locally convergent rotationally invariant particle[J]. Swarm Intelligence, 2014, 8(3): 159-198. DOI:10.1007/s11721-014-0095-1 |
| [16] |
Tan Yue, Tan Guanzheng, Deng Shuguang. Hybrid particle swarm optimizationwith chaotic search for solving integer and mixed integer programming problems[J]. Journal of Central South University, 2014, 21(7): 2731-2742. DOI:10.1007/s11771-014-2235-6 |
| [17] |
Samani M, Tafreshi M, Shafieenejad I, et al. Minimumtime open-loop and closed-loop optimal guidance with GA-PSO and neural fuzzy for Samarai MAV flight[J]. IEEE Aerospace & Electronic Systems Magazine, 2015, 30(5): 28-37. |
| [18] |
彭刘亚, 任川. 基于粒子群算法的瑞雷波频散曲线反演研究[J]. 地球物理学进展, 2018, 33(4): 1682-1686. PENG Liuya, REN Chuan. Inversion of Rayleigh wave dispersion curve using particle swarm optimization algorithm[J]. Progress in Geophysics, 2018, 33(4): 1682-1686. |
| [19] |
邵广周, 李庆春, 吴华. 基于波场数值模拟的瑞利波频散曲线特征及各模式能量分布[J]. 石油地球物理勘探, 2015, 50(2): 306-315. SHAO Guangzhou, LI Qingchun, WU Hua. Characte-ristics of Rayleigh wave dispersion curve based on wave field numerical simulation and energy distribution of each mode[J]. Oil Geophysical Prospecting, 2015, 50(2): 306-315. |
| [20] |
罗银河, 夏江海, 刘江平, 等. 基阶与高阶瑞利波联合反演研究[J]. 地球物理学报, 2008, 51(1): 242-249. LUO Yinhe, XIA Jianghai, LIU Jiangping, et al. Joint inversion of fundamental and higher mode Rayleigh waves[J]. Chinese Journal of Geophysics, 2008, 51(1): 242-249. DOI:10.3321/j.issn:0001-5733.2008.01.030 |
| [21] |
侯征, 熊盛青, 杨进, 等. 基于人工蜂群算法的瑞雷波多阶模式非线性联合反演研究[J]. 地球物理学进展, 2018, 33(1): 362-371. HOU Zheng, XIONG Shengqing, YANG Jin, et al. Research on nonlinear joint inversion of multimode Rayleigh wave based on artificial bee colony algorithm[J]. Progress in Geophysics, 2018, 33(1): 362-371. |
| [22] |
Vinh P C, Malischewsky P G. Improved approxi-mations of the Rayleigh wave velocity[J]. Journal ofThermoplastic Composite Materials, 2008, 21(4): 337-352. DOI:10.1177/0892705708089479 |
| [23] |
Kennedy J and Eberhart R C.Particle swarm optimization[C].Proceedings of IEEE International Conference on Neural Networks, Perth, 1995, 4, 1942-1948.
|
| [24] |
龚纯, 王正林. 精通MATLAB优化计算[M]. 第4版. 北京: 电子工业出版社, 2016.
|
| [25] |
刘雪明, 凡友华, 翟佳羽, 等. 四种典型地层的瑞雷波"之"字型频散曲线数值模拟研究[J]. 地球物理学报, 2009, 52(12): 3042-3050. LIU Xueming, FAN Youhua, ZHAI Jiayu, et al. Numerical simulation of Rayleigh wave zigzag dispersion curve of four typical strata[J]. Chinese Journal of Geophysics, 2009, 52(12): 3042-3050. DOI:10.3969/j.issn.0001-5733.2009.12.013 |
| [26] |
Xia J, Miller R D, Park C B, et al. A pitfall in shallow shear-wave refraction surveying[J]. Journal of A-pplied Geophysics, 2002, 51(1): 1-9. DOI:10.1016/S0926-9851(02)00197-0 |



 张大洲, 湖南省长沙市岳麓区麓山南路932号中南大学地球科学与信息物理学院应用地球物理系, 410083。Email:
张大洲, 湖南省长沙市岳麓区麓山南路932号中南大学地球科学与信息物理学院应用地球物理系, 410083。Email: