② 中国石油勘探开发研究院西北分院, 甘肃兰州 730020
② Northwest Branch, Research Institute of Petro-leum Exploration and Development, PetroChina, Lanzhou, Gansu 730020, China
在反射波法地震勘探中,面波是主要的规则干扰波,具有低速、低频、强振幅和椭圆极化等特征。随着多分量地震勘探技术的发展,现场数据采集过程中通常会采用单点数字检波器接收方式,舍弃了传统检波器组合接收方式[1]。单点接收虽然会带来一些优势,但采集到的地震数据往往信噪比低、面波干扰严重。当采用宽方位或全方位观测系统时,面波和部分线性干扰在远离炮点的排列上,其视速度与转换波的传播速度接近;另外,转换波与面波在频率上有较大重叠范围,常规去噪方法难以在不损害有效波的情况下去除面波干扰[2]。陆上三分量地震记录中的面波干扰往往会掩盖较弱的反射信号,给后续处理与反演解释带来困难[3]。
在地震数据处理中,传统的面波压制方法主要有高通滤波、FK滤波、Radon变换等[4-5]。区域滤波是在面波分布区内对地震记录进行高通滤波以达到压制面波的目的。此类方法简单实用,只对面波区域内信号进行处理,对区域外的资料无影响[6]。但由于其本质仍是高通滤波,因此难免会对低频信号造成一定程度的损害。1965年Flinn[7]最早将极化滤波应用于天然地震中不同波型的分离,提出了协方差矩阵的统计方法。随着多分量地震勘探技术的发展,极化滤波也开始应用于地震记录的去噪。Perelberg等[8]对Flinn的经典极化滤波法做了改进,并引入基于椭圆率和方向性的权重函数。
Deighan等[9]率先将一维小波变换应用于面波压制,随后以小波变换为代表的时频分析法逐渐被广泛地应用于地震数据处理[10-14]。Meersman等[15]利用SVD极化滤波成功地压制了低频地震数据中的面波;Diallo等[16]利用极化滤波在小波域实现了三分量地震数据波型分离;Chen等[17]提出一种自适应三分量地震记录极化滤波法,取得了较好去噪效果;马见青等[18]构建了时频域自适应协方差矩阵,提出一种时频域极化滤波压制面波的方法。
在利用极化滤波压制面波时,极化分析的时窗选择对面波压制效果有很大影响,使用固定/单一时窗会带来很大局限性。实际应用中,时窗大小若能随面波主频对应的波长变化,则会在很大程度上改善极化滤波效果。
本文针对三分量地震数据特点,综合考虑面波低频、低速和椭圆极化的特征,提出一种基于区域自适应极化滤波的面波压制方法:首先利用S变换进行区域滤波,但去除的面波干扰中不可避免地还残留一部分低频有效信号;再通过HHT计算面波干扰的瞬时频率从而设计自适应极化滤波窗口,使窗口大小可随面波波长的变化而改变;最后,利用自适应极化滤波所得低频有效信号对区域滤波结果进行补偿,得到面波压制后的最终地震记录。模型测试和实际数据处理结果表明,本文方法能在有效压制三分量面波干扰的同时,避免有效信号遭受损害。
1 方法原理 1.1 基于S变换的区域滤波区域滤波是一种针对目标区域的带通滤波。在面波压制的过程中,利用面波的低频特性对面波区域进行带通滤波。它与常规带通滤波的区别在于:带通滤波是针对整个数据体,而区域滤波则需根据面波的视速度设计合适的滤波窗口,从而减少对区域外信号的影响,最大限度地保留有效信息[19]。由于面波速度较低(通常为100~1000m/s),在地震记录中往往呈双曲线型或扇型分布,因此宜选择双曲线型或线型滤波窗口。面波线型滤波窗口定义为
| $ t(x)=t_{0}+\frac{x}{v} $ | (1) |
式中:t(x)表示炮检距为x的地震道窗口起始时间;v为面波视速度;t0为零炮检距处的窗口起始时间。在实际地震数据处理中,由于面波存在频散特性,其视速度会随着炮检距的增大而变化。为了得到更好的处理效果,可采用分段线型窗口(图 1)。
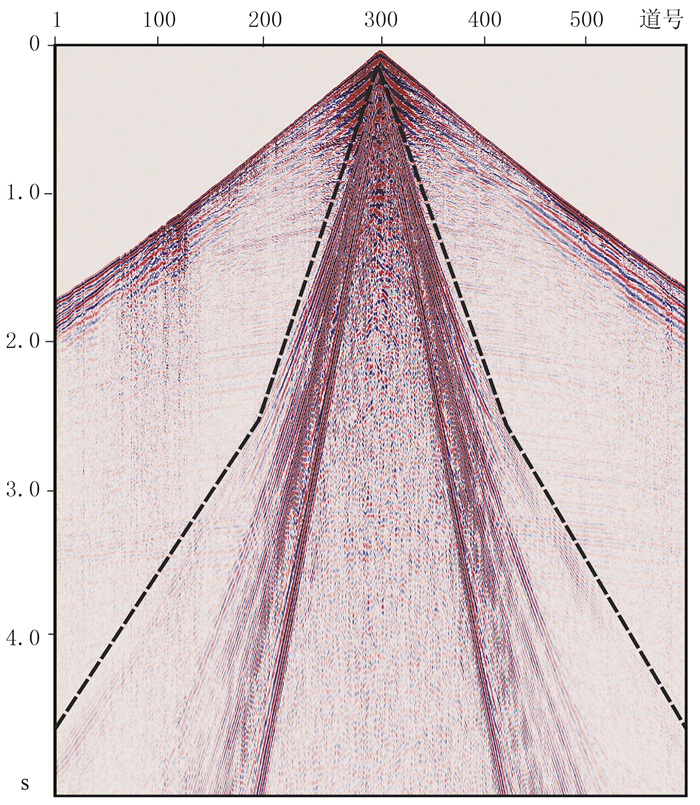
|
图 1 线型窗口示意图 |
S变换可看作是小波变换的一种延伸,其主要优点是分辨率可随频率的变化而改变,且在时频表示中各频率分量的相位谱与原始信号保持直接联系[20]。由于S变换具有可变的时窗宽度,能有效克服常规傅里叶变换的时频域分辨率差的缺点。因此,选用S变换做区域滤波,并在时频域设计滤波器,能提高区域滤波的精度。图 2b为利用S变换对图 1地震记录中第400道数据做时频分析的结果,其中红色框标示面波干扰的主要分布区域。
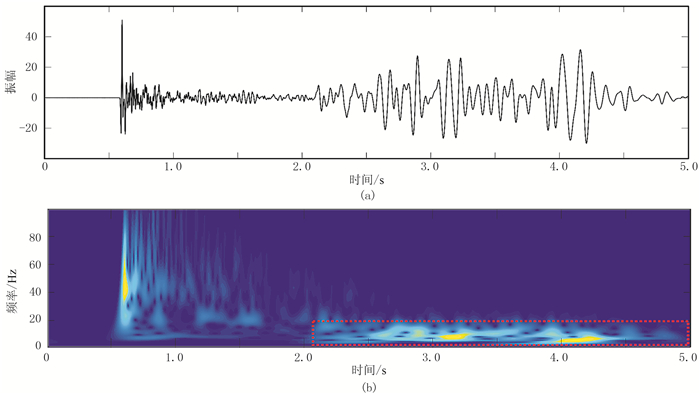
|
图 2 S变换时频域中的面波干扰 (a)图 1中第400道地震数据波形;(b)S变换时频谱 |
面波除了具有低速、低频特征外,另一重要特征是椭圆极化。在传播过程中,体波和面波质点的极化方式不同,可利用其不同的极化特征,采用基于极化分析技术的滤波方法压制面波干扰。在陆上三分量地震勘探中,采用单点数字检波器能记录到完整的波场矢量信息,这为利用极化滤波法压制面波创造了有利条件。在利用极化滤波压制面波过程中,极化分析的时窗大小是固定的,这种固定时窗在滤波时具有很大局限性。本文利用HHT计算地震记录中面波的瞬时频率,并根据面波主频求取对应波长,从而设计自适应极化滤波时窗。
HHT主要分为以下两步:首先对信号做经验模态分解(EMD),得到若干固有模态函数(IMF),并假设这些固有模态函数均为窄带信号;再对这些信号进行Hilbert变换,从而得到具有明确物理意义的瞬时参数。固有模态函数需同时满足两个条件:①该信号极值点的数目相等或至多相差一个;②在任何时间点上,由该信号的局部极大值点形成的包络线和由局部极小值点形成的包络线的平均值为零。
假设单道地震信号为x(t),找出x(t)的所有极值点,将所有的局部极大值点和极小值点利用三次样条函数进行拟合,得到上、下包络线u(t)和v(t),计算上、下包络的平均值得到原信号的平均包络线
| $ m(t)=\frac{u(t)+v(t)}{2} $ | (2) |
将原信号减去平均包络,可得不含低频成分的新信号
| $ h(t)=x(t)-m(t) $ | (3) |
若h(t)满足IMF条件,则为第一固有模态函数;否则,循环k次,使h1k(t)满足IMF条件,记为
| $ c_{1}=h_{1 k}(t)=h_{1(k-1)}(t)-m_{1 k}(t) $ | (4) |
从x(t)中分离出c1,得到去高频成分残余信号
| $ r_{1}=x(t)-c_{1} $ | (5) |
将r1作为原始信号重复以上步骤,得到第2,3,…,n个IMF分量,直至rn成为一个单调函数,不能再从中提取IMF分量时,循环停止;此时,原信号可表示为
| $ x(t)=\sum\limits_{i=1}^{n} c_{i}(t)+r_{n}(t) $ | (6) |
则原始地震信号x(t)被分解为n个IMF分量和一个残余量rn(t)。对IMF分量做Hilbert变换,得到具有物理意义的瞬时参数
| $ \hat{c}_{i}(t)=\frac{1}{{\rm{ \mathsf{ π} }}} \int_{-\infty}^{\infty} \frac{c_{i}(\tau)}{t-\tau} \mathrm{d} \tau $ | (7) |
据解析函数定义,ci(τ)和
| $ X(t)=c_{i}(\tau)+\mathrm{j} \hat{c}_{i}(t)=a_{i}(t) \mathrm{e}^{\mathrm{j} \phi_{i}(t)} $ | (8) |
则瞬时振幅、瞬时相位及瞬时频率可表示为
| $ \left\{\begin{array}{l}{a_{i}(t)=\sqrt{c_{i}^{2}(\tau)+\hat{c}_{i}^{2}(t)}} \\ {\phi_{i}(t)=\arctan \frac{\hat{c}_{i}(t)}{c_{i}(\tau)}} \\ {f_{i}(t)=\frac{\mathrm{d} \phi_{i}(t)}{\mathrm{d} t}}\end{array}\right. $ | (9) |
自适应极化滤波的时窗Tn(n为样点数)定义为
| $ T_{n}=k_{\mathrm{T}} \bar{\lambda}_{\mathrm{R}}=\frac{3 k_{\mathrm{T}} v_{\mathrm{R}}}{f_{x}+f_{y}+f_{z}} $ | (10) |
式中:kT为自适应时窗的调节因子,经实验测试,kT取2时效果较好;fx、fy和fz对应为同一位置三分量地震数据的瞬时频率;vR为瑞雷波的速度;λR为瑞雷波的平均波长。以三分量地震记录为例,说明基于协方差矩阵的自适应极化滤波基本原理。首先,将同一位置的三分量地震数据放在一个自适应时窗Tn内,形成如下矩阵
| $ \boldsymbol{M}=[\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}] $ | (11) |
式中:x, y, z分别为列向量,若每列都含有n个采样点,则M就是一个n×3矩阵。令协方差矩阵Mc=MTM,“T”表示矩阵的转置,那么
| $ \boldsymbol{M}_{\mathrm{c}}=\boldsymbol{M}^{\mathrm{T}} \boldsymbol{M}=\sum\limits_{i=1}^{n}\left[\begin{array}{ccc}{x_{i}^{2}} & {x_{i} y_{i}} & {\boldsymbol{z}_{i} x_{i}} \\ {x_{i} y_{i}} & {y_{i}^{2}} & {z_{i} y_{i}} \\ {z_{i} x_{i}} & {z_{i} y_{i}} & {z_{i}^{2}}\end{array}\right] $ | (12) |
由于MT是3×n的矩阵,则Mc为一个3×3的矩阵。极化分析通过对Mc进行分解,得到其特征值和特征向量,分别用于判别能量大小及传播方向。奇异值分解可用下式表示
| $ \boldsymbol{M}=\boldsymbol{U} \boldsymbol{M} \boldsymbol{V}^{\mathrm{T}} $ | (13) |
式中:V表示Mc的特征向量,为一个3×3的矩阵;W是一个对角矩阵,其对角元素是矩阵M的奇异值,每一个奇异值是Mc对应特征值的正平方根。滤波器的设计主要是依据对椭圆率及传播方向主轴的估计,因此分别定义椭圆权重函数G1(t)和方向权重函数G2(t)为
| $ \left\{\begin{array}{l}{G_{1}(t)=1-\varepsilon} \\ {G_{2}(t)=|\cos \Delta \theta(t)|}\end{array}\right. $ | (14) |
式中:ε是反椭圆率;Δθ(t)是期望入射角与实际入射角的夹角。图 3为G1(t)、G2(t)示意图。
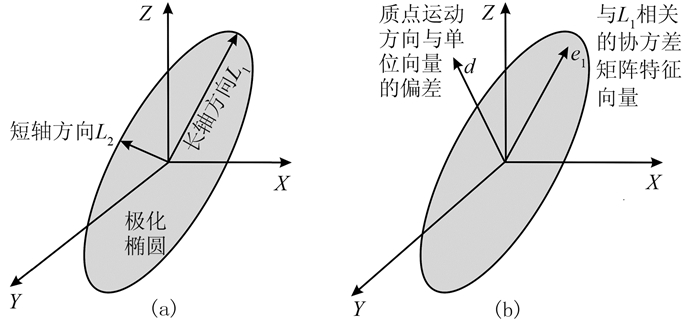
|
图 3 权重函数示意图 (a)椭圆( |
引入高斯权重函数代替上式中的线性和余弦函数,可将式(14)改写为
| $ \left\{\begin{array}{l}{G_{1}(t)=\exp \left[-\frac{\lambda(t)-\lambda_{0}(t)^{2}}{2 \sigma_{\lambda}^{2}}\right]} \\ {G_{2}(t)=\exp \left[-\frac{\Delta \theta(t)^{2}}{2 \sigma_{\theta}^{2}}\right]}\end{array}\right. $ | (15) |
式中:λ0(t)是期望椭圆率;σλ2和σθ2是椭圆率和入射角的方差;Δθ是期望的与实际的入射方向角度差。
质点的振动方向是协方差矩阵主特征值所对应的特征向量的方向。滤波过程可表示为
| $ R(t)=G_{1}(t) G_{2}(t) S(t) $ | (16) |
式中:S(t)表示输入的含有面波的地震记录;R(t)表示自适应极化滤波的结果。
1.3 基于区域自适应极化滤波的面波压制方法由前文的分析可知,基于S变换的区域滤波考虑了面波的低速、低频特征,但是会损害面波区域内与面波频带相同的低频有效信号。极化滤波考虑到面波与体波极化特征的不同,可据此将体波和面波进行分离。两种方法针对面波的不同特征,在面波压制的过程中具有一定的互补效果,因此本文提出了一种基于区域自适应极化滤波的面波压制方法,该方法通过自适应极化滤波提取的低频有效信号对区域滤波结果进行低频补偿,能够取得较好的面波压制效果。该方法的流程如图 4所示。
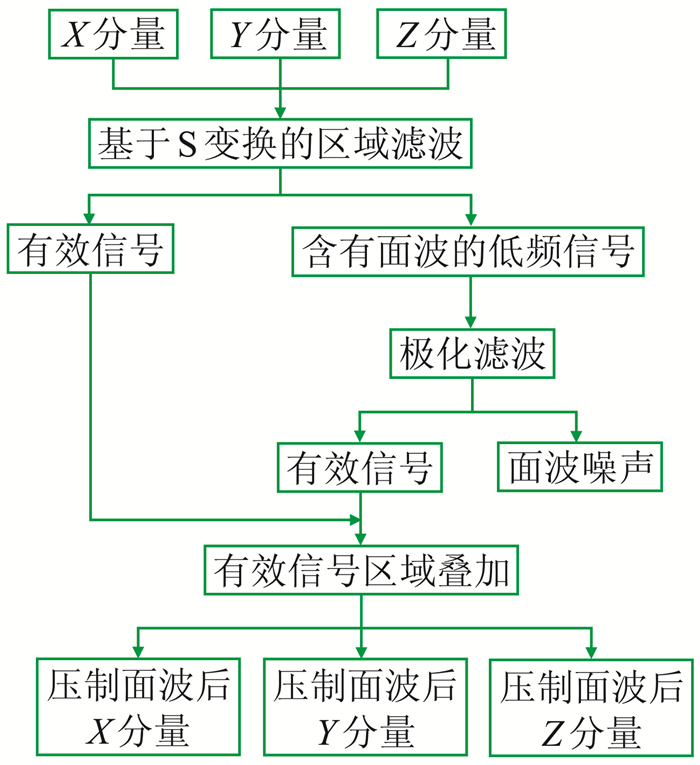
|
图 4 三分量面波干扰压制方法流程图 |
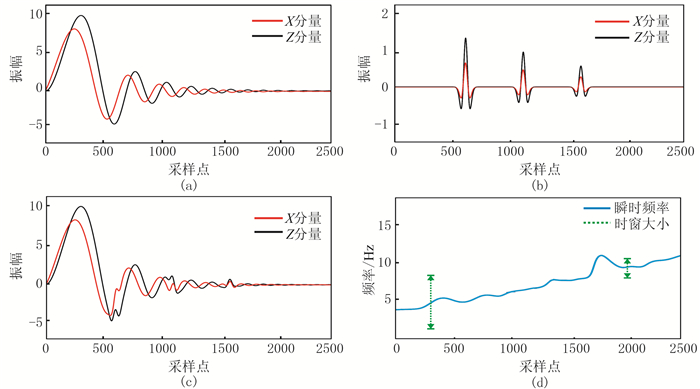
为了测试自适应极化滤波法的有效性,利用正弦扫描信号和指数函数模拟得到面波干扰(图 5a),与通过褶积合成的有效信号(图 5b)叠加,就得到图 5c所示的合成信号。利用HHT求出该信号的瞬时频率(图 5d,绿色线段表示自适应时窗大小),可见低频时取较大时窗,而在高频时取较小时窗。
|
图 5 一维合成信号 (a)面波干扰;(b)有效信号;(c)合成测试信号;(d)测试信号对应的瞬时频率 |
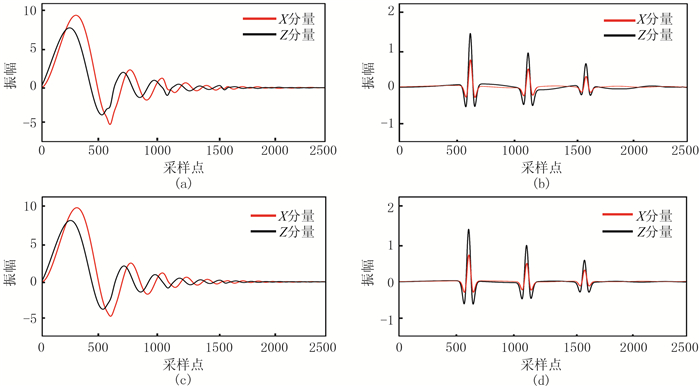
图 6为利用固定时窗和自适应时窗做极化滤波得到的信号分离结果。可见虽然两种方法都可分离出有效信号,但固定时窗极化滤波法对有效信号造成了损害,有效信号发生畸变(图 6b);相比之下,自适应极化滤波能更彻底地分离有效信号,且有效信号未遭受明显损害(图 6d)。
|
图 6 固定时窗(a、b)与自适应时窗(c、d)极化滤波分离得到的面波干扰(a、c)及有效信号(b、d) |
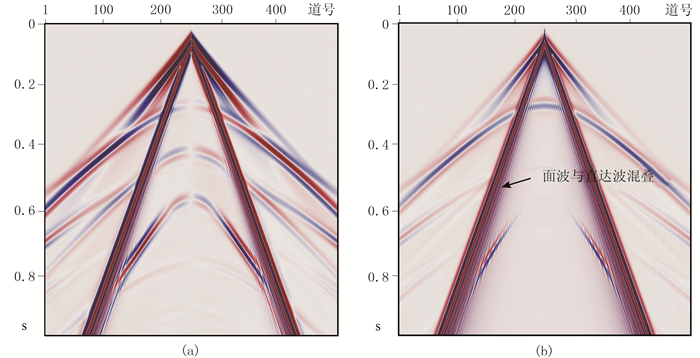
为验证本文方法的正确性和有效性,设计了一个水平层状模型,共包含三层,具体参数见表 1。针对该模型进行有限差分正演模拟,得到一个含有面波的二分量单炮记录(图 7)。图 7b中箭头处为与直达S波混叠在一起的面波干扰,可见其频散现象明显,严重干扰了有效信号的识别。
|
|
表 1 地层参数模型 |
|
图 7 含面波干扰的X(a)、Z(b)二分量正演记录 |
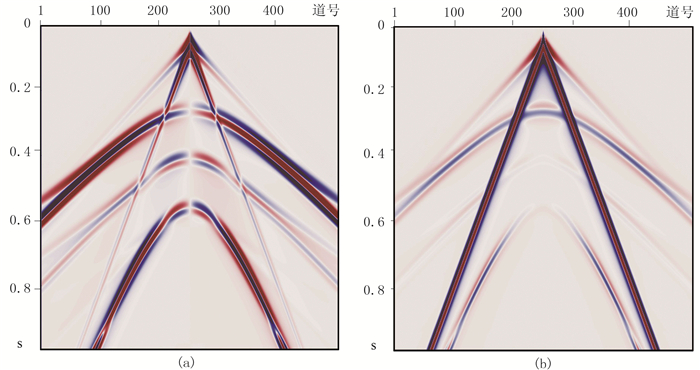
利用本文方法对正演记录做面波压制处理,得到如图 8所示的地震记录。从去噪后记录可见,箭头所指处(图 8b)面波得到了很好的压制,面波残留能量较少,直达波和面波被较彻底分离开,有效信号基本未受影响,易于识别。
|
图 8 使用本文方法压制面波后的X(a)、Z(b)二分量记录 |
图 9为分离出的面波成分,图中除了极少量的反射S波残留,大部分为面波噪声。从而验证了本文方法的有效性。
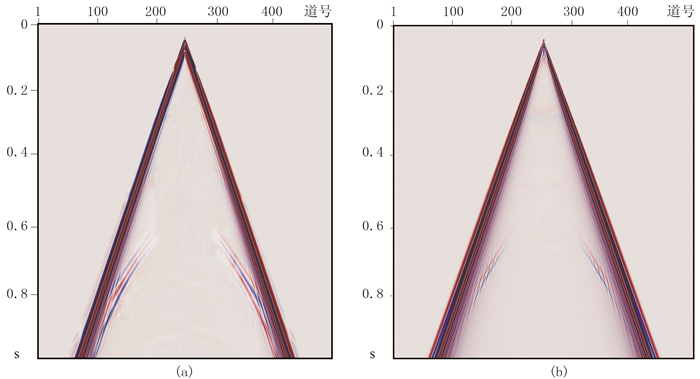
|
图 9 去除的面波的X(a)、Z(b)二分量成分 |
为验证本文方法的实际应用效果,针对实际地震资料进行了测试。图 10中三分量地震记录采集于胜利油田M工区,共有125道,记录长度为2.5s,时间采样率为0.5ms。从图 10c的Z分量黄色圈中可见明显的面波噪声,它基本呈扇形分布,频率分布范围是5~15Hz,严重干扰了有效信号的识别。
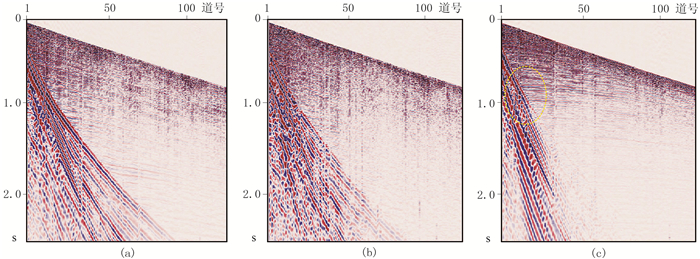
|
图 10 X(a)、Y(b)、Z(c)三分量原始单炮记录 |
图 11为利用区域滤波处理得到的结果,可见面波干扰虽被去除,但低频有效信号也受到了损害。对分离出的面波干扰应用HHT计算,得到三个分量地震数据的瞬时频率(图 12a~图 12c)及其平均值(图 12d)。

|
图 11 单独使用区域滤波压制面波后的X(a)、Y(b)、Z(c)三分量记录 |
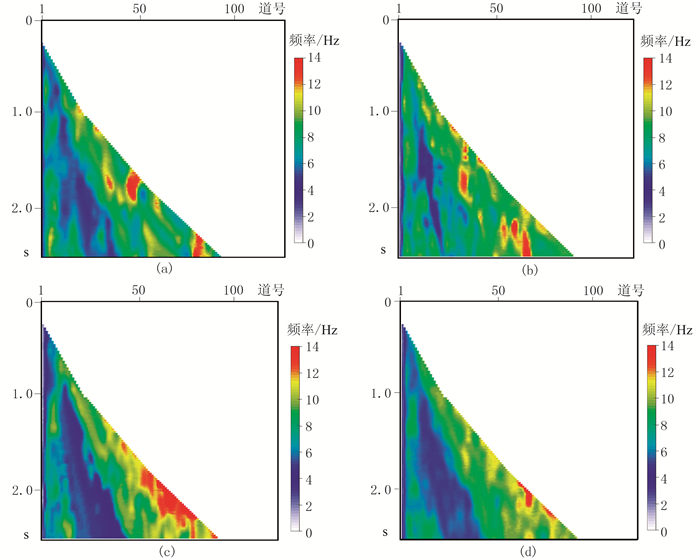
|
图 12 利用HHT计算的X(a)、Y(b)、Z(c)三分量地震数据的瞬时频率及其平均值(d) |
根据瞬时频率做自适应极化滤波,利用分离出的低频有效信号对区域滤波结果进行补偿(图 13)。
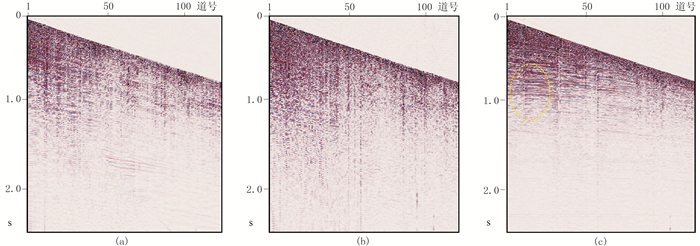
|
图 13 本文方法压制面波后的X(a)、Y(b)、Z(c)三分量记录 |
对比去噪前、后地震记录,可见原始记录中的面波成分已经得到较好压制,如图 13c的Z分量黄色圈中,被面波掩盖的有效反射波能清晰地显现出来,且同相轴连续性较好。
图 14为滤除的面波噪声,在其中未见到有效波同相轴,说明有效信号受到了较好保护。
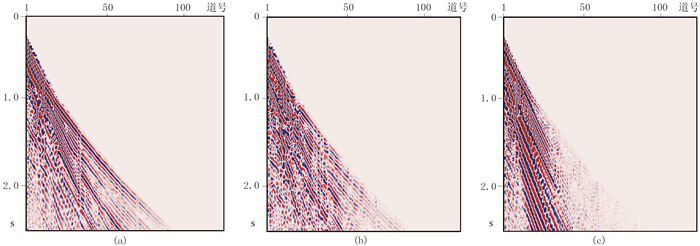
|
图 14 本文方法分离出的X(a)、Y(b)、Z(c)三分量面波 |
图 15为单独使用固定时窗极化滤波得到的面波压制记录。从图中容易看到,虽然大部分的面波能量已被滤除,但记录中仍残留了部分面波,不利于对有效信号的识别。
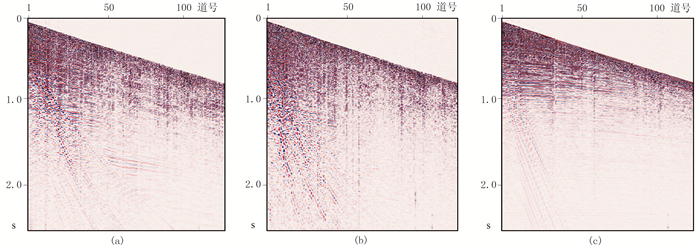
|
图 15 单独使用极化滤波压制面波后的X(a)、Y(b)、Z(c)三分量记录 |
利用本文方法压制面波前(黑线)、后(蓝线)第20道地震记录的波形及其放大显示的对比如图 16所示。可见其中的低频面波被较彻底地压制,有效信号得到了较好保护。尤其通过去噪前、后的波形放大对比,发现面波区域的噪声得到压制,其他区域的有效信号并未受到损害,故具有较好保幅性。

|
图 16 本文方法去噪前、后第20道X(a)、Y(c)、Z(e)三分量地震记录波形及其对应的局部放大(b、d、f) |
将本文方法与区域滤波法和极化滤波法压制面波前、后第20道地震记录的频谱(图 17~图 19)进行对比,可以看到:区域滤波法压制面波后的频谱(图 17)中,低频信号明显被损害;采用极化滤波法处理所得频谱(图 18)中,低频部分仍有少量面波残留,且其他频段的有效信号也受到一定程度的影响;采用本文方法在有效压制低频面波的同时,能够保护其他频段的有效信号(图 19)。这就再次验证了本文方法的有效性和保幅性。
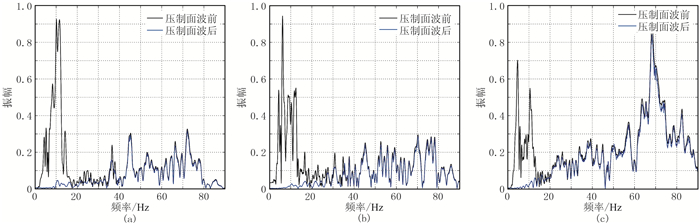
|
图 17 区域滤波去噪前、后第20道的X(a)、Y(b)、Z(c)三分量地震记录频谱 |

|
图 18 极化滤波去噪前、后第20道的X(a)、Y(b)、Z(c)三分量地震记录频谱 |

|
图 19 本文方法去噪前、后第20道的X(a)、Y(b)、Z(c)三分量地震记录频谱 |
全面考虑了面波具有的低速、低频和椭圆极化的特征,并综合区域滤波与极化滤波的优势,本文提出了一种基于区域自适应极化滤波的面波压制方法:利用S变换对区域滤波法进行改进,提高了其时频域的分辨率,摒弃单独使用区域滤波法,以免对低频有效信号造成损害;通过HHT变换计算面波干扰的瞬时频率,设计自适应极化滤波窗口,克服固定窗口在极化滤波过程中的局限性;利用自适应极化滤波的多分量去噪优势对区域滤波结果进行低频补偿,以取得更佳的面波压制效果。
模型测试和实际数据处理结果表明,本文方法能在有效压制地震记录中面波干扰的同时,较好地保护有效信号, 效果明显,实用性强。
| [1] |
姜福豪, 李培明, 张翊孟, 等. 多道面波频散分析在实际大炮数据中的应用[J]. 石油地球物理勘探, 2018, 53(1): 17-24, 46. JIANG Fuhao, LI Peiming, ZHANG Yimeng, et al. Frequency dispersion analysis of MASW in real seismic data[J]. Oil Geophysical Prospecting, 2018, 53(1): 17-24, 46. |
| [2] |
唐建明, 程冰洁, 徐天吉. 三维三分量地震勘探[M]. 北京: 地质出版社, 2011: 20-23. TANG Jianming, CHENG Bingjie, XU Tianji. 3D/3-C Seismic Exploration[M]. Beijing: Geological Publishing House, 2011: 20-23. |
| [3] |
Sun Chengyu, Wang Yanyan, Wu Dunshi, et al. Non-linear Rayleigh wave inversion based on the shuffled frog-leaping algorithm[J]. Applied Geophysics, 2017, 14(4): 551-558. DOI:10.1007/s11770-017-0641-x |
| [4] |
张军华. 地震资料去噪方法[M]. 山东青岛: 中国石油大学出版社, 2010: 30-33. ZHANG Junhua. Seismic Data Denoising Method[M]. Qingdao, Shandong: China University of Petroleum Press, 2010: 30-33. |
| [5] |
李振春, 张军华. 地震数据处理方法[M]. 山东东营: 中国石油大学出版社, 2004: 48-50. LI Zhenchun, ZHANG Junhua. Seismic Data Processing Method[M]. Dongying, Shandong: China University of Petroleum Press, 2004: 48-50. |
| [6] |
胡国斌, 王智杰. 几种面波压制方法的讨论[J]. 石化技术, 2016, 23(3): 65-66. HU Guobin, WANG Zhijie. Discussion on several surface wave suppression methods[J]. Petrochemical Technology, 2016, 23(3): 65-66. |
| [7] |
Flinn E A. Signal analysis using rectilinearity and direction of particle motion[J]. Proceedings of the IEEE on Teleseismic Signal Data Techniques, 1965, 53(12): 1874-1876. |
| [8] |
Perelberg A I, Hornbostel S C. Applications of seismic polarization analysis[J]. Geophysics, 1994, 59(1): 119-130. DOI:10.1190/1.1443522 |
| [9] |
Deighan A J, Watts D R. Ground-roll suppression using the wavelet transform[J]. Geophysics, 1997, 62(6): 1896-1903. DOI:10.1190/1.1444290 |
| [10] |
王西文, 刘全新, 高静怀, 等. 地震资料在小波域的分频处理与重构[J]. 石油地球物理勘探, 2001, 36(1): 78-85. WANG Xiwen, LIU Quanxin, GAO Jinghuai, et al. Frequency-shared processing and reconstitution of seismic data in wavelet domain[J]. Oil Geophysical Prospecting, 2001, 36(1): 78-85. DOI:10.3321/j.issn:1000-7210.2001.01.012 |
| [11] |
罗国安, 杜世通. 小波变换及信号重建在压制面波中的应用[J]. 石油地球物理勘探, 1996, 31(3): 337-349. LUO Guoan, DU Shitong. Application of wavelet transform and signal reconstruction in surface wave elimination[J]. Oil Geophysical Prospecting, 1996, 31(3): 337-349. |
| [12] |
陈文超, 高静怀, 包乾宗. 基于连续小波变换的自适应面波压制方法[J]. 地球物理学报, 2009, 52(11): 2854-2861. CHEN Wenchao, GAO Jinghuai, BAO Qianzong. Adaptive attenuation of ground roll via continuous wavelet transform[J]. Chinese Journal of Geophysics, 2009, 52(11): 2854-2861. |
| [13] |
邵婕, 孙成禹, 唐杰, 等. 基于字典训练的小波域稀疏表示微地震去噪方法[J]. 石油地球物理勘探, 2016, 51(2): 254-260. SHAO Jie, SUN Chengyu, TANG Jie, et al. Micro-seismic data denoising based on sparse representations over learned dictionary in the wavelet domain[J]. Oil Geophysical Prospecting, 2016, 51(2): 254-260. |
| [14] |
曹鹏涛, 张敏, 李振春. 基于广义S变换及高斯平滑的自适应滤波去噪方法[J]. 石油地球物理勘探, 2018, 53(6): 1128-1136, 1187. CAO Pengtao, ZHANG Min, LI Zhenchun. An adaptive filtering denoising method based on genera-lized S-transform and Gaussian smoothing[J]. Oil Geo-physical Prospecting, 2018, 53(6): 1128-1136, 1187. |
| [15] |
Meersman K D and Kendall R.A complex SVD-polarization filter for ground roll attenuation on multi-component data[C].Extended Abstracts of 67th EAGE Conference & Exhibition, 2005, B019.
|
| [16] |
Diallo M S, Kulesh M, Holschneider M, et al. Instantaneous polarization attributes based on adaptive approximate covariance method[J]. Geophysics, 2006, 71(5): V99-V104. DOI:10.1190/1.2227522 |
| [17] |
Chen Haifeng, Li Xiangyang, Qian Zhongping, et al. Robust adaptive polarization analysis method for elimi-nating ground roll in 3C land seismic[J]. Applied Geo-physics, 2013, 10(3): 295-304. |
| [18] |
马见青, 李庆春. 利用时频域极化滤波压制地震面波[J]. 石油地球物理勘探, 2015, 50(6): 1089-1097. MA Jianqing, LI Qingchun. Seismic surface wave suppression with polarization filtering method in time-frequency domain[J]. Oil Geophysical Prospecting, 2015, 50(6): 1089-1097. |
| [19] |
金守利. 区域滤波参数分析及效果[J]. 石油地球物理勘探, 2003, 38(增刊1): 52-56. JIN Shouli. Parameter analysis and effect of region filter[J]. Oil Geophysical Prospecting, 2003, 38(S1): 52-56. |
| [20] |
Tan Yuyang, He Chuan, Wang Yandong, et al. Ground roll attenuation using a time-frequency dependent polarization filter based on the S transform[J]. Applied Geophysics, 2013, 10(3): 279-294. DOI:10.1007/s11770-013-0383-3 |



 孙成禹, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
孙成禹, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: