从缺失的原始数据重建完整地震波场是经典的反问题。显然,地震数据重建可为后续的偏移成像、全波形反演等处理提供可靠的基础数据[1]。现今,地震数据的重建方法主要有以下六类。
基于滤波的重建方法是通过褶积插值滤波器实现插值,较常用的有基于预测误差滤波方法等[2]。此类方法的优点是不需反射同相轴的先验信息,不受假频影响;缺点是运算量较大,且只适用于规则采样的地震数据。
基于波场延拓算子的重建方法是通过Kirchhodff积分算子实现插值,主要有炮域延拓法[3]、炮检距域延拓法[4-5]和倾角时差校正法[6]等。该类方法的优点是灵活度高,能最大程度地利用地下信息;缺点是计算复杂度较高。
基于变换域重建的方法常采用Randon变换[7-8]、Fourier变换[9-10]、Curvelet变换[11-12]等,再在变换域完成地震数据的重建。该类方法的优点是计算速度快,可处理不同缺失形式的地震数据;缺点是不适用于有限带宽和含有空间假频的地震数据。
基于相干倾角插值的重建方法主要包括最大相干倾角插值法[13]和多倾角同相轴方法[14]。其优点是可自适应地做倾角扫描;缺点是不适用于含噪地震数据,对于高维地震数据的计算复杂度很高。
基于压缩感知理论的地震数据重建[15-18],其思想是利用变换域的稀疏性,将重建作为反问题求解。其主要方法有正交匹配追踪算法[19]、字典学习法[20-21]、光滑L1范数法[22]和Bregman迭代算法[23]等。它们的优点是计算速度快,可处理大规模问题;缺点是受噪声干扰影响较大。
近年来,作为压缩感知的二维推广形式,“矩阵补全”得到快速发展,基于“低秩补全”的地震数据重建也成为现今主流方法。其优点是比现有方法更简单、高效;缺点是须通过预变换建立低秩结构。基于低秩补全理论的重建方法的主要原理是:有限个线性同相轴的无缺失或无噪声污染的地震数据在频率切片上是低秩结构[24],而数据的缺失和噪声的存在导致地震数据构造的Hankel矩阵的秩的增加,因此可通过降秩处理实现数据重建。
经典的矩阵秩最小化是一个“NP难”(高复杂度)问题。对此,人们尝试将秩最小化近似转化为核范数最小化问题,再利用凸优化法进行求解。Trickett等[25]提出基于频率切片降秩的方法。Oropeza等[26]证明地震时频切片形成的块Hankel矩阵是低秩矩阵。Yang等[27]梳理了矩阵补全与地震数据重建的关系,针对地震数据重建提出核范数最小化模型,且说明了低秩矩阵补全的可靠性。Cai等[28]提出的奇异值阈值(Singular Value Thresholding,SVT)算法,主要是利用交替更新和梯度下降法求解核范数最小化问题,而SVT的加速算法可参见文献[29-30]。Goldfarb等[31]通过分离变量后,利用参数交替迭代更新和软阈值收缩算子求解,实现了不动点延续(Fixed Point Continuation,FPC)算法,且提出利用迭代方式更新观测数据,即FPC与Bregman迭代[32]相结合的算法。Toh等[33]通过利用目标函数的二阶泰勒逼近函数,再利用不同变量的相互交替更新,实现了加速近端梯度(Accelerated Proximal Gradient,APG)算法;并给出了改进的加速算法(Accelerated Proximal Gradient by Linesearch-like technique,APGL)。
FPC算法在每次迭代更新时都需进行奇异值分解(Singular Value Decomposition,SVD),因此会降低算法效率。传统解决方法是利用PROPACK加速包,该方法能对矩阵进行快速SVD。为了进一步提高计算效率,本文提出一种快速不动点延续(Fast Fixed Pointed Continuation,FFPC)算法,利用块克雷洛夫迭代近似奇异值分解算法(Block Krylov Iteration Methods for Approximate SVD,BKIMASVD)和子空间复用技术,在保证重构精度的同时可大幅度缩短运行时间。BKIMASVD是基于随机投影形式实现的,其计算复杂度远小于PROPACK中所采用的快速算法;子空间复用技术则通过减少迭代次数,大幅度缩短运行时间。通过以上两种技术的运用,相比传统加速算法,FFPC有更高的计算效率。
1 基于FPC算法的地震数据重建 1.1 基于低秩理论的地震数据重建模型地震数据重建的秩最小化模型为
| $ \min\limits_{\boldsymbol{X}} \operatorname{Rank}(\boldsymbol{X}) \quad \text { s. t. } \quad \mathscr{A}(\boldsymbol{X})=\boldsymbol{b} $ | (1) |
式中:X∈Rm×n为重建的地震数据,其中m、n为重建地震数据的维度,且有p=m×n;Rank(X)表示求X的秩;
式(1)的求解是个“NP难”问题,因此通常可将目标函数凸松弛为核范数最小化进行求解。
假设矩阵X有r个正奇异值σ1≥σ2≥…≥σr>0,则X的核范数定义为
| $ \|\boldsymbol{X}\|_{*} \triangleq \sum\limits_{i=1}^{r} \sigma_{i}(\boldsymbol{X}) $ |
则基于核范数最小化的地震数据重建的模型如下
| $ \min\limits_{\boldsymbol{X}}\left[\mu\|\boldsymbol{X}\|_{*}+\frac{1}{2}\|\mathscr{A}(\boldsymbol{X})-\boldsymbol{b}\|_{2}^{2}\right] $ | (2) |
式中μ为正则化参数。
1.2 FPC重建算法的步骤式(2)目标函数关于X的次梯度为
| $ \mu \partial\|\boldsymbol{X}\|_{*}+g(\boldsymbol{X}) $ | (3) |
式中:∂‖X‖*为核范数的导数;
假设重构矩阵X*为式(2)的最优解,则满足
| $ \begin{array}{l}{0 \in \tau_{ \mu} \partial\left\|\boldsymbol{X}^{*}\right\|_*+\tau g\left(\boldsymbol{X}^{*}\right)} \\ {\quad=\tau \mu \partial\left\|\boldsymbol{X}^{*}\right\|_*+\boldsymbol{X}^{*}-\left[\boldsymbol{X}^{*}-\tau g\left(\boldsymbol{X}^{*}\right)\right]}\end{array} $ | (4) |
式中变量τ>0。定义Y*=X*-τg(X*),式(4)等价于
| $ 0 \in \tau \mu \partial\left\|\boldsymbol{X}^{*}\right\|_*+\boldsymbol{X}^{*}-\boldsymbol{Y}^{*} $ | (5) |
对式(5)关于X*求积分,可知X*也是下式最优解
| $ \min\limits_{\boldsymbol{X} \in \boldsymbol{R}^{m \times n}} \tau \mu\|\boldsymbol{X}\|_{*}+\frac{1}{2}\left\|\boldsymbol{X}-\boldsymbol{Y}^{*}\right\|_{F}^{2} $ | (6) |
这样,式(2)的秩最小化问题即可利用文献[32]中定理3求解。表 1给出了具体的FPC算法步骤。
|
|
表 1 不动点延续算法(FPC)步骤 |
表 1中μ>0为常数,是正则化约束项μt的下限;0<ημ<1为常数;ε为迭代精度;M为最大循环迭代次数;Sτμt为非负向量收缩算子,定义为
| $ \begin{array}{c}{\boldsymbol{S}_{\tau \mu_{t}}(\sigma)=\left(\bar{\sigma}_{1}, \bar{\sigma}_{2}, \cdots, \bar{\sigma}_{\min (m, n)}\right)} \\ {\bar{\sigma}_{i}=\max \left(\sigma_{i}-\tau \mu_{t}, 0\right) \quad i \in\{1, 2, \cdots, \min (m, n)\}}\end{array} $ |
FPC算法中最重要的部分为循环体中的第2~第4步。假设循环终止迭代次数为M,由于第2步的截断SVD主要是针对稀疏矩阵Y操作的,再假设Y∈Rm×n中非零个数为Φ,选取的奇异值个数为k,则第2步复杂度为cSVDk|Φ|=O[mnmin(m, n)],其中cSVD为标准SVD复杂度常数;利用PROPACK加速包,可将计算复杂度降低为O(kmn)。计算第3步的复杂度为O[m(k+n)(2k-1)],第4步的复杂度为O(1)。
综上所述,FPC算法的平均复杂度为
| $ \begin{array}{c} k O[m m \min (m, n)]+k O[m(k+n)(2 k-1)]+k O(1) \\=M\left\{c_{\mathrm{SVD}}[m n \min (m, n)]+\right.\\\left.c_{\mathrm{mul}}[m(k+n)(2 k-1)+1]\right\} \end{array} $ | (7) |
传统加速型FPC算法的平均复杂度为
| $ M\left\{c_{\mathrm{SVD}}(k m n)+c_{\mathrm{mul}}[m(k+n)(2 k-1)+1]\right\} $ | (8) |
式中cmul为矩阵乘法的复杂度常数。
2 FFPC算法为了解决SVD算法复杂度较高的问题,本文提出的FFPC算法采用随机投影的分解方法,即将高维矩阵投影到低维矩阵,再进行SVD运算;同时利用子空间复用的方法减少迭代次数,降低计算复杂度,以进一步提高运行效率。
2.1 块克雷洛夫迭代近似奇异值分解算法BKIMASVD算法的主要思想是基于RandQB过程[34-35],将需要进行SVD的矩阵A降维分解,通过对维度更低的矩阵B进行SVD以达到快速分解的目的。RandQB过程可表示为
| $ \boldsymbol{A} \approx Q \boldsymbol{B} \quad \boldsymbol{A} \in \boldsymbol{R}^{n \times n}, \boldsymbol{Q} \in \boldsymbol{R}^{m \times l}, \boldsymbol{B} \in \boldsymbol{R}^{l \times n} $ | (9) |
式中l≪min(m, n)。
BKIMASVD的具体步骤为:首先对观测矩阵A随机采样得到采样矩阵AΩ,其中Ω∈Rn×(k+s)为随机产生的矩阵;将采样矩阵AΩ通过QR分解(将一个矩阵分解为一个正交矩阵与上三角矩阵的乘积)得到正交矩阵H0,在P次循环迭代过程中通过[Hi, ~]=QR[A(ATHi-1), 0]迭代方法逐步更新子空间Hi, i∈{1, 2, …, P};再将迭代产生的子空间Hi按列依次排列,扩充为更高维度的空间H;然后对高维空间H进行QR分解得到子空间矩阵Q,这样便得到低维矩阵B=QTA;最后对B进行SVD即可提高其计算效率。迭代参数P可提升子空间维度,提高重建精度[34],详细原理参见文献[35-38]。表 2为BKIMASVD的具体算法步骤。
|
|
表 2 BKIMASVD算法步骤 |
在FPC算法中,每个观测矩阵需进行多次SVD迭代更新。事实上,当FPC算法执行多次迭代后,迭代更新的矩阵Yt会趋于稳定,因此在后续对Yt进行迭代更新时,可复用第P次迭代产生的子空间Q,再对B=QTYt进行SVD[34]。当FPC算法中迭代次数t超过P后,复用技术可省去高维空间H和Q的迭代计算,从而有效缩短运行时间。
具体操作步骤为:当迭代次数小于P时,利用BKIMASVD对迭代更新的矩阵进行分解;当迭代次数超过P后,保留第P次产生的Q,直接从BKIMASVD算法(表 2中)的第6步开始执行,这样就可保证在高精度范围内提高计算效率。迭代中可将P设置较小,只要满足(k+s)P≪min(m, n)就可保证多次循环迭代时SVD的计算量大幅度降低,也就可在确保精度的情况下显著缩短运行时间。
本文提出的FFPC算法是以BKIMASVD替代SVD,同时利用子空间复用技术减少迭代更新次数,可极大地提高计算效率。表 3给出了FFPC算法的具体步骤。
|
|
表 3 FFPC算法步骤 |
FFPC与FPC算法最大的不同点在第2步,因此需首先分析BKIMASVD的复杂度。对于矩阵A∈Rm×n,BKIMASVD的第3步(表 2)中的每一次循环迭代所需计算量为2cmul(k+s)Nnnz+cQRm(k+s)2,则循环P次的计算量为
| $ 2 c_{\mathrm{mul}}(k+s) P N_{\mathrm{nnz}}+c_{\mathrm{QR}} m(k+s)^{2} P $ | (10) |
生成Q的计算量为cQRm(kP+sP)2,生成B的计算量为
| $ c_{\mathrm{mul}}(k+s) P N_{\mathrm{nnz}} $ | (11) |
对B进行SVD的计算量为
| $ c_{\mathrm{SvD}}[m(k P+s P) \min (m, k P+s P)] $ | (12) |
第8步(表 2)计算量为cmul[(k+s)P]2m,第9步(表 2)计算量为cmul[m(k+n)(2k-1)]。因此,BKIMASVD的复杂度为
| $ \begin{array}{c} 3 c_{\text {mul }} k P N_{\text {nnz }} +\left(\frac{c_{\mathrm{QR}}}{P}+c_{\mathrm{QR}}+c_{\text {mul }}\right) m(k P+s P)^{2}+\\ c_{\text {SVD }} m(k P+s P) \min (m, k P+s P)+ \\ c_{\text {mul }} m(k+s)(2 k-1) \end{array} $ | (13) |
式中:Nnnz表示矩阵A中的非零元素的个数;cQR表示QR分解的复杂度常数。且(k+s)P≪min(m, n),而传统SVD算法的复杂度为cSVD[mnmin(m, n)]=O[mnmin(m, n)],所以利用该算法可实现快速SVD。
同样,假设循环终止迭代次数为M,因第2步(表 3)的SVD主要针对稀疏矩阵Yt,假设Yt∈Rm×n中非零个数为Φ,选取奇异值个数为k,子空间复用个数为P,则第2步(表 2)主要复杂度为
| $ \begin{array}{l} P\left[3 c_{\text {mul }} k P N_{\text {nnz }}\right.+\left(\frac{c_{{\rm Q R}}}{P}+c_{{\rm Q R}}+c_{\text {mul }}\right) \times \\~~~~~(k P+s P)^{2} m+c_{\text {SVD }} m(k P+s P) \times \\~~~~~\left.\min (m, k P+s P)+c_{\text {mul }} m(k+s)(2 k-1)\right] \end{array} $ | (14) |
当次数超过P以后,由于复用前面计算的Q,所以只需计算B的分解,那么循环所需时耗为
| $ \begin{array}{l}(M-P)\left[c_{\text {mul }}(k+s) P N_{\text {nnz }}+\right.\\~~~~~ c_{\text {SVD }} m(k P+s P) \min (m, k P+s P)+\\~~~~~\left.c_{\text {mul }}(k P+s P)^{2} m+c_{\text {mul }} m(k+s)(2 k-1)\right] \end{array} $ | (15) |
则FFPC算法的复杂度为
| $ \begin{aligned} 3 c_{\text {mul }} & k P^{2} N_{\text {nnz }}+\left(c_{\mathrm{QR}}+c_{\mathrm{QR}} P\right) m(k P+s P)^{2}+\\ & M\left[c_{\mathrm{SVD}} m(k P+s P) \min (m, k P+s P)+\right.\\ &\left.c_{\text {mul }} m(k P+s P)^{2}+c_{\text {mul }} m(k+n)(2 k-1)\right] \end{aligned} $ | (16) |
当矩阵维度m、n较大、P很小(P≪M),且满足条件(k+s)P≪min(m, n)时,FFPC算法的复杂度近似为
| $ \begin{array}{l} M\left[c_{\mathrm{SVD}} m(k P+s P) \min (m, k P+s P)+\right.\\~~~~~\left.c_{\mathrm{mul}} m(k P+s P)^{2}+c_{\mathrm{mul}} m(k+n)(2 k-1)\right] \\~~~~~=M\left[\left(c_{\mathrm{SVD}}+c_{\mathrm{mul}}\right) m(k P+s P)^{2}+\right.\\ ~~~~~\left.c_{\mathrm{mul}} m(k+n)(2 k-1)\right] \end{array} $ | (17) |
而传统加速型FPC算法的复杂度可近似为
| $ M\left[c_{\mathrm{SVD}} k m n+c_{\mathrm{mul}} m(k+n)(2 k-1)\right] $ | (18) |
当P、k、s满足以上条件时,对比FFPC与FPC算法的复杂度,可知FFPC算法相对FPC具有更高的计算效率。
3 基于FFPC算法的地震数据重建理论证明了地震数据在频率切片上具有低秩结构特性,但地震数据的缺失会导致其构造Hankel矩阵的秩增加,于是缺失位置信息就可通过降秩进行重建。针对地震数据,图 1给出了基于FPC和FFPC算法的重建流程图。具体操作过程如下。
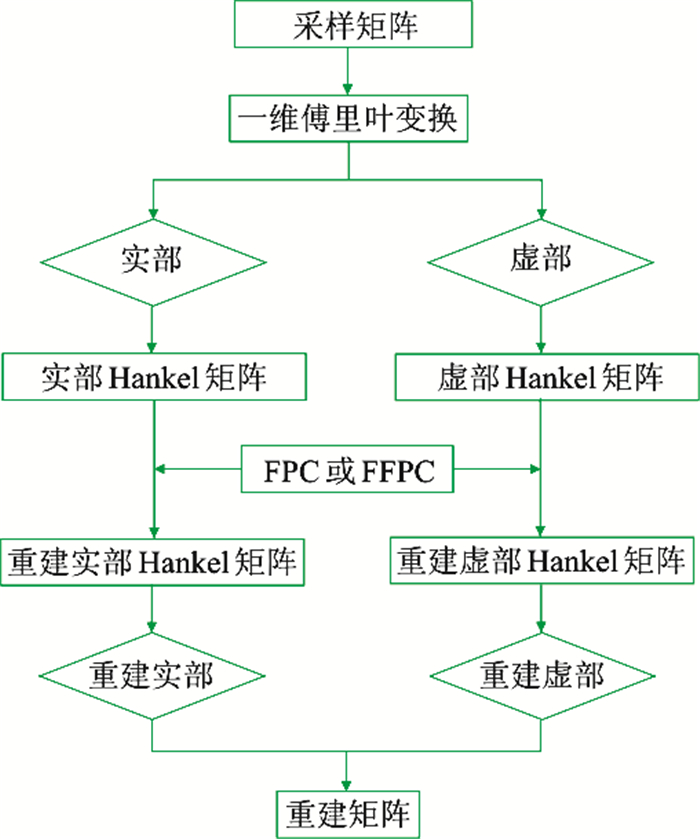
|
图 1 基于FPC和FFPC算法的地震数据重建流程 |
首先对缺失观测地震数据做一维傅里叶变换,得到实部和虚部两部分,再在频率域的每个切片上构造Hankel矩阵;对于每个Hankel矩阵,分别利用FPC和FFPC算法进行降秩重建;针对重建的Hankel矩阵用反对角取平均,即可得重建的频率切片;最后将重建的实部和虚部频率切片通过逆傅里叶变换到时间域,即完成了地震数据重建(图 1)。
4 实验测试实验选用两个主要衡量指标,即信噪比和运算耗时。信噪比的计算公式为
| $ \left\{\begin{array}{l}{R_{\mathrm{S} / \mathrm{N}}=10 \lg \frac{P_{\mathrm{s}}}{P_{\mathrm{n}}}} \\ {P_{\mathrm{s}}=\|\boldsymbol{I}\|_{F}^{2}} \\ {P_{\mathrm{n}}=\left\|\boldsymbol{I}_{\mathrm{n}}-\boldsymbol{I}\right\|_{F}^{2}}\end{array}\right. $ | (19) |
式中:Ps是信号能量;Pn是噪声能量;I为原始信号;In为噪声信号。此处运算耗时为重建过程所消耗的CPU时间。采用重建信噪比相对误差表征不同算法重建信噪比的差异,其计算表达式为
| $ \frac{\left|R_{\mathrm{S} / \mathrm{N}}^{(1)}-R_{\mathrm{S} / \mathrm{N}}^{(2)}\right|}{\left|R_{\mathrm{S} / \mathrm{N}}^{(2)}\right|} $ | (20) |
式中:RS/N(1)为FFPC算法的重建信噪比;RS/N(2)为FPC算法重建信噪比。主要参数设置:精度为0.01;迭代次数为100;秩选取为k;超采样参数(s)为5;幂迭代次数(P)为3。其中k=[0.1min(m,n)](其中[·]表示取整)是因为奇异值的前10%就占据整个矩阵的80%以上的能量,且需满足条件:(k+s)P≪min(m, n)。
4.1 仿真地震数据实验仿真数据由Ricker子波产生,它包含两条交叉的线性同相轴,仿真地震数据(图 2a)尺寸为256(道)×256(个)。对比原始仿真地震数据(图 2a)、随机缺失50%数据(图 2b)及其对应的频率—波数图(图 3a、图 3b),可见图 3b上有很明显的假频;从基于FFPC与FPC算法的重建结果(图 2c、图 2d)及其对应频率—波数图(图 3c、图 3d)上,清晰可见抗假频重构特征。当缺失率为50%时(表 4),FFPC与FPC的重建信噪比相对误差为0.38%,但FFPC算法耗时为FPC算法的1/1.66。显然,针对仿真地震数据,在确保高精度重建效果的同时,FFPC算法比FPC具有更高的计算效率。
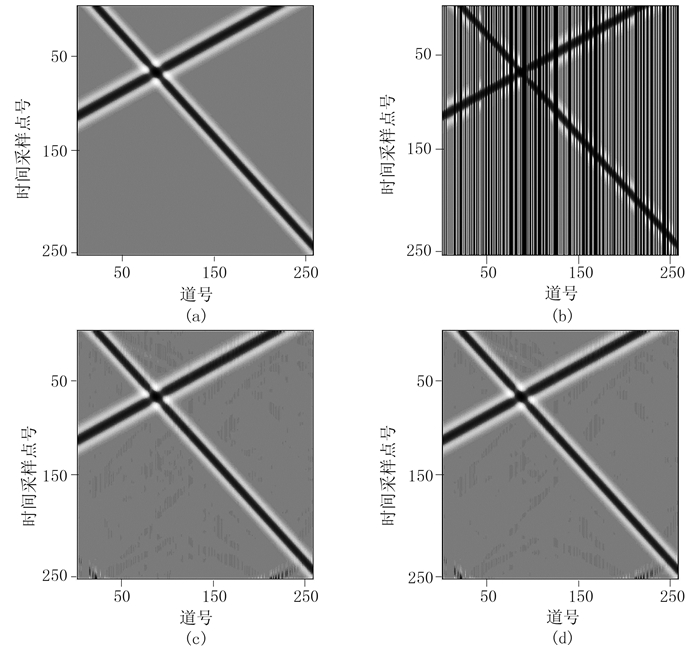
|
图 2 缺失率为50%的仿真地震数据重建效果对比 (a)原始数据;(b)随机缺失50%的数据;(c)基于FFPC重建的数据;(d)基于FPC重建的数据 |
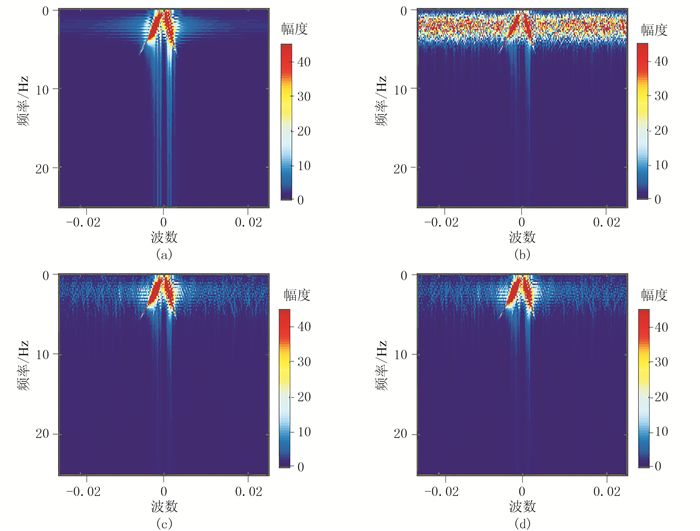
|
图 3 缺失率为50%时仿真地震数据频率—波数对比 (a)原始数据;(b)随机缺失50%的数据;(c)基于FFPC重建的数据;(d)基于FPC重建的数据 |
|
|
表 4 不同缺失率下仿真数据FPC与FFPC算法性能对比 |
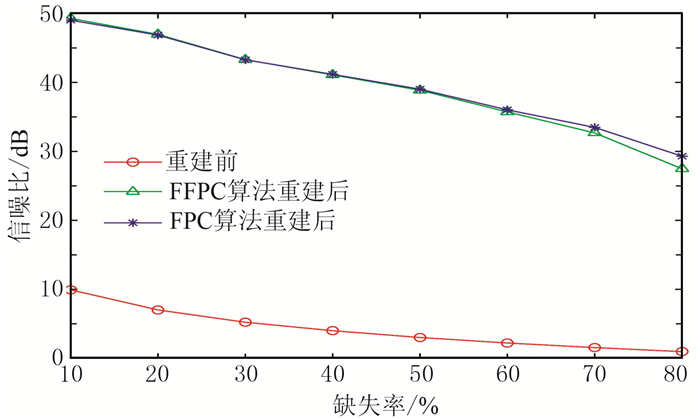
为了更详实地对比不同缺失率下FFPC和FPC算法的重建效果,分别测试了缺失率为10%~80%情况下基于两算法的重建信噪比和耗时(表 4、图 4和图 5)。可知在固定缺失率情况下,FFPC与FPC算法重建信噪比误差范围为0.38%~7.00%,而FFPC算法的重建耗时为FPC算法的1/3.53~1/1.59。FFPC和FPC算法的重建信噪比都随缺失率的增加而降低;重建耗时也随缺失率的增加总体上逐渐降低,且FFPC算法提升的倍率为先降后升(以60%缺失率为界)。当缺失率≤50%时,FPC算法耗时较长;而利用FFPC算法能在确保高精度重建的同时,显著缩短运行时间,提高计算效率。
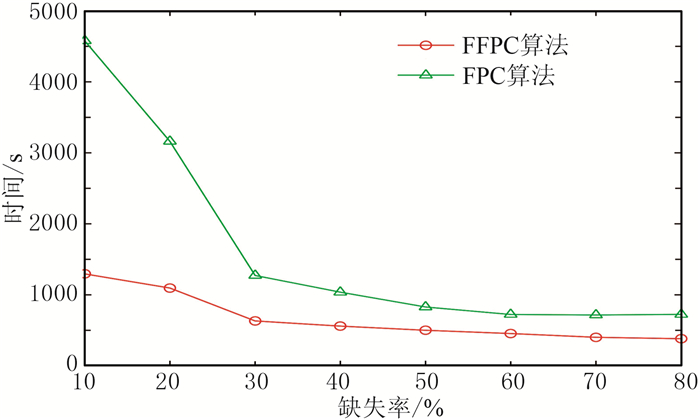
|
图 4 不同缺失率下仿真数据FPC与FFPC算法重建耗时 |
|
图 5 不同缺失率下仿真数据FPC与FFPC算法重建信噪比 |
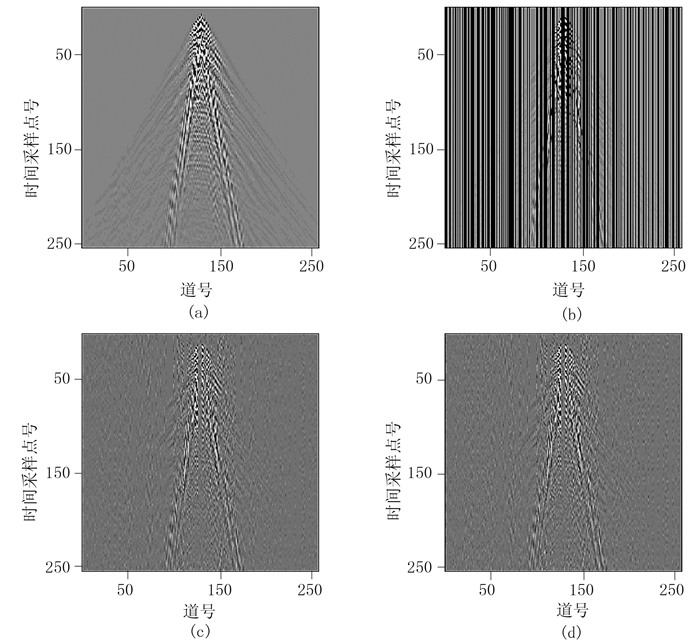
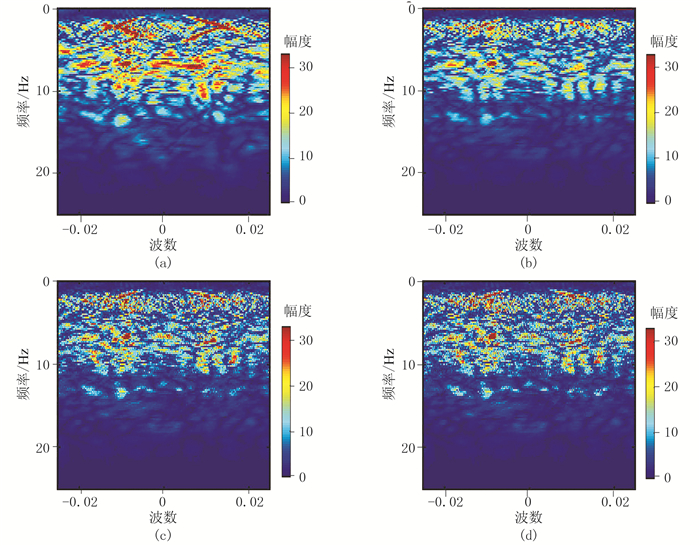
选取实际叠前地震数据(256(道)×256(个))进行实验。对比原始叠前数据(图 6a)、随机缺失50%数据(图 6b)及其对应频率—波数图(图 7a、图 7b)、基于FFPC和FPC算法的重建结果(图 6c、图 6d)及其对应频率—波数图(图 7c、图 7d),可见基于FFPC的重建效果与FPC基本相当,都可较好地对随机缺失数据进行插值。当缺失率为50%时(表 5),FFPC与FPC的重建信噪比相对误差为0.58%;但FPC算法的耗时是FFPC的3.83倍,表明针对叠前数据,在确保高精度重建效果的同时,FFPC计算效率更高。
|
图 6 缺失率为50%的叠前地震数据重建效果对比 (a)原始数据;(b)随机缺失50%的数据;(c)基于FFPC重建的数据;(d)基于FPC重建的数据 |
|
图 7 缺失率为50%时叠前地震数据频率—波数对比 (a)原始数据;(b)随机缺失50%的数据;(c)基于FFPC重建的数据;(d)基于FPC重建的数据 |
|
|
表 5 不同缺失率下叠前数据FPC与FFPC算法性能对比 |
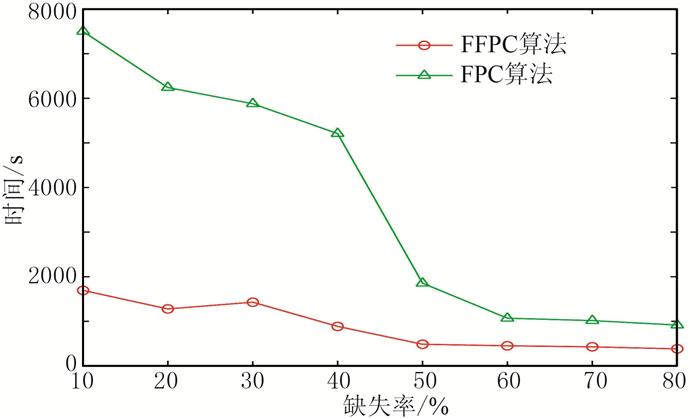
表 5给出缺失率为10%~80%的叠前地震数据的重建信噪比和耗时(图 8、图 9)。可见在固定缺失率时,FFPC与FPC算法重建信噪比的相对误差范围是0.37%~3.80%,即二者重建的精度接近;而FPC算法的重建耗时却是FFPC算法的2.37~5.88倍。随着缺失率的增加,FFPC和FPC算法的重建信噪比都降低,二者的重建耗时也逐渐降低。当缺失率≤50%时,FPC算法耗时很长,而FFPC算法在确保高精度重建的前提下能显著缩短运行时间,具有更高计算效率。
|
图 8 不同缺失率下叠前数据FPC和FFPC算法重建耗时 |
|
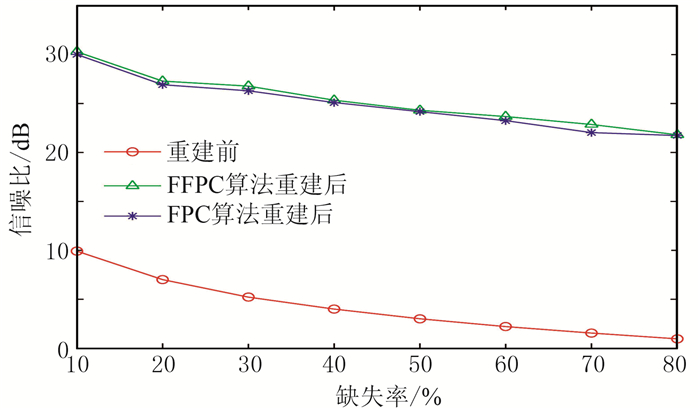
图 9 不同缺失率下叠前数据FPC和FFPC算法重建信噪比 |
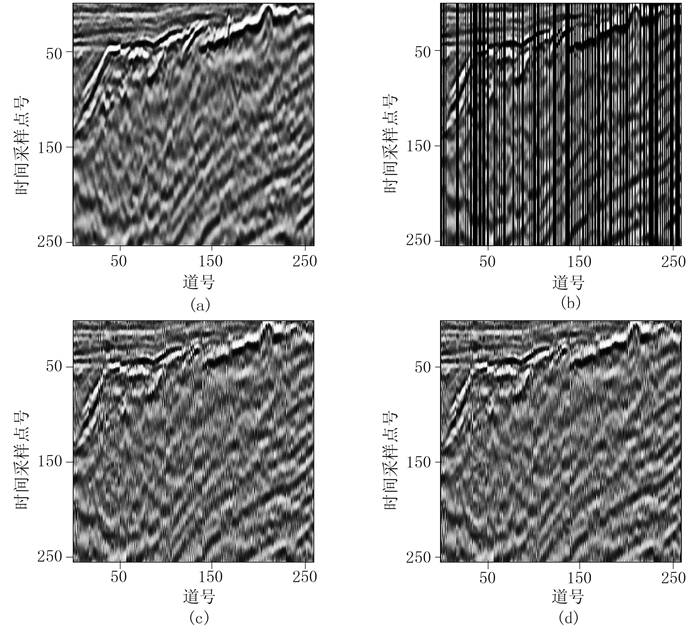
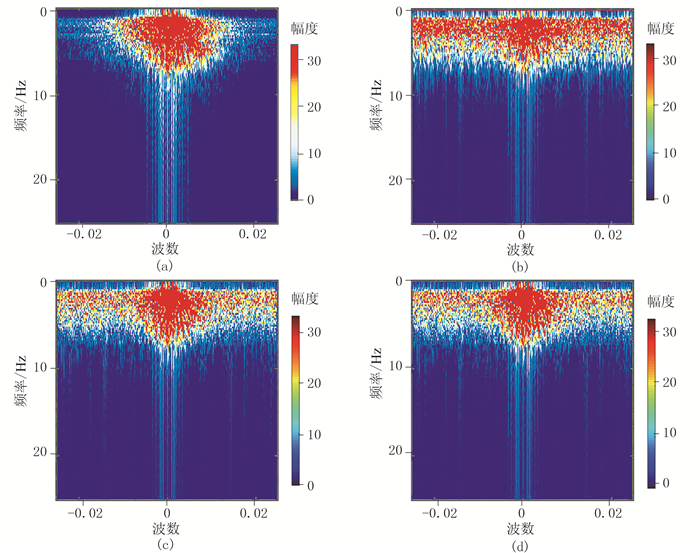
选取相同尺度和特征参数的实际叠后地震数据做进一步测试。得到并对比原始叠后数据(图 10a)、随机缺失50%的数据(图 10b)、基于FFPC(图 10c)和FPC(图 10d)的重建结果及其对应的频率—波数图(图 11a~图 11d),可见基于FFPC和FPC的重建结果对抑制假频都起了较好作用。当缺失率为50%时(表 6),FFPC与FPC重建信噪比误差为0.15%,但FFPC算法的重建耗时是FPC的1/1.75。
|
图 10 缺失率为50%的叠后地震数据重建效果对比 (a)原始数据;(b)随机缺失50%的数据;(c)基于FFPC重建的数据;(d)基于FPC重建的数据 |
|
图 11 缺失率为50%的叠后地震数据的频率—波数对比 (a)原始数据; (b)随机缺失50%的数据; (c)基于FFPC重建的数据; (d)基于FPC重建的数据 |
|
|
表 6 不同缺失率下叠后数据FPC与FFPC算法性能对比 |
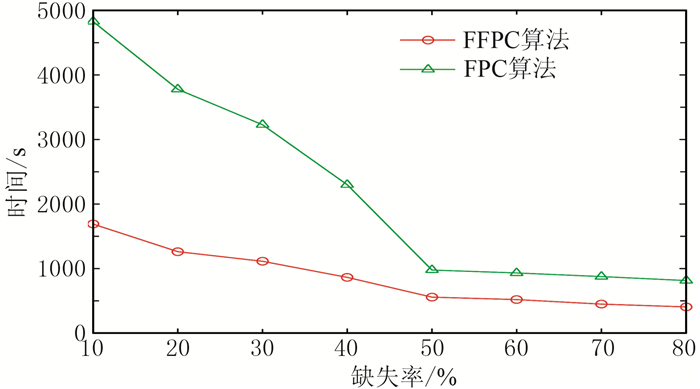
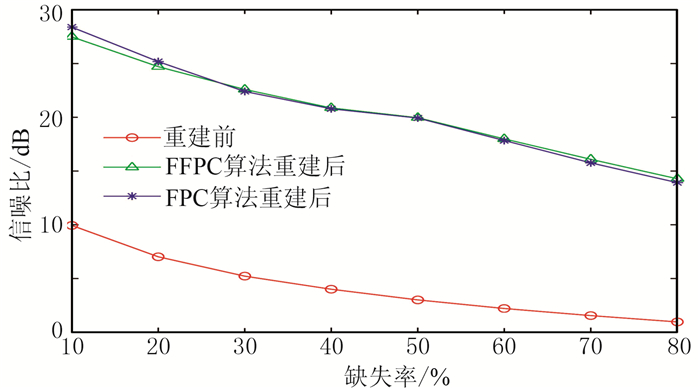
表 6给出缺失率为10%~80%的实际叠后地震数据的重建信噪比和耗时(图 12、图 13)。可见在固定缺失率时,基于FFPC与FPC算法的重建信噪比的相对误差范围是0.15%~5.20%;而FPC算法的重建耗时是FFPC的1.75~2.99倍。FFPC和FPC算法的重建信噪比都随缺失率的增加而降低;重建耗时也都随缺失率的增加而逐渐降低,且FFPC算法提升的倍率为先降后升。当缺失率≤50%时,FPC算法耗时很长,但利用FFPC算法却能在确保高精度重建效果的同时,有效缩短运行时间,提高计算效率。
|
图 12 不同缺失率下叠后数据FPC与FFPC算法重建耗时 |
|
图 13 不同缺失率下叠后数据FPC与FFPC算法重建信噪比 |
因此,基于BKIMASVD算法与子空间复用的FFPC算法比传统加速型的FPC算法的效率至少可提升1.75倍。
5 结论与展望基于核范数最小化的FPC算法在每次迭代过程中需进行SVD,导致算法的计算复杂度较高;传统的加速方法为直接利用PROPACK包,但仍然耗时较长。本文提出利用BKIMASVD算法和子空间复用的FFPC算法,并分析了该算法的计算复杂度。仿真数据和实际地震数据的实验表明:基于FFPC算法与基于FPC算法的地震数据重建精度基本相当,都可较好地对随机缺失地震数据进行插值,实现抗假频重构,但本文提出的FFPC算法进一步提高了计算效率。
实验过程中还发现:对于m≤n类型的矩阵,FFPC算法提速效果更明显。由于算法所涉及的参数较多,它们的选取和设定都会一定程度地影响重建效果。其中幂迭代次数P可通过前后两次迭代的重构矩阵误差满足一定精度而自适应地改变。
| [1] |
Fu L H, Zhang M, Liu Z H, et al. Reconstruction of seismic data with missing traces using normalized Gaussian weighted filter[J]. Journal of Geophysics and Engineering, 2018, 15(5): 2009-2020. DOI:10.1088/1742-2140/aac31c |
| [2] |
Spitz S. Seismic traces interpolation in F-X domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [3] |
Spagnolini U, Opreni S.3D shot continuation operator[C]. SEG Technical Program Expanded Abstracts, 1996, 15: 439-442.
|
| [4] |
Ronen J. Wave-equation trace interpolation[J]. Geophysics, 1987, 52(7): 973-984. DOI:10.1190/1.1442366 |
| [5] |
Fomel S. Seismic reflection data interpolation with differential offset and shot continuation[J]. Geophy-sics, 2003, 68(2): 733-744. |
| [6] |
Deregowski S M. What is DMO?[J]. First Break, 1986, 4(7): 7-24. |
| [7] |
Wang J F, Ng M, Perz M. Seismic data interpolation by greedy local Radon transform[J]. Geophysics, 2010, 75(6): WB225-WB234. DOI:10.1190/1.3484195 |
| [8] |
薛亚茹, 王敏, 陈小宏. 基于SL0的高分辨率Radon变换及数据重建[J]. 石油地球物理勘探, 2018, 53(1): 1-7. XUE Yaru, WANG Min, CHEN Xiaohong. High re-solution Radon transform based on SL0 and its application in data reconstruction[J]. Oil Geophysical Prospecting, 2018, 53(1): 1-7. |
| [9] |
Naghizadeh M, Innanen K A. Seismicdatainter-polation using a fast generalized Fourier transform[J]. Geophysics, 2011, 76(1): V1-V10. DOI:10.1190/1.3511525 |
| [10] |
Ma J W, Yu S W.Seismic data interpolation with polar Fourier transform[C].SEG Technical Program Expanded Abstracts, 2016, 35: 480-481.
|
| [11] |
Shahidi R, Tang G, Ma J, et al. Application of ran-domized sampling schemes to curvelet based sparsity-promoting seismic data recovery[J]. Geophysics Prospecting, 2013, 61(4): 973-997. |
| [12] |
Wang B F, Chen X H, Li J Y, et al. An improved weighted projection onto convex sets method for seismic data interpolation and denoising[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(1): 228-235. DOI:10.1109/JSTARS.2015.2496374 |
| [13] |
Larner K, Gibson B, Rothman D. Trace interpolation and the design of seismic survey[J]. Geophysics, 1981, 46(4): 407-415. |
| [14] |
Pieprzak A W, Mclean J W.Trace interpolation of severely aliased events[C].SEG Technical Program Expanded Abstracts, 1988, 7: 658-660.
|
| [15] |
温睿, 刘国昌, 冉扬. 压缩感知地震数据重建中的三个关键因素分析[J]. 石油地球物理勘探, 2018, 53(4): 682-693. WEN Rui, LIU Guochang, RAN Yang. Three key factors in seismic data reconstruction based on compre-ssive sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 682-693. |
| [16] |
刘争光, 韩立国, 张良, 等. 压缩感知理论下基于快速不动点连续算法的地震数重建[J]. 石油物探, 2018, 57(1): 50-57. LIU Zhengguang, HAN Liguo, ZHANG Liang, et al. Seismic data reconstruction using FFPC algorithm based on compressive sensing[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 50-57. DOI:10.3969/j.issn.1000-1441.2018.01.007 |
| [17] |
Qin N, Liang H X, Liu P T.Compressed sensing seismic data reconstruction based on Shearlet transformation[C].International Geophysical Conference, 2018, 1719-1722.
|
| [18] |
王新全, 耿瑜, Ru-Shan Wu, 等. 基于压缩感知的Dreamlet域数据重构方法及应用[J]. 石油地球物理勘探, 2015, 50(3): 399-404. WANG Xinquan, GENG Yu, Ru-Shan Wu, et al. Seismic data reconstruction in Dreamlet domain based on compressive sensing[J]. Oil Geophysical Prospecting, 2015, 50(3): 399-404. |
| [19] |
刘晓晶, 印兴耀, 吴国忱, 等. 基于正交匹配追踪算法的叠前地震反演方法[J]. 石油地球物理勘探, 2015, 50(5): 925-935. LIU Xiaojing, YIN Xingyao, WU Guochen, et al. Pre-stack seismic inversion based on orthogonal matching pursuit algorithm[J]. Oil Geophysical Prospecting, 2015, 50(5): 925-935. |
| [20] |
周亚同, 王丽莉, 蒲青山. 压缩感知框架下基于K-奇异值分解字典学习的地震数据重建[J]. 石油地球物理勘探, 2014, 49(4): 652-660. ZHOU Yatong, WANG Lili, PU Qingshan. Seismic data reconstruction based on K-SVD dictionary lear-ning under compressive sensing framework[J]. Oil Geophysical Prospecting, 2014, 49(4): 652-660. |
| [21] |
Zhou Y H, Chen W C, Shi Z S, et al.Seismic reconstruction via constrained dictionary learning[C].SEG Technical Program Expanded Abstracts, 2018, 37: 4608-4612.
|
| [22] |
李欣, 杨婷, 孙文博, 等. 一种基于光滑L1范数的地震数据插值方法[J]. 石油地球物理勘探, 2018, 53(2): 251-256. LI Xin, YANG Ting, SUN Wenbo, et al. A gradient projection method for smooth L1 norm regularization based seismic data sparse interpolation[J]. Oil Geophysical Prospecting, 2018, 53(2): 251-256. |
| [23] |
Gao X, Zhao H.Seismic data interpolation based on Bregman iteration method[C].International Geophy-sical Conference, 2018, 1727-1731.
|
| [24] |
梁硕博.基于Hankel矩阵的去躁方法研究[D].山东青岛: 中国石油大学(华东), 2014. LIANG Shuobo.Research on Denoising Method Based on Hankel Matrix[D].China University of Petroleum(East China), Qingdao, Shandong, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10425-1016711717.htm |
| [25] |
Trickett S, Burroughs L, Milton A, et al.Rank-reduction-based trace interpolation[C].SEG Technical Program Expanded Abstracts, 2010, 29: 3829-3833.
|
| [26] |
Oropeza V, Sacchi M. Simultaneous seismic data de-noising and reconstruction via multichannel singular spectrum analysis[J]. Geophysics, 2011, 76(3): V25-V32. DOI:10.1190/1.3552706 |
| [27] |
Yang Y, Ma J, Osher S. Seismic data reconstruction via matrix completion[J]. Inverse Problems and Imaging, 2013, 4(4): 1379-1392. |
| [28] |
Cai J F, Candes E J, Shen Z W. A singular value thre-sholding algorithm for matrix completion[J]. SIAM Journal on Optimaztion, 2010, 20(4): 1956-1982. DOI:10.1137/080738970 |
| [29] |
Oh T, Matsushita Y, Tai Y, et al. Fast randomized singular value thresholding for low rank optimization[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2018, 40(2): 376-391. DOI:10.1109/TPAMI.2017.2677440 |
| [30] |
Cai J F, Osher S. Fast singular value thresholding without singular value decomposition[J]. Methods and Applications of Analysis, 2013, 20(4): 335-352. DOI:10.4310/MAA.2013.v20.n4.a2 |
| [31] |
Goldfarb D, Ma S Q. Convergence of fixed point continuation algorithm for matrix rank minimization[J]. Foundations of Computational Mathematics, 2011, 11(2): 183-210. DOI:10.1007/s10208-011-9084-6 |
| [32] |
Ma S Q, Goldfarb D, Chen L F. Fixed point and Bregman iterative methods for matrix rank minimization[J]. Mathematical Programming, 2011, 128(1-2): 321-353. DOI:10.1007/s10107-009-0306-5 |
| [33] |
Toh K C, Yun S. An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems[J]. Pacific Journal of Optimization, 2010, 6(3): 615-640. |
| [34] |
冯栩, 李可欣, 喻文健, 等. 基于随机奇异值分解的快速矩阵补全算法及其应用[J]. 计算机辅助设计与图形学报, 2017, 29(12): 2343-2348. FENG Xu, LI Kexin, YU Wenjian, et al. Fast matrix completion algorithm based on randomized singular value decomposition and its applications[J]. Journal of Computer-Aided Design & Computer Graphics, 2017, 29(12): 2343-2348. |
| [35] |
Martinsson P G.Randomized methods for matrix computations and analysis of high dimensional data[J/OL].2018, arXiv: 1607.01649.
|
| [36] |
Larsen R M.PROPACK-software for large and sparse SVD calculations, 2017.http://sun.stanford.edu/~rmunk/PROPACK/.
|
| [37] |
Halko N, Martinsson P G, Shkolnisky Y. An algorithm for the principal component analysis of large data sets[J]. SIAM Journal on Scientific Computing, 2011, 33(5): 2580-2594. DOI:10.1137/100804139 |
| [38] |
Musco C, Musco C.Randomized block Krylov methods for stronger and faster approximate singular value decomposition[C].Proceeding of the 28th International Conference on Neural Information Processing Systems, MIT Press, Cambridge, 2015, 1396-1404.
|



 付丽华, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)数学与物理学院, 430074。Email:
付丽华, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)数学与物理学院, 430074。Email: