0 引言

地震数据中噪声严重影响资料处理和解释结果^[1]，压制噪声对后期地震资料的处理、反演和解释等具重要作用^[2]。地震资料常用的去噪方法一般分为空间域方法和变换域方法两大类。空间域去噪方法包括均值滤波、中值滤波^[3]和维纳滤波^[4]等，变换域去噪方法包括傅里叶变换、小波变换、曲波变换和Randon变换等阈值方法^[5-6]。这些去噪算法本质都是利用了图像本身的局部相关性，没有充分挖掘、利用图像的非局部相关性，因此在压制噪声的同时也会损害部分有效信号，不能精确保持断层、裂缝等地质体的边缘特征，甚至会出现伪影等现象^[7]。

针对这一问题，Buades等^[8]提出利用原始数据的结构相似性进行非局部去噪，与传统的局部去噪算法相比，该算法能有效地保护图像的边缘细节信息。在非局部去噪算法中，Kostadin等^[9]提出的三维块匹配(Block-Matching 3D，BM3D)去噪算法利用块匹配和三维变换域滤波技术进行串联去噪，该方法综合了非局部算法和变换域算法的优势^[10-11]，对随机噪声具有很好的去噪效果。BM3D去噪是将图像分割成许多个不同的小块，根据不同小块之间的相似性进行块匹配，然后在三维变换域中去除噪声，充分利用了数据的自相似性和冗余性信息，能较好地保留信号细节^[12]。韩玉兰等^[13]针对BM3D算法运算量大、运行时间过长的问题，采用积分图计算块的相似性，代替相应的滤波过程，提高了计算效率；李文静等^[14]将改进后的BM3D算法引入地震数据处理领域，得到了较为理想的去噪效果。但该方法依然存在一些不足，滤波阈值参数需要根据经验人为设定^[15]，而阈值选取的不确定性严重影响基础估计部分的降噪效果。由于在实际计算中，噪声方差对阈值大小和块匹配相似度的影响最大，而实际数据噪声的方差却是未知的^[16]，极大地限制了该算法在地震资料去噪中的应用。

在变换域地震资料去噪方法中，Candès等^[17]在脊波变换的基础上提出了第一代曲波变换。张恒磊等^[18]利用曲波尺度分解得到较为准确的噪声方差估计值，使后续的曲波变换阈值选取更加精确。但是由于实际地震数据的复杂性，单一曲波变换方法的去噪精度不足，处理结果常常存在伪影和过度平滑等现象。针对这些问题，薛诗桂等^[19]将曲波变换和循环平移技术结合，消除了曲波变换产生的伪吉布斯效应。姚振岸等^[20]将各向异性扩散滤波和曲波变换结合保护地震数据的边界特征；杨会等^[21]将曲波变换和二维经验模态分解结合，在去除噪声的同时较好地保护了弱信号。曹静杰等^[22]将曲波变换作为稀疏变换自适应地进行稀疏反演去噪。

为了弥补曲波变换和常规BM3D去噪方法的缺陷，本文结合两种方法的优势，提出了一种基于曲波噪声估计的BM3D地震资料去噪方法。该方法无需人为设定相关参数，根据曲波变换得到的地震资料噪声估计作为先验信息，准确计算块匹配相似度，自适应选取合适的滤波阈值进行去噪，可以得到更好的效果。数值模型和实际资料测试表明，与常规BM3D去噪方法、曲波变换去噪法相比，该方法去噪效果明显、实用性较高。

1 基本原理 1.1 三维块匹配去噪原理

BM3D去噪是图像处理中的一种方法。其基本算法是：将含噪数据看作一个图像，将其划分为若干块，并根据各块与其他块的相似度进行匹配分组；对组内数据进行三维线性变换，在变换域内对噪声进行滤波后反变换回原来的域内，并将每个组内的块像素返回到图像原来的位置；最后对重叠的块进行加权平均，得到去噪后的结果。为了提高匹配分组的正确性，通常对含噪数据进行前置硬约束阈值滤波作为地震信号的基础估计，获取维纳滤波的收缩系数。因此，整个过程就包含基础估计和重新估计两个阶段。每个阶段也都包含块匹配、变换域去噪和聚集三个环节。

在基础估计的块匹配阶段，将含噪地震数据视为二维图像，划分成尺寸为N×N的多个块Z_i(i=1，2，…，n，n为块总数)，依次选取各块作为参考块Z_r(r=1，2，…，n)，定义块与参考块之间的距离为

$ d\left( {{\mathit{\boldsymbol{Z}}_r}, {\mathit{\boldsymbol{Z}}_i}} \right) = \frac{{{{\left\| {{\mathit{\boldsymbol{Z}}_r} - {\mathit{\boldsymbol{Z}}_i}} \right\|}_2}}}{{{N^2}}} $

(1)

式中‖·‖₂表示L₂范数。若位块Z_i与参考块Z_r之间的距离不超过阈值τ_match，则将Z_i作为Z_r的相似块，Z_r的所有相似块组成相似群组S_r^Z，即

$ \boldsymbol{S}_{r}^{Z}=\left\{\boldsymbol{Z}_{i} \in \boldsymbol{Z}: d\left(\boldsymbol{Z}_{r}, \boldsymbol{Z}_{i}\right) \leqslant \tau_{\text {match }}\right\} $

(2)

将相似群组S_r^Z中的所有块按距离由小到大顺序排列，形成大小为N×N×M的三维矩阵Y_r，其中M为集合S_r^Z中块的个数。将Y_r进行三维线性变换，在变换域作硬阈值滤波处理，再通过三维逆变换得到估计值。具体过程可表示为

$ \hat{\boldsymbol{Y}}_{r}=T_{3 \mathrm{D}}^{-1}\left[\gamma_{1} T_{3 \mathrm{D}}\left(\boldsymbol{Y}_{r}\right)\right] $

(3)

式中：$ \hat{\boldsymbol{Y}}_{r}$为滤波处理后的估计值；T_3D和T_3D^-1分别为三维线性变换和逆变换算子；γ1=λ_3Dσ为滤波时硬阈值(λ_3D为三维系数)。该阈值与输入的噪声强度σ(即零均值噪声的标准差)成正比。实际处理中对含噪地震资料估计得到的噪声标准差往往无法直接用于计算该系数，需要进一步处理。显然，当距离阈值τ_match选取较大时，同一块Z_i可能出现在不同参考块Z_r对应的相似群组中，因而在滤波后就会存在交叠现象。为此可以对交叠块进行加权平均得到图像基础估计值

$ {\mathit{\boldsymbol{\hat Z}}_i} = \frac{{\sum\limits_r {{w_r}} {{\mathit{\boldsymbol{\hat Y}}}_r}(i)}}{{\sum\limits_r {{w_r}} {\chi _r}(i)}} $

(4)

式中：w_r为基础估计的权值；χ_r(i)为相似块Z_i的特征函数。对所有块Z_i进行处理后，得到初始估计${\mathit{\boldsymbol{\hat Z}}_i} $。

与基础估计类似，在重新估计阶段，将${\mathit{\boldsymbol{\hat Z}}_i} $分成大小为N₁×N₁的图像块$ {\mathit{\boldsymbol{\hat Z}}_i}$(i=1, 2, …, m)，以τ_match¹为阈值对参考块${\mathit{\boldsymbol{\hat Z}}_r} $进行匹配得到相似群组$\mathit{\boldsymbol{S}}_r^{\mathit{\boldsymbol{\hat Z}}} $

$ \mathit{\boldsymbol{S}}_r^{\mathit{\boldsymbol{\hat Z}}} = \left\{ {{{\mathit{\boldsymbol{\hat Z}}}_i} \in \mathit{\boldsymbol{\hat Z}}:\frac{{{{\left\| {{{\mathit{\boldsymbol{\hat Z}}}_i} - {{\mathit{\boldsymbol{\hat Z}}}_r}} \right\|}_2}}}{{N_1^2}} \le \tau _{{\rm{match }}}^1} \right\} $

(5)

利用集合$ \mathit{\boldsymbol{S}}_r^{\mathit{\boldsymbol{\hat Z}}}$的构建准则，可以得到两个三维矩阵，分别是由基础估计处理后集合$ \mathit{\boldsymbol{S}}_r^{\mathit{\boldsymbol{\hat Z}}}$排列得到的三维矩阵$ {\mathit{\boldsymbol{\hat Y}}}$和由原始含噪数据按照$ \mathit{\boldsymbol{S}}_r^{\mathit{\boldsymbol{\hat Z}}}$的构建准则得到的三维矩阵Y_r。利用$ {\mathit{\boldsymbol{\hat Y}}}$的三维线性变换T_3D($ {\mathit{\boldsymbol{\hat Y}}}$)计算维纳滤波的收缩系数

$ \phi_{r}=\frac{\left|T_{3 \mathrm{D}}\left(\hat{\boldsymbol{Y}}_{r}\right)\right|^{2}}{\left|T_{3 \mathrm{D}}\left(\hat{\boldsymbol{Y}}_{r}\right)\right|^{2}+\sigma^{2}} $

(6)

将维纳滤波应用于噪声数据矩阵Y_r，即将噪声数据矩阵三维变换后的系数与维纳滤波收缩系数相乘，再进行反变换后得到新的估计值为

$ \hat{\hat{\boldsymbol{Y}}}_{r}=T_{3 \mathrm{D}}^{-1}\left[\phi_{r} T_{3 \mathrm{D}}\left(\boldsymbol{Y}_{r}\right)\right] $

(7)

最后将不同群组中的重叠块进行加权平均得到重新估计值

$ {{\mathit{\boldsymbol{\hat {\hat Z}}}}_i} = \frac{{\sum\limits_r {{{\hat w}_r}} {{\mathit{\boldsymbol{\hat {\hat Y}}}}_r}(i)}}{{\sum\limits_r {{{\hat w}_r}} {{\hat \chi }_r}(i)}} $

(8)

式中：$ {{\mathit{\boldsymbol{\hat {\hat Z}}}}_i}$为BM3D去噪完成后的图像；$ {{{\hat w}_r}}$和${{{\hat \chi }_r}(i)} $为重新估计的权值和特征函数。

1.2 基于曲波噪声估计的BM3D地震资料去噪方法

常规的BM3D去噪方法需要根据噪声方差σ²作为先验信息求取滤波阈值和块匹配参数。在实际地震资料的处理中，常用的噪声方差估计方法是中值噪声方差估计和基于小波分析的细节估计。当原始地震资料信噪比较高、噪声方差较小时，这两种方法的估计值与真值较为接近。但是，当原始地震资料的噪声水平较高时，前者的估计值与真值偏差较大，而后者则不能完整地估计噪声，导致估计值比实际噪声方差偏小。

在地震资料去噪领域，曲波变换是一种成熟且实用的方法^[23]，可以在曲波域利用曲波分解系数进行噪声方差估计^[24]，再根据噪声水平确定阈值大小，从而进行更精确的去噪^[25-26]。在曲波域根据一阶系数可以较为准确地估计出噪声标准差$\hat{\sigma}_{0} $，通过多次测试确定一个适用于BM3D去噪算法的γ因子，从而得到噪声强度σ

$ \sigma=\hat{\sigma}_{0} \gamma $

(9)

根据σ可以进一步确定BM3D去噪算法中的滤波阈值γ₁及收缩系数ϕ_r。这样滤波参数成为噪声强度σ的自适应函数，弱反射和边界细节信息可以得到有效的保护。

BM3D去噪算法结合了非局部算法和变换域算法的优势，可以有效去除高斯随机噪声。由于事先无法得到噪声方差，需要人为设定滤波参数，因而去噪效果难以保证。本文将曲波变换估计出的噪声方差作为先验信息，求取适用于BM3D去噪算法的输入噪声强度σ，进而自适应地调整滤波阈值和块匹配参数，完成去噪处理。当σ较小时，可直接应用式(1)计算块匹配相似度；当σ为中等或较大时，直接块匹配可能会导致错误的块匹配分组，需要先对图像块进行预滤波处理，即先对两个图像块进行正则二维线性变换，对其进行阈值滤波，然后再计算两者之间的距离，即

$ d\left(\boldsymbol{Z}_{r}, \boldsymbol{Z}_{i}\right)=\frac{\left\|\gamma_{0}\left[T_{2 \mathrm{D}}\left(\boldsymbol{Z}_{r}\right)\right]-\gamma_{0}\left[T_{2 \mathrm{D}}\left(\boldsymbol{Z}_{i}\right)\right]\right\|_{2}}{N^{2}} $

(10)

式中：γ₀=λ_2Dσ为二维预滤波处理的阈值(λ_2D为二维系数)；T_2D为正则二维线性变换算子。去噪阈值参数通常都设为常量，为了有效地保护有效信号，将其设定为噪声强度σ的自适应函数。当σ较小时，无需进行预滤波处理，图像块可以取值较小(如N取为8)；当σ中等时，需要进行预滤波处理，滤波阈值γ₀取为1.0，图像块应适当增大(如N取为9~10)；当原始资料噪声强度σ较大时，二维预滤波阈值γ₀可取为2.0，图像块应取值较大(如N取为11~12)。

2 模型试算

为了测试自适应选取阈值的改进方法的优越性，建立楔状体模型，对其正演数据加入随机噪声，得到含噪记录如图 1a所示。分别利用常规BM3D方法和改进的BM3D法进行去噪处理，结果如图 1b和图 1c所示。

选用峰值信噪比和信噪比两个参数对去噪效果进行定量比较。二者分别定义为

$ \mathrm{PSNR}=10 \times \lg \frac{\max \left(S_{0}^{2}\right)}{\mathrm{MSE}} $

(11)

$ {\rm{SNR}} = 10 \times \lg \frac{{\sum\limits_{i = 1}^K {{\mathop{\rm var}} } {{\left( {S_0^2} \right)}_i}}}{{\sum\limits_{i = 1}^K {{\mathop{\rm var}} } {{\left( {{S_{\rm{N}}}} \right)}_i}}} $

(12)

式中：max(S₀²)表示整个数据中样点的最大能量值；MSE为数据的均方误差；K为数据道数；var(S₀)_i和var(S_N)_i分别为第i道信号和噪声的能量。显然，PSNR表示信号最大功率与噪声功率的比值，SNR则是有效信号S₀与噪声S_N总能量的比值，显然PSNR大于SNR。

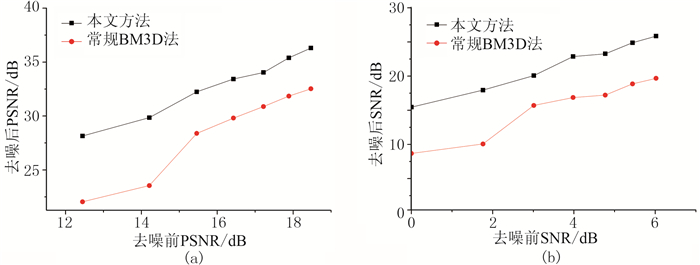
对图 1a所示的模型正演数据，变化所加入噪声的强度，分别使用常规BM3D和改进BM3D方法进行去噪处理，并计算其PSNR和SNR，结果如图 2所示。从图中曲线可以看出，改进BM3D去噪方法相对常规BM3D方法去噪后SNR和PSNR均更高，尤其是低信噪比情况下去噪效果更显著。

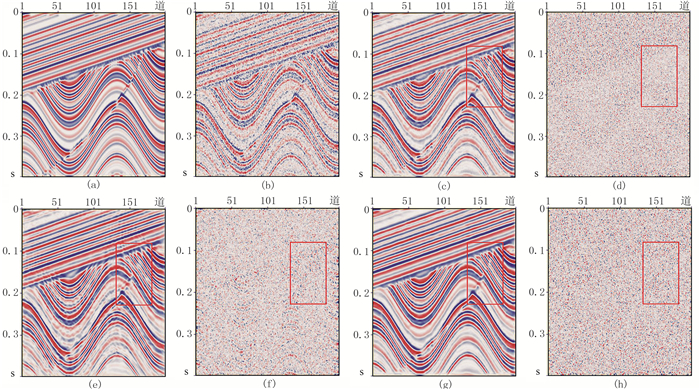
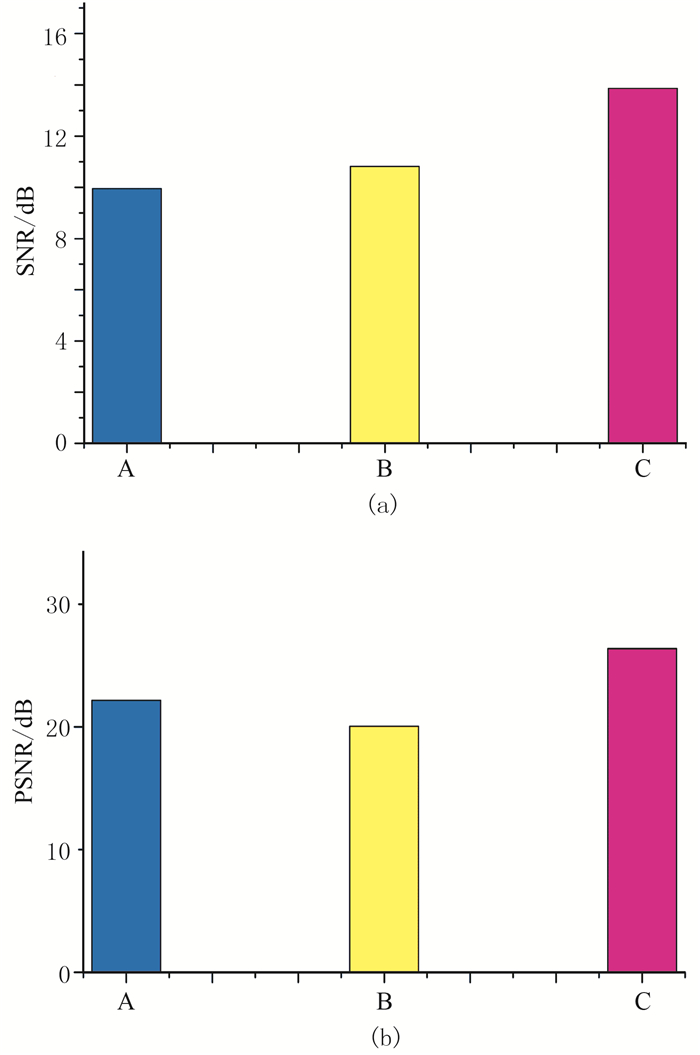
为了进一步说明本文方法相对于常规方法的优越型，使用图 3a所示的模型数据进行测试。对模型数据加入随机噪声，得到信噪比为3dB(即信号与噪声的能量之比为2)的含噪记录，如图 3b所示。分别使用常规BM3D方法、曲波变换滤波方法和本文方法进行去噪处理，结果如图 3c、图 3e和图 3g所示，去噪前后的差值剖面即去除的噪声如图 3d、图 3f和图 3h所示。由图可以看出，加入随机噪声后模型断点处的反射基本淹没在噪声中，断层边缘位置模糊不清。常规BM3D方法能够在一定程度上去除部分噪声，但去噪后同相轴连续性降低(图 3c)；曲波变换滤波后的剖面(图 3e)同相轴弯曲部分连续性降低，断层边缘有效信号在残差剖面中明显(图 3f中红框处)，对断层细节信息保持较差。本文方法不仅能明显去除随机噪声，且去噪后反射同相轴清晰，断层边界特征也得到了良好的保持(图 3g)。从图 3h所示的去除噪声剖面上可以看出，本方法未将有效信号作为噪声去除，很好地保留了有效信息，去噪效果相对最佳。图 4为三种方法去噪后的SNR和PSNR对比，可以看出本文方法的去噪效果最好。

3 实际资料试算

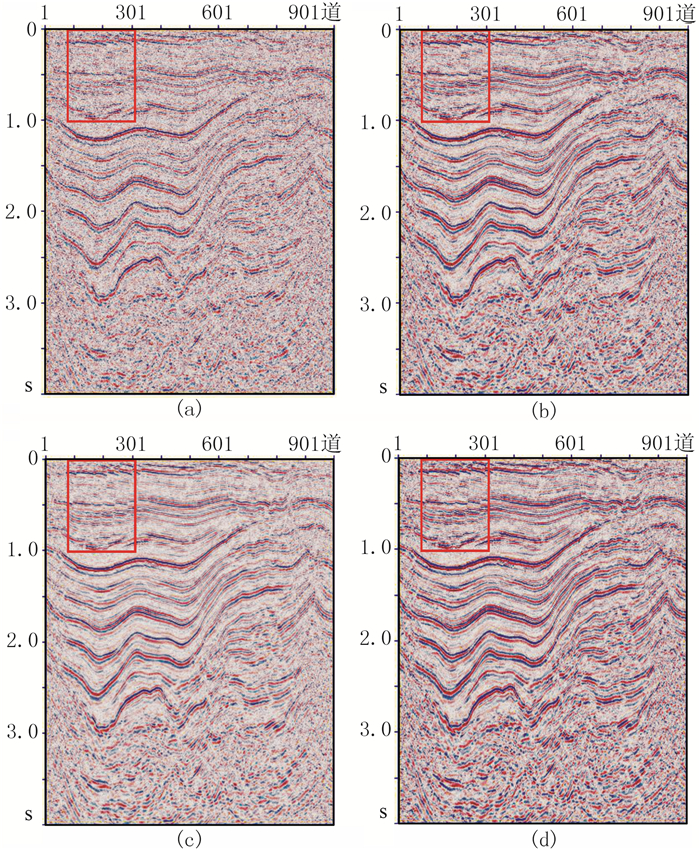
图 5a为实际叠后地震剖面，其中含有随机噪声，影响了资料品质。分别使用常规BM3D法、曲波变换法和本文方法进行去噪，结果如图 5b、图 5c和图 5d所示。

在常规BM3D方法去噪过程中，首先对噪声强度作初步估计，确定其所在范围为10~20，通过逐点测试，最终确定为15，以此选取滤波参数N为8，硬阈值为2.7。在曲波变换法去噪过程中，根据张恒磊等^[18]所述，在细尺度上阈值取$3 \hat{\sigma}_{0} $，考虑蒙特卡罗噪声衰减，选用半软阈值为$ 2.4 \hat{\sigma}_{0}$。本文方法中，根据曲波变换计算得到的噪声方差为0.07，由此计算出的噪声强度为15.846。对比三者的去噪结果，可以看出，本文方法去噪处理后能有效地压制随机噪声，得到较为清晰的剖面，且省去了驻点测试的过程，提高了计算效率。

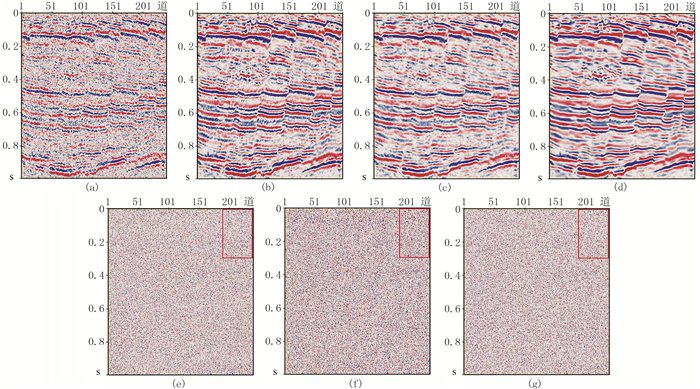
为了说明本方法对断层边界信息的保持能力，从图 5中截取存在多个断层的红框区域进行放大显示，如图 6a~图 6d所示。可见：常规BM3D去噪结果边界信息不够清楚，弱反射层同相轴连续性较差(图 6b)；曲波变换方法保持边界能力较差，断层边缘模糊(图 6c)；本文去噪方法在去噪后断点清晰，断层解释更准确，较弱的反射同相轴连续性强(图 6d)。图 6e~图 6g为三种方法去除的噪声剖面，可见常规BM3D法和本文方法去除的噪声剖面均匀，表明未去除有效信号；而曲波变换去除的噪声剖面中部分断点处存在有效信号(红框所示)。综合去噪后剖面和残差剖面可以看出，本文的方法去噪效果最好。

4 结论

BM3D方法在地震资料去噪中具有良好的效果，但因无法准确估计噪声方差并选取合适的处理参数，在实际应用中受到一定的限制。本文联合曲波噪声估计和BM3D去噪方法，通过曲波分析，实现了滤波阈值和块匹配参数的自适应选取和去噪处理，提高了去噪精度和计算效率，具有较强的实际意义。理论模型及实际资料处理结果表明：

(1) 基于曲波噪声估计的BM3D去噪方法能准确选取滤波参数，去噪后剖面的信噪比和峰值信噪比更高；

(2) 本文方法避免了参数选取的多次测试，提高了计算效率；

(3) 由于实现了滤波阈值的自适应选取，本文方法较好地保护弱反射信号和边界细节信息，为后续地震资料的精细解释提供保障。