0 引言

在浅海OBS(Ocean Bottom Seismic)勘探过程中，需布放和定位大量海底地震检波器或海洋节点设备^[1-2]。声学二次定位技术及系统因为具有精度高、低成本、体积小且重量轻的优点，通过将声学应答器与海底地震检波器进行捆绑定位，可实现高精度海底地震检波器定位，满足浅海地震勘探的需求。在浅海声学定位中，声波在海水中传播时，会在介质常数不同的两个界面上产生反射、折射和某种程度的反向散射，从而导致波束声线弯曲和传播速度发生改变。入射角越大，声速变化越大，弯曲越显著^[3-9]。此外，声学测距的时延误差、船的行差和姿态转换误差等都在一定程度上影响声学定位精度。

为减弱各类观测误差对声学定位平面精度的影响，工程人员通常利用潮汐矫正后的水深作为海底应答器的高程，实施海底应答器的高精度二维定位。该方法观测模型简单稳定，具有良好的抗粗差能力。但由于潮汐模型的不匹配及区域水深数据造成的误差，平面测距信息中会再次引入新的深度误差，影响定位结果的收敛性和精度。

船载星站差分系统可实时测量和记录任意时刻高精度的位置信息，能达到约20cm的水平精度和30cm垂直精度，从而得到较高精度的实时潮汐信息^[10-11]。而在实际的浅海地震勘探中，通常搭载较高精度的单波束测深设备，也能达到分米级到厘米级的实时测深精度。基于星站差分技术和单波束测深技术可得到较高精度的浅海应答器深度约束信息，进而改善声学二次定位的平面精度。

本文主要研究充分利用上述高精度的星站差分信息和单波束测深信息提高海底多应答器的平面定位精度。针对声学二次定位的对称观测结构和浅海海底局部范围内地形平坦的特性，基于区域插值方法，设计了基于深度约束的浅海多目标定位算法。通过实测实验，将本文算法与传统二维几何法、三维几何法的测量结果进行对比，以验证本文方法的高精度和强稳定性。

1 浅海声学定位算法 1.1 声学二次定位原理

如图 1所示，浅海声学二次定位传感器包括声学换能器、应答器及相关辅助设备。声学定位实际是一种前方交会测量法。假设t_i时刻由GPS得到测量船的位置为X_i^k，海底应答器坐标为X_T^k，测得的测量船至应答器的距离为ρ_i^k。若不考虑姿态测量误差的影响，仅考虑与声速有关的误差和测量随机误差，则观测方程可写为^[12-13]

$ \rho_{i}^{k}=f\left(\boldsymbol{X}_{i}^{k}-\boldsymbol{X}_{\mathrm{T}}^{k}\right)+\delta \rho_{\mathrm{V}i}^{k}+\varepsilon_{i}^{k} $

(1)

$ f\left(\boldsymbol{X}_{\mathrm{T}}^{k}-\boldsymbol{X}_{i}^{k}\right)\\=\sqrt{\left(x_{\mathrm{T}}^{k}-x_{i}^{k}\right)^{2}+\left(y_{\mathrm{T}}^{k}-y_{i}^{k}\right)^{2}+\left(z_{\mathrm{T}}^{k}-z_{i}^{k}\right)^{2}} $

(2)

式中：f(X_T^k-X_i^k)为测量船到海底应答器的真实距离；δρ_Vi^k为声线弯曲误差及其他与声速(入射角)有关的误差；ε_i^k为其他测距随机误差；i是区域内采样点序号，其总数为M。

如果声速剖面已知，可得到Harmonic平均声速或其他加权平均声速。则式(1)线性化为

$ \rho _{{\rm{o}}i}^k - f_{{\rm{o}}i}^k = a_{{\rm{o}}i}^k{\rm{d}}x + \delta \rho _{{\rm{V}}i}^k + \varepsilon _i^k $

(3)

式中：ρ_oi^k=C_et_i^k，其中C_e为平均声速，t_i^k是单程传播时间；$a_{\mathrm{o}i}^{k}=\left[\frac{\partial f_{\mathrm{o}i}^{k}}{\partial x} \frac{\partial f_{\mathrm{o}i}^{k}}{\partial y} \frac{\partial f_{\mathrm{o}i}^{k}}{\partial z}\right] $为雅可比矩阵，且$\frac{\partial f_{\mathrm{o} i}^{k}}{\partial x}=\frac{x_{\mathrm{oT}}^{k}-x_{i}^{k}}{f_{\mathrm{o} i}^{k}}, \frac{\partial f_{\mathrm{o} i}^{k}}{\partial y}=\frac{y_{\mathrm{oT}}^{k}-y_{i}^{k}}{f_{\mathrm{o} i}^{k}}, \frac{\partial f_{\mathrm{o} i}^{k}}{\partial z}=\frac{z_{\mathrm{oT}}^{k}-z_{i}^{k}}{f_{\mathrm{o} i}^{k}} $$ f_{\mathrm{o} i}^{k}=\sqrt{\left(x_{\mathrm{oT}}^{k}-x_{i}^{k}\right)^{2}+\left(y_{\mathrm{oT}}^{k}-y_{i}^{k}\right)^{2}+\left(z_{\mathrm{oT}}^{k}-z_{i}^{k}\right)^{2}}$；下标“o”表示近似坐标。

若已知采集施工区域的平均水深，基于当地的潮汐表信息，可插值取得施工时刻的潮汐值。结合平均水深，可得到水下应答器的高程值。假设该区应答器的平均高程为z_T，式(3)进一步简化为

$ \rho_{\mathrm{h}}i^{k}-g_{\mathrm{o}i}^{k}=b_{\mathrm{o}i}^{k} \mathrm{d} x+\varepsilon_{\mathrm{b}i}^{k} $

(4)

式中：$\rho_{\mathrm{h}i}^{k}=\sqrt{\left(C_{\mathrm{e}} t_{i}^{k}\right)^{2}-\bar{z}_{\mathrm{T}}^{2}} $；$b_{\mathrm{o} i}^{k}=\left[\frac{\partial g_{\mathrm{o}i}^{k}}{\partial x} \frac{\partial g_{\mathrm{o}i}^{k}}{\partial y}\right] $，且$ \frac{\partial g_{{\rm o} i}^{k}}{\partial x}=\frac{x_{{\rm o} \mathrm{T}}^{k}-x_{i}^{k}}{g_{{\rm o} i}^{k}}, \quad \frac{\partial g_{{\rm o} i}^{k}}{\partial y}=\frac{y_{{\rm o} T}^{k}-y_{i}^{k}}{g_{{\rm o} i}^{k}}$；$g_{{\rm o} i}^{k}= \sqrt{\left(x_{ \mathrm{oT}}^{k}-x_{i}^{k}\right)^{2}+\left(y_{\mathrm{oT}}^{k}-y_{i}^{k}\right)^{2}}$。

式(4)与式(3)相比，无须解算应答器的高程信息，因此观测结构更稳定。由于沿测线方向上水平观测结构的对称性，高程误差造成的平距测距误差可沿测线方向较好地消除。

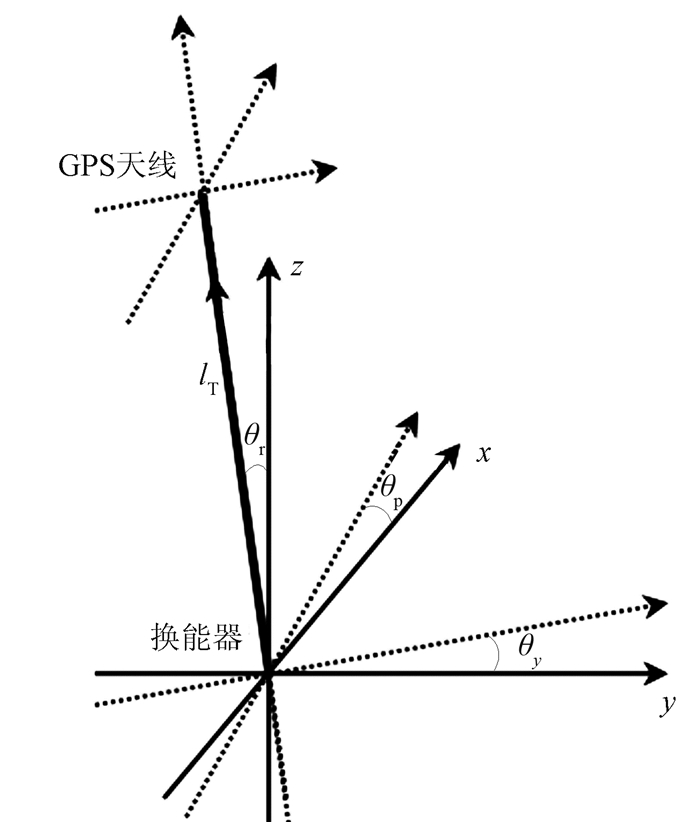
1.2 深度约束信息获取

由于GPS接收机得到的是GPS天线相位中心在WGS-84下的坐标，需将GPS的坐标转换到水下换能器和单波束测深仪探头的坐标(图 2)。计算换能器在以GPS天线相位中心为原点的天顶坐标系中的坐标改正数方法如下

$ \left(\begin{array}{l}{\Delta x} \\ {\Delta y} \\ {\Delta z}\end{array}\right)=\boldsymbol{R}_{{\rm y}} \boldsymbol{R}_{{\rm p}} \boldsymbol{R}_{{\rm r}}\left[\begin{array}{c}{0} \\ {0} \\ {l_{\mathrm{T}}}\end{array}\right] $

(5)

其中

$ \boldsymbol{R}_{\mathrm{y}}=\left(\begin{array}{ccc}{\cos \theta_{\mathrm{y}}} & {-\sin \theta_{\mathrm{y}}} & {0} \\ {\sin \theta_{\mathrm{y}}} & {\cos \theta_{\mathrm{y}}} & {} \\ {} & {} & {1}\end{array}\right)\\ \boldsymbol{R}_{\mathrm{p}}=\left(\begin{array}{ccc}{\cos \theta_{\mathrm{p}}} & {0} & {-\sin \theta_{\mathrm{p}}} \\ {0} & {1} & {0} \\ {\sin \theta_{\mathrm{p}}} & {0} & {\cos \theta_{\mathrm{p}}}\end{array}\right)\\ \boldsymbol{R}_{\mathrm{r}}=\left(\begin{array}{ccc}{1} & {0} & {0} \\ {0} & {\cos \theta_{\mathrm{r}}} & {-\sin \theta_{\mathrm{r}}} \\ {0} & {\sin \theta_{\mathrm{r}}} & {\cos \theta_{\mathrm{r}}}\end{array}\right) $

式中：θ_y为方位角；θ_p为升沉角；θ_r为横滚角；l_T为DGPS天线到换能器的垂直距离。中国石油集团东方地球物理公司(BGP)勘探二号探测船的链接杆长度约为20m。当摇摆角为10°时，未姿态补偿在垂直方向造成的误差约为10cm。

图 3为GPS大地高和单波束测深原始观测数据，采样率为1s。设t时刻船载DGPS大地高为H(t)，单波束测深值为D(t)，DGPS天线到换能器的垂直距离为l_s，则该地理坐标下的海底高程H_F(t)为

$ H_{\mathrm{F}}(t)=\boldsymbol{R}_{\mathrm{y}} \boldsymbol{R}_{\mathrm{p}} \boldsymbol{R}_{\mathrm{r}}\left(\begin{array}{l}{0} \\ {0} \\ {l_{\mathrm{s}}}\end{array}\right)+D(t)+H(t) $

(6)

受测量信号及复杂水环境因素影响，单波束测量值中含有少量的噪声观测值(图 3)。因此需采用适宜滤波方法去噪，如中值滤波或低通滤波等。

2 深度约束的浅海多目标定位算法 2.1 高精度深度约束信息处理

由图 3易知DGPS天线的大地高约为22m，施工区域水深约为77m，结合式(4)并采用IGG3(中科院测量与地球物理所首创的权函数)抗差估计^[7]可得初步稳定的海底应答器近似坐标，精度约为1m。

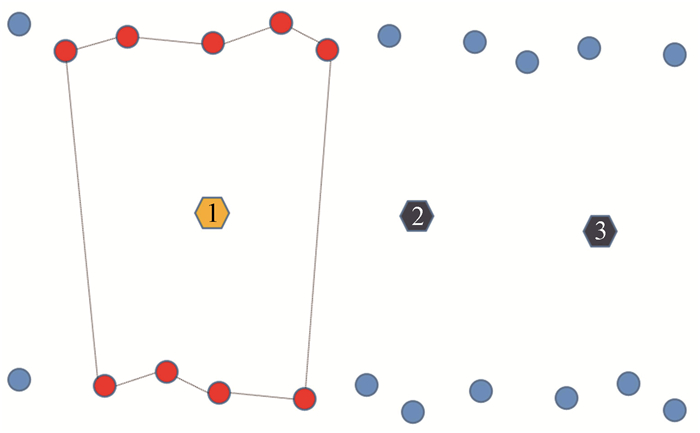
在图 4中沿测线方向可选择一定数量的采样点，并结合其平面地理坐标和对应的海底大地高信息，进行空间插值。

本文采用自然邻点插值法对应答器的近似平面坐标做深度插值^[14]。自然邻点插值方法即是根据各自然邻点对待插值点函数值的贡献率计算该节点的插值结果。所用插值公式^[12-14]为

$ H_{k}^{\mathrm{T}}=\sum\limits_{i} \phi\left(x_{i}\right) f\left(x_{i}\right) \quad x_{i} \in R^{2}, i \in 1 \sim M $

(7)

式中：H_k^T为第k个应答器对应的大地高；x_i为采样点平面坐标；f(x_i)是采样点x_i对应的大地高；(x_i)为采样点x_i对应的基函数。

2.2 基于深度约束的浅海多目标定位算法

考虑浅海声学二次定位中较大声线入射角造成的声线弯曲问题，对于不同的应答器，若声学观测的入射角相近，由于采集时间和距离相近，水深几乎不变，可认为其声学环境类似、声线弯曲误差相同^{[3, 15]}，因此可利用所有应答器对应的观测数据削弱声线弯曲对平面定位精度的影响。此时待估参数为dX_T^k=$=\left[\mathrm{d} x_{\mathrm{T}}^{k}, \mathrm{d} y_{\mathrm{T}}^{k}, \underbrace{u_{1}, \cdots, u_{m}}_{\boldsymbol{X}_{\mathrm{c}}}\right]^{\mathrm{T}} $。结合式(4)和式(6)可得到深度约束后的新观测方程为

$ \boldsymbol{L}_{a}=\boldsymbol{B}_{a} \mathrm{d} \boldsymbol{X}_{\mathrm{T}}^{k}+\Delta $

(8)

$ \boldsymbol{B}_{1}=\left[\begin{array}{c}{b_{\mathrm{o} 1}^{k}} \\ {b_{\mathrm{o} 2}^{k}} \\ {\vdots} \\ {b_{\mathrm{o}n}^{k}}\end{array}\right]_{n \times 2}\\ \boldsymbol{B}_{2}=\left[\begin{array}{cccc}{0_{n_{2} \times 1}} & {0_{n_{2} \times 1}} & {0_{n_{2} \times 1}} & { 0_{n_{2} \times 1}} \\ {\frac{1}{\left(\cos \theta_{\mathrm{W}_{1}}\right)^{N}}} & {0} & {0} & {0} \\ {0} & {\frac{1}{\left(\cos \theta_{\mathrm{W}_{2}}\right)^{N}}} & {0} & {0} \\ {0} & {0} & {\ddots} & {0} \\ {0} & {0} & {0} & {\frac{1}{\left(\cos \theta_{\mathrm{W}_{m}}\right)^{N}}}\end{array}\right]_{n \times m} $

(9)

式中：B_a=[B₁ B₂]；L_a=(ρ_h1^k-g_o1^k, ρ_h2^k-g_o2^k, …, ρ_hn^k-g_on^k)^T；Δ为误差项；θ表示入射角；W_l(l=1~m)表示按入射角分m组，其编号为l；N一般取2或3。因同时解算上千观测数据会非常费时，须对非公共参数进行约化，并采用序贯最小二乘(LS)法^[16-19]求解全部应答器观测数据对应的最优解

$ \boldsymbol{R}_{B_{1}} \boldsymbol{B}_{2} \boldsymbol{X}_{\mathrm{c}}=\boldsymbol{R}_{B_{1}} \boldsymbol{L}_{a} $

(10)

式中：R_B1=I-B₁(B₁^TΣ₁^-1B₁)^-1B₁^TΣ₁^-1，其中I表示单位矩阵，Σ₁为观测值的协方差矩阵；X_c为声线弯曲模型参数。

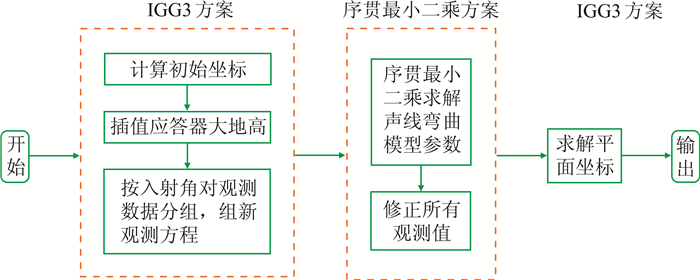
基于深度约束的浅海多目标定位算法的流程如图 5所示，主要分为以下三步。

(1) 采用IGG3抗差方法^[16-17]解算应答器初始坐标和对应的观测数据入射角。该过程可选择平均水深进行深度约束或直接解算应答器初始坐标。根据水平距离约束，选取一定范围内的采样点，并采用自然邻点插值法内插初始坐标对应的大地高。

(2) 基于式(8)和式(9)，采用序贯最小二乘计算声线弯曲模型参数，并利用最终解算的声线弯曲参数修正大入射角情形下的观测值。

(3) 采用IGG3方法和修正后的平距观测值解算应答器的平面坐标。

3 实验验证

为验证本文算法的精度和可靠性，选择中国南海M海域开展海上实际数据测试。如图 6所示，测试人员搭乘BGP勘探二号探测船，船上搭载了电罗经、星站差分定位系统、测深仪、声速剖面仪、Sonardyne公司生产的OBC声学定位系统和Kongsberg-EA600型单波束测深仪等。

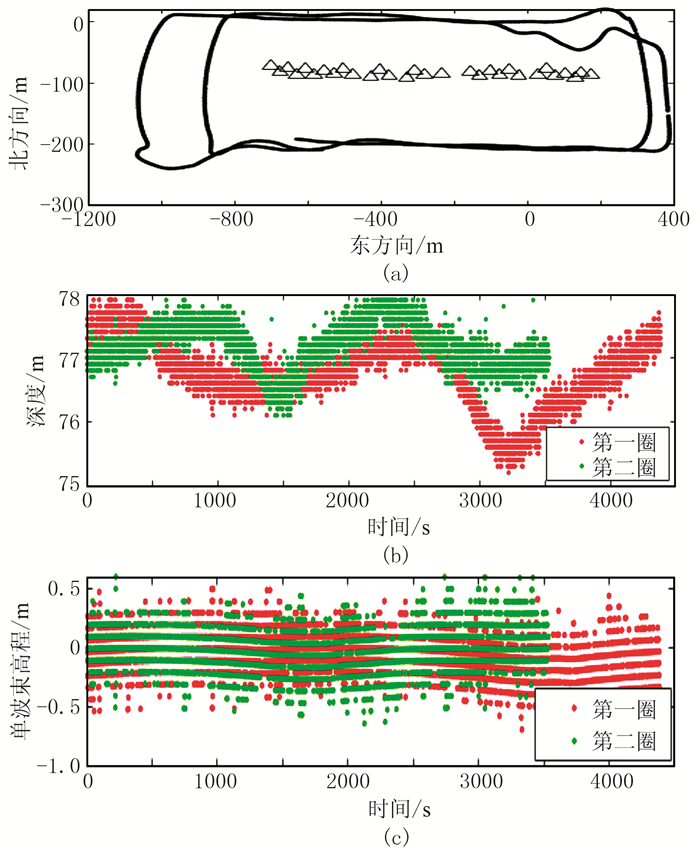
缆绳上每隔50m钩挂检波器和应答器(图 7a)，共30个。利用声速剖面仪测量该区的声速，并与时间相乘得到换能器与应答器之间的距离观测值。

通常认为沉入海底的缆绳位置在短时间内不变。本次实验对所选缆绳上的应答器做两次独立重复测试，分别采用不同经验水深的LS方法、普通三维解算方法(LS1)、截止入射角方法(LS2)、抗差IGG3方法和本文方法进行解算，并比较各方法的水平定位精度。由于本次实验同时采用两次独立观测对30个应答器定位，累计两次测量解算的定位偏差具有一定的统计意义。

图 8和图 9是分别在东方向和北方向上以不同固定经验水深的LS方法和本文方法的定位偏差柱状图。实测水深约78m，从图中可见当经验高程与应答器实际高程存在较大偏差时，使用固定经验水深作为高程会影响应答器水平定位的精度。

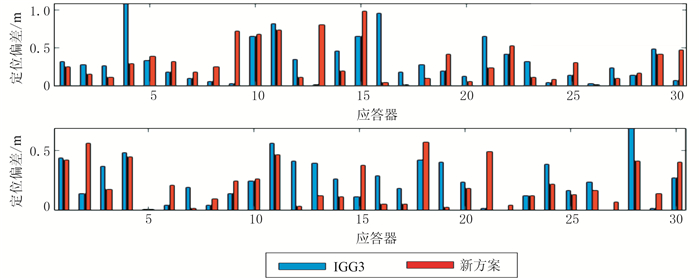
在一些观测极端情况下，基于固定经验水深的方法的定位偏差超过1m(精度较低)。将本文方法与较稳定可靠的IGG3抗差方法进行比较(图 10)。

IGG3方法在一定程度上可减弱粗差对定位的影响，该方法的各方向定位精度(偏差)都优(小)于1m。注意不同方法的解算结果在东方向上的定位精度明显优于北方向。由图 7可知勘探船主要沿东方向进行对称观测，参考点主要沿东方向分布，因而东方向的观测结构比北方向更稳定。

不失一般性，采用下列偏差指标统计定位精度

$ \mathrm{MPB}=\frac{\sum\limits_{i=1}^{n} \operatorname{norm}\left[(\hat{x}, \hat{y})_{1 i}-(\hat{x}, \hat{y})_{2 i}\right]}{K} $

(11)

式中：norm(·)表示向量求模；K为应答器个数。

由表 1可知本文方法与传统的LS1、LS2和IGG3等方法相比，平均定位精度更高。分析得知主要原因是本文方法使用了高精度的单波束测深和船载DGPS系统进行应答器高程插值，因此观测方程的观测结构的稳定性更强。

同时，本文方法还估计了大入射角情况下的声线弯曲的影响，采用序贯最小二乘模式对全局声线弯曲参数进行求解，可进一步减弱声线弯曲对水平定位精度的影响。

4 结束语

本文分析了浅海石油地震勘探中声学二次定位过程中固定经验水深不准对水平定位精度的影响；依托船载单波束和DGPS，使用自然邻点插值法对应答器进行空间高程插值；根据入射角计算声线弯曲后的综合速度场，以提高每次声信号的测距精度；采用序贯最小二乘求解模型参数，提高了水下应答器的解算精度。南海实测实验结果表明：本文算法可显著提高水下多目标定位精度，在约80m水深条件下，平均平面定位偏差小于0.4m。