② 中国石油西南油气田勘探开发研究院, 四川成都 610000;
③ 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580
② Exploration and Development Research Institute, Southwest Oil & Gas Field Company, PetroChina, Chengdu, Sichuan 610000, China;
③ School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China
在实际地震勘探中,面波是影响原始地震数据信噪比的重要因素。在道集记录上主要表现为频率低、速度低、能量强,呈扫帚状发散分布。针对面波的压制,现今已研发出多种成熟的配套技术,包括频率域滤波、F-K滤波、F-X滤波、小波变换、Curvelet变换等[1-5]。总的发展趋势是由单一特征差异向多特征差异发展,由频域向时频域发展。
在频率域,主要依据面波与有效波的频率差异压制面波,这是单一特征差异的面波压制方法。F-K滤波、F-X滤波相对于频率域滤波而言,增加了一项差异特征,如速度差异、空间位置差异等。频率域滤波、F-K滤波和F-X滤波都具有“频率时不变”的共同特性。小波变换是一种多尺度分析方法,它在将数据变换到频率域的同时还保留了时间特性,可呈现信号在各尺度下的频率特征。由于小波变换角度分辨率不高[6],它不能很好地表达图像边缘的方向特征。
Curvelet变换是一种多尺度、多方向的分析方法。1999年,Candès等[7]基于Rideglet变换提出了第一代Curvelet变换。第一代Curvelet变换的数字实现比较繁琐,且具有很大的数据冗余。随后,Candès等[8-10]进一步提出了一种改进的快速离散傅里叶变换方法,即第二代Curvelet变换。Curvelet变换具有较强的方向特征,针对高维信号的线奇异特征具有最优的非线性表达,能克服小波变换对于图像边缘方向特征表达不足的欠缺。
Curvelet变换的多尺度、多方向特性被广泛应用于地震资料去噪,主要包括随机噪声压制、面波分离、多次波预测等[11-18]。张恒磊等[13]通过Curvelet多尺度分解,在曲线变化特征良好逼近的基础上采用非线性阈值压制随机噪声,取得了良好效果。董烈乾等[15]利用面波与有效波在Curvelet域不重叠的特性,对Curvelet系数进行处理,在Curvelet域成功地压制了面波;他们还提出利用曲波多方向特性,自动选取遵循斯奈尔定律的多次波贡献道集,对多次波模型道进行构建,弥补了自由表面多次波压制方法(SRME)预测多次波时产生的振幅误差。
针对基于Curvelet变换压制面波的方法,已有许多学者提出了多种不同的阈值计算公式[19-21],且具有各自的优缺点。但其压制效果都受到面波与有效波在Curvelet域的重叠程度影响。鉴于此,本文提出一种基于能量比值的Curvelet阈值迭代压制面波方法,通过将面波与有效波进行多次阈值迭代,可以更彻底地分离面波与有效波。
1 基于二代Curvelet变换的面波压制 1.1 第二代Curvelet变换原理Curvelet变换属于多尺度分析理论范畴,其实质是设定一个基函数与信号进行内积,实现信号的多尺度表达。假设一个二维空间,其空间域参数为x,频率域参数为w,r、θ为极坐标参数,l为方向参数。
先定义两个时窗:半径时窗为W(r),
| $ \sum\limits_{j = - \infty }^\infty {{W^2}} \left( {{2^j}r} \right) = 1\quad r \in \left( {\frac{3}{4},\frac{3}{2}} \right) $ | (1) |
| $ \sum\limits_{l = - \infty }^\infty {{V^2}} (t - l) = 1\quad t \in \left( { - \frac{1}{2},\frac{1}{2}} \right) $ | (2) |
对于每一个尺度参数j≥j0(j0为起始值),都可利用傅里叶变换定义一个频率窗
| $ {U_j}(r,\theta ) = {2^{ - 3j/4}}W\left( {{2^{ - j}}r} \right)V\left( {\frac{{2\left\lfloor {\frac{j}{2}} \right\rfloor \theta }}{{2{\rm{ \mathsf{ π} }}}}} \right) $ | (3) |
式中
定义Curvelet“母”函数为Φj(x), 通过傅里叶变换,可得
| $ {{\mathit{\hat \Phi }}_j}(w) = {U_j}(w) $ | (4) |
则其他2-j尺度的Curvelet函数都可由该母函数Φj(x)经过旋转、平移得到。
定义旋转角度θl=
| $ {\mathit{\Phi }_{j,l,k}}(x) = {\mathit{\Phi }_j}\left[ {{\mathit{\boldsymbol{R}}_{{\theta _l}}}\left( {x - x_k^{j,l}} \right)} \right] $ | (5) |
式中:
| $ C(j,l,k) = \left\langle {f,{\mathit{\Phi }_{j,l,k}}} \right\rangle = \int_{{R^2}} f (x)\overline {{\mathit{\Phi }_{j,l,k}}(x)} {\rm{d}}x $ | (6) |
由此可知,给定一个Curvelet函数,经过伸缩、平移和旋转可生成L2(R2)(平方可积函数空间)的紧标架,这意味着它具有重构公式
| $ f(x) = \sum\limits_{(j,l,k) = \mathit{\boldsymbol{M}}} {\left\langle {f(x),{\mathit{\Phi }_{j,l,k}}} \right\rangle {\mathit{\Phi }_{j,l,k}}} $ | (7) |
式中:Φj, l, k表示由指标(j, l, k)确定的Curvelet簇;M表示指标。
Curvelet函数具有很强的方向敏感性。由式(5)可知,在尺度j上总共有
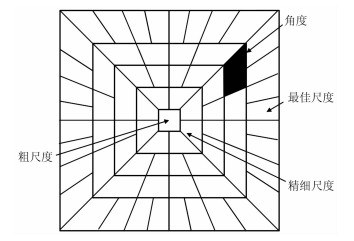
图 1是Curvelet变换频率域尺度分割示意图,图中阴影区为楔形,每个楔形对应一个Curvelet基函数。由Curvelet定义可知,每个Curvelet基函数有一个特定的尺度、方向和位置,这些特定因素可由式(6)中的下标(j, l, k)表征。
|
图 1 Curvelet变换频率域分割示意图 |
整个Curvelet变换按照频率由低到高划分尺度,由最内层粗尺度(Coarse)、中间层精细尺度(Detail)和最外层最佳尺度(Fine)组成。每个尺度沿着顺时针划分方向,每个方向由相应频率的Curvelet系数组成。其中:粗尺度包含了低频系数信息,不具有方向性;最佳尺度包含了高频系数信息,具有方向特性;精细尺度主要用于方向分割,具有方向特性。
在利用Curvelet变换进行信号处理过程中,通常会将信号进行尺度和方向划分。其中粗尺度与最佳尺度下的数据包含了信号的原本概貌,不作为处理对象,而精细尺度下的数据包含了待处理的信息,是主要研究对象。
1.2 Curvelet域面波压制原理面波具有频率低、速度低、能量强,在道集记录中呈扫帚状发散分布等特点,根据面波与有效波在频率、速度、方向上的特征差异,利用Curvelet变换的多尺度、多方向等特性,将面波与有效波变换到Curvelet域,可更细致地描述面波与有效波的差异。与其他传统面波压制方法相比,Curvelet变换的多尺度、多方向特性具有明显优势。
假设一个地震数据体由下式表示
| $ S = {x_1} + {x_2} + n $ | (8) |
式中:x1为有效信号;x2为面波;n为高斯白噪声。
对地震数据体做Curvelet变换,可将x1、x2和n用Curvelet系数表示
| $ \left\{ {\begin{array}{*{20}{l}} {{x_1} = {C_{\rm{T}}}\left( {{C_1}} \right)}\\ {{x_2} = {C_{\rm{T}}}\left( {{C_2}} \right)}\\ {n = {C_{\rm{T}}}\left( {{C_3}} \right)} \end{array}} \right. $ | (9) |
式中:CT表示Curvelet变换;C1、C2、C3对应有效波、面波及高斯白噪声的Curvelet系数。
由式(9)可知,通过合适的尺度、方向等变换参数,可将有效波与面波变换到Curvelet域中,将面波系数置零,实现面波与有效波的分离。
2 基于能量比值的阈值迭代方法Curvelet变换压制面波的效果受面波与有效波在Curvelet域中的重叠程度影响,两者重叠程度越低,压制效果越好。在实际地震采集资料中,因不同的地质环境、采集工艺,造成面波分布特征不尽相同。针对面波与有效波重叠程度较高的资料,Curvelet变换也难以较彻底地分离面波与有效波。本文尝试提出一种基于能量比的阈值迭代压制面波方法:将面波与有效波在Curvelet域进行不同频带的多次分解;在不同尺度和方向上,根据面波与有效波的分布特征,以不同的阈值进行多次迭代,力求更彻底地分离面波与有效波。
2.1 能量比值在信号处理过程中,分析两信号的不同点及相同点时,通常采用对比法,如能量对比法等。本文基于能量对比法,通过面波模型与地震数据体中的面波在Curvelet域中进行能量对比,根据相似程度,将地震数据体中的面波分离出来。
假设面波x2已知,将地震数据体S与面波x2进行相同参数的Curvelet变换,得到CT(S)和CT(x2)。
将相同尺度和方向下的CT(S)与CT(x2)进行能量对比
| $ \zeta = \frac{{{A_{{{(j,l)}_1}}}}}{{{A_{{{(j,l)}_2}}}}} $ | (10) |
式中A(j, l)1和A(j, l)2分别为地震数据体S和面波x2在j尺度、l方向分量的振幅。
由式(10)可知,通过分析能量比值ζ的大小,便可知地震数据体S在j尺度和l方向分量下的面波与面波模型x2在相应尺度和方向分量下的面波的相似程度。其中,ζ越大,表明地震数据体在该尺度和方向分量下的面波与面波模型在相应尺度和方向分量下的面波的相似性越小,表征面波含量越小;反之越大。
2.2 阈值选取Curvelet变换压制面波,很重要的一个环节阈值处理。在阈值去噪中,通常分为软阈值处理和硬阈值处理两种。由于硬阈值处理存在间断点,容易造成重构失真现象,本文采用软阈值处理方法。
由式(10)可知,根据不同尺度j和方向l下ζ的大小,采用基于能量比值的软阈值面波压制方法。重构系数设定为
| $ {\hat C_{j,l}} = \left\{ {\begin{array}{*{20}{c}} 0&{\zeta < 0.8\alpha }\\ { {\rm{sign}} \left( {{C_{j,l}}} \right) \cdot \left( {\left| {{C_{j,l}}} \right| - \zeta } \right)}&{0.8\alpha \le \zeta < \alpha }\\ {{C_{j,l}}}&{\zeta \ge \alpha } \end{array}} \right. $ | (11) |
式中:Cj, l为地震数据体S在j尺度和l方向分量下的Curvelet系数;sign(·)为符号函数;α为阈值,根据面波与有效波在Curvelet域中各尺度和方向分量下的分布特点而有所不同,一般为试验值或经验值,它决定了压制面波的程度;
从式(11)可知:当ζ<0.8α时,表明面波含量高,则将重构系数
上述处理方法,只要给定一个与地震数据体中的面波相似的含面波数据体,便可由式(11)分离出等同或者更多、更少的面波。
图 2为处理流程图,可细分为以下具体步骤:

|
图 2 面波压制迭代处理流程 |
(1) 将原始地震数据体进行Curvelet变换;
(2) 选取含有面波的尺度和方向分量做Curvelet反变换,得到预估面波模型;
(3) 将预估面波模型与原始地震数据做相同参数的Curvelet变换,并进行阈值处理;
(4) 通过多次设置不同的Curvelet变换参数(尺度、方向等)、尺度频率范围,根据面波与有效波的分布特征,针对不同区域设置不同的阈值进行多次迭代,直至达到满意效果。
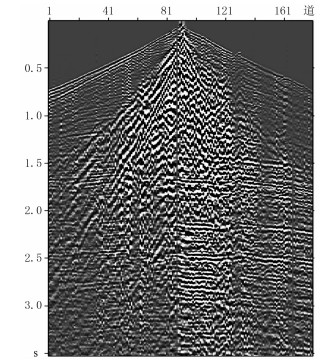
3 实际应用实际资料来源于四川盆地M工区(图 3)。主要采集参数分别为:道距30m,接收道数180,采样间隔2ms,中点炸药激发,记录长度5s,本文记录显示长度为3.5s。
|
图 3 四川盆地某工区采集数据 |
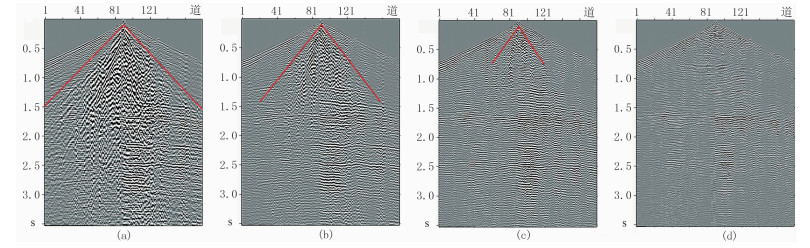
首先对采集数据中的面波做速度分析和频率分析。通过速度扫描得知,面波视速度最高约达2100m/s。图 4为采集数据的频率扫描结果,采用高通滤波器扫描,扫描间隔为8Hz。图中频率扫描到24Hz时仍能看到部分面波(图 4c红色直线下方区域),该部分面波能量强,线性相关性低,与有效波重叠程度高。但在实际应用中,利用传统方法压制这部分面波时,由于其线性相关性低,且频率高,往往难以达到理想压制效果。
|
图 4 采集数据不同低截频率时的频率扫描结果 (a)8Hz;(b)16Hz;(c)24Hz;(d)32Hz |
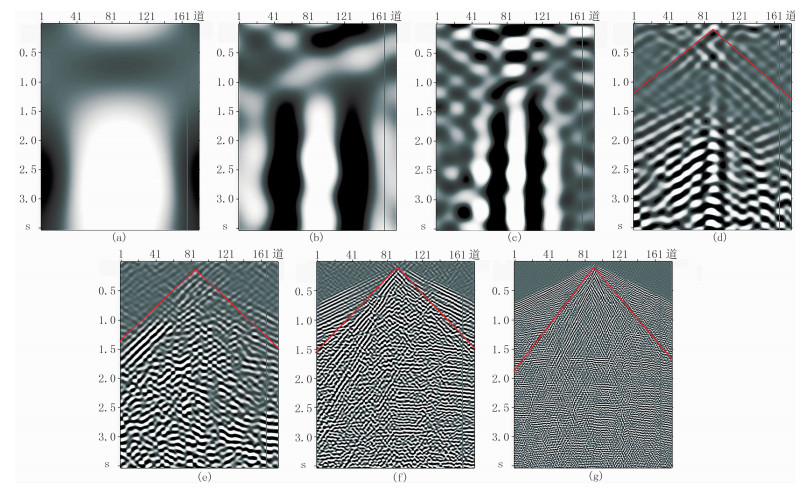
针对该区面波分布特征,基于第二代Curvelet变换,采用能量比值的阈值迭代方法进行压制。即首先对原始数据做Curvelet变换,得到各尺度下T-X域的地震数据体(图 5)。尺度分析所采用的频带范围是0~40Hz,尺度依次为1~7。
|
图 5 原始数据在各尺度下的T-X域数据体 (a)尺度1;(b)尺度2;(c)尺度3;(d)尺度4;(e)尺度5;(f)尺度6;(g)尺度7 |
从图 5可见:尺度1~3主要是一些超低频信息,这部分信息属于低频系数部分,涵盖了原始数据的概貌(图 5a~图 5c);尺度4~7中都含有面波(图 5d~图 5g中红色直线下方区域)。含有面波的尺度是重点研究对象,需进行方向细分。
将尺度4~7下的数据体再做方向细分,根据面波分布的视速度范围,确定面波在Curvelet域所处角度方向,选取含有面波的角度范围做Curvelet反变换,所得数据体作为预估面波模型。
根据工区内面波分布特点,遵循先强后弱、先低频后高频、先低速后高速的原则,对原始地震数据体进行了3次阈值迭代。此3次Curvelet变换参数如表 1所示。
|
|
表 1 多次迭代的Curvelet变换参数表 |
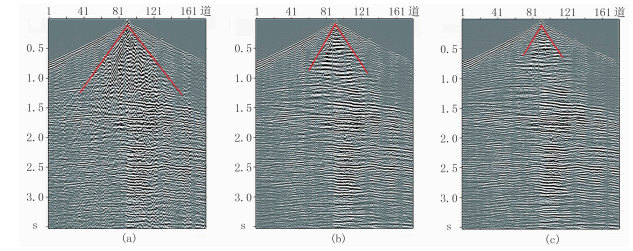
图 6是多次迭代后的道集记录对比。可见原始采集数据经3次阈值迭代后面波含量逐渐减少,同相轴连续性增强;被面波掩盖的有效波在3次迭代后,逐渐突显出来,信噪比得到显著提高。
|
图 6 多次迭代后的道集记录对比图 (a)第一次;(b)第二次;(c)第三次 |
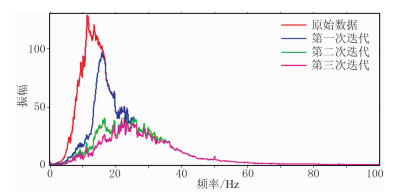
图 7是多次迭代前、后的频谱曲线对比。可见低频面波在每一次设定的尺度频率范围内被多次衰减,中高频有效波频谱特征与原先基本一致,同时还保留了部分低频信息。
|
图 7 多次迭代前、后的频谱曲线对比图 |
为了对比验证本文方法的可靠性和优越性,分别对原始数据再做传统Curvelet变换阈值面波压制和F-K滤波,三种方法参数如表 2所示。
|
|
表 2 三种方法参数对照表 |
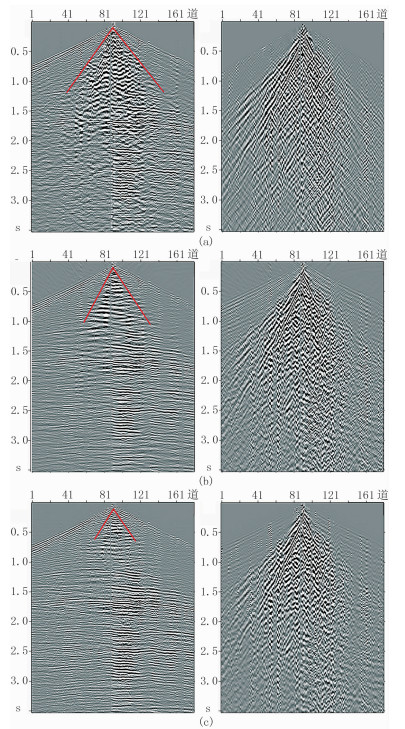
图 8是三种方法压制面波后的道集记录及噪声记录对比图。从总体上看,三种方法都具有一定的面波压制作用,且基于Curvelet变换的面波压制方法(图 8b和图 8c)效果明显优于F-K滤波(图 8a)。
|
图 8 三种方法去噪后的道集(左)及其噪声(右)记录对比 (a)F-K滤波法;(b)传统Curvelet变换阈值法;(c)本文方法 |
图 8a是利用传统F-K滤波压制面波后的道集及其噪声记录。可见面波压制欠彻底,尚存较多低频的残留面波(红线下方区域)。这部分强能量面波掩盖了有效波,使波组特征表现不突出,严重影响了整个资料的信噪比及后期资料处理和解释。
由于传统F-K滤波需满足线性相关的前提条件,该局限性使其对在道集记录中表现为低频、低线性相关、能量强,且与有效波重叠程度较高的这部分面波,难以达到理想效果。
图 8b是利用传统Curvelet变换压制面波后的道集及其噪声记录。可见在F-K滤波后(图 8a)仍残留的面波也得到较好压制(红线下方区域),其有效波较突显,同相轴连续性变强,波组特征明显,资料的整体信噪比显著提高。充分利用Curvelet变换具有的多尺度、多方向特性,通过合适的尺度、方向等Curvelet变换参数,在Curvelet域将地震数据体中有效波与低线性相关的残留面波进行有效分隔,进而消除。
图 8c是基于本文方法压制面波后的道集及其噪声记录。可见在图 8b(传统Curvelet变换阈值法)道集记录上仍然残留的部分能量强、与有效波重叠程度高的面波被较彻底地消除(图 8c红线下方区域),该去噪后道集记录信噪比更高,同相轴连续性更强,波组特征更明显。
图 9为图 8b和图 8c去噪后道集记录的局部放大图,对比可见图 9a的背景记录上存在很多反向线性噪声,即Curvelet系数脚印。因此,本文方法不仅可很好地分离面波与有效波,还能消除Curvelet变换遗留下来的Curvelet系数脚印。
图 10是三种方法压制面波前、后的频谱曲线对比,可见其对面波频带的压制效果有所差异。基于本文的压制面波方法,面波频带的压制效果优于传统的面波压制方法。

|
图 10 三种方法去噪前、后的频谱曲线对比 |
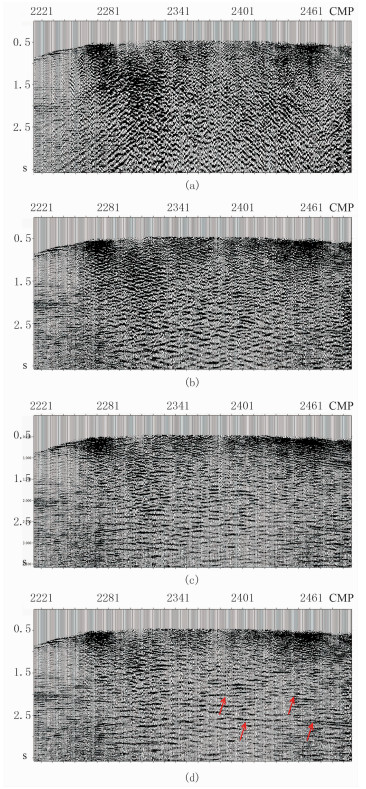
为了验证本文方法应用效果,将三种压制面波方法处理后的剖面(图 11)进行对比。从图 11中可以看出:利用F-K滤波方法压制面波后,存在面波压制不干净,有效波被掩盖的不足;利用传统Curvelet变换阈值法压制面波后,剖面整体信噪比明显提高,有效波出露;基于本文方法压制面波后,剖面有效波连续性更强,信噪比更高。
|
图 11 三种方法去噪前、后的地震剖面对比 (a)原始地震剖面;(b)F-K滤波法;(c)传统Curvelet阈值去噪法;(d)本文方法 |
Curvelet变换是一种多尺度、多方向、多分辨率的分析方法,它将信号进行多尺度分解,得到多方向上的Curvelet域信息;通过分析面波与有效波的分布特征,可在Curvelet域有效分离面波与有效波。但是,Curvelet变换压制面波受有效波与面波在Curvelet域重叠程度影响。本文提出的基于能量比值的阈值迭代压制面波方法,将面波与有效波在Curvelet域进行不同频带的多次分隔,在不同的尺度和方向上,根据面波与有效波的分布特征,采用不同的阈值进行多次迭代,对面波的压制达到了很好的效果。理论分析与实际应用效果对比均表明,相对于传统面波压制方法,本文方法面波压制更彻底,所获资料信噪比更高,同相轴更连续。
| [1] |
李振春, 张军华. 地震数据处理方法[M]. 山东东营: 石油大学出版社, 2004: 23-54.
|
| [2] |
张军华, 吕宁, 田连玉, 等. 地震资料去噪方法技术综合评述[J]. 地球物理学进展, 2006, 21(2): 546-553. ZHANG Junhua, LYU Ning, TIAN Lianyu, et al. An overview of the methods and techniques for seismic data noise attenuation[J]. Progress in Geophysics, 2006, 21(2): 546-553. DOI:10.3969/j.issn.1004-2903.2006.02.033 |
| [3] |
刘志刚, 谢言光, 陈峰. 地震数据处理中噪声衰减方法的探讨[J]. 石油地球物理勘探, 2009, 44(增刊1): 67-71. LIU Zhigang, XIE Yanguang, CHEN Feng. Discussion on noise attenuation methods in seismic data processing[J]. Oil Geophysical Prospecting, 2009, 44(S1): 67-71. |
| [4] |
臧胜涛, 苏勤, 王建华, 等. 山地复杂构造带地震资料处理方法[J]. 石油地球物理勘探, 2018, 53(增刊1): 62-68. ZANG Shengtao, SU Qin, WANG Jianhua, et al. Seismic data processing methods for complex mountai-nous areas[J]. Oil Geophysical Prospecting, 2018, 53(S1): 62-68. |
| [5] |
董烈乾, 张慕刚, 张翊孟. 预测自适应相减面波压制方法[J]. 石油地球物理勘探, 2016, 51(6): 1089-1093. DONG Lieqian, ZHANG Mugang, ZHANG Yimeng. A ground roll suppression method based on predictive and adaptive subtraction[J]. Oil Geophysical Prospecting, 2016, 51(6): 1089-1093. |
| [6] |
Mallat S. A theory for multiresolution signal decomposition:The wavelet representation[J]. IEEE Tran-sactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693. DOI:10.1109/34.192463 |
| [7] |
Candès E J, Donoho D J. Curvelets:A Surprisingly Effective Non-adaptive Representation of Objects with Edges[M]. Vanderbilt University Press, 1999.
|
| [8] |
Candès E J, Donoho D L. New tight frames of Curvelets and optimal representations of objects with piecewise-C2 singularities[J]. Communications on Pure and Applied Mathematics, 2004, 57(2): 219-266. DOI:10.1002/cpa.10116 |
| [9] |
Candès E J, Donoho D L. Continuous curvelet transform[J]. Applied Computational Harmonic Analysis, 2005, 19(2): 198-222. |
| [10] |
Candès E J, Demanet L, Donoho D L, et al. Fast discrete curvelet transforms[J]. SIAM Multiscale Mo-deling and Simulation, 2006, 5(3): 861-899. DOI:10.1137/05064182X |
| [11] |
张华, 陈小宏, 李红星, 等. 曲波变换三维地震数据去噪技术[J]. 石油地球物理勘探, 2017, 52(2): 226-232. ZHANG Hua, CHEN Xiaohong, LI Hongxing, et al. 3D seismic data de-noising approach based on Curvelet transform[J]. Oil Geophysical Prospecting, 2017, 52(2): 226-232. |
| [12] |
郑静静, 印兴耀, 张广智, 等. 基于第二代Curvelet变换的面波压制[J]. 应用地球物理, 2010, 7(4): 325-335. ZHENG Jingjing, YIN Xingyao, ZHANG Guangzhi, et al. The surface wave suppression using the second generation Curvelet transform[J]. Applied Geophy-sics, 2010, 7(4): 325-335. |
| [13] |
张恒磊, 张云翠, 宋双, 等. 基于Curvelet域的叠前地震资料去噪方法[J]. 石油地球物理勘探, 2008, 43(5): 508-513. ZHANG Henglei, ZHANG Yuncui, SONG Shuang, et al. Curvelet domain-based prestack seismic data denoise method[J]. Oil Geophysical Prospecting, 2008, 43(5): 508-513. DOI:10.3321/j.issn:1000-7210.2008.05.004 |
| [14] |
张恒磊, 刘天佑. Curvelet变换及其在地震波场分离中的应用[J]. 煤田地质与勘探, 2010, 38(1): 76-80. ZHANG Henglei, LIU Tianyou. Curvelet transform and its application in seismic wave field separation[J]. Coal Geology & Exploration, 2010, 38(1): 76-80. DOI:10.3969/j.issn.1001-1986.2010.01.018 |
| [15] |
董烈乾, 李振春, 王德营, 等. 第二代Curvelet变换面波压制方法[J]. 石油地球物理勘探, 2011, 46(6): 897-904. DONG Lieqian, LI Zhenchun, WANG Deying, et al. Ground-roll suppression based on the second generation Curvelet transform[J]. Oil Geophysical Prospecting, 2011, 46(6): 897-904. |
| [16] |
曹静杰, 杨志权, 孙秀丽. 一种基于曲波变换的自适应地震随机噪声消除方法[J]. 石油物探, 2018, 57(1): 72-78. CAO Jingjie, YANG Zhiquan, SUN Xiuli. An adaptive seismic random noise elimination method based on Curvele transfrom[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 72-78. DOI:10.3969/j.issn.1000-1441.2018.01.010 |
| [17] |
董烈乾, 李培明, 张奎, 等. 利用曲波变换预测多次波模型[J]. 石油地球物理勘探, 2015, 50(6): 1098-1104. DONG Lieqian, LI Peiming, ZHANG Kui, et al. Multiple model prediction based on Curvelet transform[J]. Oil Geophysical Prospecting, 2015, 50(6): 1098-1104. |
| [18] |
彭才, 常智, 朱仕军. 基于曲波变换的地震数据去噪方法[J]. 石油物探, 2008, 47(5): 461-464. PENG Cai, CHANG Zhi, ZHU Shijun. Noise elimination method based on curvelet transform[J]. Geophysical Prospecting for Petroleum, 2008, 47(5): 461-464. DOI:10.3969/j.issn.1000-1441.2008.05.006 |
| [19] |
Donoho D L. Ten-minute tour[J]. Progress in Wavelet Analysis and Application, 1993, 338(2): 639-654. |
| [20] |
Donoho D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory, 2002, 41(3): 613-627. |
| [21] |
Li C Z, Wang J D, Zhang L. Curvelet transform for image denoising based on Bayes shrink[J]. Video Engineering, 2007, 31(6): 14-16. |



 李继伟, 四川省成都市天府新区华阳大道一段216号中国石油集团东方地球物理公司西南物探研究院, 610213。Email:
李继伟, 四川省成都市天府新区华阳大道一段216号中国石油集团东方地球物理公司西南物探研究院, 610213。Email:
