陆上地震勘探中,疏松表层介质对地震波高频成分有强烈的吸收衰减作用,导致地震资料垂向分辨率降低;由于表层岩性、速度、厚度的横向变化,吸收衰减程度会不同,造成地震波道间能量、频率和相位的不一致,影响同相叠加结果的横向分辨率。地震波的吸收和频散特性与介质的成分、饱和度、孔隙度等密切相关,研究衰减补偿时一般用品质因子Q描述这种吸收与衰减的总体效应。
目前改善地表一致性、提高分辨率的常规方法有基于地表一致性(或单道)的反褶积(含振幅补偿)和基于深层地层的Q补偿方法。前者基于统计方法,通常难以满足假设条件,因此对消除表层影响能力有限。而且反褶积存在不同程度的保真性问题,甚至产生副作用[1-5]。后者忽略了表层严重的吸收衰减作用,因此难以获得理想的处理成果。
近年来,对地震信号的吸收衰减研究日趋重视[6-7],但大多数的地层Q值求取及吸收补偿方法针对的是深层成岩介质[8-13],Q模型的估算难度大,存在不确定性;反Q滤波振幅补偿的稳定性、补偿结果的评价等问题都亟待解决。针对反Q滤波振幅补偿的稳定性问题,Wang[14]基于Kolsky-Futterman模型,从一维波动方程出发,考虑能量的吸收和频散,导出能量补偿和相位校正公式,实现了稳健有效的频率域反Q滤波方法。
随着油气勘探领域对地震数据精度要求的提高,学者们开始重视表层吸收补偿问题[15-20]。尹喜玲等[18]就沙漠地区的近地表吸收规律进行了初步探讨,认为多次反射和透射是造成近地表衰减的主要原因。于承业等[19]提出利用双井微测井资料,通过频移法估算近地表Q值,强调了近地表衰减补偿的重要性,指出现有处理系统的地表一致性振幅补偿和地表一致性反褶积是定性的,不能在时间、频率、空间三个域有效消除近地表影响。
为了有效解决表层吸收补偿问题,本文提出了一种确定性表层Q求取和空变吸收补偿方法。该方法基于地表一致性原理,实现了表层相对衰减系数统计估算、表层Q模型建立、表层Q标定以及稳定的空变Q补偿,有效解决表层横向多变的吸收问题。经模型计算验证了方法的正确性和保真性,目前已应用于新疆、青海、大庆等多个地区实际生产。生产实践表明:该方法能合理拓宽有效频带并大幅提高地震数据分辨率,且不降低数据信噪比。经表层吸收补偿后,数据一致性更高,波组关系更加明确,地质现象和构造特征更加清楚。井标定和属性分析等均证明了补偿结果的可靠性,相比常规处理方法效果明显。
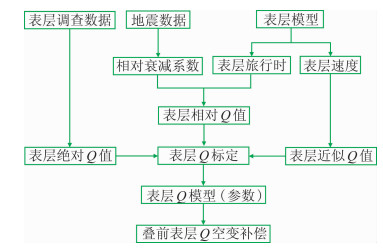
1 方法原理首先利用野外表层吸收调查数据的直达波计算调查点的表层实测Q值。在没有表层实测Q值的情况下,也可利用表层调查的速度模型计算近似Q值:基于共炮检域统计迭代求出炮检点相对衰减系数,并结合表层旅行时得到表层相对Q值;再利用实测Q值或近似Q值对相对Q值的大小和空间变化趋势进行标定,得到表层Q场;最后利用表层Q场和表层旅行时,通过有效稳定的Q补偿算法对地震数据进行表层Q空变补偿。表层吸收补偿即相当于将炮点和检波点从地表延拓至高速顶界的过程。该方法流程如图 1示。
|
图 1 表层Q空变补偿流程 |
实测Q值的求取是表层吸收补偿方法研究的基础,其结果对计算整个工区的Q值起着约束标定作用。利用微测井数据井底道和地面道直达波的频率属性和振幅属性,通过改进的峰值频移法或谱比法计算实测Q值[13, 19-20]。
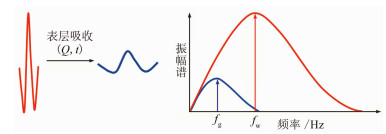
改进峰值频率频移法:表层对地震波的吸收会导致峰值频率由高变低,通过分析井底道峰值频率fw到地面道峰值频率fg的移动可反演调查点的表层Q值,如图 2所示。改进峰值频率频移法结合了质心频率频移法和峰值频率频移法的优点,目的是先求质心频率fwc,再通过式(1)将质心频率换算成峰值频率fw,提高算法的稳定性。
| $ {f_{\rm{w}}} = \frac{{2{f_{{\rm{wc}}}}}}{{\sqrt {\rm{ \mathsf{ π} }} }} $ | (1) |
|
图 2 峰值频率频移法示意图 |
峰值频率频移法的计算公式为
| $ Q=\frac{\pi t f_{\mathrm{g}} f_{\mathrm{w}}^{2}}{2\left(f_{\mathrm{w}}^{2}-f_{\mathrm{g}}^{2}\right)} $ | (2) |
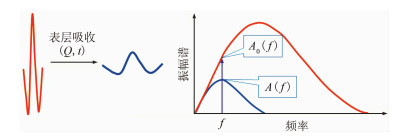
频谱比率法(改进的谱比法):表层对地震波的吸收还会造成振幅减弱,谱比法通过分析井中道振幅A0与地面道振幅A的比值计算Q值
| $ \frac{A(f)}{A_{0}(f)}=\mathrm{e}^{-\frac{\pi f t}{Q}} $ | (3) |
计算两道之间振幅(A1、A2)比值的对数可得到
|
图 3 谱比法示意图 |
实际应用中,应先评价吸收调查记录是否可用。由于表层的吸收作用,地面道信号相对井底道信号其振幅明显更弱,主频明显降低。有时由于采集中井中道的耦合不好,所求出的Q值比较大,这样的值不可用。野外表层Q值调查点的设计密度应以能控制区域的表层Q的长波长变化为宜。
对于表层较厚的沙漠区,也可以利用多项式拟合质心频移法估算近地表Q值[19]。
1.2 表层相对Q值表层吸收会造成反射信号的振幅减弱。若表层速度低或旅行时长,则表现出较强的吸收特征,这种吸收衰减具有地表一致性特点,把这种比例关系定义为相对衰减系数,作为求取表层相对Q值的重要属性参数。具体方法为:先对原始数据去噪,选取给定时窗内信噪比较高的反射同相轴数据作为输入,计算每道的均方根振幅,然后统计求取共炮检点的平均振幅,迭代求出炮检点相对衰减系数R,并结合表层旅行时、根据谱比法得到表层相对Q值。
R相当于谱比法中衰减前、后的能量比值。检波点位置的R与表层Q值之间的关系式为
| $ R \times \text { scale }=\frac{A(f)}{A_{0}(f)}=\mathrm{e}^{-\frac{\pi ft}{Q}} $ | (4) |
式中:t表示旅行时,根据表层模型求得;f表示地震波主频,可根据去噪后频谱分析计算得到;scale表示调节系数,该系数可改变Q的趋势大小,逼近于实测Q值。
实际工作中对R做异常值过滤处理,由式(4)可以推导出表层Q值为
| $ Q=-\frac{\pi f t}{\ln (R \times \text { scale })} $ | (5) |
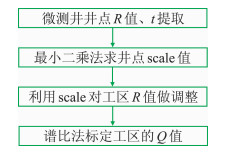
基于野外实测数据求取的实测Q值及通过大炮数据统计求取炮检点表层的相对Q值,采用图 4给出的表层Q约束标定流程可实现相对Q值的标定约束,并建立表层空变Q场,标定结果不改变表层Q值的短波长,但校正了表层Q值的长波长问题。
|
图 4 表层Q约束标定流程图 |
除表层Q值外,表层旅行时也是表层Q补偿的重要参数,可通过静校正计算得到。具体过程如图 4所示。
求得了每个炮检点的Q和t,也就完整地建立了表层Q模型和补偿参数,为叠前数据表层Q空变补偿奠定了基础。
1.4 表层Q补偿建立表层Q场后,用稳定的表层补偿算法就可以对叠前数据在频率域进行表层Q空变补偿
| $ \begin{aligned} U(\tau+\Delta \tau, \omega)=& U(\tau, \omega) \exp \left[\left(\frac{\omega}{\omega_{\mathrm{h}}}\right)^{-\gamma} \frac{\omega \Delta \tau}{2 Q}\right] \times \\ & \exp \left[\mathrm{i}\left(\frac{\omega}{\omega_{\mathrm{h}}}\right)^{-\gamma} \omega \Delta \tau\right] \end{aligned} $ | (6) |
式中:U(τ, ω)为未经Q补偿的频率域数据,即对输入地震道数据进行傅里叶变换的结果;U(τ+Δτ, ω)为经过Q补偿后的频率域数据;τ为传播时间;Δτ为表层旅行时;ω为角频率;ωh是地震频带内与最高频率有关的调谐频率;
Wang[14]提出了稳定的Q补偿算法,对振幅项做了改进,提出稳定的振幅补偿量
| $ \mathit{\Lambda}(\omega)=\frac{\beta(\omega)+\sigma^{2}}{\beta^{2}(\omega)+\sigma^{2}} $ |
式中:
上述Q补偿算法的稳定性体现在可以通过增益限制控制补偿的频带范围,防止高频噪声的过分补偿。由于补偿量随频率和时间的增大逐渐增大,通常的补偿算法都会对高频端过分补偿,造成噪声过量、信号失真,而Wang[14]采用对完全吸收的频率成分不再进行补偿的策略,避免了对高频噪声的过量补偿。该算法的另一优点是补偿振幅的同时也可调整相位,可以同时解决地层吸收造成的地震波能量损失和频散问题。
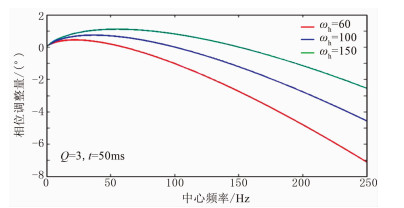
算法中的参数scale对补偿起着重要作用,在实际工作中需要根据具体情况给定合理的值。图 5是参数scale中心频率对相位调整项的影响。由图可见,中心频率发生变化时,相位调整量也随之变化,仅仅在频率为ωh时相位不做调整,其他情况都需要调整。
|
图 5 相位调整量随中心频率的变化曲线 |
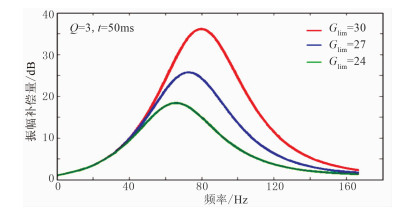
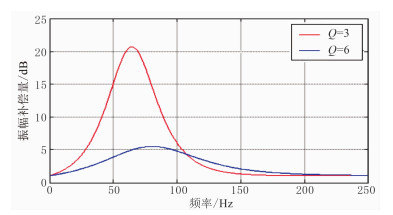
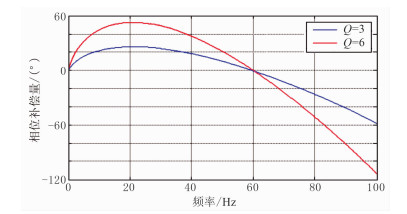
图 6是在固定Q、t的情况下,给定不同Glim时的振幅补偿曲线。由图可见,Glim控制了拐点频率(即截止频率fh),在实际数据补偿中控制高频端的补偿量,因此合理设定Glim能降低补偿结果中的噪声水平。图 7和图 8分别为不同表层Q值、相同旅行时的振幅和相位补偿曲线,也进一步说明了表层Q补偿算法的自适应性。
|
图 6 增益限制Glim对振幅补偿量影响曲线 |
|
图 7 相同旅行时(t=60ms)、不同Q值时的振幅补偿曲线 |
|
图 8 相同旅行时(t=60ms)、不同Q值时的相位补偿曲线 |
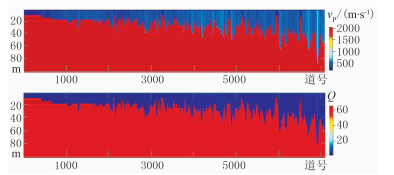
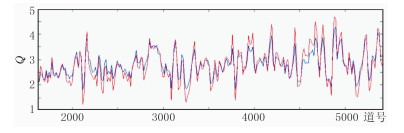
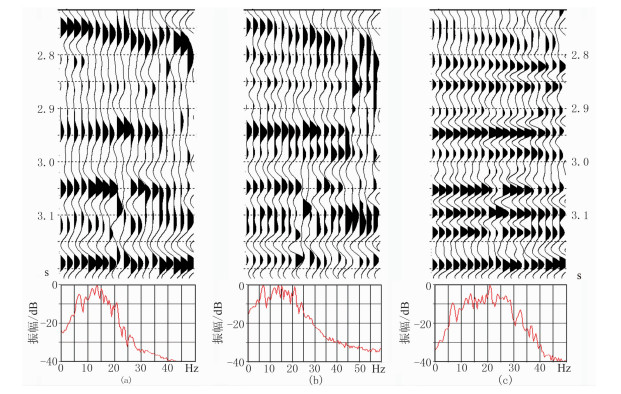
为了测试方法的正确性及适应性,利用理论模型进行正、反演论证。参照一口实际井的数据建立黏弹模型。图 9是表层速度模型和Q模型,表层Q是横向变化的。通过波动方程正演获得二维地震数据,利用本文方法对数据求取相对衰减系数、建立表层Q模型并验证表层Q补偿。图 10为正演Q值和反演相对Q值曲线,可见两者吻合较好。图 11是模型正演、反褶积、表层Q补偿道集及频谱对比图。需要说明的是试验采用的是地表一致性反褶积,参数是经扫描后优选得到的。模型1的计算结果证明了本文法求取Q值及表层Q补偿是准确且稳定的。
|
图 9 表层速度理论模型(上)和Q值理论模型(下) |
|
图 10 理论模型正演Q值(蓝色)和反演相对Q值(红色) |
|
图 11 模型正演、反褶积、表层Q补偿道集及频谱对比图 (a)表层吸收模型正演道集及频谱; (b)图a经反褶积后的单炮记录及频谱;(c)图a经表层Q补偿后的单炮记录及频谱 |
图 12为模型正演、反褶积、表层Q补偿叠加剖面及模型合成记录对比图,剖面中内嵌的蓝色信号为合成记录(模型)。可以看出表层Q补偿的数据与合成记录吻合性更好,分辨率更高。进一步验证了本文方法的保真性。

|
图 12 理论模型正演、反褶积、表层Q补偿叠加剖面与模型合成记录对比图 (a)表层吸收的模型正演数据叠加;(b)对图a做反褶积和表层Q补偿后的剖面;(c)模型合成记录 |
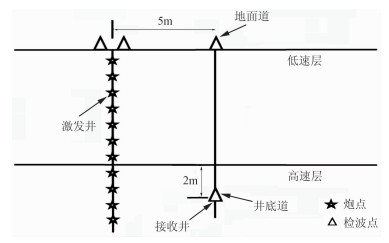
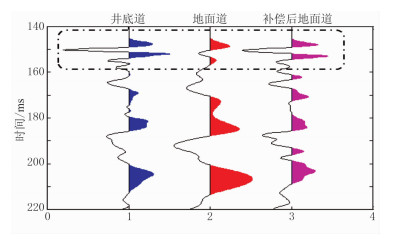
模型2来自于实际的表层吸收调查数据。图 13为吸收调查的现场观测方式示意图,通过激发井和接收井构成双微测井调查,分别取井底道与地面道信号,用频移法或谱比法求取野外实测Q值。用得到的实测Q值补偿地面道,与井底道对比如图 14所示。可以看出:地面道相对与井底道的衰减更显著、振幅更弱、主频更低,经反演Q值补偿的信号与井底道的信号很相似。模型2的计算结果进一步证实,表层吸收严重的信号经衰减处理后,通过表层补偿可以近似得到恢复。
|
图 13 吸收调查的现场观测方式示意图 |
|
图 14 表层吸收调查数据与Q补偿数据对比 |
实例1数据来自中国西部典型丘陵地区,该区地表发育两个大型冲积扇,表层纵、横向速度和厚度变化较大,且浅层干燥,导致近地表有效信号高频吸收衰减严重,对中深目的层地震资料成像、储层描述、砂体识别、流体检测等造成很大影响。
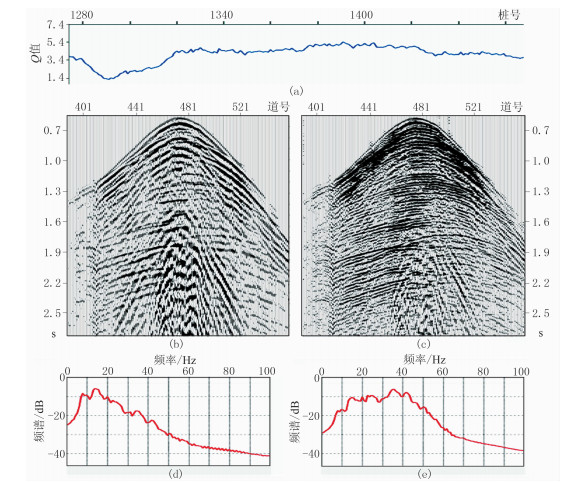
图 15为表层Q值曲线及Q空变补偿处理前、后单炮及频谱对比图。从图 15b可以看到,补偿后的记录中浅、中、深层有效反射信噪比、分辨率均有显著提高;从图 15c、图 15d所示的频谱分析结果可以看出,低频信号保持较好,中、高频成分得到较好的恢复,有效频带拓宽了20Hz。
|
图 15 表层Q值曲线及Q补偿前、后单炮记录及频谱对比 (a)表层Q值;(b)补偿前原始单炮记录;(c)表层定量Q补偿后单炮记录;(d)表层Q补偿前频谱;(e)表层Q补偿后频谱 |
图 16为经地表一致性反褶积和表层Q空变补偿的剖面对比。由图可见,经表层Q补偿获得了高质量的地震剖面,地表一致性问题得到了较好的解决,反射层信噪比、连续性增强,分辨率、保真度提高,地质现象清晰,其效果明显优于传统方法。

|
图 16 地表一致性反褶积(a)与表层Q补偿(b)剖面对比 |
实例2来自中国西部典型大沙漠地区。该地区沙丘起伏剧烈,厚度约为30~200m,地表干燥松散,表层横向速度和厚度变化大,地震波吸收衰减严重,分辨率、保真度的提高是该区地震勘探的瓶颈问题。
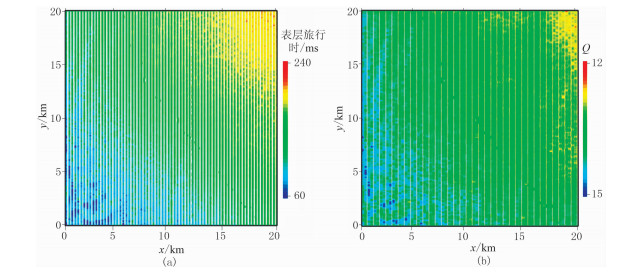
图 17为表层补偿参数平面图对比,可见表层旅行时与表层Q值有明显的正相关性。
|
图 17 表层补偿参数平面图 (a)表层旅行时;(b)表层Q值 |
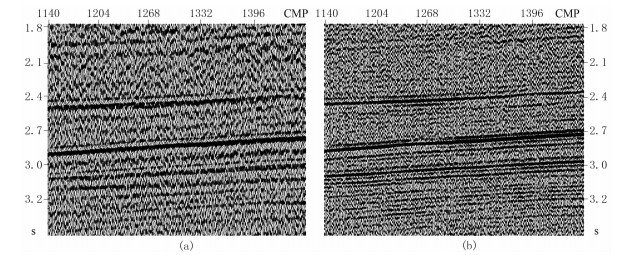
图 18为表层Q补偿前、后的单炮记录对比,图 19为表层Q补偿前、后叠加剖面对比。可以看出:表层Q补偿后有效反射的连续性得到改善,信噪比和分辨率均有显著提高。

|
图 18 表层Q补偿前(a)、后(b)单炮记录对比 |
|
图 19 表层Q补偿前(a)、后(b)剖面对比 |
图 20为分别应用地表一致性反褶积与表层Q补偿处理的剖面对比。可以看出:表层Q补偿后反射波组特征稳定、清晰,便于追踪对比,信噪比、分辨率均优于常规处理剖面。

|
图 20 地表一致性反褶积(a)与表层Q补偿(b)剖面对比 |
本文从地表一致性问题入手,引入表层相对衰减系数的概念,并由此推导表层相对Q值的计算公式。表层Q模型由野外实测的绝对Q值(或李氏经验公式Q值)对相对Q值进行约束标定完成,然后基于空变表层旅行时、表层Q值、补偿参数等实现稳定的表层Q空变补偿,使表层横向吸收衰减的信号得到最大程度的补偿。
通过实测调查分析了表层吸收对信号的影响。采用确定的表层Q补偿方法基本可以恢复近地表衰减前的信号。
理论模型和两个不同地表类型的地区实测资料的计算结果验证了该方法可有效提高计算精度。总体来说,经表层Q补偿的地震资料振幅谱震荡关系得到相对保持,反射波有效频带得到大幅度拓宽,叠前单炮记录和叠加剖面的信噪比、分辨率均有较大幅度的提高。该方法为攻克表层吸收补偿难题提供了新思路。
| [1] |
王西文, 赵邦六, 吕焕通, 等. 地震资料相对保真处理方法研究[J]. 石油物探, 2009, 48(4): 319-331. WANG Xiwen, ZHAO Bangliu, LYU Huantong, et al. Relative amplitude preservation method for seismic data processing[J]. Geophysical Prospecting for Petroleum, 2009, 48(4): 319-331. DOI:10.3969/j.issn.1000-1441.2009.04.001 |
| [2] |
王丹, 孙赞东, 王迪, 等. 基于模型数据的不同反褶积方法保幅性分析[J]. 石油地球物理勘探, 2013, 48(3): 359-365. WANG Dan, SUN Zandong, WANG Di, et al. Analysis of the amplitude preservation of deconvolution methods based on physical model data[J]. Oil Geophysical Prospecting, 2013, 48(3): 359-365. |
| [3] |
王军, 吕小伟, 王立歆. 基于正演模型的地震处理技术保幅性分析与评价[J]. 油气地质与采收率, 2012, 19(4): 46-49. WANG Jun, LYU Xiaowei, Wang Lixin. Analysis and evaluation of seismic processing technique based on forward modeling[J]. Petroleum Geology and Reco-very Efficiency, 2012, 19(4): 46-49. DOI:10.3969/j.issn.1009-9603.2012.04.013 |
| [4] |
郭树祥. 地震资料保幅处理的讨论[J]. 油气地球物理, 2009, 7(1): 1-7. GUO Shuxiang. Discussion of preserved amplitude processing of seismic data[J]. Petroleum Geophysics, 2009, 7(1): 1-7. |
| [5] |
云美厚, 党鹏飞, 李伟娜, 等. 地层品质因子Q值地震反演问题剖析[J]. 石油地球物理勘探, 2017, 52(1): 189-198. YUN Meihou, DANG Pengfei, LI Weina, et al. On issues of formation quality factor Q inversion[J]. Oil Geophysical Prospecting, 2017, 52(1): 189-198. |
| [6] |
李振春, 王清振. 地震波衰减机理及能量补偿研究综述[J]. 地球物理学进展, 2007, 22(4): 1147-1152. LI Zhenchun, WANG Qingzhen. A review of research on mechanism of seismic attenuation and energy compensation[J]. Progress in Geophysics, 2007, 22(4): 1147-1152. DOI:10.3969/j.issn.1004-2903.2007.04.021 |
| [7] |
马昭军, 刘洋. 地震波衰减反演研究综述[J]. 地球物理学进展, 2005, 20(4): 1074-1082. MA Zhaojun, LIU Yang. A summary of research on seismic attenuation[J]. Progress in Geophysics, 2005, 20(4): 1074-1082. DOI:10.3969/j.issn.1004-2903.2005.04.031 |
| [8] |
ZHANG C J, Tadeusz J U. Estimation of quality factors from CMP records[J]. Geophysics, 2002, 67(5): 1542-1547. DOI:10.1190/1.1512799 |
| [9] |
冯玮, 胡天跃, 常丁月, 等. 基于时变子波的品质因子估计[J]. 石油地球物理勘探, 2018, 53(1): 136-146. FENG Wei, HU Tianyue, CHANG Dingyue, et al. Quality factor Q estimation based on time-varying wavelet[J]. Oil Geophysical Prospecting, 2018, 53(1): 136-146. |
| [10] |
凌云, 高军, 吴琳. 时频空间域球面发散与吸收补偿[J]. 石油地球物理勘探, 2005, 40(2): 176-182. LING Yun, GAO Jun, WU Lin. Compensation for spherical dispersion and absorption in time-frequency-space domain[J]. Oil Geophysical Prospecting, 2005, 40(2): 176-182. DOI:10.3321/j.issn:1000-7210.2005.02.018 |
| [11] |
Zhang X W, Han L G. An inverse Q-filter algorithm based on stable wavefield continuation[J]. Applied Geophysics, 2007, 4(4): 263-270. DOI:10.1007/s11770-007-0040-9 |
| [12] |
宫同举, 孙成禹, 彭洪超, 等. 几种提取品质因子方法的对比分析[J]. 勘探地球物理进展, 2009, 32(4): 253-256. GONG Tongju, SUN Chengyu, PENG Hongchao, et al. Comparison and analysis of several methods for extracting quality factors[J]. Progress in Exploration Geophysics, 2009, 32(4): 253-256. |
| [13] |
张宇生, 晋志刚, 李可恩. 利用微测井及VSP资料确定地面地震采集资料的频率[J]. 天然气地球科学, 2010, 21(2): 300-304. ZHANG Yusheng, JIN Zhigang, LI Keen. Determination of surface seismic data frequency by micro logging and vertical seismic profile(VSP) data[J]. Natural Gas Geoscience, 2010, 21(2): 300-304. |
| [14] |
Wang Y H. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 2002, 67(2): 657-663. DOI:10.1190/1.1468627 |
| [15] |
王晓涛, 谭佳, 毛海波, 等. 强衰减条件下能量比法的修正及其应用[J]. 石油地球物理勘探, 2017, 52(1): 42-47. WANG Xiaotao, TAN Jia, MAO Haibo, et al. A modified energy ratio method in strong attenuation condition[J]. Oil Geophysical Prospecting, 2017, 52(1): 42-47. |
| [16] |
裴江云, 陈树民, 刘振宽, 等. 近地表Q值求取及振幅补偿[J]. 地球物理学进展, 2001, 16(4): 18-22. PEI Jiangyun, CHEN Shumin, LIU Zhenkuan, et al. Near surface Q value extraction and amplitude compensation[J]. Progress in Geophysics, 2001, 16(4): 18-22. DOI:10.3969/j.issn.1004-2903.2001.04.004 |
| [17] |
Nizare E Y, Fabian E, Wim M. Near-surface attenuation estimation using wave-propagation modeling[J]. Geophysics, 2008, 73(6): U27-U37. DOI:10.1190/1.2976548 |
| [18] |
尹喜玲, 石战结, 田钢. 近地表低降速带地震波传播规律初探[J]. 地球物理学进展, 2009, 24(2): 398-407. YIN Xiling, SHI Zhanjie, TIAN gang. Study on transmittable laws of seismic waves in unconsolidated layers[J]. Progress in Geophysics, 2009, 24(2): 398-407. DOI:10.3969/j.issn.1004-2903.2009.02.005 |
| [19] |
于承业, 周志才. 利用双井微测井资料估算近地表Q值[J]. 石油地球物理勘探, 2011, 46(1): 89-92. YU Chengye, ZHOU Zhicai. Estimation of near surface Q value based on the datasets of the uphole survey in double hole[J]. Oil Geophysical Prospecting, 2011, 46(1): 89-92. |
| [20] |
罗勇, 毛海波, 薛卫平, 等. 利用多项式拟合质心频移法估算近地表Q值[J]. 石油地球物理勘探, 2016, 51(3): 589-595. LUO Yong, MAO Haibo, XUE Weiping, et al. Nearsurface Q estimation based on polynomial fitting centroid frequency shift[J]. Oil Geophysical Prospecting, 2016, 51(3): 589-595. |



 苏勤, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email:
苏勤, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email: