0 引言

地震数据为探测地质构造和地层分布提供了有效的地球物理信息。地震数据的质量直接影响地震处理和解释结果^[1-4]。地震数据在空间上可能出现不规则采样^[5-6]，造成有效信号的缺失，从而增加地震数据处理难度^[7-8]。因此，对地震数据进行有效重建，使后续数据处理能够更好地刻画复杂地质结构非常必要^[9]。随着地震勘探研究的不断深入, 更多的数学方法被用于地震数据重建^[10-12]。其中一类是基于滤波的重建方法，该类方法通过褶积插值滤波器实现^[13-16]。另一类重要方法是基于变换域的地震数据重建，主要有Radon域变换^[17-19]、Fourier域变换^[20-22]、Curvelet域变换^[23-25]和Shearlet变换^[26]等，即基于数学变换理论，把数据转换到不同的域进行重建。基于波动方程的地震数据重建方法也得到广泛研究，如炮域延拓法^[27]、炮检距域延拓法^[28]、DMO法^[29]和拓展成像条件法^[30]，该类方法计算量大，运算耗时，且当地下信息未知或精度较低时会影响重建效果，所以实际应用较少。

近年来，基于降秩重建的方法引起广泛关注。Trickett等^[31]和Naghizadeh等^[32]提出基于Cadzow滤波的三维地震数据随机噪声衰减方法，建立了Hankel矩阵并对其进行奇异值分解，通过降秩压制线性干扰。Oropeza等^[33]提出多道奇异谱分析(Multichannel Singular Spectrum Analysis, MSSA)将地震数据变换到频率域，然后对每个频率切片构造块Hankel矩阵，通过随机奇异值分解对块Hankel矩阵降秩，得到重建的地震数据。Kreimer等^[34]将该框架直接运用于五维地震数据重建，通过高阶奇异值分解(Higher Order Singular Value Decomposition)进行降秩。Abma等^[35]提出凸集投影迭代方法，在频率切片上进行傅里叶变换后，对幅值进行阈值处理，最后进行反傅里叶变换并插值。Jia等^[36]提出正交矩阵匹配追踪Hankel重建方法(Orthogonal Matrix Pursuit HankelReconstruction, OMPHR)，利用秩1正交匹配追踪方法(Orthogonal Rank-one Matrix Pursuit)代替SVD分解进行降秩，大幅提升运算效率。Siahsar等^[37]提出最优奇异值收缩法，根据随机矩阵理论产生最优低秩估计量，并利用衰减因子约束奇异值，提高低秩估计的鲁棒性^[38]。Gao等^[39]引入一种基于构建块Toeplitz矩阵的快速降秩方法，运用Lanczos双对角化算法代替截断奇异值分解操作，提升了计算效率。Ma^[40]提出基于构建纹理块的低秩矩阵补全方法，通过三维纹理块映射将三维数据变换到二维空间进行地震数据重建。

对于稀疏信号的恢复和低秩矩阵补全，一般建立秩最小化模型并将该模型凸松弛到核范数最小化模型。相对于凸核范数松弛模型，非凸L_p范数松弛模型可以以较低的采样率恢复缺失数据，通过在迭代中设置权重约束奇异值，很好地保证了数据结构的低秩性^[41-42]。Lu等^[43]成功地将非凸L_p范数松弛模型应用到彩色图像恢复上，并取得较好的效果。

基于降秩理论，本文提出非凸L_p范数Hankel重建(Non-convex L_p Norm Hankel Reconstruction，NLPHR)方法对三维地震数据进行重建。非凸L_p范数比核范数更接近秩函数，因此通过求解最小L_p范数问题可以得到更接近于真实值的解。此外，MSSA方法和OMPHR方法均要求给定秩的大小，通过多次重复实验选取合适的秩。本文方法不需要给定秩的大小，而是通过设置权重约束奇异值，迭代减小奇异值，保证了重建数据的低秩性。

1 基于非凸L_p范数的地震数据重建 1.1 三维地震数据低秩重建

考虑三维地震数据体D(t, x, y)∈R^{N_t×N_y×N_x}，其中N_t为时间采样点数，N_y和N_x分别为x方向和y方向地震道数目。对每道数据进行傅里叶变换，得到频率域数据D(ω, x, y)。取每一个频率切片D_ω∈R^N_y×N_x构成矩阵

$ {\mathit{\boldsymbol{D}}_\omega } = \left( {\begin{array}{*{20}{c}} {D(1,1)}&{D(1,2)}& \cdots &{D\left( {1,{N_x}} \right)}\\ {D(2,1)}&{D(2,2)}& \cdots &{D\left( {2,{N_x}} \right)}\\ \vdots & \vdots & \ddots & \vdots \\ {D\left( {{N_y},1} \right)}&{D\left( {{N_y},2} \right)}& \cdots &{D\left( {{N_y},{N_x}} \right)} \end{array}} \right) $

(1)

首先对D_ω的每行构造Hankel矩阵，以第j(1≤j≤N_y)行为例，格式如下

$ {\mathit{\boldsymbol{h}}_j} = \left( {\begin{array}{*{20}{c}} {D(j,1)}&{D(j,2)}& \cdots &{D\left( {j,{K_x}} \right)}\\ {D(j,2)}&{D(j,3)}& \cdots &{D\left( {j,{K_x} + 1} \right)}\\ \vdots & \vdots & \ddots & \vdots \\ {D\left( {j,{L_x}} \right)}&{D\left( {j,{L_x} + 1} \right)}& \cdots &{D\left( {j,{N_x}} \right)} \end{array}} \right) $

(2)

式中：L_x=floor(N_x/2)+1，其中floor(·)为向下取整函数；K_x=N_x-L_x+1。再对每一行的h_j(1≤j≤N_y)进行Hankel矩阵化，建立块Hankel矩阵

$ \mathit{\boldsymbol{\widetilde H}} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}_1}}&{{\mathit{\boldsymbol{h}}_2}}& \cdots &{{\mathit{\boldsymbol{h}}_{{K_y}}}}\\ {{\mathit{\boldsymbol{h}}_2}}&{{\mathit{\boldsymbol{h}}_3}}& \cdots &{{\mathit{\boldsymbol{h}}_{{K_y} + 1}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{\mathit{\boldsymbol{h}}_{{L_y}}}}&{{\mathit{\boldsymbol{h}}_{{L_y} + 1}}}& \cdots &{{\mathit{\boldsymbol{h}}_{{N_y}}}} \end{array}} \right) $

(3)

类似地，L_y=floor(N_y/2)+1，K_y=N_y-L_y+1，则块Hankel矩阵$ {\mathit{\boldsymbol{\tilde H}}}$的大小为(L_x×L_y)×(K_x×K_y)。块Hankel矩阵映射定义如下

$ \mathit{\boldsymbol{\tilde H}}: = {P_{\rm{H}}}(\mathit{\boldsymbol{D}}) $

(4)

式中算子${P_{\rm{H}}}:{\mathit{\boldsymbol{R}}^{{N_t} \times {N_y} \times {N_x}}} \to {\mathit{\boldsymbol{R}}^{\left( {{L_x} \times {L_y}} \right)\left( {{K_x} \times {K_y}} \right)}} $表示将三维数据映射为二维块Hankel矩阵。理论证明，同相轴数量无缺失的或无噪的地震数据是低秩的^[33]，数据的缺失会增加矩阵的秩^{[40, 44]}。

记待恢复数据为$ {\mathit{\boldsymbol{\tilde X}}}$，首先根据矩阵$ {\mathit{\boldsymbol{\tilde H}}}$重建$ {\mathit{\boldsymbol{\tilde X}}}$，然后通过逆映射$ \boldsymbol{X} :=P_{\mathrm{H}}^{-1}(\tilde{\boldsymbol{X}})$得到原始数据X。为了简化符号表达，下文中的符号“~”都省去。

1.2 NLPHR方法

低秩矩阵补全问题的一般形式为

$ \mathop {\min }\limits_\mathit{\boldsymbol{X}} rank (\mathit{\boldsymbol{X}})\quad {P_\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}(\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{H}}) = 0 $

(5)

式中：原始数据X∈R^m×n; rank(·)表示矩阵的秩；H∈R^m×n为观测数据；Ω是采样指标集；P_Ω:R^m×n→R^m×n是线性算子，确保观测数据H未缺失位置元素与原始数据X对应位置元素相同，而缺失位置元素赋值为0。式(5)中秩最小问题求解是一个NP-hard(Non-deterministic Polynomial)问题，通常运用凸松弛的方法求解。一般用核范数‖X‖_*= $\sum\limits_{i = 1}^m {{\sigma _i}} (\mathit{\boldsymbol{X}}) $代替秩函数求解，其中σ_i(X)代表矩阵X的第i个奇异值。式(5)转化为求解如下凸松弛问题

$ \mathop {\min }\limits_\mathit{\boldsymbol{X}} \lambda {\left\| \mathit{\boldsymbol{X}} \right\|_ * } + \frac{1}{2}\left\| {{P_\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}(\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{H}})} \right\|_{\rm{F}}^2 $

(6)

式中：λ为超参数；‖·‖_F²为Frobenius范数。该凸问题可以通过交替方向乘子法等凸优化方法解决。但是，核范数是秩函数的凸松弛近似，所以式(6)得到的解往往是次优解^[41]。

对于地震数据重建问题，考虑建立非凸L_p范数松弛模型

$ \mathop {\min }\limits_\mathit{\boldsymbol{X}} \lambda \sum\limits_{i = 1}^m h \left[ {{\sigma _i}(\mathit{\boldsymbol{X}})} \right] + \frac{1}{2}\left\| {{P_\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}(\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{H}})} \right\|_{\rm{F}}^2 $

(7)

式中: $h(x)=x^{p}(0 <p <1) $为非凸L_p范数；$\sum\limits_{i=1}^{m} h\left[\sigma_{i}(\boldsymbol{X})\right] $是秩函数的非凸替代。矩阵的奇异值为非负值，所以仅考虑定义在R⁺上的非凸函数h(x)。为了方便描述，以下均用d(x)代表式(7)中的损失函数项$ \frac{1}{2}\left\| {{P_\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}(\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{H}})} \right\|_{\rm{F}}^2$。式(7)是一个非凸低秩最小化问题，求解较困难。为此，本文提出NLPHR法求解式(7)，其中非凸L_p函数h(x)和损失函数d(x)满足以下假设和定义。

假设1：h(x):R⁺→R⁺在[0, +∞)是凹函数且单调递增，可以为非光滑函数；

假设2：d(x):R^m×n→R⁺是一个光滑函数，即其梯度为Lipschitz常数L_f，满足

$ \begin{array}{*{20}{c}} {{{\left\| {\nabla d(\mathit{\boldsymbol{A}}) - \nabla d(\mathit{\boldsymbol{B}})} \right\|}_{\rm{F}}} \le {L_{\rm{f}}}{{\left\| {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}} \right\|}_{\rm{F}}}}\\ {\forall \mathit{\boldsymbol{A}},\mathit{\boldsymbol{B}} \in {\mathit{\boldsymbol{R}}^{m \times n}}} \end{array} $

(8)

定义1：h(x):Rⁿ→R是凹函数，如果对任意的b∈Rⁿ，v满足

$ h(\mathit{\boldsymbol{b}}) \le h(\mathit{\boldsymbol{a}}) + \langle \mathit{\boldsymbol{v}},\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{a}}\rangle $

(9)

就称v为函数h(x)在点a∈Rⁿ处的超梯度，记为$ \partial h\left( \mathit{\boldsymbol{a}} \right)$。超梯度在非光滑点可能不唯一。函数h(x)在点a处所有的超梯度称为h(x)在a处的超微分。如果h(x)在a处可微，那么$ \nabla h\left( \mathit{\boldsymbol{a}} \right)$为h(x)在点a处的唯一超梯度，即$ \partial h\left( \mathit{\boldsymbol{a}} \right) = \left\{ {\nabla h\left( \mathit{\boldsymbol{a}} \right)} \right\}$。

由非凸L_p范数h(x)=x^p(0＜p＜1)，可知其超梯度为

$ \partial h(x) = \left\{ {\begin{array}{*{20}{l}} { + \infty }&{x = 0}\\ {p{x^{p - 1}}}&{x > 0} \end{array}} \right. $

(10)

方便起见，以σ₁≥σ₂≥…≥σ_m代表矩阵X的奇异值，X的第k次迭代记为X^(k)，X^(k)的第i个奇异值记为σ_i^(k)=σ_i(X^(k))。

根据假设1及定义1(式(9))，有

$ h\left( {{\sigma _i}} \right) \le h\left[ {\sigma _i^{(k)}} \right] + w_i^{(k)}\left[ {{\sigma _i} - \sigma _i^{(k)}} \right] $

(11)

其中

$ w_i^{(k)} \in \partial h\left[ {\sigma _i^{(k)}} \right] $

(12)

由h(x)的增量性及超梯度的反单调特性，有

$ 0 \le w_1^{(k)} \le w_2^{(k)} \le \cdots \le w_m^{(k)} $

(13)

因为d(x)是一个L_f光滑函数，可将d(X)在X^(k)处线性变换为

$ \begin{array}{l} d(\mathit{\boldsymbol{X}}) \approx d\left[ {{\mathit{\boldsymbol{X}}^{(k)}}} \right] + \left\langle {\nabla d\left[ {{\mathit{\boldsymbol{X}}^{(k)}}} \right],\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}^{(k)}}} \right\rangle + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{\mu }{2}\left\| {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}^{(k)}}} \right\|_{\rm{F}}^2 \end{array} $

(14)

式中：μ为常数，且μ＞L_f；$\frac{\mu}{2}\left\|\boldsymbol{X}-\boldsymbol{X}^{(k)}\right\|_{\mathrm{F}}^{2} $为添加的近邻项。

用式(11)右边项代替式(7)的第一项，用式(14)右边项代替式(7)第二项，得到式(7)解的更新值

$ \begin{array}{l} {\mathit{\boldsymbol{X}}^{(k + 1)}} = \arg \mathop {\min }\limits_\mathit{\boldsymbol{X}} \left[ {\sum\limits_{i = 1}^m h \left[ {\sigma _i^{(k)}} \right] + w_i^{(k)}\left[ {{\sigma _i} - \sigma _i^{(k)}} \right]} \right. + \\ \;\;\;\;\;\;\;\;\;\;\;\;d\left[ {{\mathit{\boldsymbol{X}}^{(k)}}} \right] + \left\langle {\nabla d\left[ {{\mathit{\boldsymbol{X}}^{(k)}}} \right],\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}^{(k)}}} \right\rangle + \\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{\mu }{2}\left\| {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}^{(k)}}} \right\|_{\rm{F}}^2} \right]\\ \;\;\;\;\;\;\;\;\; = \arg \mathop {\min }\limits_\mathit{\boldsymbol{X}} \left\{ {\sum\limits_{i = 1}^m {w_i^{(k)}} {\sigma _i} + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\frac{\mu }{2}\left\| {\mathit{\boldsymbol{X}} - \left[ {{\mathit{\boldsymbol{X}}^{(k)}} - \frac{1}{\mu }\nabla d\left( {{\mathit{\boldsymbol{X}}^{(k)}}} \right)} \right]} \right\|_{\rm{F}}^2} \right\} \end{array} $

(15)

求解式(15)等价于计算加权核范数的逼近算子，根据式(15)的非凸性及式(13), 可得到式(15)的闭式解。根据

定理1^[45]：对任意λ＞0, Y∈R^m×n, 0≤w₁≤w₂≤…≤w_q, q=min(m, n)，Y=UΣV^T是Y的奇异值分解，S_λw(Σ)=Diag[max(Σ_ii-λw_i, 0)]。对于问题

$ \min \left[ {\lambda \sum\limits_{i = 1}^k {{w_i}} {\sigma _i}(\mathit{\boldsymbol{X}}) + \frac{1}{2}\left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{Y}}} \right\|_{\rm{F}}^2} \right] $

(16)

其全局最优解可通过加权奇异值阈值(WSVT)算法得到

$ {\mathit{\boldsymbol{X}}^*} = \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{S}}_{\lambda w}}(\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}){\mathit{\boldsymbol{V}}^{\rm{T}}} $

(17)

式(15)可以通过式(17)求解，其中式(13)起重要作用，式(13)保证了非凸L_p函数h(x)满足假设1。如果h(x)=x，那么$\sum\limits_{i=1}^{m} h\left[\sigma_{i}(\boldsymbol{X})\right] $就变为凸核范数‖X‖_*。需要注意的是，如果σ_i^(k)=0，那么σ_i^(k+1)=0，这样就保证了序列{X^(k)}的秩不会增加。

通过求解式(15)更新X^(k+1)后，根据

$ w_i^{(k + 1)} \in \partial h\left[ {{\sigma _i}\left( {{\mathit{\boldsymbol{X}}^{(k + 1)}}} \right)} \right]\quad i = 1,2, \cdots ,m $

(18)

可更新权重w_i^(k+1)。

通过奇异值迭代更新X^(k+1)和w_i^(k+1)后，降秩可得到每个频率切片对应的块Hankel矩阵的近似矩阵。

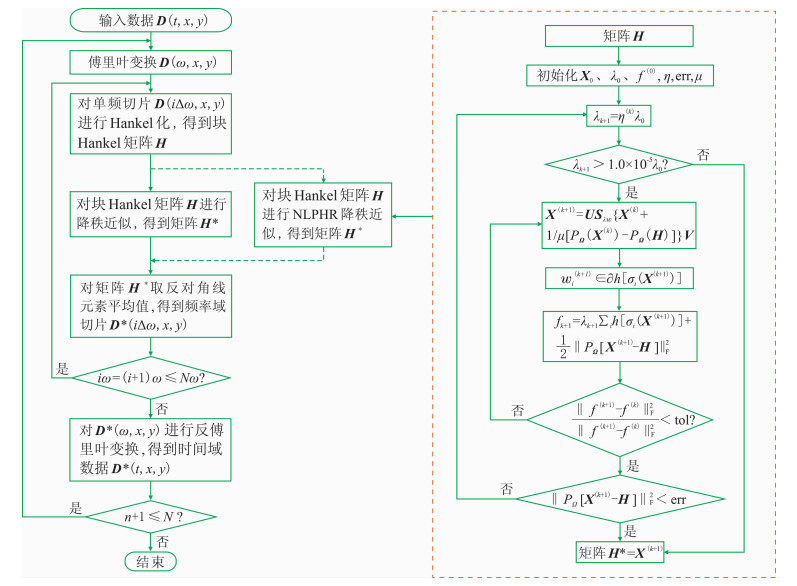
基于NLPHR的三维地震数据低秩重建流程(图 1)如下。

(1) 首先将三维数据D(t, x, y)从时间域变换至频率域，得到频率域数据D(ω, x, y)，然后对每个频率切片D(iΔω, x, y)分别构建相应的块Hankel矩阵H。

(2) 对每个频率切片的块Hankel矩阵H进行降秩操作。首先初始化λ，其初始值设置为一个较大的值λ₀，其中λ₀=‖P_Ω(H)‖_∞, ‖·‖_∞为矩阵的无穷范数。当λ＞1.0×10^-5λ₀时，进行N次迭代循环，依据式(15)~式(17)得到X的当前迭代值X^(k+1)，由式(18)得到权重w_i的更新w_i^(k+1)。由于式(17)需要进行SVD，对于大的数据体计算十分耗时，故用LANSVD(MATLAB中自带函数)替代SVD来进行奇异值分解。二者的区别是SVD返回所有的奇异值，LANSVD只返回前面较大的几个奇异值，由于数据主要信息是包含在前面较大的几个奇异值中，所以用LANSVD替代SVD重建信噪比基本保持不变，但运算效率大幅提升。

(3) 第k次和k+1次迭代时目标函数值分别为f^(k)和f^(k+1)(式(7))，当$ \frac{\left\|f^{(k+1)}-f^{(k)}\right\|_{\mathrm{F}}^{2}}{\left\|f^{(k+1)}+f^{(k)}\right\|_{\mathrm{F}}^{2}} <\mathrm{tol}$, tol为相邻两次迭代目标函数值之间的相对误差，根据λ_k+1=η^(k)λ₀更新λ，其中超参数η满足0＜η＜1。当‖P_Ω[X^(k+1)-H]‖_F³＜err(err为重建数据与原始数据之间的误差)，迭代循环结束。

(4) 迭代停止后，从降秩得到的近似矩阵H^*反对角线平均值获取频率域数据D^*(ω, x, y)，将频率域数据变换回时间域，得到时间域数据D^*(t, x, y)。

2 实验

通过对三维模拟地震数据和实际地震数据分别利用NLPHR法与MSSA方法、OMPHR方法进行对比。衡量重建质量的指标为信噪比

$ {\rm{SNR}} = \lg \frac{{\left\| \mathit{\boldsymbol{D}} \right\|_{\rm{F}}^2}}{{\left\| {\mathit{\boldsymbol{D}} - {\mathit{\boldsymbol{D}}^*}} \right\|_{\rm{F}}^2}} $

(19)

2.1 模拟数据实验

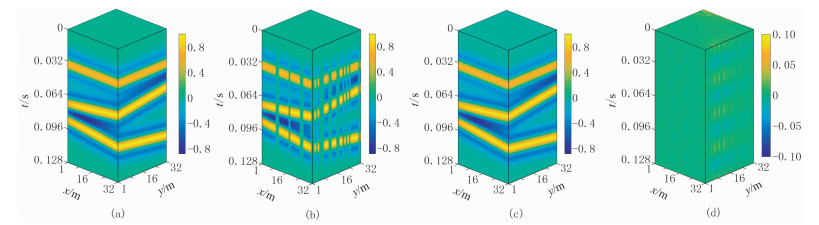
测试选用的模拟数据包含三条线性同相轴，x方向和y方向各有32道，道间距为1m。共有64个时间采样点，采样间隔为2ms。图 2a为原始模拟三维数据，其大小为64×32×32。每个块Hankel矩阵大小为256×289。图 2b为随机缺失40%道集的数据，图 2c为NLPHR重建结果。

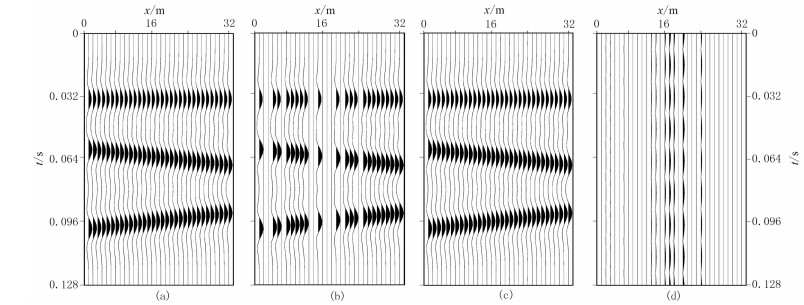
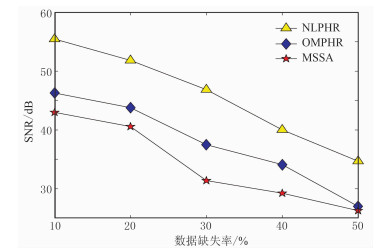
为了更清楚地说明文中所提出方法的重建效果，分别取图 2中三维数据的二维剖面(y=19m)进行显示(图 3)。图 3直观地展示了NLPHR法重建前、后地震数据的吻合程度。图 4为OMPHR与MSSA方法重建效果对比，两种方法中秩的大小均选取为3。NLPHR方法重建数据的信噪比为40.0dB，耗时3.8s；OMPHR和MSSA方法重建数据的信噪比分别为34.1dB和29.2dB，耗时分别为1.5s和94.5s。图 5为分别随机缺失10%、20%、30%、40%、50%道集情况下NLPHR法、OMPHR法以及MSSA方法重建数据的信噪比曲线，可以看出，NLPHR方法重建信噪比明显高于OMPHR法和MSSA法。

2.2 实际数据实验

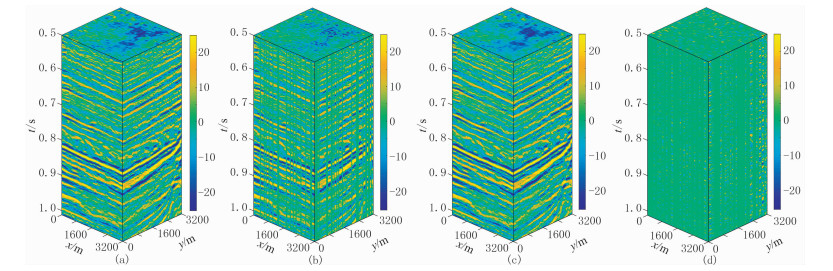
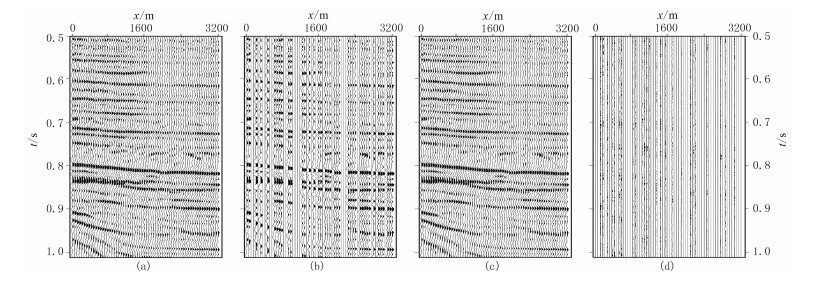
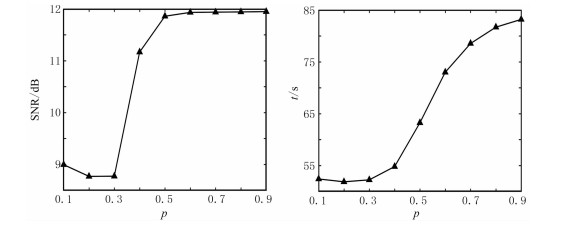
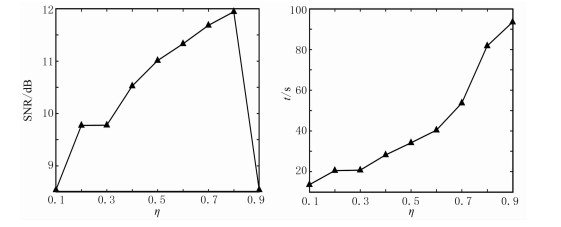
实际三维叠后地震资料(图 6a)参数如下：x方向和y方向各有64道，道距为50m，时间采样间隔为2ms，采样点数为256。随机缺失40%道集数据见图 6b，采用NLPHR法重建的地震数据如图 6c所示。图 7是从该三维数据体(图 6)中抽取的二维剖面(y=1000m)。从图 6和图 7的重构结果可知，基于NLPHR方法的三维数据重建方法能有效恢复缺失道集，较好地实现(含缺失道)地震数据的重建。图 8为随机缺失40%道集情况下OMPHR法及MSSA法重构结果。OMPHR法和MSSA法的秩均取为20。由于数据体较大，实验中实行分块并行重建。将大小为256×64×64的数据均分成四块，每块大小为256×32×32，对四块同时进行重建。NLPHR法重建数据的信噪比为11.9dB，耗时81.7s；OMPHR法重建数据的信噪比为9.3dB，耗时66.6s；MSSA重建数据的信噪比为7.7dB，耗时203.2s。可以看出，NLPHR法较好地恢复了缺失道集，而OMPHR法和MSSA法均未能完全恢复缺失道集。图 9为不同缺失率下三种方法重建数据的信噪比对比。可以看出，NLPHR法具有较高的输出信噪比，比OMPHR法和MSSA法更具有稳健性。表 1为三种数据重建方法在不同缺失率下三维叠后地震资料上重建数据的信噪比及计算耗时对比。从表 1可以看出，NLPHR法重建数据的信噪比高于OMPHR法和MSSA法，耗时比MSSA方法短。图 10和图 11分别为缺失40%数据下该三维叠后数据体在参数p和η不同取值时重建数据信噪比及耗时对比。由图可见，参数p在(0.5, 1)范围内重建数据的信噪比较高；p=0.6时重建信噪比最高，且重建耗时相对较短。由图 11可以看出，η在(0.1, 0.8)范围内，重建信噪比随η呈现增大趋势；在(0.8, 0.9)范围内呈下降趋势。图 12为数据缺失40%时三维叠后数据在三种重建方法下的SNR收敛曲线及收敛时间。由图可知，三种方法均较快收敛，其中NLPHR法收敛最快，重建数据的信噪比高于OMPHR法和MSSA法，迭代时间比MSSA法短。

3 结束语

MSSA法通过随机奇异值分解直接降秩，得到的解往往不是最优解，并且在低采样率下重建效果欠佳。针对此问题，文章提出非凸L_p范数Hankel重建方法(NLPHR)，对三维地震数据进行重建。该方法将地震数据每个频率切片转换成块Hankel矩阵，再运用NLPHR法对块Hankel矩阵进行降秩处理，从而实现地震数据低秩重建。三维模拟地震数据和实际地震数据实验证明，与MSSA法和OMPHR法相比，本文方法数据重建信噪比最高，耗时较少，效果最优。