② 吉林大学地球探测科学与技术学院, 吉林长春 130026
② College of Geo-Exploration Sciences and Technology, Jilin University, Changchun, Jilin 130026, China
地震勘探是矿产资源勘查的一种重要手段[1-3]。强随机噪声的干扰直接影响地震资料处理和解释。随机噪声一般表现为无规律振动,由多种不确定因素形成。因此,去除随机噪声是地震数据弱信号提取与增强的重要环节。目前,常用的随机噪声压制方法包括频率域滤波、f-x域去噪、Radon域[4-6]去噪等。20世纪80年代,小波变换[7]作为一种多尺度变换,在图像分析、去噪等方面得到快速发展,能够稀疏表示一维信号,但不能简单地扩展到二维或高维信号。因此Ridgelet变换[8]、Curvelet变换[9-11]和Contourlet变换[12-13]作为多尺度几何分析方法应运而生,在二维和高维信号的稀疏表示和图像处理方面发挥了重要作用,但它们的数学结构复杂,而且变换域的某一尺度的系数矩阵尺度与原始数据不同。
Shearlet变换[14-17]作为一种新的稀疏变换方法,具有多尺度、多方向特性,且能最优地刻画信号的局部特征。与其他多尺度分析方法相比,Shearlet变换具有更简单的数学结构,对尺度和方向表征更细腻,采用更少的系数逼近曲线。对于一个N×N阶的图像,经过Shearlet变换后,各尺度方向的系数仍是N×N阶,且各方向系数仍然保留时间的维度。Shearlet变换可最优地稀疏表示信号,宜于处理包含纹理、轮廓和边缘信息的地震数据。含噪地震数据经Shearlet变换后,通常将有效信号映射到某些特定方向的Shearlet系数上,且对应的Shearlet系数值较大,而随机噪声分布在所有方向的Shearlet系数上,对应的Shearlet系数值较小。因此设置合理的阈值函数可以有效分离有效信号与随机噪声。
刘成明等[18]利用地震数据在二维Shearlet域的稀疏性去除随机噪声,获得了较好效果。程浩等[19]基于Shearlet变换的自适应阈值方法去噪,在提高地震数据信噪比的同时,最大限度地保留有效信号。上述方法都是针对二维单炮记录,并没有考虑到单炮记录间的相关性。
三维Shearlet变换[20]与二维Shearlet变换相比,兼顾了信号的空间相关性,在三维Shearlet域中能更稀疏地表示有效信号。与常用的三维Curvelet变换[21-23]相比,通过三维Shearlet变换得到某一尺度、某一方向的Shearlet系数与原始数据尺度相同,具有更明确的物理意义。段昶等[24]利用三维Shearlet变换融合处理磁共振图像,证明其稀疏性明显优于二维Shearlet变换。Negi等[25]分析了三维Shearlet变换的特点,并用于视频去噪,取得了较好的效果。
本文应用尺度自适应三维Shearlet变换压制多炮地震数据随机噪声,通过将多炮数据变换到三维Shearlet域,充分考虑单炮记录及其间的相关性,在三维Shearlet域更稀疏地表示地震数据。由于有效信号主要分布在低尺度,随机噪声分布在各个尺度,因此在硬阈值的基础上,结合尺度自适应因子压制随机噪声。再通过三维Shearlet反变换,得到去噪地震数据。数值模拟和实际多炮地震数据去噪结果表明,尺度自适应三维Shearlet变换的去噪效果优于二维Shearlet变换、不结合尺度自适应因子的三维Shearlet变换。
1 三维Shearlet变换 1.1 基本理论Shearlet变换[15]作为一种稀疏变换方法,不仅受尺度和位置变化影响,还受剪切矩阵控制的正交变换影响。当空间维度参数D=3时,利用3个近似锥形区域P(D)和1个中心区域C函数构成Shearlet系统
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{P}}_1} = \left\{ {\left( {{\xi _1},{\xi _2},{\xi _3}} \right) \in {\mathit{\boldsymbol{R}}^3}:\left| {{\xi _2}/{\xi _1}} \right| \le 1,\left| {{\xi _3}/{\xi _1}} \right| \le 1} \right\}}\\ {{\mathit{\boldsymbol{P}}_2} = \left\{ {\left( {{\xi _1},{\xi _2},{\xi _3}} \right) \in {\mathit{\boldsymbol{R}}^3}:\left| {{\xi _1}/{\xi _2}} \right| \le 1,\left| {{\xi _3}/{\xi _2}} \right| \le 1} \right\}}\\ {{\mathit{\boldsymbol{P}}_3} = \left\{ {\left( {{\xi _1},{\xi _2},{\xi _3}} \right) \in {\mathit{\boldsymbol{R}}^3}:\left| {{\xi _1}/{\xi _3}} \right| \le 1,\left| {{\xi _2}/{\xi _3}} \right| \le 1} \right\}}\\ {\mathit{\boldsymbol{C}} = \left\{ {\left( {{\xi _1},{\xi _2},{\xi _3}} \right) \in {\mathit{\boldsymbol{R}}^3}:{{\left\| {\left( {{\xi _1},{\xi _2},{\xi _3}} \right)} \right\|}_\infty } < 1} \right\}} \end{array}} \right. $ | (1) |
此处,3个近似锥形区域将频率空间
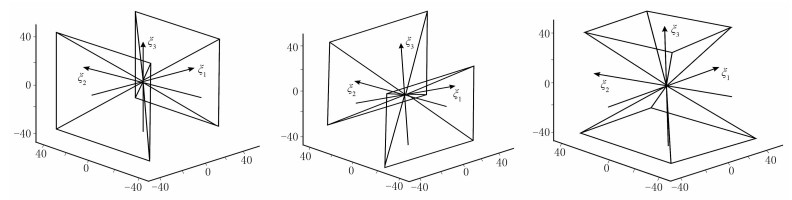
|
图 1 频率空间 |
为了定义这样一个系统,假设ϕ是一元函数,且0≤
令ξ=(ξ1,ξ2,ξ3)∈
| $ \mathit{\hat \Phi }(\xi ) = \mathit{\hat \Phi }\left( {{\xi _1},{\xi _2},{\xi _3}} \right) = \hat \phi \left( {{\xi _1}} \right)\hat \phi \left( {{\xi _2}} \right)\hat \phi \left( {{\xi _3}} \right) $ | (2) |
并且使
| $ W(\mathit{\boldsymbol{\xi }}) = \sqrt {{{\mathit{\tilde \Phi }}^2}\left( {{2^{ - 2}}\mathit{\boldsymbol{\xi }}} \right) - {{\mathit{\tilde \Phi }}^2}(\mathit{\boldsymbol{\xi }})} $ | (3) |
满足
| $ {\mathit{\hat \Phi }^2}(\xi ) + \sum\limits_{j \ge 0} {{W^2}} \left( {{2^{ - 2j}}\mathit{\boldsymbol{\xi }}} \right) = 1\quad \mathit{\boldsymbol{\xi }} \in {\mathit{\boldsymbol{R}}^3} $ | (4) |
当D=1,2,3,l=(l1, l2)∈Z2, 与三维Shearlet系统相关的锥形区域P(D)可以定义为
| $ \left\{ {\psi _{j,l,k}^{(D)}:j \ge 0, - {2^j} \le {l_1},{l_2} \le {2^j},k \in {\mathit{\boldsymbol{Z}}^3}} \right\} $ | (5) |
其中
| $ \begin{array}{*{20}{c}} {\hat \psi _{j,l,k}^D(\mathit{\boldsymbol{\xi }}) = {{\left| {{\rm{det}} {\mathit{\boldsymbol{A}}_{(D)}}} \right|}^{ - \frac{j}{2}}}W\left( {{2^{ - 2j}}\mathit{\boldsymbol{\xi }}} \right) \times }\\ {{F_{(D)}}\left\{ {\mathit{\boldsymbol{\xi A}}_{(D)}^{ - j}\mathit{\boldsymbol{B}}_{(D)}^{[ - \mathit{\boldsymbol{l}}]}} \right\}{{\rm{e}}^{2{\rm{ \mathsf{ π} i}}\mathit{\boldsymbol{\xi A}}_{(D)}^{ - j}\mathit{\boldsymbol{B}}_{(D)}^{\left[ { - \mathit{\boldsymbol{l}}} \right]}k}}} \end{array} $ | (6) |
式中:A(D)表示各向异性矩阵;B(D)[-l]表示剪切矩阵;F为尺度方向函数。则对于任意f∈L2(R3),三维Shearlet变换可以定义为
| $ {\sum {\left| {\langle f,\tilde \psi \rangle } \right|} ^2} = {\left\| f \right\|^2} $ | (7) |
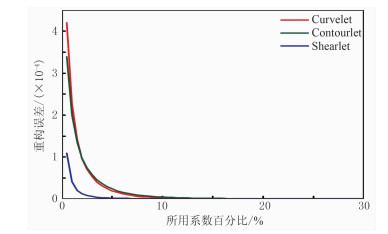
基于信号分解的随机去噪方法的去噪效果依赖于方法对有效信号的逼近程度。为了展现Shearlet变换的稀疏特性,将其与Curvelet变换和Contourlet变换进行稀疏度对比。首先,利用不同的变换方法分解不含噪地震数据。然后,将变换域中的系数从大到小排列,保留不同百分比的系数重构,计算重构结果与原始数据的误差。图 2为重构误差曲线。由图可见,保留的最大系数百分比从0.5%~30.0%,当保留4.0%的最大系数时,Shearlet变换的重构误差趋近于零,而Curvelet变换和Contourlet变换保留10.0%的最大系数时,重构误差才近乎为零,说明Shearlet变换具有更好的稀疏特性。
|
图 2 重构误差曲线 |
Shearlet变换通过多尺度、多角度的特性,可以分解地震数据。由于地震同相轴是连续的,在局部同相轴具有一定的方向性,当同相轴的方向与某一Shearlet基的方向大致相同时,在Shearlet域对应较大Shearlet系数,同相轴的局部方向不同,在Shearlet域可被分解到不同的方向。由于随机噪声不具有方向性,在Shearlet域对应较小的Shearlet系数,因此通过设置合理的阈值可去除随机噪声。
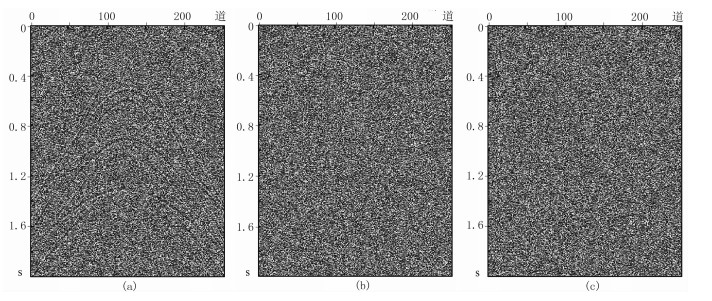
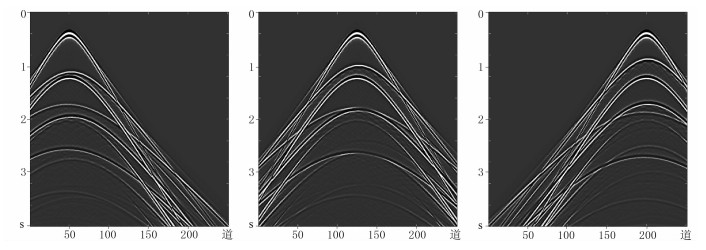
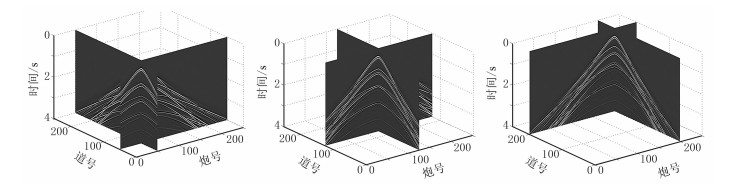
图 3为第50、125、200炮模拟单炮记录。利用二维Shearlet变换处理单炮记录,仅利用共炮点道集自身的特点压制随机噪声。但对于多炮记录,还可以利用共检波点方向的相关性。图 4为多炮地震数据的空间切片。由图可见,各单炮记录间存在一定联系,类似于三维数据的单炮记录,即多炮地震数据可以看成一个伪三维数据。在变换域随机噪声压制过程中,不仅考虑单炮记录自身的特点,还兼顾单炮记录间的相关性,可获得更好的效果。
|
图 3 第50(左)、125(中)、200炮(右)模拟单炮记录 |
|
图 4 多炮地震数据的空间切片 |
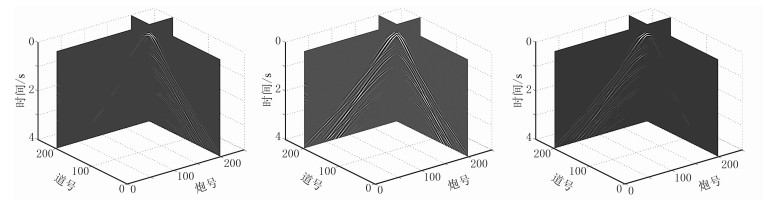
图 5为三维Shearlet变换分解多炮地震数据的3组系数,可见由于Shearlet变换的方向性,地震同相轴根据自身的方向匹配到Shearlet域的不同方向,说明Shearlet变换可将地震数据分解到不同方向刻画。
|
图 5 三维Shearlet变换分解多炮地震数据的3组系数 |
在随机噪声压制过程中,假设待处理的含噪地震数据为
| $ f(t) = s(t) + n(t) $ | (8) |
式中:s(t)为有效信号;n(t)为随机噪声。
三维Shearlet变换随机噪声压制过程与二维Shearlet变换类似,但后者仅考虑共炮点道集(单炮记录)中有效信号的分布特点,而前者不仅考虑共炮点道集有效信号的分布特点,还兼顾共检波点或共炮检距方向有效信号的分布特点,可更好地去除随机噪声,保护有效信号。三维Shearlet去噪主要包括以下步骤。
(1) 通过三维Shearlet变换,对含噪地震数据进行多尺度、多角度剖分,获取对应的系数
| $ C(j,l,k) = SH [f(t)] = \left\langle {f(t),{{\tilde \psi }_{j,l,k}}} \right\rangle $ | (9) |
式中:C(j, l, k)为参数尺度j、方向l、位置k对应的三维Shearlet系数;SH(·)为三维Shearlet正变换。
(2) 在步骤(1)中,当信号的某一方向与对应某一角度的Shearlet基函数方向大致相同时,将获得较大的Shearlet系数,相反,当所选Shearlet基函数方向与信号方向偏差较大时,将获得较小的Shearlet系数。因为地震同相轴都具有一定方向性,所以在Shearlet域对应尺度、角度上将获得较大的Shearlet系数,而随机噪声不具有方向性,将获得相对较小的Shearlet系数。通过阈值函数对Shearlet系数进行阈值化处理,保留大于阈值的Shearlet系数,去除小于阈值的Shearlet系数,达到去除随机噪声的目的。常用硬阈值函数为
| $ T(x) = \left\{ {\begin{array}{*{20}{l}} {T(x)}&{|T(x)| \ge M\lambda \sigma }\\ 0&{|T(x)| < M\lambda \sigma } \end{array}} \right. $ | (10) |
式中:M为常数变量,根据不同工区环境的噪声级别选取不同值,同一工区采集的多炮地震数据,由于所处环境基本一致,所以所选值相同;λ为某一尺度和角度的Shearlet系数均方差;σ为噪声标准差。
由于有效地震信号主要分布在相对低频的尺度,随机噪声则分布在各个尺度,因此为了尽可能地保留有效信号,在硬阈值函数中加入尺度自适应因子ε,将式(10)变为尺度自适应阈值,即
| $ T(x) = \left\{ {\begin{array}{*{20}{l}} {T(x)}&{|T(x)| \ge \varepsilon M\lambda \sigma }\\ 0&{|T(x)| < \varepsilon M\lambda \sigma } \end{array}} \right. $ | (11) |
其中
| $ \varepsilon = {2^{ - \frac{{J - j}}{2}}} $ | (12) |
式中J为所选的尺度值。
(3) 通过三维Shearlet反变换,将阈值处理以后的Shearlet系数Cnew(j, l, k)进行反变换(SH-1),可得到期望输出的
| $ \bar s(t) = {\rm{S}}{{\rm{H}}^{ - 1}}\left[ {{C_{{\rm{new}}}}(j,l,k)} \right] = \sum\limits_{j,l,k} {{C_{{\rm{new}}}}} (j,l,k){\phi _{j,l,k}} $ | (13) |
为了体现所提方法的有效性,分别计算地震数据去噪前、后的信噪比(SNR)、峰值信噪比(Peak signal to noise ratio, PSNR)和均方差(Mean square error,MSE)进行对比[17]。
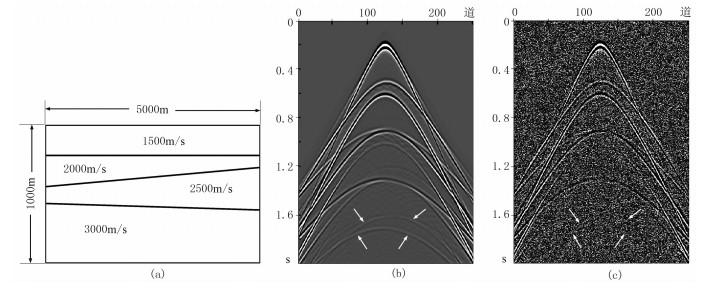
3 理论数据测试利用模拟的多炮地震数据作为伪三维数据,验证尺度自适应三维Shearlet变换去噪方法。图 6为数值模型及第125炮原始单炮记录、加噪单炮记录。由图可见:第125炮原始单炮记录浅部有效信号能量较强,底部有效信号能量较弱,对应两个能量较弱的反射同相轴(图 6b箭头所示位置);在模拟记录中添加一定程度的随机噪声,仍可以有效识别浅部能量较强的信号,但底部能量较弱的信号被随机噪声完全淹没(图 6c箭头所示位置)而无法识别。
|
图 6 数值模型(a)及第125炮原始单炮记录(b)、加噪单炮记录(c) 利用有限差分法进行模拟,共251炮模拟地震数据,每炮记录包含251道和1000个样点,采样间隔为0.002s,采样时间为2s。经计算可知,添加随机噪声地震记录的SNR、PSNR和MSE分别为-1.2772dB、74.1516dB和2.5×10-3 |
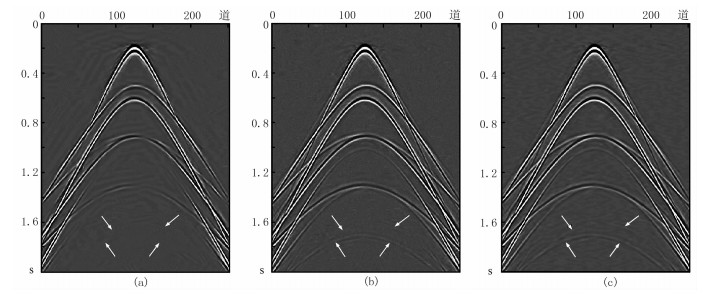
分别利用二维(图 7a)、三维(图 7b)Shearlet变换和尺度自适应三维Shearlet变换(图 7c)处理加噪多炮地震记录。可见:①二维Shearlet变换硬阈值去噪结果较充分地去除了随机噪声,图像清晰,但在去噪的同时损害了有效信号(图 7a箭头位置),还产生一定的边界效应;对应的差剖面具有清晰可见的有效信号(图 8a),SNR、PSNR和MSE分别为15.1687dB、89.9425dB和6.589×10-5(表 1),说明二维Shearlet硬阈值去噪方法具有一定的随机噪声压制能力,但一定程度上损害了能量较弱的有效信号。②三维Shearlet变换硬阈值去噪结果在去除随机噪声的同时,保留了底部能量较弱的有效信号,且由变换产生的边界效应也较弱,不影响数据的成像效果(图 7b);对应的差剖面基本不残留有效信号(图 8b),SNR、PSNR和MSE分别为19.4816dB、94.9103dB和2.0992×10-5(表 1)。因此与二维Shearlet变换相比,三维Shearlet变换不但考虑了单炮记录的特点,还考虑了单炮记录间的相关性,在三维Shearlet域地震数据更稀疏,对随机噪声的去除更彻底。③与二维(图 7a)、三维(图 7b)Shearlet变换去噪结果相比,尺度自适应三维Shearlet变换阈值去噪结果对随机噪声的去除效果更好,充分保留了底层能量较弱的有效信号,由变换产生的边界效应更小,反射同相轴连续性更好、更清晰(图 7c箭头所示位置);对应的差剖面不存在有效信号(图 8c),SNR、PSNR和MSE分别为20.1058dB、95.5345dB和1.8181×10-5(表 1),在信噪比和保真度方面得到进一步提高。因此尺度自适应三维Shearlet变换去噪方法在去除随机噪声的同时,最大限度地保留了有效信号。
|
图 7 二维(a)、三维(b)Shearlet变换和尺度自适应三维Shearlet变换(c)对图 6c数据去噪结果 所选尺度参数为4,对应的方向剖分参数为[1 1 2 2] |
|
|
表 1 信噪比、峰值信噪比、均方差对比 |
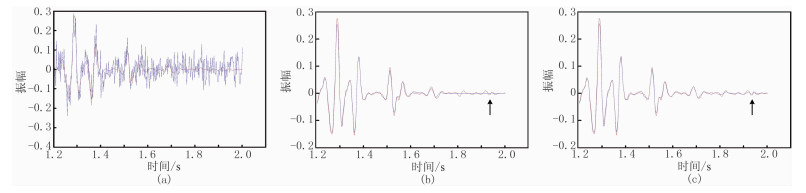
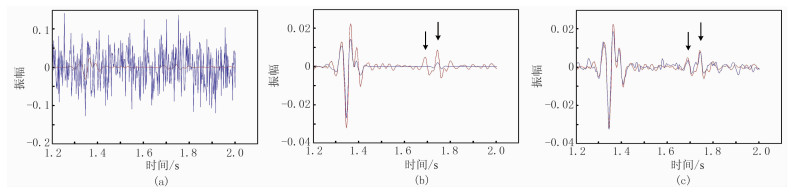
分别抽取第125炮第40道(图 9)和第90道(图 10)的1.2~2.0s的记录进行振幅分析。由图 9可见:原始有效信号淹没在含噪数据中(图 9a);三维Shearlet变换去噪方法大致在1.7s前去噪效果与保幅性较好,振幅基本与原始信号吻合,在1.7s以后振幅基本归零,与有效信号差异较大(图 9b);尺度自适应三维Shearlet变换去噪方法的整体去噪效果与保幅性都很好,振幅与原始信号吻合(图 9c)。由图 10可见:原始有效信号淹没在含噪数据中(图 10a);三维Shearlet变换去噪方法在1.5s前振幅拟合相对较好,但是幅值存在一定差异,大致在1.75s又出现一定振幅响应,差异较大,其他幅值基本为零(图 10b);尺度自适应三维Shearlet变换去噪方法在1.5s前振幅拟合较好,幅值差异相对较小,较好地拟合了1.65~1.80s的有效振幅响应(图 10c)。由图 9、图 10可知:由于存在炮检距变化,第40道的有效信号幅值相对较大,去噪效果较好,振幅拟合程度高,保幅性好(图 9);第90道有效信号的幅值相对较小,去噪效果和振幅拟合程度受到影响(图 10)。
通过上述分析可知,尺度自适应三维Shearlet变换去噪方法不但考虑了单炮记录自身的特点,还顾及了单炮记录间的相关性,充分地利用了地震数据在三维Shearlet域的稀疏性。同时,结合有效信号与随机噪声在三维Shearlet域的分布特点,利用尺度自适应因子最大限度地保留有效信号,提高信噪比和保真度。
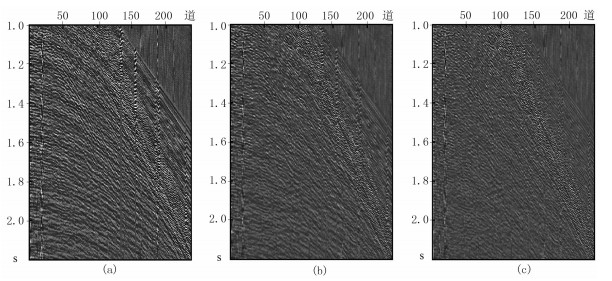
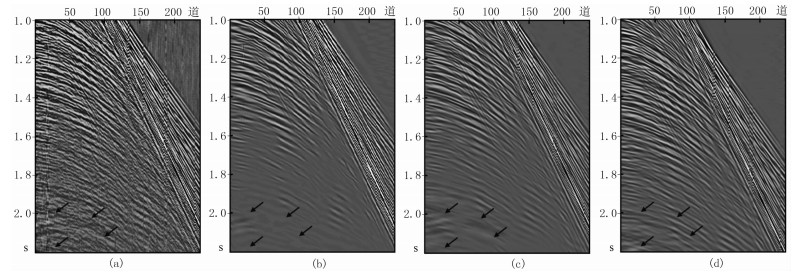
4 实际数据测试选取A区实际地震数据测试尺度自适应三维Shearlet变换的去噪效果。图 11为第123炮记录及去噪结果。由图可见:①单炮记录上部同相轴较清晰,能量最强,连续性好,底部有效信号几乎被随机噪声淹没,同相轴相对能量较弱,连续性差,不易识别,影响层位和断层解释(图 11a)。②二维Shearlet变换较好地压制了随机噪声,去噪结果上部同相轴连续性变好,整体清晰,但底部有效信号被损害,同相轴连续性差,严重影响底部层位解释(图 11b);在对应的差剖面上可较清晰地看到有效信号的趋势(图 12a)。③三维Shearlet变换充分地压制了随机噪声,去噪结果上部反射同相轴连续性更好,去噪结果较好地保留了底部信号,底部反射同相轴连续性较好,并保留了部分能量较弱的有效信号(图 11c);在对应的差剖面上几乎不残留有效信号(图 12b)。④与前两种去噪方法相比,尺度自适应三维Shearlet变换去噪结果上部反射同相轴连续性最好、最清晰,能量最强,并最大限度地保留了底部有效信号,有效改善了反射同相轴的连续性(图 11d);在对应的差剖面上基本上不残留有效信号(图 12c)。
|
图 11 第123炮记录及去噪结果 (a)单炮记录;(b)二维Shearlet变换;(c)三维Shearlet变换;(d)尺度自适应三维Shearlet变换 实际地震数据共236炮记录,每炮记录有236道、1500个样点,采样间隔为0.002s,采样时间为3s。尺度和对应的方向剖分参数分别为4和[1 1 2 2] |
5 结束语
在传统稀疏变换去噪方法的基础上,笔者应用尺度自适应三维Shearlet变换去除地震数据噪声。尺度自适应三维Shearlet变换去噪方法不但考虑了单炮记录自身的特点,还顾及了单炮记录间的相关性,充分地利用了地震数据在三维Shearlet域的稀疏性。同时,结合有效信号与随机噪声在三维Shearlet域的分布特点,利用尺度自适应因子,最大限度地保留有效信号,提高信噪比和保真度。
尚需指出,由于对多炮地震数据进行三维Shearlet变换,对应的任意尺度、方向上的系数矩阵规模均与原始数据一致,所以本文方法对服务器的内存有一定要求。此外,通过对比理论数据单道振幅可知,由于炮检距的变化,有效信号的幅值在横向产生变化,因此所提方法可能对幅值相对较小的有效信号产生损害。
| [1] |
解吉高, 刘春成, 刘志斌, 等. 下刚果盆地北部中新统深水浊积岩储层及含油性地震预测[J]. 石油学报, 2015, 36(1): 33-40. XIE Jigao, LIU Chuncheng, LIU Zhibin, et al. Seismic prediction of the reservoir and oil-bearing property of Miocene deep-water turbidite in northern Lower Congo Basin[J]. Acta Petrolei Sinica, 2015, 36(1): 33-40. |
| [2] |
陈志德, 王成, 刘国友, 等. 近地表Q值模型建立方法及其地震叠前补偿应用[J]. 石油学报, 2015, 36(2): 188-196. CHEN Zhide, WANG Cheng, LIU Guoyou, et al. Modeling method of near-surface Q value and its seismic pre-stack compensation application[J]. Acta Petrolei Sinica, 2015, 36(2): 188-196. |
| [3] |
崔永福, 彭更新, 吴国忱, 等. 孔洞型碳酸盐岩储层地震正演及叠前深度偏移[J]. 石油学报, 2015, 36(7): 827-836. CUI Yongfu, PENG Gengxin, WU Guochen, et al. Seismic forward modeling and pre-stack depth migration of porous-type carbonate reservoirs[J]. Acta Petrolei Sinica, 2015, 36(7): 827-836. |
| [4] |
薛亚茹, 王敏, 陈小宏. 基于SL0的高分辨Radon变换及数据重建[J]. 石油地球物理勘探, 2018, 53(1): 1-7. XUE Yaru, WANG Min, CHEN Xiaohong. Seismic data reconstruction based on high order high resolution Radon transform[J]. Oil Geophysical Prospecting, 2018, 53(1): 1-7. |
| [5] |
徐彦凯, 曹思远, 何元. 双曲Radon-ASVD方法压制叠前地震数据随机噪声[J]. 石油地球物理勘探, 2017, 52(3): 451-457. XU Yankai, CAO Siyuan, HE Yuan. Hyperbolic Radon-ASVD method for suppressing seismic random noise[J]. Oil Geophysical Prospecting, 2017, 52(3): 451-457. |
| [6] |
陈泓竹, 王彦春. 频率域拉东变换加权约束反演压制层间多次波[J]. 石油地球物理勘探, 2018, 53(4): 666-673. CHEN Hongzhu, WANG Yanchun. Weighted constraint inversion to suppress the internal multiples in the frequency domain by Radon transform[J]. Oil Geo-physical Prospecting, 2018, 53(4): 666-673. |
| [7] |
曹小玲, 刘开元, 严良俊. 大地电磁的小波变换——独立分量分析去噪[J]. 石油地球物理勘探, 2018, 53(1): 206-213. CAO Xiaoling, LIU Kaiyuan, YAN Liangjun. Magnetotelluric wavelet transform:Independent component analysis denoising[J]. Oil Geophysical Prospecting, 2018, 53(1): 206-213. |
| [8] |
包乾宗, 高静怀, 陈文超. 面波压制的Ridgelet域方法[J]. 地球物理学报, 2007, 50(4): 1210-1215. BAO Qianzong, GAO Jinghuai, CHEN Wenchao. Ridgelet domain method of ground-roll suppression[J]. Chinese Journal of Geophysics, 2007, 50(4): 1210-1215. DOI:10.3321/j.issn:0001-5733.2007.04.030 |
| [9] |
Wang D L, Tong Z F, Tang C, et al. An iterative curvelet thresholding algorithm for seismic random noise attenuation[J]. Applied Geophysics, 2010, 7(4): 315-324. DOI:10.1007/s11770-010-0259-8 |
| [10] |
Mortezanejad R, Gholami A. Optimization of wavelet and curvelet-based denoising algorithms by multivariate SURE and GCV[J]. Journal of Geophysics and Engineering, 2016, 13(3): 378-390. DOI:10.1088/1742-2132/13/3/378 |
| [11] |
孟大江, 王德利, 冯飞, 等. 基于Curvelet变换的稀疏反褶积[J]. 石油学报, 2013, 34(1): 107-114. MENG Dajiang, WANG Deli, FENG Fei, et al. Sparse deconvolution based on the Curvelet transform[J]. Acta Petrolei Sinica, 2013, 34(1): 107-114. |
| [12] |
赵娴.基于Contourlet变换二维TFPF压制地震勘探随机噪声[D].吉林长春: 吉林大学, 2016. ZHAO Xian.2-D TFPF Based on Contourlet Transform for Seismic Random Noise Attenuation[D]. Jilin University, Chang Chun, Jilin, 2016. |
| [13] |
唐飞.基于Contourlet变换和Shearlet变换的图像去噪算法研究[D].湖南湘潭: 湘潭大学, 2014. TANG Fei.Research on Image Denoising Methods based on Contourlet Transform and Shearlet Transform[D]. Xiangtan University, Xiangtan, Hunan, 2014. |
| [14] |
Guo K, Labate D. Optimally sparse multidimensional representation using shearlets[J]. SIAM Journal on Mathematical Analysis, 2007, 39(1): 298-318. DOI:10.1137/060649781 |
| [15] |
Guo K, Labate D, Lim W Q, et al. Wavelets with composite dilations[J]. Electronic Research Announcements of the American Mathematical Society, 2004, 10(10): 78-87. |
| [16] |
Guo K, Labate D, Lim W Q, et al. Wavelets with composite dilations and their MRA properties[J]. Applied and Computational Harmonic Analysis, 2006, 20(2): 202-236. DOI:10.1016/j.acha.2005.07.002 |
| [17] |
张良, 韩立国, 许德鑫, 等. 基于压缩感知技术的Shearlet变换重建地震数据[J]. 石油地球物理勘探, 2017, 52(2): 220-225. ZHANG Liang, HAN Liguo, XU Dexin, et al. Seismic data reconstruction with Shearlet transform based on compressed sensing technology[J]. Oil Geophysical Prospecting, 2017, 52(2): 220-225. |
| [18] |
刘成明, 王德利, 王通, 等. 基于Shearlet变换的地震随机噪声压制[J]. 石油学报, 2014, 35(4): 692-699. LIU Chengming, WANG Deli, WANG Tong, et al. Random seismic noise attenuation based on the Shearlet transform[J]. Acta Petrolei Sinica, 2014, 35(4): 692-699. |
| [19] |
程浩, 陈刚, 王恩德, 等. 基于Shearlet变换的自适应阈值地震数据去噪方法[J]. 石油学报, 2018, 39(1): 82-91. CHENG Hao, CHEN Gang, WANG Ende, et al. Seismic data de-noising method of adaptive threshold based on Shearlet transform[J]. Acta Petrolei Sinica, 2018, 39(1): 82-91. |
| [20] |
Guo K, Labate D. Analysis and detection of surface discontinuities using the 3D continuous shearlet transform[J]. Applied and Computational Harmonic Ana-lysis, 2011, 30(2): 231-242. DOI:10.1016/j.acha.2010.08.004 |
| [21] |
孟阁阁, 王德利, 陈鑫. 基于三维曲波变换的地震数据去噪方法研究[J]. 石油物探, 2014, 53(3): 313-323. MENG Gege, WANG Deli, CHEN Xin. Study on seismic data denoising method based on 3D Curvelet transform[J]. Geophysical Prospecting for Petroleum, 2014, 53(3): 313-323. DOI:10.3969/j.issn.1000-1441.2014.03.009 |
| [22] |
张之涵, 孙成禹, 姚永强, 等. 三维曲波变换在地震资料去噪处理中的应用研究[J]. 石油物探, 2014, 53(4): 421-430. ZHANG Zhihan, SUN Chengyu, YAO Yongqiang, et al. Research on the application of 3D curvelet transform to seismic data denoising[J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 421-430. DOI:10.3969/j.issn.1000-1441.2014.04.007 |
| [23] |
胡雨, 谢凯, 阮宁君, 等. 基于三维曲波变换的弱信号恢复方法研究[J]. 计算机工程与应用, 2016, 52(18): 199-202. HU Yu, XIE Kai, RUAN Ningjun, et al. Method of weak signal recovery based on 3D curvelet transform[J]. Computer Engineering and Applications, 2016, 52(18): 199-202. DOI:10.3778/j.issn.1002-8331.1511-0202 |
| [24] |
段昶, 汪学刚, 王洪, 等. 基于三维带限剪切波变换的磁共振图像融合[J]. 生物医学工程学杂志, 2015, 32(1): 181-186. DUAN Chang, WANG Xuegang, WANG Hong, et al. Magnetic resonance image fusion based on three dimensional band limited Shearlet transform[J]. Journal of Biomedical Engineering, 2015, 32(1): 181-186. |
| [25] |
Negi P S, Labate D. 3D discrete Shearlet transform and video processing[J]. IEEE Transactions on Image Processing, 2012, 21(6): 2944-2954. DOI:10.1109/TIP.2012.2183883 |



 程浩, 辽宁省沈阳市和平区文体路三巷11号东北大学资源与土木工程学院, 110819。Email:
程浩, 辽宁省沈阳市和平区文体路三巷11号东北大学资源与土木工程学院, 110819。Email: