② 长安大学地质工程与测绘学院, 陕西西安 710154;
③ 西安石油大学地球科学与工程学院, 陕西西安 710065
② School of Geological Engineering and Geoma-tics, Chang'an University, Xi'an, Shaanxi 710154, China;
③ School of Earth Sciences and Engineering, Xi'an Shiyou University, Xi'an, Shaanxi 710065, China
随着波动方程叠前偏移方法的发展,利用波场的聚焦效果评估背景速度对波场传播的影响更为有效[1-3]。聚焦之后的局部成像结果包含速度信息,以此可以形成基于共成像点道集的偏移速度分析方法[4-5]。因此,共成像点道集的精度及其对速度的敏感性决定着偏移速度分析的可行性,也影响着偏移速度分析的收敛速度和效果[6]。
由于射线多路径问题的影响,常规CMP道集或炮检距域共成像点道集存在不同程度的构造假象,而角道集对射线多路径具有自适应性,通过波动方程偏移提取的角度道集(ADCIG)不存在假象[7-8],而且其偏移深度仅是局部入射角的函数,影响速度分析的变量因素少,适合于做偏移速度分析[9-10]。Biondi等[11]分析了ADCIG上的入射角与剩余时差关系;刘守伟等[12-13]推导了波动方程炮检距域共成像点道集(ODCIG)和ADCIG与偏移速度的关系,分析了剩余时差对偏移速度误差的敏感性,并基于ADCIG推导了水平层状介质条件下的速度更新公式,统一了常用的深度聚焦分析和剩余曲率分析的速度判别准则;Zhang等[14]基于剩余曲率速度分析的原理,利用ADCIG建立了入射角与偏移深度之间的联系,以此进行剩余速度分析修正、更新偏移速度;徐嘉亮等[15]分析了角度域剩余深度对剩余速度的敏感性,为偏移速度分析中初始模型的选择提供了依据;任芳等[16]基于微分相似优化速度反演方法的原理,利用ADCIG建立了目标泛函判定速度的准确性;秦宁等[17]将角度道集作为输入数据,在剩余曲率法速度更新的基础上建立了相应的层析速度建模方程,为角度道集用于速度分析开辟了新途径。
前人研究表明,ADCIG对速度误差非常敏感,且可以更为准确、直观地进行速度判别,非常有利于速度分析。但目前基于ADCIG的速度分析方法多以水平层状介质为基础,且研究内容集中于建立偏移深度与速度误差之间的函数关系,以此探讨ADCIG用于速度分析的可行性和优越性。面对实际地层复杂的构造特征,有必要推导实用性更强的倾斜界面或复杂构造情况下的ADCIG更新方程。另外,ADCIG作为偏移速度分析的一种输入,如何直观定量地判别速度误差也是提高速度分析建模精度的重要研究内容。
本文基于波动方程叠前偏移过程中波场角度域转化的运动学属性,推导了倾斜地层情况下ADCIG的剩余深度方程,拓展了ADCIG用于速度分析的适用性。为了准确判断速度误差,本文在相关法速度分析[18]的基础上,通过道集信噪比的估计发展了匹配相关的剩余曲率谱计算方法,从而可以定量拾取剩余曲率值进行速度更新。理论模型和实际资料试算表明,本文匹配相关算法提高了剩余曲率谱的分辨率和抗噪能力,可以更为准确地拾取剩余曲率值,提高速度分析的精度。
1 ADCIG剩余深度方程基于ADCIG的运动学属性可知,当偏移速度不准确时,波动方程偏移无法使波场在零炮检距处聚焦,这时波场的角度域转换将沿着与局部炮检距正交方向移动成像点,即角度转换将成像点从不同位置的炮检距域(Ixh、Izh、I0)变换到同一位置处的角度域(Iβ),也就是法向移动校正了炮检距方向对成像点位置的影响[11],其几何关系如图 1所示。
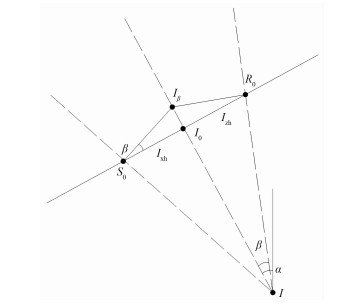
|
图 1 速度偏小时角度域转换的几何关系 α为视地层倾角;β为波场入射角;S0为震源位置;R0为检波点位置;I为震源射线与检波点射线的交点;I0为准确速度角度域成像点;Iβ为不准确速度时角度域成像点;Ixh为水平炮检距成像点,在S0与I0间随速度变化;Izh为垂直炮检距成像点,在R0与I0间随速度变化 |
此时角度域偏移的成像点(Iβ)位于视地层倾角法线方向,且穿过震源S0和检波器R0的射线交点I。由图中几何关系可知,角度域转换引起的沿反射层的法线移动量为Δnβ
| $ \Delta {\mathit{\boldsymbol{n}}_\beta } = \Delta {\mathit{\boldsymbol{n}}_{{h_0}}}{\tan ^2}\beta $ | (1) |
式中:Δnh0=nh0/tanβ表示地层倾角域的成像点法线移动量;β为入射角;h0表示半炮检距距;n为地层界面法向。由零炮检距处波场聚焦引起的全部法向移动量为
| $ \Delta {\mathit{\boldsymbol{n}}_{{\rm{total}}}} = \Delta {\mathit{\boldsymbol{n}}_{{h_0}}} + \Delta {\mathit{\boldsymbol{n}}_\beta } = \Delta {\mathit{\boldsymbol{n}}_{{h_0}}}\left( {1 + {{\tan }^2}\beta } \right) = \frac{{\Delta {\mathit{\boldsymbol{n}}_{{h_0}}}}}{{{{\cos }^2}\beta }} $ | (2) |
根据式(2),利用三角关系和Fermat定理,可以推出Δntotal和由速度误差引起的旅行时扰动间的关系为
| $ \Delta {\mathit{\boldsymbol{n}}_{{\rm{total}}}} = \frac{{{v_{\rm{m}}}\Delta t}}{{2\cos \beta }}\mathit{\boldsymbol{n}} $ | (3) |
式中:vm是成像点附近的偏移速度;Δt为背景旅行时和扰动旅行时的差值。倾斜地层情况下任意入射角时的波场传播旅行时表达式为[19]
| $ t = \frac{{2z}}{v}\frac{{\cos \alpha \cos \beta }}{{{{\cos }^2}\alpha - {{\sin }^2}\beta }} $ | (4) |
式中:z为反射点深度;v为波场传播速度。相应地,在速度不准确的情况下(偏移速度为vm),可得波场旅行时
| $ {t_{\rm{m}}} = \frac{{2z}}{{{v_{\rm{m}}}}}\frac{{\cos \alpha \cos \beta }}{{{{\cos }^2}\alpha - {{\sin }^2}\beta }} $ | (5) |
定义剩余曲率p=vm/v,可得vm引起的波场传播旅行时时差为
| $ \Delta t = t - {t_{\rm{m}}} = \frac{1}{v}\left( {1 - \frac{1}{p}} \right)\frac{{\cos \alpha \cos \beta }}{{{{\cos }^2}\alpha - {{\sin }^2}\beta }} $ | (6) |
将式(6)代入式(3),可得
| $ \Delta {\mathit{\boldsymbol{n}}_{{\rm{total }}}} = (p - 1)\frac{{\cos \alpha }}{{{{\cos }^2}\alpha - {{\sin }^2}\beta }}{\mathit{\boldsymbol{z}}_{\rm{m}}}\mathit{\boldsymbol{n}} $ | (7) |
式中zm为成像深度。剩余深度描述了成像点任意入射角β与法线入射方向时(β=0)的深度之差。由式(7)可得
| $ \begin{array}{l} \Delta {\mathit{\boldsymbol{n}}_{{\rm{RMO}}}} = \Delta {\mathit{\boldsymbol{n}}_{{\rm{total}}}}(\beta ) - \Delta {\mathit{\boldsymbol{n}}_{{\rm{total}}}}(0)\\ \;\;\;\;\;\;\;\;\;\; = \frac{{(p - 1){{\sin }^2}\beta }}{{\left( {{{\cos }^2}\alpha - {{\sin }^2}\beta } \right)\cos \alpha }}{\mathit{\boldsymbol{z}}_{\rm{m}}}\mathit{\boldsymbol{n}} \end{array} $ | (8) |
式中ΔnRMO为沿地层法向的剩余深度。速度分析利用垂直方向的深度剩余量,因此,需将沿地层法向的剩余深度投影到垂向,即
| $ \Delta {z_{{\rm{RMO}}}} = \left| {\Delta {\mathit{\boldsymbol{n}}_{{\rm{RMO}}}}} \right| \cdot \cos \alpha = \frac{{(p - 1){{\sin }^2}\beta }}{{{{\cos }^2}\alpha - {{\sin }^2}\beta }}{z_{\rm{m}}} $ | (9) |
式中ΔzRMO为垂向剩余深度。为更一般性地表示地下反射点深度z,可以用zm=zp近似替换,则
| $ \Delta {z_{{\rm{RMO}}}} = p(p - 1)\frac{{z{{\sin }^2}\beta }}{{{{\cos }^2}\alpha - {{\sin }^2}\beta }} $ | (10) |
上式即为地层任意倾角情况下ADCIG上的深度剩余量计算公式。当α=0°时,上式退化为水平层状介质的公式。图 2为z=2000m、α=10°时用式(10)计算的剩余深度随剩余曲率的变化曲线。同一入射角时不同剩余曲率引起不同的剩余深度量,通过剩余曲率扫描得到一系列剩余深度进行道集更新。当同相轴拉平时对应的剩余曲率值就可以用作速度修正
| $ {v_{{\rm{update}}}} = \frac{{{v_i}}}{{{p_i}}} $ | (11) |
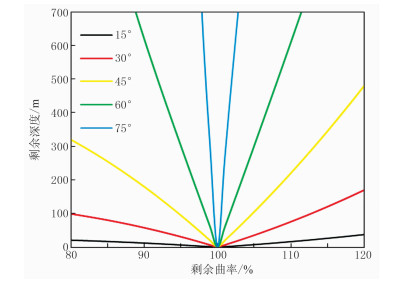
|
图 2 入射角β不同时的理论计算的剩余深度随剩余曲率的变化曲线 |
式中:vupdate示第i层更新后的速度;vi是初始偏移速度;pi是拾取的剩余曲率值。由上式可以看出,速度更新对拾取的剩余曲率值pi较为敏感,因此需要在空间上先进行一定的平滑和插值,然后进行速度更新,得到整个模型空间更新后的速度。
2 速度分析方法通过ADCIG同相轴的弯曲情况仅能判断速度是否正确,为了进行速度更新还需获得准确的剩余曲率。依据常规速度分析方法的思路[20-22],本文给出一系列剩余曲率值,根据式(10)计算剩余深度量并进行道集更新,以此制作剩余曲率谱,然后拾取剩余曲率谱极值对应的剩余曲率值,进而求取更新后的速度模型。因此,获得计算精度高、分辨率高的剩余曲率谱,是拾取准确剩余曲率值的关键。
2.1 叠加法叠加法是最常用的一种速度分析方法,将它用于ADCIG来判断速度误差,基本过程可以描述为:选取一系列剩余曲率值计算剩余深度量;然后进行深度更新,如果剩余曲率值选取合适,弯曲的ADCIG同相轴被校平,各个角度的波形一致;将不同入射角的成像道集叠加后其能量最大,最大能量或最大振幅对应的剩余曲率值就是可用于速度更新的最佳值。叠加能量法速度分析公式可表示为
| $ {C_{\rm{E}}}(z,p) = {\left[ {\frac{1}{{{N_{{\rm{tr}}}}}}\sum\limits_{i = 1}^{{N_{{\rm{tr}}}}} U \left( {{z_i},i} \right)} \right]^2} $ | (12) |
式中:U(zi,i)表示深度zi处更新后的ADCIG;Ntr表示数据的总道数;CE为平均振幅能量。进行剩余曲率谱扫描,当剩余曲率值准确时,计算可获得准确的剩余深度量,更新后的ADCIG同相轴是水平的,成像深度不随入射角变化,叠加之后能量最大;当剩余曲率值不准确时,剩余深度量也存在误差,更新后的同相轴无法校平,这样同一深度不同角度的地震道集叠加之后能量将大大削弱。
2.2 相关法基于相关计算的速度分析方法将能量叠加改为相关计算[23],以此提高剩余曲率谱的计算精度。Al-Yahya[24]于1989年提出了能量相关计算剩余曲率谱的方法,其公式为
| $ {C_{\rm{S}}}(z,p) = \frac{{{{\left[ {\sum\limits_{i = 1}^{{N_{{\rm{tr}}}}} U \left( {{z_i},i} \right)} \right]}^2}}}{{\sum\limits_{i = 1}^{{N_{{\rm{tr}}}}} {{U^2}} \left( {{z_i},i} \right)}} $ | (13) |
式中CS为相似系数。当扫描的剩余曲率值准确时,剩余深度计算准确,ADCIG被校平,不同角度之间波形一致,CS=1;否则,道集无法校平,CS < 1。在信噪比较低的情况下,为了提高复杂道集剩余曲率值的拾取精度,对式(13)做如下改造
| $ {C_{\rm{S}}}(z,p) = \frac{{{{\left[ {\sum\limits_{i = 1}^{{N_{{\rm{tr}}}}} U \left( {{z_i},i} \right)} \right]}^{2n}}}}{{\sum\limits_{i = 1}^{{N_{{\rm{tr}}}}} {{U^{2n}}} \left( {{z_i},i} \right)}} $ | (14) |
当n取1、2、3时,相关剩余曲率谱的分辨率可随阶数增大而提高,从而更有利于提高剩余曲率值的拾取精度。
2.3 匹配相关法由于缺乏子波约束,使用叠加类或相关类方法计算的剩余曲率谱分辨率一般较低。假设地震道集振幅谱和原始数据频谱近似匹配的情况下,可以用信噪比(RS/N)定量描述道集质量。假设地震数据中噪声与有效信号不相关,则道集的RS/N估算公式为[25]
| $ {R_{{\rm{S}}/{\rm{N}}}} = \frac{{{\lambda _1} - \sum\limits_{i = 2}^{{N_{{\rm{tr}}}}} {\frac{{{\lambda _i}}}{{{N_{{\rm{tr}}}} - 1}}} }}{{\sum\limits_{i = 2}^{{N_{{\rm{tr}}}}} {\frac{{{\lambda _i}}}{{{N_{{\rm{tr}}}} - 1}}} }} $ | (15) |
式中λi表示ADCIG协方差矩阵按降序排列的特征值,一般可以通过奇异值分解或QR分解等方法求解[26]。对于上式有如下认识:如果剩余曲率扫描值合适,道集时窗内计算的信噪比较大;当剩余曲率扫描值不合理时,则计算得到的信噪比数值较小。
利用相关系数(式(14))和信噪比(式(15))可以构造如下相关函数
| $ {C_{{\rm{SG}}}}(z,p) = {C_{\rm{S}}} \times {R_{{\rm{S}}/{\rm{N}}}} $ | (16) |
当剩余曲率值准确时,道集相关性最好,信噪比最高,该方程将这两者进行了匹配,能进一步提高剩余曲率谱的分辨率。另外,如果ADCIG包含多次波或转换波等交互干扰时,在信噪比估算中,这些干扰均会被视为噪声,不会影响有效信号的估计,即在低信噪比情况下,不会降低有效信号的分辨率,因此式(16)在低信噪比数据中同样可以获得较高的分辨率。
3 模型数据测试通过模型数据对几种剩余曲率谱计算方法进行对照测试。对理论数据进行偏移成像时,首先采用准确的偏移速度,因此可以获得同相轴平直的ADCIG,进行剩余曲率速度分析时,剩余曲率谱极值处对应的剩余曲率值p=100%。以此数据为基础,分别采用叠加法、相关法和匹配相关法计算ADCIG对应的剩余曲率谱,对比不同算法的分辨率,然后对ADCIG添加不同幅度的随机噪声以测试方法的抗噪性。最后,采用有误差的速度进行偏移,以此测试速度分析方法对速度误差判断的准确性。
3.1 分辨率分析图 3a为未添加噪声时的ADCIG,可以看出主要目的层位的ADCIG同相轴平直,说明偏移速度准确。图 3b~图 3d分别为叠加法、相关法和匹配相关法计算的剩余曲率谱,可见,几种方法均能较好地反映速度误差情况,能量团峰值基本都在p=100%处,但不同的方法在剩余曲率横向分辨率和深度分辨率上存在差别。叠加法总体效果最差,仅在浅部具有相对较高的纵向分辨率,在中深层其能量团被拉伸,分辨率明显降低,特别是在深层,基本没有可分辨的能量团;相关法相对于叠加法其纵、横向分辨率均得到提高,纵向上可分辨的层位增多,对于深层也有反映;匹配相关法获得了分辨率最高的剩余曲率谱,其横向分辨率大大提高,主要是因为通过信噪比的加权约束,正确剩余曲率谱时的相似系数得到加强,而剩余曲率存在误差时的相似系数相对弱化了,因此能量团收敛、更为集中。
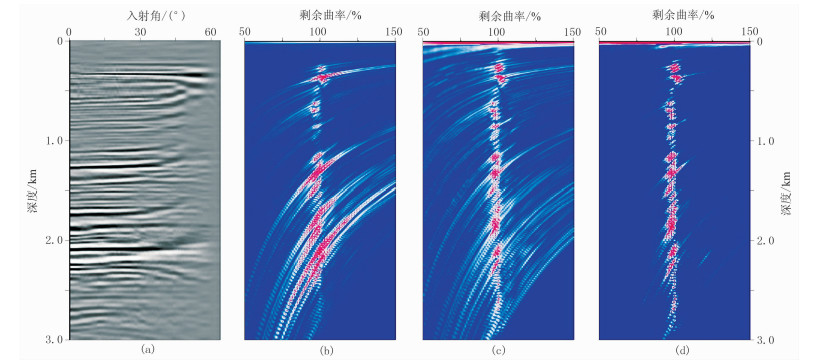
|
图 3 原始ADCIG及其不同方法计算的剩余曲率谱 (a)准确速度偏移的ADCIG;(b)叠加法;(c)相关法;(d)匹配相关法 |
处理方法的抗噪性测试是检验其实用性的有效途径,对于实际资料中经常出现的随机噪声,本文通过一般性的理论模型,研究其对几种剩余曲率谱计算方法的影响。在图 3a所示的ADCIG中加入不同程度的高斯白噪声,使其信噪比分别为2.0和0.4,即代表高、低信噪比两种情况下的数据。图 4为高信噪比情况下的ADCIG及不同方法计算的剩余曲率谱,可以看出,由于随机噪声的干扰,各种方法获得的剩余曲率谱随深度增加分辨率均有所下降,但总体仍具有较好的效果,从中均可以拾取到较为准确的剩余曲率值,说明这些方法都具有一定的抗噪性。从叠加法、相关法到匹配相关法,其分辨率和信噪比逐渐提高。但在随机噪声的影响下,叠加法和相关法计算的剩余曲率谱中均受到噪声干扰,而匹配相关法几乎没有受到噪声干扰,仍具有较高的分辨率和信噪比。
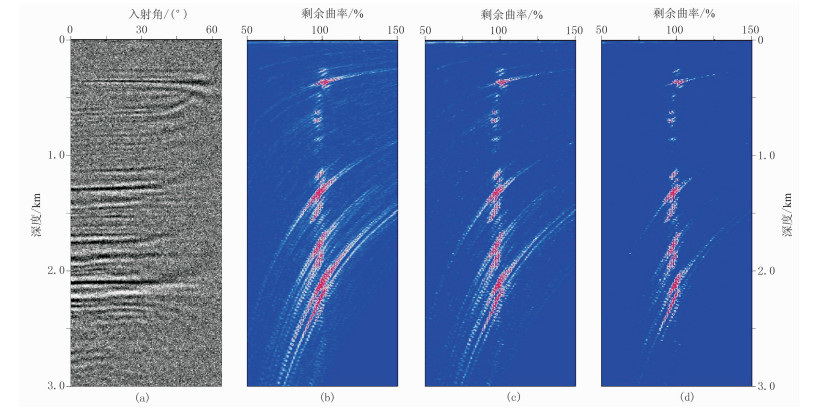
|
图 4 高信噪比ADCIG及其不同方法计算的剩余曲率谱 (a)含弱噪声的ADCIG;(b)叠加能量法;(c)相关法;(d)匹配相关法 |
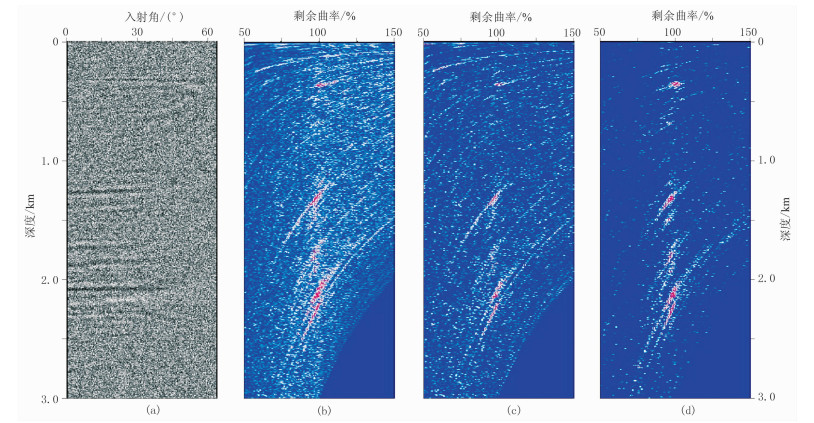
图 5为低信噪比时的ADCIG及其剩余曲率谱。由图 5a可以看出,原始ADCIG中能量较弱的同相轴已经完全被噪声淹没,只有中深部反射能量较强的几个同相轴可以识别。用不同方法计算其剩余曲率谱,其中叠加法受噪声干扰严重,信噪比也较低,但峰值计算的能量较强,仍具有一定的分辨率;相关法剩余曲率谱信噪比相对得到提高,但由于噪声能量较强,相关法也无法突出最佳剩余曲率值,其剩余曲率谱峰值能量相对较弱;匹配相关法取得了较好的效果,由于噪声对有效信号的估计不产生影响,因此低信噪比时信噪比估计尤为有效,通过信噪比和相似系数的联合,有效增强了最佳剩余曲率值时的相关系数,因此剩余曲率谱的分辨率得到提高。对于含噪声ADCIG中无法识别的同相轴,匹配相关计算仍可对其进行剩余曲率谱扫描,获得高分辨率的剩余曲率谱,进而拾取较为准确的剩余曲率值。
|
图 5 低信噪比ADCIG及其不同方法计算的剩余曲率谱 (a)含强噪声的ADCIG;(b)叠加能量法;(c)相关法;(d)匹配相关法 |
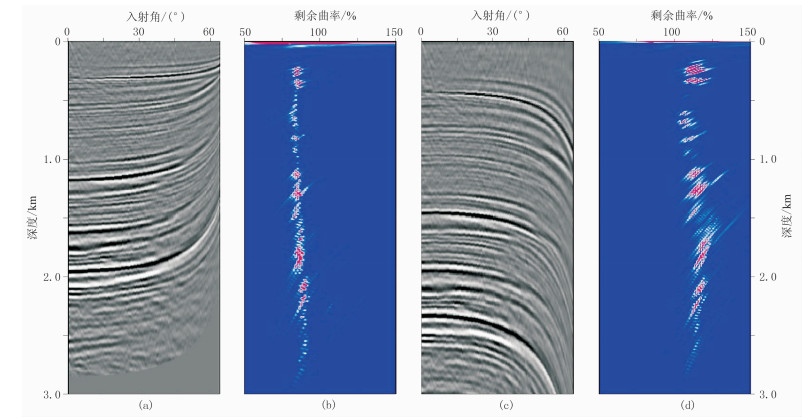
偏移速度分析的目的即是通过成像道集识别并提取速度误差,进而更新偏移速度场。首先采用偏小的速度进行偏移,偏移速度设计为真实速度的0.80~0.90倍,且随深度线性变化,图 6a为速度偏小时偏移获得的ADCIG,可以看到道集同相轴向上弯曲。通过匹配相关法计算获得的剩余曲率谱如图 6b所示,可见该剩余曲率谱较为准确地反映了速度误差。进一步采用偏大的速度进行偏移,偏移速度设计为真实速度的1.05~1.20倍,且随深度任意变化。图 6c为速度偏大时偏移提取的ADCIG,可以看到该道集同相轴向下弯曲,且不同深度同相轴弯曲程度不同,直观地表明不同深度存在不同的速度误差。图 6d为匹配相关法计算获得的剩余曲率谱,它更为清晰地反映了不同深度的速度误差量。
|
图 6 速度存在误差时的ADCIG及匹配相关算法计算的剩余曲率谱 (a)速度偏小时提取的ADCIG;(b)图a数据计算的剩余曲率谱;(c)速度偏大时提取的ADCIG;(d)图c数据计算的剩余曲率谱 |
上面测试表明,ADCIG的同相轴弯曲情况仅反映了偏移速度存在偏小或偏大的误差,而通过本文剩余曲率谱的计算,可以拾取较为精确的剩余曲率值,以此进行速度更新,使速度向正确的方向收敛。
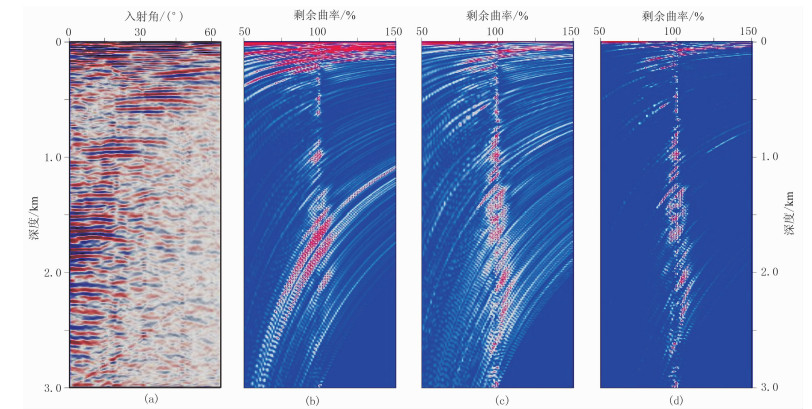
4 实际数据试算图 7a为实际资料通过角度域偏移获得的ADCIG,图 7b~图 7d为不同方法计算的剩余曲率谱。可以看出:叠加法在中部其能量团峰值较分散,分辨率较低;相似法计算的剩余曲率谱能量收敛,横向分辨率大大提高,可以进行剩余曲率值拾取;匹配相关法计算的剩余曲率谱分辨率和信噪比进一步提高,可以拾取较为准确的剩余曲率值。
|
图 7 实际数据提取的ADCIG及其不同方法计算的剩余曲率谱 (a)ADCIG;(b)叠加能量法;(c)相关法;(d)匹配相关法 |
波动方程偏移提取的ADCIG正确地反映了地下的构造和岩性信息,是目前唯一没有假象的道集,它对速度误差较为敏感,非常适用于偏移速度分析。本文从ADCIG的运动学属性出发,推导了倾斜地层情况下的ADCIG剩余深度方程,在相关法基础上发展了匹配相关法进行剩余曲率扫描以计算剩余曲率谱,从而可以准确、直观地进行初始模型速度误差的判断和更新,提高偏移速度建模的准确性。本文的匹配相关速度分析方法具有较好的抗噪性,在低信噪比数据中仍可提取到弱反射信号,因此具有更高的分辨率。由理论模型和实际资料的数值实验结果可以看出,相关法和匹配相关法可以获得较为近似的结果,但匹配相关法具有更高的分辨率,特别是在横向上,其对剩余曲率的分辨率更高。但是匹配相关法一般要通过奇异值分解或QR分解来计算ADCIG协方差矩阵的特征值,因此计算量一般较大。
| [1] |
Herve C, Emmanuel C. From migration to inversion velocity analysis[J]. Geophysics, 2017, 82(3): S207-S223. DOI:10.1190/geo2016-0359.1 |
| [2] |
刘奇琳, 刘伊克, 常旭. 双平方根波动方程偏移速度分析[J]. 地球物理学报, 2009, 52(7): 1891-1898. LIU Qilin, LIU Yike, CHANG Xu. Wave equation migration velocity analysis by double square method[J]. Chinese Journal of Geophysics, 2009, 52(7): 1891-1898. |
| [3] |
徐嘉亮, 周东红, 贺电波, 等. 高精度深度域层析速度反演方法[J]. 石油地球物理勘探, 2018, 53(4): 737-744. XU Jialiang, ZHOU Donghong, HE Dianbo, et al. High-precision velocity tomography inversion in the depth domain[J]. Oil Geophysical Prospecting, 2018, 53(4): 737-744. |
| [4] |
Guo B, Schuster G T. Wave-equation migration velocity analysis using plane-wave common-image gathers[J]. Geophysics, 2017, 82(5): S327-S340. DOI:10.1190/geo2016-0653.1 |
| [5] |
李江. 基于奇异值分解的角度域去噪方法[J]. 石油物探, 2019, 58(3): 427-432. LI Jiang. Seismic denoising in the angle domain based on singular value decomposition[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 427-432. |
| [6] |
Zhang Y, Biondi B. Moveout based wave equation migration velocity analysis[J]. Geophysics, 2013, 78(2): U31-U39. DOI:10.1190/geo2012-0082.1 |
| [7] |
张广智, 常德宽, 王一惠, 等. 波动方程叠前深度偏移角度道集求取方法[J]. 石油地球物理勘探, 2016, 51(3): 529-536. ZHANG Guangzhi, CHANG Dekuan, WANG Yihui, et al. Angle domain common-image gather calculation based on wave equation prestack depth migration[J]. Oil Geophysical Prospecting, 2016, 51(3): 529-536. |
| [8] |
李海强, 杨国权, 李振春, 等. 基于局部平面波分解的逆时偏移角道集提取方法[J]. 石油地球物理勘探, 2017, 52(6): 1177-1183. LI Haiqiang, YANG Guoquan, LI Zhenchun, et al. A method for extracting angle-domain common-image gathers based on local plane wave decomposition[J]. Oil Geophysical Prospecting, 2017, 52(6): 1177-1183. |
| [9] |
Save P, Biondi B. Wave equation migration velocity analysis 1:Theory[J]. Geophysics Prospecting, 2004, 52(6): 593-606. DOI:10.1111/j.1365-2478.2004.00447.x |
| [10] |
Stork C, Symes W. Kinematic artifacts in prestack depthmigration[J]. Geophysics, 2004, 69(2): 562-575. DOI:10.1190/1.1707076 |
| [11] |
Biondi B, William S. Angle domain common image gathers for migration velocity analysis by wave field continuation imaging[J]. Geophysics, 2004, 69(5): 1283-1298. DOI:10.1190/1.1801945 |
| [12] |
刘守伟, 程玖兵, 王华忠, 等. 炮检距域/角度域共成像点该道集与偏移速度的关系[J]. 地球科学——中国地质大学学报, 2007, 32(4): 575-582. LIU Shouwei, CHENG Jiubing, WANG Huazhong, et al. Relationships between offset domain/angle domain common image gathers and migration velocity[J]. Earth Science:Journal of China University of Geosciences, 2007, 32(4): 575-582. |
| [13] |
刘守伟, 王华忠, 程玖兵, 等. 时空移动成像条件及偏移速度分析[J]. 地球物理学报, 2008, 51(6): 1883-1891. LIU Shouwei, WANG Huazhong, CHENG Jiubing, et al. Space-time shift imaging condition and migration velocity analysis[J]. Chinese Journal of Geophysics, 2008, 51(6): 1883-1891. |
| [14] |
Zhang K, Li Z C, Zeng T S, et al. Residual curvature migration velocity analysis for angle domain common imaging gather[J]. Applied Geophysics, 2010, 7(1): 49-56. DOI:10.1007/s11770-010-0006-1 |
| [15] |
徐嘉亮, 常旭, 王一博. 角度与剩余深度对剩余速度的敏感性分析[J]. 地球物理学报, 2015, 58(8): 2927-2934. XU Jialiang, CHANG Xu, WANG Yibo. Sensitivity analysis of the residual depth about the residual velocity in the angle domain[J]. Chinese Journal of Geophysics, 2015, 58(8): 2927-2934. |
| [16] |
任芳, 李振春, 张敏, 等. 基于角道集的微分相似优化法偏移速度分析[J]. 物探与化探, 2017, 41(5): 872-880. REN Fang, LI Zhenchun, ZHANG Min, et al. Diffe-rential semblance optimization migration velocity ana-lysis based on angle domain CIGs[J]. Geophysical and Geochemical Exploration, 2017, 41(5): 872-880. |
| [17] |
秦宁, 王延光, 杨晓东, 等. 基于角道集剩余曲率分析的层析速度建模[J]. 石油地球物理勘探, 2015, 50(1): 61-66. QIN Ning, WANG Yanguang, YANG Xiaodong, et al. Tomography velocity modelbuildingbased on ADCIGs residual curvature[J]. Oil Geophysical Prospecting, 2015, 50(1): 61-66. |
| [18] |
高妍. 几种速度分析方法的对比分析与应用[J]. 工程地球物理学报, 2014, 11(4): 436-450. GAO Yan. Comparison of several velocity methods and application[J]. Chinese Journal of Engineering Geophysics, 2014, 11(4): 436-450. |
| [19] |
Sava P, Fomel S. Angle-domain common-image ga-thers by wave field continuation methods[J]. Geophy-sics, 2003, 68(3): 1065-1074. |
| [20] |
张建彬, 林年添, 张栋, 等. 基于非线性函数的速度谱智能拾取[J]. 地球物理学进展, 2016, 31(2): 856-860. ZHANG Jianbin, LIN Niantian, ZHANG Dong, et al. Intelligent picking of velocity spectrum based on nonlinear function[J]. Progress in Geophysics, 2016, 31(2): 856-860. |
| [21] |
Andrea T, Eusebio S, Alessia R, et al. High resolution coherency functional for velocity analysis:An application for subbasalt seismic exploration[J]. Geophysics, 2013, 78(5): U53-U63. DOI:10.1190/geo2012-0544.1 |
| [22] |
王珊. 层速度求取方法及速度谱横向密度对速度场精度的影响[J]. 石油地球物理勘探, 2016, 51(2): 355-360, 375. WANG Shan. Influences of interval velocity calculation method and spectrum lateral density on velocity field accuracy[J]. Oil Geophysical Prospecting, 2016, 51(2): 355-360, 375. |
| [23] |
刘国华. 高分辨率归一化自举微分相似系数速度分析方法[J]. 石油物探, 2014, 53(5): 530-536. LIU Guohua. High-resolution velocity analysis based on normalized bootstrapped differential semblance[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 530-536. |
| [24] |
Al-Yahya K. Velocity analysis by iterative profile migration[J]. Geophysics, 1989, 54(6): 718-729. DOI:10.1190/1.1442699 |
| [25] |
张军华, 藏胜涛, 周振晓, 等. 地震资料信噪比定量计算及方法比较[J]. 石油地球物理勘探, 2009, 44(4): 481-486. ZHANG Junhua, ZANG Shengtao, ZHOU Zhenxiao, et al. Quantitative computation and comparison of S/N ratio in seismic data[J]. Oil Geophysical Prospecting, 2009, 44(4): 481-486. |
| [26] |
郑晓, 薄华, 孙强. QR分解与特征值优化观测矩阵的算法研究[J]. 智能系统学报, 2015, 10(1): 149-155. ZHENG Xiao, BO Hua, SUN Qiang. An algorithm for measurement matrix based on QR decomposition and eigenvalue optimization[J]. Transactions on Intelligent Systems, 2015, 10(1): 149-155. |



 李庆春, 陕西省西安市雁塔区雁塔路南段126号长安大学地质工程与测绘学院, 710064。Email:
李庆春, 陕西省西安市雁塔区雁塔路南段126号长安大学地质工程与测绘学院, 710064。Email: