② 中国石化胜利油田油气勘探管理中心, 山东东营 257000
② Center for Oil & Gas Exploration Management, Shengli Oilfield Branch Co., SINOPEC, Dongying, Shandong 257000, China
微地震监测技术是通过监测致密储层压裂改造产生的微地震事件,以评价与分析储层改造效果的一种地球物理技术[1]。微地震震源能量相对较弱,信号在传播过程中能量又被地层强烈吸收,造成微地震事件湮没在噪声中,所获得的资料通常存在微震事件少、有效信号能量弱、信噪比低等缺点[2]。为了有效地提高初至拾取的精度及反演结果的可靠性,需要压制微震资料中的随机噪声,提高数据的信噪比[3]。
微地震信号的去噪方法有很多,根据微地震监测方式的不同,可分为井中微地震资料去噪及地面微地震资料去噪两大类[4],前者去噪结果信噪比相对较高,后者的信噪比较低。微地震数据中的不规则干扰和有源噪声类型非常多,包括压裂井场干扰、抽油机噪声、钻机干扰、建筑工地噪声、工业电干扰、车辆噪声、风吹草动、人畜活动和物体坠落噪声等。近年来针对井中微地震数据的主要去噪方法包括偏振滤波、τ-p变换、F-K滤波等[5-6];针对地面微地震数据当前有效去噪方法主要包括基于独立分量分析的方法、基于局部相关谱约束的多道匹配追踪算法、基于压缩连续小波变换方法及基于多尺度形态学的方法等[7-11]。由于地面微地震资料具有强噪声、弱有效信号的特点,很多常规的去噪方法难以得到理想的去噪效果,因此研究针对地面微地震资料的去噪方法也十分重要。
稀疏表示(稀疏编码)是压缩感知理论的先验条件,能够从多维数据中自适应地构造字典,通过该字典的线性组合表示地震数据。稀疏表示理论的关键问题包括字典构造方法及稀疏优化方法,字典构造就是确定字典中的基函数,基函数的性能决定了信号表示的稀疏程度。姜宇东等[12]采用曲波变换算法进行了微地震数据的自适应阈值噪声压制,Zhang等[13]研究了基于三维Shearlet变换的多分量微地震去噪方法,两种方法都是基于固定基的稀疏变换。固定基的稀疏变换没有利用地震数据的先验信息,而字典学习方法通过原始数据训练得到稀疏变换,将字典的训练与去噪过程有机地结合,能够实现在数据稀疏表示的同时压制数据中的噪声。李稳等[14]研究了基于稀疏分布特征的井下微地震信号识别与提取方法;Tang等[15]研究了基于学习型超完备稀疏表示的随机噪声压制方法,可以有效地压制伪吉布斯现象引起的扰动;Chen等[16]研究了基于双稀疏字典的地震信号去噪方法,获得了较好的去噪效果;Liang等[17]采用数据驱动紧框架方法完成了地震数据的重构。
针对地面微地震数据的特征,本文利用基于弱纹理块的噪声估计方法求取含噪微地震数据中的噪声方差,采用具有多分辨率性质和冗余性质的数据驱动紧框架方法进行微地震资料去噪,取得了较好的去噪效果。
1 基本理论与技术流程 1.1 基于弱纹理块的噪声方差估计在去噪算法中,需要知道噪声的分布模型和统计参数,噪声的方差估计是含噪数据处理中的常见问题之一[18]。目前有代表性的噪声估计算法有很多,常见的有基于小波分解的噪声方差估计、基于主成分分析的方差估计[19]、基于尺度不变性的噪声估计方法[20]及基于弱纹理块的噪声方差估计[21]等。小波变换估计方法是对数据进行小波变换,数据的能量主要集中在尺度大的子带,而尺度小的高频子带系数的幅值较小、能量较低。因此,当噪声较大时,可将最高频率子带的系数全部看成是噪声,由此估计噪声的标准方差,但当噪声较强时小波变换的估计误差较大。
基于弱纹理块的噪声方差估计利用概率统计思想,通过统计数据分割结果拟合每个分割块的标准差。该方法把含噪声的地震记录x看成N个有效信息块和噪声块的组合
| $ \boldsymbol{x}_{i}=\boldsymbol{s}_{i}+\boldsymbol{n}_{i} \quad i=1, 2, \cdots, N $ | (1) |
式中:si是第i个无噪声的有效信号块;ni是第i个噪声块,假设噪声独立于有效信号。将含噪数据块协方差矩阵的最小特征值分解为
| $ {\lambda _{\min }}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_\mathit{\boldsymbol{x}}}} \right) = {\lambda _{\min }}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_\mathit{\boldsymbol{s}}}} \right) + \sigma _{\rm{n}}^2 $ | (2) |
则可计算出噪声方差σn2。式中:λmin(Σx)是含噪声数据块协方差矩阵Σx的最小特征值;λmin(Σs)是不含噪声的有效信号块协方差矩阵Σs的最小特征值。
实际上λmin(Σs)是未知的,基于弱纹理块的噪声方差估计就是利用局部梯度矩阵及其统计特性的纹理强度来选择弱纹理块,用弱纹理块集合的协方差矩阵的最小特征值代替式(2)中的无噪数据块的λmin(Σs),进而求得噪声方差。数据块的纹理强度ξi定义为
| $ {\xi _i} = {\mathop{\rm tr}\nolimits} \left( {{\mathit{\boldsymbol{C}}_{{\mathit{\boldsymbol{x}}_i}}}} \right) $ | (3) |
式中:Cxi为数据块xi的梯度协方差矩阵;tr(·)表示求矩阵的迹。设定一个阈值τ,将纹理强度小于τ的数据块定为弱纹理块。首先利用输入数据的协方差矩阵估计初始噪声方差σ02,用第k个噪声方差σk2确定第k+1个阈值τk+1,然后从噪声数据中选择第k+1次的弱纹理块集合,进而计算出第k+1个噪声方差估计σk+12。重复上述迭代过程,直到噪声方差估计结果不再变化。
图 1为基于弱纹理块方法与小波分解方法的噪声方差估计结果对比,可以看出,基于弱纹理块方法的噪声估计结果要优于小波分解估计结果,稳定性较好,基本不会受到实际噪声水平的影响。

|
图 1 基于弱纹理块与小波分解的噪声方差估计对比 |
紧框架基的多分辨率性质和冗余性质有助于数据的稀疏表示,数据驱动紧框架优化的目标函数[22-23]为
| $ \begin{array}{l} \arg {\min _{\mathit{\boldsymbol{v, w}}}}\parallel \mathit{\boldsymbol{v}} - {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{x}}\parallel _2^2 + \sigma _{\rm{n}}^2\parallel \mathit{\boldsymbol{v}}{\parallel _0}\\ {\rm{满足}}\;\;\;\;\;\;{\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{W}} = \mathit{\boldsymbol{I}} \end{array} $ | (4) |
式中:v为变换系数向量;WT(a1, a2, …, am)为滤波器组(字典)矩阵,其每一列表示由每一个滤波器(a1, a2, …, am)生成的紧框架算子,m为定义的滤波器的个数,单个滤波器由r×r个元素组成;x为原始微地震数据,令地震数据的噪声方差估计σn2作为权重参数;I为单位矩阵。式(4)的第一项‖v-WTx‖22是为了确保去噪的保真性;第二项‖v‖0控制系数的稀疏性;约束条件WTW=I是为了保证W为紧框架。式(4)有两个未知变量,变换系数向量v和生成紧框架的字典矩阵滤波器组{ai}i=1m,采用迭代的方法交替更新系数向量v和{ai}i=1m,分为两个子问题进行循环求解[24-26]。
(1) 稀疏编码——固定W,求v
| $ {\mathit{\boldsymbol{v}}^{(k)}} = \arg \mathop {\min }\limits_\mathit{\boldsymbol{v}} \sigma _{\rm{n}}^2\parallel \mathit{\boldsymbol{v}}{\parallel _0} + \frac{1}{2}\left\| {\mathit{\boldsymbol{v}} - {{\left[ {{\mathit{\boldsymbol{W}}^{(k)}}} \right]}^{\rm{T}}}\mathit{\boldsymbol{x}}} \right\|_2^2 $ | (5) |
这一步可通过阈值法求解。
(2) 字典更新——固定v,求W
| $ \begin{array}{l} {\mathit{\boldsymbol{W}}^{(k + 1)}} = \arg \mathop {\min }\limits_\mathit{\boldsymbol{W}} \left\| {{\mathit{\boldsymbol{v}}^{(k)}} - {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{x}}} \right\|_2^2\\ {\rm{满足}}\;\;\;\;\;\;{\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{W}} = \mathit{\boldsymbol{I}} \end{array} $ | (6) |
这一步存在显式解。首先将vxT进行奇异值分解,即vxT=UDXT,则W(k+1)=XUT/r。其中U为m×m阶正交矩阵,其每一列为vxT(vxT)T的特征向量;X为r2×r2阶正交矩阵,其每一列为(vxT)T vxT的特征向量;D为m×r2阶对角阵,对角线上的元素是矩阵vxT的奇异值。
经过k次迭代后,适应于数据x的紧框架被定义为
| $ \boldsymbol{W}^{\mathrm{T}}\left[\boldsymbol{a}_{1}^{(k)}, \boldsymbol{a}_{2}^{(k)}, \cdots, \boldsymbol{a}_{m}^{(k)}\right] $ | (7) |
第一,计算地震数据x的噪声方差估计σn2;
第二,预设块大小为r×r、数量为r2(令m=r2)的紧框架滤波器组{ai(0)}i=1r2,并使用现有的紧框架条件进行初始化,滤波器的阈值由噪声方差估计σn2决定;
第三,通过{ai(k)}i=1r2定义W(k),令v(k)=Tσn2×[W(k)x],其中Tσn2为硬阈值算子,其值由噪声方差估计σn2确定;
第四,对vxT进行奇异值分解,得到W(k+1)=XUT/r,其中矩阵W(k+1)的第i个列向量为ai(k+1)。
对式(4)的优化流程如图 2所示。利用流程中求取的{ai(k)}i=1r2构成的滤波器组矩阵WT和变换系数向量v,对数据进行去噪处理。由于加入了噪声估计,该算法能够自适应地去除数据中的噪声,是一种盲去噪方法。
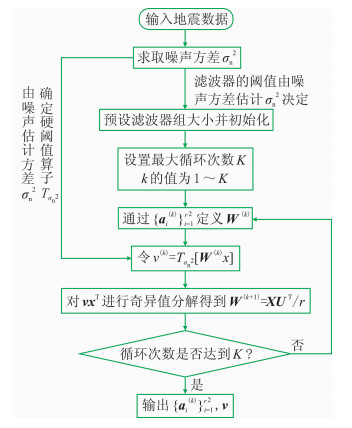
|
图 2 紧框架滤波器组构建流程 |
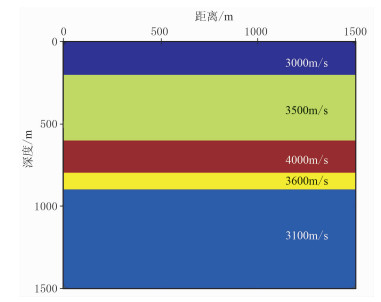
为了验证本文去噪算法的可行性和有效性,建立如图 3所示的速度模型。震源位于(750m,750m)处,在地表处接收,品质因子Q=50,采用黏声有限差分方法合成的微地震数据如图 4a所示。首先根据合成微地震数据中有效信号的能量加入噪声,含噪数据如图 4b所示,其信噪比大幅降低。为了对比数据驱动紧框架方法与传统去噪方法的去噪效果,首先对加噪数据进行曲波阈值去噪,结果如图 4c所示,图 4d为去除的噪声。然后采用数据驱动紧框架方法去噪,结果如图 4e所示,图 4f为去除的噪声。从图 4可以看出,经过曲波阈值去噪方法处理后,噪声虽然被压制,但是去噪剖面上引入背景斑块,部分有效信号被压制,去噪效果不理想;数据驱动紧框架方法的去噪剖面上噪声基本被压制,信噪比得到提升,残差剖面上基本没有有效信号的残留,说明本文方法在去噪的同时能够较好地保护有效信号。
|
图 3 速度模型 |
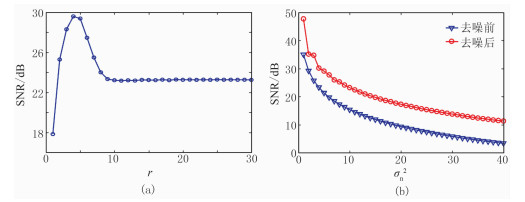
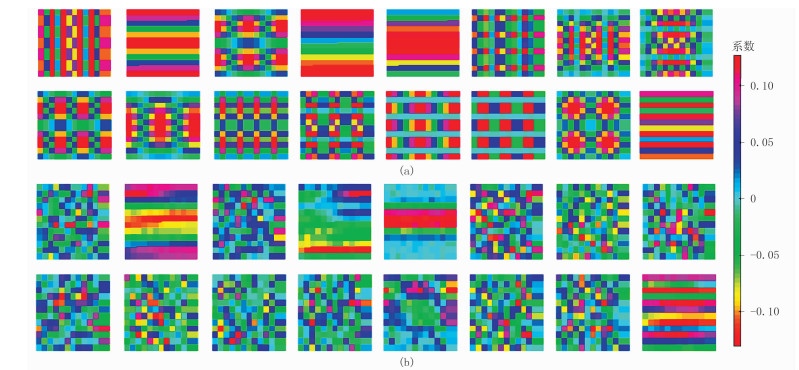
为了分析预设块参数r和噪声方差估计σn2对去噪效果的影响,对图 4所示数据使用不同的预设块参数和不同噪声方差的数据进行处理试验。图 5a为含噪数据中预设块参数r对去噪结果的影响分析,可以看出,随着r的增加,去噪结果信噪比(SNR)先增加后减小,并在10之后趋于平稳。所以,在进行去噪处理时,预设块的大小并不是越大越好,应当在合适范围内选取最优值。本模型试验在预设块参数r取值为4时,达到最高信噪比,当r超过9后,处理结果的信噪比趋于稳定。图 5b为加入不同方差噪声时去噪前、后的SNR结果对比,可以看出去噪后的SNR整体都有所提高。图 6为该模型数据处理过程中相应的滤波器组(只显示了144个中的16个),大小为12×12。图 6a为初始滤波器组,图 6b为训练后滤波器组,在滤波器组中显示了数据中细小的结构特征,与初始滤波器组相比训练后的滤波器组包含了从低频到高频的结构信息。

|
图 4 理论合成数据测试 (a)合成数据;(b)含噪数据;(c)曲波阈值法去噪结果;(d)曲波阈值法去除的噪声;(e)本文方法去噪结果;(f)本文方法去除的噪声 |
|
图 5 预设块参数r对去噪结果的影响分析(a)及不同噪声方差σn2条件下的去噪效果分析(b) |
|
图 6 训练前(a)、后(b)滤波器组 |
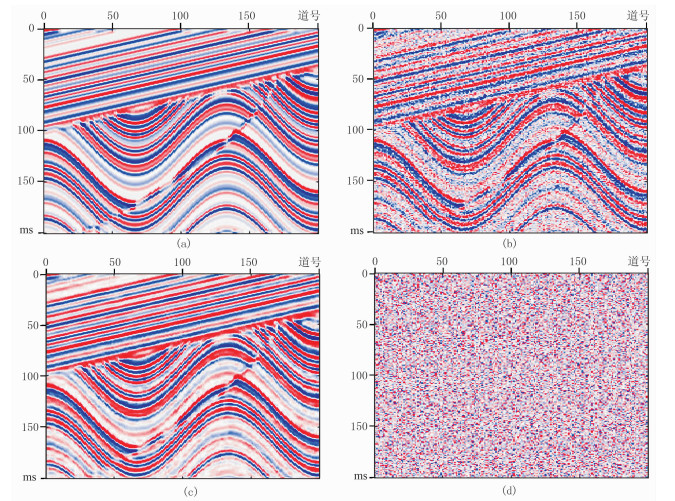
为了验证该方法对低信噪比复杂地震数据的应用效果,在图 7a所示的地震记录中加入噪声,得到图 7b所示数据。采用数据驱动紧框架去噪方法进行处理,结果如图 7c所示。可以看出,该方法可以有效地压制剖面中的随机噪声,同时能保护边缘处不连续性信息,断点及尖灭点处的同相轴没有发生畸变,弯曲同相轴处的能量也没有损失,说明该方法在弯曲同相轴以及断层等处具有较好的保边效果。
|
图 7 复杂数据模型处理效果 (a)合成数据;(b)加噪数据;(c)去噪结果;(d)去除的噪声 |
图 8为含噪数据和去噪数据的相干体属性和瞬时频率计算结果。从相干体属性图上可以看出,去噪前地震相干体剖面较为杂乱,难以识别断层和岩性突变点,去噪后这些信息可以从剖面中拾取。从瞬时频率属性图上可以看出,去噪处理后瞬时频率得到了平滑,较好地压制了毛刺现象。

|
图 8 复杂数据模型去噪效果分析 (a)去噪前相干体属性;(b)去噪后相干体属性;(c)去噪前瞬时频率;(d)去噪后瞬时频率 |
为了验证本文方法对实际地面微地震监测数据的应用效果,对实测的微震监测数据进行处理。图 9a为原始微地震资料,有效信号完全淹没在随机噪声中,各道间的相关性较差,难以有效地拾取到有效信息,严重影响反演结果的可靠性。采用数据驱动紧框架方法进行去噪处理,结果如图 9b所示,可见去噪后的剖面中背景噪声得到了有效的压制,连续性较好,信噪比显著提高,可以清晰地得到微震事件的波形,提高旅行时拾取的精度,为震源定位提供有效数据。图 9c为去除的噪声,去除的噪声中没有掺杂有效信号,有效信息得到了很好的保留。

|
图 9 实际微地震数据压噪结果 (a)原始数据;(b)去噪后结果;(c)去除的噪声 |
图 10a为原始微地震记录单道时频分布,图 10b为去噪后的单道时频分布,可以明显看出:在去噪前的时频分布中有效信号(图 10a红色箭头所示)的能量较弱,噪声能量强,有效信号被淹没在噪声中,很难识别;去噪处理后,噪声得到很好的压制,突出了有效信号(图 10b红色箭头所示),有效提高了微地震数据的信噪比,在时频图中更易识别微地震事件,保障了较高的微地震事件初至拾取精度和定位准确度。

|
图 10 实际微地震数据压噪前(a)、后(b)单道时频分布 |
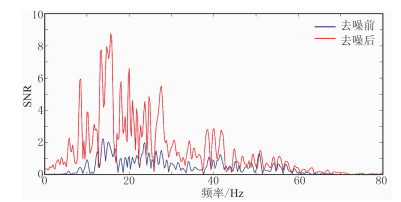
图 11为微地震记录单道信噪比谱,可见,去噪之后数据的信噪比要明显大于去噪前的数据,尤其在中、低频区信噪比提升显著。
|
图 11 实际微地震记录去噪前、后信噪比谱 |
本文研究了基于数据驱动紧框架方法在地面微地震随机噪声压制中的应用。通过理论模型及实际资料的处理结果得到如下的结论与认识。
(1) 地面微地震监测数据噪声干扰严重、信噪比低,制约着地面微地震监测技术的应用,基于自适应数据驱动紧框架的去噪方法能够根据微地震数据中的噪声方差,对微地震数据中的噪声进行有效的压制,实现对微地震数据信噪比的有效提升,有助于后续的微地震数据处理。
(2) 稀疏表示方法假设原始数据的方差已知,且方差的微小变化会对去噪结果产生较大的影响,需要解决方差的选取问题,基于弱纹理块的噪声估计结果优于小波分解估计。
(3) 数据驱动紧框架方法具有多分辨率性质和冗余性质,应用于去噪处理,既能够显著提高地震资料的信噪比,同时也能够有效保护有效信号,特别是对于复杂构造地区,该方法能充分保留地震资料中的不连续性信息。对实际微地震数据去噪后可以清晰地得到微震事件的波形,提高旅行时拾取的精度,为微地震震源精确定位奠定基础。
| [1] |
唐杰, 温雷, 王浩, 等. 正交各向异性介质中的剪张源震源机制与矩张量特征研究[J]. 石油地球物理勘探, 2018, 53(6): 1247-1255. TANG Jie, WEN Lei, WANG Hao, et al. Focal mechanisms and moment tensor in orthorhombic anisotropic media[J]. Oil Geophysical Prospecting, 2018, 53(6): 1247-1255. |
| [2] |
唐杰, 王浩, 温雷, 等. 剪张型微地震震源机制与振幅分布特征[J]. 石油地球物理勘探, 2018, 53(3): 502-510. TANG Jie, WANG Hao, WEN Lei, et al. Focal me-chanism of shear-tensile microseismic and amplitude distribution characteristics[J]. Oil Geophysical Prospecting, 2018, 53(3): 502-510. |
| [3] |
谭玉阳, 于静, 冯刚. 微地震事件初至拾取SLPEA算法[J]. 地球物理学报, 2016, 59(1): 185-196. TAN Yuyang, YU Jing, FENG Gang. Arrival picking of microseismic events using the SLPEA algorithm[J]. Chinese Journal of Geophysics, 2016, 59(1): 185-196. |
| [4] |
宋维琪, 刘太伟. 地面微地震资料τ-p变换噪声压制[J]. 石油地球物理勘探, 2015, 50(1): 48-53. SONG Weiqi, LIU Taiwei. Surface microseismic noise suppression with τ-p transform[J]. Oil Geophysical Prospecting, 2015, 50(1): 48-53. |
| [5] |
朱卫星, 宋维琪, 修金磊, 等. 微地震信号的偏振-位置对比法震相分离技术[J]. 石油地球物理勘探, 2009, 44(4): 425-429. ZHU Weixing, SONG Weiqi, XIU Jinlei, et al. Seismic phase separation technique of micro-seismic signal by polarization-position correlation[J]. Oil Geophysical Prospecting, 2009, 44(4): 425-429. DOI:10.3321/j.issn:1000-7210.2009.04.008 |
| [6] |
孙成禹, 邵婕, 蓝阳. 基于独立分量分析基的地震随机噪声压制[J]. 石油物探, 2016, 55(2): 196-204. SUN Chengyu, SHAO Jie, LAN Yang. Seismic random noise suppression based on independent component analysis basis functions[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 196-204. DOI:10.3969/j.issn.1000-1441.2016.02.005 |
| [7] |
宋维琪, 李艳清, 刘磊. 独立分量分析与压缩感知微地震弱信号提取方法[J]. 石油地球物理勘探, 2017, 52(5): 984-989. SONG Weiqi, LI Yanqing, LIU Lei. Microseismic weak signal extraction based on the independent component analysis and compressive sensing[J]. Oil Geophysical Prospecting, 2017, 52(5): 984-989. |
| [8] |
曹俊海, 顾汉明, 尚新民. 基于局部相关谱约束的多道匹配追踪算法识别微地震信号[J]. 石油地球物理勘探, 2017, 52(4): 704-714. CAO Junhai, GU Hanming, SHANG Xinmin. Microseismic signal identification with multichannel ma-tching pursuit based on local coherence spectrum constraint[J]. Oil Geophysical Prospecting, 2017, 52(4): 704-714. |
| [9] |
Mousavi M, Langston C A, Horton S P. Automatic microseismic denoising and onset detection using the synchrosqueezed continuous wavelet transform[J]. Geophysics, 2016, 81(4): V341-V355. DOI:10.1190/geo2015-0598.1 |
| [10] |
李会俭, 王润秋, 曹思远, 等. 利用多尺度形态学识别微地震监测中的弱信号[J]. 石油地球物理勘探, 2015, 50(6): 1105-1111. LI Huijian, WANG Runqiu, CAO Siyuan, et al. Weak signal identification in microseismic monitoring with multi-scale morphology[J]. Oil Geophysical Prospecting, 2015, 50(6): 1105-1111. |
| [11] |
邵婕, 孙成禹, 唐杰, 等. 基于字典训练的小波域稀疏表示微地震去噪方法[J]. 石油地球物理勘探, 2016, 51(2): 254-260. SHAO Jie, SUN Chengyu, TANG Jie, et al. Micro-seismic data denoising based on sparse representations over learned dictionary in the wavelet domain[J]. Oil Geophysical Prospecting, 2016, 51(2): 254-260. |
| [12] |
姜宇东, 宋维琪, 郭晓中, 等. 地面微地震监测资料静校正方法研究[J]. 石油物探, 2013, 52(2): 136-154. JIANG Yudong, SONG Weiqi, GUO Xiaozhong, et al. Static correction method for surface microseismic monitoring data[J]. Geophysical Prospecting for Petro-leum, 2013, 52(2): 136-140. DOI:10.3969/j.issn.1000-1441.2013.02.004 |
| [13] |
Zhang C, van der Baan M. Multicomponent microseismic data denoising by 3D shearlet transform[J]. Geophysics, 2018, 83(3): A45-A51. DOI:10.1190/geo2017-0788.1 |
| [14] |
李稳, 刘伊克, 刘保金. 基于稀疏分布特征的井下微地震信号识别与提取方法[J]. 地球物理学报, 2016, 59(10): 3869-3882. LI Wen, LIU Yike, LIU Baojin. Downhole microseismic signal recognition and extraction based on sparse distribution features[J]. Chinese Journal of Geophysics, 2016, 59(10): 3869-3882. DOI:10.6038/cjg20161030 |
| [15] |
Tang G, Ma J W, Yang H Z. Seismic data denoising based on learning-type overcomplete dictionaries[J]. Applied Geophysics, 2012, 9(1): 27-32. DOI:10.1007/s11770-012-0310-z |
| [16] |
Chen Y, Ma J, Fomel S. Double sparsity dictionary forseismic noise attenuation[J]. Geophysics, 2016, 81(2): V103-V106. DOI:10.1190/geo2014-0525.1 |
| [17] |
Liang J, Ma J, Zhang X. Seismic data restoration via data-driven tight frame[J]. Geophysics, 2014, 79(3): V65-V74. DOI:10.1190/geo2013-0252.1 |
| [18] |
Zou H, Hastie T, Tibshirani R. Sparse principal component analysis[J]. Journal of Computational and Graphical Statistics, 2006, 15(2): 265-286. DOI:10.1198/106186006X113430 |
| [19] |
Pyatykh S, Hesser J, Zheng L. Image noise level estimation by principal component analysis[J]. IEEE Transactions on Image Processing, 2013, 22(2): 687-699. DOI:10.1109/TIP.2012.2221728 |
| [20] |
Daniel Z, Yair W.Scale invariance and noise innatural images[C]. 2009 IEEE 12th International Conference on Computer Vision, 2009, 2209-2216.
|
| [21] |
Liu X, Tanaka M, Okutomi M. Single-image noise le-vel estimation for blind denoising[J]. IEEE Transactions on Image Processing, 2013, 22(12): 5226-5237. DOI:10.1109/TIP.2013.2283400 |
| [22] |
Cai J F, Ji H, Shen Z, et al. Data-driven tight frame construction and image denoising[J]. Applied & Computational Harmonic Analysis, 2014, 37(1): 89-105. |
| [23] |
Yu S, Ma J, Zhang X, et al. Interpolation and denoising of high-dimensional seismic data by learning tight frame[J]. Geophysics, 2015, 80(5): V119-V132. DOI:10.1190/geo2014-0396.1 |
| [24] |
Daubechies I, Han B, Ron A, et al. Framelets:MRA-based constructions of wavelet frames[J]. Applied & Computational Harmonic Analysis, 2003, 14(1): 1-46. |
| [25] |
Cai J F, Ji H, Liu C, et al.Blind motion deblurring from a single image using sparse approximation[C]. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2009, 104-111.
|
| [26] |
Cai J F, Dong B, Osher S, et al. Image restoration:Total variation, wavelet frames, and beyond[J]. Journal of the American Mathematical Society, 2012, 25(4): 1033-1089. DOI:10.1090/S0894-0347-2012-00740-1 |
| [27] |
Chui C K, He W, Stöckler J. Compactly supported tight and sibling frames with maximum vanishing moments[J]. Applied & Computational Harmonic Analysis, 2002, 13(3): 224-262. |
| [28] |
Ma J. Three-dimensional irregular seismic data recon-struction via low-rank matrix completion[J]. Geophysics, 2013, 78(5): V181-V192. DOI:10.1190/geo2012-0465.1 |



 唐杰, 山东省青岛市长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
唐杰, 山东省青岛市长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: