在本世纪初,地球物理工作者就提出宽方位采集概念并逐步尝试。早在2003年前,凌云研究小组[1]通过对中国西部宽方位资料的研究,认为宽方位角地震勘探在岩性和方向性裂缝勘探领域具有广阔应用前景。受当时设备条件和成本限制,宽方位高密度采集技术的推广举步维艰。凌云等[2]进一步分析了在上覆地层相对平缓、资料具有一定信噪比的情况下,宽方位比窄方位三维采集能获得更高成像分辨率资料,并不需很高覆盖次数,如60~80次。也有其他地球物理工作者根据中国东部滩海地区特点构建地质模型,对比宽方位与窄方位三维采集正演模拟资料,在上覆地层相对平缓、速度横向变化不大的背景下,宽方位和窄方位三维采集都能实现地下目标可信的地震成像,且两者的成像分辨率基本相当[3]。此阶段地震资料评价仅限于成像效果,且前提是地质条件简单的较高信噪比资料。
自从第七代十万道级地震仪诞生后,“两宽一高”地震采集技术、高效采集技术才真正得到推广应用[4]。如在塔里木[5]、柴达木[6]、渤海湾[7]、准噶尔[8]、大庆[9]、吐哈[10]以及乍得邦戈[11]等盆地或地区都取得了较好应用效果。
宽方位采集技术也促进了处理、解释技术的发展,如催生了面向宽方位地震数据的炮检距向量片(OVT)处理技术[5]、宽方位角地震资料噪声压制技术[12]、宽方位层析速度建模技术、深度域成像技术[13]和针对断层的“两宽一高”地震资料[14]处理—解释配套技术,这些技术日臻完善并被推广应用。同时,宽方位高密度处理、解释技术的进步也反推“两宽一高”现场数据采集技术的逐步完善。
高密度宽方位采集技术是当今石油物探采集领域重要的方法创新,以此集成的“高密度宽方位地震勘探技术创新及重大成效”成功入选了2015~2016年“中国石油石化科技创新十大进展”。
宽方位地震采集的目的是获取观测方位、炮检距和覆盖次数分布尽可能均匀的三维数据体,但宽方位高密度观测必然会带来现场采集成本的大量增加。因此,研究高效便捷、经济实用的观测系统及相应的采集方法,就成为宽方位高密度地震采集设计的核心理念[15],而其中三维排列片尺寸及其纵横比的设计显得尤为重要。
Cordsen等[16]给出了一种“折中”方法,这就是一直指导大家进行三维地震勘探观测系统设计的“85%法则”——排列片纵向长度选择为最大炮检距长度的85%,横向长度又选择为纵向长度的85%。李庆忠[17]随后指出“Andreas Cordsen主张排列片的最佳纵、横比为85%,而没有深入讨论其缺点”,显然此处的“缺点”有更宽泛的地球物理内涵。然而,Cordsen等二十多年前提出的85%法则,至今尚未见到有人深入分析其合理性并详细论证何种排列片才是更经济高效的?
本文质疑依据85%法则设计出来的排列片是否就是最佳排列片?进而探讨是否还有其他更佳方案或能否给设计者更大的选择自由度?因此,本文基于数学积分计算,得到基于最大炮检距限制的有效和无效地震采集信息及其相对变化信息随排列片纵、横长度的函数关系,生成函数图像;通过研究函数图像,提供有助于三维观测系统设计的系列图表。在数学推导过程中,剖析了Cordsen的“85%法则”;提供了设定三维观测系统排列尺寸和横纵比更理想的方案。
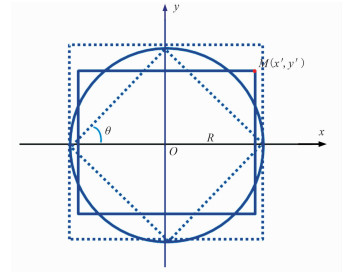
1 数学模型排列片通常纵向选为x方向、横向为y方向,取排列片中心为原点,建立直角坐标系。以论证的最大炮检距为半径(R)画圆,圆心与坐标原点重合(图 1)。
|
图 1 通用数学模型 |
在三维采集设计时,根据动校拉伸限制、反射系数稳定性、主要目的层埋藏深度和实际资料效果分析等方面论证设定最大炮检距。大于最大炮检距的地震信号,由于动校拉伸畸变等原因,无益于偏移叠加成像,也会造成反射系数不稳定,在后期资料处理时常须切除大于最大炮检距的信息。定义大于论证最大炮检距的地震道信息为“无效信息”,小于最大炮检距地震道信息为“有效信息”。
结合数学模型(图 1),排列片在圆内部分接收道为采集有效信息,圆外部分接收道为无效信息。排列片右上角M点坐标为M(x′,y′),该坐标值决定了排列片尺寸和横纵比,即纵向最大炮检距、横向最大炮检距及其比值。M(x′,y′)变化会引起采集有效信息和无效信息的面积变化。为研究方便,选取最大炮检距长度R为单位1,则M(x′,y′)坐标即为排列片纵、横向炮检距与论证最大炮检距的比值(倍数)。
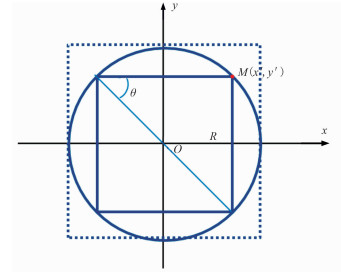
2 数学分析 2.1 坐标点M(x′,y′)在圆内或圆周上从图 2可知,坐标点M(x′,y′)在外接圆内和圆周上时,采集到的数据都是有效炮检距信息。考察圆周上四个点,它们构成的矩形的面积为
| $ S_{\mathrm{rect}}=2 R \sin \theta \times 2 R \cos \theta=2 R^{2} \sin 2 \theta $ | (1) |
|
图 2 点在圆周上的矩形排列片数学模型 |
当θ=45°时,排列片为正方形,M(x′,y′)点坐标为
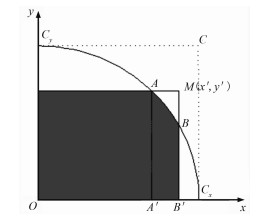
坐标点在圆内移动,最大采集面积仅为圆面积的64%,这显然是不够的。希望在圆外寻找合适点,使采集的有效信息(灰色面积)尽可能地多,无效信息(ABM)尽可能少(图 3)。当x′,y′大于1(R)时,增加的均为无效信息,故坐标点M(x′,y′)取值范围应在圆外、且在正方形OCxCCy之内区域。较合理的数学方程式是以(x′,y′)为自变量,以有效信息面积Sv和无效信息面积Sinv及其间的差值Sv-inv、比值Sinv/v为因变量,建立二元函数关系,分析随M点变化时有效信息和无效信息的变化规律。因四个象限是对称的,故只需研究第一象限即可。
|
图 3 点在圆外的矩形排列片数学模型 |
由几何关系可知,A点坐标为
| $ \begin{aligned} S_{\text {inv }} &=\int_{\sqrt{1-y^{2}}}^{x^{\prime}}\left(y^{\prime}-\sqrt{1-x^{2}}\right) \mathrm{d} x \\ &=x^{\prime} y^{\prime}-\frac{x^{\prime} \sqrt{1-x^{2}}}{2}-\frac{y^{\prime} \sqrt{1-y^{2}}}{2}-\\ & \frac{\arcsin x^{\prime}}{2}+\frac{\arcsin \sqrt{1-y^{2}}}{2} \end{aligned} $ | (2) |
有效信息面积为
| $ \begin{array}{l} {S_{\rm{v}}} = {x^\prime }{y^\prime } - {S_{{\rm{inv}}}} = \frac{{{x^\prime }\sqrt {1 - {x^2}} }}{2} + \frac{{{y^\prime }\sqrt {1 - {y^2}} }}{2} + \\ \frac{{\arcsin {x^\prime }}}{2} - \frac{{\arcsin \sqrt {1 - {y^2}} }}{2} \end{array} $ | (3) |
有效信息面积减去无效信息面积,可得
| $ \begin{aligned} S_{\text {v-inv}}=& x^{\prime} y^{\prime}-2 S_{\text {inv }}=x^{\prime} \sqrt{1-x^{2}}+y^{\prime} \sqrt{1-y^{2}}+\\ & \arcsin x^{\prime}-\arcsin \sqrt{1-y^{\prime}}-x^{\prime} y^{\prime} \end{aligned} $ | (4) |
式(2)反映了M点位置变化引起的无效信息面积变化;式(3)反映了M点位置变化引起的有效信息面积变化;式(4)反映M点位置变化有效信息面积与无效信息面积相互关系的变化。这三个函数式较为复杂,很难用求导法或极值法等数学手段了解它们随M点移动的变化规律。随后分析函数值随M点的移动的空间变化规律。为了表达方便,以下文(图表)中x′,y′均用x、y代替。
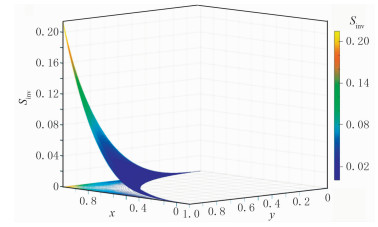
2.3 数据分析图 4为无效信息面积Sinv变化函数图,邻近圆周的点的Sinv值接近0或非常小;随着M点远离原点O,无效信息急剧增加,且沿OC方向移动,增加速度最慢,OC是Sinv图形下凹轴线。
|
图 4 无效信息面积变化函数图 |
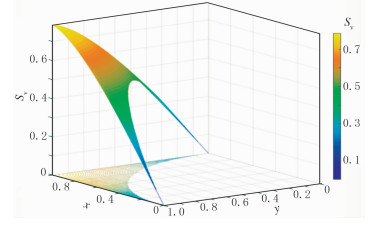
图 5为有效信息面积Sv函数图,M点在x轴或y轴上时面积为0,随着远离坐标轴面积迅速增加。与图 4相反,Sv是个上凸形状,OC为高点轴线。但随着M点接近C点,Sv增加变慢。M点在圆周上移动时,射线OC与圆交点处有效信息面积最大,佐证了2.1节结论。
|
图 5 有效信息面积变化函数图 |
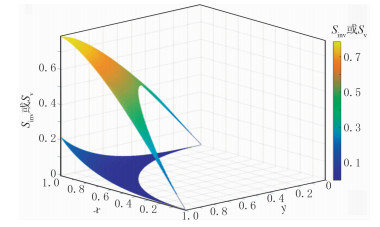
图 6是无效信息与有效信息面积函数叠合图,在轴线部位Sinv表现为向下凹,Sv表现为上凸。这为M点最佳位置选择提供了思路。
|
图 6 无效信息与有效信息面积变化叠合图 |
图 7是据式(4)得到的Sv-inv函数图,可见并不是M点移动到C点函数达到极大值;连接OC,从与圆周的交点到C点,考察函数Sv-inv在OC向的方向导数,数值由大逐渐变小,至“0”,再到负值。函数在OC向的方向导数巧妙地反映了有效信息与无效信息相对空间变化。随着远离中心点,有效信息面积虽然持续增加,但增加的“加速度”逐渐减小,且在到达极值点前比无效信息面积增加的快;再往C点方向移动,有效信息面积增加逐渐变慢,无效信息面积的增加却逐渐加快;在达到最大值时,有效信息面积增量与无效信息面积增量相同,极值点附近区域都是函数值变化平缓带;从极值点到C点,为无效信息面积增量大于有效信息面积增量的区域。
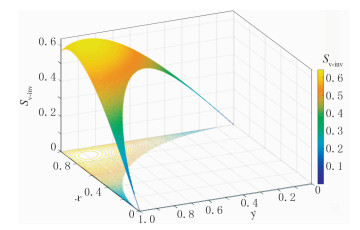
|
图 7 有效信息面积与无效信息面积差函数(Sv-inv)图 |
图 8是函数Sv-inv数值的等高线平面图,反映了函数Sv-inv空间梯度变化。连接对角线OC,发现等高线是关于OC轴对称的,在趋向极大值点前,沿着OC方向等高线最密,也是函数Sv-inv增长最快的方向。
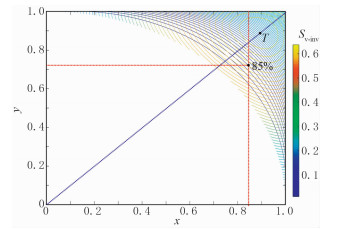
|
图 8 Sv-inv函数等高线平面图 |
三维地震采集排列片横、纵参数包括排列片横、纵长度和横纵比两个方面。由2.3节分析可知,M点应选择在图 8等高线最密处,有效信息面积增加速度远大于无效信息面积增加速度;极值对应的点为T(0.895,0.895)。当设计排列片的纵、横向炮检距大于该极值点坐标时,有效信息面积增加速度迅速减小、而无效信息面积迅速增大。因此,设计时应尽量避免使纵、横向炮检距大于论证的最大炮检距的0.895倍,点T也被称为90拐点。
Cordsen等提出的85%法则在图 8中如红线交点所示,排列参数对应的Sv =0.5999,Sinv=0.0142,Sv-inv=0.5857。排列片有效面积相对于R圆面积为4Sv/π=76.4%,该比值并不等于Cordsen等提出的78%[16],而85%法则点和原点构成的矩形面积与四分之一圆面积比为0.85×0.852/(π/4)=78%,该比值显然包含了无效信息的面积,可见Cordsen在提出85%法则时,并没有经过严谨的微积分计算;其所有数值都是基于几何学关系近似求得,“85%法则”虽然较为理想,但数学论证并不充分、系统。
当M点移动至C点时,排列片相当于最大炮检距半径圆的外接正方形(图 2),这时Sv=0.785,Sinv=0.215,则Sv-inv=0.570,排列片无效信息面积相对于R圆面积为4Sinv/π=27%。
除27%无效信息面积外,外接正方形排列片还存在一个隐形的无效信息面积,即当接收线距较大时,最外边的第一条排列与圆相切的有效信息只有一道,而这一道占据了第二条排列与圆弧(切点)构成的有效信息面积。造成实际的无效信息与R圆面积之比大于27%的情况。接收线距越小,比值越接近27%。
因此,排列片长和宽不应大于论证的最大炮检距的0.895倍(M点没超出T点与坐标轴构成矩形的范围)。
用面积绝对差值函数还不能直接反映无效信息相对于有效信息面积大小。图 9是无效信息面积除以有效信息面积函数Sinv/v的函数值空间分布图。与Sinv图像有些相似,反映出在M点移动过程中,无效信息面积变化影响函数Sinv/v较大。
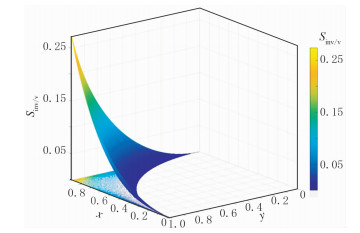
|
图 9 Sinv/v函数图 |
将Sv-inv函数等高线与Sinv/v函数等高线叠合起来(图 10),取名为排列片横纵参数量板,图中蓝线为Sinv/v函数等值线,色标值为Sv-inv值(为显示效果,图件在前文等高线图基础上抽稀一半)。为最大限度增加有效信息面积和减少无效信息面积,M点最佳选择区域应为Sv-inv等值线密集且穿越Sinv/v(蓝)函数等值线值尽可能小、线数尽可能少的区域,即理想区域是等高线与OC交点附近(T点前),最佳位置点在等值线与OC交点上。
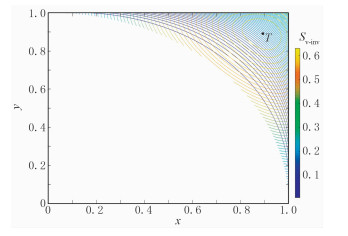
|
图 10 排列片横纵参数量板 |
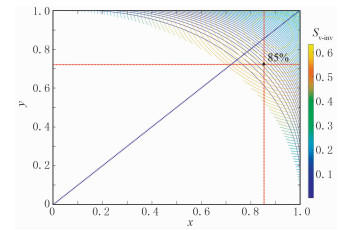
图 11在量板上标注了85%法则点对应的M点位置,可见85%法则虽较为理想,但不是最经济的,沿0.5858等值线靠近OC线,都是不错的选择。
|
图 11 Sinv/v(蓝)与Sv-inv函数等高线叠合图 |
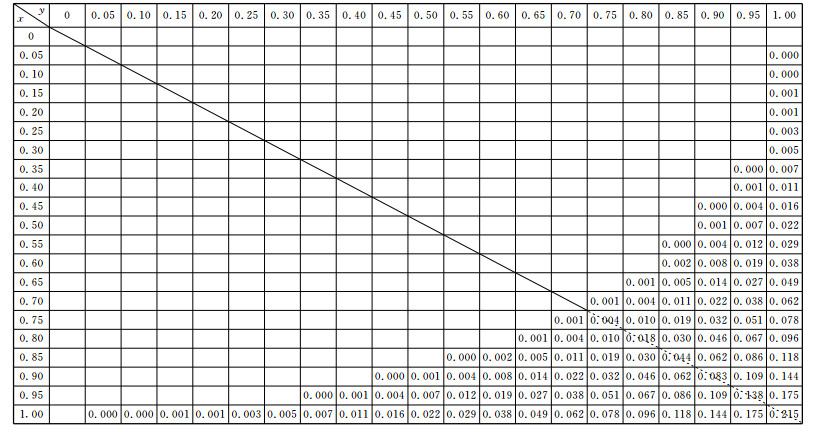
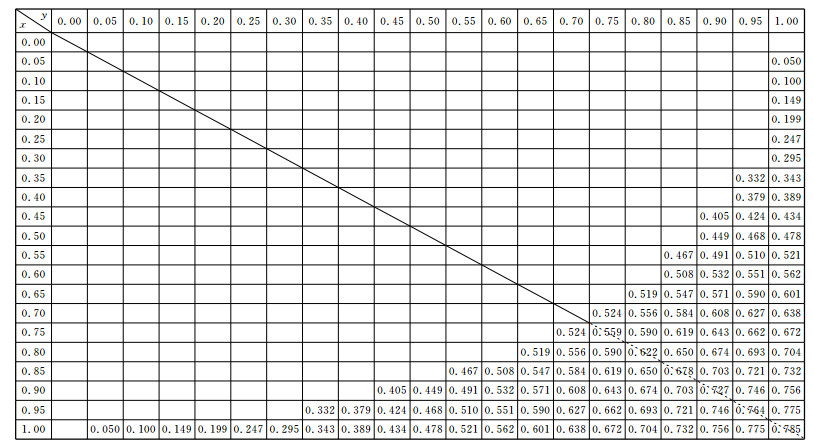
结合排列片横纵参数量板,提供两个表格供三维设计参考,表 1是空间20×20个样点的无效信息面积Sinv真值表,对角线连线即为OC连线,对角线上真值都较左右数值小;表 2为有效信息面积Sv真值表,对角线上真值都较左右数值大。所以,观测系统设计从经济效益来说,沿对角线是最佳选择,这时排列片横纵比为1。实际应用中,结合勘探地质任务和设备条件,可在对角线附近数值差别不大范围内选择排列片横、纵长度和比例。
|
|
表 1 无效信息面积Sinv真值表 |
|
|
表 2 有效信息面积Sv真值表 |
在实际运用中,还可以根据式(2)~式(4)制作更加精细表格和不同精度的量板。
4 结束语在观测系统设计时,一方面考虑尽可能多地获取各个方位的有效炮检距信息,另一方面还要考虑尽可能减少大于有效炮检距的道数所占的比例。Cordsen给出了观测系统设计的双“85%”法则,但未给出严格的论证。数学计算证明,只要纵横向最大炮检距小于设计的最大炮检距的0.895倍,就可以达到既尽可能多地获取有效信息又最大程度减少无效信息的目的。所提供的“一板二表”是三维观测系统设计的经济效益参考指标,对宽方位高密度观测系统设计具有一定的指导作用。通过分析也说明,在“两宽一高”实施中,如果纵、横向最大炮检距均取为工区论证的最大炮检距,横纵比选为1,至少27%的采集信息都是无效信息,从经济效益角度考虑是不科学的。
| [1] |
凌云研究小组. 宽方位角地震勘探应用研究[J]. 石油地球物理勘探, 2003, 38(4): 350-357. LING Yun Study Group. Application and study on wide-azimuth seismic ploration[J]. Oil Geophysical Prospecting, 2003, 38(4): 350-357. DOI:10.3321/j.issn:1000-7210.2003.04.003 |
| [2] |
凌云, 高军, 孙德胜, 等. 宽/窄方位角勘探实例分析与评价(一)[J]. 石油地球物理勘探, 2005, 40(3): 305-308. LING Yun, GAO Jun, SUN Desheng, et al. Analysis and appreciation of wide/narrow azimuth exploration cases(Ⅰ)[J]. Oil Geophysical Prospecting, 2005, 40(3): 305-308. DOI:10.3321/j.issn:1000-7210.2005.03.018 |
| [3] |
狄帮让, 孙作兴, 顾培成, 等. 宽/窄方位三维观测系统对地震成像的影响分析——基于地震物理模拟的采集方法研究[J]. 石油地球物理勘探, 2007, 42(1): 1-6. DI Bangrang, SUN Zuoxing, GU Peicheng, et al. Analysis of influence of 3-D wide/narrow geometry on seismic imaging (1):Acquisition study based on seismic physical simulation[J]. Oil Geophysical Prospecting, 2007, 42(1): 1-6. DOI:10.3321/j.issn:1000-7210.2007.01.002 |
| [4] |
刘振武, 撒利明, 董世泰, 等. 地震数据采集核心装备现状及发展方向[J]. 石油地球物理勘探, 2013, 48(4): 663-675. LIU Zhenwu, SA Liming, DONG Shitai, et al. Current status of kernel seismic acquisition equipment and its development direction[J]. Oil Geophysical Prospecting, 2013, 48(4): 663-675. |
| [5] |
段文胜, 李飞, 王彦春, 等. 面向宽方位地震处理的炮检距向量片技术[J]. 石油地球物理勘探, 2013, 48(2): 206-213. DUAN Wensheng, LI Fei, WANG Yanchun, et al. Offset vector tile for wide-azimuth seismic processing[J]. Oil Geophysical Prospecting, 2013, 48(2): 206-213. |
| [6] |
杨柳, 沈亚, 管俊亚, 等. 多维数据裂缝检测技术探索及应用[J]. 石油地球物理勘探, 2016, 51(增刊1): 58-63. YANG Liu, SHEN Ya, GUAN Junya, et al. Fracture detection based on multi-dimension data[J]. Oil Geophysical Prospecting, 2016, 51(S1): 58-63. |
| [7] |
白辰阳, 张保庆, 耿玮, 等. 多方位地震数据联合解释技术在KN复杂断裂系统识别和储层描述中的应用[J]. 石油地球物理勘探, 2015, 50(2): 351-356. BAI Chenyang, ZHANG Baoqing, GENG Wei, et al. Complex fault system identification and reservoir characterization in KN area with multi-azimuth seismic data cubes[J]. Oil Geophysical Prospecting, 2015, 50(2): 351-356. |
| [8] |
林娟, 娄兵, 张淑萍, 等. 准噶尔盆地玛湖1井区高密度三维OVT域裂缝预测的应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 146-152. LIN Juan, LOU Bing, ZHANG Shuping, et al. Fracture prediction with the high-density 3D OVT domain in the Well Mahu 1 area, Junggar Basin[J]. Oil Geophysical Prospecting, 2017, 52(S2): 146-152. |
| [9] |
丁吉丰, 裴江云, 包燚, 等. "两宽一高"资料处理技术在大庆油田的应用[J]. 石油地球物理勘探, 2017, 52(增刊1): 10-16. DING Jifeng, PEI Jiangyun, BAO Yi, et al. Broadband, wide-azimuth and high-density (BWH) seismic data processing technology in Daqing Oilfield[J]. Oil Geophysical Prospecting, 2017, 52(S1): 10-16. |
| [10] |
冉建斌, 张明玉, 李海银, 等. "两宽一高"三维地震资料的纵向分辨率探讨及应用[J]. 石油地球物理勘探, 2018, 53(3): 520-527. RAN Jianbin, ZHANG Mingyu, LI Haiyin, et al. Vertical resolution of broadband, wide-azimuth and high-density seismic data[J]. Oil Geophysical Prospecting, 2018, 53(3): 520-527. |
| [11] |
王景春, 窦立荣, 徐建国, 等. "两宽一高"地震资料在花岗岩潜山储层表征中的应用[J]. 石油地球物理勘探, 2018, 53(2): 320-329. WANG Jingchun, DOU Lirong, XU Jianguo, et al. Granitic buried-hill reservoir characterization based on broadband, wide-azimuth and high-density seismic data:A case study of Bangor Basin in Chad[J]. Oil Geophysical Prospecting, 2018, 53(2): 320-329. |
| [12] |
田彦灿, 王西文, 彭更新, 等. 宽方位角地震噪声压制技术[J]. 石油地球物理勘探, 2013, 48(2): 187-191. TIAN Yancan, WANG Xiwen, PENG Gengxin, et al. Noise attenuation technology on wide azimuth seismic data[J]. Oil Geophysical Prospecting, 2013, 48(2): 187-191. |
| [13] |
段文胜, 李飞, 黄录忠, 等. OVT域宽方位层析速度建模与深度域成像[J]. 石油地球物理勘探, 2016, 51(3): 521-528. DUAN Wensheng, LI Fei, HUANG Luzhong, et al. Wide azimuth tomographic velocity model building and depth imaging in the OVT domain[J]. Oil Geophysical Prospecting, 2016, 51(3): 521-528. |
| [14] |
汪关妹, 周赏, 张宏伟, 等. "两宽一高"地震资料的断层解释技术[J]. 石油地球物理勘探, 2017, 52(增刊1): 77-83. WANG Guanmei, ZHOU Shang, ZHANG Hongwei, et al. Fault interpretation on broadband, wide-azimuth, and high-density (BWH) 3D seismic data[J]. Oil Geophysical Prospecting, 2017, 52(S1): 77-83. |
| [15] |
刘依谋, 印兴耀, 张三元, 等. 宽方位地震勘探技术新进展[J]. 石油地球物理勘探, 2014, 49(3): 596-610. LIU Yimou, YIN Xingyao, ZHANG Sanyuan, et al. Recent advances in wide-azimuth seismic exploration[J]. Oil Geophysical Prospecting, 2014, 49(3): 596-610. |
| [16] |
Cordsen A, Peirce J W著; 俞寿朋译.陆上三维地震勘探的设计与施工[M].河北涿州: 石油地球物理勘探局, 1996, 51-53.
|
| [17] |
李庆忠. 对宽方位角三维采集不要盲从——到底什么叫"全三维采集"[J]. 石油地球物理勘探, 2001, 36(1): 122-124. LI Qingzhong. Don't follow blindly wide azimuth 3-D acquisition-what on earth is "full 3-D acquisition"?[J]. Oil Geophysical Prospecting, 2001, 36(1): 122-124. DOI:10.3321/j.issn:1000-7210.2001.01.018 |



 张华, 河北省涿州市华阳东路东方地球物理公司科技园采集技术中心, 072751。Email:
张华, 河北省涿州市华阳东路东方地球物理公司科技园采集技术中心, 072751。Email: