② 中南大学地球科学与信息物理学院, 湖南长沙 410083
② School of Geosciences and Info-Physics, Central South University, Changsha, Hunan 410083, China
直流电阻率法是资源和工程勘探中广泛应用的一种地球物理方法[1-5]。有限单元法能够精细刻画地下真实的复杂地质体,且计算精度高,因而受到广泛关注[6-11]。区域剖分是有限单元法计算的重要环节,直接影响计算结果。传统的结构化网格难以解决构造复杂模型边界及解决源场的奇异性问题,往往造成较大的视电阻率误差[12-13]。为获得更精确的结果,必须以增加网格为代价,这无疑会成倍地增加计算量及内存需求。非结构化网格通过网格加密技术在关注区域(如场源、观测点、异常体、地形)进行网格细化,可以有效地处理异常体边界及场源点的奇异性问题,进而得到更为精确的解[14]。
采用有限阶精度的插值函数进行有限单元正演时,网格越精细得到的结果往往越精确,然而这样无疑增加了反演的不适定性。通过网格数量与质量的控制可以有效增加反演的稳定性[15]。在地震弹性波层析成像中,基于单元所通过的射线数量进行网格优化的技术得到了应用[16];通过组合具有相似物性的邻近单元以减少单元数量的技术,提高了医学中电阻率图像重建的质量[17];非线性反演中,基于灵敏度信息的多尺度自适应优化方法很好地避免了总目标函数陷入局部极小值的风险[18]。上述“粗化”类网格优化方法旨在通过减少单元数以减少反演不适定性,按照一定标准“细化”并得到高质量网格是提高反演稳定性的另一种思路。物性梯度可以反映异常体边界,以物性梯度为依据逐步细化网格,能更好地反演出异常体形状[19];将精度逐渐增加的三重网格分别用于二次场和总场模拟以及反演,在保证正演精度的情况下有效提高了反演效率[20]。此外,小波多尺度变换技术也受到了关注[21]。
自适应网格技术在地球物理反演中逐渐成为热点,但网格优化缺少评价标准,因此本文研究了依据模型灵敏度的自适应网格生成技术,并开展了三维直流电阻率反演。模型灵敏度反映模型改变量对于所有观测数据集的影响,若较小的模型改变量造成了较大观测数据的改变时,则应对该反演区域进行网格优化,同时通过设置最小单元体积以避免产生增加反演不确定性的过小网格。该方法在反演中构建了非结构化网格条件下的最小结构稳定因子;使用高斯—牛顿法最优化求解目标函数;通过稳定双共轭梯度法(BICGSTAB)迭代求解高斯—牛顿系统。理论与实测数据反演证明了本文方法的有效性。
1 直流电阻率法三维正演直流电法的边值问题可以表示为[8]
| $ \left\{ {\begin{array}{*{20}{l}} {\nabla \cdot [\sigma \nabla \mathit{\boldsymbol{u}}] = - I\delta \left( {\mathit{\boldsymbol{r}} - {\mathit{\boldsymbol{r}}_0}} \right)}\\ {{{\left. {\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial \mathit{\boldsymbol{n}}}}} \right|}_{{\mathit{\Gamma }_0}}} = 0}\\ {\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial \mathit{\boldsymbol{n}}}} + {{\left. {\cos \left\langle {\mathit{\boldsymbol{r}} - {\mathit{\boldsymbol{r}}_0}, \mathit{\boldsymbol{n}}} \right\rangle \frac{\mathit{\boldsymbol{u}}}{\mathit{\boldsymbol{r}}}} \right|}_{{\mathit{\Gamma }_{\rm{R}}}}} = 0} \end{array}} \right. $ | (1) |
式中:u为电位;r表示位置矢量;r0为电流源位置;δ为狄拉克函数;σ为电导率;I为电流强度;Γ0表示地表界面;ΓR表示无穷远处边界;n为边界外法线方向矢量;〈·,·〉表示两个矢量的夹角。边值问题等价于下式泛函极值问题[5]
| $ \begin{aligned} F(\boldsymbol{u})=& \int\left[\frac{1}{2} \sigma(\nabla \boldsymbol{u})^{2}-2 I \delta\left(\boldsymbol{r}-\boldsymbol{r}_{0}\right) \boldsymbol{u}\right] \mathrm{d} {\mathit{\Omega }}+\\ & \frac{1}{2} \int_{{\mathit{\Gamma }_{\mathrm{R}}}} \sigma \frac{\cos \langle\boldsymbol{r}, \boldsymbol{n}\rangle}{\boldsymbol{r}} \boldsymbol{u}^{2} \mathrm{d} {\mathit{\Gamma }} \end{aligned} $ | (2) |
采用有限单元法[22]求解式(2)的极值问题
| $ F(\mathit{\boldsymbol{u}}) = \frac{1}{2}\sum\limits_{e = 1}^{{N_e}} {{\mathit{\boldsymbol{U}}^{\rm{T}}}} \overline {\mathit{\boldsymbol{K}}_{\rm{e}}^1\mathit{\boldsymbol{U}}} + \frac{1}{2}\sum\limits_{{\mathit{\Gamma }_{{\rm{Re}}}}} {\mathit{\boldsymbol{U}}_{\rm{e}}^{\rm{T}}} \overline {\mathit{\boldsymbol{K}}_{\rm{e}}^2\mathit{\boldsymbol{U}}} - {\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{P}} $ | (3) |
式中:Ke1和Ke2为组成矩阵Ke的两个小矩阵;Ne为区域内剖分单元个数;ΓRe为边界面单元;P代表电流源分布的右端项;U为全部节点的电位值构成的矩阵;令
| $ \boldsymbol{K} \boldsymbol{U}=\boldsymbol{P} $ | (4) |
求解式(4)可得节点电位,进而计算视电阻率。
2 非结构化自适应网格反演 2.1 正则化反演正则化是求解不适定性地球物理反问题的重要手段,Tikhonov正则化公式[23]为
| $ \mathit{\Phi } = \phi (\mathit{\boldsymbol{d}}) + \alpha \phi (\mathit{\boldsymbol{m}}) $ | (5) |
式中:Φ为总目标函数,反演就是求解Φ极小值的过程;ϕ(d)为数据误差函数,d为数据向量; ϕ(m)为稳定因子,m为模型参数向量;α为正则化因子,是权衡数据拟合误差与稳定因子的一个折中系数。α的选取方式,一般包括经验定值法、无偏风险估计预测方法(UPRE)[24]、广义交叉验证方法(GCV)[25-26]、“L”型曲线法[27]、自适应求取方法[28]等。本文采用一种修正的“L”型曲线方法[29]。
目标函数的数据拟合泛函为
| $ \phi(\boldsymbol{d})=[\boldsymbol{A}(\boldsymbol{m})-\boldsymbol{d}]^{\mathrm{T}} \boldsymbol{W}_{\mathrm{d}}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{d}}[\boldsymbol{A}(\boldsymbol{m})-\boldsymbol{d}] $ | (6) |
式中:Wd为数据权重矩阵;A为正演算子。稳定因子能对模型解的空间进行限制,以减少多解性,常用的稳定因子有平滑模型约束稳定因子[30](一阶导数、二阶导数)、最小结构稳定因子[31-32]、最小支持稳定因子[33-34]和最小梯度支持稳定因子[35-36]等。本文采用最小结构稳定因子
| $ \begin{aligned} \phi(\boldsymbol{m})=& \alpha_{S} \int\left(\boldsymbol{m}-\boldsymbol{m}_{\mathrm{apr}}\right)^{2} \mathrm{d} v+\alpha_{x} \int\left(\frac{\partial \boldsymbol{m}}{\partial x}\right)^{2} \mathrm{d} v+\\ & \alpha_{y} \int\left(\frac{\partial \boldsymbol{m}}{\partial y}\right)^{2} \mathrm{d} v+\alpha_{z} \int\left(\frac{\partial \boldsymbol{m}}{\partial \boldsymbol{z}}\right)^{2} \mathrm{d} v \end{aligned} $ | (7) |
式中:αS、αx、αy、αz为比例系数;mapr为先验模型。
Zhdanov[37]给出稳定因子的一般形式为
| $ \phi(\boldsymbol{m})=\left(\boldsymbol{m}-\boldsymbol{m}_{\mathrm{apr}}\right)^{\mathrm{T}} \boldsymbol{W}_{\mathrm{m}}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{m}}\left(\boldsymbol{m}-\boldsymbol{m}_{\mathrm{apr}}\right) $ | (8) |
式中Wm为模型权重矩阵。由此可以得到总目标函数
| $ \begin{aligned} \mathit{\Phi }=&[\boldsymbol{A}(\boldsymbol{m})-\boldsymbol{d}]^{\mathrm{T}} \boldsymbol{W}_{\mathrm{d}}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{d}}[\boldsymbol{A}(\boldsymbol{m})-\boldsymbol{d}]+\\ & \alpha\left(\boldsymbol{m}-\boldsymbol{m}_{\mathrm{apr}}\right)^{\mathrm{T}} \boldsymbol{W}_{\mathrm{m}}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{m}}\left(\boldsymbol{m}-\boldsymbol{m}_{\mathrm{apr}}\right) \end{aligned} $ | (9) |
| $ \Delta \boldsymbol{m}=\boldsymbol{m}_{k+1}-\boldsymbol{m}_{k} $ | (10) |
求解目标函数对Δm的一阶导数,并令其为0,得到
| $ \begin{array}{l}{\left(\boldsymbol{J}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{d}}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{d}} \boldsymbol{J}+\alpha \boldsymbol{W}_{\mathrm{m}}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{m}}\right) \Delta \boldsymbol{m}} \\ {\quad=-\left[\boldsymbol{J}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{d}}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{d}} \Delta \boldsymbol{d}_{\mathrm{k}}+\alpha \boldsymbol{W}_{\mathrm{m}}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{m}}\left(\boldsymbol{m}_{k}-\boldsymbol{m}_{\mathrm{apr}}\right)\right]}\end{array} $ | (11) |
式中:Δdk=A(mk)-d;灵敏度矩阵J的元素为
| $ \boldsymbol{H}_{k}=\boldsymbol{J}^{\mathrm{T}} \hat{\boldsymbol{W}}_{\mathrm{d}}^{\mathrm{T}} \hat{\boldsymbol{W}}_{\mathrm{d}} \boldsymbol{J}+\alpha \hat{\boldsymbol{W}}_{\mathrm{m}}^{\mathrm{T}} \hat{\boldsymbol{W}}_{\mathrm{m}} $ | (12) |
| $ \nabla \phi=\boldsymbol{J}^{\mathrm{T}} \hat{\boldsymbol{W}}_{\mathrm{d}}^{\mathrm{T}} \hat{\boldsymbol{W}}_{\mathrm{d}} \Delta \boldsymbol{d}_{k}+\alpha \hat{\boldsymbol{W}}_{\mathrm{m}}^{\mathrm{T}} \hat{\boldsymbol{W}}_{\mathrm{m}}\left(\boldsymbol{m}_{k}-\boldsymbol{m}_{\mathrm{apr}}\right) $ | (13) |
则式(11)可写成高斯—牛顿方程
| $ \boldsymbol{H}_{k} \Delta \boldsymbol{m}=-\nabla \phi $ | (14) |
BICGSTAB算法是一种基于双边Lanczos算法和残差正交子空间的迭代方法,在Krylov子空间中选取序列,并选择合适的搜索方向及步长,使误差最小。该算法收敛规则、平滑且只需要较小的迭代次数,在求解大型线性方程组时优势明显[42]。具体过程参见文献[43]。
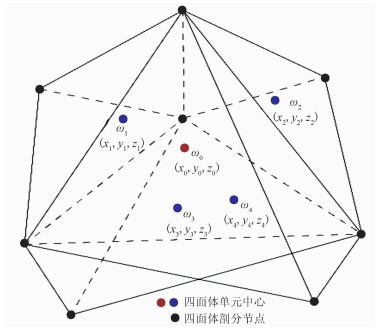
2.4 非结构化网格粗糙度计算Sethian等[44]提出,单元的空间梯度可以通过方向梯度的线性组合得到。在二维条件下,空间梯度通过计算单元中心点与其相邻单元中心点之间的方向导数线性组合得到。拓展到三维,在非结构化网格中任选四个相邻单元,假设其中心点(xi, yi, zi)的某一物性参数为ωi,则中心单元的空间梯度等于ω0对相邻四个单元中心方向上的导数之和(图 1)。
|
图 1 非结构化网格单元 |
ωi的值可以通过一个与x、y、z有关的线性函数拟合
| $ \omega(x, y, z)=a x+b y+c z+d $ | (15) |
5个单元形成5个方程组
| $ \left\{\begin{array}{llll}{x_{0}} & {y_{0}} & {z_{0}} & {1} \\ {x_{1}} & {y_{1}} & {z_{1}} & {1} \\ {x_{2}} & {y_{2}} & {z_{2}} & {1} \\ {x_{3}} & {y_{3}} & {z_{3}} & {1} \\ {x_{4}} & {y_{4}} & {z_{4}} & {1}\end{array}\right)\left(\begin{array}{c}{a} \\ {b} \\ {c} \\ {d}\end{array}\right)=\left(\begin{array}{c}{\omega_{0}} \\ {\omega_{1}} \\ {\omega_{2}} \\ {\omega_{3}} \\ {\omega_{4}}\end{array}\right) $ | (16) |
式(16)可写为矩阵形式
| $ \boldsymbol{F} \boldsymbol{q}=\boldsymbol{\omega} $ | (17) |
式中
| $ \boldsymbol{q}=\left(\boldsymbol{F}^{\mathrm{T}} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{T}} \boldsymbol{\omega} $ |
使用最小二乘方法得到超定方程的解,中心单元中任意一点p0处的梯度为
| $ \nabla_{\omega}(x, y, z)=a \hat{x}+b \hat{y}+c \hat{z} $ | (18) |
式中
设N为数据点数,定义模型灵敏度为
| $ {S_j} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {J_{i, j}^2} } $ |
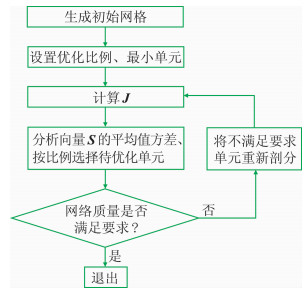
Sj是模型参数mj改变对整体数据影响的综合响应,反之也反映了整个数据集对mj改变的识别能力。不考虑数据方差与正则化,Sj实质上是矩阵H的主对角元素的平方根。一般而言,灵敏度矩阵的奇异值与Hessian的特征值是网格质量评判的依据。显然,如果Hessian是主对角占优的矩阵,则有利于反问题的优化求解[15]。基于Sj进行网格优化实质上是对Hessian矩阵的主对角元素进行优化,所以通过Sj对网格进行优化可以生成适用于反演的高质量网格,计算流程如图 2,运算过程如下:
|
图 2 网格优化流程 |
(1) 生成初始网格,设置优化比例、最小单元;
(2) 计算J;
(3) 分析向量S的平均值方差,并按比例选择待优化单元;
(4) 设置优化单元质量标准;
(5) 判断网格质量,不满足要求则返回步骤(2),满足要求则退出。
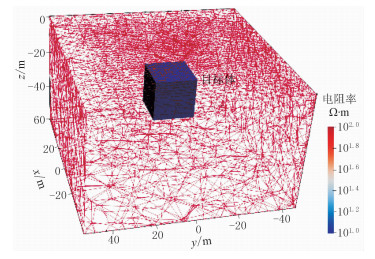
3 模型验证设地下15m处有一体积为20m×20m×20m的低阻异常体(图 3),电阻率为10Ω·m,地层背景电阻率为100Ω·m,地面布设15×15个接收电极,极距为5m,电极按E-SCAN[4]观测方法布设。
|
图 3 理论模型 |
比较图 4a与图 4b可见,在场源及异常体周边进行了网格细化,这些区域内很小的模型改变量往往会造成模型灵敏度大幅度的改变;在距离异常体较远的区域并未进行网格加密,因为这些区域内的模型灵敏度值往往较低,无需优化。随着距离的增加,网格逐渐粗糙的过程也更符合真实的地电模型。

|
图 4 网格优化前(a)、后(b)对比 |
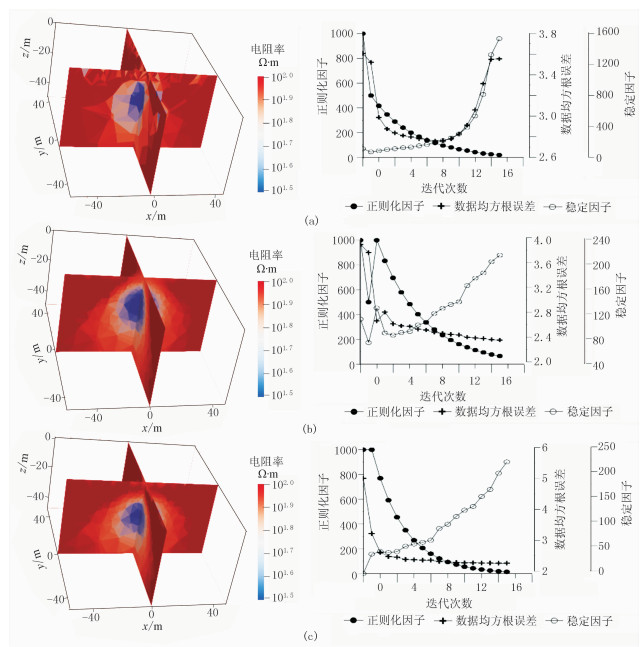
图 5所示为不同网格条件下的反演结果及反演迭代过程中相关因素变化曲线(右)对比。
|
图 5 不同网格条件下的反演结果(左)及反演迭代过程中相关因素变化曲线(右)对比 (a)网格未做自适应处理;(b)网格自适应优化一次;(c)网格自适应优化两次 |
图 5a为未进行网格优化的反演结果,由于网格过于粗糙,对异常体边界刻画不清晰,导致异常体形态偏离真实模型;场源附近过于粗糙的网格导致了严重的奇异性问题,具体表现在场源附近反演出多个低阻假异常;反演电阻率大于理论模型。图 5b为采用本文所述网格优化策略进行一次优化得到的结果,可见对模型灵敏度较大的区域进行网格细化后,地表附近未见明显异常,反演的异常体位置及电阻率更接近真实模型。从表 1可见,网格优化一次后,均方根误差明显下降,从3.60降至2.38。两次优化后的反演结果(图 5c)显示,第二次优化网格过程中,网格增加数量较第一次少,说明网格优化趋于稳定。
|
|
表 1 不同网格条件下反演次数及误差 |
因此,反演结果在一次优化的基础上得到了进一步改善,表现为边界的分辨率更高,异常体形态也更接近真实情况。
使用粗网格进行反演时(图 5a),迭代前期数据误差迅速下降,迭代中、后期出现稳定因子与数据误差同时上升的情况。分析可能的原因是网格过于粗糙,较低的正演精度直接影响反演结果,导致迭代中后期数据误差随正则化因子的减小而增大。该方案由于网格数量较少,反演所需时间较短,但反演效果不理想。运用本文所述网格优化策略进行两次网格细化(图 5c)则有效改善了这一问题。随着迭代进行,均方根误差随稳定因子的增加而下降,在迭代后期逐步趋于稳定。网格的细化意味着计算量的增加,通过设置网格细化阈值避免了产生过多过细网格,以兼顾计算效率。
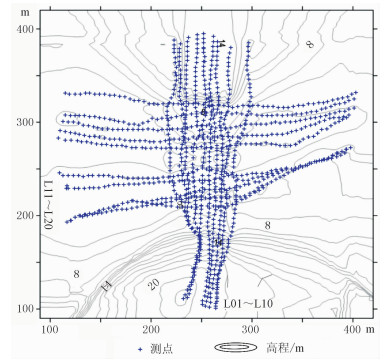
4 实测数据反演将本文所述算法运用于某区岩溶探测数据的反演。布设南北、东西方向测线各10条(图 6)。采用温纳和温纳—施伦贝尔[4]两种工作装置共采集有效测点12775个。
|
图 6 直流电阻率勘探测线部署图 |
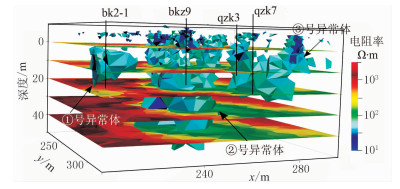
根据数据反演结果,得到如下的结论:反演区域发育3个低阻异常体(图 7)。①号异常体推测为被低阻物质填充的完整溶洞;②号异常体部分出露地表,底部深度为-40m,推测为被低阻物质填充的、出露地表的漏斗状溶洞;③号异常体同样出露地表,底部深度为-23m,推测为被低阻物质填充的漏斗状溶洞。钻探记录显示这3个异常体是被低阻物质填充的溶洞反映,异常体周围的高阻体是致密灰岩。
|
图 7 实测数据反演结果 |
综上分析,利用本文所述算法结合地质资料,大致确定地下3个被低阻物质填充的溶洞,其规模和形态与实际钻井信息吻合,证实了本文所述算法的正确性。
5 结束语本文采用基于模型灵敏度的网格优化算法,生成了高质量的反演网格,进而有效提高了反演的效果。将本文算法运用于理论模型及实际地下溶洞探测,均取得了理想的反演结果。基于模型灵敏度的网格优化算法从反演需求出发进行模型剖分,为高效、精确地进行三维反演提供了一种新思路。
| [1] |
傅良魁. 电法勘探教程[M]. 北京: 地质出版社, 1983.
|
| [2] |
吴小平, 刘洋, 王威. 基于非结构网格的电阻率三维带地形反演[J]. 地球物理学报, 2015, 58(8): 2706-2717. WU Xiaoping, LIU Yang, WANG Wei. 3D resistivity inversion incorporating topography based on unstructured meshes[J]. Chinese Journal of Geophysics, 2015, 58(8): 2706-2717. |
| [3] |
Zhang J, Mackie R L, Madden T R. Three-dimensional resistivity forward modeling and inversion using conjugate gradients[J]. Geophysics, 1995, 60(5): 1313-1325. DOI:10.1190/1.1443868 |
| [4] |
Loke M H, Barker R D. Rapid least-squares inversion of apparent conductivity pseudosection using a quasi-Newton method[J]. Geophysical Prospecting, 1996, 44(1): 131-152. DOI:10.1111/j.1365-2478.1996.tb00142.x |
| [5] |
刘洋.基于非结构网格的电阻率三维正反演及其应用硏究[D].安徽合肥: 中国科学技术大学, 2016. LIU Yang.Study of 3D Resistivity Modeling and Inversion Using Unstructured Grids and Their Applications[D].University of Science and Technology of China, Hefei, Anhui, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10358-1016103159.htm |
| [6] |
Coggon J H. Electromagnetic and electrical modeling by the finite element method[J]. Geophysics, 1971, 36(1): 132-155. DOI:10.1190/1.1440151 |
| [7] |
周熙襄, 钟本善. 电法勘探数值模拟技术[M]. 四川成都: 四川科学技术出版社, 1986.
|
| [8] |
徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.
|
| [9] |
Sasaki Y. 3D resistivity inversion using the finite-element method[J]. Geophysics, 1997, 59(11): 1839-1848. |
| [10] |
Rücker C, Günther T, Spitzer K. Three dimensional modeling and inversion of DC resistivity data incorporating topography I:Modeling[J]. Geophysical Journal International, 2006, 166: 495-505. DOI:10.1111/j.1365-246X.2006.03010.x |
| [11] |
任政勇, 汤井田. 基于局部加密非结构化网格的三维电阻率法有限元数值模拟[J]. 地球物理学报, 2009, 52(10): 2627-2634. REN Zhengyong, TANG Jingtian. Finite element mo-deling of 3-D resistivity using locally refined unstructured meshes[J]. Chinese Journal of Geophysics, 2009, 52(10): 2627-2634. DOI:10.3969/j.issn.0001-5733.2009.10.023 |
| [12] |
Lowry T, Allen M B, Shive P N. Singularity removal:a refinement of resistivity modeling techniques[J]. Geophysics, 1989, 54(6): 766-774. DOI:10.1190/1.1442704 |
| [13] |
Williams N C.Geologically-Constrained Ubc-Gif Gravity and MagneticInversions with Examples from the Agnew-Wiluna Greenstone Belt[D].University of British Columbia, 2008.
|
| [14] |
Blome M, Maurer H R, Schmidt K. Advances in three-dimensional geoelectric forward solver techniques[J]. Geophysical Journal International, 2009, 176: 740-752. DOI:10.1111/j.1365-246X.2008.04006.x |
| [15] |
Menke W. Geophysical Data Analysis:Discrete Inverse:Theory[M]. San Diego: Academic Press, 1989.
|
| [16] |
Bohm G, Vesnaver A. Inquest of the grid[J]. Geophysics, 1999, 64(4): 1116-1125. DOI:10.1190/1.1444618 |
| [17] |
Kim M, Kim S, Lee K, et al. Improvement of the electrical impedance tomographic image for the two-phase system with adaptive element grouping technique[J]. Measurement Science & Technology, 2004, 15(7): 1391-1401. |
| [18] |
Pessel M, Gibert D. Multiscale electrical impedancetomography[J]. Journal of Geophysical Research, 2003, 108: 2054. |
| [19] |
Molinar M, Blott B, Cox S, et al. Optimal imaging with adaptive mesh refinement in electrical impedance tomography[J]. Physiological Measurement, 2002, 23(1): 121-128. DOI:10.1088/0967-3334/23/1/311 |
| [20] |
Günther. Three-dimensional modelling and inversion of DC resistivity data incorporating toporating Ⅱ:Inversion[J]. Geophysical Journal International, 2006, 166: 506-517. DOI:10.1111/j.1365-246X.2006.03011.x |
| [21] |
Plattner. 3-D electrical resistivity tomography using adaptive waveletparameter grids[J]. Geophysical Journal International, 2012, 189: 317-330. DOI:10.1111/j.1365-246X.2012.05374.x |
| [22] |
Wang W, Wu X P, Spitzer K. Three-dimensional DC anisotropic resistivity modelling using finite elements on unstructured grids[J]. Geophysical Journal International, 2013, 193: 734-746. DOI:10.1093/gji/ggs124 |
| [23] |
吉洪诺夫·阿尔先宁著, 王秉忱译. 不适定问题的解法[M]. 北京: 地质出版社, 1979.
|
| [24] |
Mallows C L. Some comments on Cp[J]. Technome-trics, 1973, 15(4): 661-675. |
| [25] |
Golub G H, Michael H, Grace W. Generalized cross-validation as a method for choosing a good Ridge parameter[J]. Technometrocs, 1979, 21(2): 215-223. DOI:10.1080/00401706.1979.10489751 |
| [26] |
Colin G, Farquharson and Douglas W, et al.Automatic estimation of the trade-off parameter in nonlinear inverse problems using the GCV and L-curve criteria[C].SEG Technical Program Expanded Abstracts, 2000, 19: 265-268.
|
| [27] |
Hansen P C, O'Leary D P. The use of the L-curve in the regularization of discrete ill-posed problems[J]. SIAM Journal on Numerical Analysis, 1993, 14(6): 1487-1530. |
| [28] |
陈小斌, 赵国泽, 汤吉, 等. 大地电磁自适应正则化反演算法[J]. 地球物理学报, 2005, 48(4): 937-946. CHEN Xiaobin, ZHAO Guoze, TANG Ji, et al. An adaptive regularized inversion algorithm for magnetotelluric data[J]. Chinese Journal of Geophysics, 2005, 48(4): 937-946. DOI:10.3321/j.issn:0001-5733.2005.04.029 |
| [29] |
李曼, 林文东. 基于最小支持的2.5维直流电阻率正则化反演研究[J]. 东华理工大学学报(自然科学版), 2014, 37(3): 292-298. LI Man, LIN Wendong. The study of regularization inversion for 2.5 dimension DC resistivity based on minimum support stabilizing factor[J]. Journal of East China Institute of Technology (Natural Science), 2014, 37(3): 292-298. DOI:10.3969/j.issn.1674-3504.2014.03.007 |
| [30] |
Constable S C, Parker R C, Constable G G. Occam's inversion:a practical algorithm for generating smooth models from EM sounding data[J]. Geophysics, 1987, 52(3): 289-300. DOI:10.1190/1.1442303 |
| [31] |
Smith J T, Booker J R. Rapid inversion of two and three-dimensional magnetotelluric data[J]. Journal of Geophysical Research, 1991, 96: 3905-3922. DOI:10.1029/90JB02416 |
| [32] |
Oldenburg D, Li Y. Inversion of induced polarization data[J]. Geophysics, 1994, 59(9): 1327-1341. DOI:10.1190/1.1443692 |
| [33] |
Last B J, Kubik K. Compact gravity inversion[J]. Geophysics, 1983, 48(6): 713-721. DOI:10.1190/1.1441501 |
| [34] |
Guillen A, Menichetti V. Gravity and magnetic inversion with minimization of a specific functional[J]. Geophysics, 1984, 49(8): 1354-1360. DOI:10.1190/1.1441761 |
| [35] |
Portniaguine O, Zhdanov M S. Focusing geophysical inversion images[J]. Geophysics, 1999, 64(3): 874-887. DOI:10.1190/1.1444596 |
| [36] |
刘小军, 王家林, 陈冰. 二维大地电磁测深数据的聚焦反演探讨[J]. 石油地球物理勘探, 2007, 42(3): 338-342. LIU Xiaojun, WANG Jialin, CHEN Bing. Discussionon focus inversion algorithm of 2-D MT data[J]. Oil Geophysical Prospecting, 2007, 42(3): 338-342. DOI:10.3321/j.issn:1000-7210.2007.03.020 |
| [37] |
Zhdanov M S.Geophysical Inverse Theory and Regularization Problems[M].Elsevier Science, Netherlands, 2002.
|
| [38] |
Mackie R L, Madden T R. Three-dimensional magnetotelluric inversion using conjugate gradients[J]. Geophysical Journal International, 1993, 115: 215-229. DOI:10.1111/j.1365-246X.1993.tb05600.x |
| [39] |
Rodi W L, Mackie R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J]. Geophysics, 2001, 66(1): 174-187. DOI:10.1190/1.1444893 |
| [40] |
McGillivray P R, Oldenburg D W. Methods for calculating Fréchet derivatives and sensitivities for the non-linear inverse problems:a comparative study[J]. Geophysical Prospecting, 1990, 38(5): 499-524. DOI:10.1111/j.1365-2478.1990.tb01859.x |
| [41] |
Colin G.Approximate Sensitivities for the Multi-Dimensional Electromagnetic Inverse Problem[D].University of Edinburgh, 1995.
|
| [42] |
柳建新. 不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用[J]. 中南大学学报(自然科学版), 2009, 40(2): 484-491. LIU Jianxin. Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling[J]. Journal of Central South University (Science and Technology), 2009, 40(2): 484-491. |
| [43] |
Saad Y.Iterative Methods for Sparse Linear Systems[M].PWS Pub, 2009.
|
| [44] |
Sethian J A, Vladimirsky A. Fast methods for the Eikonal and related Hamilton-Jacobi equations on unstructured meshes[J]. Proceedings of the National Acdemy of Sciences of the United States of America, 2000, 97(11): 5699-5703. DOI:10.1073/pnas.090060097 |
| [45] |
Peter G, Leliéver, Colin G. Farquharson gradient and smoothness regularization operators for geophysical inversion on unstructured meshes[J]. Geophysical Journal International, 2013, 195: 330-341. DOI:10.1093/gji/ggt255 |



 张志勇, 江西省南昌市经济开发区广兰大道418号东华理工大学, 330013。Email:
张志勇, 江西省南昌市经济开发区广兰大道418号东华理工大学, 330013。Email: