重力场向下延拓能够突出局部或浅部异常,对重力数据的定量解释起重要作用。重力场下延是经典的不适定问题。当前,该问题的求解方法除了边界单元法[1]、样条函数法[2-3]、等效源法[4]等少数空间域方法以外,绝大部分下延方法需要在波数域加速[5-11],即便是基于泰勒级数[12]、中值定理[13]、Milne法[14]等原理的下延方法,也需要利用波数域方法快速获得垂向导数。换言之,目前绝大部分下延方法均基于Fourier变换。Fourier变换要求输入的重力数据无空白区,且数据长度满足快速Fourier变换(FFT)对数据长度(2的幂次方)的要求。显然,实测重力数据很难完全满足上述两个条件。因此,对实测重力数据进行下延处理前,必须对数据空白部分进行插值,且波数域下延方法还需对数据进行扩边,这将直接关系到重力数据下延的精度。重力数据的插值和扩边对应于信号的重构和外推。信号重构和外推是信号处理的逆问题,也是不适定的[15]。因此,可以将重力数据的插值、扩边和向下延拓统一考虑。
凸集投影(Projection onto Convex Sets,POCS)是带限信号重构的重要理论方法之一,在图像重建[16-17]和地震数据插值[18-21]等领域应用广泛,具有原理简单、易于执行和精度较高的特点。文献[22]基于凸集投影方法进行了重磁网格数据插值重建,结果表明该方法的插值精度优于克里金方法和反距离加权法,与最小曲率法相当。实际工程往往是计算实测重力数据与模型正演数据的差获得目标体的重力异常。因此,实测重力异常数据可以视为带限信号[23],满足采用凸集投影方法处理的条件。本文基于凸集投影原理,将重力数据的插值、扩边与下延这三个不适定问题统一考虑,提出重力数据同时填充、扩边和下延的一体化方法。
1 原理方法 1.1 基于POCS的重力插值扩边方法POCS对网格化后的重力数据缺失部分的插值扩边,其原理与图像缺失重建方法类似,主要基于Gerchberg-Saxton迭代计算,每次迭代计算的核心是二维Fourier变换。通过二维Fourier正变换将数据从空间域转换到波数域,给定一个阈值,保留大于和等于该阈值的谱分量,其余谱分量置零;然后,对保留的谱分量做二维Fourier反变换,并将原始已知数据重置回反变换后的数据中;照此过程逐次迭代,并逐渐减小每次迭代的阈值,以便恢复缺失数据和边界的更多细节信息,直至达到设置的最大迭代次数即完成插值扩边。从以上的方法实现过程描述可以看出,POCS方法是利用整个数据的谱(能量)进行插值和扩边的。
设含缺失数据的重力网格数据为g(x, y),则其POCS插值扩边计算公式为
| $ \begin{array}{c}{g_{k}(x, y)=g(x, y)+\boldsymbol{M} \mathrm{F}^{-1} \boldsymbol{T}_{k} \mathrm{F} g_{k-1}(x, y)} \\ {k=1, 2, \cdots, K}\end{array} $ | (1) |
式中:gk(x, y)表示第k次迭代插值扩边后的数据;M为采样矩阵,矩阵元素为0或1,0代表该点有数据,无需插值,为1则代表该点无数据,需要进行插值;F和F-1分别表示Fourier正、反变换;K表示最大迭代次数;Tk表示阈值矩阵,其元素满足
| $ T_{k}(u, v)=\left\{\begin{array}{ll}{1} & {\left|S_{k-1}(u, v)\right| \geqslant p_{k}} \\ {0} & {\left|S_{k-1}(u, v)\right|<p_{k}}\end{array}\right. $ | (2) |
式中:Sk-1(u, v)表示第k-1次迭代得到的插值扩边数据的频谱,满足Sk-1(u, v)=Fgk-1(x, y),其中u和v分别是x和y方向的波数;pk∈{p1, p2, …, pK}表示第k次迭代的阈值,满足p1>p2>…>pK和min{|Sk-1(u, v)|}<pk<max{|Sk-1(u, v)|}。一般先确定pk的最大值和最小值,再按照一定模式完成从最大值到最小值的下降过程。现有文献一般只关注阈值pk的下降模式,仅指出最大值和最小值的确定与原始数据的噪声水平有关[18-21]。
Tk(u, v)实质等同于理想低通滤波器。为减少参数个数,将Tk(u, v)设置为
| $ T_{k}(u, v)=\left\{\begin{array}{ll}{1} & {D(u, v) \leqslant c_{k}} \\ {0} & {D(u, v)>c_{k}}\end{array}\right. $ | (3) |
式中:ck表示第k次迭代的截止波数,满足c1≤c2≤…≤cK和1<ck≤min(M, N),M和N是插值扩边后重力数据的大小;D(u, v)表示波数域中点(u, v)与波数矩形中心的距离
| $ D(u, v)=\left[\left(u-\frac{M}{2}\right)^{2}+\left(v-\frac{N}{2}\right)^{2}\right]^{\frac{1}{2}} $ | (4) |
显然,式(3)与式(2)等价。式(3)只是将式(2)的阈值pk转化成截止波数ck。同理,最大截止波数cK的大小与原始数据的噪声水平相关。
1.2 重力数据向下延拓原理若观测平面(z=0, z轴向下为正)上的重力场g(x, y)已知,则由g(x, y)求z=d(d>0, 场源深度大于d)平面上的重力数据f(x, y)称为重力场的向下延拓
| $ g(x, y)=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} h(x-\xi, y-\eta) f(\xi, \eta) \mathrm{d} \xi \mathrm{d} \eta $ | (5) |
式中:
| $ G(u, v)=H(u, v) F(u, v) $ | (6) |
式中:G(u, v)和F(u, v)分别是g(x, y)和f(x, y)的Fourier变换结果;
针对该不适定性问题,Tikhonov正则化和各类迭代法是常用的处理方法。这些方法将对应的算子变换到波数域,其实质是进行低通滤波。以Tikhonov正则化为例,其对应的波数域正则化算子为[6, 9]
| $ R_{\alpha}=\mathrm{e}^{2 \pi d \sqrt{u^{2}+v^{2}}} \frac{\mathrm{e}^{-4 \pi d \sqrt{u^{2}+v^{2}}}}{\mathrm{e}^{-4 \pi d \sqrt{u^{2}+v^{2}}}+\alpha}=\mathrm{e}^{2 \pi d \sqrt{u^{2}+v^{2}}} T_{a} $ | (7) |
式中α为正则参数。该正则化方法的实质是利用正则化低通滤波算子Tα压制高频噪声的影响。同理,也可以利用类似式(3)的理想低通滤波器实现稳定的向下延拓
| $ f_{k}(x, y)=\mathrm{F}^{-1} \mathrm{e}^{2 \pi d \sqrt{u^{2}+v^{2}}} T_{\mathrm{DC}}(u, v) \mathrm{Fg}_{k}(x, y) $ | (8) |
式中的TDC(u, v)与式(3)中的理想滤波器的区别在于其阈值为cDC,而式(3)滤波器的阈值为cK。
式(8)可称为谱截断正则化,其作用等同于截断奇异值分解正则化(Truncated Singular Value Decomposition,TSVD)方法[24]。TDC(u, v)的阈值cDC对应于Tikhonov的正则参数α。用于下延的理想低通滤波器TDC(u, v)只需要滤除高频噪声即可确保向下延拓稳定,因此,正则参数cDC一般比较大且主要与数据的噪声水平相关。上一节的插值扩边迭代中,最大截止波数cK也与原始数据的噪声水平相关,由此,将正则参数cDC设置为最大截止波数cK具有合理性,这是因为插值和扩边同样不需要噪声谱。此外,现有确定正则参数的方法比较成熟,故将正则参数cDC设置为cK,即利用正则参数cDC确定式(3)中插值和扩边迭代过程的最大截止波数cK。因此经插值和扩边后的下延场为
| $ f_{K}(x, y)=\mathrm{F}^{-1} \mathrm{e}^{2 \pi(t) \sqrt{u^{2}+v^{2}}} T_{K} \mathrm{F} g_{K-1}(x, y) $ | (9) |
这样,通过理想低通滤波器以及截止波数与正则参数的关系实现了重力数据的插值、扩边和下延一体化。
1.3 正则化参数的选取正则化的关键在于最优正则参数的选取,其关系到正则化的精度和计算效率。常用的正则参数选取方法有L—曲线法、GCV法、偏差准则等[15],本文采用L—曲线法。
常规L—曲线法使用对数尺度描述正则解的范数‖fcK(x, y)‖和残差范数‖g(x, y)-h(x, y)fcK(x, y)‖。Hansen定义L—曲线的隅角为最大曲率,但最大曲率的求解相对复杂,本文采用极小化泛函[25]
| $ \begin{aligned} c_{K}=& \arg \min\limits_{1<c_{k} \leqslant \min (M, N)}[ \| g(x, y)-\\ &\left.h(x, y) f_{c_{k}}(x, y)\| \times\| f_{c_{k}}(x, y) \|\right] \end{aligned} $ | (10) |
确定最优正则参数cK。然后结合迭代次数K,阈值ck按线性方式从c1递增到最大值cK。本文所述的一体化方法流程可归纳为图 1。

|
图 1 频率域POCS迭代插值、扩边、下延一体化流程 |
构建一个由位于不同深度、大小不同的5个球体组合而成的理论球体模型(图 2a),各球体的具体参数见表 1。

|
图 2 理论模型及重力数据计算结果 (a)理论模型示意图; (b)地面理论重力异常场; (c)加噪后地面之上1km处的理论重力异常场; (d)从图c中挖去边界和内部部分数据的重力异常场; (e)本文方法求cK的曲线; (f)本文方法计算结果的误差随k的变化曲线 |
|
|
表 1 理论模型球体参数 |
设观测点、线距均为50m,正演计算地面(0高度,201×201个观测点,10km×10km观测范围)的重力场,如图 2b所示。以地面之上1km高度处(256×256个观测点,12.8km×12.8km观测范围)的重力数据为观测数据,并加入均值为零、方差为0.01mGal2的高斯白噪声(信噪比为40.51dB)模拟实际情况,其结果如图 2c所示。为检验方法的插值和扩边能力,将图 2c所示数据的内部部分数据(40×30个数据点)和边界(四个边界各28个数据点,共25536个数据点)“挖去”构成空白区(图 2d)。采用本文一体化方法,对图 2d所示的重力数据进行填充、扩边后,下延1km(20倍网格距)到地面,并用1km高度处的理论重力数据检验本文方法的填充和扩边精度,以图 2b所示的理论地面重力数据检验方法的下延精度。
为定量分析算法的精度,填充、扩边和下延精度都以均方根误差(Root Mean Square Error, RMSE)进行定量分析
| $ {\mathop{\rm RMSE}\nolimits} = \sqrt {\frac{1}{Q}\sum\limits_{i = 1}^Q {{{\left[ {{D_{\rm{c}}}(i) - {D_{\rm{t}}}(i)} \right]}^2}} } $ | (11) |
式中:Dc(i)和Dt(i)分别表示计算值和理论值;Q表示参与误差统计的数据个数。
根据图 1的流程,首先利用式(10)求解截止波数cK(图 2e),最小值cK=7。选定迭代次数K=100,然后按照算法步骤进行迭代计算。图 2f为填充、扩边和向下延拓均方根误差随迭代次数k的变化曲线。由图可知,本文算法具有收敛性,最终的填充、扩边和下延的均方根误差分别为0.04、0.36、1.43mGal。最终的插值和扩边结果见图 3a,与真实值在数据缺失处的残差见图 3b。图 3a的下延结果见图 3c,其与真实值(图 2b)的残差见图 3d。
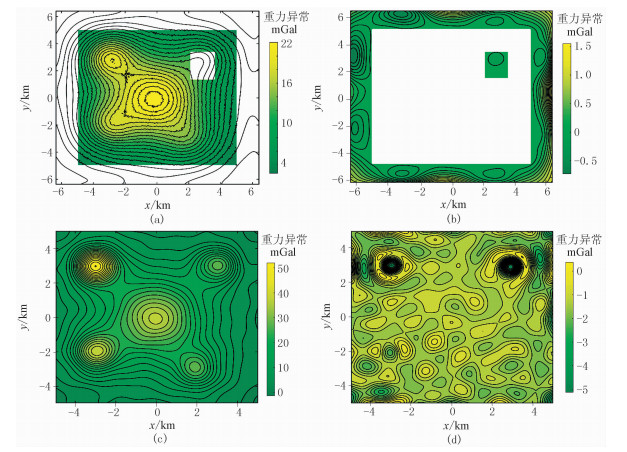
|
图 3 理论模型本文方法插值、扩边、下延的结果及误差 (a)本文方法扩边插值结果; (b)本文方法插值和扩边结果误差分布图; (c)图a下延1km的结果; (d)图c误差分布图 |
为了对比分析,采用经典的最小曲率插值法、余弦函数扩边法和Tikhonov正则化下延法组合方法对图 2d所示的数据分步进行插值、扩边和下延,并与本文方法的处理结果进行对比。最小曲率法的插值在软件Golden Surfer上实现,其最大残差和最大迭代次数分别选定为1.0×10-5和1.0×10-5;余弦函数扩边法采用文献[26]提供的“taper2d”程序;Tikhonov正则化参数选定为使下延均方根误差最小的最优正则化参数,经对比计算选定为0.005。插值扩边结果见图 4a,与真实值在数据缺失处的残差见图 4b。图 4a的下延(下延1km)结果见图 4c,与真实值(图 2b)的残差见图 4d。经统计,采用经典组合方法进行插值、扩边和下延结果的均方根误差分别为0.15、1.88、2.23mGal。
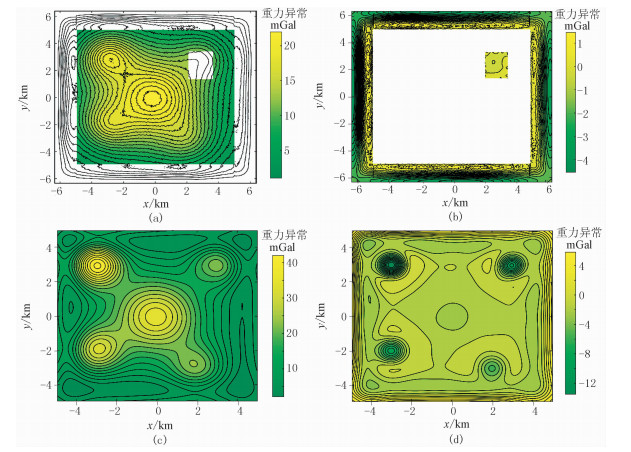
|
图 4 理论模型经典组合方法插值、扩边、下延的结果及误差 (a)经典组合方法扩边插值结果; (b)图a误差分布; (c)图a下延1km的结果; (d)图c误差分布 |
对比本文方法与经典组合方法的插值、扩边、下延结果及其残差和均方根误差可知,本文方法的插值、扩边和下延结果与理论值更接近,残差和均方根误差更小。
3 实测航空重力数据实验为检验本文方法在实际数据处理中的实用性,对美国地质勘探局(United States Geological Survey, USGS)2006年在阿富汗实测的航空重力数据进行计算。
该航空重力测量数据经各项处理并最终归算至离地7000m高度,形成网格距为1000m的布格重力异常(图 5a)。由图可知,实际航空重力测区范围很不规则。将图 5a的布格重力异常采用本文方法进行填充、扩边(扩边至1024×1024个点)并下延至地面。首先,采用式(10)求得截止波数cK=70,如图 5b所示。选定迭代次数K=100,按照图 1所示的步骤,图 5a数据经填充和扩边的结果见图 6a,图 6a下延至地面的结果见图 6b。将图 6b的布格重力异常场上延7000m恢复至原数据高度,结果如图 6c所示(仅展示有原始数据的区域)。图 6c与图 5a所示真实值的残差见图 6d,其均方根误差仅0.05mGal,验证了本文方法的有效性和高精度。

|
图 5 实测航空重力数据实验 (a)实测航空布格重力异常图; (b)本文方法求cK的曲线图 图a数据来自美国地质勘探局(USGS) |
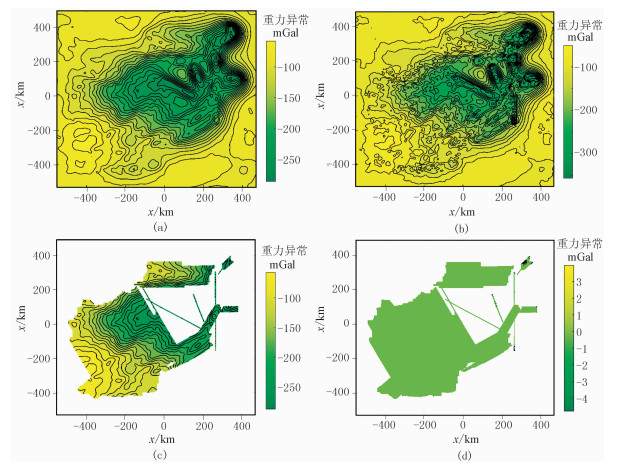
|
图 6 实测数据本文方法插值、扩边、下延结果和误差 (a)图 5a经本文方法填充扩边后结果; (b)图 6a下延7000m的重力异常场; (c)图 6b上延7000m的结果; (d)图 6c与图 5a的残差分布 |
同理论模型实验一样,同样采用经典的最小曲率插值法、余弦函数扩边法和Tikhonov正则化下延法对图 5a所示数据分步进行插值、扩边和下延。最小曲率插值法采用与理论模型计算部分一致的参数;Tikhonov正则化下延法的正则化参数采用使下延结果经上延后均方根误差最小的正则参数,经计算确定为0.001。采用经典组合方法对图 5a数据进行插值和扩边,其结果见图 7a~图 7d,其中图 7c仅展示有原始数据的区域。图 7c与图 5a的均方根误差达5.94mGal(图 7d)。

|
图 7 实测数据经典方法插值、扩边、下延结果和误差 (a)图 5a经经典方法插值、扩边后的结果; (b)图 7a经Tikhonov下延7000m的结果; (c)图 7b上延7000m的结果; (d)图 7c与图 5a的残差分布图 |
对比图 6与图 7可知,本文方法的插值、扩边和下延结果远优于经典组合方法,其计算残差和均方误差也远低于后者。
4 结束语本文针对实测重力数据不规则且存在空白区的实际情况,结合重力数据填充、扩边和向下延拓同属不适定反问题的理论基础,基于带限信号重建的经典算法——凸集投影算法,提出了重力插值、扩边、下延的一体化方法,并利用理论模型和实测数据验证了方法的收敛性和有效性。从算法流程来看,方法采用FFT运算,在波数域仅涉及理想低通滤波器,且只需要预先设定迭代次数,具有原理简单、实际操作方便和运算高效的特点。理论模型数据和实测数据处理结果显示,本文方法的扩边效果光滑、无畸变且插值和向下延拓结果精度较高,优于经典的组合方法。因此,本文方法适宜于实测规则网格重力数据的插值、扩边和向下延拓。
目前该方法的局限在于只能处理规则网格数据,基于该方法的不均匀采样重力数据的处理是后续进一步研究的内容。
| [1] |
刘保华, 焦湘恒, 王重德. 位场向下延拓的边界单元法[J]. 石油地球物理勘探, 1990, 25(4): 495-499. LIU Baohua, JIAO Xiangheng, WANG Chongde. Downward continuation of potential field based on boundary element method[J]. Oil Geophysical Prospecting, 1990, 25(4): 495-499. |
| [2] |
于增慧, 王硕儒. 用样条函数建立位场转换系统的研究[J]. 石油地球物理勘探, 2000, 35(1): 64-69. YU Zenghui, WANG Shuoru. Constructing a potential field conversion system by spline function[J]. Oil Geo-physical Prospecting, 2000, 35(1): 64-69. DOI:10.3321/j.issn:1000-7210.2000.01.009 |
| [3] |
Wang B Z. 2D and 3D potential-field upward continuation using splines[J]. Geophysical Prospecting, 2006, 54(2): 199-209. DOI:10.1111/j.1365-2478.2006.00526.x |
| [4] |
李端, 陈超, 杜劲松, 等. 多层等效源曲面磁异常转换方法[J]. 地球物理学报, 2018, 61(7): 3055-3073. LI Duan, CHEN Chao, DU Jinsong, et al. Transformation of magnetic anomaly data on an arbitrary surface by multi-layer equivalent sources[J]. Chinese Journal of Geophysics, 2018, 61(7): 3055-3073. |
| [5] |
Pilkington M, Boulanger O. Potential field continua-tion between arbitrary surfaces:Comparing methods[J]. Geophysics, 2017, 82(3): J9-J25. DOI:10.1190/geo2016-0210.1 |
| [6] |
陈生昌, 肖鹏飞. 位场向下延拓的波数域广义逆算法[J]. 地球物理学报, 2007, 50(6): 1816-1822. CHEN Shengchang, XIAO Pengfei. Wavenumber domain generalize inverse algorithm for potential field downward continuation[J]. Chinese Journal of Geophysics, 2007, 50(6): 1816-1822. DOI:10.3321/j.issn:0001-5733.2007.06.023 |
| [7] |
王彦国, 张凤旭, 王祝文, 等. 位场向下延拓的泰勒级数迭代法[J]. 石油地球物理勘探, 2011, 46(4): 657-662. WANG Yangguo, ZHANG Fengxu, WANG Zhuwen, et al. Taylor series iteration for downward continuation of potential field[J]. Oil Geophysical Prospecting, 2011, 46(4): 657-662. |
| [8] |
姚长利, 李宏伟, 郑元满, 等. 重磁位场转换计算中迭代法的综合分析与研究[J]. 地球物理学报, 2012, 55(6): 2062-2078. YAO Changli, LI Hongwei, ZHENG Yuanman, et al. Research on iteration method using in potential field transformations[J]. Chinese Journal of Geophysics, 2012, 55(6): 2062-2078. |
| [9] |
曾小牛, 李夕海, 牛超, 等. 位场向下延拓的波数域正则-积分迭代法[J]. 石油地球物理勘探, 2013, 48(4): 643-650. ZENG Xiaoniu, LI Xihai, NIU Chao, et al. Regularization-integral iteration in wavenumber domain for downward continuation of potential fields[J]. Oil Geo-physical Prospecting, 2013, 48(4): 643-650. |
| [10] |
Zhang H L, Ravat D, Hu X Y. An improved and stable downward continuation of potential field data:The truncated Taylor series iterative downward continuation method[J]. Geophysics, 2013, 78(5): J75-J86. DOI:10.1190/geo2012-0463.1 |
| [11] |
李晓杰, 王真理. 正则化等效层重力向下延拓方法[J]. 地球物理学报, 2018, 61(7): 3028-3036. LI Xiaojie, WANG Zhenli. A study on gravity field downward continuation using the regularized equivalent-layer method[J]. Chinese Journal of Geophysics, 2018, 61(7): 3028-3036. |
| [12] |
Fedi M, Florio G. A stable downward continuation by using the ISVD method[J]. Geophysical Journal International, 2002, 151(1): 146-156. DOI:10.1046/j.1365-246X.2002.01767.x |
| [13] |
Zhang C, Lü Q, Yan J, et al. Numerical solutions of the mean-value theorem:new methods for downward continuation of potential fields[J]. Geophysical Research Letters, 2018, 45(8): 3461-3470. DOI:10.1002/2018GL076995 |
| [14] |
张冲, 黄大年, 刘杰. 重力场向下延拓Milne法[J]. 地球物理学报, 2017, 60(11): 4212-4220. ZHANG Chong, HUANG Danian, LIU Jie. Milne method for downward continuation of gravity field[J]. Chinese Journal of Geophysics, 2017, 60(11): 4212-4220. DOI:10.6038/cjg20171109 |
| [15] |
王彦飞. 反演问题的计算方法及其应用[M]. 北京: 高等教育出版社, 2007.
|
| [16] |
Youla D C, Webb H. Image restoration by the method of convex projections:Part 1-Theory[J]. IEEE Tran-sactions on Medical Imaging, 1982, 1(2): 81-94. DOI:10.1109/TMI.1982.4307555 |
| [17] |
Wang S Q, Zhang J H. Fast image inpainting using exponential-threshold POCS plus conjugate gradient[J]. The Imaging Science Journal, 2014, 62(3): 161-170. |
| [18] |
Abma R, Kabir N. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 2006, 71(6): E91-E97. DOI:10.1190/1.2356088 |
| [19] |
刘国昌, 陈小宏, 郭志峰, 等. 基于Curvelet变换的缺失地震数据插值方法[J]. 石油地球物理勘探, 2011, 46(2): 237-246. LIU Guochang, CHEN Xiaohong, GUO Zhifeng, et al. Missing seismic data rebuilding by interpolation based on Curvelet transform[J]. Oil Geophysical Prospecting, 2011, 46(2): 237-246. |
| [20] |
王本锋, 陈小宏, 李景叶, 等. POCS联合改进的Jitter采样理论曲波域地震数据重建[J]. 石油地球物理勘探, 2015, 50(1): 20-28. WANG Benfeng, CHEN Xiaohong, LI Jingye, et al. Seismic data reconstruction based on POCS and improved Jittered sampling in the curvelet domain[J]. Oil Geophysical Prospecting, 2015, 50(1): 20-28. |
| [21] |
温睿, 刘国昌, 冉扬. 压缩感知地震数据重建中的三个关键因素分析[J]. 石油地球物理勘探, 2018, 53(4): 682-693. WEN Rui, LIU Guochang, RAN Yang. Three key factors in seismic data reconstruction based on compressive sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 682-693. |
| [22] |
闫浩飞, 刘国峰, 薛典军, 等. 基于凸集投影方法的重磁数据规则缺失重建[J]. 地球物理学进展, 2016, 31(5): 2192-2197. YAN Haofei, LIU Guofeng, XUE Dianjun, et al. Reconstruction of gravity/magnetic data with the projection-onto-convex-sets methods[J]. Progress in Geophysics, 2016, 31(5): 2192-2197. |
| [23] |
Novák P, Heck B. Downward continuation and geoid determination based on band-limited airborne gravity data[J]. Journal of Geodesy, 2002, 76(5): 269-278. DOI:10.1007/s00190-002-0252-y |
| [24] |
Xu P. Truncated SVD methods for discrete linear ill-posed problems[J]. Geophysical Journal Internatio-nal, 1998, 135(2): 505-514. DOI:10.1046/j.1365-246X.1998.00652.x |
| [25] |
Regińska T. A regularization parameter in discrete ill-posed problems[J]. SIAM Journal on Scientific Computing, 1996, 17(3): 740-749. DOI:10.1137/S1064827593252672 |
| [26] |
Cooper G R J, Cowan D R. Enhancing potential field data using filters based on the local phase[J]. Computers & Geosciences, 2006, 32(10): 1585-1591. |



 李夕海, 陕西省西安市灞桥区洪庆同心路2号, 710025。Email:
李夕海, 陕西省西安市灞桥区洪庆同心路2号, 710025。Email: