② 山东科技大学地质学院, 山东青岛 266590
② Geological College, Shandong University of Science and Technology, Qingdao, Shandong 266590, China
测井数据是衔接岩心与地震资料的中间尺度信息,也是认识井点地质信息的主要途径。从20世纪50年代提出测井相[1]的概念以来,如何准确而快速地识别测井相成为油藏地质研究的一项重要内容。早期测井相研究主要通过对比、分析测井曲线形态与录井资料,确定沉积相或地层层序,是一种费时、费力的全人工分析模式[2]。随着计算机技术尤其是人工智能的发展,使精准、快速、自动识别测井相成为可能,判别分析法、数理统计法、聚类分析法、模糊识别、曲线拟合、支持向量机和神经网络等方法逐渐用于测井相识别与分析[3]。
Lim等[4]使用主成分分析和分层聚类分析方法定量分析测井曲线,取得了较好的效果;Sang等[5]应用非参数回归结合多变量统计分析(主成分分析和判别分析)方法识别测井相并预测渗透率;Lim等[6]针对数据模糊问题,提出模糊逻辑和神经网络结合方法,描述了测井相与储层性质之间的非线性关系,并能够预测孔隙度或渗透率;Tang等[7]利用概率神经网络(PNN)方法分析测井相以精确地预测测井数据,模型预测精度达70%;汪忠德等[8]提取测井资料中的对应特征建立标准模式样本并使用反向传播(BP)神经网络分析建模。但是,上述由机器学习算法定量识别测井相的模型也存在许多不足:首先,特征提取繁琐,需要将数据归一化等操作,不同的归一化方法对模型训练结果也有影响,而且在识别测井相时还要调整数据维度;其次,泛化能力不足,由这种定量分析方法训练得到的模型只适用于某地区或具相同沉积环境的地区。
近年来,随着人工智能的发展,在图像识别方面,许多深度学习模型表现出优异的性能,对某些数据集的处理水平已经超越人类[9-15]。从图像角度识别测井相正是模仿人类基于测井曲线形态分类识别的工作流程,使用深度神经网络模型可获得较高的分类精度,这种使用曲线形态作为特征的模型泛化能力较强,广泛用于识别不同沉积环境。
本文选用东海F气田的砂质辫状河三角洲的测井数据,基于测井曲线形态,选取自然伽马(GR)数据作为训练数据构建深度卷积神经网络,并首次用于测井相识别,结合沉积微相与测井相对应表识别沉积微相。结果表明,本文提出的卷积神经网络模型可有效识别测井相,在分类精度和模型泛化能力上优于其他算法。
1 测井相自动识别原理 1.1 卷积神经网络原理自20世纪80年代提出卷积神经网络(Convolutional Neural Network,CNN)并在手写数字识别中取得了优异成果[16-17]。CNN的结构主要由输入层、卷积层、池化层(也称下采样层)、全连接层和输出层构成,卷积层与池化层相邻构建,根据实际需要可以设置多个。
卷积层可视为由多个特征映射(Feature Map)组成,多个神经元组成特征映射,每个神经元通过卷积核(Kernel)与上层特征映射的一部分神经元相连。其中卷积核为一个随机初始化的权值矩阵,其作用是与上一层计算得到的特征映射进行如下卷积操作
| $ y = \sum\limits_{i = 1}^{n \times n} {{x_i}} {w_i} + b $ |
式中:n×n为卷积核大小;xi为区域内第i个像素点的输入值;wi为对应的权值矩阵元素值;b为计算后加入的偏置;y为卷积运算结果。
卷积运算使用卷积核操作整个特征映射,可使权值共享,大大减少了网络参数,这也是CNN的一大优势。卷积结束使用激励函数将y归一化,作为下一层的输入
| $ x=f(y) $ |
式中:f(·)是为激励函数,有多种形式,在实际实验中可以根据情况自行选择;x是为激励函数的输出,也是下一层网络的输入值。
池化层也由多个特征映射组成,其特征映射与上一层是一一对应的[18]。以最大池化为例
| $ y_{i}=\max \left\{x_{1}, x_{2}, \cdots, x_{n \times n}\right\} $ |
式中:x为池化区域的每个点的值;yi为从n×n个点中选取的最大值,也是池化操作的输出。
池化操作降低了特征映射的分辨率,从而具有平移、旋转不变形的特征[18],并且减少了神经元个数,从而降低了模型的复杂度,提高了泛化能力。
1.2 多尺度识别原理由于沉积旋回具有级次性,对测井相的探讨必须建立在一个确定的尺度或地层单元上,本文采用多尺度小波变换划分沉积单元,在此基础上再识别多尺度测井相。小波变换是通过改进傅里叶变换得到的变换方法,通过信号的伸缩、平移在局部分析时间或空间频率,并且能以不同尺度细化。由于小波变换具有优异的时频局部化特点,被广泛用于信号去噪。如,能够抑制高频噪声,从而保护有用突变和尖峰信息。本文利用小波变换进行滤波,以保持测井曲线的突变段,在去除噪声的同时不会丢失曲线的有效信息。
采用小波变换去噪分为两个过程,即:首先对原始信号进行小波分解,然后再重构分解的信号。小波变换使用的函数各有不同,常用的小波函数有Harr、Daubechies、Symlets、Morlet、Gauss等。在选定一个母小波作为小波基时,将母小波经过尺度变化和位移得到一簇小波,该簇小波能够表达一个信号,而得到一簇小波的过程就是多尺度小波变换过程。选用合适的小波函数和尺度处理测井曲线,可使测井曲线在整体趋势上保持不变,但在细节上有所不同。
GR测井是对地层放射性的探测,其曲线变化可反映不同时间尺度的沉积环境变化,从而指示测井相和沉积相变化。经过分解后,GR曲线的地质意义发生变化,曲线本身已经不再反映泥质含量等与地层放射性密切相关的地质特征,GR曲线的垂向变化趋势以及变化界面有效地指示沉积级次,从而划分不同级次地层单元。
2 测井相自动识别方法识别测井相的前提是准确划分识别单元。陆相沉积类型复杂,在同一个地质时间单元内不同平面位置的地层可能存在较大的厚度差异,如何划分、识别单元是一个难题;地下的沉积结构复杂多变,导致同一种沉积微相的测井相存在差异,对经验丰富的解释人员识别难度不大,但是对于计算机自动识别是严峻的挑战。本文采用多尺度小波变换合理划分识别单元,提出了深度CNN模型自动识别测井相的方法(图 1)。

|
图 1 深度CNN模型自动识别测井相基本框架 |
本文选用东海凹陷F气田的砂质辫状河三角洲沉积环境的测井数据作为研究对象。因为不同沉积环境的物源和水动力等条件存在差异,使测井曲线形态、特征不同,所以在实际测井解释时,基于区块的沉积环境划分测井曲线形态很重要。GR响应能够区分泥岩和砂岩,可反映垂向序列中砂岩和泥岩的相对含量,还可反映沉积环境、沉积韵律和沉积速率等地质特征,具有良好的指示性[19-20],其测井曲线形态可反映沉积相类型。
不同沉积环境的水动力和物源条件差异造成沉积特征差异,导致GR曲线形态差异。GR曲线形态主要有箱形、钟形、漏斗形、齿形及其复合形态,复合形态是前几种形态的组合。箱形反映了水动力条件稳定的快速堆积或者环境稳定的沉积;钟形反映了水流能量逐渐减弱或物源供应逐渐减少的沉积环境;漏斗形与钟形正好相反,反映了水动力变强或物源供应逐渐增多的沉积环境[19]。
本文选用四种GR曲线形态作为特征,将数值转变为图像形式。由于形态标定存在人为误差,从不同井段的测井数据中选取无歧义的形态特征人工截取和标定(图 2),首先对图像做标准化、添加噪声、旋转和转灰度等处理,再对数据增强与扩充,最终建立训练和测试数据集,共计4000余张图片。

|
图 2 训练数据集样例 从左到右依次为箱形、钟形、漏斗形和齿形 |
GR曲线是与深度有关的一串具有特定形态的数据,针对其具有特定形态这一特性,本文基于基本CNN结构,提出了基于CNN的测井相分类模型,主体结构如图 3所示。具体构建策略及解释如下。

|
图 3 基于深度CNN的测井相分类模型主体结构 整个CNN由8层网络构成:第1层、第3层和第5层为卷积层,主要用于提取特征;第2层和第4层为池化层,主要用于降低模型复杂度;第6层和第7层为全连接层,主要用于将二维特征转变为一维特征向量;第8层为输出层,主要用于分类 |
(1) 输入图像像素为227×227,在第1层使用64个11×11的卷积核对输入图像做卷积运算,随后使用激活函数ReLU激活每个点。ReLU函数为
| $ f(x)=\max(0, x) $ |
式中F(x)是经过激活函数得到的新数值,其中x为该点数值。
激活函数有多种,一般使用饱和非线性函数,如Sigmoid或Tanh函数等(图 4),ReLU是不饱和非线性函数(图 5)。与Sigmoid和Tanh相比,ReLU在梯度下降时更容易求得一阶导数,不易出现梯度消失或爆炸,还能加快收敛速度[21],所以本文选用ReLU作为激活函数。

|
图 4 激活函数Sigmoid和Tanh 横坐标表示激活函数的输入值,为实数(无单位),纵坐标表示经过激活函数运算得到的输出值,图 5同 |

|
图 5 激活函数ReLU |
(2) 将经过一层卷积之后得到的特征映射作为池化层的输入,第2层使用192个5×5的池化核对其进行池化操作。常用的池化方法有最大池化和平均池化,即分别取池化核部分中的最大值和所有值的平均值。本文针对所建数据集的特性,即整个图片大部分为空白部分,真正有价值的特征区域占比很小,因此选用最大池化操作,充分利用其适用于分离稀疏特征的特点。
(3) 第3层和第5层为卷积层,分别使用384个和256个3×3的卷积核,随后再用ReLU做激活处理;第4层使用256个3×3的池化核对特征映射进行最大池化处理;第6层将上述256个特征映射变换成长度为4096的特征向量;第7层对第6层的结果再进行一次全连接操作,同样得到长度为4096的特征向量。
(4) 本文在网络中加入了Dropout、局部响应归一化(Local Response Normalization,LRN)和L2正则化等策略。Dropout的原理是以一定概率随机抑制神经元,使一部分神经元在训练阶段处于休眠状态,不参加前向传播和反向回馈过程,降低了网络之间的连接性,从而提高了模型的鲁棒性;LRN的作用是对局部神经元建立竞争机制,增强响应强烈的神经元效果,从而抑制反馈较小的神经元;L2范数是所有向量模的平方和的平方根,在CNN的目标函数中加入L2范数,在最小化过程中,会使L2范数也最小,而其中的参数为训练时得到的卷积核的权值矩阵,这样在最小化过程中权值矩阵中所有元素都更加趋近于0,最终使模型参数接近0,致使模型的泛化能力更强且计算速度更快。
2.3 数据分割在识别实际测井数据时,需要分割一段深度序列数据,并转换为图像形式由模型识别。由于GR的数据范围为0~200(API),本文首先以120为阈值,找出大于120的极值点,将数据分割一次;接着以100为阈值,找出前述分割段之间大于100的极值,对数据进行二次分割;再以85为阈值,找出前述分割段之间大于85的极值,对数据进行三次分割;最后将这些数据段转换成二维灰度图像形式。
2.4 多尺度划分本文提出一种多尺度测井相单元划分方法,经过分析对比实验,选用Daubechies小波基对测井数据进行不同尺度的小波变换,使测井数据具有不同细节特征。本文选用Daubechies小波基作为小波基函数的原因为:本文的思想是将一维数据转换为二维图像进行识别,选用合适阶数和分解层数的Daubechies小波可以保持曲线的整体趋势,并且不会在识别大尺度测井相时造成不良影响;Daubechies小波支持尺度变换,可根据实际数据特征和识别精度自由变换尺度;Daubechies小波具有良好的正则性,使信号重构过程较为光滑。Daubechies小波基简写为dbN,N为小波的阶数,N越大表示小波滤波器越长。db小波还能进行多层分解,分解层数越多表示信号分解次数越多。由不同阶数和不同层数db小波的分解发现,选用db6小波4层分解和db4小波4层分解能有效地对本文数据进行降噪和滤波处理,同时不破坏GR曲线的主体形态与增减趋势。图 6为原始数据与经过小波变换去噪、平滑处理数据。由图可见:db6小波4层分解进一步扩大了尺度;db4小波4层分解使测井曲线在大体形态不变的情况下,过滤了同一深度范围内GR曲线的细节,只保留了主要趋势,从而合理地划分、识别单元。

|
图 6 原始数据与经过小波变换去噪、平滑处理数据(3213.8~3273.1m井段) |
为了验证深度CNN测井相识别模型的有效性,对构建的测井相数据集进行实验,并对比与传统的分类算法(BP神经网络、支持向量机(Support Vector Machine,SVM)和传统CNN(不添加Dropout、LRU和L2正则化))的实验结果(表 1),证明深度CNN模型在测井相分类中性能更好。在训练达到2000代时,传统CNN模型已经出现过拟合情况,深度CNN模型达到最高准确率,表明模型具有良好的泛化能力。经过数据分割操作,使用本文提出的测井相识别方法识别某一段GR数据(图 7),可以看出,db6小波4层分解(图 7a)识别的测井相类型多于db4小波4层分解(图 7b),这是因为前者仅仅使用了降噪处理,处理数据基本与原始数据无异,后者使用滤波处理使对应同一深度段内识别的测井相与前者有差异,但两者在大范围内保持一致。
|
|
表 1 不同模型分类性能 |

|
图 7 模型识别结果(3212.7~3316.0m井段) (a)db6小波4层分解降噪处理;(b)db4小波4层分解滤波处理 |
测井曲线形态从多个方面反映沉积特征,不同的测井曲线形态通常对应不同的沉积相。根据“沃尔索相律”可知,只有在横向上成因相似或者相邻发育的沉积相,才能在垂向上依次叠覆相邻。根据具体的沉积环境,可以由特定测井曲线形态判别沉积微相。本文选用砂质辫状河三角洲的GR数据,利用测井相判别沉积相。砂质辫状河三角洲前缘的沉积微相主要为水下分流河道、分流间湾和河口坝(表 2)。
|
|
表 2 沉积微相与测井曲线形态对应表 |
利用测井曲线形态与沉积微相的对应关系(表 2),通过分析得到目标井段的沉积微相。图 8为A井部分模型分析与实际结果对比。由图可见:基于深度CNN的测井相识别模型与BP神经网络、SVM算法识别结果差异较大;对比沉积微相分析结果与取心分析结果表明,基于深度CNN的测井相识别模型具有较高的准确率和泛化能力,但是还会出现误判,尤其是对于齿形与漏斗形、钟形之间的识别,这是由于有些曲线对应的深度距离较小,存在歧义,使基于深度CNN的测井相识别模型不能准确地识别。
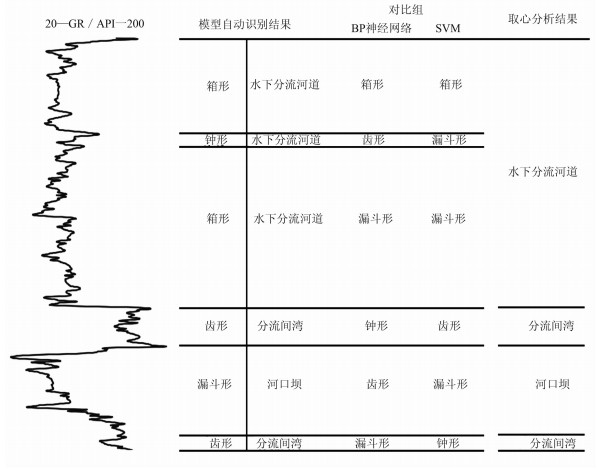
|
图 8 A井部分模型分析与实际结果对比(3966.6~4120.0m井段) |
本文基于人工智能技术,提出了基于卷积神经网络的多尺度测井相识别方法,利用L2范数、Dropout和LRN有效地限制了模型的复杂程度,提高了模型泛化能力,获得了优于其他算法的97.87%的模型分类准确率,利用Daubechies小波划分不同尺度的测井相单元,可便捷、高效地自动识别测井曲线形态。由于文中方法选用二维测井相图像数据进行分类,无关具体数值,即结合研究区的沉积环境背景即可分析测井相,因此比经典方法的泛化能力更强。对比沉积微相与取心分析结果表明,文中方法具有较高的准确率和泛化能力。
尚需指出,卷积神经网络模型作为有监督学习,受训练数据影响很大,难以得到令人满意的结果。因此,扩充数据集、区分相似数据是未来的研究方向。
| [1] |
吴灿灿, 李壮福. 基于BP神经网络的测井相分析及沉积相识别[J]. 煤田地质与勘探, 2012, 40(1): 68-71. WU Cancan, LI Zhuangfu. Logging facies analysis and sedimentary facies identification based on BP neural network[J]. Coalfield Geology and Exploration, 2012, 40(1): 68-71. DOI:10.3969/j.issn.1001-1986.2012.01.016 |
| [2] |
赵希刚, 吴汉宁, 王靖华, 等. 综合测井资料在研究油气藏沉积相中的应用——以川口油田长六油层组为例[J]. 地球物理学进展, 2004, 19(4): 918-923. ZHAO Xigang, WU Hanning, WANG Jinghua, et al. Application of comprehensive logging information for research the sedimentary facies of oil/gas reservoirs in the Chang-6 oil layer of Chuankou oil field[J]. Progress in Geophysics, 2004, 19(4): 918-923. DOI:10.3969/j.issn.1004-2903.2004.04.036 |
| [3] |
张福明, 李洪奇, 邵才瑞, 等. 应用神经网络模式识别技术进行测井沉积学研究[J]. 石油勘探与开发, 2003, 30(3): 121-123. ZHANG Fuming, LI Hongqi, SHAO Cairui, et al. Application of artificial neural network pattern recognition technology to the study of well logging sedimentology[J]. Petroleum Exploration and Development, 2003, 30(3): 121-123. DOI:10.3321/j.issn:1000-0747.2003.03.033 |
| [4] |
Lim J S, Kang J, Kim J.Multivariate statistical analysis for automatic electrofacies determination from well log measurements[C].SPE Asia Pacific Oil and Gas Conference and Exhibition, 1997, 14-16.
|
| [5] |
Sang H L, Arun K, Akhil D G. Electrofacies characterization and permeability predictions in complex reservoirs[J]. SPE Reservoir Evaluation & Engineering, 2002, 5(3): 237-248. |
| [6] |
Lim J S, Kim J.Reservoir porosity and permeability estimation from well logs using fuzzy logic and neural networks[C].SPE Asia Pacific Oil and Gas Confe-rence and Exhibition, 2004, 18-20.
|
| [7] |
Tang H, Meddaugh W S, Toomey N. Using an artificial-neural-network method to predict carbonate well log facies successfully[J]. SPE Reservoir Evaluation & Engineering, 2011, 14(1): 35-44. |
| [8] |
汪忠德, 王新海, 张汶, 等. BP人工神经网络法(ANNS)在塔中地区碳酸盐岩测井评价中的应用[J]. 石油天然气学报, 2008(2): 253-255. WANG Zhongde, WANG Xinhai, ZHANG Wen, et al. BP neural network model to recognize carbonate reservoir in Tazhong of Tarim Oilfield[J]. Journal of Oil and Gas Technology, 2008(2): 253-255. |
| [9] |
Guo Y, Liu Y, Oerlemans A, et al. Deep learning for visual understanding:A review[J]. Neurocomputing, 2016, 187(2): 27-48. |
| [10] |
Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527 |
| [11] |
Krizhevsky A, Sutskever I, Hinton G E.Image net classification with deep convolutional neural networks[C].International Conference on Neural Information Processing Systems, 2012, 1097-1105.
|
| [12] |
Niu X X, Suen C Y. A novel hybrid CNN-SVM classifier for recognizing handwritten digits[J]. Pattern Recognition, 2012, 45(4): 1318-1325. DOI:10.1016/j.patcog.2011.09.021 |
| [13] |
Szegedy C, Liu W, JiaY, et al.Going deeper with convolutions[C].Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, 1-9.
|
| [14] |
He K, Zhang X, Ren S, et al.Deep residual learning for image recognition[C].Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, 770-778.
|
| [15] |
Sainath T N, Mohamed A R, Kingsbury B, et al.Deep convolutional neural networks for LVCSR[C].IEEE International Conference on Acoustics, Speech and Signal Processing, 2013, 8614-8618.
|
| [16] |
Lawrence S, Giles C L, Tsoi A C, et al. Face recognition:a convolutional neural-network approach[J]. IEEE Transactions on Neural Networks, 1997, 8(1): 98-113. DOI:10.1109/72.554195 |
| [17] |
Nebauer C. Evaluation of convolutional neural net-works for visual recognition[J]. IEEE Transactions on Neural Networks, 1998, 9(4): 685-696. DOI:10.1109/72.701181 |
| [18] |
Gu J, Wang Z, Kuen J, et al. Recent advances in con-volutional neural networks[J]. Pattern Recognition, 2018, 77(12): 354-377. |
| [19] |
王贵文, 郭荣坤. 测井地质学[M]. 北京: 石油工业出版社, 2015.
|
| [20] |
丁次乾. 矿场地球物理[M]. 山东东营: 石油大学出版社, 1992.
|
| [21] |
Xu B, Wang N, Chen T, et al. Empirical evaluation of rectified activations in convolutional network[J]. Computer Science, 2015, 27(10): 6-14. |



 何旭, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)计算机与通信工程学院, 266580。Email:
何旭, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)计算机与通信工程学院, 266580。Email: