② 黑龙江省油气藏形成机理与资源评价重点实验室, 黑龙江大庆 163318;
③ 西安交通大学电子与信息工程学院, 陕西西安 710049
② Heilongjiang Key Laboratory of Hydrocarbon Reservoir Forming Mechanism and Resource Evaluation, Daqing, Heilongjiang 163318, China;
③ School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an, Shaanxi 710049, China
长期以来,薄层、薄互层的预测与评价一直是地震处理与解释人员的重点研究内容之一。为此,人们从不同角度广泛研究了薄层、薄互层预测,研究方向大致分为四类:一是各类地震属性参数与薄层、薄互层间的关系[1-2];二是基于各类时频分析方法的谱分解和谱反演技术[3-5];三是以提高地震资料分辨率为主的伪反褶积和频带拓宽方法[6-7];四是建立峰值频率、调谐厚度和调谐频率等参数的薄层、薄互层厚度预测方法[8-11]。上述研究为薄层、薄互层研究奠定了基础。
近年来,通过对不同厚度、不同极性、不同反射系数的薄层和不同单层厚度、不同互层数的等厚薄互层的研究,已经逐步认识到地质体结构特别是厚度结构与时频响应间存在重要的调控关系[12-22],即特定的地质体结构存在特定的时频变化规律。反之,依据相应的时频变化规律可以断推地质体结构,这为根据地震数据的时频变化规律认识、判别和解释地下地质体结构提供了重要的线索和思路。
砂泥岩薄互层是中国东部油田的主要岩石组合类型,而厚度有序递变型薄互层(简称递变型薄互层)又是其中较典型的类型,研究递变型薄互层的时频变化规律对认识其他更复杂的薄互层类型的时频变化规律具有重要指导意义。刘传虎等[23-24]、崔凤林等[25]和张玉芬等[26]研究了沉积旋回的时频变化规律,认为随着地层减薄,瞬时频率逐渐增大,随着地层增厚,瞬时频率降低。随后,人们通过不同时频分析方法进一步认识了上述规律[27-29]。但上述研究主要集中于大尺度沉积旋回的总体时频变化,对超薄沉积旋回体和沉积旋回内部超薄单层组合体的时频变化特征鲜有涉及,存在以下不足:没有考虑单层厚度变化对薄互层时域波形特征、时频谱及瞬时频谱变化的影响;对时频变化厚度响应区间缺乏严格的界定;没有探讨递变型薄互层与等厚薄互层、单一薄层间的时频关系;没有给出递变型薄互层的内部结构特征与时频响应间的调控机制。补充和完善上述缺陷是探究其他类型薄互层时频响应变化规律的重要基础。
鉴于此,本文建立了厚度有序递增型(递增型)、厚度有序递减型(递减型)、厚度先有序递增后有序递减型(先增后减型)、厚度先有序递减后有序递增型(先减后增型)等4种典型的薄互层地质模型,采用波动方程正演模拟获取理论数据,通过仿射类平滑伪Wigner分布获取瞬时频谱,进而总结了4种模型的时域波形、时频谱和瞬时频谱的特征及变化规律。在此基础上,着重探究不同厚度变化量、不同互层数和不同厚度区间对递变型薄互层时频变化的控制作用,厘清递变型薄互层内部结构特征与时频响应之间的内在调控机理,为建立地质体时频响应特征统一框架奠定基础。
1 仿射类双线性时频分布Cohen类双线性时频分布以时移和频移不变性为基础[30],仿射类双线性时频分布则由时移和伸缩变换实现。因此,仿射类时频分布也是一类时频能量分布,与Cohen类时频分布很相似,只是变换方式不同。能够从时间和尺度角度分析信号,且转换后的理想性质中具有时移和伸缩变换不变性的分布类,此变换群称为仿射群[31]。
如果一个双线性时间尺度的广义分布函数Ωx(t, a)对仿射变换具有时间和尺度不变性,即
| $ {\mathit{\Omega }_{{x_{a' , b' }}}}\left( {t, a} \right) = {\mathit{\Omega }_x}\left( {\frac{{t - b' }}{{a' }}, \frac{a}{{a' }}} \right) $ | (1) |
则有
| $ {\mathit{\Omega }_x}\left( {t, a;\mathit{\Pi }} \right) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\mathit{\Pi }\left( {\frac{{s - t}}{a}, a\xi } \right)} } {W_x}(s, \xi ){\rm{d}}s{\rm{d}}\xi $ | (2) |
式中:t、b′、s为时间变量;a、a′为尺度变量;Π(t, v)是一个任意平滑函数;Wx(s, ξ)是信号x(t)的Wigner-Ville变换,ξ、v为频率变量。式(2)表示时间尺度分布的全体定义了仿射类时频分布。仿射类时频分布是一种通过时移和伸缩变换实现的时频能量分布函数,其核心思想就是设计affine平滑函数,尽可能减少交叉项,提高频率分辨率。很明显,Wigner-Ville分布(WVD)是仿射类时频分布的组成部分,是连接Cohen类和仿射类时频分布的纽带。
1.1 尺度图尺度图是一种仿射类时频分布。实际上,它可作为WVD的平滑形式
| $ {\left| {{T_x}\left( {t, a;\mathit{\Psi }} \right)} \right|^2}\\ \;\;\;\;\;\;\; = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {{W_x}\left( {s, \xi } \right)} } {W_\mathit{\Psi }}\left( {\frac{{s - t}}{a}, a\xi } \right){\rm{d}}s{\rm{d}}\xi $ | (3) |
因此,尺度图就是对应于平滑函数Π(t, v)=WΨ(t, v)的仿射类分布。在Cohen类分布中,谱图可以用平滑后的WVD形式[32]
| $ {S_x}\left( {t, \upsilon } \right) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {{W_h}\left( {s - t, \xi - \upsilon } \right)} } {W_x}(s, \xi ){\rm{d}}s{\rm{d}}\xi $ | (4) |
通过比较谱图的定义,发现尺度图是谱图在仿射类中的对应者。谱图是由WVD通过平滑得到的时频分布,而尺度图是由WVD经过仿射变换得到的时频分布。由上述定义可知:尺度是仿射相对应的频谱(信号→频谱,仿射→尺度),且尺度图总是取正值。
1.2 仿射类平滑伪Wigner分布为了克服尺度图时域与频域分辨率之间的相互制约性,采用一个时域和频域分离的平滑窗函数,由此得到的分布称为仿射类平滑伪Wigner分布[31],即
| $ \begin{array}{l} {\rm{ASP}}{W_x}\left( {t, a} \right) = \frac{1}{a}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {h\left( {\frac{\tau }{a}} \right)} } \cdot\\ \;\;\;\;\;\;\;\;\;\;g\left( {\frac{{s - t}}{a}} \right)x\left( {s + \frac{\tau }{2}} \right){x^*}\left( {s - \frac{\tau }{2}} \right){\rm{d}}s{\rm{d}}\tau \end{array} $ | (5) |
式中:τ为时间变量;上角“*”表示取共轭。由上述定义可知,通过选择不同的时域平滑窗函数g和频域平滑窗函数h,独立地确定时间和尺度分辨率,并很好地抑制时域和频域两个方向的交叉项。
WVD具有最好的时间和频率分辨率,但同时也带来严重的交叉干扰;尺度图具有最低的时间和频率分辨率,但几乎没有交叉项。因此,仿射类平滑伪Wigner分布很好地结合了二者的优点,明显增强了频率分辨能力,是一种十分实用的时频分析方法。因此,本文采用仿射类平滑伪Wigner分布。
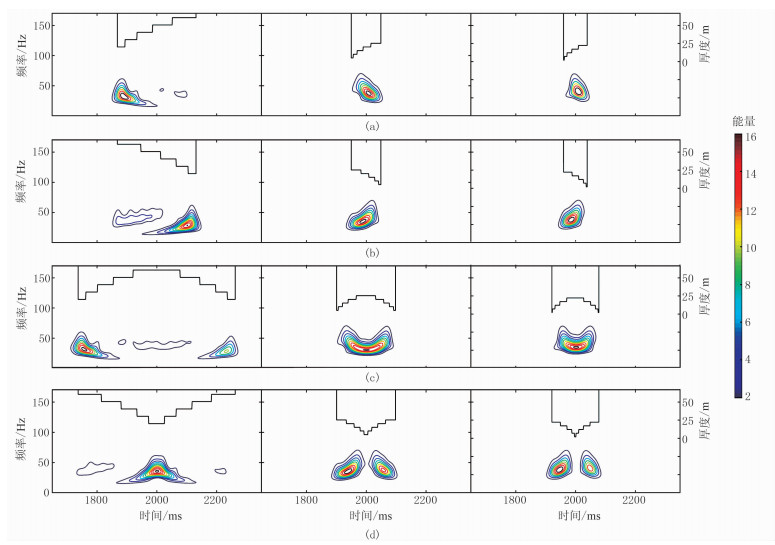
2 典型时频特征分析 2.1 地质模型的建立及波动方程正演模拟根据大庆探区地层韵律类型,将递变型薄互层分为递增型、递减型、先增后减型、先减后增型等4种类型。在均匀泥岩背景下,设计3种地层总厚度、互层数为5的递变型薄互层地质模型,设相邻砂、泥岩厚度相等,并按照一定的厚度变化量增、减。递减型薄互层结构是递增型的逆序排列;先增后减型、先减后增型是递增型和递减型的不同组合。基于波场延拓理论,采用深度域相移法正演模拟获取单炮记录;从炮记录零炮检距位置抽取地震道进行仿射类时频分析,得到不同递变型薄互层的时频谱(图 1)。
|
图 1 递变型薄互层典型模型的仿射类时频分布
(a)递增型;(b)递减型;(c)先增后减型;(d)先减后增型 左:第一层砂、泥岩厚度均为20m,砂、泥岩厚度变化量为10m,则最后一层砂岩厚度为60m,整个薄互层总厚度为340m;中:第一层砂、泥岩厚度均为5m,砂、泥岩的厚度变化量为5m,则最后一层砂岩厚度为25m,整个薄互层总厚度为125m;右:第一层砂、泥岩厚度均为2m,砂、泥岩的厚度变化量为5m,则最后一层砂岩厚度为22m,整个薄互层总厚度为98m。黑色折线代表不同薄互层地层厚度变化,下同。设砂岩速度为2918m/s,密度为2.14g/cm3,泥岩速度为3180m/s,密度为2.32g/cm3,反射系数为0.084。震源为零相位雷克子波,主频为39Hz(峰值频率为30Hz);采取中间放炮、两边接收的采集方式,地震道采样点数为4000,采样间隔为0.001s,道间距为10m,共1000道 |
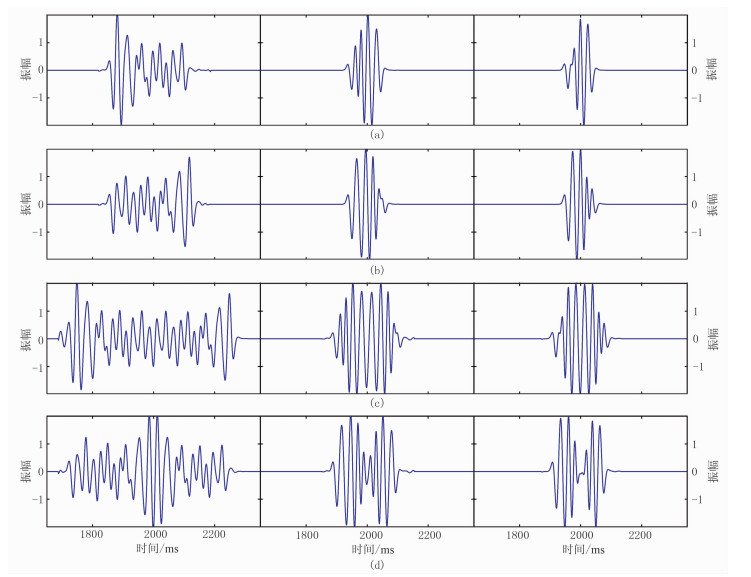
从波形上看,不同厚度的递变型薄互层波形特征具有相同的变化规律:薄层处波形密集,厚层处波形稀疏(图 2);整个波形最大振幅总是位于1/4波长调谐厚度处,其他位置无论是地层增厚还是减薄,振幅均相对减小;当单层厚度大于1/2波长时,振幅趋于恒定。此外,当地层很厚时,递减型(图 2b)的波形是递增型(图 2a)的镜像,当地层减薄时,由于地震波球面扩散效应导致递减型与递增型的振幅略有不同。对于先增后减型(图 2c)和先减后增型(图 2d)两种复合类型,其基本组成单元具有相对独立性,在顶、底界面附近保持递增型或递减型的波形特性;复合类型的中部如果是厚地层与厚地层相遇,则振幅增强;如果是薄地层与薄地层相遇,则振幅减弱。
|
图 2 递变型薄互层典型模型的时域波形 (a)递增型;(b)递减型;(c)先增后减型;(d)先减后增型 |
从时频谱上看,4种薄互层类型的时频响应特征具有相同的变化规律:在薄互层内部,随着地层减薄,频率逐渐升高,谱宽增大,呈“薄升厚降”、“薄宽厚窄”的变化规律(图 1),即高频端指向地层变薄方向,低频端指向地层变厚方向,地层厚度变化越大,这种趋势越明显。此外,在厚度1/4波长处时频能量最强,谱宽最大。当单层厚度小于1/8波长时,由于破坏性干涉作用,时频能量大幅衰减,薄层处时频能量被相对压制,使频谱能量向地层中心移动(图 1c中、图 1c右);当地层总厚度较大时,单层厚度小于1/2波长的地层对单层厚度大于1/2波长地层的时频能量具有相对压制作用,二者之间存在较宽的陷频区,将时频谱割裂(图 1b左、图 1c左、图 1d左)。
当地层总厚度很大时,复合类型时频谱分别呈基本类型的时频特点,二者呈镜像关系;当地层总厚度减小时,两种基本类型时频谱相互接近、融合(图 1c中、图 1c右);当中部单层厚度大于1/4波长时,厚层与厚层相遇,时频能量相对增强;当中部单层厚度小于1/8波长时,薄层与薄层相遇,时频能量相对压制,整体表现为时频谱中断(图 1d中、图 1d右)。
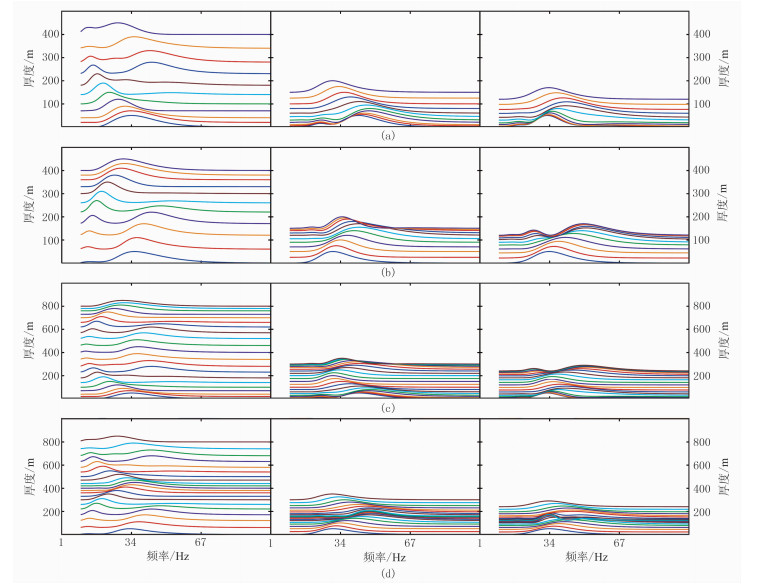
由所有厚度大于1/8波长的单层中部抽取的瞬时频谱可见,“薄升厚降”,“薄宽厚窄”的变化规律更明显:递增型瞬时频谱的峰值频率随着地层增厚逐渐降低,频带宽度逐渐减小(图 3a左);递减型瞬时频谱的峰值频率随着地层减薄逐渐升高,频带宽度逐渐增大(图 3b左);先增后减型瞬时频谱的峰值频率随着地层厚度变化先降低再升高,频带宽度先变窄后变宽(图 3c左);先减后增型瞬时频谱的峰值频率随着地层厚度变化先升高后降低,频带宽度先变宽后变窄(图 3d左)。同时,厚层方向出现第二频率峰,与第一频率峰之间存在较宽的陷频带。
|
图 3 递变型薄互层典型模型的瞬时频谱 (a)递增型;(b)递减型;(c)先增后减型;(d)先减后增型 |
当单层厚度小于1/8波长,随着单层厚度变小,各单层瞬时频谱的峰值频率呈逐渐降低的趋势,频宽逐渐变窄,主峰左侧存在陷频(图 3a中、图 3a右、图 3b中、图 3b右),这种变化规律是笔者的新发现。
3 控制因素分析从上述分析可知,不同递变型薄互层的时频谱主要受薄互层的总厚度和厚度变化量两个因素影响。由于地层厚度变化规律、组合关系相同的递增型与递减型薄互层时频特征具有镜像关系,而复合型又是递增型、递减型的某种组合,因此,下述研究均以递增型薄互层为例。
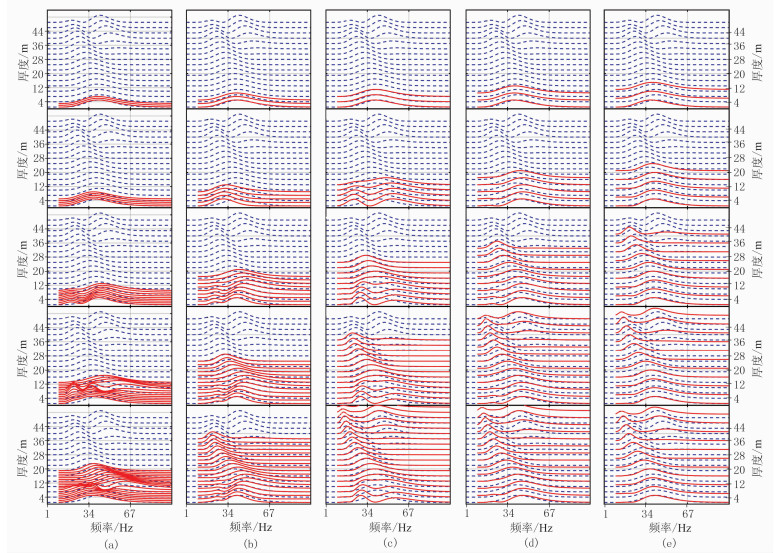
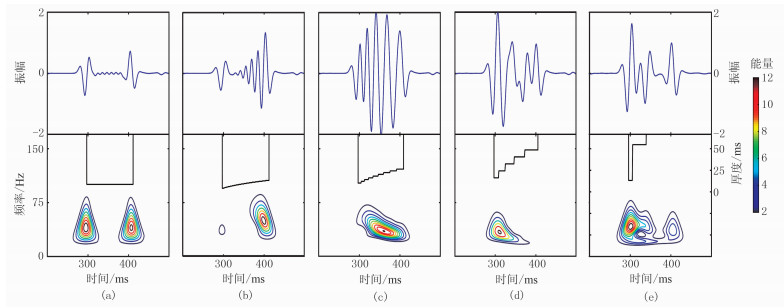
3.1 总厚度不变,互层数、厚度变化量不同固定薄互层总厚度,改变互层数,探讨不同厚度变化量的时频变化规律。图 4为递增型的波形及时频分布。由图可见,单层厚度变化量为0.5m(图 4b)是等厚薄互层(图 4a,单层厚度为8.5m(1/8波长))向单层厚度变化量为2m(图 4c)的过渡类型,定义为过渡性递变型薄互层。此类型上半部分(单层厚度小于1/8波长)保留了等厚薄互层波形和频谱特性,而下半部分却表现为递增型薄互层的时频特性,说明递增型薄互层的“薄升厚降”、“薄宽厚窄”时频特征变化规律只发生在单层厚度大于1/8波长的厚度区间,同时也证明了等厚薄互层是递变型薄互层的一个特例。
|
图 4 递增型的波形(上)及时频分布(下) 薄互层总厚度为162m,互层数依次为10、10、5、3、2,单层厚度变化量依次为0(a)、0.5(b)、2(c)、8(d)、41m(e) |
对比单层厚度变化量为2m(图 4c上)、8m(图 4d上)、41m(图 4e上)的波形可见:除了具有递增型典型特征外,随着单层厚度变化量增大和第一单层厚度增大(大于1/8波长),表现为振荡波(图 4c上),界面子波、复合波(图 4d上),界面子波、复合波、独立子波(图 4e上);当所有单层厚度小于1/2波长时,表现为幅值不等的振荡波,并在1/4波长处振幅取得最大值;当所有单层厚度大于1/2波长且小于1个波长时,相邻各层反射波叠加在一起,形成复合波,每一个复合波的振幅近似相等,不反映单层厚度;当单层厚度大于1个波长时,形成独立反射子波,表征通常意义上的厚层。
随着单层厚度变化量的增加,递增型薄互层的“薄升厚降”、“薄宽厚窄”时频谱在向厚层方向拉伸的同时向薄层方向挤压(图 4d下),厚层方向的频谱能量、谱宽、峰值频率迅速降低;此后,当单层厚度进一步加大并大于1/2波长时,各单层之间彼此干涉作用减弱而使子波谱趋于分离,形成相对独立的子波谱。单层厚度变化量较小时,顶界面子波谱不完整,低频方向出现明显陷频,使子波谱呈现明显向高频内凹的月牙形(图 4c下);当厚度变化量增大时,顶界面子波谱虽然完整,但厚层方向出现明显向低频内凹的陷频带,从而挤压厚层的第一频率峰,使第一频峰逐渐变窄(图 4d下);当单层厚度变化量超过1/2波长时,表现为强顶界面子波谱,形态清晰完整;厚度超过波长的单层表现为完全独立的子波谱,能量较顶界面子波谱弱;中间层子波谱虽有子波谱形态,但由于其与顶界面存在一定干涉作用而遭到破坏(图 4e下)。
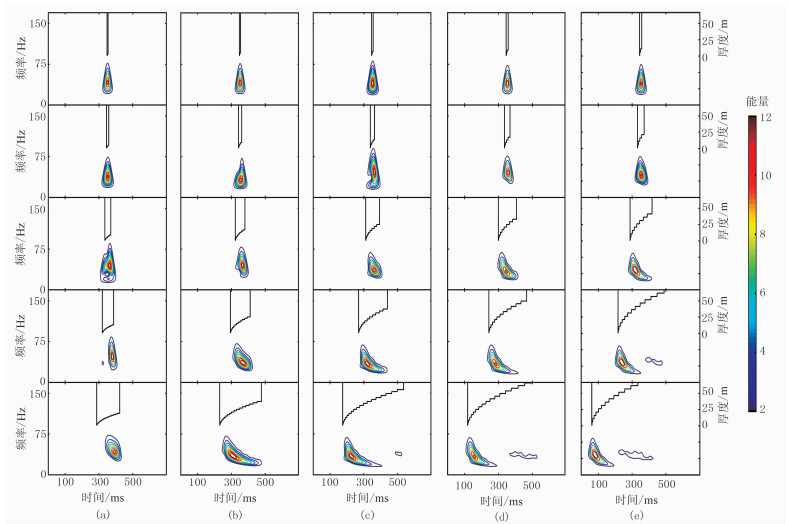
3.2 不同厚度区间、互层数、厚度变化量地下实际薄互层的单层厚度变化量很少大于5m,同时具有超薄单层组合的薄互层也是本文研究的重点。因此,设计25种地质模型,设置不同互层数和厚度变化量,因此总厚度也不同。将25种地质模型、时频谱叠合(图 5),以研究不同厚度区间、不同互层数和不同厚度变化量的递增型薄互层时频变化规律。
|
图 5 递增型薄互层时频分布 (a)厚度变化量为1m,从上至下互层数分别为2(a1)、3(a2)、5(a3)、7(a4)、10(a5);(b)厚度变化量为2m,从上至下互层数分别为2(b1)、3(b2)、5(b3)、7(b4)、10(b5);(c)厚度变化量为3m,从上至下互层数分别为2(c1)、3(c2)、5(c3)、7(c4)、10(c5);(d)厚度变化量为4m,从上至下互层数分别为2(d1)、3(d2)、5(d3)、7(d4)、10(d5);(e)厚度变化量为5m,从上至下互层数分别为2(e1)、3(e2)、5(e3)、7(e4)、10(e5) |
当薄互层总厚度小于1/4波长时,递增型薄互层时频谱均表现为单子波谱(图 5a1、图 5b1、图 5c1、图 5d1、图 5e1、图 5a2),与单一薄层时频谱类似,只是频谱能量随着地层总厚度增大略有增大。因此,当地层总厚度小于1/4波长时,无论是哪类薄互层,均不可分辨,定义为等效薄层。
当薄互层总厚度大于1/4波长且薄互层最大单层厚度小于1/8波长时,底界面出现类子波谱,高频尖峰指向薄互层底界面(图 5b2、图 5a3),而顶界面薄层的时频谱与底界面子波谱出现干涉融合,总体上表现出与典型递增型频谱特征相反的变化规律,即频带“薄窄厚宽”,频率“薄降厚升”;随着地层总厚度增加,整个频谱低频端能量被干涉压制,出现较宽的陷频区(图 5a3)。
当最大单层厚度大于1/8波长而小于1/4波长时,子波谱能量出现“厚强薄弱”特征,频谱略向厚层方向拉伸,高频端指向地层中部,低频端部分能量被压制,表现为薄层端出现明显的陷频区(图 5c2、图 5d2、图 5b3);当厚度变化量不大于1m、地层总厚度大于波长、最大单层厚度小于1/4波长时,薄互层上部所有厚度小于1/8波长地层的能量均遭受破坏性干涉,由于能量弱导致顶界面子波谱被压制,只在薄互层中下部保留能量(图 5a4、图 5a5),频谱最高频指向单层厚度为1/8波长位置处,并随着地层增厚向厚层方向拉伸变窄,反映了等厚薄互层向递变型薄互层的过渡类型。
当最大单层厚度大于1/4波长且小于1/2波长、厚度变化量小于3m时,递增型薄互层薄层端由于单层厚度小于1/8波长而产生强烈破坏性干涉作用,导致高频能量损失,频谱能量被压制;时频谱向厚层方向伸展拉伸,形成“薄升厚降”、“薄宽厚窄”的典型频谱特征;随着地层总厚度的增加和厚度变化量增大,时频谱拉伸程度加大,并扩展到薄互层的最底部(图 5c3、图 5b4、图 5c4、图 5b5)。
当厚度变化量大于3m、最大单层厚度约为1/2波长时,时频谱覆盖地层整个区域,薄层端和厚层端无明显压制、挤压现象,反映了中间过渡类型(图 5e2、图 5d3、图 5e3)。
当最大单层厚度大于1/2波长时,所有单层厚度小于1/2波长的地层对大于1/2波长的地层具有一定的能量压制作用,中间存在明显的陷频区而将二者割裂;时频谱主要位于薄互层顶部,高频端指向薄层方向,低频端指向厚层方向,地层越厚,时频谱向薄层方向挤压越强烈,导致厚层方向频带变窄(图 5d4、图 5e4、图 5c5、图 5d5、图 5e5)。
综上所述,递变型薄互层的频谱特征是渐变的,由等效薄层、过渡性递变型薄互层向递变型薄互层变化,时频谱也相应地由单一子波谱(图 5a1、图 5b1、图 5c1、图 5d1、图 5e1、图 5a2)、低频薄向拉伸底峰子波谱(图 5b2、图 5a3)、顶弱底强“藻”型子波谱(图 4b下、图 5a4、图 5a5)、低频厚向内凹型子波谱(图 4c下、图 5c2、图 5b3)、单楔形子波谱(图 4d下、图 5d2、图 5e2、图 5c3、图 5b4)向双楔形子波谱(图 5d3、图 5e3、图 5c4、图 5d4、图 5e4、图 5b5、图 5c5、图 5d5、图 5e5)变化。从递变型薄互层判别来说,上述时频特征分别对应不可判定区、难分辨区和可判定区。不同的递变型薄互层的主要时频能量出现在特定的厚度区间;在相同厚度变化量的情况下,地层总厚度越大,递变型薄互层时频特征越明显。
3.2.2 瞬时频谱特征分析为了探究递增型薄互层瞬时频谱随单层厚度的变化规律,从每一个地质模型各小层中心位置对应时刻抽取瞬时频谱,经归一化处理后与相同厚度的单一薄层的瞬时频谱叠合(图 6),借以考察瞬时频谱不同频率成分随单层厚度的变化规律。
总体上来说,当地层总厚度小于1/4波长时,递增型薄互层各单层的瞬时频谱与对应厚度的薄层瞬时频谱相重合,此时,无法区分薄层和薄互层(图 6a1、图 6b1、图 6c1、图 6d1、图 6e1、图 6a2)。
递变型薄互层内部厚度大于1/8波长的各小层均表现为“薄升厚降”、“薄宽厚窄”的瞬时频谱特性,与该区间范围内单一薄层的瞬时频谱变化规律一致,说明此部分薄互层的时频特性受薄层时频特性调控。
当互层数大于3、厚度变化量大于1m时,在相同厚度变化量、顶层厚度的情况下,随着互层数的增加,薄层方向的瞬时频谱表现出很好的继承性,说明相同的薄层组合特征具有相同的瞬时频谱特性(图 6e3、图 6e4、图 6e5);随着总厚度的增大,厚层方向第一频峰被压缩,与单一薄层相比频带急剧变窄,峰值频率降低并向低频移动;厚度超过1/2波长的单层出现第二频峰,与第一频峰之间存在较大的陷频带,与单一薄层相比,陷频带较薄层宽(图 6d3、图 6d4、图 6d5)。说明地层总厚度的增大对厚层方向的瞬时频谱产生一定影响,表现出明显不同于单一薄层的时频特征。
当厚度变化量为1、2m、递增型薄互层总厚度大于1/4波长时,厚度小于1/8波长各小层的瞬时频谱表现为幅度很弱的“薄降厚升”、“薄窄厚宽”时频特性(图 6b2、图 6a3、图 6b3、图 6a4、图 6b4、图 6a5、图 6b5),但在厚度变化量不大于1m的情况下,由于强烈干涉作用,导致薄互层中部厚度接近1/8波长的地层能量损失殆尽,出现低幅陷频区(图 6a4、图 6a5);
互层数为3与互层数较大、相同地层结构的薄互层的瞬时频谱总体趋势一致,但还存在差别;如图 6c2中前4小层主频附近的能量被干涉压制,陷频带将频谱分割为2个频峰,不同单层的峰值频率及陷频近似相等;但由图 6c3、图 6c4、图 6c5可见,第一频峰较窄,随着单层减薄峰值频率逐渐降低,第二频峰幅度较小,说明地层总厚度增大对薄层方向的瞬时频谱产生一定影响,明显表现出不同于单一薄层的时频特征。
3.2.3 时域波形特征分析不同互层数、厚度变化量、厚度区间对应的时域波形不同,归纳如下:
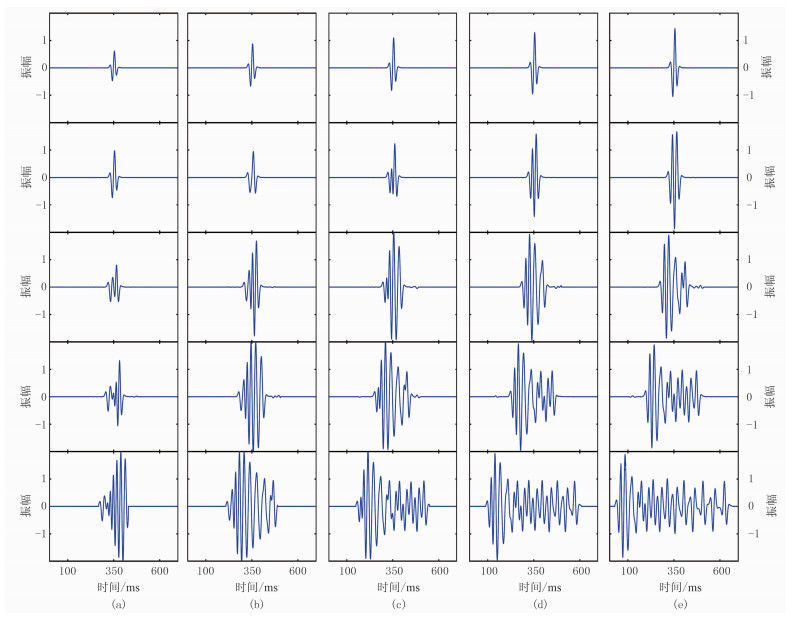
(1) 等效薄层独立子波。对应地层总厚度小于1/4波长、最大单层厚度小于1/8波长,振幅较小,但随着地层总厚度增加略有增大(图 7a1、图 7b1、图 7c1、图 7d1、图 7e1、图 7a2)。
|
图 7 厚度递增型薄互层时域波形 |
(2) 薄层复合波。对应地层总厚度大于1/4波长、最大单层厚度小于1/8波长,各薄单层之间产生破坏性干涉作用,中高频能量损失,形成振幅较小的复合波(图 7b2、图 7c2、图 7a3)。
(3) 界面子波+渐增型振荡波。为等厚薄互层向递变型薄互层过渡的波形特征,厚度变化量不大于1m、最大单层厚度为1/8~1/4波长。厚度小于1/8波长的各单层相互干涉,能量大部分损失殆尽,只保留了界面子波波形;厚度大于1/8波长的各单层随着地层增厚形成振幅渐增型振荡波形,表现出递增型薄互层波形特征(图 4b上、图 7a4、图 7a5)。
(4) 振荡波。对应最大单层厚度小于1/2波长,波形表现为中高频不等幅振荡,在1/4波长厚度处振幅取得最大值,是递增型薄互层时频谱主体波形(图 2a中、图 2b右,图 4c上,图 7d2、图 7e2、图 7b3、图 7c3、图 7b4)。
(5) 厚层复合波。对应最大单层厚度为1/2~1个波长,各单层反射波叠合时发生干涉,高频成分存在不同程度的损失,形成中低频等幅复合波(图 2a左、图 2b左、图 2c左、图 2d左,图 4d上,图 7d3、图 7e3、图 7c4、图 7d4、图 7e4、图 7b5、图 7c5)。
(6) 厚层独立子波。对应地层厚度大于波长,与邻近的复合波发生明显分离,为独立子波特性,实际上该单层已经属于厚层范畴(图 7d5、图 7e5)。
由于不同厚度区间、单层组合特征薄互层的时域波形特征不同,因此可以依据波形特点分析单层组合特征、解释厚度和划分地层。
4 讨论虽然不同厚度变化量、不同互层数的递变型薄互层的时频特征千差万别,但其中还是存在一定调控机理。笔者注意到:当单层厚度大于1/8波长时,递变型薄互层总体时频特征呈“薄升厚降”,“薄宽厚窄”的时频特性;厚度为1/4波长的单层,其时域波形振幅最大,瞬时频谱与相同厚度的单一薄层完全重合,说明该厚度区间的时频特性主要受薄层时频特性调控,这是递变型薄互层最主要的时频调控机制。
研究发现,文中所讨论的薄层分为单一薄层、地层总厚度小于1/4波长的等效薄层和厚度小于1/8波长各单层组合成的递变型薄层(厚层递变型薄互层中的一部分),三者的时频特性完全不同。厚度小于1/4波长的单一薄层具有升频降幅特性[19],随着薄层减薄,峰值频率逐渐增大,谱宽增加,频谱幅度降低;等效薄层的时域波形和子波谱均与单一薄层一致,但是各小层的瞬时频谱不随单层厚度发生变化,各种频谱特征均相同(图 5a1、图 5b1、图 5c1、图 5d1、图 5e1、图 5a2)。递变型薄互层中的渐变型薄层的时域波形特征和频谱特征均与单一薄层不同,瞬时频谱表现为随着地层减薄,峰值频率降低、频宽变窄的特性。这三类薄层在地层中广泛分布,时频特征又完全不同,在实际解释应用时应予以特别重视。
与时域波形存在厚度分区特性一样,时频谱也表现出厚度分区特性,不同类型递变型薄互层的主要时频能量出现在特定的厚度区间(1/8~1/2波长),对其他厚度区间的能量具显著压制作用。同样,瞬时频谱也存在厚度分区特性:厚度小于1/8波长的各小层的瞬时频谱表现为随着单层减薄,频率逐渐降低的现象;厚度大于1/8波长且小于1/2波长的各小层的瞬时频谱特征与单一薄层相近;厚度大于1/2波长各小层的瞬时频谱特征表现为第一频峰被压缩,频带变窄,相比于单一薄层,峰值频率向低频方向移动,第一峰与第二峰之间存在明显的陷频带。
5 结论(1) 总体上,总厚度大于1/4波长的递变型薄互层表现为峰值频率“薄升厚降”、频带“薄宽厚窄”时频变化规律;厚度组合特征相同的递增型和递减型时频特征呈现镜像关系,复合类型是二者时频特征的某种组合。总厚度小于1/4波长的递变型薄互层形成等效薄层,其时频特征与单一薄层类似,无法区分。
(2) 在厚度变化量小于2m的递变型薄互层中,厚度小于1/8波长的各单层的时频特征与整体时频特征明显不同,即随着地层减薄,峰值频率降低,频宽变窄。这种特性往往被厚层方向的时频特征所压制、掩盖。
(3) 递变型薄互层中厚度大于1/8波长的各小层的时频变化主要受薄层时频特性调控,这是递变型薄互层最主要的时频响应调控机制。厚度小于1/8波长的各小层由于受破坏性干涉作用,导致高频能量损失,且层越薄,能量损失越严重,导致峰频低移、频带变窄、幅度减弱。这是递变型薄互层辅助调控机制。
(4) 递变型薄互层的时频特征存在明显厚度分区现象。在不同厚度区间,其时域波形特征不同,时频谱主要能量只出现在特定的厚度区间(1/8~1/2波长),对其他厚度区间的能量具显著压制作用;瞬时频谱在不同厚度区间表现出“薄低”、“中同”、“厚窄”特性。
| [1] |
Taner M T.Attributes revisited.http://www.rocksolidimages.com/pdf/attrib_revisited.htm[DB/OL], 2000.
|
| [2] |
Coléou T, Poupon M, Azbel K. Unsupervised seismic facies classification:A review and comparison of techniques and implementation[J]. The Leading Edge, 2003, 22(10): 942-953. DOI:10.1190/1.1623635 |
| [3] |
Partyka G, Gridley J, Lopez J. Interpretational applications of spectral decomposition in reservoir cha-racterization[J]. The Leading Edge, 1999, 18(3): 353-360. DOI:10.1190/1.1438295 |
| [4] |
Portniaguine O and Castagna J P.Inverse spectral decomposition[C]. SEG Technical Program Expanded Abstracts, 2004, 23: 1786-1789.
|
| [5] |
Puryear C I, Castagna J P. Layer-thickness determination and stratigraphic interpretation using spectral inversion:Theory and application[J]. Geophy-sics, 2008, 73(2): R37-R48. |
| [6] |
Matos M C and Marfurt K J.Inverse continuous wavelet transform "deconvolution"[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 1861-1865.
|
| [7] |
Smith M, Perry G, Stein J, et al. Extending seismic bandwidth using the continuous wavelet transform[J]. First Break, 2008, 26(6): 97-102. |
| [8] |
Zeng H L. Frequency-dependent seismic-stratigraphic and facies interpretation[J]. AAPG Bulletin, 2013, 97(2): 201-221. DOI:10.1306/06011212029 |
| [9] |
Chung H, Lawton D C. Frequency characteristics of seismic reflections from thin beds[J]. Canadian Journal of Exploration Geophysicists, 1995, 31(1): 32-37. |
| [10] |
范明霏, 吴胜和, 曲晶晶, 等. 基于广义S变换模极大值的薄储层刻画新方法[J]. 石油地球物理勘探, 2017, 52(4): 805-814. FAN Mingfei, WU Shenghe, QU Jingjing, et al. A new interpretation method for thin beds with the maximum modulus based on the generalized S transform[J]. Oil Geophysical Prospecting, 2017, 52(4): 805-814. |
| [11] |
王鹏, 胡向阳, 魏水建. 基于改进的相位目标函数估算薄层厚度[J]. 石油地球物理勘探, 2018, 53(1): 178-185. WANG Peng, HU Xiangyang, WEI Shuijian. Thin bed thinckness estimation based on improved phase objective function[J]. Oil Geophysical Prospecting, 2018, 53(1): 178-185. |
| [12] |
Widess M B. How thin is a thin bed?[J]. Geophysics, 1973, 38(6): 1176-1180. DOI:10.1190/1.1440403 |
| [13] |
Kallweitt R S, Wood L C. The limits of resolution of zero-phase wavelets[J]. Geophysics, 1982, 47(7): 1035-1046. DOI:10.1190/1.1441367 |
| [14] |
赵晨光. 薄互层地震反射波的特征分析[J]. 石油地球物理勘探, 1986, 21(1): 32-46. ZHAO Chen'guang. The analysis of seismic reflection from thin interbedding[J]. Oil Geophysical Prospecting, 1986, 21(1): 32-46. |
| [15] |
苏盛甫. 薄储集层的反射特征和定量解释方法[J]. 石油地球物理勘探, 1988, 23(4): 387-402. SU Shengfu. Thin-reservoir reflection and the quantitative interpretation method[J]. Oil Geophysical Prospecting, 1988, 23(4): 387-402. |
| [16] |
Knapp R W. Vertical resolution of thick beds, thin beds, and thin-bed cyclothems[J]. Geophysics, 1990, 55(9): 1183-1190. DOI:10.1190/1.1442934 |
| [17] |
张玉芬, 熊维纲. 石油地震勘探中薄互层的反射系数序列振幅谱特征分析[J]. 地球科学——中国地质大学学报, 1994, 19(5): 685-693. ZHANG Yufen, XIONG Weigang. Characteristic analysis of amplitude spectra of reflection coefficient of thin interbedding in oil prospecting[J]. Earth Science:Journal of China University of Geosciences, 1994, 19(5): 685-693. |
| [18] |
孙鲁平, 郑晓东, 首皓, 等. 薄层地震峰值频率与厚度关系研究[J]. 石油地球物理勘探, 2010, 45(2): 254-259. SUN Luping, ZHENG Xiaodong, SHOU Hao, et al. The study of relation between thin-layer thickness and peak frequency[J]. Oil Geophysical Prospecting, 2010, 45(2): 254-259. |
| [19] |
李雪英, 陈树民, 王建民, 等. 薄层时频特征的正演模拟[J]. 地球物理学报, 2012, 55(10): 3410-3419. LI Xueying, CHEN Shumin, WANG Jianmin, et al. Forward modeling studies on the time-frequency cha-racteristics of thin layers[J]. Chinese Journal of Geophysics, 2012, 55(10): 3410-3419. DOI:10.6038/j.issn.0001-5733.2012.10.024 |
| [20] |
李雪英, 文慧俭, 陈树民, 等. 等厚薄互层时频特征的正演模拟[J]. 地球物理学报, 2013, 56(3): 1033-1042. LI Xueying, WEN Huijian, CHEN Shumin, et al. Forward modeling studies on the time-frequency characteristics of isopachous thin interbeding[J]. Chinese Journal of Geophysics, 2013, 56(3): 1033-1042. |
| [21] |
刘力辉, 李建海, 孙莹频, 等. 时频属性法薄互层预测[J]. 石油地球物理勘探, 2017, 52(6): 1261-1268. LIU Lihui, LI Jianhai, SUN Yingpin, et al. Thin interbed prediction with time and frequency attributes[J]. Oil Geophysical Prospecting, 2017, 52(6): 1261-1268. |
| [22] |
杨昊, 郑晓东, 李劲松, 等. 基于匹配追踪的薄层自动解释方法[J]. 石油地球物理勘探, 2013, 48(3): 429-435. YANG Hao, ZHENG Xiaodong, LI Jingsong, et al. Thin-bed automatic interpretation based on matching pursuit[J]. Oil Geophysical Prospecting, 2013, 48(3): 429-435. |
| [23] |
刘传虎, 刘福贵, 李卫忠. 时频分析方法及在储层预测中的应用[J]. 石油地球物理勘探, 1996, 31(增刊1): 11-20. LIU Chuanhu, LIU Fugui, LI Weizhong. Time frequency analysis method and its application in reservoir predicting[J]. Oil Geophysical Prospecting, 1996, 31(S1): 11-20. |
| [24] |
刘传虎, 王学忠. 构造-层序分析模型地震响应特征与应用[J]. 石油地球物理勘探, 2011, 46(6): 938-943. LIU Chuanhu, WANG Xuezhong. Seismic responses of structure-sequence models and their applications in hydrocarbon exploration[J]. Oil Geophysical Prospecting, 2011, 46(6): 938-943. |
| [25] |
崔凤林, 管叶君. 时频分析-薄互层结构研究的新途径[J]. 石油物探, 1992, 31(2): 1-15. CUI Fenglin, GUAN Yejun. Time-frequency analysis:A new way for thin interbeds examination[J]. Geophysical Prospecting for Petroleum, 1992, 31(2): 1-15. |
| [26] |
张玉芬, 熊维纲, 杜聿麟. 时频分析方法在薄储集层横向预测中的应用[J]. 地质科技情报, 1995, 14(1): 83-88. ZHANG Yufen, XIONG Weigang, DU Yulin. Application of time frequency analysis method to thin re-servoir lateral prediction[J]. Geological Science and Technology Information, 1995, 14(1): 83-88. |
| [27] |
雷克辉, 朱广生, 毛宁波, 等. 在小波时频域中研究沉积旋回[J]. 石油地球物理勘探, 1998, 33(增刊1): 72-78. LEI Kehui, ZHU Guangsheng, MAO Ningbo, et al. Study of sedimentary cycles in time-frequency domain of wavelet[J]. Oil Geophysical Prospecting, 1998, 33(S1): 72-78. |
| [28] |
魏学强, 李辉峰, 杨超. 基于广义S变换的沉积旋回分析方法研究[J]. 西安石油大学学报(自然科学版), 2013, 28(4): 35-40. WEI Xueqiang, LI Huifeng, YANG Chao. Study of sedimentary cycle analysis method based on genera-lized S transform[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 2013, 28(4): 35-40. DOI:10.3969/j.issn.1673-064X.2013.04.006 |
| [29] |
崔永谦, 刘延利, 王孟华, 等. 利用地震资料Hilbert-Huang变换划分沉积旋回[J]. 石油地球物理勘探, 2016, 51(5): 983-989, 1001. CUI Yongqian, LIU Yanli, WANG Menghua, et al. Sedimentary cycle demarcation based on seismic Hilbert-Huang transformation[J]. Oil Geophysical Prospecting, 2016, 51(5): 983-989, 1001. |
| [30] |
Cohen L. Time-frequency distribution:A review[J]. Proceedings of the IEEE, 1989, 77(7): 941-981. DOI:10.1109/5.30749 |
| [31] |
司文荣, 李军浩, 袁鹏, 等. 局部放电脉冲的仿射类时频分布特性研究[J]. 仪器仪表学报, 2008, 29(10): 2168-2173. SI Wenrong, LI Junhao, YUAN Peng, et al. Study on characteristic of affine class time-frequency distribution for partial discharge pulse signal[J]. Chinese Journal of Scientific Instrument, 2008, 29(10): 2168-2173. DOI:10.3321/j.issn:0254-3087.2008.10.029 |
| [32] |
Hlawatsch F, Manickam T G, Urbanke R, et al. Smoothed pseudo-winger distribution, Choi-Williams distribution, and Cone-kernel representation:ambiguity domain analysis and experimental comparison[J]. Signal Processing, 2005, 43(2): 149-168. |



 李雪英, 黑龙江省大庆市高新技术开发区学府街99号东北石油大学地球科学学院, 163318。Email:
李雪英, 黑龙江省大庆市高新技术开发区学府街99号东北石油大学地球科学学院, 163318。Email: