② 中国石化胜利油田分公司物探研究院, 山东东营 257022
② Geophysical Research Institute, Shengli Oilfield Branch Co., SINOPEC, Dongying, Shandong 257022, China
速度是地震数据处理、解释的重要参数之一。全波形反演(FWI)充分利用了地震记录的各种信息(波形、相位和振幅等),相比于其他反演方法(如走时反演、射线反演等)具有更高精度。声波FWI已经被广泛应用于工业界。与声波FWI相比,弹性波FWI(EFWI)能同时获取纵、横波速度、密度等参数[1-4]。由于不同模式的波之间互相干扰,会出现更严重的非线性问题[5]。特别是转换横波受纵波影响严重,反演的横波速度精度远低于纵波速度[6-7]。对于部分异常体区域,纵、横波会互相影响,使得这些区域的反演结果不准确[8]。针对压制FWI多参数间的串扰效应,很多学者进行了深入的研究,其中主要有辐射模式法[6, 9-11]和Hessian矩阵法[8, 12-13]。辐射模式法根据不同波的辐射模式差异,基于反演的不同阶段数据对弹性参数的敏感性不同,选择不同的参数化方式和数据子集,从而降低参数之间的影响[11]。Operto等[12]和Wang等[8]分析块Hessian矩阵的非对角元素区域的值(为零时串扰效应最小),对其进行预处理,但块Hessian矩阵的计算成本巨大;Wang等[13]除了考虑Hessian矩阵的对角线元素之外,还采用了描述相同位置处的纵波速度、横波速度和密度之间的权重的非对角线元素压制串扰效应,提出了一种新的块对角拟Hessian逆矩阵对梯度进行预处理的方法,在不增加计算量的同时加快迭代效率。
纵、横波分离很早就被运用于弹性波逆时偏移过程中的串扰噪声压制[14-15],但纵、横波分离的EFWI直到近年才被提出。针对多参数反演的敏感核(梯度)有很强的串扰效应的问题,Ren等[6]首先提出在波数域采用纵、横波分离降低梯度串扰,以提高反演精度;Qu等[7]运用矢量纵、横波分离方法直接对纵、横波速度进行扰动,以求取PP梯度和SS梯度,也取得了很好的效果;Wang等[8]运用二阶弹性波方程的纵、横波解耦的方法分析Hessian矩阵以及分辨率矩阵,证实纵、横波分离的共轭梯度预处理能有效压制串扰影响。
常规FWI分别对每个震源进行处理,因此其计算成本与震源的数量成正比,计算量巨大。多震源处理是一种比较实用的降低计算量和存储量的方法,但同时会引入严重的串扰噪声。震源编码技术可以有效缓解多震源的串扰噪声,黄建平等[16]和李闯等[17]将所有单炮地震记录合成为若干个不同射线参数的平面波地震记录,极大提高了声波最小二乘逆时偏移的计算效率,但其要求炮间距不能太大,且不同射线参数的平面波不能太少。Krebs等[18]首先将随机相位震源编码技术运用到声波FWI,虽然大大提高了计算效率,但是存在较强的串扰噪声。随后,不同学者在此基础上做了改进[19-20]。Moghaddam等[21]研究发现,相位编码算法的目标泛函是真实目标泛函的随机无偏差估计,其梯度也是随机的。因此,李庆洋等[22]和李娜[23]考虑梯度的随机特性,将随机最优化思想推广到相位编码声波最小二乘逆时偏移。张盼等[24]采用各向异性全变分约束的动态震源随机编码实现了EFWI,取得了较好的效果。
弹性介质中波场复杂,在没有其他约束的情况下,多震源EFWI的结果精度较低[24],放炮数量较大时反演极易陷入局部极小值。为此,本文提出了基于纵横波分离的动态震源随机编码EFWI。采用动态震源随机编码技术将所有单炮随机分成几组超级炮,提高计算效率和压制串扰噪声;采用纵、横波分离的方法,分别用PP波和PS波计算纵、横波速度的梯度,缓解不同波模式之间的串扰。通过Marmousi模型和Marmousi-Ⅱ模型的试算,对比常规EFWI、常规多震源弹性波全波形反演(ES_EFWI)和纵、横波分离的多震源弹性波全波形反演(ES_SEFWI)的效率和效果,验证本文方法的优越性。
1 方法原理 1.1 常规EFWI原理时域二维一阶弹性波速度—应力波动方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\rho \frac{{\partial {v_x}}}{{\partial t}} = \frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{xz}}}}{{\partial z}}}\\ {\rho \frac{{\partial {v_z}}}{{\partial t}} = \frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}}} \end{array}} \right. $ | (1a) |
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {\tau _{xx}}}}{{\partial t}} = (\lambda + 2\mu )\frac{{\partial {v_x}}}{{\partial x}} + \lambda \frac{{\partial {v_z}}}{{\partial z}}}\\ {\frac{{\partial {\tau _{zz}}}}{{\partial t}} = \lambda \frac{{\partial {v_x}}}{{\partial x}} + (\lambda + 2\mu )\frac{{\partial {v_z}}}{{\partial z}}}\\ {\frac{{\partial {\tau _{xz}}}}{{\partial t}} = \mu \left( {\frac{{\partial {v_x}}}{{\partial z}} + \frac{{\partial {v_z}}}{{\partial x}}} \right)} \end{array}} \right. $ | (1b) |
式中:λ和μ为拉梅常数;ρ为密度;(vx, vz)为质点振动速度矢量;(τxx, τzz, τxz)为应力矢量。其伴随状态法为
| $ \left\langle {L\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{u}}^*}} \right\rangle = \left\langle {\mathit{\boldsymbol{u}},{L^*}{\mathit{\boldsymbol{u}}^*}} \right\rangle $ | (2) |
式中:L为正演算子;u为质点振动速度和应力矢量;“*”为伴随状态。将式(1)代入式(2),并进行相应的积分变换可得常规伴随方程
| $ \left\{ \begin{array}{l} \rho \frac{{\partial v_x^*}}{{\partial t}} = \frac{\partial }{{\partial x}}\left[ {(\lambda + 2\mu )\tau _{xx}^* + \lambda \tau _{zz}^*} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{\partial }{{\partial z}}\left( {\mu \tau _{xz}^*} \right) + \left( {d_{{v_x}}^{{\rm{cal}}} - d_{{v_x}}^{{\rm{obs}}}} \right)\\ \rho \frac{{\partial v_z^*}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {\mu \tau _{xz}^*} \right) + \frac{\partial }{{\partial z}}\left[ {\lambda \tau _{xx}^* + (\lambda + 2\mu )\tau _{zz}^*} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\left( {d_{{v_z}}^{{\rm{cal}}} - d_{{v_z}}^{{\rm{obs}}}} \right)\\ \frac{{\partial v_{xx}^*}}{{\partial t}} = \frac{{\partial v_x^*}}{{\partial x}}\\ \frac{{\partial \tau _{zz}^*}}{{\partial t}} = \frac{{\partial v_z^*}}{{\partial z}}\\ \frac{{\partial {\tau _{xz}}}}{{\partial t}} = \frac{{\partial v_x^*}}{{\partial z}} + \frac{{\partial v_z^*}}{{\partial x}} \end{array} \right. $ | (3) |
式中dobs、dcal分别代表观测和模拟地震记录。式(3)和式(1)差别较大,为了方便计算,对应力波场进行线性化处理
| $ {\mathit{\boldsymbol{\tau }}^{\rm{w}}} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{\tau }}^*} $ | (4) |
式中:τ*=(τxx*, τzz*, τxz*)T;过渡伴随波场τw=(τxxw, τzzw, τxzw)T;T是算子,具体形式为
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {\lambda + 2\mu }&\lambda &\\ \lambda &{\lambda + 2\mu }&\\ & & {\mu} \end{array}} \right] $ | (5) |
将式(4)代入式(3),通过变量替换可推得与式(1)形式一样的过渡伴随波动方程。采用相同的差分算法和程序代码对原始弹性波方程和过渡伴随方程进行求解。得到变换后的τw后,计算梯度时只需对式(4)做逆变换就可得到τ*。其中逆变换算子为
| $ {T^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\lambda + 2\mu }}{{4\mu (\lambda + \mu )}}}&{ - \frac{\lambda }{{4\mu (\lambda + \mu )}}}&\\ { - \frac{\lambda }{{4\mu (\lambda + \mu )}}}&{\frac{{\lambda + 2\mu }}{{4\mu (\lambda + \mu )}}}&\\ & &{\frac{1}{\mu }} \end{array}} \right] $ | (6) |
常规纵、横波梯度表示为[25]
| $ \frac{{\partial E}}{{\partial {v_{\rm{P}}}}} = 2\rho {v_{\rm{P}}}\sum {\left( {\frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_z}}}{{\partial z}}} \right)} \left( {\tau _{zz}^* + \tau _{xx}^*} \right) $ | (7) |
| $ \begin{array}{l} \frac{{\partial E}}{{\partial {v_{\rm{S}}}}} = 2\rho {v_{\rm{S}}}\sum {\left( {\frac{{\partial {v_x}}}{{\partial z}} + \frac{{\partial {v_z}}}{{\partial x}}} \right)} \tau _{xz}^* - \\ \;\;\;\;\;\;\;2\left( {\frac{{\partial {v_z}}}{{\partial z}}\tau _{xx}^* + \frac{{\partial {v_x}}}{{\partial x}}\tau _{zz}^*} \right) \end{array} $ | (8) |
式中E为目标泛函
| $ E = \frac{1}{2}{\left\| {d_{{v_x}}^{{\rm{cal}}} - d_{{v_x}}^{{\rm{obs}}}} \right\|^2} + \frac{1}{2}{\left\| {d_{{v_z}}^{{\rm{cal}}} - d_{{v_z}}^{{\rm{obs}}}} \right\|^2} $ | (9) |
式(7)中纵波梯度上正传波场项是个散度,即正传波场为纯纵波。因此纵波串扰比横波小,所以常规纵波反演精度比横波高。
1.2 基于波场分离的弹性波全波形反演(CSEFWI)原理李振春等[26]提出弹性波纵、横波分离方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{v_x} = {v_{x{\rm{P}}}} + {v_{x{\rm{S}}}}}\\ {{v_z} = {v_{z{\rm{P}}}} + {v_{z{\rm{S}}}}} \end{array}} \right. $ | (10) |
| $ \left\{ {\begin{array}{*{20}{l}} {\rho \frac{{\partial {v_{x{\rm{P}}}}}}{{\partial t}} = \frac{{\partial {\tau _{xx{\rm{P}}}}}}{{\partial x}}}\\ {\rho \frac{{\partial {v_{z{\rm{P}}}}}}{{\partial t}} = \frac{{\partial {\tau _{zz{\rm{P}}}}}}{{\partial z}}}\\ {\frac{{\partial {\tau _{xx{\rm{P}}}}}}{{\partial t}} = (\lambda + 2\mu )\left( {\frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_z}}}{{\partial z}}} \right)}\\ {\frac{{\partial {\tau _{zz{\rm{P}}}}}}{{\partial t}} = (\lambda + 2\mu )\left( {\frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_z}}}{{\partial z}}} \right)} \end{array}} \right. $ | (11a) |
| $ \left\{ {\begin{array}{*{20}{l}} {\rho \frac{{\partial {v_{x{\rm{S}}}}}}{{\partial t}} = \frac{{\partial {\tau _{xx{\rm{S}}}}}}{{\partial x}} + \frac{{\partial {\tau _{xz{\rm{S}}}}}}{{\partial z}}}\\ {\rho \frac{{\partial {v_{z{\rm{S}}}}}}{{\partial t}} = \frac{{\partial {\tau _{xz{\rm{S}}}}}}{{\partial x}} + \frac{{\partial {\tau _{zz{\rm{S}}}}}}{{\partial z}}}\\ {\frac{{\partial {\tau _{xx{\rm{S}}}}}}{{\partial t}} = - 2\mu \frac{{\partial {v_z}}}{{\partial z}}}\\ {\frac{{\partial {\tau _{zz{\rm{S}}}}}}{{\partial t}} = - 2\mu \frac{{\partial {v_x}}}{{\partial x}}}\\ {\frac{{\partial {\tau _{xz{\rm{S}}}}}}{{\partial t}} = \mu \left( {\frac{{\partial {v_x}}}{{\partial z}} + \frac{{\partial {v_z}}}{{\partial x}}} \right)} \end{array}} \right. $ | (11b) |
式中:(vxP, vzP)为纵波偏振速度分量;(vxS, vzS)为横波偏振速度分量;(τxxP, τzzP)为纵波应力分量;(τxxS, τzzS, τxzS)为横波应力分量。式(11a)为纯纵波波动方程,式(11b)为纯横波波动方程,两式相加与式(1)等价。
在纵波源激发条件下,纵波速度界面只反射纵波,横波速度界面既反射纵波也反射横波[27]。因此,借鉴逆时偏移方法,在计算纵、横波速度梯度时,正向传播波场都只采用纵波波场,计算纵波速度梯度时反传波场只用纵波伴随波场,计算横波速度梯度时反传波场只用横波伴随波场,保证具有相同物理意义的波场参与计算,最大限度压制纵、横波之间的串扰噪声。同理, 既然式(11)与式(1)等价,可由式(11)求得过渡纵、横波分离的伴随应力波场τsw=(τxxPw, τzzPw, τxxSw, τzzSw, τxzSw)T,再对τSw做线性逆变换得到纵、横波分离的伴随应力波场τS*=(τxxP*, τzzP*, τxxS*τzzS*, τxzS*)T,且
| $ \mathit{\boldsymbol{\tau }}_{\rm{S}}^ * = \mathit{\boldsymbol{T}}_{\rm{S}}^{ - 1}{\mathit{\boldsymbol{\tau }}^{{\rm{Sw}}}} $ | (12) |
式中TS-1是线性算子,表达式为
| $ \mathit{\boldsymbol{T}}_{\rm{S}}^{ - 1} = \left[ {\begin{array}{*{20}{c}} {\frac{{\lambda + 2\mu }}{{4\mu \left( {\lambda + \mu } \right)}}}&{ - \frac{\lambda }{{4\mu \left( {\lambda + \mu } \right)}}}&{}&{}&{}\\ { - \frac{\lambda }{{4\mu \left( {\lambda + \mu } \right)}}}&{\frac{{\lambda + 2\mu }}{{4\mu \left( {\lambda + \mu } \right)}}}&{}&{}&{}\\ {}&{}&{\frac{{\lambda + 2\mu }}{{4\mu \left( {\lambda + \mu } \right)}}}&{ - \frac{\lambda }{{4\mu \left( {\lambda + \mu } \right)}}}&{}\\ {}&{}&{ - \frac{\lambda }{{4\mu \left( {\lambda + \mu } \right)}}}&{\frac{{\lambda + 2\mu }}{{4\mu \left( {\lambda + \mu } \right)}}}&{}\\ {}&{}&{}&{}&{\frac{1}{\mu }} \end{array}} \right] $ | (13) |
得到纵、横波分离的伴随应力波场后,参照文献[6]给出波场分离纵、横波速度的梯度为
| $ {\left. {\frac{{\partial E}}{{\partial {v_{\rm{P}}}}}} \right|_{{\rm{PP}}}} = 2\rho {v_{\rm{P}}}\sum {\left( {\frac{{\partial {v_{x{\rm{P}}}}}}{{\partial x}} + \frac{{\partial {v_{z{\rm{P}}}}}}{{\partial z}}} \right)} \left( {\tau _{z{\rm{zP}}}^* + \tau _{xx{\rm{P}}}^*} \right) $ | (14) |
| $ \begin{array}{l} {\left. {\frac{{\partial E}}{{\partial {v_{\rm{S}}}}}} \right|_{{\rm{PS}}}} = 2\rho {v_{\rm{S}}}\sum {\left( {\frac{{\partial {v_{x{\rm{P}}}}}}{{\partial z}} + \frac{{\partial {v_{z{\rm{P}}}}}}{{\partial x}}} \right)} \tau _{xz{\rm{S}}}^* - \\ \;\;\;\;\;\;\;\;\;\;\;2\left( {\frac{{\partial {v_{z{\rm{P}}}}}}{{\partial z}}\tau _{xx{\rm{S}}}^* + \frac{{\partial {v_{x{\rm{P}}}}}}{{\partial x}}\tau _{zz{\rm{S}}}^*} \right) \end{array} $ | (15) |
新的纵、横波目标泛函变为
| $ {E_{\rm{P}}} = \frac{1}{2}{\left\| {d_{{v_{x{\rm{P}}}}}^{{\rm{cal}}} - d_{{v_{x{\rm{P}}}}}^{{\rm{obs}}}} \right\|^2} + \frac{1}{2}{\left\| {d_{{v_{z{\rm{P}}}}}^{{\rm{cal}}} - d_{{v_{z{\rm{P}}}}}^{{\rm{obs}}}} \right\|^2} $ | (16) |
| $ {E_{\rm{S}}} = \frac{1}{2}{\left\| {d_{{v_{x{\rm{S}}}}}^{{\rm{cal}}} - d_{{v_{x{\rm{S}}}}}^{{\rm{obs}}}} \right\|^2} + \frac{1}{2}{\left\| {d_{{v_{z{\rm{S}}}}}^{{\rm{cal}}} - d_{{v_{z{\rm{S}}}}}^{{\rm{obs}}}} \right\|^2} $ | (17) |
式(16)和式(17)中模拟的纯纵、横波地震记录是在波场传播的每一个采样时间自然分离并记录的。对于提取实际的纯纵、横波观测地震记录可以参照文献[28]在频率—波数域直接进行纵、横波分离。
基于纵、横波分离EFWI(SEFWI)的主要步骤概括:
(1) 求解纵、横波分离的弹性波方程,得到每一时间步长的正传纵波速度波场和分离的纵横波地震记录;
(2) 求解纵、横波分离的伴随弹性波方程,得到每一时间步的伴随应力波场;
(3) 用正传的纵波波场和反传的纵波伴随波场计算纵波速度梯度,用正传的纵波波场和反传的横波伴随波场计算横波速度梯度;
(4) 分别用纯纵波目标泛函和和纯横波目标泛函、采用三点抛物线插值法计算纵横波速度迭代步长;
(5) 采用非线性共轭梯度法对模型进行更新。
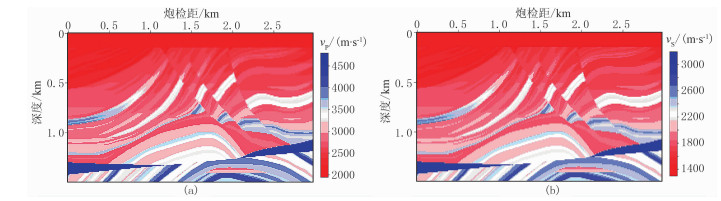
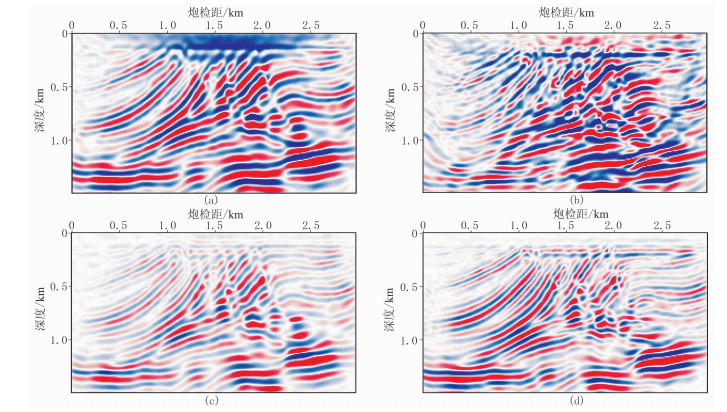
通过纵、横波分离的梯度公式和新的目标泛函缓解不同波模式间的串扰噪声,提高反演精度。以Marmousi模型为例进行说明。图 1为真实的纵、横波速度模型,采用12×12个节点的高斯平滑获得初始纵、横波速度模型。计算区域包含301×151个节点,节点间隔为10m;地表每隔10m布置1个检波器,共301个检波器。从地表x=50m处每隔100m放一炮,共30炮,采用主频为20Hz的雷克子波纵波源。图 2a和图 2b为第15炮的(vx, vz)分量地震记录;图 2c~图 2f为采用式(11)得到的合成(vxP, vxS, vzP, vzS)分量的地震记录;图 2g~图 2j为直接对(vx, vz)分量地震记录在频率—波数域进行分离得到的(vxP, vxS, vzP, vzS)分量地震记录[28]。由图 2g~图 2j可见,频率—波数域分离的纵、横波地震记录满足实际资料处理的精度要求。图 3a~图 3d分别为常规EFWI和SEFWI得到的第一次迭代的纵、横波速度梯度,从图 3a和图 3c可见纵波速度梯度串扰噪声相对较弱,与前文分析结果一致。图 3b中常规横波速度梯度受纵波波场影响串扰噪声较强,而图 3d中纵、横波分离的横波速度梯度同相轴连续、干净,几乎没有串扰影响。因此,通过波场分离可以压制多波引起的串扰影响。但求解式(11)的计算量约为式(1)的2倍,即缓解串扰的同时增加了时间成本。
|
图 1 Marmousi模型 (a)纵波速度;(b)横波速度 |

|
图 2 Marmousi模型第15炮地震记录 (a)vx;(b)vz;(c)模拟vxP地震记录;(d)模拟vxS地震记录;(e)模拟vzP地震记录;(f)模拟vzS地震记录;(g)频率—波数域分离的vxP地震记录; (h)频率—波数域分离的vxS地震记录;(i)频率—波数域分离的vzP地震记录;(j)频率—波数域分离的vzS地震记录 |
|
图 3 Marmousi模型第一次迭代梯度剖面 (a)EFWI迭代的纵波梯度;(b)EFWI迭代的横波梯度;(c)SEFWI迭代的纵波梯度;(d)SEFWI迭代的横波梯度 |
FWI需要多次迭代,计算量与震源个数成正比,因此计算量巨大。采用SEFWI方法的计算量约为EFWI方法的2倍。因此如何提高计算效率是一个必须考虑的问题。参考前人方法[19-20, 24],采用一种动态震源随机编码技术,对所有单炮记录编码,然后随机分成若干组,每组(包括Ns个单炮)即为一个超级炮,以超级炮为单位进行常规FWI计算流程。第k组超级炮的动态震源随机编码为
| $ \begin{array}{*{20}{c}} {{S_k} = \sum\limits_{i = 1}^{{N_{\rm{s}}}} {{A_{{\rm{rand }}}}} {\gamma _{{\rm{rand }}}}\left[ {{s_i}\left( {{x_{{\rm{rand }}}},t} \right)*\delta \left( {t - \Delta {t_{{\rm{rand }}}}} \right)} \right]}\\ {k = 1,2, \cdots ,N/{N_{\rm{S}}}} \end{array} $ | (18) |
式中:随机振幅因子Arand=sinθrand,
从式(18)可知,将所有单炮随机组成若个超级炮,每个超级炮中震源位置随机、极性随机、振幅随机和时间延迟随机,这样可以最大限度地压制串扰噪声的影响。由于编码是随机的,而反演收敛依赖于目标泛函,所以可能会造成照明不均匀和收敛等问题。因此本文每迭代数次后更换一套随机编码,这样可以避免串扰都在同一个地方和目标泛函变化不定时影响反演收敛。
本文的动态随机震源编码步骤为:
(1) 对观测地震记录进行分组,每组包括随机选取的Ns个单炮记录;
(2) 对每组的每个单炮记录的极性、振幅、时间延迟进行随机化处理;
(3) 对模拟地震震源函数式(18)进行与步骤(1)和步骤(2)相同的编码处理。
2 模型试算 2.1 Marmousi模型试算以图 1的Marmousi速度模型为例,分别运用EFWI、ES_EFWI和ES_SEFWI方法进行计算,以此验证本文方法的有效性。
观测系统设计为:炮间距为100m,共30炮;在地表每隔10m布置1个检波器,共301个。计算参数为:纵波源为主频20Hz的雷克子波;采用时间2阶、空间10阶精度有限差分进行数值模拟;检波器采样间隔为1ms,总采样时间为3s。采用式(18)将30个单炮组成3个超级炮,每个超级炮有10个位置随机的单炮, 每个单炮的振幅、极性和延迟时间随机。总共迭代200次,每10次迭代更换一次震源随机编码。
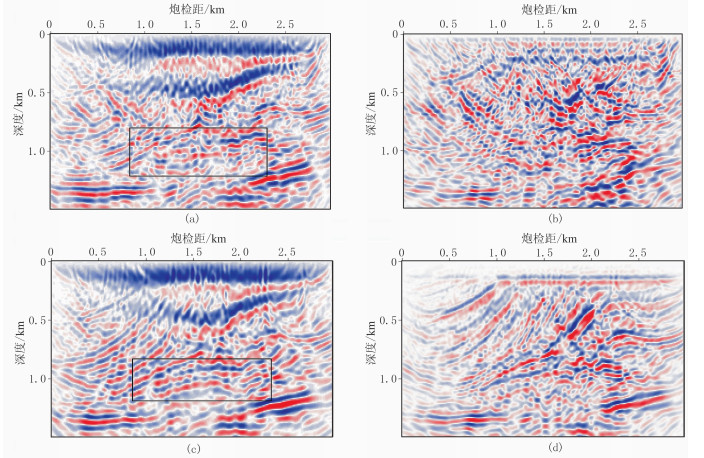
分别采用ES_EFWI和ES_SEFWI得到第一次迭代速度梯度剖面见图 4。对比图 4a与图 4c可见,结果与与前文分析一致,由于正传波场都为纯纵波,因此梯度串扰区别较小,但在图 4a中的方框区域串扰比较严重,而图 4c的同一区域则明显刻画出了背斜形态。对比图 4b与图 4d所示的横波速度梯度剖面可见,用本文方法计算的结果中串扰得到了明显压制,而用常规方法计算的横波速度梯度由于受纵波和多震源的影响,出现严重的串扰噪声。
|
图 4 Marmousi模型多震源激发数据第一次迭代梯度剖面 (a)ES_EFWI反演的纵波梯度;(b)ES_EFWI反演的横波梯度;(c)ES_SEFWI反演的纵波梯度;(d)ES_SEFWI反演的横波梯度 |
ES_EFWI和ES_SEFWI的反演结果见图 5。从图 5a与图 5b可见,利用常规方法反演的结果中离散噪声分布于整个计算区域,反演质量很差;由图 5c和图 5d可见,本文方法反演结果中的中浅层串扰噪声几乎完全被消除,反演质量更高。
|
图 5 Marmousi模型多震源反演结果 (a)ES_EFWI反演的纵波速度;(b)ES_EFWI反演的横波速度;(c)ES_SEFWI反演的纵波速度;(d)ES_SEFWI反演的横波速度 |
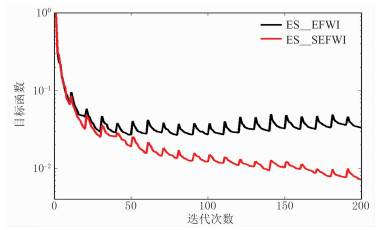
图 6为ES_EFWI和ES_SEFWI方法得到的目标泛函收敛曲线。由图可见,ES_EFWI方法在迭代到第50次就不再下降,而ES_SEFWI方法收敛特性很好,在200次迭代后仍有下降的趋势。
|
图 6 ES_EFWI与ES_SEFWI目标泛函曲线对比 |
图 7为常规逐炮激发的EFWI反演结果。由图可见,纵、横波速度反演结果质量都较高,但在图中箭头所示区域,由于受纵波干扰,横波速度的几个高速体都没能展现出来,整体分辨率明显低于纵波速度,说明横波速度的反演质量比纵波速度差。在图 5c和图 5d中深层可见轻微的离散噪声,但与图 7a和图 7b中箭头所对应的区域相比,可见高速体都能被有效恢复,纵、横波速度的分辨率相当。

|
图 7 Marmousi模型EFWI计算结果 (a)纵波速度;(b)横波速度 |
采用下式评价反演精度
| $ {\rm{err}} = \frac{{{{\left\| {{v_{{\rm{real }}}} - {v_{{\rm{result }}}}} \right\|}^2}}}{{{{\left\| {{v_{{\rm{real }}}}} \right\|}^2}}} \times 100\% $ | (19) |
式中:vreal为真实速度;vresult为反演速度。不同反演方法的计算量和反演精度对比如表 1所示。表中将EFWI的计算量设定为1,ES_EFWI的计算量为EFWI的0.1倍,但反演精度较低。ES_SEFWI的计算量约为常规ES_EFWI计算量的2倍。因此本文ES_SEFWI方法的计算量约为常规逐炮激发弹性波全波形反演(EFWI)的0.2倍。由于图 1中模型的横波速度是由纵波速度根据经验公式除以1.5得到的,为更好地对比纵、横波速度的反演精度,将反演的横波速度乘以1.5使其量化到与纵波速度同一个数量级。由表 1可知,ES_SEFWI与EFWI反演的精度相差不大,EFWI方法反演的横波速度精度略低于纵波速度,而ES_SEFWI方法反演的纵波与横波的速度精度差别相对较小。
|
|
表 1 Marmousi模型不同方法计算量和精度统计 |
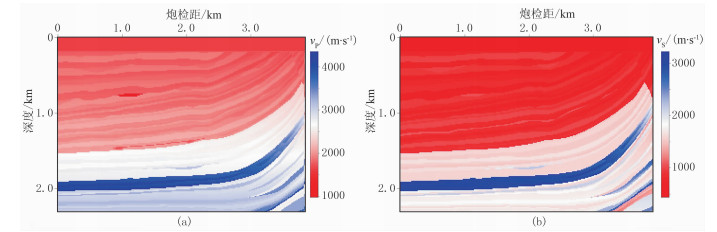
图 8为不相关速度模型Marmousi-Ⅱ的局部区域速度剖面,分别用其测试三种方法的计算效果。初始纵、横波速度模型采用12×12个节点高斯平滑。计算区域包含315×185个节点,节点间隔为12.5m。观测系统设计为:炮间距为137.5m,共28炮;在地表每隔12.5m布置1个检波器,共315个检波器。震源编码参数为:每个超级炮由7个单炮组成,共4个超级炮;共迭代120次,每迭代7次更换一组震源编码。其他的计算参数都与Marmousi模型算例相同。
|
图 8 Marmousi-Ⅱ模型纵(a)、横(b)波速度模型(局部) |
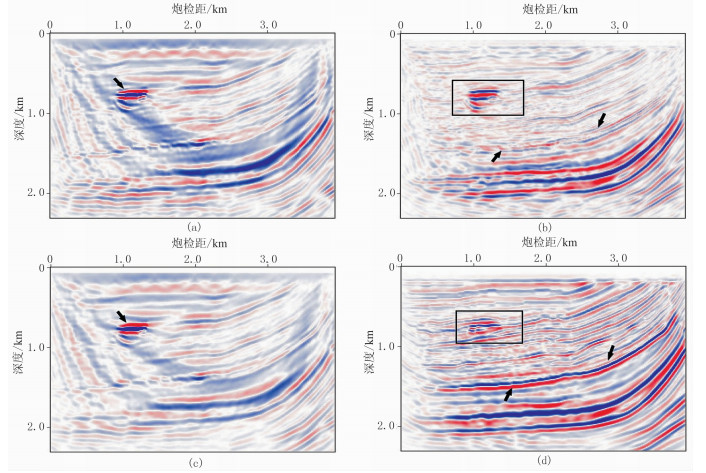
用不同方法计算的逐炮激发第一次迭代纵波、横波梯度剖面见图 9。由图可见,EFWI与SEFWI方法得到的纵波速度梯度相差不大,由于受低速气体带(箭头位置)的影响,该区域的反射能量很强,因此前几次迭代以该区域为主。EFWI与SEFWI方法的横波速度梯度区别比较明显,尤其在与纵波低速气体带相同的位置,由于横波速度与周围的速度相差不大,因此该区域能量不会太强。图 9d用波场分离方法计算得到的横波速度梯度在该位置能量与周围相当(见方框位置),而图 9b是用常规方法的计算结果,由于受纵波影响,方框区域能量很强,其周围的更新方向也相对较乱。
|
图 9 Marmousi-Ⅱ速度模型常规逐炮激发第一次迭代梯度剖面 (a)EFWI纵波梯度;(b)EFWI横波梯度;(c)SEFWI纵波梯度;(d)SEFWI横波梯度 |
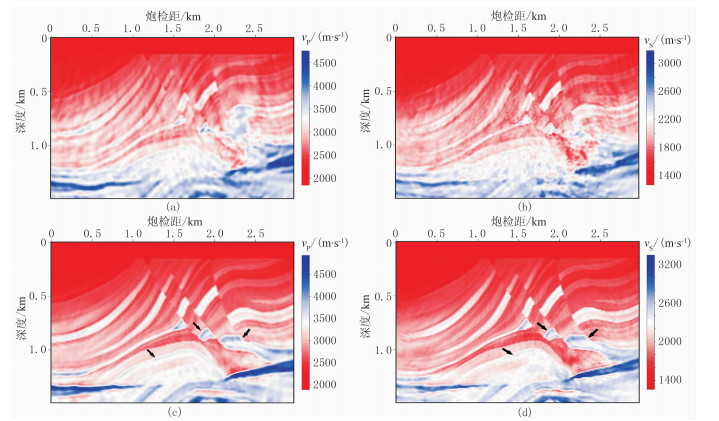
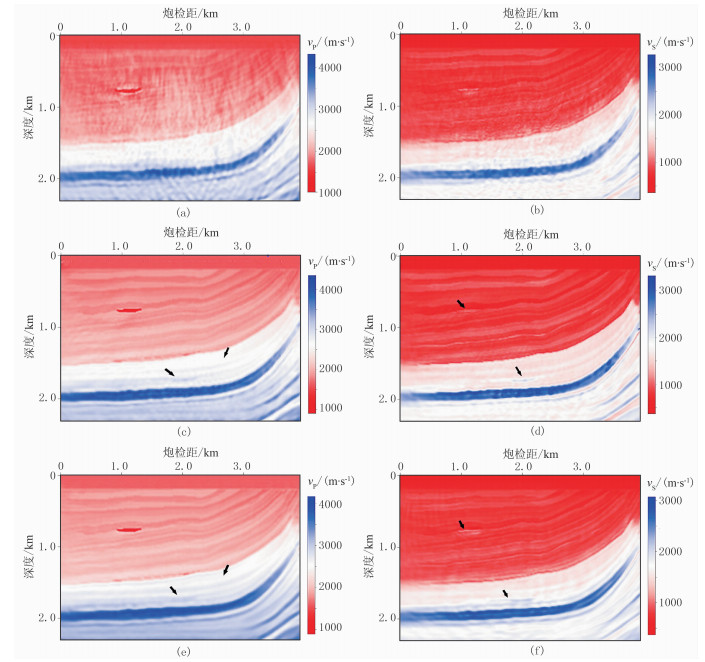
图 10为分别用ES_EFWI、ES_SEFWI和EFWI反演得到的纵、横波速度剖面。由图可见,图 10a和图 10b中离散串扰噪声相当严重;图 10c和图 10e中纵波速度相差不大,只是前者在深层有微小的离散噪声,但在深层箭头位置反演精度稍高;而图 10d和图 10f中横波速度相差较大,可见ES_SEFWI方法反演精度明显更高,特别在箭头所指区域。
|
图 10 Marmousi-Ⅱ模型不同方法速度反演剖面 (a)ES_EFWI纵波速度;(b)ES_EFWI横波速度;(c)ES_SEFWI纵波速度;(d)ES_SEFWI横波速度;(e)EFWI纵波速度;(f)EFWI横波速度 |
Marmousi-Ⅱ模型的计算量和反演效果对比如表 2所示。可见ES_SEFWI方法不仅大大减少了计算量,同时反演的纵、横波速度精度比EFWI方法略高。三种方法结果对比说明本文方法对弹性速度模型也是适用和有效的。
|
|
表 2 Marmousi-Ⅱ模型不同方法计算量和精度统计 |
精度和计算效率是弹性波全波形反演的两个关键参数。本文采用动态震源随机编码技术提高了弹性波全波形反演的计算效率并压制了多震源的串扰效应。在纵波源激发情况下,采用PP波场计算纵波速度梯度、利用PS波场计算横波速度梯度压制多参数反演造成的串扰噪声。通过Marmousi模型和Marmousi-Ⅱ模型分别测试了本文提出的基于纵横波分离动态震源随机编码弹性波全波形反演(ES_SEFWI)方法,得到如下结论:
(1) 动态震源随机编码技术能大大提高全波形反演的计算效率并缓解波场之间的相干性;
(2) 纵、横波分离能够降低波场的复杂度、缓解不同模式的波场间互相干扰造成的梯度串扰噪声;
(3) 将纵、横波波场分离与动态震源随机编码技术相结合,可以有效提高弹性波全波形反演的精度和计算效率。
感谢中国石油大学(华东)SWPI课题组全体成员对本研究的帮助与支持!
| [1] |
Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [2] |
Vigh D, Jiao K, Watts D, et al. Elastic full-waveform inversion application using multicomponent measurements of seismic data collection[J]. Geophysics, 2014, 79(2): R63-R77. DOI:10.1190/geo2013-0055.1 |
| [3] |
Borisov D, Singh S C. Three-dimensional elastic full waveform inversion in a marine environment using multicomponent ocean-bottom cables:a synthetic study[J]. Geophysical Journal International, 2015, 201(3): 1215-1234. DOI:10.1093/gji/ggv048 |
| [4] |
王毓玮, 董良国, 黄超, 等. 降低弹性波全波形反演强烈非线性的分步反演策略[J]. 石油地球物理勘探, 2016, 51(2): 288-294. WANG Yuwei, DONG Liangguo, HUANG Chao, et al. A multi-step strategy for mitigation severe non-linearity in elastic full-waveform inversion[J]. Oil Geophysical Prospecting, 2016, 51(2): 288-294. |
| [5] |
Virieux J, Operto S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 |
| [6] |
Ren Z, Liu Y. A hierarchical elastic full-waveform inversion scheme based on wavefield separation and the multistep-length approach[J]. Geophysics, 2016, 81(3): R99-R123. DOI:10.1190/geo2015-0431.1 |
| [7] |
Qu Y, Li J, Li Z, et al. An elastic full-waveform inversion based on wave-mode separation[J]. Exploration Geophysics, 2018, 49(4): 530-552. DOI:10.1071/EG16158 |
| [8] |
Wang T F, Cheng J B. Elastic full waveform inversion based on mode decomposition:The approach and mechanism[J]. Geophysical Journal International, 2017, 209(2): 606-622. DOI:10.1093/gji/ggx038 |
| [9] |
Prieux V, Brossier R, Operto S, et al. Multiparameter full waveform inversion of multicomponent ocean-bottom-cable data from the Valhall field, Part 2:Imaging compressive-wave and shear-wave velocities[J]. Geophysical Journal International, 2013, 194(3): 1665-1681. DOI:10.1093/gji/ggt178 |
| [10] |
Zhou W, Brossier R, Operto S, et al. Full waveform inversion of diving & reflected waves for velocity model building with impedance inversion based on scale separation[J]. Geophysical Journal Internatio-nal, 2015, 202(3): 1535-1554. DOI:10.1093/gji/ggv228 |
| [11] |
王毓玮, 董良国, 黄超, 等. 弹性波全波形反演目标函数性态与反演策略[J]. 石油物探, 2016, 55(1): 123-132. WANG Yuwei, DONG Liangguo, HUANG Chao, et al. Objective function behavior and inversion strategy in elastic full-waveform inversion[J]. Geophysical Prospecting for Petroleum, 2016, 55(1): 123-132. |
| [12] |
Operto S, Gholami Y, Prieux V, et al. A guided tour of multiparameter full-waveform inversion with multicomponent data:From theory to practice[J]. The Leading Edge, 2013, 32(9): 1040-1054. DOI:10.1190/tle32091040.1 |
| [13] |
Wang Y, Dong L, Liu Y, et al. 2D frequency-domain elastic full-waveform inversion using the block-diagonal pseudo-Hessian approximation[J]. Geophysics, 2016, 81(5): R247-R259. DOI:10.1190/geo2015-0678.1 |
| [14] |
Sun R, McMechan G A. Scalar reverse-time depth migration of prestack elastic seismic data[J]. Geophy-sics, 2001, 66(5): 1519-1527. |
| [15] |
Gu B, Li Z, Ma X, et al. Multi-component elastic reverse time migration based on the P- and S-wave se-parated velocity-stress equations[J]. Journal of Applied Geophysics, 2015, 112: 62-78. DOI:10.1016/j.jappgeo.2014.11.008 |
| [16] |
黄建平, 李闯, 李庆洋, 等. 一种基于平面波静态编码的最小二乘逆时偏移方法[J]. 地球物理学报, 2015, 58(6): 2046-2056. HUANG Jianping, LI Chuang, LI Qingyang, et al. Least-square reverse time migration with static plane-wave encoding[J]. Chinese Journal of Geophysics, 2015, 58(6): 2046-2056. |
| [17] |
李闯, 黄建平, 李振春, 等. 平面波最小二乘逆时偏移编码策略分析[J]. 石油物探, 2015, 54(5): 592-601. LI Chuang, HUANG Jianping, LI Zhenchun, et al. Analysis of plane wave least squares inverse time migration coding strategy[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 592-601. |
| [18] |
Krebs J R, Anderson J E, Hinkley D, et al. Fast full-wavefield seismic inversion using encoded sources[J]. Geophysics, 2009, 74(6): WCC177-WCC188. DOI:10.1190/1.3230502 |
| [19] |
Boonyasiriwat C, Schuster G T.3D multisource full-waveform inversion using dynamic random phase encoding[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 1044-1049.
|
| [20] |
Schuster G T, Wang X, Huang Y, et al. Theory of multisource crosstalk reduction by phase-encoded statics[J]. Geophysical Journal International, 2015, 184(3): 1289-1303. |
| [21] |
Moghaddam P P, Keers H, Herrmann F J, et al. A new optimization approach for source-encoding full-waveform inversion[J]. Geophysics, 2013, 78(3): R125-R132. DOI:10.1190/geo2012-0090.1 |
| [22] |
李庆洋, 黄建平, 李振春, 等. 优化的多震源最小二乘逆时偏移[J]. 石油地球物理勘探, 2016, 51(2): 334-341. LI Qingyang, HUANG Jianping, LI Zhenchun, et al. Optimized multi-source least-squares reverse time migration[J]. Oil Geophysical Prospecting, 2016, 51(2): 334-341. |
| [23] |
李娜. 基于Huber范数的多震源最小二乘逆时偏移[J]. 石油地球物理勘探, 2017, 52(5): 941-947. LI Na. Multi-source least squares inverse time migration based on Huber norm[J]. Oil Geophysical Prospecting, 2017, 52(5): 941-947. |
| [24] |
张盼, 韩立国, 巩向博, 等. 基于各向异性全变分约束的多震源弹性波全波形反演[J]. 地球物理学报, 2018, 61(2): 716-719. ZHANG Pan, HAN Liguo, GONG Xiangbo, et al. Full waveform inversion of multi-seismic elastic waves based on anisotropic total variational constraints[J]. Chinese Journal of Geophysics, 2018, 61(2): 716-719. |
| [25] |
Mora P. Nonlinear two-dimensional elastic inversion of multioffset seismic data[J]. Geophysics, 1987, 52(12): 1211-1228. |
| [26] |
李振春, 张华, 刘庆敏, 等. 弹性波交错网格高阶有限差分法波场分离数值模拟[J]. 石油地球物理勘探, 2007, 42(5): 510-515. LI Zhenchun, ZHANG Hua, LIU Qingmin, et al. Numeric simulation of elastic wavefield separation by staggering grid high-order finite-difference algorithm[J]. Oil Geophysical Prospecting, 2007, 42(5): 510-515. |
| [27] |
Forgues E, Lambaré G. Parameterization study for acoustic and elastic ray plus Born inversion[J]. Journal of Seismic Exploration, 1997, 6(2-3): 253-277. |
| [28] |
Li Z Y, Ma X N, Fu C, et al. Frequency-wavenumber implementation for P- and S-wave separation from multi-component seismic data[J]. Exploration Geophysics, 2016, 47(1): 32-43. DOI:10.1071/EG14047 |



 任志明, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
任志明, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 