② 中国石油东方地球物理公司, 河北涿州 072750
② BGP Inc., CNPC, Zhuozhou, Hebei 072750, China
在地震勘探早期,人们普遍粗略地认为地下介质为各向同性,即假定地震波场在地下介质中沿各个方向的传播速度相同。但随着地震勘探技术的不断发展、勘探程度的不断加深,地下介质的各向异性问题愈发受到人们的重视。因为相对于浅层介质,各向异性在深层介质中更为明显,地震波沿各个方向的传播速度不同,单一的速度建模已经不能适应地震勘探开发的需要。如果忽略地下介质的各向异性,就会造成成像结果中绕射波不收敛、层位归位不准确、成像分辨率低等问题,从而降低地震成像和反演精度[1-5]。
许多学者对层析反演技术进行过深入研究。传统的层析速度建模方法由三部分组成,首先利用Dix公式或基于层位约束的Dix公式生成初始层速度模型,然后利用炮检距道集对初始速度进行迭代,最后利用网格层析方法局部修饰速度模型[6]。Woodward等[7]利用反射层析对深度域速度进行建模;Tsvankin等[8]认为速度和各向异性参数对地震波旅行时的影响相互耦合,反演很可能存在多解性;Chapman等[9]基于线性扰动理论,导出了二维非均匀弱各向异性介质中的射线旅行时方程,该方程仅依赖于有限的几个参数;Watanabe等[10]采用四周全方位观测方式实现了VTI介质中三参数的同步反演。
现有的深度域建模技术主要包括偏移速度分析、层析反演及全波形反演[11]。其中偏移速度分析是以成像质量最佳作为判别准则,利用深度聚焦分析或剩余曲率分析获取相应的剩余深度以更新速度;层析反演既可在叠前数据域实现(常规反射层析),也可在成像域实现(共成像点道集层析),利用旅行时或波形残差进行速度更新;全波形反演是以模型数据与观测数据的最佳拟合作为判别准则,通过地震全波形信息实现速度恢复。从计算效率上看,常规反射层析最高,但也存在难点:①旅行时差获取困难,特别是对于信噪比低的叠前数据更是如此;②射线追踪过程中通过大量的插值和试射拟合炮检点坐标,且需要解决复杂的反射问题[7]。全波形反演计算量巨大,虽然精度很高,但如果在震源子波未知、低波数约束信息存在较大误差时,容易陷入局部极值[12]。Koren等[13]提出采用角度域共成像点道集(ADCIG)开展反演的策略,利用近炮检距内的数据求取各向异性参数δ值,利用远炮检距数据求取ε值。由于ADCIG反映了每一个共反射点处不同角度反射波对该点成像的贡献,所以局部信息更为丰富。通过ADCIG叠加,压制了由于绕射波不收敛或炮点的强能量产生的低频噪声,局部成像效果得到改善。Rickett等[14]分析了角道集的动力学和运动学特征,用ADCIG迭代更新深度域层速度模型,从而大大提高了层析速度建模精度[15-17]。
本文研究了一种基于角道集的各向异性参数层析反演方法,通过分析各向异性参数对不同角度范围内角道集影响,定量分析参数误差,进而拾取对应部位残差,更新参数。
1 方法原理逆时偏移(RTM)可以提供精确的成像结果,能有效确保各向异性参数反演的准确性[18]。但RTM对参数场的要求相对较高,特别是速度场。基于这方面考虑,本文首先采用各向同性单程波偏移成像确定速度场大致层位,进行单一速度层析,得到基础速度场。在此基础上进行VTI介质RTM,并利用Poynting矢量法提取角道集。采用自动拾取策略得到角道集深度残差,并进一步转化为时间残差。利用各向异性射线追踪获得灵敏度矩阵,使用LSQR方法解方程,最终获得三参数更新量。
1.1 基于一阶拟声波近似方程的RTMRTM波场延拓时沿时间轴对波场进行逆时外推,本文采用一阶速度—应力拟声波波动方程构建波场延拓算子。Duveneck等[19]提出的一阶应力—速度形式的VTI介质拟声波方程为
| $ \left\{ \begin{array}{l} \frac{{\partial u}}{{\partial t}} = \frac{1}{\rho }\;\frac{{\partial p}}{{\partial x}}\\ \frac{{\partial v}}{{\partial t}} = \frac{1}{\rho }\;\frac{{\partial p}}{{\partial y}}\\ \frac{{\partial w}}{{\partial t}} = \frac{1}{\rho }\;\frac{{\partial p}}{{\partial z}} \end{array} \right. $ | (1a) |
| $ \left\{ \begin{array}{l} \frac{{\partial p}}{{\partial t}} = \rho V_{{\rm{Px}}}^2\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right) + \rho {V_{{\rm{P0}}}}{V_{{\rm{Pn}}}}\frac{{\partial w}}{{\partial z}}\\ \frac{{\partial q}}{{\partial t}} = \rho {V_{{\rm{P0}}}}{V_{{\rm{Pn}}}}\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right) + \rho V_{{\rm{P0}}}^2\frac{{\partial w}}{{\partial z}} \end{array} \right. $ | (1b) |
式中:u、v、w分别为沿x、y、z方向的速度分量;p=σ11=σ22和q=σ33分别为水平应力分量和垂直应力分量;VPx为对称平面内的qP波速度,且VPx2=VP02(1+2ε);VPn为波的正常时差速度,且VPn2=VP02(1+2δ);VP0、ε、δ为VTI介质Thmosen参数[20]。对上式采用交错网格高阶有限差分格式进行求解。
1.2 Poynting矢量法提取角道集RTM利用双程波动方程进行时间外推,能精准还原沿不同方向传播的波场,成像不受地层倾角限制,但成像结果常伴随强振幅低频噪声。利用不同方向的波场进行成像可以有效压制低频噪声[21]。Yoon等[22]利用Poynting矢量对震源波场和检波点波场进行分解,只对反射波进行成像从而压制低频噪声。Yan等[23]通过倾斜叠加计算角度并选择小角度信息进行成像以减少噪声。
波场在t时刻的Poynting矢量为
| $ \mathit{\pmb{S}} = - {\mathit{\pmb{r}}}p = - \nabla p\frac{{\partial p}}{{\partial t}}p $ | (2) |
式中r为射线方向矢量,可以通过p的一阶空间导数
| $ \left\{ \begin{array}{l} {\mathit{\pmb{S}}_{\rm{s}}} = - \left( {\frac{{\partial {u_{\rm{s}}}}}{{\partial t}}\frac{{\partial {p_{\rm{s}}}}}{{\partial t}}, \frac{{\partial {w_{\rm{s}}}}}{{\partial t}}\frac{{\partial {q_{\rm{s}}}}}{{\partial t}}} \right)\\ {\mathit{\pmb{S}}_{\rm{r}}} = - \left( {\frac{{\partial {u_{\rm{r}}}}}{{\partial t}}\frac{{\partial {p_{\rm{r}}}}}{{\partial t}}, \frac{{\partial {w_{\rm{r}}}}}{{\partial t}}\frac{{\partial {q_{\rm{r}}}}}{{\partial t}}} \right) \end{array} \right. $ | (3) |
式中:ps、qs分别为震源波场的p和q分量;pr、qr分别为检波点波场的p和q分量;us、ws分别为震源波场x和z方向的速度分量;ur、wr分别为检波点波场x和z方向的速度分量。
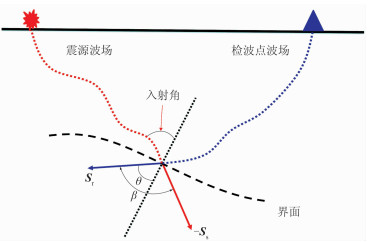
在逆时延拓中提取ADCIG的原理如图 1所示。图中-Ss、Sr之间的夹角为β,入射角θ为
| $ \theta = \frac{1}{2}\beta = \frac{1}{2}{\rm{arc}}\;\;{\rm{cos}}\frac{{ - {\mathit{\pmb{S}}_s}\mathit{\pmb{\cdot}}{\mathit{\pmb{S}}_r}}}{{\left| { - {\mathit{\pmb{S}}_s}} \right|\left| {{\mathit{\pmb{S}}_r}} \right|}} $ | (4) |
|
图 1 Poynting矢量法计算入射角 |
qP波成像不同于各向同性声波,需要同时考虑qP波的p、q分量,这一点在式(2)、式(3)中得以体现。大量试算证明,拟声波p分量的成像结果无异于q分量,本文不讨论qP波p、q分量成像差异,仅采用p分量进行偏移成像。
1.3 各向异性参数层析反演层析的基础理论是Radon变换,将一系列观测到的地震数据沿射线路径反投影得到地下介质的速度信息[24]。基于射线类的旅行时层析沿着射线传播方向对慢度进行线积分得到射线旅行时[11],即
| $ t = \int_s^{\rm{T}} {{s_{\text{g}}}(x, z){\rm{d}}l} $ | (5) |
式中:sg为群速度的倒数;l表示积分路径,积分上、下限分别为检波点(射线终止点)和震源(射线起点)。模型群慢度变化会造成旅行时产生差异,引入Δt和Δsg,有
| $ L(\theta )\Delta {s_{\rm{g}}}\left( \theta \right) = \Delta t(\theta ) $ | (6) |
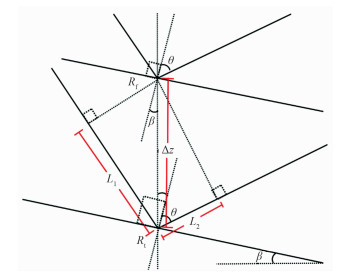
由此建立时间残差与慢度扰动量的关系。式中L即为射线路径长度;θ为相角。时间残差可从角道集剩余曲率中获得,如图 2所示[25]。
|
图 2 深度残差与时间残差转换示意图 Rf是错误成像点,Rt是正确成像点 |
为了使围绕地震波传播的相速度公式在进行理论研究和实际应用时更为方便,并且也能准确阐释公式的物理意义,本文采用Thmosen[20]提出的三个参数VP0、ε和δ表征各向异性性质。由于这三个参数的误差,导致反射界面成像错位,即角道集存在剩余曲率。成像点深度变化量为Δz,射线路径改变量为
| $ \Delta L = {L_1} + {L_2} $ | (7) |
由图 2的几何关系可得
| $ \Delta z = \frac{{\Delta {V_{\rm{P}}}\Delta t}}{{2{\rm{cos}}\theta \;{\rm{co}}s\beta }} $ | (8) |
式中VP为VTI介质相速度。
根据时间一致性原理和波场可逆原理,这种由于参数误差造成的波场传播误差,造成的成像点的位置偏差,可以利用射线路径进行近似还原。
各向异性参数层析反演方程组[26]为
| $ {\mathit{\pmb{L}}}\Delta {\mathit{\pmb{s}}} = \Delta {\mathit{\pmb{t}}} $ | (9) |
式中
| $ \left\{ \begin{array}{l} \mathit{\pmb{L}} = \left[ {l\;{\rm{cos}}\phi \frac{{\partial {s_{\rm{p}}}}}{{\partial {s_0}}}\;\;\;\;lcos\phi \frac{{\partial {s_{\rm{p}}}}}{{\partial \varepsilon }}{\rm{ }}lcos\phi \frac{{\partial {s_{\rm{p}}}}}{{\partial \delta }}} \right]\\ \Delta {\mathit{\pmb{s}}} = {[\Delta {s_0}\;\;\;\;\Delta \varepsilon \;\;\;\;\Delta \delta ]^{\rm{T}}} \end{array} \right. $ | (10) |
其中:s是相慢度;s0=1/VP0;ϕ是群慢度向量和相慢度向量的夹角;l是网格内射线长度。
1.4 角道集Thmosen参数敏感性测试根据Zhou等[27]提出的层析理论,不考虑横波速度对P波速度的影响,令沿对称轴的剪切波速度为零的VTI介质相速度为
| $ \begin{array}{l} {V_{\rm{P}}} = {V_{{\rm{P0}}}}[0.5 + \varepsilon {\sin ^2}\theta + \\ \;\;\;\;\;\;0.5\sqrt {{{\left( {1 + 2\varepsilon {{\sin }^2}\theta } \right)}^2} - 8\left( {\varepsilon - \delta } \right){{\sin }^2}\theta {{\cos }^2}\theta } {]^{\frac{1}{2}}}\\ \;\;\;\; = {V_{{\rm{P0}}}}A \end{array} $ | (11) |
由式(11)可得相慢度对Thmosen的参数的导数为
| $ \left\{ \begin{array}{l} \frac{{\partial {s_{\rm{p}}}}}{{\partial {s_{\rm{0}}}}}{\rm{ = }}A\\ \frac{{\partial {s_{\rm{p}}}}}{{\partial \varepsilon }} = - 0.5{s_{\rm{0}}}{A^3} \times \\ \;\;\;\;\;\left[ {1 + B\left( {1 + 2\varepsilon {{\sin }^2}\theta - 2{{\cos }^2}\theta } \right)} \right]{\sin ^2}\theta \\ \frac{{\partial {s_{\rm{p}}}}}{{\partial \delta }} = - {s_{\rm{0}}}{A^3}B{\sin ^2}\theta {\cos ^2}\theta \end{array} \right. $ | (12) |
联合式(10)~式(12)可得走时t与三参数的关系
| $ \left\{ \begin{array}{l} \frac{{\partial t}}{{\partial {V_{{\rm{P0}}}}}} = \frac{{\partial {s_{\rm{p}}}}}{{\partial {V_{{\rm{P0}}}}}}\;l\cos \phi \\ \frac{{\partial t}}{{\partial \varepsilon }} = \frac{{\partial {s_{\rm{p}}}}}{{\partial \varepsilon }}\;l\cos \phi \\ \frac{{\partial t}}{{\partial \delta }} = \frac{{\partial {s_{\rm{p}}}}}{{\partial \delta }}\;l\cos \phi \end{array} \right. $ | (13) |
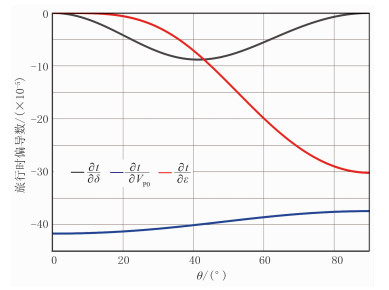
如果给定了具体的模型参数VP0=3000m/s、ε=0.2、δ=0.15,就可以计算旅行时对Thmosen参数的偏导数(图 3)。从图 3可以看出,
|
图 3 旅行时对Thmosen参数导数随入射角的变化 |
对于上文中提到的三类角道集的范围,业界目前尚无准确定义。为了定义角道集范围,用旅行时对三参数的导数对相角θ求导,即
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}t}}{{\partial {s_{\rm{0}}}\partial \theta }} = - \frac{{l\cos \phi }}{2}{\left[ {\frac{1}{2}D + \frac{1}{2}{{\left( {{D^2} - E} \right)}^{\frac{1}{2}}}} \right]^{\frac{3}{2}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\left[ {\varepsilon \sin 2\theta + \frac{F}{4}{{\left( {{D^2} - 4E{{\cos }^2}\theta } \right)}^{\frac{1}{2}}}} \right]\\ \frac{{{\partial ^2}t}}{{\partial \varepsilon \partial \theta }} = - \frac{{{A^2}l\cos \phi }}{{2{V_{{\rm{P0}}}}}}\{ 3A'\left( {1 + BC} \right){\sin ^2}\theta + \\ \;\;\;\;\;\;\;\;\;\;\;\;A[\left( {1 + BC} \right)\sin 2\theta + {\sin ^2}\theta (2B\left( {\varepsilon + 1} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\sin 2\theta + CG)]\} \\ \frac{{{\partial ^2}t}}{{\partial \delta \partial \theta }} = - \frac{{{A^2}l\cos \phi }}{{2{V_{{\rm{P0}}}}}}[\frac{{3A'B{{\sin }^2}2\theta }}{4} + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}A\left( {B\sin 4\theta + \frac{1}{2}G{{\sin }^2}2\theta } \right)] \end{array} \right. $ | (14) |
式中
| $ \left\{ \begin{array}{l} A' = \frac{{{\partial ^2}t}}{{\partial {s_{\rm{0}}}\partial \theta }}\\ B = \frac{1}{{\sqrt {1 + 2\varepsilon {{\sin }^2}\theta - 8\left( {\varepsilon - \delta } \right){{\sin }^2}\theta {{\cos }^2}\theta } }}\\ C = D - 2{\cos ^2}\theta \\ D = 1 + 2\varepsilon {\sin ^2}\theta \\ E = 2\left( {\varepsilon - \delta } \right){\sin ^2}\theta \\ F = 4\left[ {D\varepsilon \;\sin 2\theta - \left( {\varepsilon - \delta } \right)\sin 4\theta } \right]\\ G = - \frac{1}{2}{B^2}F \end{array} \right. $ | (15) |
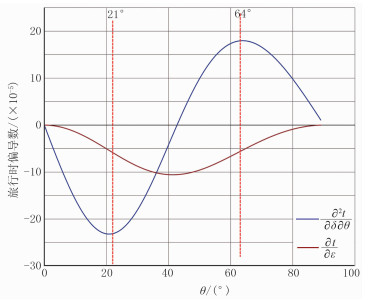
如果给定了VP0、ε、δ,就可以利用式(14)计算旅行时对三参数和相角的二次导数。因为中角度信息用来反演δ,中角度确定后,大角度、小角度也随之确定。当VP0=2000m/s、ε=0.12、δ=0.08时,图 4为计算的
|
图 4 |
|
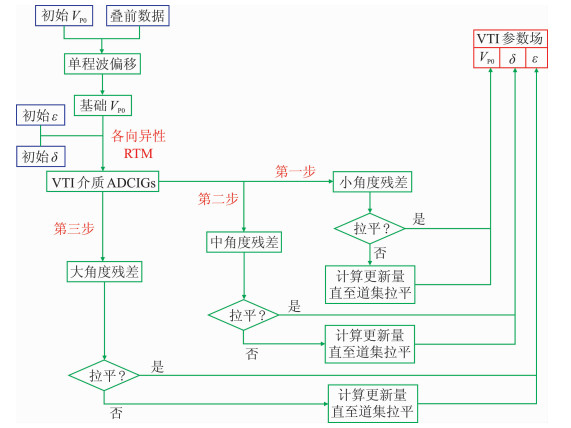
图 5 层析反演流程 |
(1) 首先选取范围小于22°的角道集,利用其剩余时间残差反演VP0,经多次迭代后判断该角度范围道集拉平程度,如果拉平则认为得到满足精度的VP0;
(2) 用步骤(1)得到的VP0进行RTM得到偏移剖面和角道集,选取22°~65°的角道集,利用其剩余时间残差反演δ,同第一步相似,经多次迭代后得到满足精度的δ;
(3) 用步骤(2)得到的δ进行偏移并提取角道集,选取大于65°的角道集,反演最后一个参数ε,经多次迭代得到满足精度的ε,完成整个反演流程。
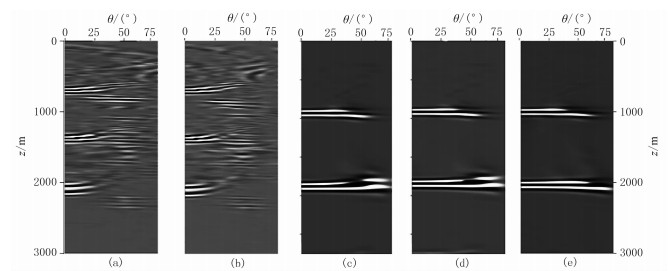
2 模型试算 2.1 角道集敏感性验证首先通过一个层状模型(图 6)验证角道集残差对三个参数的敏感性。图 7为不同参数误差下获得的逆时偏移角道集,可以看出:角道集受速度影响最大,特别是深层,当速度不准时,即使另两个参数完全准确,角道集效果也较差;当速度准确时,小角度范围内角道集已经拉平,但中、大角度范围角道集仍然不平;当δ准确时,中等角度范围角道集拉平;当ε也准确时,所有角度范围的角道集拉平。

|
图 6 层状模型 |
|
图 7 不同参数误差下水平层状模型的逆时偏移角道集 (a)VP0、ε、δ皆小30%;(b)VP0小30%,ε、δ准确;(c)VP0准确,ε、δ小30%;(d)VP0和δ准确,ε小30%;(e)VP0、ε、δ皆准确 |
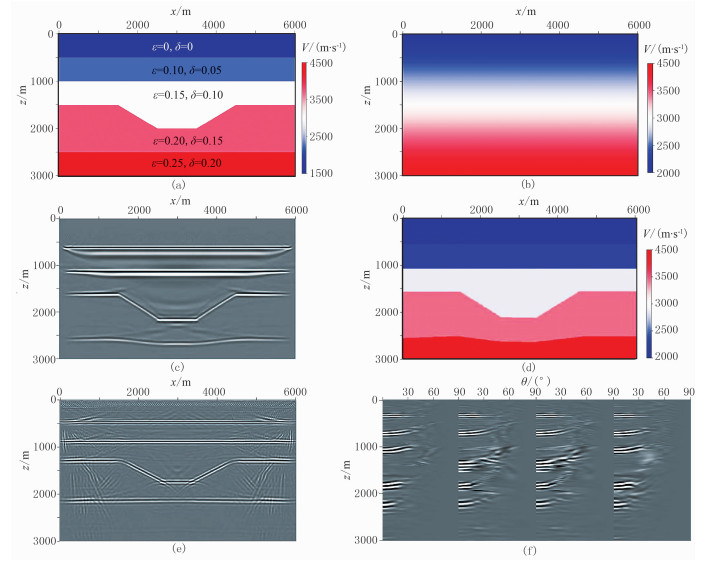
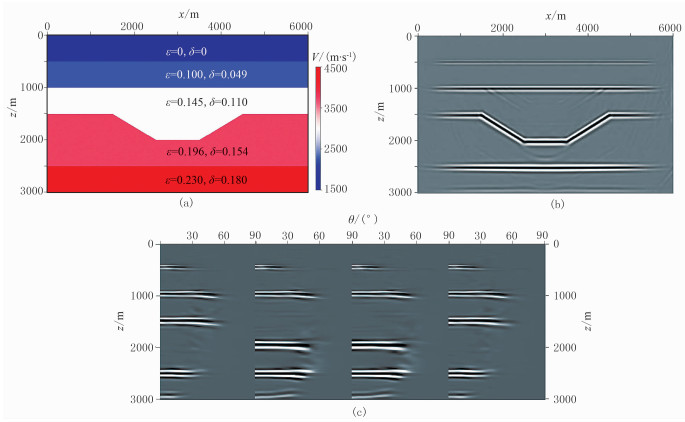
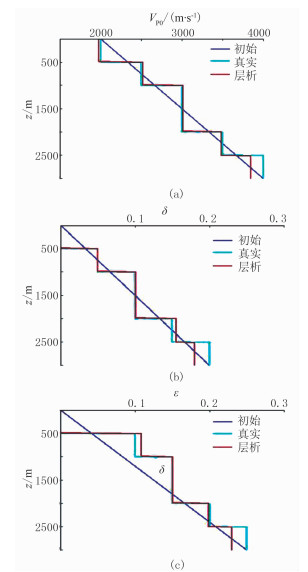
用洼陷模型(图 8a)验证文中反演策略的合理性。模型横向采样点601,纵向采样点301,横、纵采样间隔为10m,正演共放50炮,地表全接收。首先以从浅至深线性变化速度场作为初始速度场(图 8b),由单程波偏移结果(图 8c)确定速度场VP0大致层位,通过各向同性速度层析反演得到基础速度场(图 8d)。初始δ场和ε场的值为从浅至深线性变化,范围分别为0~0.2和0~0.25。由基础速度模型、初始ε场、初始δ场经各向异性RTM得到初始偏移剖面和初始角道集(图 8e、图 8f)。由于参数不准确,导致偏移剖面层位不准,画弧现象严重,对应的角道集同相轴上翘。采用图 5所示的反演策略,进行VTI介质各向异性参数层析。图 9a~图 9c为各向异性层析后的参数模型、偏移剖面、角道集,偏移剖面中深层结构清晰,角道集也基本拉平。对比图 8e和图 9b可见,相比于单一的速度层析反演,各向异性参数层析反演后深层能量显著加强,且成像假象减少。图 10为x=3000m处的层析后模型参数与初始、真实参数的对比,说明本文方法具有较高反演精度。
|
图 8 洼陷模型 (a)真实模型;(b)初始VP0模型;(c)单程波方程偏移剖面;(d)基础速度模型;(e)RTM剖面;(f)RTM角道集 |
|
图 9 洼陷模型层析反演结果 (a)层析后模型;(b)RTM剖面;(c)RTM角道集 |
|
图 10 洼陷模型层析后模型参数与初始、真实参数的对比 (a)VP0;(b)δ;(c)ε |
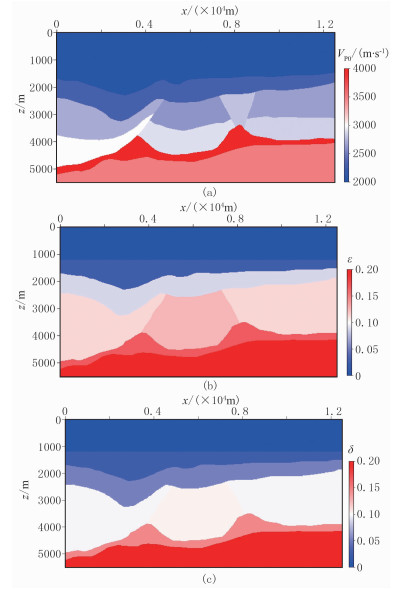
该模型为弱各向异性VTI介质,表层为海水,包含断块、异常高速体、高陡断层等(图 11)。模型CDP范围是1~1251,深度采样点数为551,纵横向采样间隔均为10m。采用文中所述的各向异性反演策略进行三参数反演,偏移过程中角道集提取范围为0°~75°。由于模型为弱各向异性VTI介质,可设ε、δ范围均为0~0.2,代入式(14),可将小角度范围设置为0~21°,中角度范围为21°~61°,大角度范围为61°~75°。
|
图 11 复杂构造模型的真实速度(a)、ε(b)和δ(c)场 |
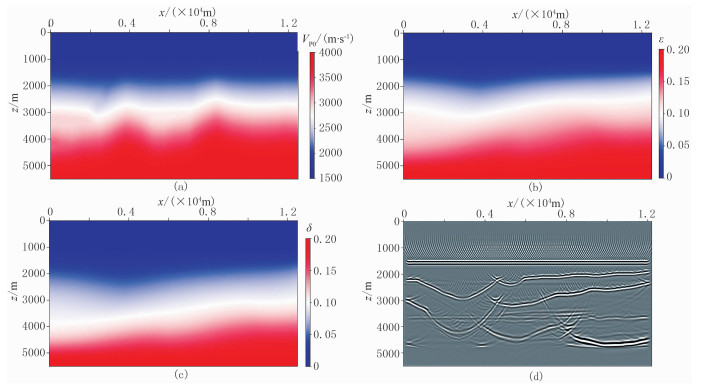
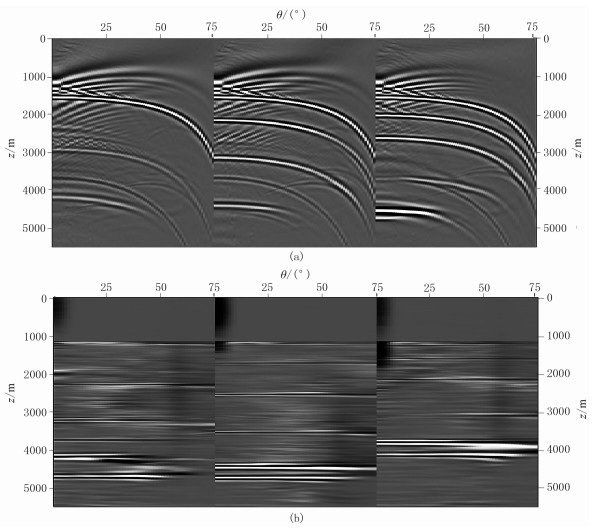
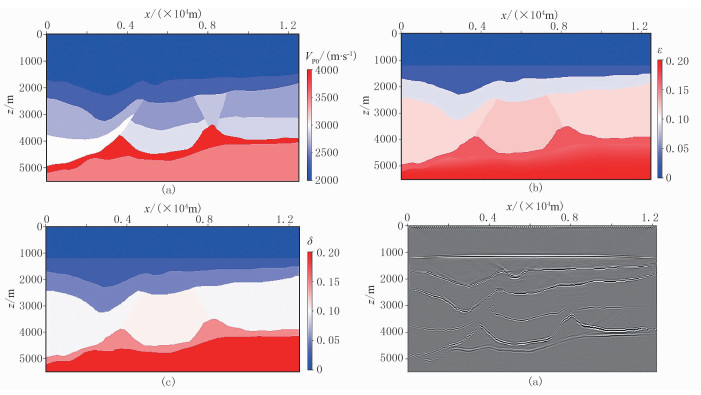
将真实模型经过大尺度平滑后再乘以一定系数得到初始模型。图 12为初始参数模型及各向同性叠前单程波偏移剖面,可以看出,由于参数不准,偏移剖面同相轴混乱,存在成像假象。应用本文方法,首先在初始剖面拾取大致层位,进行各向同性速度层析。当得到较为准确的基础速度模型后,按照各向异性反演策略进行处理。图 13是抽取x=3000m、6000m、9000m处的VTI介质层析前、后偏移角道集,可以看出,由于参数不准,层析前角道集弯曲严重;层析后角道集已基本拉平,说明三个参数基本准确(图 14a~图 14c)。各向异性层析后偏移剖面反射界面归位正确,海底以下断块、高陡构造和高速异常层得到较为清晰反映,成像效果良好(图 14d)。抽取x=4260m处初始模型、层析后模型、真实模型的三参数(图 15)进行对比,可以看出,各向异性参数层析后Thmosen三参数均与真实值吻合较好,特别是浅层精度较高。
|
图 12 复杂构造模型的初始速度(a)、ε(b)和δ(c)场及初始单程波偏移剖面(d) |
|
图 13 初始单程波偏移角道集(a)和各向异性层析完成后RTM角道集(b) |
|
图 14 层析后速度(a)、ε(b)、δ(c)场及RTM偏移剖面(d) |
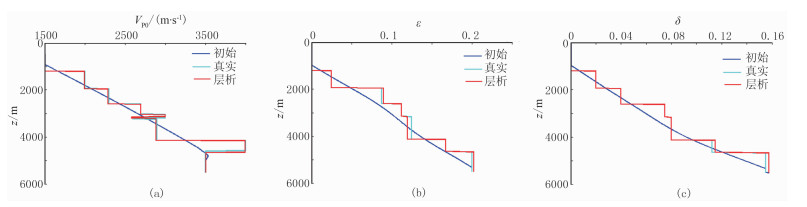
|
图 15 x=4260m处层析参数与初始和真实参数对比 (a)VP0;(b)ε;(c)δ |
本文通过分析角道集剩余曲率的影响因素,提出了一种适用于VTI介质各向异性参数的层析反演策略。针对速度是最关键的影响因素,并考虑逆时偏移中对速度模型的高要求,首先通过各向同性双平方根(DSR)偏移得到速度场层位,进行单一速度层析。然后利用RTM得到较高精度的成像结果,同时用Poynting矢量法求取角道集。根据各参数对不同角道信息的敏感性,在前人研究基础上,精确划分了不同的角度范围,改进了传统的各向异性参数层析反演方法。洼陷模型试算结果表明,该方法能有效反演各向异性Thmosen三参数;复杂构造模型试算结果验证了本文方法的适用性。
| [1] |
李勤, 李庆春, 张林. VTI介质多波各向异性参数分析[J]. 石油地球物理勘探, 2010, 49(3): 503-507. LI Qin, LI Qingchun, ZHANG Lin. Anisotropic parameter analysis of multi-component data in VTI media[J]. Oil Geophysical Prospecting, 2010, 49(3): 503-507. |
| [2] |
王世清, 贺玉山, 王建民, 等. 基于时移双曲方程的各向异性速度分析[J]. 石油地球物理勘探, 2013, 48(5): 700-706. WANG Shiqing, HE Yushan, WANG Jianmin, et al. Anisotropic velocity analysis based on shift hyperbolic equation[J]. Oil Geophysical Prospecting, 2013, 48(5): 700-706. |
| [3] |
刘瑞合, 赵金玉, 印兴耀, 等. VTI介质各向异性参数层析反演策略与应用[J]. 石油地球物理勘探, 2017, 52(3): 484-490. LIU Ruihe, ZHAO Jinyu, YIN Xingyao, et al. Strategy of anisotropic parameter tomography inversion in VTI medium[J]. Oil Geophysical Prospecting, 2017, 52(3): 484-490. |
| [4] |
娄婷婷, 李振春, 张凯.各向异性参数层析反演方法研究[C].中国地球物理2013——第十九分会场论文集, 2013.
|
| [5] |
白海军, 孙赞东, 李彦鹏. 3D VSP共检波点道集各向异性分析及参数提取[J]. 石油地球物理勘探, 2011, 46(增刊1): 53-59. BAI Haijun, SUN Zandong, LI Yanpeng. Anisotropy analysis and parameters extraction on 3D VSP common receiver gathers[J]. Oil Geophysical Prospecting, 2011, 46(S1): 53-59. |
| [6] |
徐嘉亮, 周东红, 贺电波, 等. 高精度深度域层析速度反演方法[J]. 石油地球物理勘探, 2018, 53(4): 737-744. XU Jialiang, ZHOU Donghong, HE Dianbo, et al. High-precision velocity tomography inversion in the depth domain[J]. Oil Geophysical Prospecting, 2018, 53(4): 737-744. |
| [7] |
Woodward M, Nichols D, Zdraveva O, et al. A decade of tomography[J]. Geophysics, 2008, 73(5): VE5-VE11. DOI:10.1190/1.2969907 |
| [8] |
Tsvankin L, Thmosen L. Inversion of reflection tra-veltimes for transverse isotropy[J]. Geophysics, 1995, 60(4): 1095-1107. DOI:10.1190/1.1443838 |
| [9] |
Chapman C H, Pratt R G. Traveltime tomography in anisotropic media Ⅰ:Theory[J]. Geophysical Journal International, 1992, 109(1): 1-19. DOI:10.1111/j.1365-246X.1992.tb00075.x |
| [10] |
Watanabe T, Hirai T, Sassa K. Seismic traveltime tomography in anisotropic heterogeneous media[J]. Journal of Applied Geophysics, 1996, 35(2-3): 133-143. DOI:10.1016/0926-9851(96)00014-6 |
| [11] |
秦宁, 王延光, 杨晓东, 等. 基于角道集剩余曲率分析的层析速度建模[J]. 石油地球物理勘探, 2015, 50(1): 61-66. QIN Ning, WANG Yanguang, YANG Xiaodong, et al. Tomography velocity model building based on ADCIG's residual curvature[J]. Oil Geophysical Prospecting, 2015, 50(1): 61-66. |
| [12] |
秦宁, 李振春, 杨晓东, 等. 自动拾取的成像空间域旅行时层析速度反演[J]. 石油地球物理勘探, 2012, 47(3): 392-398. QIN Ning, LI Zhenchun, YANG Xiaodong, et al. Im-age domain travel-time tomography velocity inversion based on automatic picking[J]. Oil Geophysical Prospecting, 2012, 47(3): 392-398. |
| [13] |
Koren Z, Ravve I, Gonzalez G, et al. Anisotropic local tomography[J]. Geophysics, 2008, 73(5): VE75-VE92.. DOI:10.1190/1.2953979 |
| [14] |
Rickett J E, Sava P C. Offset and angle-domain common image-point gathers for shot-profile migration[J]. Geophysics, 2002, 67(3): 883-889. DOI:10.1190/1.1484531 |
| [15] |
刘文卿, 王西文, 王宇超, 等. 角度域叠前偏移成像研究及应用[J]. 石油地球物理勘探, 2010, 45(增刊1): 62-65. LIU Wenqing, WANG Xiwen, WANG Yuchao, et al. Angle domain pre-stack migration imaging studies and application[J]. Oil Geophysical Prospecting, 2010, 45(S1): 62-65. |
| [16] |
Sava P, and Fomel S.Angle-gathers by Fourier Transform[R].Stanford Exploration Project Report, 2000, 103: 123-133.
|
| [17] |
Sava P C, Fomel S. Angle-domain common-image ga-thers by wavefield continuation methods[J]. Geophy-sics, 2003, 68(3): 1065-1074. |
| [18] |
Robert G C.Reverse time migration with random boundary[C].SEG Technical Program Expanded Abstracts, 2009, 28: 2809-2813.
|
| [19] |
Duveneck E, Milcik P, Bakker P M.Acoustic VTI wave equations and their application for anisotropic reverse time migration[C].SEG Technical Program Expanded Abstracts, 2008, 27: 2186-2190.
|
| [20] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 661-672. |
| [21] |
李志晔, 李振春, 刘玉金, 等. 基于波场分离的层析波形反演方法[J]. 石油地球物理勘探, 2016, 51(2): 295-300. LI Zhiye, LI Zhenchun, LIU Yujin, et al. Tomography waveform inversion with wave-field decomposition[J]. Oil Geophysical Prospecting, 2016, 51(2): 295-300. |
| [22] |
Yoon K, Marfurt K J. Reverse-time migration using the Poynting vector[J]. Exploration Geophysics, 2006, 59(1): 102-107. |
| [23] |
Yan R, Xie X B.A new angle-domain imaging condition for pre-stack reverse-time migration[C].SEG Technical Program Expanded Abstracts, 2009, 28: 2784-2788.
|
| [24] |
Culter R T, Bishop T N.Seismic tomography: Formulation and methodology[C].SEG Technical Program Expanded Abstracts, 1984, 3: 711-712.
|
| [25] |
Stork C. Reflection tomography in the post migrated domain[J]. Geophysics, 1992, 57(5): 680-692. DOI:10.1190/1.1443282 |
| [26] |
胡博凯.基于ADCIGs的VTI介质旅行时层析反演方法研究[D].山东青岛: 中国石油大学(华东), 2017, 41-42.
|
| [27] |
Zhou C, Jiao J, Lin S, et al. Multiparameter joint tomography for TTI model building[J]. Geophysics, 2011, 76(5): WB183-WB190. DOI:10.1190/geo2010-0395.1 |



 张凯, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
张凯, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: