基于全波场模拟从地震观测记录中获取定量信息的全波形反演(Full waveform inversion,FWI)是一项充满挑战的高精度速度反演技术。相对于常规的速度建模方法(如旅行时层析成像),FWI兼顾了数据中所有的信息分量,因此它具备更高分辨率的速度建模的潜力。20世纪80年代Tarantola[1]提出时间域FWI技术,但受当时计算能力的限制,FWI技术发展缓慢;90年代Pratt[2]将该技术引入频率域并促成其快速发展。通过进一步研究,Pratt[3]发现,使用低频和大炮检距信息做频率域FWI,更有利于准确构建复杂的地下地质构造模型。
FWI是高分辨率的反演方法,在最佳情况下,其分辨精度可达波长一半[4-5]。基于最优化理论,FWI目标泛函的梯度可由伴随状态法有效构建,从而避免了Fréchet矩阵的大规模运算[6-7]。然而,波动方程的强非线性使FWI在实际应用时须依赖于较准确的宏观速度模型(尤其是中低波数部分)和观测数据的低频信息。Shi等[8]指出FWI是高度非线性和“病态”的问题,当初始模型与真实模型足够接近时,目标泛函才能避开局部极值而收敛到全局最优点。
近年来,随着计算机技术的快速发展和一系列优化算法的出现,三维声波FWI的应用陆续出现[9-11]。但这些成功案例大多应用于海上数据。杨勤勇等[12]分析了陆地资料的应用难点,并展望了陆地资料的应用前景。胡光辉等[13]提出了利用早至波波形反演解决近地表建模问题的方案。
本文研发了基于高斯束层析的速度建模技术,有效弥补了速度模型中的中波数成分,降低了FWI技术对数据低频的依赖;利用基于相位匹配的目标泛函和伪保守波动方程,降低了FWI局部极值性并解决了海量计算量难题,从而实现了射线层析→高斯束层析→全波形反演的递进式速度建模方案,并成功应用于三维陆地实际资料。
1 高斯束层析宏观速度建模反演过程的强非线性特征是制约FWI方法在实践中取得突破的关键,使FWI在应用层面依赖于高精度的初始速度模型。针对这一问题,本文研发了高斯束层析速度建模技术,利用波动方程波路径替代传统射线层析的高频传播路径,弥补了射线层析无法分辨的中波数速度成分,为FWI提供了高精度宏观速度模型,有效避免了周波跳跃现象。此外,本文基于高斯束传播算子计算波动方程旅行时层析核函数,在兼顾精度的同时,提高了层析核函数计算效率。
1.1 成像域波动旅行时层析核函数层析反演是构建宏观速度模型最为重要的方法之一,结合偏移算法在成像域进行旅行时层析速度反演是当前较成熟、有效且广泛应用的技术。本文应用成像域高斯束层析反演技术为FWI提供宏观速度模型,以缓解FWI面临的初始速度建模难题。
成像域波路径层析核函数的推导与成像条件相关,角度域高斯束偏移(GBM)单炮成像条件表示为
| $ {I_{{\rm{GBM}}}}(\mathit{\boldsymbol{x}},\theta ,\varphi ,\omega ) = S\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){R^*}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) $ | (1) |
式中:ps和pr分别代表从炮点和检波点传播到成像点x的慢度矢量;IGBM(x, θ, φ, ω)是频率域表示的角度成像结果(共方位—反射角成像道集);S(x, ps, ω; xs)表示从炮点出发的下行高斯束波场;R(x, pr, ω; xs)表示从检波点出发的上行高斯束波场;x=(x, y, z)表示成像点坐标;θ、φ分别表示成像点的反射张角及方位角;“*”表示共轭;下标“s”和“r”均分别对应炮点和检波点。
与熟知的单程波成像条件(在波场传播时没有显式地得到慢度矢量p)类似,高斯束成像也是激励时间成像条件。
在波动方程的一阶Born近似下,波场U可分解为背景波场U0和扰动波场ΔU,即
| $ \mathit{\boldsymbol{U}} = {\mathit{\boldsymbol{U}}_0} + \Delta \mathit{\boldsymbol{U}} $ | (2) |
因此从式(1)可近似得到扰动像
| $ \begin{array}{l} \Delta {I_{{\rm{CBM}}}}(\mathit{\boldsymbol{x}},\theta ,\varphi ,\omega ) \\ \;\;\;\;\approx\Delta S\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)R_0^*\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) + \\ \;\;\;\;\;\;\;\;{S_0}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\Delta {R^*}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) \end{array} $ | (3) |
式中:S0(x, ps, ω; xs)和R0(x, pr, ω; xs)分别表示在背景速度模型中从炮点和检波点传播到空间任意一点x的波场;ΔS、ΔR为对应的一阶Born近似散射场。式(3)表明,成像点x处像的扰动来自炮点端和检波点端两个分支的影响。
进一步地,根据一阶Born近似散射场的表达和分解原理[14],ΔS与ΔR*可分别表示为
| $ \left\{ \begin{array}{l} \Delta S(\left. {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\\ \;\; = \int_{{L_{\rm{s}}}} 2 k_0^2\frac{{\Delta v(\mathit{\boldsymbol{y}})}}{{{v_0}(\mathit{\boldsymbol{y}})}}{G_{\rm{s}}}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ,\mathit{\boldsymbol{y}}} \right){S_0}\left( {\mathit{\boldsymbol{y}};{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){\rm{d}}\mathit{\boldsymbol{y}}\\ \Delta {R^*}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\\ \;\; = \int_{{L_{\rm{r}}}} 2 k_0^2\frac{{\Delta v(\mathit{\boldsymbol{y}})}}{{{v_0}(\mathit{\boldsymbol{y}})}}{G_{\rm{r}}}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ,\mathit{\boldsymbol{y}}} \right)R_0^*\left( {\mathit{\boldsymbol{y}};{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){\rm{d}}\mathit{\boldsymbol{y}} \end{array} \right. $ | (4) |
式中Ls和Lr分别表示从炮点和从检波点到成像点的Born波路径;
将式(4)代入式(3),从形式上可给出像的扰动(左端项)与速度扰动(右端项)的关系式。但在实际操作时,显然不能直接利用该式进行层析反演!通过对比、分析可知:数据域层析反演利用的是正演数据与实测数据的差在某种范数(如L2)下的最小值作为误差泛函,其实测数据是客观的,可直接用来做逼近标准;而若直接用式(3)做成像域反演,则因客观上无法得到真实像IGBM(x, θ, φ, ω)而无法得到扰动像ΔIGBM(x, θ, φ, ω),故其本质是利用一个未知的中间量估计另一未知量Δv。直接利用像的扰动进行反演缺乏严格的判断标准。
从另一个角度分析,像的扰动是一个综合概念,其实质包括了旅行时(位置)扰动和振幅扰动。实际计算时需将像的扰动退化为旅行时(深度)扰动或振幅扰动,从而分别建立与速度扰动的关系式。由于像域的振幅扰动影响因素太复杂,包括地表一致性、震源及检波器耦合效应等,即使是在准确模型下的保幅成像,其角度道集仍存在AVA效应,因此角度道集上能用来层析反演的仅仅是其同相轴的剩余旅行时差(RMO),不包括其振幅,此时实际层析反演一般退化为仅利用旅行时扰动。
考虑退化到仅利用旅行时扰动进行层析反演,进一步地,将式(3)改写为
| $ \begin{array}{l} \Delta {I_{{\rm{GBM}}}}(\mathit{\boldsymbol{x}},\theta ,\varphi ,\omega )\\ \;\;\; \approx \frac{{\Delta S\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{{S_0}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{S_0}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)R_0^*\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) + \\ \;\;\;\;\;\frac{{\Delta {R^*}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{R_0^*\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{S_0}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)R_0^*\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\\ = {I_0}(\mathit{\boldsymbol{x}},\theta ,\varphi ,\omega )\left[ {\frac{{\Delta S\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{{S_0}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}} + \frac{{\Delta {R^*}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{R_0^*\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}} \right. \end{array} $ | (5) |
整理得
| $ \begin{array}{l} \frac{{I(\mathit{\boldsymbol{x}},\theta ,\varphi ,\omega )}}{{{I_0}(\mathit{\boldsymbol{x}},\theta ,\varphi ,\omega )}} - 1 \approx \frac{{\Delta S\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{{S_0}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\Delta {R^*}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{R_0^*\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}} \end{array} $ | (6) |
在波动方程的Rytov近似下,波场可表示为
| $ \mathit{\boldsymbol{u}} = \left( {{\mathit{\boldsymbol{A}}_0} + \Delta \mathit{\boldsymbol{A}}} \right){{\rm{e}}^{{\rm{i}}\left( {{\varphi _0} + \Delta \varphi } \right)}} $ |
其成像值是两个波场的相关,故也可表示为
| $ \mathit{\boldsymbol{I}} = \left( {{\mathit{\boldsymbol{A}}_0} + \Delta \mathit{\boldsymbol{A}}} \right){{\rm{e}}^{{\rm{i}}\left( {{\varphi _0} + \Delta \varphi } \right)}} $ |
| $ {\mathit{\boldsymbol{I}}_0}(\mathit{\boldsymbol{x}},\theta ,\varphi ,\omega ) = {\mathit{\boldsymbol{A}}_0}{{\rm{e}}^{{\rm{i}}{\varphi _0}}} $ |
由于ΔA≪A0,则式(6)可进一步表示为
| $ {{\rm{e}}^{{\rm{i}}\Delta \varphi }} - 1 \approx \frac{{\Delta S\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{{S_0}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}} + \frac{{\Delta {R^*}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{R_0^*\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}} $ | (7) |
因Δφ趋近于零,则式(7)左端项近似等于iΔφ。两边取虚部,得到
| $ \begin{array}{*{20}{c}} {\Delta \varphi \left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = Im \left[ {\frac{{\Delta S\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{{S_0}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}} \right] + }\\ { Im \left[ {\frac{{\Delta {R^*}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{R_0^*\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}} \right]} \end{array} $ | (8) |
式中Im(·)表示虚部。
单频相位扰动与单频旅行时扰动也有近似关系
| $ \Delta t(\mathit{\boldsymbol{x}},\theta ,\varphi ,\omega ) = \frac{{\Delta \varphi (\mathit{\boldsymbol{x}},\theta ,\varphi ,\omega )}}{\omega } $ | (9) |
同时将式(4)及式(9)代入式(8),整理得到成像域单频旅行时扰动与速度扰动的关系式
| $ \begin{array}{*{20}{c}} {\Delta t(\mathit{\boldsymbol{x}},\theta ,\varphi ,\omega ) = \int_{{L_{\rm{s}}}} {K_{\rm{s}}^{\rm{F}}} \left( {\mathit{\boldsymbol{y}};\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\Delta v(\mathit{\boldsymbol{y}}){\rm{d}}\mathit{\boldsymbol{y}} + }\\ {\int_{{L_{\rm{r}}}} {K_{\rm{r}}^{\rm{F}}} \left( {\mathit{\boldsymbol{y}};\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\Delta v(\mathit{\boldsymbol{y}}){\rm{d}}\mathit{\boldsymbol{y}}} \end{array} $ | (10) |
式中:Δt(x, θ, φ, ω)为高斯束偏移的旅行时扰动,即剩余时差;KF为单频旅行时层析核函数,其两个分支分别表示为[15]
| $ \left\{ \begin{array}{l} K_{\rm{s}}^{\rm{F}}\left( {\mathit{\boldsymbol{y}};\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\\ \;\;\;\; = Im \left[ {\frac{{2\omega }}{{v_0^3(\mathit{\boldsymbol{y}})}}\frac{{{G_{\rm{s}}}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ,\mathit{\boldsymbol{y}}} \right){G_0}\left( {\mathit{\boldsymbol{y}};{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{{G_0}\left( {\mathit{\boldsymbol{y}};{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}} \right]\\ K_{\rm{r}}^{\rm{F}}\left( {\mathit{\boldsymbol{y}};\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\\ \;\;\;\;\; = Im \left[ {\frac{{2\omega }}{{v_0^3(\mathit{\boldsymbol{y}})}}\frac{{{G_{\rm{r}}}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ,\mathit{\boldsymbol{y}}} \right)G_0^*\left( {\mathit{\boldsymbol{y}};{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{G_0^*\left( {\mathit{\boldsymbol{y}};{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}} \right] \end{array} \right. $ | (11) |
式中G0(y; ps, ω,xs)表示对应的背景格林函数。
带限地震信号的旅行时扰动可用单频旅行时扰动加权叠加[16]得到
| $ \Delta t = \int_{{\omega _0} - \Delta \omega }^{{\omega _0} + \Delta \omega } H (\omega )\Delta t(\omega ){\rm{d}}\omega $ | (12) |
式中H(ω)表示归一化的加权函数,那么,成像域带限旅行时扰动与速度扰动的关系可以表示为
| $ \begin{array}{l} \Delta t(\mathit{\boldsymbol{x}},\theta ,\varphi ) = \int_{{L_{\rm{s}}}} {K_{\rm{s}}^{\rm{T}}} \left( {\mathit{\boldsymbol{y}};\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\Delta v(\mathit{\boldsymbol{y}}){\rm{d}}\mathit{\boldsymbol{y}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_J {K_{\rm{r}}^{\rm{T}}} \left( {\mathit{\boldsymbol{y}};\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\Delta v(\mathit{\boldsymbol{y}}){\rm{d}}\mathit{\boldsymbol{y}} \end{array} $ | (13) |
式中KT为带限旅行层析核函数,其两个分支为
| $ \left\{ {\begin{array}{*{20}{l}} {K_{\rm{s}}^{\rm{T}}\left( {\mathit{\boldsymbol{y}};\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = \int W (\omega ) \times }\\ { Im \left[ {\frac{{2\omega }}{{v_0^3(\mathit{\boldsymbol{y}})}}\frac{{{G_{\rm{s}}}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ,\mathit{\boldsymbol{y}}} \right){G_0}\left( {\mathit{\boldsymbol{y}};{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{{G_0}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{p}}_{\rm{s}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}} \right]{\rm{d}}\omega }\\ {K_{\rm{r}}^{\rm{T}}\left( {\mathit{\boldsymbol{y}};\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{p}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = \int W (\omega ) \times }\\ { Im \left[ {\frac{{2\omega }}{{v_0^3(\mathit{\boldsymbol{y}})}}\frac{{{G_{\rm{r}}}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ,\mathit{\boldsymbol{y}}} \right)G_0^ * \left( {\mathit{\boldsymbol{y}};{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{G_0^ * \left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{p}}_{\rm{r}}},\omega ,{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}} \right]{\rm{d}}\omega } \end{array}} \right. $ | (14) |
该式即为推导的成像域带限旅行时核函数。
至此,基于式(14)计算带限旅行时层析核函数的层析反演方法即为高斯束层析速度建模技术。
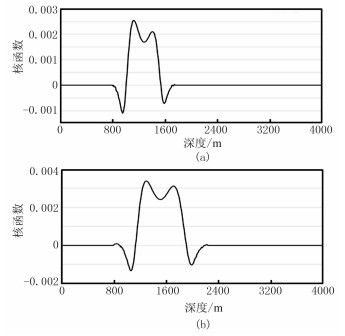
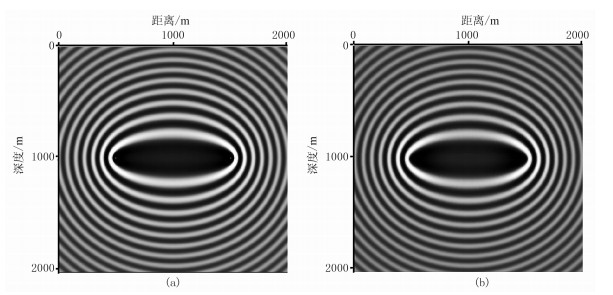
1.2 高斯束计算格林函数式(11)给出单频旅行时层析核函数表达式,计算该核函数的关键是求取背景模型格林函数,高斯束传播算子的具体计算请参考文献[17]。本文主要通过数值实验展示基于高斯束传播算子计算带限波动旅行时层析核函数(式(14))的精度与可行性。图 1为常速情况下20Hz高斯束计算核函数与解析解对比,为直观分析两者差别,抽取图 1中x=1000m处核函数纵截面数值进行对比;从图 2可见20Hz高斯束计算的核函数与解析解基本一致。
|
图 1 常速情况下20Hz高斯束计算核函数(b)与解析核函数(a)的对比 |
|
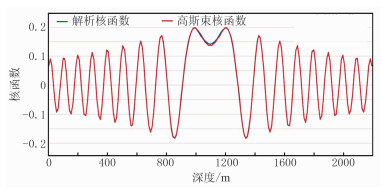
图 2 20Hz高斯束计算核函数与解析解在x=1000m处纵截面的精度对比 |
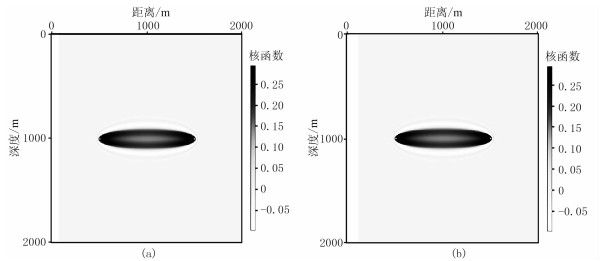
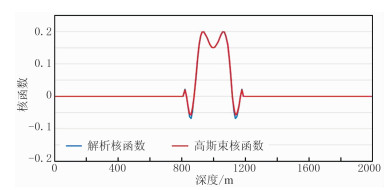
进一步地,根据式(14)对频率加权积分可计算带限旅行时层析核函数,积分频段为0~
从图 3、图 4可看出,利用高斯束计算带限旅行时层析核函数与解析解基本一致,完全满足后续旅行时层析成像的需求。
|
图 3 解析解带限核函数(a)与高斯束计算的带限旅行时层析核函数(b)的对比 |
|
图 4 高斯束计算带限核函数与解析解在x=1000m处纵截面的精度对比 |
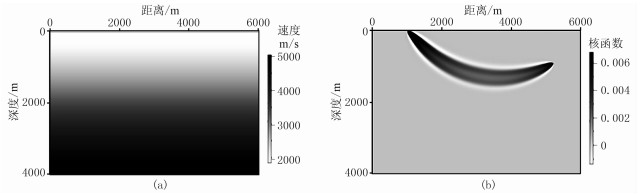
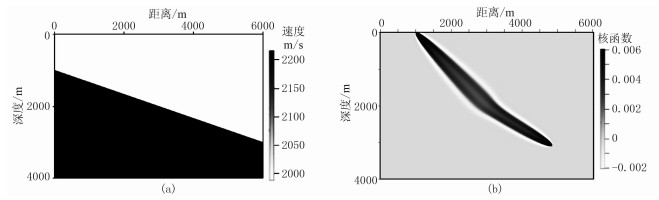
图 5和图 6分别为常梯度速度模型(震源位于(1000m,0),接收点位于(5200m,900m))、层状介质速度模型(震源位于(1000m,0),接收点位于(4900m,3100m))的核函数计算结果,两种核函数均通过高斯束积分得到,积分频段同上。图 7对比了两种模型层析核函数的截面,可见核函数的中心值较小,远离中心射线后逐渐增大,在某点达到最大后又逐渐减小直至为0。形状表现为双驼峰型。
|
图 5 常梯度速度模型(a)及其带限核函数(b) |
|
图 6 层状速度模型(a)及其带限核函数(b) |
1.3 高斯束层析反演流程
成像域高斯束层析反演的基本流程同常规射线层析反演的流程基本一致,其具体步骤如下:
(1) 基于初始速度模型进行高斯束叠前深度偏移(GBM),并输出(方位)反射角度道集(ADCIGs);
(2) 在深度偏移剖面上全自动解释反射界面,拾取层析控制点;
(3) 参数化速度模型;
(4) 在界面约束下,在ADCIGs上全自动拾取相应的同相轴的剩余深度差/时间差;
(5) 利用式(5)计算高斯束层析核函数,构建高斯束层析Fréchet导数矩阵;
(6) 建立旅行时误差泛函(可考虑各种约束);
(7) 利用并行化的LSQR算法求解法方程,得到速度更新量;
(8) 更新速度模型;
(9) 重新进行GBM。视ADCIGs是否拉平决定是否进行下一轮的速度反演。
2 FWI高波数精细建模充分利用叠前地震波场的运动学和动力学信息重建地下物理参数,FWI的分辨率可达传播波长的二分之一,能揭示复杂地质背景下构造细节及岩性,是现今精度最高的速度建模方法之一。但受目前数据采集条件的限制,地震数据的振幅和相位常呈强非一致性。本文采用基于相位匹配的目标泛函增强数据相位匹配,从而降低陷入局部极值的风险;采用伪保守一阶速度—应力方程计算速度的梯度函数,大幅度提升了计算效率,推动了FWI实用化进程。
2.1 基于相位匹配的目标泛函陆地数据受激发和接受条件限制,各震源和检波点之间存在较为明显的能量差异。当采用此类数据反演时,各炮和检波点之间的不均衡带来残差能量的不一致,在波场残差反传时引起模型更新量在不同地区存在较大差异,进而导致反演不稳定甚至不收敛。为了削弱这种不均衡的影响,采用基于相位拟合的互相关目标泛函较L2泛函更优,其主要优势在于强调匹配相位信息,其凸性更优,不易陷入局部极值。Brossier等[18]给出了非零延迟归一化互相关目标泛函,其表达式为
| $ \begin{array}{l} E(m) = - \frac{1}{2}\sum\limits_{{x_{\rm{s}}}} {\sum\limits_{{x_{\rm{r}}}} {\sum\limits_\tau {} } } \\ \;\;\;\;\;\;\;{\left[ {W(\tau )\frac{{\sum\limits_t {{d_{{\rm{cal}}}}} \left( {t,{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){d_{{\rm{obs}}}}\left( {t + \tau ,{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{\left\| {{d_{{\rm{cal}}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right\| \cdot \left\| {{d_{{\rm{obs}}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right\|}}} \right]^2} \end{array} $ | (15) |
式中:τ为延迟时间;xr为检波点;xs为炮点;W(τ)是惩罚函数;dcal(t, xr; xs)为人工合成地震记录;dobs(t+τ, xr; xs)是时延观测地震记录。
为了实现分步FWI,本文采用了时间加窗的归一化互相关目标泛函
| $ \left\{ \begin{array}{l} E(m) = - \frac{1}{2}\sum\limits_h {\sum\limits_\tau {{{\left[ {P(\tau ){X_{\cos .n}}(\tau ,h)} \right]}^2}} } \\ {X_{{\mathop{\rm co}\nolimits} {\rm{r}},{\rm{n}}}}\left( {\tau ,h} \right)\\ \;\;\;\; = \frac{{win (t,h)\sum\limits_t {{d_{{\rm{cal}}}}} (t,h){d_{{\rm{obs}}}}(t + \tau ,h)}}{{\left\| {win(t,h){d_{{\rm{cal}}}}(h)} \right\| \cdot \left\| {win(t,h){d_{{\rm{obs}}}}(h)} \right\|}} \end{array} \right. $ | (16) |
式中: P(τ)=-eατ2为加权互相关时窗函数, 其中α控制计算归一化互相关目标泛函时窗大小,α越大时窗越小,α越小时窗越大;win(t,h)是与炮检距h相关的时窗函数。
2.2 基于伪保守一阶速度—应力方程的梯度计算梯度计算是FWI技术最核心的部分[19],梯度计算效率决定了FWI对于实际问题的处理能力,而梯度计算效率主要取决于波动方程数值模拟的计算效率以及存储能力[20-21]。常用的Fréchet矩阵计算具有计算量大、实现性差的弊端,本文采用共轭状态法求取梯度,该方法的实现仅使用炮点正向传播波场与接收点逆时传播残差波场的互相关生成梯度。通过互相关目标泛函式(15)对模型参数求导,即可得其梯度。具体表达式为
| $ \begin{array}{l} \frac{{\partial E(m)}}{{\partial m}} = - \sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{s}}}} {\sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{r}}}} {\sum\limits_t {\frac{{\partial {d_{{\rm{cal}}}}\left( {t,{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{\partial m}}} } } \sum\limits_\tau {{W^2}} (\tau ) \times \\ \;\;\;\;\;\;\;\;\;\frac{{\sum\limits_t {{d_{{\rm{cal}}}}} \left( {t,{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){d_{{\rm{obs}}}}\left( {t + \tau ,{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{\left\| {{d_{{\rm{cal}}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right\| \cdot \left\| {{d_{{\rm{obs}}}}\left( {{{\bf{x}}_{\rm{r}}};{{\bf{x}}_{\rm{s}}}} \right)} \right\|}} \times \\ \;\;\;\;\;\;\;\;\;\;\left[ {\frac{{{d_{{\rm{obs}}}}\left( {t + \tau ,{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{\left\| {{d_{{\rm{cal}}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right\| \cdot \left\| {{d_{{\rm{obs}}}}\left( {{{\bf{x}}_{\rm{r}}};{{\bf{x}}_{\rm{s}}}} \right)} \right\|}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{{{d_{{\rm{cal}}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\sum\limits_t {{d_{{\rm{cal}}}}} \left( {t,{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){d_{{\rm{obs}}}}\left( {t + \tau ,{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}{{{{\left\| {{d_{{\rm{cal}}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right\|}^3} \cdot \left\| {{d_{{\rm{obs}}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}};{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right\|}}} \right] \end{array} $ | (17) |
对于不同的数据匹配,不论是求解两个信号的波形振幅残差还是计算两个信号的相似程度,目标泛函关于模型参数的梯度求解表达式是相同的,即都是采用正向传播波场和逆时传播的伴随波场互相关叠加求得。唯一不同的是对不同的匹配方式,伴随方程右端的伴随震源项不相同。
传统的一阶速度—应力方程的声波正演模拟算子为非自伴随算子,由于正演算子为非自伴随,在求取震源正传波场和残差反传波场时不能使用同一个正演算子,且需要对正演算子求导数,增加了计算的复杂度。Castellanos[7]把一阶速度—应力方程转化为伪保守形式使正演模拟算子自伴随,利用伪保守形式的波动方程
| $ \frac{{\partial E(m)}}{{\partial {m_i}}}(\mathit{\boldsymbol{u}}) = - {\left( {{\partial _t}\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{s}}} \right)^i}{\left( {\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}}{{\partial {m_i}}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{p}}_l} $ | (18) |
式中:梯度散射核
| $ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = \left( {\begin{array}{*{20}{c}} {1/k}&0&0&0\\ 0&\rho &0&0\\ 0&0&\rho &0\\ 0&0&0&\rho \end{array}} \right) $ | (19) |
| $ \mathit{\boldsymbol{G'}} = \left( {\begin{array}{*{20}{c}} 0&{{\partial _x}}&{{\partial _y}}&{{\partial _z}}\\ {{\partial _x}}&0&0&0\\ {{\partial _y}}&0&0&0\\ {{\partial _z}}&0&0&0 \end{array}} \right) $ | (20) |
从数学的角度可看出伴随状态法计算梯度的有效性。为了进一步验证这种方法的准确性和精度,将伴随状态法计算所得的梯度与经典的有限差分算法计算的梯度做对比分析。使用有限差分法计算梯度公式如下
| $ \frac{{\partial E(m)}}{{\partial m}} \approx \frac{{E(m + \Delta m) - E(m)}}{{\Delta m}} $ | (21) |
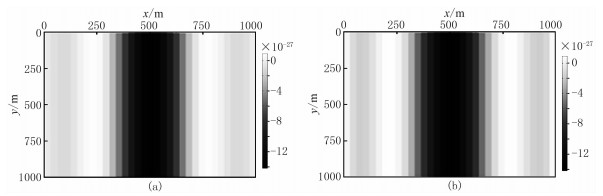
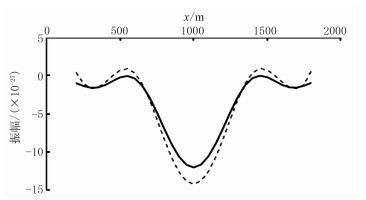
选用41×41×41的均质立方体模型,模型中心嵌入一个半径为50m的绕射体,其x、y、z三个方向的步长(50m)相同;震源采用主频为5Hz的雷克子波。图 8a为使用伴随状态法计算所得的梯度水平方向切片。如前文所述,该梯度使用频率域反演联合时间域正演而得到。正演使用有限差分交错网格空间4阶、时间2阶。梯度计算仅使用5Hz单频。图 8b为有限差分法获取的梯度。图 9显示伴随状态法(实线)和有限差分法(虚线)计算的梯度一维曲线的直接对比。不难看出二者形状近似一致,仅存在可接受的误差。这是因为有限差分法对步长敏感,当采用不同的步长时,该误差随步长而改变,因此可认为该误差来自有限差分的离散化。
|
图 8 在z=800m深度处计算的梯度水平切片 (a)伴随状态法;(b)有限差分法 |
|
图 9 伴随状态法(实线)与有限差分法(虚线)计算的梯度一维曲线对比 y=800m,z=800m |
FWI强烈的依赖于观测数据,因此在开展全波形迭代反演之前需要对实际数据进行特殊的精细处理:保早至波的去噪处理、振幅一致性处理、有效数据提取。FWI具体计算流程如下:
(1) 利用高斯束层析建立包含中波数速度信息的FWI初始模型;
(2) 地震子波估计;
(3) 基于伪保守形式波动方程地震波模拟;
(4) 计算观测数据与模拟数据的互相关,并得到波场反传的震源;
(5) 采用与地震波正演模拟相同的算子进行波场反向传播;
(6) 正传与反传波场在时间域的互相关形成梯度;
(7) 计算初始迭代步长,得到初始速度更新量;
(8) 利用LBFGS算法优化迭代步长,最优速度更新量,完成一次迭代反演;
(9) 利用新的速度作为初始速度进行步骤(3)~步骤(8)的循环迭代,直到满足迭代终止条件。
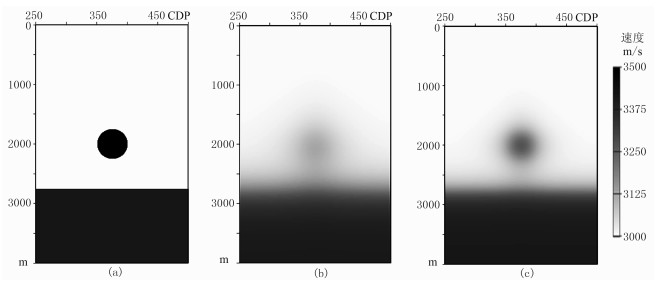
3 模型测试本文设计了简单的球状模型,CDP范围0~750,为了更清晰地显示反演的球体,在图 10a中显示的CDP范围只有250~500,球体中心位于CDP500处,深度为2000m。数据采集最大炮检距为7500m。图 10b和图 10c分别是射线层析和高斯束层析反演得到的速度。高斯束层析比射线层析具有更丰富的中波数成分,分辨率提高。分别将射线层析和高斯束层析速度作为FWI初始模型进行高波数速度反演。这两种模型作为初始速度时FWI速度梯度在首次迭代时差异并不明显,随着迭代次数的增加速度更新量逐步差异化。
|
图 10 理论速度模型(a)、射线层析(b)和高斯束层析(c)速度模型 |
迭代次数较高时,速度梯度已无法直观展示与真实速度模型的关系,因而本文分别展示了经10次迭代后速度更新量的总和(图 11)。从图 11清晰可见:射线层析作为初始模型时反演结果无法聚焦,呈现出周波跳跃现象;高斯束层析速度作为初始模型时,FWI速度逼近于真实速度,避免反演结果陷入局部极值。同时,基于该模型对比分析其计算效率,可知利用自伴随算子可使波场传播数值模拟的总体计算效率提高约40%。

|
图 11 FWI模型测试 (a)射线层析速度作为初始速度做10次迭代后的总速度更新量; (b)高斯束层析速度作为初始速度做10次迭代后的总速度更新量 |
本文利用高斯束层析与FWI联合速度建模技术对中国东北某复杂构造工区进行了攻关处理。该区基底之下是上古生界变质岩,变质岩之上发育火山岩。目的层波场复杂,存在多组断裂系统,速度变化大,深度域建模困难,精确成像难度较大。成像处理要求纵向上能刻画火山机构特征和喷发期次,横向上能分辨接触关系,合理突出与火山岩接触的地层反射。前期进行了射线层析速度建模,以此作为深度域初始模型进行后续高斯束层析与FWI联合速度建模。
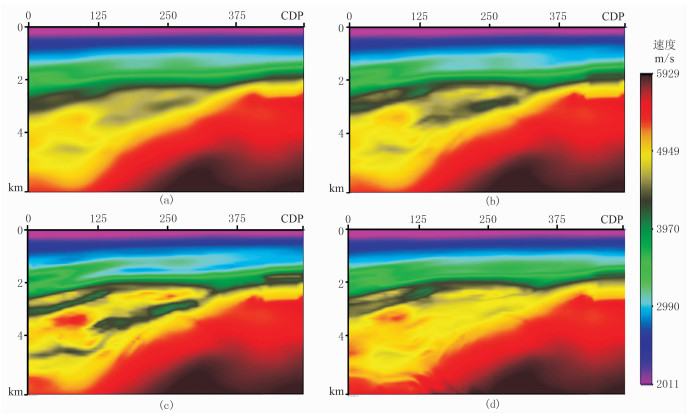
图 12为该地区二维速度反演结果对比,射线层析包含了低波数速度,高斯束层析反演得到了中波数的速度成分,相对于射线层析速度分辨率更高。图 12c为利用图 12b高斯束层析反演作为初始模型反演得到的高波数速度,速度结构层次明确,岩石接触关系清晰;图 12d是以图 12a射线层析速度作为初始模型的反演结果,无法辨识速度结构关系。
|
图 12 实际资料二维速度反演结果对比 (a)射线层析速度;(b)高斯束层析速度;(c)以高斯束层析速度为初始模型的FWI速度;(d)以射线层析速度为初始模型的FWI速度 |
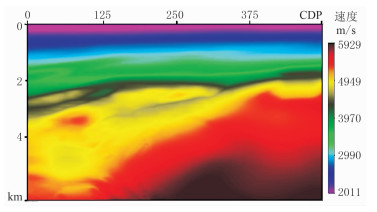
图 13为采用常规互相关泛函得到的FWI速度,可见分辨率不足,且由于缺失了中波数成分,反演收敛性较弱。
|
图 13 采用常规互相关泛函得到的FWI速度 |
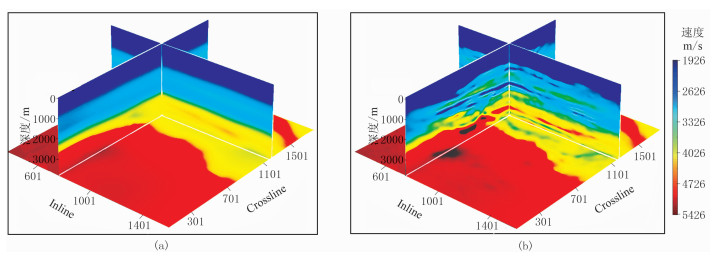
图 14展示了该实际资料常规射线层析与本文方法反演出的三维速度体对比。图 14a为传统射线层析获得的速度场,较好体现速度模型的宏观变化规律,但仅恢复出低波数速度成分,存在反演分辨率不足的问题。高斯束层析与FWI联合建模获得的速度场(图 14b)具有丰富的中、高波数信息,与常规射线层析(图 14a)相比,速度场的横向和纵向分辨率均明显提高,速度建模精度得到提升。
|
图 14 实际资料速度模型对比 (a)射线层析;(b)高斯束层析与FWI联合反演 |
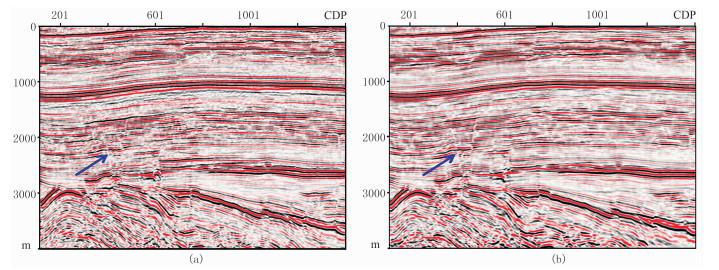
图 15为针对实际数据分别利用射线层析模型及本文高精度FWI反演模型获得的RTM偏移结果,可见后者断裂成像质量更高,断点更干脆,同相轴更连续,整体成像质量更高。从该实际资料处理可以认识到,结合高斯束层析与FWI的联合速度建模处理技术,可以更好地适应复杂陆地资料的深度域速度建模,提供更高质量的成像结果。
|
图 15 实际资料使用不同速度模型的RTM偏移结果对比 (a)射线层析模型;(b)高斯束层析与FWI联合反演模型 |
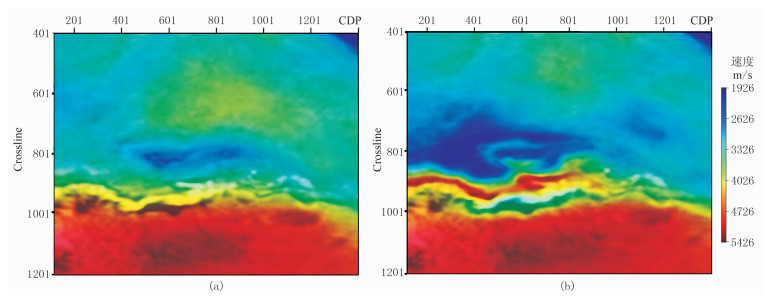
图 16以水平切片方式显示常规射线层析速度与本文方法反演速度模型,可见本文方法反演的速度模型在基底火成岩高速区域具备理想的反演分辨率;特别地,速度场的空间变化规律与该区地质构造特征匹配一致,体现出良好的地质合理性。
|
图 16 实际资料水平切片速度与偏移结果叠合对比 (a)射线层析;(b)高斯束层析与FWI联合反演 |
(1) 陆地资料FWI面临噪声严重、地表复杂及炮检距受限等问题,在实用化进程中存在多重困难。对于复杂构造地区,基于射线层析的低波数初始建模精度不能满足FWI对初始速度的严苛要求。鉴于高斯束层析兼具射线和波动的特征,本文利用高斯束层析构建中波数速度成分,为FWI提供了高精度的初始速度模型,避免了周波跳跃现象。
(2) 针对陆地数据采集各炮和检波点之间的不均衡导致的FWI不稳定甚至不收敛问题,本文采用基于相位匹配的互相关目标泛函取代L2范数,增强目标泛函凸性,降低了FWI陷入局部极值的风险,提高了反演的稳定性和可靠性。
(3) 采用伪保守一阶波动方程形成了自伴随的正演算子,伴随波场梯度计算与正演算子保持一致性,进而提高了FWI速度更新梯度计算效率和计算能力,推动了FWI实用化发展。
(4) 针对中国东北某复杂构造工区目的层波场复杂、断裂系统发育、速度变化大的难题,本文利用高斯束层析结合FWI的深度域速度建模提高了成像精度。从成像剖面上可见火成岩结构特征及接触关系,有助于后续精细解释。高斯束层析与FWI联合的建模方法对于陆地资料深度域速度建模具有广泛的实用价值。
| [1] |
Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [2] |
Pratt R G. Frequency-domain elastic wave modeling by finite differences: a tool for crosshole seismic imaging[J]. Geophysics, 1990, 55(5): 626-632. DOI:10.1190/1.1442874 |
| [3] |
Pratt R. Velocity models from frequency-domain waveform tomography: past, present and future[C]. Extended Abstracts of 76th EAGE Conference & Exhibition, Workshops, 2004.
|
| [4] |
Sirgue L, Pratt R G. Efficient waveform inversion and imaging:a strategy for selecting temporal frequencies[J]. Geophysics, 2004, 69(1): 231-248. DOI:10.1190/1.1649391 |
| [5] |
Ravaut C, Operto S, Improta S, et al. Multi-scale imaging of complex structures from multi-fold wide-aperture seismic data by frequency-domain full-waveform tomography:application to a thrust belt[J]. Geophysical Journal International, 2004, 159(3): 1032-1056. DOI:10.1111/j.1365-246X.2004.02442.x |
| [6] |
Plessix R. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal of the Royal Astronomical Society, 2006, 167(2): 495-503. DOI:10.1111/j.1365-246X.2006.02978.x |
| [7] |
Castellanos C, Etienne V, Hu G, et al. Algorithmic and methodological developments towards full waveform inversion in 3D elastic media[J]. SEG Technical Program Expanded Abstracts, 2011, 30: 2793-2798. |
| [8] |
Shi Y M, Zhao W Z, Cao H. Nonlinear process control of wave-equation inversion and its application in the detection of gas[J]. Geophysics, 2007, 72(1): R9-R18. DOI:10.1190/1.2399450 |
| [9] |
Plessix R. Three-dimensional frequency-domain full-waveform inversion with an iterative solver[J]. Geophysics, 2009, 74(6): WCC149-WCC157. DOI:10.1190/1.3211198 |
| [10] |
Plessix R, Perkins C. Full waveform inversion of a deep water ocean bottom seismometer dataset[J]. First Break, 2010, 28(4): 71-78. |
| [11] |
Sirgue L, Barkved O, Dellinger J, et al. Full waveform inversion: the next leap forward in imaging at Valhall[J]. First Break, 2010, 28(4): 65-70. |
| [12] |
杨勤勇, 胡光辉, 王立歆. 全波形反演研究现状及发展趋势[J]. 石油物探, 2014, 53(1): 78-84. YANG Qinyong, HU Guanghui, WANG Lixin. Research status and development trend of full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2014, 53(1): 77-83. DOI:10.3969/j.issn.1000-1441.2014.01.011 |
| [13] |
胡光辉, 王立歆, 王杰, 等. 基于早至波的特征波波形反演建模方法[J]. 石油物探, 2015, 54(1): 71-76. HU Guanghui, WANG Lixin, WANG Jie, et al. Cha-racteristics waveform inversion based on early arrival wave[J]. Geophysical Prospecting for Petroleum, 2015, 54(1): 71-76. DOI:10.3969/j.issn.1000-1441.2015.01.010 |
| [14] |
蔡杰雄, 方伍宝, 王华忠. 高斯束深度偏移的实现与应用研究[J]. 石油物探, 2012, 51(5): 119-125. CAI Jiexiong, FANG Wubao, WANG Huazhong. Realization and application of Gaussian beam depth migration[J]. Geophysical Prospecting for Petroleum, 2012, 51(5): 119-125. |
| [15] |
蔡杰雄, 王华忠, 陈进, 等. 基于高斯束传播算子的成像域走时层析成像方法[J]. 地球物理学报, 2017, 60(9): 3539-3554. CAI Jiexiong, WANG Huazhong, CHEN Jin, et al. Traveltime tomography in the image domain based on the Gaussian-beam-propagator[J]. Chinese Journal of Geophysics, 2017, 60(9): 3539-3554. |
| [16] |
刘玉柱. 菲涅尔体地震层析成像理论与应用研究[M]. 上海: 同济大学出版社, 2011. LIU Yuzhu. Theory and Applications of Fresnel Vo-lume Seismic Tomography[M]. Shanghai: Tongji University Press, 2011. |
| [17] |
Cerveny V. Seismic Ray Theory[M]. New York: Cambridge University Press, 2001.
|
| [18] |
Brossier R, Operto S, Virieux J. Velocity model building from seismic reflection data by full-waveform inversion[J]. Geophysical Prospecting, 2015, 63(2): 354-367. DOI:10.1111/1365-2478.12190 |
| [19] |
李海山, 杨午阳, 雍学善. 三维一阶速度—应力声波方程全波形反演[J]. 石油地球物理勘探, 2018, 53(4): 730-736. LI Haishan, YANG Wuyang, YONG Xueshan. Three-dimensional full waveform inversion based on the first-order velocity-stress acoustic wave equation[J]. Oil Geophysical Prospecting, 2018, 53(4): 730-736. |
| [20] |
梁展源, 吴国忱, 王玉梅. 基于波动方程重建震源子波的三维全波形反演[J]. 石油地球物理勘探, 2017, 52(6): 1200-1207. LIANG Zhanyuan, WU Guochen, WANG Yumei. A 3D full waveform inversion method based on reconstructed source wavelet with wave equation[J]. Oil Geophysical Prospecting, 2017, 52(6): 1200-1207. |
| [21] |
史才旺, 何兵寿. 基于主成分分析和梯度重构的全波形反演[J]. 石油地球物理勘探, 2018, 53(1): 95-104. SHI Caiwang, HE Bingshou. Full waveform inversion based on principal component analysis and gradient reconstruction[J]. Oil Geophysical Prospecting, 2018, 53(1): 95-104. |



 刘定进, 江苏省南京市江宁区上高路219号中国石化石油物探技术研究院, 211103。Email:
刘定进, 江苏省南京市江宁区上高路219号中国石化石油物探技术研究院, 211103。Email: