地震波场数值模拟是应用数值方法模拟地震波在地下介质中的传播过程,得到在地面或地下各观测点地震记录的一种方法,是地球物理勘探和地震学的重要基础。随着有限差分数值模拟技术的发展,针对实际应用中提高有限差分计算效率[1]、模拟精度[2]、算法稳定性[3-4],处理复杂介质[5-7]、吸收边界条件[8-10]和压制数值频散[11-13]等多方面需求,已研发了多种实用技术,并取得相应研究成果。
提高差分格式数值计算精度最直接的方法就是在模拟时增加(加密)网格节点数,但随之也增加了运算量和存储空间。紧致差分方法能较好地解决这个矛盾;同时紧致差分是一种隐式差分格式,稳定性较强。这些优势使其成为目前颇受关注的有限差分方法之一,并被广泛应用于声波、弹性波和复杂介质等地震波场数值模拟中[14-22],提高了地震波场数值模拟的精度和计算效率。
而Madariaga[23]提出的交错网格差分格式既可提高数值模拟的局部精度,还能加快收敛速度。将交错网格与紧致差分技术结合,可进一步提高数值模拟的精度和压制数值频散的能力[24-26]。
为使差分格式在较大波数范围内减少频散误差,Kim等[27]基于频散关系保持(Dispersion relation preserving,DRP)的思路优化了紧致差分格式,指明采用这种优化差分系数方法可使差分算子最大程度地逼近空间偏导数算子。Liu等[28]基于频散关系提出了优化的时空域有限差分系数,在不增加计算成本的情况下可显著提高模拟精度。Zhang等[29-30]应用最大范数的目标函数及模拟退火算法求解目标函数,优化了一阶和二阶常规中心差分格式的差分系数。Liu[31-32]利用最小平方法优化了二阶导数中心差分和一阶导数交错差分系数。Yu等[33]基于DRP思想,优化得到5阶精度的组合型紧致差分系数。Ren等[34]以优化后时空域差分格式进行声波和弹性波方程的数值模拟。Yang等[35-36]利用极值逼近(Minimax approximation)算法优化了交错网格差分系数,当波数较大时可提高模拟精度。
本文首先讨论了一阶导数的2N阶紧致交错差分格式的建立方法;基于频散关系保持的思想,通过最小平方法建立了最小数值波数误差的目标函数,利用拉格朗日乘数法求解目标函数,得到优化后的4~10阶精度差分系数;然后分析和对比优化前、后的紧致交错网格差分格式的模拟精度、数值频散和声波方程的稳定性条件,并用优化后的紧致交错差分格式对一阶速度—应力声波方程组进行数值模拟。研究结果表明,采用优化差分算子能有效压制数值频散,提高差分近似导数的精度。
1 二维声波方程的高阶差分近似Madariaga[23]早年提出的波动方程交错网格数值模拟方法的差分精度为O(Δt2+Δx2);Levander[37]应用交错网格方法求解P-SV波方程,将差分精度提高到O(Δt2+Δx4);董良国等[3]提出了一阶弹性波方程交错网格高阶差分解法,其差分精度达到O(Δt2M+Δx2N)。现今,交错网格有限差分方法已成为一种高效且应用广泛的数值模拟方法。
根据弹性力学分析,二维情况下一阶应力—速度声波方程组(假设体力为零)可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {V_x}}}{{\partial t}} = \frac{1}{\rho }\frac{{\partial P}}{{\partial x}}}\\ {\frac{{\partial {V_z}}}{{\partial t}} = \frac{1}{\rho }\frac{{\partial P}}{{\partial z}}}\\ {\frac{{\partial P}}{{\partial t}} = \rho {v^2}\left( {\frac{{\partial {V_z}}}{{\partial x}} + \frac{{\partial {V_z}}}{{\partial z}}} \right)} \end{array}} \right. $ | (1) |
式中:P为应力(标量);Vx和Vz分别表示x和z方向质点振动速度分量;ρ为介质密度;v为地震波速度。
1.1 时间2M阶近似用交错网格法进行声波方程数值模拟时,速度和应力分量分别是在t和t+Δt/2时刻计算的,其中Δt为时间步长。用泰勒公式可得速度分量Vx的2M阶精度时间递推式
| $ \begin{array}{l} {V_x}\left( {t + \frac{{\Delta t}}{2}} \right) = {V_x}\left( {t - \frac{{\Delta t}}{2}} \right) + 2\sum\limits_{m = 1}^M {\frac{1}{{(2m - 1)!}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {\frac{{\Delta t}}{2}} \right)^{2m - 1}}\frac{{{\partial ^{2m - 1}}{V_x}}}{{\partial {t^{2m - 1}}}} + O\left( {\Delta {t^{2M}}} \right) \end{array} $ | (2) |
当M=1时,即可得到时间二阶精度差分近似
| $ {V_x}\left( {t + \frac{{\Delta t}}{2}} \right) = {V_x}\left( {t - \frac{{\Delta t}}{2}} \right) + \Delta t\frac{{\partial {V_x}}}{{\partial t}} $ | (3) |
同理可得速度分量Vz和应力分量P的时间二阶精度差分近似
| $ {V_z}\left( {t + \frac{{\Delta t}}{2}} \right) = {V_z}\left( {t - \frac{{\Delta t}}{2}} \right) + \Delta t\frac{{\partial {V_z}}}{{\partial t}} $ | (4) |
| $ P(t + \Delta t) = P(t) + \Delta t\frac{{\partial P}}{{\partial t}} $ | (5) |
利用应力—速度方程组,将式(3)~式(5)中的变量对时间的导数转换为对空间的导数,则可得
| $ \left\{ {\begin{array}{*{20}{l}} {{V_x}\left( {t + \frac{{\Delta t}}{2}} \right) = {V_x}\left( {t - \frac{{\Delta t}}{2}} \right) + \frac{{\Delta t}}{\rho }\frac{{\partial P}}{{\partial x}}}\\ {{V_z}\left( {t + \frac{{\Delta t}}{2}} \right) = {V_z}\left( {t - \frac{{\Delta t}}{2}} \right) + \frac{{\Delta t}}{\rho }\frac{{\partial P}}{{\partial z}}}\\ {P(t + \Delta t) = P(t) + \Delta t\rho {v^2}\left( {\frac{{\partial {V_x}}}{{\partial x}} + \frac{{\partial {V_z}}}{{\partial z}}} \right)} \end{array}} \right. $ | (6) |
紧致交错差分格式最早由Nagarajan等[38]提出,用于大涡模拟(Large eddy simulation)问题,该差分格式利用4个网格节点可得到6阶空间精度。随后,Boersma[39]提出最高可达12阶空间精度的紧致交错差分格式,用于可压缩流体的Navier-Stokes方程的数值模拟。类似于常规交错网格数值模拟,紧致交错网格法求取变量的导数时,也是在相应的变量网格点之间的半程上进行的。
一阶导数的2N阶精度紧致交错差分格式为
| $ \begin{array}{l} a\left( {f_{i - 1}^\prime + f_{i + 1}^\prime } \right) + f_i^\prime = \frac{1}{h}\sum\limits_{n = 1}^{N - 1} {{b_n}} \left\{ {f\left[ {{x_i} + \frac{{(2n - 1)h}}{2}} \right] - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {f\left[ {{x_i} - \frac{{(2n - 1)h}}{2}} \right]} \right\} \end{array} $ | (7) |
式中:h为空间网格尺寸;a和bn是差分系数。利用式(7)近似计算式(6)中变量对空间的一阶导数,确保2N阶差分精度的关键是确定差分系数a和bn。利用泰勒级数展开和待定系数法,即用
| $ \left[ {\begin{array}{*{20}{c}} { - 2}&{{1^1}}&{{3^1}}& \cdots &{2N - 3}\\ { - 3 \times {2^3}}&{{1^3}}&{{3^3}}& \cdots &{{{(2N - 3)}^3}}\\ { - 5 \times {2^5}}&{{1^5}}&{{3^5}}& \cdots &{{{(2N - 3)}^5}}\\ { - 5 \times {2^5}}&{{1^5}}&{{3^5}}& \cdots &{{{(2N - 3)}^5}}\\ { - \left( {2N - 1} \right) \times {2^{2N - 1}}}&{{1^{2N - 1}}}&{{3^{2N - 1}}}& \cdots &{{{(2N - 3)}^{2N - 1}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} a\\ {{b_1}}\\ {{b_2}}\\ \vdots \\ {{b_{N - 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1\\ 0\\ 0\\ \vdots \\ 0 \end{array}} \right] $ | (8) |
可求得紧致交错网格2N阶空间差分精度的差分系数。如当差分精度2N=10时,上述方程组共有5个方程,可确定a和bn(n=1~4)共5个差分系数。
此外,从上述公式可看出,常规交错差分格式(Staggered finite difference,SD)求取中心点处的导数值时,仅用到周围网格点的函数值,而紧致交错差分格式(Staggered compact finite difference,SCD)却还用到相邻点导数值。紧致交错网格法只需利用2N-2个节点即可达到2N阶空间差分精度,而常规交错网格法则须使用2N个节点,因此SCD方法可节省存储空间。表 1列出4~10阶泰勒级数展开得到的差分系数。
|
|
表 1 紧致交错差分格式一阶导数的差分系数 |
利用式(7)表示的SCD格式求取式(6)中的各项偏导数。假设二维地震波场网格化后x方向有n个节点,z方向有m个节点。利用紧致交错差分格式求取一阶导数时,是将变量和导数分别放在两套网格系统中,故差分格式分为向前差分和向后差分。以
| $ \frac{{\partial P}}{{\partial x}}\mathit{\boldsymbol{A}} = \frac{1}{{\Delta x}}P\mathit{\boldsymbol{B}} $ | (9) |
其中
| $ \frac{{\partial P}}{{\partial x}} = {\left[ {\begin{array}{*{20}{c}} {{{\left( {\frac{{\partial P}}{{\partial x}}} \right)}_{1,1}}}&{{{\left( {\frac{{\partial P}}{{\partial x}}} \right)}_{1,2}}}& \cdots &{{{\left( {\frac{{\partial P}}{{\partial x}}} \right)}_{1,n}}}\\ {{{\left( {\frac{{\partial P}}{{\partial x}}} \right)}_{2,1}}}&{{{\left( {\frac{{\partial P}}{{\partial x}}} \right)}_{2,2}}}& \cdots &{{{\left( {\frac{{\partial P}}{{\partial x}}} \right)}_{2,n}}}\\ {}&{}& \vdots &{}\\ {{{\left( {\frac{{\partial P}}{{\partial x}}} \right)}_{m,1}}}&{{{\left( {\frac{{\partial P}}{{\partial x}}} \right)}_{m,2}}}& \cdots &{{{\left( {\frac{{\partial P}}{{\partial x}}} \right)}_{m,n}}} \end{array}} \right]_{m \times n}} $ |
| $ \mathit{\boldsymbol{A}} = {\left[ {\begin{array}{*{20}{c}} 1&a&{}&{}&{}&{}&{}\\ a&1&a&{}&{}&{}&{}\\ {}&a&1&{}&{}&{}&{}\\ {}&{}&{}& \ddots &{}&{}&{}\\ {}&{}&{}&a&1&a&{}\\ {}&{}&{}&{}&a&1&a\\ {}&{}&{}&{}&{}&a&1 \end{array}} \right]_{m \times n}} $ |
向前差分为
| $ \mathit{\boldsymbol{B}} = {\mathit{\boldsymbol{B}}_1} = {\left[ {\begin{array}{*{20}{c}} { - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}&{}&{}&{}&{}&{}&{}&{}\\ {{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}&{}&{}&{}&{}&{}&{}\\ {{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}&{}&{}&{}&{}&{}\\ {{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}&{}&{}&{}&{}\\ {{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}&{}&{}&{}\\ {}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}&{}&{}\\ {}&{}&{}&{}&{}&{}& \ddots &{}&{}&{}&{}&{}\\ {}&{}&{}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}\\ {}&{}&{}&{}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}\\ {}&{}&{}&{}&{}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}\\ {}&{}&{}&{}&{}&{}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}\\ {}&{}&{}&{}&{}&{}&{}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}} \end{array}} \right]_{m \times n}} $ |
向后差分为
| $ \mathit{\boldsymbol{B}} = {\mathit{\boldsymbol{B}}_2} = {\left[ {\begin{array}{*{20}{c}} {{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}&{}&{}&{}&{}&{}&{}\\ {{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}&{}&{}&{}&{}&{}\\ {{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}&{}&{}&{}&{}\\ {{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}&{}&{}&{}\\ {}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}&{}&{}\\ {}&{}&{}&{}&{}&{}& \ddots &{}&{}&{}&{}&{}\\ {}&{}&{}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}&{}\\ {}&{}&{}&{}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}&{ - {b_4}}\\ {}&{}&{}&{}&{}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}&{ - {b_3}}\\ {}&{}&{}&{}&{}&{}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}&{ - {b_2}}\\ {}&{}&{}&{}&{}&{}&{}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}}&{ - {b_1}}\\ {}&{}&{}&{}&{}&{}&{}&{}&{{b_4}}&{{b_3}}&{{b_2}}&{{b_1}} \end{array}} \right]_{m \times n}} $ |
据式(9),由应力(标量)场P求取其空间一阶导数
| $ \frac{{\partial P}}{{\partial x}} = \frac{{P \cdot \mathit{\boldsymbol{B}} \cdot {\mathit{\boldsymbol{A}}^{ - 1}}}}{{\Delta x}} $ | (10) |
上述各式中差分系数a和bn(n=1~4)由表 1给出,可求得一阶导数的4~10阶空间差分精度近似值。
2 紧致交错格式差分系数优化及分析在地震波场数值模拟中,为得到清晰的波场记录,需要高精度的空间离散差分算子。差分算子的精度取决于差分系数和差分阶数,差分阶数越高,差分算子越精确,但其运算量也会随之增加。优化差分系数可使差分算子最大程度地逼近空间偏导数算子,本节对一阶导数的紧致交错差分系数进行优化,进一步提高紧致交错差分格式的分辨率,并分析优化后的差分格式的精度、频散和稳定性。
2.1 优化差分系数首先对一阶导数的紧致交错差分格式(式(7))进行数值频散分析。令
| $ \left\{ {\begin{array}{*{20}{l}} {{f_i} = A{{\rm{e}}^{l({\rm{i}}hk)}}}\\ {\frac{{\partial {f_l}}}{{\partial x}} = B{{\rm{e}}^{l({\rm{i}}hk)}}} \end{array}} \right. $ | (11) |
式中:h为网格尺寸;k为真波数。若数值模拟时不存在误差,则B=(ik)A。但在差分计算中,可能会产生不同结果,即产生数值波数(又称修正波数)。可令B=(ik′)A, k′为修正波数。
将式(11)代入式(7),并用欧拉公式化简可得
| $ \omega '(\omega ) = \frac{{2\sum\limits_{n = 1}^{N - 1} {{b_n}} \sin \frac{{(2n - 1)\omega }}{2}}}{{2a\cos \omega + 1}} $ | (12) |
式中:ω=kh; ω′=k′h。
在理想情况下,若不存在数值频散,则ω′=ω。它们的差异越大,说明该方法的数值频散越严重;反之则说明该方法能更好地压制数值频散。依据修正波数尽可能在大范围内接近真波数,以4点紧致交错差分格式为例说明优化的思路和方法。
由式(7)可得
| $ \begin{array}{*{20}{c}} {a\left( {f_{i - 1}^\prime + f_{i + 1}^\prime } \right) + f_i^\prime = \frac{1}{{\Delta x}}\left\{ {{b_1}\left[ {f\left( {{x_i} + \frac{{\Delta x}}{2}} \right) - } \right.} \right.}\\ {\left. {f\left( {{x_i} - \frac{{\Delta x}}{2}} \right)} \right] + {b_2}\left[ {f\left( {{x_i} + \frac{{3\Delta x}}{2}} \right) - \left( {{x_i} - \frac{{3\Delta x}}{2}} \right)} \right]} \end{array} $ | (13) |
为了满足2阶和4阶精度泰勒公式截断误差的要求,式中差分系数a、b1和b2须满足下列方程组
| $ \left\{ {\begin{array}{*{20}{l}} {{b_1} + 3{b_2} = 1 + 2a}\\ {{b_1} + 27{b_2} = 24a} \end{array}} \right. $ | (14) |
即为式(8)表示的前两个方程。
为了确定上述方程中的未知差分系数,按照Tam等[40]的思路和方法,在某个选定波数范围内,确定式(13)中3个未知差分系数,使得修正波数尽可能地接近真波数,故定义误差函数为
| $ E = \int_0^{\frac{{3{\rm{ \mathsf{ π} }}}}{4}} {{{\left\{ {W(\omega )\left[ {\omega - {\omega ^\prime }(\omega )} \right]} \right\}}^2}} {\rm{d}}\omega $ | (15) |
式中W(ω)为加权函数,目标是使误差函数解析可积,它是ω-ω′(ω)的分母部分。选定a为变量,则b1=(9-6a)/8,b2=(22a-1)/24。确定E的最小值为条件极值问题,采用拉格朗日乘数法进行求解,即根据
| $ \int_0^{\frac{{3\pi }}{4}} 2 QW{\rm{d}}\omega = 0 $ | (16) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {Q = 2a\omega \cos \omega + \omega - 2{b_1}\sin \frac{\omega }{2} - 2{b_2}\sin \frac{{3\omega }}{2}}\\ {W = 2\omega \cos \omega + \frac{3}{2}\sin \frac{\omega }{2} - \frac{{11}}{6}\sin \frac{{3\omega }}{2}} \end{array}} \right. $ | (17) |
由式(14)和式(16)中的3个方程,可确定3个优化后差分系数,即a=0.185715、b1=0.985714、b2=0.128572。将优化后的差分系数代入式(13),则得到优化后的紧致交错差分格式(Optimized staggered compact finite difference,OSCD)。
需要说明的是:4阶精度OSCD格式在式(14)基础上,需加入一个表示DRP要求的积分方程,所以不能严格满足空间6阶精度泰勒公式截断误差的要求,只能达到空间4阶精度近似;而常规SCD格式的3个方程即能满足空间6阶精度截断误差的要求。因此,若要达到2N阶空间差分精度,SCD方法只需利用2N-2个节点,而OSCD方法需使用2N个节点,与SD方法使用的节点数相同。
采用同样方法,对式(7)表示的6~10阶OSCD格式做差分系数优化,优化后差分系数列于表 2。
|
|
表 2 优化的紧致交错网格一阶导数的差分系数 |
本文方法与文献[33]方法基本一样,不同之处在于:文献中原差分格式是3点6阶组合型紧致差分格式,为了加入代表DRP思路的积分方程,在原差分格式基础上构造了新格式,增加了1个网格节点,降低了1阶精度,得到的是4点5阶迎风型组合紧致差分格式;本文的优化格式与原紧致交错差分格式相比,在使用同样网格节点进行差分计算时,降低了2阶精度。
本文求取优化差分系数的方法本质上是根据泰勒级数展开式,而文献[35]和[36]则是根据函数逼近的思路。文献[35]首先根据紧致交错差分格式的频散关系和极小极大原则建立了误差函数,在所有逼近格式中寻找误差最小且满足误差标准的三角函数多项式,求取过程中使用的是列梅兹(Remez)迭代算法。文献[35]指出该方法求得的差分系数在中等和大波数条件下比泰勒级数得到的要好,但算法复杂,实现难度较大,这也限制了该方法的应用。此外,该方法得到的差分格式是在给定的误差标准条件下得到的,但不能明确差分格式的近似精度,即通常意义上的2N阶。
2.2 频散分析对优化前、后一阶导数的紧致交错差分格式进行数值频散分析,通过数值波数与真波数的比值评判优化效果并确定适用的空间网格尺寸。
据式(12),修正波数与真波数之比可定义为
| $ R = \frac{{k'}}{k} = \frac{{\omega '}}{\omega } = \frac{{2\sum\limits_{n = 1}^{N - 1} {{b_n}} \sin \frac{{(2n - 1)\omega }}{2}}}{{(2a\cos \omega + 1)\omega }} $ | (18) |
在理想情况下,若不存在数值频散则波数比R恒等于1。R偏离1越大,说明该方法的数值频散越严重;反之则说明该方法能较好地压制数值频散。利用表 1和表 2中不同精度的差分系数可求取优化前后的波数比曲线。为了比较,计算得到常规交错差分格式(SD)的波数比,计算公式见文献[35],不再赘述公式。
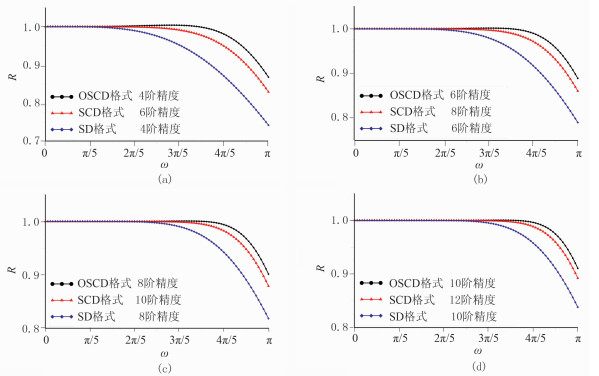
图 1为3种差分格式在不同差分网格节点个数(即差分算子长度)情况下的波数比曲线,如图 1a为4个差分节点,根据前文分析,SD、SCD和OSCD格式分别可达到4阶、6阶和4阶差分精度。
|
图 1 不同网格节点数三种差分格式的波数比曲线 (a)4节点;(b)6节点;(c)8节点;(d)10节点 |
取ω∈[0, π]作为横坐标,它是波数与空间步长的乘积,单位波长内采样点数
此外,从图中可见:低阶差分精度时,三者波数比曲线差别最大;随差分精度增加,差异变小。显然,OSCD格式在压制数值频散方面的优势主要体现在低阶差分精度时。因此,可用较低(4或6)阶OSCD格式达到高阶SCD或SD格式的效果。
2.3 精度分析为了比较SD、SCD和OSCD三种格式的近似精度,对比分析其截断误差。从表 3可见:在达到相同空间近似精度的条件下,4和6阶精度的OSCD格式具有更小的截断误差,8和10阶时误差介于SD和SCD之间,所以低阶差分时OSCD格式的精度优势更明显。
|
|
表 3 不同差分格式的一阶导数截断误差主项系数比较 |
利用一维平面简谐波初值问题,比较SD、SCD和OSCD格式的数值模拟精度。一维平面谐波初值问题可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\partial ^2}u}}{{\partial {t^2}}} = {v^2}\frac{{{\partial ^2}u}}{{\partial {x^2}}}}&{ - \infty < x < \infty ,t > 0}\\ {{{\left. u \right|}_{t = 0}} = \sin \frac{x}{\omega }}&{{{\left. {\frac{{\partial u}}{{\partial t}}} \right|}_{t = 0}} = 1} \end{array}} \right. $ | (19) |
该偏微分方程的达朗贝尔解,即精确的解析解为
| $ u(x,t) = \frac{1}{2}\left( {\sin \frac{{x - vt}}{\omega } + \sin \frac{{x + vt}}{\omega } + 2t} \right) $ | (20) |
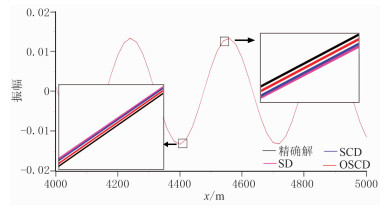
设置一维介质模型长度为8km,平面波v=4000m/s,ω=50Hz,数值模拟时的时间步长为1ms,空间网格尺寸为20m×20m。数值模拟时,三种差分格式的空间差分均为4阶精度。通过数值模拟,可得图 2所示的0.5s时刻的
|
图 2 三种差分格式的一维声波方程数值模拟快照 |
通过定量计算,可得到该时刻、4000~5000m之间,OSCD、SCD和SD格式数值解与解析解之间的相对误差依次为0.33%、0.77%和0.97%,这正是由于它们在计算空间导数时存在不同截断误差造成的,这也与表 3的理论分析结果相一致。相对误差定义为
| $ E = {\left\{ {\frac{{\sum\limits_{i = 1}^N {{{\left[ {u_i^n - u\left( {{t_n},{x_i}} \right)} \right]}^2}} }}{{\sum\limits_{i = 1}^N {{u^2}} \left( {{t_n},{x_i}} \right)}}} \right\}^{\frac{1}{2}}} \times 100\% $ | (21) |
式中:ui, jn表示数值解;u(tn, xi, zj)表示解析解。
2.4 稳定性分析按照董良国等[3]和杜启振等[4]使用的Fourier方法对差分格式进行稳定性分析,略去推导过程,直接给出式(22)表示的二维声波一阶速度—应力方程组(2M,2N)阶差分精度的紧致交错网格差分格式的稳定性条件。
| $ 0 \le \sum\limits_{m = 1}^M {\frac{{{{( - 1)}^{m - 1}}}}{{(2m - 1)!}}} {L^{2m}}{d^{2m}} \le 1 $ | (22) |
其中
| $ L = \sqrt 2 \frac{{v\Delta t}}{h} $ |
| $ d = \sum\limits_{n = 1}^N {\frac{{{{( - 1)}^{n - 1}}{b_n}}}{{1 - 2a}}} $ |
定义
|
|
表 4 二维声波方程不同差分格式的Courant数 |
采用OSCD差分格式对简单模型和复杂的Marmousi模型进行二维声波方程进行数值模拟,检验该方法数值模拟的适用性。
3.1 均匀介质模型为比较SD、SCD和OSCD三种差分方法的差异,设置模型尺寸为3000m×3000m,纵波速度为2000m/s,模型中心加载正弦衰减子波,峰值频率为30Hz,空间网格为12m×12m,时间步长为1ms。采用三种格式的时间2阶、空间4~8阶差分精度对一阶速度—应力声波方程进行波场模拟,得到同一时刻的应力P分量的波场快照(图 3)。

|
图 3 4阶(左)、6阶(中)、8阶(右)三种格式模拟的600ms时刻波场快照 (a)SD格式;(b)SCD格式;(c)OSCD格式 |
在时间和空间网格尺寸相同的情况下,图 3a所示的4~8阶SD格式的波场快照频散非常严重;图 3b的4~8阶SCD格式波场快照好于SD格式,但4阶SCD格式频散依然明显,6阶在0°和90°方向上也存在较明显频散,8阶精度时波场快照较清晰,频散得到较好压制;图 3c的4~8阶OSCD格式波场快照均很清晰,几乎看不到数值频散。与图 1的理论分析结果一致,4阶OSCD格式(图 3c左)不仅明显好于4阶SCD格式(图 3b左),也要好于使用了相同节点数的6阶SCD格式(图 3b中),达到了8阶SCD格式(图 3b右)的效果。若要SD和SCD格式达到与OSCD相同的数值模拟效果,在相同网格步长条件下,必须增加差分节点提高差分精度,所以OSCD格式能使用较少的差分节点,从而减少了运算量,提高了计算效率。
3.2 水平层状介质模型设置四层水平层状介质模型,模型长度和深度均为2000m,各层厚度均为500m,纵波速度以500m/s间隔,从3000m/s增至4500m/s,密度由Gardner经验公式得到。在地表(1000m,0)处激发主频为20Hz的雷克子波(震源),时间步长Δt=1ms,记录时间长度为1s。边界处理采用分裂的PML边界条件对边界反射进行吸收衰减,其控制方程见文献[7],此处不赘述。
理论分析和均匀介质模拟都说明了常规SD格式与SCD和OSCD格式相比,不利于压制数值频散,所以下文中不再对常规SD格式进行分析,只比较SCD和OSCD的数值模拟结果。在都使用4个网格节点情况下,也就是利用4阶OSCD格式和6阶SCD格式进行数值模拟,并采用不同的网格尺寸进行计算,数值模拟地表接收的单炮记录(长度为1s)如图 4所示。所有地震记录使用同样的参数进行增益处理,并提取x=1000m处质点模拟得到的不含直达波单道地震记录(图 5)。

|
图 4 水平层状介质的不同网格尺寸时6阶SCD (a)和4阶OSCD (b)格式模拟地面地震记录 |

|
图 5 不同网格尺寸的6阶SCD(上)、4阶OSCD(下)格式单道地震记录对比 (a)h=15m;(b)h=16m;(c)h=17m;(d)h=18m |
从图 4和图 5可看出,随着网格尺寸h的增加,数值频散总体上逐渐变得严重。图 4显示6阶SCD格式和4阶OSCD格式分别最大在15m和17m时地震记录清晰,无明显数值频散和边界反射;图 5中单道记录在波尾处也无抖动,SCD和OSCD分别从16m和18m开始出现“拖尾”现象。仅以该模型的单个变量而言,15m网格SCD格式的网格数约为133×133,17m网格OSCD格式的网格数为117×117,相对减少内存23%,也减少了运算时间,这对于大尺度模型的数值模拟或逆时偏移还是比较有意义的。
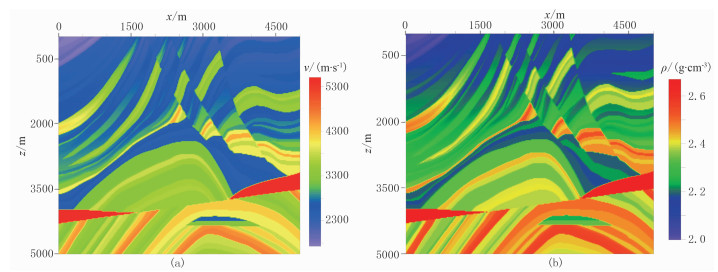
3.3 Marmousi模型为了验证OSCD格式对复杂介质的适用性,用经典二维Marmousi纵波速度模型(图 6)做数值模拟。模型的速度范围是1729~5500m/s,根据Gardner公式ρ=0.31v0.25,得到密度范围是2.00~2.67g/cm3。模型范围是501×501个网格点,空间网格尺寸取12m,时间步长取0.8ms,纵波震源位于地表中心位置,激发30Hz的Ricker子波,采样时间3s,采用20层PML吸收边界。
|
图 6 速度(a)和密度(b)表征的Marmousi模型 |
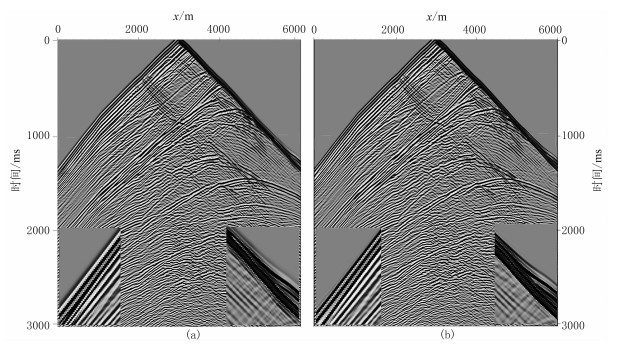
在上节主要对比了4阶OSCD与6阶SCD格式,本节对比6阶OSCD与8阶SCD格式数值模拟的结果。一方面验证OSCD格式对复杂介质的适用性;另一方面验证本文方法对其他精度SCD格式的优化效果。图 7是分别使用优化前8阶SCD和优化后6阶OSCD格式得到的地震记录,时间精度均为2阶。为了显示清晰,对地震记录进行了瞬时自动增益控制(AGC)处理,时窗为500ms。
|
图 7 Marmousi模型的优化前8阶SCD格式(a)和优化后6阶OSCD格式(b)地面地震记录 |
从图 7中虚线方框所圈定范围的地震波场看,优化前的8阶SCD格式存在较明显的数值频散,不利于波场特征分析或偏移成像处理;而优化差分系数后的6阶OSCD格式数值频散减弱,直达波、反射波及绕射波等波型清晰可见,且边界吸收效果较好,验证了本文算法对复杂模型的适用性。
4 结论基于频散关系保持的思想,本文利用最小平方法和拉格朗日乘数法对一阶导数的紧致交错差分格式的差分系数进行了优化,对比了优化前、后差分格式的频散关系和模拟精度,以及一阶速度—应力声波方程组优化前、后紧致交错差分格式的稳定性条件,获得以下认识。
(1) 相同的差分精度时,与常规SD和SCD格式相比,OSCD格式具有更小的数值频散、更小的截断误差、更高的计算精度。
(2) 相同的网格参数时,优化后4阶OSCD格式在压制数值频散方面优于6阶SCD格式,能达到8阶SCD格式的效果,即可使用更少的计算节点(算子长度),提高了计算效率。
(3) 相同的计算节点时,优化后的OSCD格式虽然比优化前的SCD格式精度降低2阶,但能更好地压制数值频散,即OSCD格式能使用更粗的空间网格进行计算,因而节省了内存容量,更适用于粗网格下的大尺度的地震波场数值模拟。
(4) 优化差分系数后,声波方程的稳定性条件比优化前略微严格,但总体上差别不大。Courant数随空间差分精度的增加而减小,随时间差分精度的增加而增加。高阶的时间精度会转换为更高阶的空间导数,势必会增加内存和运算时间,所以数值模拟中,应兼顾计算精度与效率,选取适宜的差分阶数、空间和时间步长。
(5) 本文从积分方程表示的修正波数与真波数之间的误差出发,利用拉格朗日乘数法求取优化差分系数,积分上限是采用多次试验得到的3π/4。后续研究中,拟从方程最优解角度选定适用于不同差分阶数的积分上限,从而得到不同的优化差分系数,并进行对比和分析,找到最佳优化差分系数。
| [1] |
唐佳, 王凡, 刘福烈. 三维波动方程正演的三级并行加速[J]. 石油地球物理勘探, 2016, 51(5): 1049-1054. TANG Jia, WANG Fan, LIU Fulie. 3D wave equation forward modeling based on three-level parallel acce-leration[J]. Oil Geophysical Prospecting, 2016, 51(5): 1049-1054. |
| [2] |
唐怀谷, 何兵寿. 一阶声波方程时间四阶精度差分格式的伪谱法求解[J]. 石油地球物理勘探, 2017, 52(1): 71-80. TANG Huaigu, HE Bingshou. Pseudo spectrum method of first-order acoustic wave equation finite-difference schemes with fourth-order time difference accuracy[J]. Oil Geophysical Prospecting, 2017, 52(1): 71-80. |
| [3] |
董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法稳定性研究[J]. 地球物理学报, 2000, 43(6): 856-864. DONG Liangguo, MA Zaitian, CAO Jingzhong. A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(6): 856-864. DOI:10.3321/j.issn:0001-5733.2000.06.015 |
| [4] |
杜启振, 郭成锋, 公绪飞. VTI介质纯P波混合法正演模拟及稳定性分析[J]. 地球物理学报, 2015, 58(4): 1290-1304. DU Qizhen, GUO Chengfeng, GONG Xufei. Hybrid PS/FD numerical simulation and stability analysis of pure P-wave propagation in VTI media[J]. Chinese Journal of Geophysics, 2015, 58(4): 1290-1304. |
| [5] |
王璐琛, 常旭, 王一博. TTI介质的交错网格伪P波正演方法[J]. 地球物理学报, 2016, 59(3): 1046-1058. WANG Luchen, CHANG Xu, WANG Yibo. Forward modeling of pseudo P waves in TTI medium using staggered grid[J]. Chinese Journal of Geophysics, 2016, 59(3): 1046-1058. |
| [6] |
汪勇, 段焱文, 安一凡, 等. 扩展的近似解析离散化方法及弹性波方程数值模拟[J]. 石油地球物理勘探, 2017, 52(5): 928-940, 955. WANG Yong, DUAN Yanwen, AN Yifan, et al. Expanded approximate analytic discretization and elastic wave numerical simulation[J]. Oil Geophysical Prospecting, 2017, 52(5): 928-940, 955. |
| [7] |
汪勇, 段焱文, 王婷, 等. 近似解析离散化方法的粘弹声波方程数值模拟及波场特征分析[J]. 石油物探, 2017, 56(3): 362-372. WANG Yong, DUAN Yanwen, WANG Ting, et al. Numerical simulation and the wave field characteristics analysis of viscoelastic acoustic wave equation based on the nearly-analytic discrete method[J]. Geophysical Prospecting for Petroleum, 2017, 56(3): 362-372. DOI:10.3969/j.issn.1000-1441.2017.03.006 |
| [8] |
Druskin V, Guttel S, Knizhnerman L. Near-optimal perfectly matched layers for indefinite Helmholtz problems[J]. Society for Industrial and Applied Mathematics Review, 2015, 58(1): 90-116. |
| [9] |
Rabinovich D, Dan G, Bielak J, et al. The double absorbing boundary method for a class of anisotropic elastic media[J]. Computer Methods in Applied Mechanics & Engineering, 2017, 315: 190-221. |
| [10] |
Lee J H, Tassoulas J L. Absorbing boundary condition for scalar-wave propagation problems in infinite media based on a root-finding algorithm[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 330(1): 207-219. |
| [11] |
Jing H, Chen Y S, Yang D H, et al. Dispersion-relation preserving stereo-modeling method beyond Nyquist frequency for acoustic wave equation[J]. Geophysics, 2017, 82(1): T1-T15. DOI:10.1190/geo2016-0104.1 |
| [12] |
Liu S L, Yang D H, Lan C, et al. Modified symplectic schemes with nearly-analytic discrete operators for acoustic wave simulations[J]. Computer Physics Communications, 2017, 213: 52-63. DOI:10.1016/j.cpc.2016.12.002 |
| [13] |
汪勇, 段焱文, 王婷, 等. 优化近似解析离散化方法的二维弹性波波场分离模拟[J]. 石油地球物理勘探, 2017, 52(3): 458-467. WANG Yong, DUAN Yanwen, WANG Ting, et al. Numerical simulation of elastic wave separation in 2D isotropic medium with the optimal nearly-analytic discretization[J]. Oil Geophysical Prospecting, 2017, 52(3): 458-467. |
| [14] |
Du Q, Li B, Hou B. Numerical modeling of seismic wavefields in transversely isotropic media with a compact staggered-grid finite difference scheme[J]. Applied Geophysics, 2009, 6(1): 42-49. DOI:10.1007/s11770-009-0008-z |
| [15] |
Liu Y, Sen M K. A practical implicit finite-difference method:Examples from seismic modeling[J]. Journal of Geophysics and Engineering, 2009, 6(3): 231-249. DOI:10.1088/1742-2132/6/3/003 |
| [16] |
Liu Y, Sen M K. An implicit staggered-grid finite- difference method for seismic modeling[J]. Geophy-sical Journal International, 2009, 179(1): 459-474. DOI:10.1111/j.1365-246X.2009.04305.x |
| [17] |
杨宽德, 宋国杰, 李静爽. Biot流动和喷射流动耦合作用下波传播的FCT紧致差分模拟[J]. 地球物理学报, 2011, 54(5): 1348-1357. YANG Kuande, SONG Guojie, LI Jingshuang. FCT compact difference simulation of wave propagation based on the Biot and squirt-flow coupling interaction[J]. Chinese Journal of Geophysics, 2011, 54(5): 1348-1357. DOI:10.3969/j.issn.0001-5733.2011.05.024 |
| [18] |
Liao W Y. On the dispersion, stability and accuracy of a compact higher-order finite difference scheme for 3D acoustic wave equation[J]. Journal of Computational and Applied Mathematics, 2014, 270: 571-583. DOI:10.1016/j.cam.2013.08.024 |
| [19] |
Akbari R, Mokhtari R. A new compact finite difference method for solving the generalized long wave equation[J]. Numerical Functional Analysis and Optimization, 2014, 35(2): 133-152. DOI:10.1080/01630563.2013.830128 |
| [20] |
Venutelli M. New optimized fourth-order compact finite difference schemes for wave propagation pheno-mena[J]. Applied Numerical Mathematics, 2015, 87: 53-73. DOI:10.1016/j.apnum.2014.07.005 |
| [21] |
Córdova L, Rojas O, Otero B, et al. Compact finite difference modeling of 2-D acoustic wave propagation[J]. Journal of Computational and Applied Mathema-tics, 2015, 295: 83-91. |
| [22] |
Wang Z K, Li J Y, Wang B F, et al. A new central compact finite difference scheme with high spectral resolution for acoustic wave equation[J]. Journal of Computational Physics, 2018, 366(1): 191-206. |
| [23] |
Madariaga R. Dynamics of an expanding circular fault[J]. Bulletin of the Seismological Society of America, 1976, 66(3): 639-666. |
| [24] |
董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3): 411-419. DONG Liangguo, MA Zaitian, CAO Jingzhong, et al. The staggered-grid high-order difference method of first-order elastic equation[J]. Chinese Journal of Geophysics, 2000, 43(3): 411-419. DOI:10.3321/j.issn:0001-5733.2000.03.015 |
| [25] |
Liu Y, Sen M K. A new time-space domain high-order finite-diffference method for the acoustic wave equation[J]. Journal of Computational Physics, 2009, 228(1): 8779-8806. |
| [26] |
Yan H, Yang L, Li X Y. Optimal staggered-grid finite-difference schemes by combining Taylor-series expansion and sampling approximation for wave equation modeling[J]. Journal of Computational Physics, 2016, 326(1): 913-930. |
| [27] |
Kim J W, Lee D J. Optimized compact finite difference schemes for computational acoustics[J]. American Institute of Aeronautics and Astronautics Journal, 1996, 34(5): 887-893. DOI:10.2514/3.13164 |
| [28] |
Liu Y, Sen M K. 3D acoustic wave modeling with time-space domain dispersion relation based finite difference schemes and hybrid absorbing boundary conditions[J]. Exploration Geophysics, 2011, 42(3): 176-189. DOI:10.1071/EG11007 |
| [29] |
Zhang J H, Yao Z X. Optimized finite-difference operator for broadband seismic wave modeling[J]. Geophysics, 2013, 78(1): A13-A18. DOI:10.1190/geo2012-0277.1 |
| [30] |
Zhang J H, Yao Z X. Optimized explicit finite-difference schemes for spatial derivatives using maximum norm[J]. Journal of Computational Physics, 2013, 250(10): 511-526. |
| [31] |
Liu Y. Globally optimal finite-difference schemes based on least squares[J]. Geophysics, 2013, 78(4): T113-T132. DOI:10.1190/geo2012-0480.1 |
| [32] |
Liu Y. Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modeling[J]. Geophysical Journal International, 2014, 197(2): 1033-1047. DOI:10.1093/gji/ggu032 |
| [33] |
Yu C H, Wang D, He Z, et al. An optimized dispersion-relation-preserving combined compact difference scheme to solve advection equations[J]. Journal of Computational Physics, 2015, 300(1): 92-115. |
| [34] |
Ren Z, Liu Y. Acoustic and elastic modeling by optimal time-space-domain staggered-grid finite-difference schemes[J]. Geophysics, 2015, 80(1): T17-T40. DOI:10.1190/geo2014-0269.1 |
| [35] |
Yang L, Yan H, Liu H. Optimal staggered-grid finite-difference schemes based on the minimax approximation methos with the Remez algorithm[J]. Geophy-sics, 2017, 82(1): T27-T42. |
| [36] |
Yang L, Yan H Y, Liu H. An optimal implicit staggered-grid finite-difference scheme based on the mo-dified Taylor-series expansion with minimax approximation method for elastic modeling[J]. Journal of Applied Geophysics, 2017, 138: 161-171. DOI:10.1016/j.jappgeo.2017.01.020 |
| [37] |
Levander A R. Fourth-order finite-difference P-SV seismograms[J]. Geophysics, 1988, 53(11): 1425-1436. DOI:10.1190/1.1442422 |
| [38] |
Nagarajan S, Lele S K, Ferziger J H. A robust high-order compact method for large eddy simulation[J]. Journal of Computational Physics, 2003, 191(2): 392-419. |
| [39] |
Boersma B J. A staggered compact finite difference formulation for the compressible Navier-Stokes equations[J]. Journal of Computational Physics, 2005, 208(2): 675-690. DOI:10.1016/j.jcp.2005.03.004 |
| [40] |
Tam C K W, Webb J C. Dispersion-relation-preserving finite difference schemes for computational acoustics[J]. Journal of Computational Physics, 1993, 107(2): 262-281. DOI:10.1006/jcph.1993.1142 |



 汪勇, 湖北省武汉市蔡甸区大学路111号长江大学地球物理与石油资源学院, 430100。Email:
汪勇, 湖北省武汉市蔡甸区大学路111号长江大学地球物理与石油资源学院, 430100。Email: