为满足地震波正、反演的需要,边界条件的研究引起人们的极大关注。目前应用最广泛的边界条件是由Berenger[1-2]在研究麦克斯韦方程时提出的完全匹配层(Perfectly matched layers,PML)。Chew等[3]和Collino等[4]将其解释为复坐标伸展变换的结果。当入射波角度很大时,衰减系数会变得很小,因此常规PML无法吸收大角度入射波,且在极低频时产生奇异值。复频移(Complex frequency shifted,CFS)技术对复坐标伸展变换(CCS)做进一步处理,原来为1的项被尺度因子替换并在大角度入射波的吸收中起作用,在分母中加上频移因子以消除低频奇异值[5]。Roden等[6]提出基于CFS卷积的PML(即C-PML);Komatitsch等[7]进一步将其推广到弹性介质中。
此外,近似PML(Nearly PML,NPML)[8]不同于上述常规PML,它是直接对波场进行变换而得到,不改变波场形式,也不需做卷积处理。该方法[8]自提出后很快被推广试用于声波介质、弹性介质以及双相介质中[9-11]。但是,由于该方法在大入射角时吸收能力较弱且在复杂介质的模拟中存在不稳定现象,因此,在地震正、反演中现今主流方法仍旧是C-PML。
对于边界条件的稳定性,Festa等[12]指出PML边界与面波之间会降低吸收效果并产生不稳定性。Mezafajardo等[13]认为常规PML在各向同性和各向异性中都不满足严格的渐进稳定性,并引入多轴技术,即在多个正交方向上同时引入衰减因子。同时,衰减因子对边界吸收效果有很大影响。Collino等[14]提出内截断边界与PML层的距离呈指数关系的衰减函数;此后Groby等[15]对其进行了改进和整理。近年来,中国学者也对PML做了许多研究[16-28]。田坤等[29]将多轴技术应用于C-PML中;陈可洋[30]提出了正弦型和余弦型衰减函数;罗玉钦等[31]对衰减因子进行了系统研究,提出的衰减因子将吸收效果提升了20%~60%。
虽然NPML拥有其自身优势,但它仍存在稳定性与吸收效果上的问题。本文基于NPML并引入频移因子、尺度因子及稳定性因子,提出了多轴复频移NPML(MCFS-NPML)吸收边界,旨在提升NPML对大角度入射波的吸收且增强其稳定性;在此基础上采用文献[31]提出的衰减函数,进一步提升MCFS-NPML的吸收能力。本文详细分析MCFS-NPML的稳定性和吸收效果,探讨各因子在改善吸收效果及稳定性方面所起的作用,证实了MCFS-NPML拥有更好的吸收效果和稳定性;同时,将该衰减函数与广泛运用的指数型衰减函数进行比对,结果表明在该衰减函数下吸收效果得到进一步改善。
1 理论研究 1.1 近似完全匹配层(NPML)吸收边界本文采用交错网格有限差分法,因此采用一阶速度—应力形式方程组。将方程组变换到频率域
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{i}}\omega {V_x} = \frac{1}{\rho }\left( {\frac{{\partial {T_{xx}}}}{{\partial x}} + \frac{{\partial {T_{zx}}}}{{\partial z}}} \right)}\\ {{\rm{i}}\omega {V_z} = \frac{1}{\rho }\left( {\frac{{\partial {T_{zz}}}}{{\partial z}} + \frac{{\partial {T_{zx}}}}{{\partial x}}} \right)}\\ {{\rm{i}}\omega {T_{xx}} = (\lambda + 2\mu )\frac{{\partial {V_x}}}{{\partial x}} + \lambda \frac{{\partial {V_z}}}{{\partial x}}}\\ {{\rm{i}}\omega {T_{zz}} = (\lambda + 2\mu )\frac{{\partial {V_z}}}{{\partial z}} + \lambda \frac{{\partial {V_x}}}{{\partial x}}}\\ {{\rm{i}}\omega {T_{zx}} = \mu \left( {\frac{{\partial {V_z}}}{{\partial x}} + \frac{{\partial {V_x}}}{{\partial z}}} \right)} \end{array}} \right. $ | (1) |
式中:ω是角频率;λ、μ是拉梅常数;ρ是密度;Vx、Vz为频率域弹性波场速度分量;Txx、Tzz、Txz为频率域弹性波场应力分量。
采用复坐标伸展变换的形式为
| $ \tilde x(x) = x - \frac{{\rm{i}}}{\omega }\int_0^x \alpha (s){\rm{d}}s $ | (2) |
| $ \left\{ {\begin{array}{*{20}{l}} {\partial \tilde x = \frac{1}{{{s_x}}}\partial x}\\ {{s_x} = 1 + \frac{{{\alpha _x}}}{{{\rm{i}}\omega }}} \end{array}} \right. $ | (3) |
将式(3)代入式(1),并直接作用在速度分量和应力分量上,得到复坐标伸展变换后的方程组
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{i}}\omega {V_x} = \frac{1}{\rho }\left[ {\frac{\partial }{{\partial x}}\left( {\frac{{{T_{xx}}}}{{{s_x}}}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{{\partial {T_{zx}}}}{{\partial z}}} \right)} \right]}\\ {{\rm{i}}\omega {V_z} = \frac{1}{\rho }\left[ {\frac{\partial }{{\partial z}}\left( {\frac{{{T_{zz}}}}{{{s_z}}}} \right) + \frac{\partial }{{\partial x}}\left( {\frac{{{T_{zx}}}}{{{s_x}}}} \right)} \right]}\\ {{\rm{i}}\omega {T_{xx}} = (\lambda + 2\mu )\frac{\partial }{{\partial x}}\left( {\frac{{{V_x}}}{{{s_x}}}} \right) + \lambda \frac{\partial }{{\partial z}}\left( {\frac{{{V_x}}}{{{s_z}}}} \right)}\\ {{\rm{i}}\omega {T_{zz}} = (\lambda + 2\mu )\frac{\partial }{{\partial z}}\left( {\frac{{{V_z}}}{{{s_z}}}} \right) + \lambda \frac{\partial }{{\partial x}}\left( {\frac{{{V_x}}}{{{s_x}}}} \right)}\\ {{\rm{i}}\omega {T_{zx}} = \mu \left[ {\frac{\partial }{{\partial x}}\left( {\frac{{{V_z}}}{{{s_x}}}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{{{V_x}}}{{{s_z}}}} \right)} \right]} \end{array}} \right. $ | (4) |
令
| $ \left( {1 + \frac{{{\alpha _x}}}{{{\rm{i}}\omega }}} \right)\bar T_{xx}^x = {T_{xx}} $ | (5) |
| $ {\rm{i}}\omega \bar T_{xx}^x + {\alpha _x}\bar T_{xx}^x = {\rm{i}}\omega {T_{xx}} $ | (6) |
同理,采用相同方法也将其他变量变换到时间域,有
| $ \left( {\begin{array}{*{20}{l}} {\frac{{\partial {v_x}}}{{\partial t}} = \frac{1}{\rho }\left( {\frac{{\partial \bar \tau _{xx}^x}}{{\partial x}} + \frac{{\partial \bar \tau _{zx}^x}}{{\partial z}}} \right)}\\ {\frac{{\partial {v_z}}}{{\partial t}} = \frac{1}{\rho }\left( {\frac{{\partial \bar \tau _{zz}^z}}{{\partial z}} + \frac{{\partial \bar \tau _{zx}^x}}{{\partial x}}} \right)}\\ {\frac{{\partial {\tau _{xx}}}}{{\partial t}} = (\lambda + 2\mu )\frac{{\partial \bar v_x^x}}{{\partial x}} + \lambda \frac{{\partial \bar v_z^z}}{{\partial z}}}\\ {\frac{{\partial {\tau _{zz}}}}{{\partial t}} = (\lambda + 2\mu )\frac{{\partial \bar v_z^z}}{{\partial z}} + \lambda \frac{{\partial \bar v_x^x}}{{\partial x}}}\\ {\frac{{\partial {\tau _{zx}}}}{{\partial t}} = \mu \left( {\frac{{\partial \bar v_z^x}}{{\partial x}} + \frac{{\partial \bar v_x^z}}{{\partial z}}} \right)} \end{array}} \right. $ | (7) |
且有
| $ \frac{{\partial {{\bar \xi }^m}}}{{\partial t}} + {\alpha _m}{{\bar \xi }^m} = \frac{{\partial \xi }}{{\partial t}} $ | (8) |
| $ \xi = {\tau _{xx}},{\tau _{zx}},{\tau _{zz}},{v_x},{v_z}\quad m = x,z $ |
式中:τxx、τzx、τzz是时间域应力;vx、vz为时间域速度参数。分别与频率域中的Txx、Tzx、Tzz和Vx、Vz相对应。
从式(7)可见主控方程的形式并未发生变化。这里需引入8个辅助变量替换原主控方程中的变量。在程序编写时不需改动主代码,易于实现。式(8)中的原始控制方程中的辅助变量是原变量经伸展变换得到,是将原波场直接变换后再代入相同形式的控制方程求解,因此易于将NPML推广到其他介质。在计算区域中衰减因子值为0,故式(8)中原变量与新变量是相同的,因此在编程时可只在PML区域中进行波场变换以减少存储空间。
1.2 复频移近似完全匹配层(CFS-NPML)吸收边界先分析NPML的平面波解,经过复坐标变换之后方程具有新的平面波解
| $ A\exp \left[ { - {\rm{i}}\left( {{k_x} \cdot x - \omega t} \right)} \right]\exp \left[ { - \frac{{{k_x}}}{\omega }\int_0^x {{\alpha _x}} (s){\rm{d}}s} \right] $ | (9) |
式中:
修改式(3),并引入尺度因子βx(x)和频移因子ηx(x),可得
| $ {s_x}(x) = {\beta _x}(x) + \frac{{{\alpha _x}(x)}}{{{\eta _x}(x) + {\rm{i}}\omega }} $ | (10) |
得到新的平面波解的衰减项为
| $ \exp \left( { - \frac{{\cos \theta }}{{{c_{\rm{P}}}}}\int_0^x {\frac{{{\omega ^2}}}{{\eta _x^2 + {\omega ^2}}}} \frac{{{\alpha _x}}}{{{\beta _x}}}{\rm{d}}s} \right) $ | (11) |
尺度因子βx(x)使大角度入射波的传播方向向法线方向弯曲,导致衰减系数增加;频移因子ηx(x)对入射角的影响不大,但可有效地避免奇异值的出现。当入射角较大时,在常规PML中波只能在很浅的介质中传播,无法达到较好的吸收效果,尺度因子的引入增强了边界对这一类波的吸收[7]。衰减函数、尺度因子与频移因子的表达式为
| $ \alpha (x) = \left\{ {\begin{array}{*{20}{c}} 0&{l < 0}\\ {\ln \frac{1}{R}{{\left( {\frac{l}{L}} \right)}^n}\frac{{(n + 1)\sqrt {\frac{\mu }{\rho }} }}{{2L}}}&{l \ge 0} \end{array}} \right. $ | (12) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\beta _x} = 1 + \left( {{\beta _0} - 1} \right){{\left( {\frac{x}{L}} \right)}^{{q_\beta }}}}\\ {{\eta _x} = {\eta _0}{\rm{ \mathsf{ π} }}f\left[ {1 - {{\left( {\frac{x}{L}} \right)}^{{q_\eta }}}} \right]} \end{array}} \right. $ | (13) |
式中:L是PML的层厚;R是理论边界反射系数;l为PML区计算点与内部边界的距离;η0的经验值范围是0~6;β0的经验值范围是1~10;指数qβ、qη与n相同,通常取1~3。
以式(10)替换式(3),如Txx
| $ \bar T_{xx}^x = \frac{{{T_{xx}}}}{{{\beta _x}(x) + \frac{{{\alpha _x}(x)}}{{{\eta _x}(x) + {\rm{i}}\omega }}}} $ | (14) |
| $ {\beta _x}(x)\bar T_{xx}^x + \frac{{{\alpha _x}(x)}}{{{\eta _x}(x) + {\rm{i}}\omega }}\bar T_{xx}^x = {T_{xx}} $ | (15) |
| $ \begin{array}{*{20}{l}} {\left[ {{\eta _x}(x) + {\rm{i}}\omega } \right]{\beta _x}(x)\bar T_{xx}^x + {\alpha _x}(x)\bar T_{xx}^x}\\ {\quad \;\;\; = \left[ {{\eta _x}(x) + {\rm{i}}\omega } \right]{T_{xx}}} \end{array} $ | (16) |
| $ \begin{array}{*{20}{l}} {\left[ {{\eta _x}(x){\beta _x}(x) + {\alpha _x}(x)} \right]\bar T_{xx}^x + {\rm{i}}\omega {\beta _x}(x)\bar T_{xx}^x}\\ {\quad = {\eta _x}(x){T_{xx}} + {\rm{i}}\omega {T_{xx}}} \end{array} $ | (17) |
转换到时间域,有
| $ \begin{array}{*{20}{c}} {\left[ {{\eta _x}(x){\beta _x}(x) + {\alpha _x}(x)} \right]\bar \tau _{xx}^x + {\beta _x}(x)\frac{{\partial \bar \tau _{xx}^x}}{{\partial t}}}\\ { = {\eta _x}(x){\tau _{xx}} + \frac{{\partial {\tau _{xx}}}}{{\partial t}}} \end{array} $ | (18) |
同理,求得其余变量的微分方程且替换式(8),则可简写为
| $ \begin{array}{*{20}{l}} {\left[ {{\eta _m}{\beta _m} + {\alpha _m}} \right]{{\bar \xi }^m} + {\beta _m}\frac{{\partial {{\hat \xi }^m}}}{{\partial t}} = {\eta _m}\xi + \frac{{\partial \xi }}{{\partial t}}}\\ {\xi = {\tau _{xx}},{\tau _{zx}},{\tau _{zz}},{v_x},{v_z}\quad m = x,z} \end{array} $ | (19) |
采用交错网格有限差分数值模拟时,将式(19)离散,得到如下离散格式
| $ \begin{array}{l} {\left( {{{\bar \xi }^m}} \right)^{n + \frac{1}{2}}} = \frac{1}{{{\beta _m}(m)}} + \frac{{{\eta _m}(m){\beta _m}(m) + {\alpha _m}(m)}}{2} \times \\ \;\;\;\;\left\{ {\left[ {\frac{{{\beta _m}(m)}}{{\Delta t}} - \frac{{{\eta _m}(m){\beta _m}(m) + {\alpha _m}(m)}}{2}} \right]{{\left( {{{\bar \xi }^m}} \right)}^{n - \frac{1}{2}}} + } \right.\\ \;\;\;\;\left. {\left[ {\frac{1}{{\Delta t}} + \frac{{{\eta _m}(m)}}{2}} \right]{{\left( {{\xi ^m}} \right)}^{\frac{{n + 1}}{2}}} + \left[ {\frac{{{\eta _m}(m)}}{2} - \frac{1}{{\Delta t}}} \right]{{\left( {{\xi ^m}} \right)}^{n - \frac{1}{2}}}} \right\} \end{array} $ | (20) |
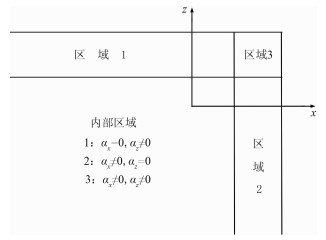
经典的分裂PML是将变量分裂为分别垂直和平行于边界的两个分量。衰减函数值的分布如图 1所示,在区域1,有αz=αz(z),αx=0。在该区域只有一个衰减剖面。现再引入一个衰减剖面
| $ \left\{ {\begin{array}{*{20}{l}} {{\alpha _z} = \alpha _z^{(z)}(z)}\\ {{\alpha _x} = \alpha _x^{(z)}(z)}\\ {\alpha _x^{(z)}(z) = {P^{(x/z)}}\alpha _z^{(z)}(z)} \end{array}} \right. $ | (21) |
|
图 1 衰减因子PML区域示意图 |
式中αx的取值不再是0,而与原衰减函数成比例,比例系数P(x/z)即是稳定性因子。
在实际应用中需调整稳定性因子,使计算稳定。稳定性因子取0时退化为常规PML。区域2与区域1采取相同的处理方法,对于区域3的处理与常规PML是一致的。在常规PML中,上边界与右边界在区域3重叠,该重叠区域内αz=αz(z)、αx=αx(x)。区域3中存在两个衰减剖面,因此不用再引入其他衰减剖面。
将双衰减剖面应用于NPML,如区域2,有
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {{\bar \xi }^z}}}{{\partial t}} + \alpha _z^z{{\bar \xi }^z} = \frac{{\partial \xi }}{{\partial t}}}\\ {\frac{{\partial {{\bar \xi }^x}}}{{\partial t}} + \alpha _x^{(z)}{{\bar \xi }^x} = \frac{{\partial \xi }}{{\partial t}} = \frac{{\partial {{\bar \xi }^x}}}{{\partial t}} + {P^{(x/z)}}\alpha _z^{(z)}{{\bar \xi }^x}} \end{array}} \right. $ | (22) |
对于CFS-NPML,在区域1和区域2中的处理方法与上面不一样。同样以区域1为例,变换函数为
| $ \left\{ {\begin{array}{*{20}{l}} {{s_z}(z) = {\beta _z}(z) + \frac{{\alpha _z^{(z)}(z)}}{{{\eta _z}(z) + {\rm{i}}\omega }}\quad \bot {\rm{PML}}}\\ {{s_x}(x) = 1 + \frac{{\alpha _x^{(z)}(x)}}{{{\rm{i}}\omega }}\quad //{\rm{PML}}} \end{array}} \right. $ | (23) |
将式(23)代入式(14)中,得到
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {{\eta _m}{\beta _m} + \alpha _m^m} \right){{\bar \xi }^m} + {\beta _m}\frac{{\partial {{\bar \xi }^m}}}{{\partial t}} = {\eta _m}\xi + \frac{{\partial \xi }}{{\partial t}}\quad \bot {\rm{PML}}}\\ {\frac{{\partial {{\bar \xi }^2}}}{{\partial t}} + \alpha _z^x{{\bar \xi }^z} = \frac{{\partial \xi }}{{\partial t}}\quad //{\rm{PML}}}\\ {\frac{{\partial {{\bar \xi }^x}}}{{\partial t}} + \alpha _x^z{{\bar \xi }^x} = \frac{{\partial \xi }}{{\partial t}}\quad //{\rm{PML}}} \end{array}} \right. $ | (24) |
这样就避免了单剖面衰减引起的平面波解呈指数增长。采用多轴衰减剖面引入了稳定性因子,使系数矩阵特征值向负半轴移动,消除了不稳定性。稳定性因子应小于1,且随介质的复杂程度而改变,不宜太大,否则会导致虚假反射增强。
2 数值模拟在地震波模拟中分别实现NPML、M-NPML、CFS-NPML及MCFS-NPML。选取的时间步长为1ms,加载震源是主频为25Hz的雷克子波。构建模型的尺寸是5200m×1200m(包含边界厚度),x方向和z方向网格步长都是10m。纵波速度为3000m/s,横波速度为1400m/s,密度为2000kg/m3,PML层数L设为10,R取10~6。将震源加载于x=2610m、z=110m处,贴近于PML边界,往两侧传播的波近似平行于上边界传播,截取上述几种近似完全匹配层下的地震波波场快照。
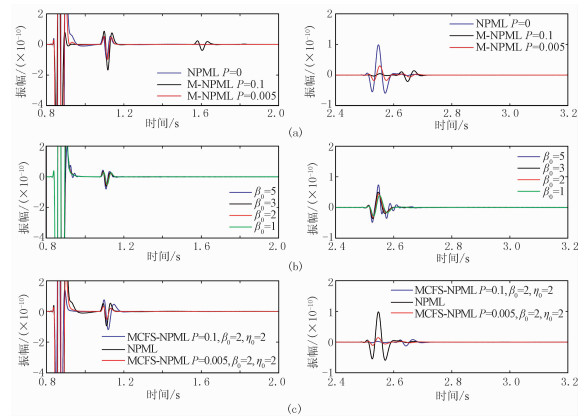
图 2a和图 2b分别显示上述四种PML在0.90s和0.95s时刻地震波传播情况。从上到下依次呈现稳定性因子、尺度因子、频移因子对匹配层的影响及三个因子共同作用下的波场;图 2a第一排标示的①、②和③分别对应直达波及在下、上边界形成的反射波;图 2b第一、第四排的第一列中黑色椭圆即匹配层中残余能量团,该能量团是因波在边界处衰减不完全产生的损耗波,且入射角度越大,能量团越明显。该能量团的存在会导致虚假反射回传到计算区域,且能量团的积累使计算不稳定。

|
图 2 三种因子不同组合下的波场快照 (a)0.90s时刻;(b)0.95s时刻,为了突显边界中的残余能量团,相对于图a进行了放大显示 |
通过图 2a第一排可见增加稳定性因子时反射波能量被增强;从图 2b第一排中可看出稳定性因子值越大,边界区域越干净,消除了大部分的残余能量团。对于CFS-NPML,选取多组参数分析频移因子和尺度因子对近似完全匹配层的影响。通过图 2a对比NPML与η0=0、β0=2时的CFS-NPML,可见残余能量团稍有减弱,且下边界处的虚假反射也得到削减,但幅度较小。
对比η0、β0分别取1、2和5这几组波场快照可知:改变η0值会显著影响吸收效果,且η0取值越大吸收效果越好,但在边界中的波“拖尾”现象更严重(图 2b第三排);但β0取值过大,反而会影响吸收效果。对于MCFS-NPML、CFS-NPML中边界处未能完全吸收的残余能量被再次削弱,MCFS-NPML能进一步清除PML层中的能量以保持匹配层的稳定且再次压制了因大角度入射所带来的虚假反射(图 2b第四排)。
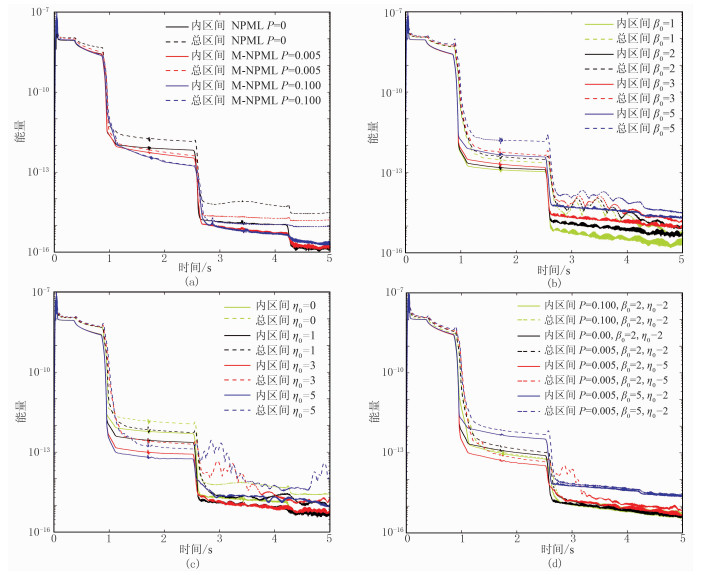
图 3中0时刻介质中的能量迅速增加,在约0.30s时因波的下侧已到达边界,波的能量逐渐减弱。图中实线和虚线分别对应内区间(不包括PML边界)和整体区域的能量曲线。在0.83s时刻波抵达左右两侧,经过PML层作用能量迅速降低,在约2.50s时残余的反射波再次抵达左、右两边界,能量再次减少。图 3a中NPML下虚线与实线的差异较大,表明有大量能量残留在边界中。该残留能量会使PML层变得不稳定,同时过多的能量积累会影响边界的吸收性能。M-NPML曲线差随稳定性因子取值增大而逐渐减小。当稳定性因子取0.1时,虚线与实线几乎重合,证明边界中的大部分能量均被消除。对于CFS-NPML,从β0取2、η0取0、1、2、3、5这几组能量曲线(图 3c)看出,η0值越大,在约0.83s时能量曲线最低。
|
图 3 能量衰减曲线 (a)不同稳定性因子下的NPML和M-NPML;(b)η0=2时不同尺度因子下的CFS-NPML;(c)β0=2时不同频移因子下的CFS-NPML;(d)三种因子不同组合下的MCFS-NPML |
正演模拟中,期望地震波在第一次达到边界处时就被尽可能地吸收,防止地震波反射回计算区域。频移因子改善了PML吸收性能,但随着η0增大,左右两侧初次未被吸收的微弱反射波再次到达边界时,整体区间的能量曲线扰动剧烈,是不稳定的。β0取值过大也会有这样的扰动,且CFS-NPML中曲线差依旧很大;而在引入稳定性因子之后(MCFS-NPML),能量扰动和曲线差过大将被压制。
图 4是模型中x=110m、z=110m点处0~3.20s时段的x方向速度分量的变化曲线,可清晰地看到上述三个因子对常规入射波吸收效果的影响。稳定性因子取0.1时,来自底界的虚假反射波最强。从反射波振幅看,CFS-NPML比NPML和M-NPML低很多,来自另一侧的反射波随η0增大而减小;对于MCFS-NPML,不仅反射波能量微弱,来自另一侧的反射波衰减也特别明显。证实了M-NPML会增强虚假反射,CFS-NPML和MCFS-NPML却有利于入射波的吸收。
|
图 4 反射波振动曲线 (a)不同稳定性因子下的NPML和M-NPML;(b)η0=2时不同尺度因子下的CFS-NPML;(c)NPML和三种因子不同组合下的MCFS-NPML |
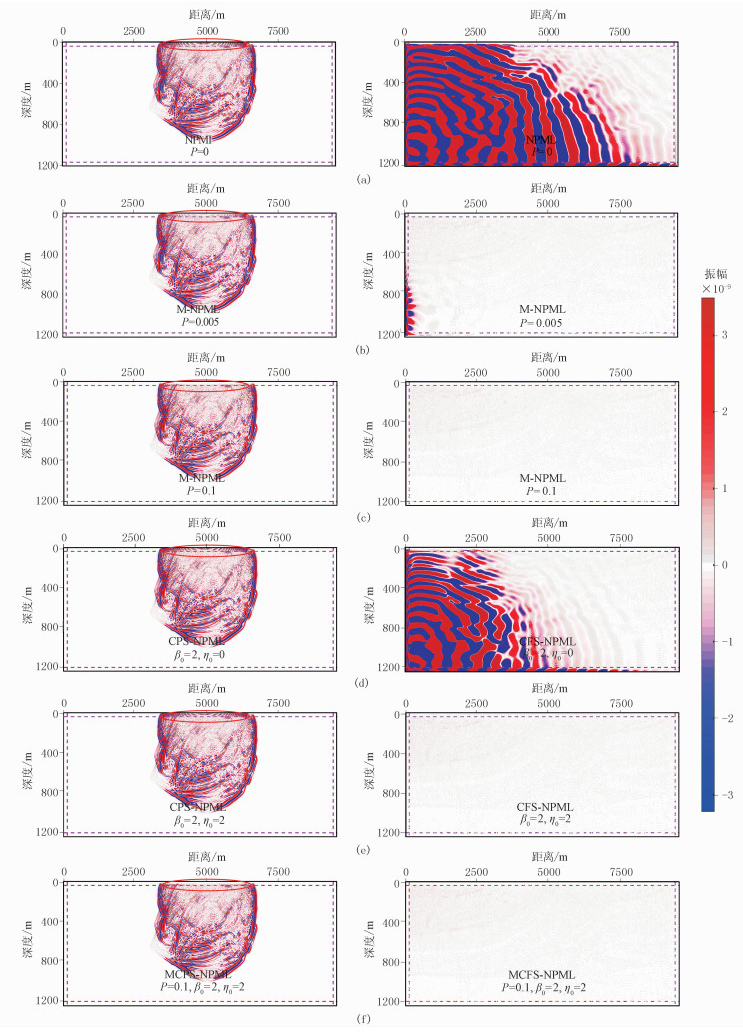
为进一步测试边界的稳定性与吸收性能,采用了复杂Marmousi模型。在该模型中不稳定性被放大,震源靠近边界,大角度的入射波进入上边界并截取0.5s和4.0s时的波场快照(图 5)。
|
图 5 0.5s (左)和4.0s(右)时刻Marmousi模型下的波场快照 (a)NPML;(b)P=0.005时的M-NPML;(c)P=0.1时的M-NPML;(d)η0=0,β0=2时的CFS-NPML;(e)η0=2,β0=2时的CFS-NPML;(f)P=0.1,η0=2,β0=2时的MCFS-NPML |
在NPML中,上边界存在强烈的地震波残留(图 5a,红色椭圆所示),CFS-NPML也是如此。从4.0s波场快照可见NPML下整个计算区域已因误差积累而发散。至于M-NPML(图 5b、图 5c),随着稳定性因子的增加,波场残留减弱。β0取2、η0取0时的CFS-NPML(图 5d)与NPML对比,虽然产生累积误差,但污染区域相对较小,表明β0有微弱压制作用;当η0取2时(图 5e)也未见波场被污染,表明频移因子对稳定性有一定作用。而MCFS-NPML(图 5f)因为稳定性因子的引入,上边界比CFS-NPML更干净。
简而言之,在提高稳定性方面,三个因子都有贡献,但机理不同。稳定性因子沿平行匹配层方向增加一个衰减剖面,吸收沿该方向传播的耗散波;频移因子避免了低频奇异值的产生;尺度因子使波向法线方向弯曲,增强对匹配层中波的吸收能力。Marmousi模型模拟中的不稳定随频移因子的引入而消除,故该不稳定是低频奇异值所致。虽然CFS-NPML下计算保持稳定,但上界残余能量团十分明显,因此需同时引入三种因子使NPML具有更好的稳定性和吸收效能。
3 衰减函数尝试通过修改衰减函数,进一步提升边界吸收能力。用网格算法模拟地震波传播,衰减函数不再是一条连续的曲线,匹配层之间的衰减函数值差异较大,引起虚假反射。通过增加层数缩小该差异,但会增加存储量,降低计算效率。探讨在不增加层数的基础上进一步削弱离散差异带来的虚假反射。设计下式
| $ \alpha (x) = K\left[ {\phi {{\left( {\frac{x}{L}} \right)}^n} + \gamma {{\rm{e}}^{ - \frac{{\delta L}}{x}}}} \right] $ | (25) |
该式分为两个部分:
| $ \alpha (x) = \ln \frac{1}{R}\frac{{(n + 1)\sqrt {\frac{\mu }{\rho }} }}{{2L}}\left[ {\phi {{\left( {\frac{x}{L}} \right)}^n} + \gamma {{\rm{e}}^{ - \frac{{\delta L}}{x}}}} \right] $ | (26) |
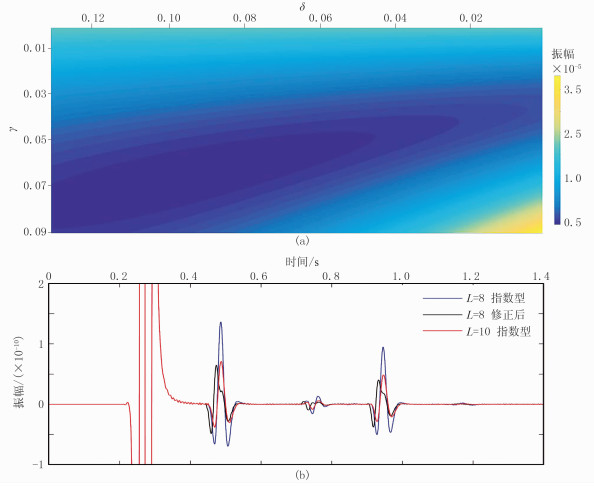
波场模拟采用MCFS-NPML,且β0=2、η0=2及P=0.005,模型尺寸为2000m×2000m。当层数取8时,γ=0.065、δ=0.094这一组系数下波反射最弱。图 6b中蓝线和黑线对应传统指数型衰减函数和式(26)给出的函数下的反射情况,可看出新函数下的虚假反射更弱。新函数取8层达到的吸收效果与原函数取10层相当。
|
图 6 吸收效果图(a)与波形曲线(b) |
为将NPML更好地应用于正反演,本文推导出MCFS-NPML吸收边界条件。该过程中引入了频移因子、尺度因子和稳定性因子,这三种因子保证了波场模拟稳定有效地进行。将它们同时引入弥补了仅引入某种单一因子的不足,相互弥补了各自固有的不利影响。通过分析衰减函数的引入过程以及分布方式,改进了衰减函数,最终达到进一步提升吸收效果的目的。
| [1] |
Berenger J P. A perfectly matched layer for the ab-sorption of electromagnetics waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. |
| [2] |
Berenger J P. On the reflection from Cummer's nearly perfectly matched layer[J]. IEEE Microwave and Wireless Components Letters, 2004, 14(7): 334-336. DOI:10.1109/LMWC.2004.829272 |
| [3] |
Chew W C, Weedon W H. A 3D perfectly matched medium from modified maxwell's equations with stretched coordinates[J]. Microwave and Optical Technology Letters, 1994, 7(13): 599-604. DOI:10.1002/mop.4650071304 |
| [4] |
Collino F, Monk P B. Optimizing the perfectly matched layer[J]. Computer Methods in Applied Mechanics & Engineering, 1998, 164(1): 157-171. |
| [5] |
Kuzuoglu M, Mittra R. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers[J]. IEEE Microwave and Guided Wave Letters, 1996, 6(12): 447-449. DOI:10.1109/75.544545 |
| [6] |
Roden J A, Gedney S D. Convolution PML (C-PML):An efficient FDTD implementation of the CFS-PML for arbitrary media[J]. Microwave and Optical Technology Letters, 2000, 27(5): 334-339. DOI:10.1002/1098-2760(20001205)27:5<334::AID-MOP14>3.0.CO;2-A |
| [7] |
Komatitsch D, Martin R. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation[J]. Geophysics, 2007, 72(5): SM155-SM167. DOI:10.1190/1.2757586 |
| [8] |
Cummer S A. A simple nearly perfectly matched layer for general electromagnetic media[J]. IEEE Microwave and Wireless Components Letters, 2003, 13(3): 128-130. DOI:10.1109/LMWC.2003.810124 |
| [9] |
Hu W Y, Abubakar A, Habashy T M. Application of the nearly perfectly matched layer in acoustic wave modeling[J]. Geophysics, 2007, 72(5): SM169-SM175. DOI:10.1190/1.2738553 |
| [10] |
Chen J Y. Application of the nearly perfectly matched layer for seismic wave propagation in 2D homoge-neous isotropic media[J]. Geophysical Prospecting, 2011, 59(4): 662-672. DOI:10.1111/j.1365-2478.2011.00949.x |
| [11] |
Chen J Y. Nearly perfectly matched layer method for seismic wave propagation in poroelastic media[J]. Canadian Journal of Exploration Geophysics, 2012, 37(1): 22-27. |
| [12] |
Festa G, Delavaud E, Vilotte J P. Interaction between surface waves and absorbing boundaries for wave propagation in geological basins:2D numerical simulations[J]. Geophysical Research Letters, 2005, 32(20): 55-102. |
| [13] |
Mezafajardo K C, Papageorgiou A S. A nonconvolutional, split-field, perfectly matched layer for wave propagation in isotropic and anisotropic elastic media:stability analysis[J]. Bulletin of the Seismological Society of America, 2008, 98(4): 1811-1836. DOI:10.1785/0120070223 |
| [14] |
Collino F, Tsogka C. Application of the PML abso-rbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1): 294-307. DOI:10.1190/1.1444908 |
| [15] |
Groby J, Tsogka C. A time domain method for mode-ling viscoacoustic wave propagation[J]. Journal of Computational Acoustics, 2006, 14(2): 201-236. DOI:10.1142/S0218396X06003001 |
| [16] |
王守东. 声波方程完全匹配层吸收边界[J]. 石油地球物理勘探, 2003, 38(1): 31-34. WANG Shoudong. Absorbing boundary condition for acoustic wave equation by perfectly matched layer[J]. Oil Geophysical Prospecting, 2003, 38(1): 31-34. DOI:10.3321/j.issn:1000-7210.2003.01.007 |
| [17] |
秦臻, 任培罡, 姚姚, 等. 弹性波正演模拟中PML吸收边界条件的改进[J]. 中国地质大学学报, 2009, 34(4): 658-664. QIN Zhen, REN Peigang, YAO Yao, et al. Improvement of PML absorbing boundary conditions in elastic wave forward modeling[J]. Journal of China University of Geosciences, 2009, 34(4): 658-664. DOI:10.3321/j.issn:1000-2383.2009.04.012 |
| [18] |
张显文, 韩立国, 黄玲, 等. 基于递归积分的复频移PML弹性波方程交错网格高阶差分[J]. 地球物理报, 2009, 52(7): 1800-1807. ZHANG Xianwen, HAN Liguo, HUANG Ling, et al. A staggered-grid high-order difference method of complex frequency-shifted PML based on recursive intergration for elastic wave equation[J]. Chinese Journal of Geophysics, 2009, 52(7): 1800-1807. |
| [19] |
熊章强, 毛承英. 声波数值模拟中改进的非分裂式PML边界条件[J]. 石油地球物理勘探, 2011, 46(1): 35-39. XIONG Zhangqiang, MAO Chengying. Improved unsplit PML boundary conditions in acoustic wave numerical simulation[J]. Oil Geophysical Prospecting, 2011, 46(1): 35-39. |
| [20] |
刘洋. 波动方程时空域有限差分数值解及吸收边界条件研究进展[J]. 石油地球物理勘探, 2014, 49(1): 35-46. LIU Yang. Research progress on time-space domain finite difference numerical solution and absorption boundary conditions of wave equation[J]. Oil Geophysical Prospecting, 2014, 49(1): 35-46. |
| [21] |
李佩笑, 林伟军, 张秀梅, 等. 常规分裂和非分裂完全匹配层吸收边界比较研究[J]. 声学学报, 2015, 40(1): 44-53. LI Peixiao, LIN Weijun, ZHANG Xiumei, et al. Comparisons for regular splitting and non-splitting perfectly matched layer absorbing boundary conditions[J]. Acta Acustica, 2015, 40(1): 44-53. |
| [22] |
廉西猛, 单联瑜, 隋志强. 地震正演模拟完全匹配层吸收边界条件研究综述[J]. 地球物理学进展, 2015, 30(4): 1725-1733. LIAN Ximeng, SHAN Lianyu, SUI Zhiqiang. An overview of research on perfectly matched layers absorbing boundary condition of seismic forward numeri-cal simulation[J]. Progress in Geophysics, 2015, 30(4): 1725-1733. |
| [23] |
黄建平, 黄金强, 李振春, 等. TTI介质一阶qP波方程交错网格伪谱法正演模拟[J]. 石油地球物理勘探, 2016, 51(3): 487-496. HUANG Jianping, HUANG Jinqiang, LI Zhenchun, et al. Staggered grid pseudo-spectral numerical simulation of first-order quasi P-wave equation for TTI media[J]. Oil Geophysical Prospecting, 2016, 51(3): 487-496. |
| [24] |
张衡, 刘洪, 李博, 等. TTI介质声波方程分裂式PML吸收边界条件研究[J]. 石油物探, 2017, 56(3): 349-361. ZHANG Heng, LIU Hong, LI Bo, et al. The research on split PML absorbing boundary conditions of acoustic equation for TTI media[J]. Geophysical Prospecting for Petroleum, 2017, 56(3): 349-361. DOI:10.3969/j.issn.1000-1441.2017.03.005 |
| [25] |
刘东洋, 彭苏萍, 师素珍, 等. 基于Lebedev网格的TTI介质二维三分量正演模拟[J]. 石油地球物理勘探, 2018, 53(2): 288-296. LIU Dongyang, PENG Suping, SHI Suzhen, et al. 2D three-component seismic forward modeling in TTI media based on the Lebedev grid[J]. Oil Geophysical Prospecting, 2018, 53(2): 288-296. |
| [26] |
成景旺, 毛宁波, 吕晓春, 等. 非分裂完全匹配层边界存储时间域全波形反演[J]. 石油地球物理勘探, 2018, 53(4): 754-764. CHENG Jingwang, MAO Ningbo, LYU Xiaochun, et al. Time-domain full waveform inversion with CFS-NPML boundary storage[J]. Oil Geophysical Prospecting, 2018, 53(4): 754-764. |
| [27] |
胡建林, 宋维琪, 张建坤, 等. 交错网格有限差分正演模拟的联合吸收边界[J]. 石油地球物理勘探, 2018, 53(5): 914-920. HU Jianlin, SONG Weiqi, ZHANG Jiankun, et al. Joint absorbing boundary in the staggered-grid finite difference forward modeling simulation[J]. Oil Geophysical Prospecting, 2018, 53(5): 914-920. |
| [28] |
汪勇, 徐佑德, 高刚, 等. 二维黏滞声波方程的优化组合型紧致有限差分数值模拟[J]. 石油地球物理勘探, 2018, 53(6): 1152-1164. WANG Yong, XU Youde, GAO Gang, et al. Numerical simulation of 2D visco-acoustic wave equation with an optimized combined compact difference scheme[J]. Oil Geophysical Prospecting, 2018, 53(6): 1152-1164. |
| [29] |
田坤, 黄建平, 李振春, 等. 多轴卷积完全匹配层吸收边界条件[J]. 石油地球物理勘探, 2014, 49(1): 143-152. TIAN Kun, HUANG Jianping, LI Zhenchun, et al. Multi-axial convolution perfectly matched layer absorption boundary condition[J]. Oil Geophysical Prospecting, 2014, 49(1): 143-152. |
| [30] |
陈可洋. 完全匹配层吸收边界条件研究[J]. 石油物探, 2010, 49(5): 472-477. CHEN Keyang. Study on perfectly matched layer absorbing boundary condition[J]. Geophysical Prospecting for Petroleum, 2010, 49(5): 472-477. DOI:10.3969/j.issn.1000-1441.2010.05.006 |
| [31] |
罗玉钦, 刘财. 近似完全匹配层边界条件吸收效果分析及衰减函数的改进[J]. 石油地球物理勘探, 2018, 53(5): 903-913. LUO Yuqin, LIU Cai. Absorption effects in nearly perfectly matched layers and damping factor improvement[J]. Oil Geophysical Prospecting, 2018, 53(5): 903-913. |



 刘财, 吉林省长春市西民主大街938号吉林大学地球探测科学与技术学院, 130026。Email:
刘财, 吉林省长春市西民主大街938号吉林大学地球探测科学与技术学院, 130026。Email: