② 同济大学海洋与地球科学学院, 上海 200092
② School of Ocean and Earth Sciences, Tongji University, Shanghai 200092, China
地震体波在地球内部非均匀介质中的传播过程中存在纵波(P波)和横波(S波)两种模式(即波型)之间的相互转换与耦合。为了获得具有明确物理含义的弹性波偏移图像,纵横波模式解耦被认为是至关重要的步骤[1-4]。模式解耦预条件对于弹性全波形反演也很有意义[5-6]。
在各向同性介质中,根据亥姆赫兹分解理论,弹性矢量波场可以分解成相应的纵波和横波成分[7-8],马德堂等[9]、李振春等[10]提出了P波和S波近似解耦的弹性波方程;吴潇等[11]比较了一系列各向同性P波和S波解耦方法。然而,地球内部介质普遍存在不同程度的弹性各向异性,表现为传播速度与偏振特征的方向相关性。此时,纵波的偏振方向与传播方向不平行,横波偏振方向与传播方向不垂直,而横波还会分裂成偏振方向相互正交的快横波和慢横波[12],它们依次被称为qP波、qS1波和qS2波。qS1和qS2波的偏振方向随着传播方向的变化通常是不连续的,而且当两种qS波相速度相等(即发生横波奇异性)时,无法确定各自的偏振方向,故而难以区分两种qS波模式。在对称性较高的横向各向同性(TI)介质中,qS1和qS2的偏振方向要么在对称轴平面以内(qSV波),要么与对称轴平面垂直(qSH波)[13-16]。
各向异性弹性波模式解耦理论和算法研究有着近三十年的发展历程。一方面,人们一直试图从方程解耦的角度实现qP和qS波场的解耦,代表性的工作包括拟声学近似[17]、纯模式近似[18]和伪纯模式波动方程[19-20]等,这些近似方程都存在动力学误差。另一方面,受亥姆赫兹分解理论的启发,人们也对各向同性介质中纵、横波分离的算法进行了扩展。最初,Dellinger等[21]提出在波数域求取伪散度和伪旋度算子,通过偏振投影分离qP与qS波。为了适应非均匀各向异性介质,Yan等[14]将偏振投影算子构建成非稳相空间滤波形式,魏石磊等[22]在此基础上研究了空间域滤波算子的特征。然而非均匀各向异性介质中基于偏振投影的模式解耦计算成本很高[16],为了突破计算瓶颈,Yan等[23]设计了一种类似于单程波偏移成像中的相移加插值(PSPI)的混合域解耦算法。而后,Cheng等[16]将模式分解表达成空间—波数域的广义傅里叶积分算子,并借用矩阵低秩近似技术[24],提出了一种分离qP、qSV和qSH波标量和矢量场的快速算法;Wang等[25]建议对介质模型进行分块,再利用低秩近似解耦算法。此外,也有学者将Yan等[14]提出的非稳相空间滤波算子简化成更经济的伪散度/伪旋度算子,实现qP和qS波近似解耦[26]。总之,从精度、成本和可操作性等角度发展各向异性弹性波模式解耦新算法仍然非常必要。
本文在回顾各向异性弹性波模式解耦的基本原理基础上,首先改进了Zhou等[27]提出的基于主能量传播与偏振方向偏差角构造的qP/qS波解耦伪散度、伪旋度算法,一定程度上考虑偏差角随传播方向的变化,进而建立精度更高的伪散度、伪旋度算子。然后,探讨低秩近似解耦算法及其模型分区、CPU-GPU异构平台实现策略。最后,应用SEG Hess VTI模型检验和评价本文的模式解耦高效算法。
1 弹性波模式解耦基本原理在各向同性介质中,弹性波场P/S波分离通常采用散度和旋度运算[8]
| $ \left\{ {\begin{array}{*{20}{l}} {{u^{({\rm{P}})}}(\mathit{\boldsymbol{x}}) = \nabla \cdot \mathit{\boldsymbol{u}}(\mathit{\boldsymbol{x}})}\\ {{\mathit{\boldsymbol{u}}^{({\rm{S}})}}(\mathit{\boldsymbol{x}}) = \nabla \times \mathit{\boldsymbol{u}}(\mathit{\boldsymbol{x}})} \end{array}} \right. $ | (1) |
式中
| $ \left\{ {\begin{array}{*{20}{l}} {{U^{({\rm{P}})}}(\mathit{\boldsymbol{K}}) = {\rm{i}}\mathit{\boldsymbol{K}} \cdot \mathit{\boldsymbol{U}}(\mathit{\boldsymbol{K}})}\\ {{\mathit{\boldsymbol{U}}^{({\rm{S}})}}(\mathit{\boldsymbol{K}}) = {\rm{i}}\mathit{\boldsymbol{K}} \times \mathit{\boldsymbol{U}}(\mathit{\boldsymbol{K}})} \end{array}} \right. $ | (2) |
式中:K=(Kx, Ky, Kz)T表示波矢量;U或U为u或u的傅里叶变换。在各向同性介质中,波的传播方向与P波的偏振方向一致,因此上面的模式解耦也可视为偏振投影的范畴。
在各向异性介质中,采用散度和旋度运算会造成模式分离不彻底,出现模式泄漏或串扰。为此,Dellinger等[21]提出以qP波偏振方向为基础的伪散度和伪旋度算子,从理论上解决了各向异性qP与qS波分离问题,即
| $ \left\{ {\begin{array}{*{20}{l}} {{U^{({\rm{qP}})}}(\mathit{\boldsymbol{K}}) = {\rm{i}}{\mathit{\boldsymbol{a}}_{\rm{P}}}(\mathit{\boldsymbol{K}}) \cdot \mathit{\boldsymbol{U}}(\mathit{\boldsymbol{K}})}\\ {{\mathit{\boldsymbol{U}}^{({\rm{qS}})}}(\mathit{\boldsymbol{K}}) = {\rm{i}}{\mathit{\boldsymbol{a}}_{\rm{P}}}(\mathit{\boldsymbol{K}}) \times \mathit{\boldsymbol{U}}(\mathit{\boldsymbol{K}})} \end{array}} \right. $ | (3) |
式中aP(K)为归一化的qP波偏振矢量。
为了求取偏振矢量,需要求解平面波解对应的Christoffel方程
| $ \left[ {\left( {\mathit{\boldsymbol{G}} - \rho \mathit{\boldsymbol{V}}_m^2\mathit{\boldsymbol{I}}} \right)} \right]{\mathit{\boldsymbol{U}}_m} = 0 $ | (4) |
式中:m为qP、qS1、qS2;I为单位对角矩阵;G为Christoffel张量
| $ {G_{ik}} = {C_{ijkl}}{n_j}{n_l}\quad i,j,k,l = 1,2,3 $ | (5) |
其中:Cijkl为刚度系数;
在VTI介质中,qS波一般分解成偏振方向连续变化的qSV和qSH波,前者在对称轴平面内垂直qP波偏振,后者在对称轴平面法向方向上偏振[13]。因此,TI介质弹性波模式解耦对应波数域的偏振投影公式为
| $ {U^{(m)}}(\mathit{\boldsymbol{K}}) = {\rm{i}}{\mathit{\boldsymbol{a}}_m}(\mathit{\boldsymbol{K}}) \cdot \mathit{\boldsymbol{U}}(\mathit{\boldsymbol{K}}) $ | (6) |
式中qSV、qSH波归一化偏振矢量满足
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{a}}_{{\rm{SH}}}}(\mathit{\boldsymbol{K}}) = \mathit{\boldsymbol{s}} \times \mathit{\boldsymbol{K}}}\\ {{\mathit{\boldsymbol{a}}_{{\rm{SV}}}}(\mathit{\boldsymbol{K}}) = {\mathit{\boldsymbol{a}}_{\rm{P}}}(\mathit{\boldsymbol{K}}) \times {\mathit{\boldsymbol{a}}_{{\rm{SH}}}}(\mathit{\boldsymbol{K}})} \end{array}} \right. $ | (7) |
式中s为TI介质的对称轴方向。
不难发现,如同散度和旋度运算一样,Dellinger等[21]构造的伪散度、伪旋度运算分离得到标量纵波和矢量横波场(其中横波场在二维情况下仅剩一个分量)。而式(6)表示偏振投影解耦得到了三种波模式的标量场。为了从总的弹性波场分离出各个波模式量纲一致、振幅和相位相对保真的矢量场,可采用Zhang等[15]提出的矢量分解算子
| $ {\mathit{\boldsymbol{U}}^{(m)}}(\mathit{\boldsymbol{K}}) = {\mathit{\boldsymbol{a}}_m}(\mathit{\boldsymbol{K}})\left[ {{\mathit{\boldsymbol{a}}_m}(\mathit{\boldsymbol{K}}) \cdot \mathit{\boldsymbol{U}}(\mathit{\boldsymbol{K}})} \right] $ | (8) |
对于非均匀VTI介质,偏振投影算子比较复杂,因为偏振方向在空间上随介质参数变化而改变。例如,Yan等[14]把式(6)改写为空间域的非稳相滤波(投影)算子
| $ {u^{(m)}} = \nabla _{\rm{a}}^{(m)} \cdot \mathit{\boldsymbol{u}} = L_x^{(m)}{u_x} + L_y^{(m)}{u_y} + L_z^{(m)}{u_z} $ | (9) |
式中
在各向异性介质中,qP波传播方向与偏振方向通常是不一致的,它们之间存在一个偏差角。一旦给定传播方向,可以借助Christoffel方程计算精确的偏振方向。为了避免采用计算复杂度非常高的精确的偏振投影算子,有学者利用相对容易估算的相(传播)方向或群方向去估计传播与偏振方向之间的夹角,进而获得偏振方向的近似估计,从而构造出比较容易计算的、近似的qP/qS波模式分离算子[27]。
三维情况下,qP波偏振矢量aP(K)的方向可用方位角α0(K)和倾角β0(K)表示,波矢量K的方向可用方位角α1(K)和倾角β1(K)表示,因此,可以用φ(K)和θ(K)表示aP(K)与K的方向偏差角,即φ(K)=α0(K)-α1(K),θ(K)=β0(K)-β1(K)。理论上,除了极个别特殊方向(如对称轴方向),这两个偏差角随传播方向变化,且都不为零。利用偏差角可从传播方向估计qP波的偏振方向,即
| $ {\mathit{\boldsymbol{a}}_{\rm{P}}}\left( \mathit{\boldsymbol{K}} \right) = \left[ {\begin{array}{*{20}{c}} {\cos \varphi \left( \mathit{\boldsymbol{K}} \right)\cos \theta \left( \mathit{\boldsymbol{K}} \right)}&{ - \sin \varphi \left( \mathit{\boldsymbol{K}} \right)}&{\cos \varphi \left( \mathit{\boldsymbol{K}} \right)\sin \theta \left( \mathit{\boldsymbol{K}} \right)}\\ {\sin \varphi \left( \mathit{\boldsymbol{K}} \right)\cos \theta \left( \mathit{\boldsymbol{K}} \right)}&{\cos \varphi \left( \mathit{\boldsymbol{K}} \right)}&{\sin \varphi \left( \mathit{\boldsymbol{K}} \right)\sin \theta \left( \mathit{\boldsymbol{K}} \right)}\\ { - \sin \theta \left( \mathit{\boldsymbol{K}} \right)}&0&{\cos \theta \left( \mathit{\boldsymbol{K}} \right)} \end{array}} \right]\mathit{\boldsymbol{K}} $ | (10) |
将式(10)施加到偏振投影算子并变换到空间域,就与式(9)完全等价。对非均匀TI介质而言,空间域非稳相滤波算子远比散度/旋度算子复杂,计算成本极高。
2.1 基于主能量传播与偏振方向夹角的伪散度与伪旋度算子为了在精确的偏振投影非稳相滤波算子和散度/旋度算子之间找到比较恰当的折中,Zhou等[27]提出了qP波偏振方向的近似估算方法,进而构造出了一种非常经济的伪散度与伪旋度算子。其思路是,首先用散度运算获得近似qP波标量场u(P),然后估计其能流密度矢量(坡印廷矢量)e=(e1,e2,e3)T
| $ {e_i} \approx \frac{{\partial {u^{({\rm{P}})}}}}{{\partial t}}\nabla {u^{({\rm{P}})}}\quad {\rm{i}} = 1,2,3 $ | (11) |
表征空间各点主能量传播方向K。针对一阶速度—应力方程计算的矢量波场,也可采用
| $ {e_j} = \sum\limits_k - {\tau _{jk}}{v_k} $ | (12) |
计算的群方向去估计相方向,从而避免估计qP波标量场引起的误差。式中:τjk表示应力分量;vk表示振动速度分量;j,k=1,2,3。再由Christoffel方程计算主能量方向qP波的偏振方向以及它与传播方向的夹角。为了简化投影滤波算子,相同空间点上可采用不随传播方向变化的偏差角去逼近qP波的偏振方向[27],即
| $ {\mathit{\boldsymbol{a}}_{\rm{P}}}(\mathit{\boldsymbol{K}}) = \left[ {\begin{array}{*{20}{c}} {\cos \varphi \cos \theta }&{ - \sin \varphi }&{\cos \varphi \sin \theta }\\ {\sin \varphi \cos \theta }&{\cos \varphi }&{\sin \varphi \sin \theta }\\ { - \sin \theta }&0&{\cos \theta } \end{array}} \right]\mathit{\boldsymbol{K}} $ | (13) |
上述近似虽可以由传播方向估计qP波的偏振方向,但无法估计qSV和qSH波的偏振方向,至多只能分离qP与qS波。另外,当qP、qS波从不同方向同时达到该点时,忽视偏差角随传播方向变化也会引入明显误差。
根据式(13),偏振投影(滤波)算子可表示成旋转后的散度/旋度算子(即伪散度/伪旋度算子),即
| $ \left\{ \begin{array}{l} {u^{({\rm{qp}})}} = {L_x}{u_x} + {L_y}{u_y} + {L_z}{u_z}\\ {\mathit{\boldsymbol{u}}^{({\rm{qS}})}} = \left( {{L_y}{u_z} - {L_z}{u_y}} \right)i + \left( {{L_z}{u_x} - {L_x}{u_z}} \right)j + \\ \;\;\;\;\;\;\;\;\;\;\left( {{L_x}{u_y} - {L_y}{u_x}} \right)\mathit{\boldsymbol{k}} \end{array} \right. $ | (14) |
式中
| $ \left\{ {\begin{array}{*{20}{l}} {{L_x} = \cos \varphi \cos \theta \frac{\partial }{{\partial x}} - \sin \varphi \frac{\partial }{{\partial y}} + \cos \varphi \sin \theta \frac{\partial }{{\partial z}}}\\ {{L_y} = \sin \varphi \cos \theta \frac{\partial }{{\partial x}} + \cos \varphi \frac{\partial }{{\partial y}} + \sin \varphi \sin \theta \frac{\partial }{{\partial z}}}\\ {{L_z} = - \sin \theta \frac{\partial }{{\partial x}} + \cos \theta \frac{\partial }{{\partial z}}} \end{array}} \right. $ | (15) |
与旋度算子类似,伪旋度算子仅从矢量总波场中分离出矢量形式的qS波,无法区分qSV和qSH波。
在Zhou等[27]仅推导了二维情况下的伪散度/伪旋度算子
| $ \left\{ {\begin{array}{*{20}{l}} {{L_x} = \cos \theta \frac{\partial }{{\partial x}} + \sin \theta \frac{\partial }{{\partial z}}}\\ {{L_z} = \cos \theta \frac{\partial }{{\partial z}} + \sin \theta \frac{\partial }{{\partial x}}} \end{array}} \right. $ | (16) |
以及相应的模式解耦非稳相滤波算子
| $ \left\{ {\begin{array}{*{20}{l}} {{u^{({\rm{qP}})}} = {L_x}{u_x} + {L_z}{u_z}}\\ {{\mathit{\boldsymbol{u}}^{({\rm{qSV}})}} = {L_z}{u_x} + {L_x}{u_z}} \end{array}} \right. $ | (17) |
本质上,这些近似的偏振投影运算用传播与偏振方向夹角相关的系数去显式地对波场的一阶偏导数进行加权求和。由于这些近似的权系数可以提前计算,偏导数波场在传播模拟过程中也预先计算好,这种空间非稳相滤波的计算复杂度大幅度降低。值得注意的是,由于传播方向是从每个时刻波场的坡印廷矢量估计的,因此每个延拓时间步上都需要构造并施加相应的伪散度/伪旋度算子。
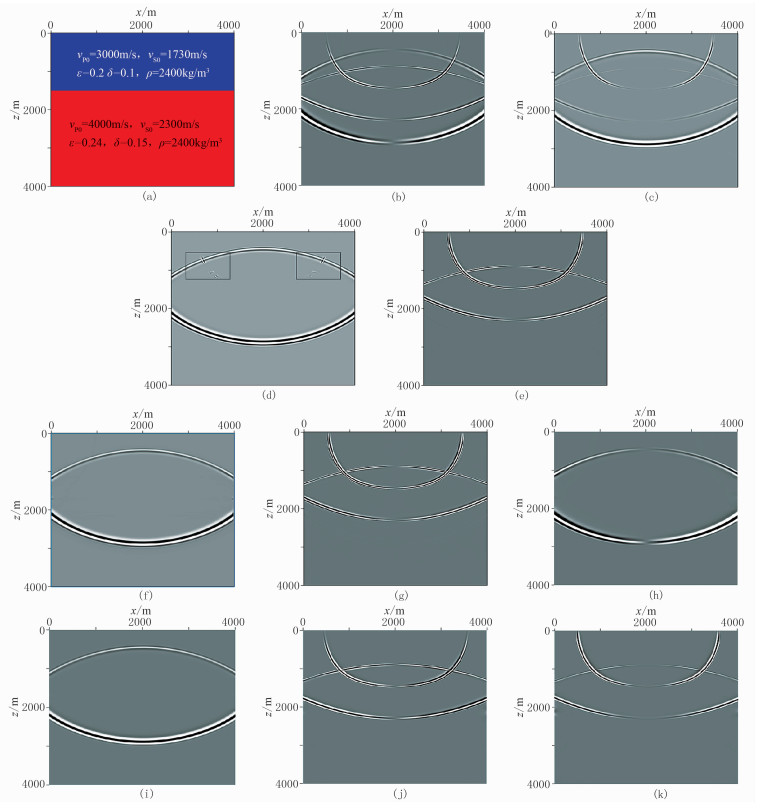
如图 1所示,在一个两层VTI介质模型中,震源位于(2000m,0),通过弹性波方程数值模拟计算得到900ms时刻的质点速度波场。然后采用主能量方向偏振投影近似投影算法,基本实现大部分空间qP、qSV波的分离。只是在一些波前面交叉区域(图 1d方框所示),存在明显的模式泄漏。其原因在于,传播与偏振矢量夹角随传播方向变化,仅依据主能量方向估计的一个偏差角构建偏振投影算子,误差较大,不能处理不同方向同时达到多种波模式的分离问题。其中采用主能量方向偏振投影近似算法得到的是标量qP和qSV波。同时,结合式(1)和式(2),波场空间偏导数运算相当于在波数域乘以iK,虚数单位i会使得纵、横波相位改变90°,与非归一化的波数K相乘会使二者的振幅发生改变(对比图 1b和图 1d)。为了保证分离得到的纵、横波在相位和振幅上尽可能保真,可以采用以式(8)为基础的矢量分解模式解耦算法,图 1f~图 1k为精确偏振投影算法分离的矢量qP和qSV波,可以看出矢量qP和qSV波的水平分量和垂直分量相位上分别与质点速度的水平分量和垂直分量保持一致。
|
图 1 两层VTI介质模型偏振投影近似算法分离结果 (a)VTI模型及其参数;(b)水平分量900ms波场快照;(c)垂直分量900ms波场快照;(d)主能量方向偏振投影算法分离的qP波;(e)主能量方向偏振投影算法分离的qSV波;(f)精确偏振投影分离的矢量qP波;(g)精确偏振投影分离的矢量qSV波;(h)精确偏振投影分离的矢量qP波的水平分量;(i)精确偏振投影分离的矢量qP波垂直分量;(j)精确偏振投影分离的矢量qSV波的水平分量;(k)精确偏振投影分离的矢量qSV波的垂直分量 |
一般来讲,波传播到某一点时能量随球面扩散,传播过程中qP波与qS波在同一时刻都经过空间某点也是非常普遍的。为了提升Zhou等[27]方法的精度,本文适当考虑传播与偏振方向偏差角随传播方向的变化,通过多方向子波场的伪散度与伪旋度运算实现更精确的模式解耦。
首先,将原始波场各个分量变换到波数域,按角度面元拆分成若干方向扇区(Ωi)的子波场[28]
| $ u(\mathit{\boldsymbol{x}}) = \sum\limits_{i = 1}^N {{u_i}} (\mathit{\boldsymbol{x}}) = \sum\limits_{i = 1}^N {\int_{{\mathit{\Omega }_i}} U } (\mathit{\boldsymbol{K}})\exp ( - {\rm{i}}\mathit{\boldsymbol{Kx}}){\rm{d}}\mathit{\boldsymbol{K}} $ | (18) |
式中u(x)和U(K)分别表示空间域、波数域的子波场。N一般取4~8,具体取值视波场复杂性和精度要求而定。然后,分别在每个方向扇区计算相应的坡印廷矢量ei,指示多个主能量传播方向。再利用Christoffel方程估计不同带区的偏差角φi和θi,进而建立各个方向扇区内偏振方向的估算公式
| $ {\mathit{\boldsymbol{a}}_{{\rm{P}}i}}(\mathit{\boldsymbol{K}}) = \left[ {\begin{array}{*{20}{c}} {\cos {\varphi _i}\cos {\theta _i}}&{ - \sin {\varphi _i}}&{\cos {\varphi _i}\sin {\theta _i}}\\ {\sin {\varphi _i}\cos {\theta _i}}&{\cos {\varphi _i}}&{\sin {\varphi _i}\sin {\theta _i}}\\ { - \sin {\theta _i}}&0&{\cos {\theta _i}} \end{array}} \right]\mathit{\boldsymbol{K}} $ | (19) |
据此构造出每个方向扇区内的偏振投影算子,将其作用于相应带区的子波场就获得解耦后的qP与qS波子波场。最后所有方向带区解耦子波场叠加就得到最终分离的qP和qS波场。
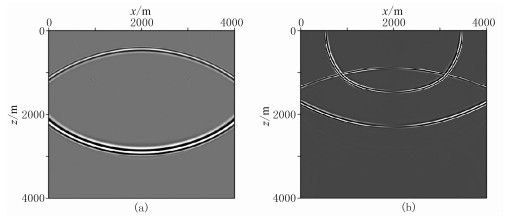
如图 2所示,对8个主能量方向子波场施加相应的偏振投影再求和,明显提升了qP与qS波重叠区域的模式分离精度。与精确偏振投影算法处理结果(图 1f和图 1g)相比,整体上效果是可接受的。不足的是,基于多个主能量传播与偏振方向夹角的伪散度与伪旋度算子分离的标量qP和qSV波在相位和振幅上仍存在一定的误差(对比图 1f和图 1g与图 2a和图 2b)。
|
图 2 两层VTI介质模型改进的偏振投影近似算法分离结果 (a)按8个主能量方向分区偏振投影分离的qP波;(b)按8个主能量方向分区偏振投影分离的qSV波 |
在非均匀VTI介质中,弹性波模式解耦的偏振投影对应空间域非稳相滤波算子。无论是Yan等[23]的PSPI算法,还是基于主能量传播与偏振方向夹角估算的非稳相滤波算法,都会损失偏振投影算子的精度,不足以应对非均匀性和各向异性都很强的地质情况。
3.1 偏振投影低秩近似算法为了既能够保证模式解耦的可靠性,又能够大幅度降低计算复杂度,Cheng等[16]提出了精确表征偏振投影的空间—波数域积分算子及其低秩近似快速算法。对非均匀VTI介质,偏振投影被表达成广义傅里叶积分公式
| $ \begin{array}{*{20}{c}} {{u^{(m)}}(\mathit{\boldsymbol{x}}) = \int {\exp } ({\rm{i}}\mathit{\boldsymbol{Kx}})\left[ {{\rm{i}}{a_{mx}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{K}})} \right]{U_x}(\mathit{\boldsymbol{K}}){\rm{d}}\mathit{\boldsymbol{K}} + }\\ {\int {\exp } ({\rm{i}}\mathit{\boldsymbol{Kx}})\left[ {{\rm{i}}{a_{my}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{K}})} \right]{U_y}(\mathit{\boldsymbol{K}}){\rm{d}}\mathit{\boldsymbol{K}} + }\\ {\int {\exp } ({\rm{i}}\mathit{\boldsymbol{Kx}})\left[ {{\rm{i}}{a_{mc}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{K}})} \right]{U_z}(\mathit{\boldsymbol{K}}){\rm{d}}\mathit{\boldsymbol{K}}} \end{array} $ | (20) |
式中am=(amx,amy,amz)T表示某种波模式对应的偏振向量。假设空间或波数采样点数为M,则这种混合域积分的计算复杂度为O(M2×lgM),现有计算条件下很难承担这样的任务。根据式(8),还可以构建纵、横波矢量分解的精确偏振投影算子,表示为广义傅里叶积分形式(以x方向为例)
| $ \begin{array}{l} u_x^{(m)}(\mathit{\boldsymbol{x}}) = \int {\exp } ({\rm{i}}\mathit{\boldsymbol{Kx}})\left[ {{a_{mx}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{K}}){a_{mx}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{K}})} \right]{U_x}(\mathit{\boldsymbol{K}}){\rm{d}}\mathit{\boldsymbol{K}} + \\ \;\;\;\;\int {\exp } ({\rm{i}}\mathit{\boldsymbol{Kx}})\left[ {{a_{mx}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{K}}){a_{mx}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{K}})} \right]{U_x}(\mathit{\boldsymbol{K}}){\rm{d}}\mathit{\boldsymbol{K}} + \\ \;\;\;\;\int {\exp } ({\rm{i}}\mathit{\boldsymbol{Kx}})\left[ {{a_{mx}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{K}}){a_{mx}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{K}})} \right]{U_x}(\mathit{\boldsymbol{K}}){\rm{d}}\mathit{\boldsymbol{K}} \end{array} $ | (21) |
根据式(20)和式(21)可知,式中的积分核同时依赖于空间域模型参数和傅里叶域波数成分。广义傅里叶积分算子可以通过核函数近似来降低积分计算的成本。通常来说,地球介质具有分层或分区变化的弹性特征,物理上也认为该混合域核函数矩阵是低秩的。因此根据低秩近似理论[24],该混合域核函数矩阵可以表示为三个矩阵的乘积
| $ \mathit{\boldsymbol{W}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{K}}) \approx \sum\limits_{l = 1}^L {\sum\limits_{n = 1}^N \mathit{\boldsymbol{B}} } \left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{K}}_l}} \right){\mathit{\boldsymbol{D}}_{ln}}\mathit{\boldsymbol{C}}\left( {{\mathit{\boldsymbol{x}}_n},\mathit{\boldsymbol{K}}} \right) $ | (22) |
式中:W表示混合域核函数矩阵;B和C分别表示降维之后的波数和空间维度的混合域矩阵;Dmn为L×N矩阵,其中L和N分别代表该算子矩阵在低秩近似意义下的列秩与行秩。如果给定矩阵分解的误差门槛值为1.0×10-6,常见各向异性介质模型偏振投影算子矩阵的秩均较小,通常为几或十几这样的数量级。对于图 1a中两层VTI模型,L和N均等于2。偏振投影模式解耦算子矩阵之所以存在上述低秩近似形式,主要是因为受地质作用的控制,大多数地层都呈现一定的层状或分块特征,从而使该算子被那些最能代表模型非均匀性和各向异性特征的空间位置和传播方向所主导[16]。
依据上述低秩分解(式(22)),式(20)中的积分式可退化成
| $ \begin{array}{*{20}{l}} {\int {\exp } ({\rm{i}}\mathit{\boldsymbol{Kx}})\left[ {{\rm{i}}{a_{mj}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{K}})} \right]{U_j}(\mathit{\boldsymbol{K}}){\rm{d}}\mathit{\boldsymbol{K}}}\\ {\left. { \approx \sum\limits_{l = 1}^L {\{ \sum\limits_{n = 1}^N {\left[ {\mathit{\boldsymbol{B}}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{K}}_l}} \right){\mathit{\boldsymbol{D}}_{ln}}} \right]} \exp ({\rm{i}}\mathit{\boldsymbol{Kx}})\mathit{\boldsymbol{C}}\left( {{\mathit{\boldsymbol{x}}_n},\mathit{\boldsymbol{K}}} \right){U_j}{\rm{d}}\mathit{\boldsymbol{K}}]} } \right\}} \end{array} $ | (23) |
式中j={x,y,z}。它们主要的计算量体现在N个矢量波场的正、反傅里叶变换,以及空间波场的N和L次加权求和。因为L和N远远小于空间或波数采样点数M,所以计算复杂度降低至O(L×M×lgM)或O(N×M×lgM)。这样就以较小的计算成本合理逼近了式(20)中的广义傅里叶积分运算[16]。更重要的是,偏振投影算子矩阵的低秩分解完全是根据介质模型本身特点自动进行的,不存在Yan等[23]的PSPI算法中设置参考模型类似的人为因素,这种模型自适应特点对实际应用非常重要。
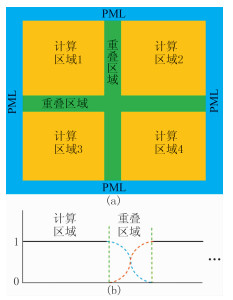
3.2 模型分区策略Wang[25]等认为,对于一些大规模应用问题,可把模型空间划分成若干区域,分别在每个区域构造低秩近似偏振投影算子,进一步提高算法效率和并行扩展潜力。如图 3a所示,首先需要将模型进行分区(黄色部分),区域之间保留一定的重叠(绿色部分),模型外围有PML吸收边界(蓝色部分),然后分别对每块区域求取偏振矢量并构建低秩近似投影算子,对弹性波场也进行同样地分区并施加窗函数。如图 3b所示,重叠区域的边界衰减函数采用的是正弦和余弦函数,且满足二者权重系数求和为1;最后,对不同区域的波场分别施加低秩近似偏振投影,并将分离后的波场按区域拼接。
|
图 3 模型分区示意图(a)及重叠区域边界衰减系数设置(b) |
尽管模型分区一定程度上可减小低秩近似解耦算法中FFT的总体成本,且一定程度降低了每个分区内偏振投影算子矩阵的秩,有助于节省单个时间片波场的模式解耦计算成本。但是,模型和波场分区需要每个分区周围的镶边处理,既带来额外计算开销,又在边界附近引入一定的误差,这些问题对弹性波逆时偏移或全波形反演等实际应用中大量延拓时间步上的模式解耦来说是不可忽略的。
3.3 GPU加速策略GPU并行加速在大规模波场数值模拟、逆时偏移成像领域已经得到广泛应用,常采用的有OpenCL和CUDA两种并行编程框架,现已开始使用OpenACC[29]。
从前文分析可知,正、反傅里叶变换在低秩近似模式解耦算法中占据大部分计算量,因此提高傅里叶变换计算效率非常关键。利用基于CUDA架构的快速傅里叶变换并行算法库cuFFT很好地解决了这个问题。其次,弹性波波模式解耦算法本身具有很好的数据独立性,因此可利用GPU进行细粒度的并行加速。
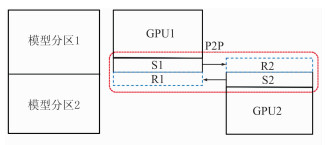
对于模型空间太大、单卡内存不足的情况,需要通过多卡并行方式来解决。多GPU并行算法的基础是沿着慢维方向对模型空间进行分区,而核心问题是GPU间的通信及其效率。单节点内GPU间的实时通信可以通过P2P技术实现,本文以单节点双卡并行作为示例。如图 4所示,整个模型空间分成两部分,分别对应在GPU1和GPU2上计算。每个计算分区都包含计算区域、数据发送区域(S1、S2)和数据接收区域(R1、R2),其中S1(S2)、R1(R2)分别对应为GPU1(GPU2)上的数据交换(发送、接收)内存区域。数据传输过程如图中箭头所示。P2P技术避免以CPU作为数据传输中转站,减小了数据传输延迟。
|
图 4 双卡并行模型分区示意图 |
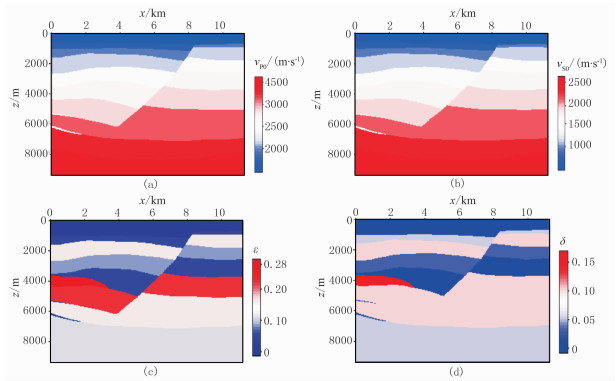
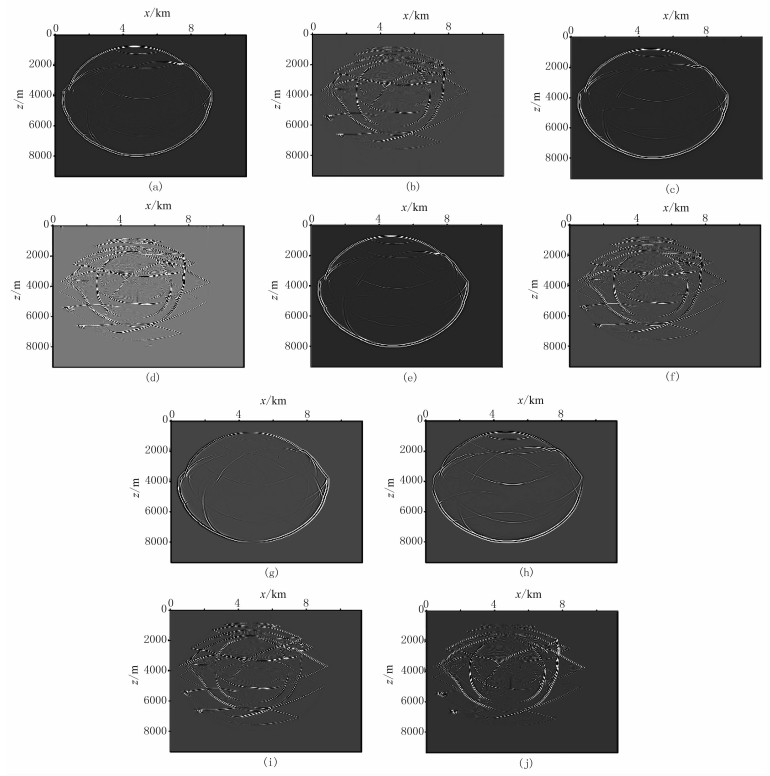
本文以SEG Hess VTI介质二维模型为例,测试本文发展的模式解耦高效算法。图 5为模型右半部分,尺寸为11.25km×9.38km(对应的空间网格数为1800×1500),震源位于(4.75km,3.81km)处。图 6为1400ms时的质点速度水平和垂直分量的波前快照。图 7分别展示了本文依据4个主能量方向传播与偏振矢量夹角构建的伪散度/伪旋度算子、偏振投影低秩近似解耦算法以及基于模型分区(以分成四个区域为例)的偏振投影低秩近似解耦算法得到的qP和qSV波场,可见几种算法都取得了比较好的模式解耦效果。
|
图 5 SEG Hess VTI模型 (a)vP0; (b)vS0; (c)ε; (d)δ |

|
图 6 SEG Hess VTI模型弹性波质点速度场1400ms时刻的水平(a)和垂直(b)分量 |
|
图 7 SEG Hess VTI模型改进的偏振投影近似算法和低秩近似算法波场分离结果 (a)和(b)为按4个主能量方向分区偏振投影分离的qP波和qSV波;(c)和(d)为精确偏振投影低秩近似分离的qP波和qSV波;(e)和(f)为基于模型分区的精确偏振投影低秩近似分离的qP波和qSV波;(g)和(h)为基于模型分区的精确偏振投影低秩近似分离的矢量qP波的水平和垂直分量;(i)和(j)为基于模型分区的精确偏振投影低秩近似分离的矢量qSV波的水平和垂直分量 |
如果采用伪散度/伪旋度算子进行模式解耦,需要在每个时间步计算坡印廷矢量,进而构建每个时间步的空间非稳相滤波器。相反,对于偏振投影低秩近似解耦算法,仅需要提前一次性构建出解耦滤波器,然后在各个时间步直接应用。在单核CPU(Intel(R) Xeon(R) CPU E5-2650 v4 @ 2.20GHz)平台上,以2000个时间步弹性qP/qSV波模式解耦为例,采用依据4个主能量方向传播与偏振矢量夹角构建的伪散度/伪旋度算子,平均每个时间片波场模式解耦耗用时间为6.8s,而偏振投影低秩近似算法的平均耗时为5.8s,两种算法在计算效率方面比较接近。
对于SEG Hess VTI模型低秩近似模式解耦,基于模型分区的低秩近似解耦GPU算法相比于常规的低秩近似解耦算法,单GPU卡(Nvidia Tesla K80)上改进后的低秩近似算法实现的加速比达到了4以上,同时从分离结果上可以看出前者精度也基本没有损失(适当选取区域划分的个数)。对于弹性波逆时偏移和全波形反演等处理而言,需要每个时间的波场都施加模式解耦,基于模型分区和GPU加速的低秩近似解耦算法在保证精度的前提下明显缩短了处理周期。此外,对于图 1的两层VTI模型而言,基于模型分区和GPU加速的低秩近似解耦算法反而比常规的耗时多,原因在于CPU-GPU异构平台涉及它们之间的数据通信开销,只有当模型规模达到一定程度时,基于模型分区和GPU加速算法优势才能凸显。
对比图 7a、图 7b与图 7g~图 7j可知,偏振投影低秩近似矢量解耦算法可以使得分离后的纵横波场的相位和振幅保真,同时结合模型分区和GPU加速策略,使算法的精度和计算效率达到最佳。
5 结论针对VTI介质qP与qS波模式解耦高昂的计算成本,本文一方面基于现有的由主能量传播与偏振方向偏差角构造的伪散度/伪旋度算法,通过波场方向分解估计的多个主能量方向逼近偏振投影算子,实现了更精确的空间域非稳相滤波算法,较好地解决了原算法在qP与qS波同时经过相同空间区域时的模式泄漏问题。由于该方法利用坡印廷矢量估计的传播与偏振矢量夹角逼近qP波的偏振方向(无法分别估计qSV和qSH波的偏振方向),它构建的模式解耦滤波只能实现qP与qS波分离,无法区分VTI介质中的qSV与qSH波。另一方面,基于现有的偏振投影低秩近似算法,通过采用模型分区和GPU加速策略进一步提高了算法效率。将模型空间分区和线程块分配有机结合,利用CUDA架构下的cuFFT快速傅里叶变换算法以及P2P数据通信技术,可以缩短这种高精度解耦算法的计算周期。对于二维VTI介质弹性波模式解耦问题,本文两种高效算法性价比相当。第二种算法因为能够对qS波进一步解耦,因此三维扩展性更强。今后将结合三维情况下的弹性波逆时偏移和全波形反演实际应用发挥该算法的优势。
| [1] |
Sun R, McMechan G A, Hsiao H, et al. Separating P- and S-waves in prestack 3D elastic seismograms using divergence and curl[J]. Geophysics, 2004, 69(1): 286-297. DOI:10.1190/1.1649396 |
| [2] |
Yan J, Sava P. Isotropic angle-domain elastic reverse-time migration[J]. Geophysics, 2008, 73(6): S229-S239. DOI:10.1190/1.2981241 |
| [3] |
Du Q, Guo C, Zhao Q, et al. Vector-based elastic reverse time migration based on scalar imaging condition[J]. Geophysics, 2017, 82(2): S111-S127. DOI:10.1190/geo2016-0146.1 |
| [4] |
王晨龙.各向异性介质多分量全波地震成像方法[D].上海: 同济大学, 2017.
|
| [5] |
Wang T F, Cheng J B. Born reflection kernel analysis and wave equation reflection traveltime inversion in elastic media[C]. SEG Technical Program Expanded Abstracts, 2017, 36: 1486-1491.
|
| [6] |
WangTF, ChengJB, Gu oQ, et al. Elasticwave-equation-based reflection kernel analysis and traveltime inversion using wave mode decomposition[J]. Geophysical Journal International, 2018, 215(1): 450-470. DOI:10.1093/gji/ggy291 |
| [7] |
Morse P M, Feshbach H. Methods of Theoretical Physics[M]. New York: McGraw-Hill Book Company, 1953.
|
| [8] |
Aki K, Richards P. Quantitative Seismology(2nd Edition)[M]. New Jersey: University Science Books, 2002.
|
| [9] |
马德堂, 朱光明. 弹性波波场P波和S波分解的数值模拟[J]. 石油地球物理勘探, 2003, 38(5): 482-486. MA Detang, ZHU Guangming. Numerical mode-ling of P-wave and S-wave separation in elastic wavefield[J]. Oil Geophysical Prospecting, 2003, 38(5): 482-486. DOI:10.3321/j.issn:1000-7210.2003.05.005 |
| [10] |
李振春, 张华, 刘庆敏, 等. 弹性波交错网格高阶有限差分法波场数值模拟[J]. 石油地球物理勘探, 2007, 42(5): 510-515. LI Zhenchun, ZHANG Hua, LIU Qingmin, et al. Numeric simulation of elastic wavefield separation by staggering grid high-order finite-difference algorithm[J]. Oil Geophysical Prospecting, 2007, 42(5): 510-515. DOI:10.3321/j.issn:1000-7210.2007.05.006 |
| [11] |
吴潇, 刘洋, 蔡晓慧. 弹性波波场分离方法对比及其在逆时偏移成像中的应用[J]. 石油地球物理勘探, 2018, 53(4): 710-721. WU Xiao, LIU Yang, CAI Xiaohui. Elastic wavefield separation methods and their applications in reverse migration[J]. Oil Geophysical Prospecting, 2018, 53(4): 710-721. |
| [12] |
Crampin S. Effective anisotropic elastic constants for wave propagation through cracked solids[J]. Geophysical Journal of the Royal Astronomical Society, 1984, 76(1): 135-145. DOI:10.1111/j.1365-246X.1984.tb05029.x |
| [13] |
Dellinger J. Anisotropic Seismic Wave Propagation[D]. Stanford University, 1991.
|
| [14] |
Yan J, Sava P. Elastic wave-mode separation for VTI media[J]. Geophysics, 2009, 74(6): WB19-WB32. DOI:10.1190/1.3256285 |
| [15] |
Zhang Q, McMechan G A. 2D and 3D elastic wavefield vector decomposition in the wavenumber domain for VTI media[J]. Geophysics, 2010, 75(3): D13-D26. DOI:10.1190/1.3431045 |
| [16] |
Cheng J B, Fomel S. Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media[J]. Geophysics, 2014, 79(4): C97-C110. DOI:10.1190/geo2014-0032.1 |
| [17] |
Alkhalifah T. An acoustic wave equation for aniso-tropic media[J]. Geophysics, 2000, 65(4): 1239-1250. DOI:10.1190/1.1444815 |
| [18] |
Liu F, Morton S A, Jiang S, et al. Decoupled wave equations for P and SV waves in an acoustic VTI media[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2844-2848.
|
| [19] |
Cheng J B, Kang W. Simulating propagation of separated wave modes in general anisotropic media, Part Ⅰ:qP-wave propagators[J]. Geophysics, 2014, 79(1): C1-C18. DOI:10.1190/geo2012-0504.1 |
| [20] |
Cheng J B, Kang W. Simulating propagation of separated wave modes in general anisotropic media, Part Ⅱ:qS-wave propagators[J]. Geophysics, 2016, 81(2): C39-C52. DOI:10.1190/geo2015-0253.1 |
| [21] |
Dellinger J, Etgen J. Wavefield separation in two-dimensional anisotropic media[J]. Geophysics, 1990, 55(7): 914-919. DOI:10.1190/1.1442906 |
| [22] |
魏石磊, 张大洲, 李明智, 等. VTI介质中波场分离算子特征研究[J]. 石油地球物理勘探, 2016, 51(3): 506-512. WEI Shilei, ZHANG Dazhou, LI Mingzhi, et al. Wave separation operator characteristics in the VTI medium[J]. Oil Geophysical Prospecting, 2016, 51(3): 506-512. |
| [23] |
Yan J, Sava P. Improving the efficiency of elastic wave-mode separation for heterogeneous tilted transverse isotropic media[J]. Geophysics, 2011, 76(4): T65-T78. DOI:10.1190/1.3581360 |
| [24] |
Engquist B, Ying L. Fast directional multilevel algorithms for oscillatory kernels[J]. SIAM Journal on Scientific Computing, 2007, 29(4): 1710-1737. DOI:10.1137/07068583X |
| [25] |
Wang W L, Hua B L, McMechan G, et al. P- and S-decomposition in anisotropic media with localized low-rank approximations[J]. Geophysics, 2018, 83(1): C13-C26. DOI:10.1190/geo2017-0138.1 |
| [26] |
芦永明, 张剑锋, 杨凯, 等. 二维TI介质非结构网格弹性波矢量逆时偏移[J]. 地球物理学报, 2017, 60(12): 4776-4789. LU Yongming, ZHANG Jianfeng, YANG Kai, et al. Vector elastic reverse time migration based on unstructured mesh for tilted TI medium[J]. Chinese Journal of Geophysics, 2017, 60(12): 4776-4789. DOI:10.6038/cjg20171219 |
| [27] |
Zhou Y, Wang H Z. Efficient wave-mode separation in vertical transversely isotropic media[J]. Geophysics, 2017, 82(2): C35-C47. DOI:10.1190/geo2016-0191.1 |
| [28] |
Tang C, McMechan G. Multidirectional slowness vector for computing angle gathers from reverse time migration[J]. Geophysics, 2016, 81(2): S55-S68. DOI:10.1190/geo2015-0134.1 |
| [29] |
赵虎, 武泗海, 尹成, 等. 基于OpenACC编程模型的逆时偏移多级并行的设计与优化[J]. 石油地球物理勘探, 2018, 53(6): 1307-1313, 1325. ZHAO Hu, WU Sihai, YIN Cheng, et al. Multi-level parallel design and optimization for reverse migration based on OpenACC programming mode[J]. Oil Geophysical Prospecting, 2018, 53(6): 1307-1313, 1325. |



 阮伦, 上海市杨浦区四平路1239号同济大学海洋与地球科学学院, 200092。Email:
阮伦, 上海市杨浦区四平路1239号同济大学海洋与地球科学学院, 200092。Email: