② 青岛海洋科学与技术试点国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China
在地震勘探数据采集中,受施工现场各种条件、因素的限制,往往会出现缺道或坏道,难以获取高质量的完整数据。而原始数据的完整性是后续处理和解释的基础,因此对缺失地震数据的插值重建,也成为地震数据处理的关键技术之一。
常用的地震数据重建方法包括基于波动方程、基于预测滤波和基于数学变换等三类。这些方法都受Nyquist采样定理限制,采样频率至少为信号频率的两倍,否则无法将信号从采集样本中完整地恢复。近年来压缩感知理论[1-2]的提出为地震数据重建方法提供了新思路。它基于信号的稀疏性,在一定条件下,通过最优化求解方式从不满足采样定理的信号中高概率地恢复出完整信号。
压缩感知理论的一个重要前提是信号的稀疏性。由于地震数据通常不是稀疏的,因此如何找到合适稀疏字典,使信号在该字典下的系数是稀疏的,即能稀疏表示信号,就显得尤为重要[3]。现今已有多种数学变换被用于地震数据重建,如Fourier变换[4]、Curvelet变换[5]、Wavelet变换[6-7]、Dreamlet变换[8]、Shearlet变换[9-10]、Contourlet变换[11]、Dreamlet变换[12]、UDWT变换[13]、DDTF变换[14]等。由于地震数据通常由不同类型元素组成,单一变换难以充分、有效地进行表达,因此形态分量分析(Morphological component analysis,MCA)方法[15]应运而生。
MCA是一种用于信号分离的理论方法,主要利用不同信号之间成分的差异分离信号。该方法最早由Starck等[15]提出并被成功地应用于图像的去噪与修复,现今被广泛地应用于信号的去噪、重建、分隔、修复及融合等众多领域。
李海山等[16]将MCA方法引入地震数据重建领域,取得了较好效果。周亚同等[17]在MCA框架下定量评价了多种稀疏字典组合数据重建效果,判定离散余弦变换(DCT)与Curvelet字典组合具有最高的重建精度。刘成明等[18]和张良等[19]指出Shearlet变换作为一种新型的多尺度几何变换,具有比Curvelet变换更好的方向性及各向异性特点,从而拥有更突出的稀疏表达能力,认为基于Shearlet变换的重建算法可望取得精度更高的重建结果。
本文基于文献[17-20]的研究成果,定量分析、对比了Shearlet字典与其他字典组合进行地震数据重建的效果,并挑选出最优的组合方式。合成数据和实际数据的重建结果都表明,Shearlet字典与DCT字典组合具有最高的重建精度。
1 基于MCA的地震数据重建方法 1.1 形态分量分析MCA方法认为,信号是由形态不同的多个分量线性组合而成,每个分量都能找到一个字典,该字典只能稀疏表示对应的形态分量,而无法稀疏表示其他分量。
给定二维信号X,假设它由K个不同形态的分量线性组合而成,即
| $ {\mathit{\pmb{X}}} = \sum\limits_{k = 1}^K {{\mathit{\pmb{X}}_k} = \sum\limits_{k = 1}^K {{\mathit{\pmb{D}}_k}{\mathit{\pmb{a}}_k}} } $ | (1) |
式中:X表示理想的完整地震数据;Xk为第k个形态分量,它可被字典Dk稀疏表示;ak为对应的稀疏系数。
1.2 地震数据重建地震数据的重建可表示为
| $ \mathit{\pmb{Y}} = \mathit{\pmb{RX}} $ | (2) |
式中:Y为实际采集的含缺失道地震数据;R为采样矩阵。
在MCA框架下,式(2)可被表示为
| $ \mathit{\pmb{Y}} = \mathit{\pmb{RX}} = {\mathit{\pmb{R}}}\sum\limits_{k = 1}^K {{\mathit{\pmb{X}}_k} = {\mathit{\pmb{R}}}\sum\limits_{k = 1}^K {{\mathit{\pmb{D}}_k}{\mathit{\pmb{a}}_k}} } $ | (3) |
将式(3)改写成无约束最优化问题,求解得
| $ {\mathit{\pmb{a}}_k} = \arg \min {\left\| {{\mathit{\pmb{a}}_k}} \right\|_1} + \lambda \left\| {{\mathit{\pmb{Y}}} - {\mathit{\pmb{R}}}\sum\limits_{k = 1}^K {{\mathit{\pmb{D}}_k}{\mathit{\pmb{a}}_k}} } \right\|_2^2 $ | (4) |
式中:||·||1表示L1范数;λ为拉格朗日乘子,平衡L1项和L2项所占比重; arg min表示函数取值最小时的自变量取值。
1.3 MCA求解算法对于式(4),Sardy等[21]结合块坐标松弛(Block coordinate relaxation,BCR)算法给出如下求解方法。
输入:采样矩阵R,字典组合D=[D1, D2, …, DK],缺失地震数据Y,总迭代次数N
输出:重建地震数据
初始化:每个形态分量Xi(0)=0, i=1, 2, …, K
(1) for n=1:N
(2) 残差
(3) for k=1:K
(4) ak(n)=Dk(Xk(n)+r(n))
(5) Xk(n)=Dk-1Tλ(ak(n))
(6) 应用阈值模型减小λ
(7) end
(8) end
(9)
其中:D-1表示字典D对应的逆变换;Tλ为阈值函数,本文选用指数阈值函数[22],其公式为
| $ T\left( {{\mathit{\pmb{X}}}, \lambda } \right) = {\mathit{\pmb{X}}}\cdot{\rm{exp}}\left[ { - {{\left( {\frac{\lambda }{{\left| {\mathit{\pmb{X}}} \right|}}} \right)}^{2 - p}}} \right] $ | (5) |
式中p∈[0, 1],本文中取0。
1.4 阈值模型算法求解过程中,需不断地对拉格朗日乘子λ进行调整,从而获得最优解。其步骤为:首先选取一个较大的变换域系数作为阈值,以此获取稀疏近似解;然后不断地减小λ取值以纳入更多的变换域系数,持续迭代以逼近最优解。阈值选取的策略称为阈值模型,它对算法求解的速度和精度都有一定影响。常见阈值模型包括线性模型、指数模型和数据驱动模型等。本文采用指数模型,其表达式为
| $ {\lambda _n} = {\lambda _{_{{\rm{max}}}}}{\delta ^{\frac{{n - 1}}{{N - 1}}}}\;\;\;\;\;\;\;n = 1, 2, \ldots , N $ | (6) |
式中:最大阈值λmax=pmax|D-1Y|∞; n为迭代次数; pmax和δ为选定的参数,本文中取pmax=0.95,δ=0.01。
1.5 稀疏字典的选取稀疏字典的选取是MCA方法的核心问题,不同的字典对稀疏表示的效果影响很大。周亚同等[17]已对Curvelet字典的不同组合方案进行了实验,最终认定离散余弦变换(DCT)与Curvelet字典组合具有最高重建精度。Curvelet具有刻画多尺度、多方向各向异性的能力,能够很好地表达地震信号中的曲线状边缘特征;但与Shearlet变换相比,其稀疏表示能力相对弱一些。Shearlet字典是目前提供对图像的最优稀疏表示的多尺度变换。与此同时,Shearlet变换的数学结构较简单,它通过对一个函数进行伸缩、平移、旋转来生成基函数,该特点与小波类似,却正是Curvelet变换所欠缺的,所以Shearlet字典非常适用于图像恢复重建。
本文尝试选取了Shearlet字典与其他稀疏字典的不同组合方案,包括:Shearlet字典与DCT字典、Shearlet字典与Curvelet字典、Shearlet单一字典,并将重建结果与Curvelet+DCT字典组合方案进行定量对比分析,最终认定Shearlet字典与DCT字典组合具有最高重建精度。
1.5.1 DCT字典DCT变换是一种在信号和图像处理中常用的数学变换,它具有一个很重要的特性——能量集中,即经DCT变换后信号能量非常集中,且大多数系数都集中在低频部分。
对M×N的二维信号f(i,j),其二维DCT变换为
| $ \begin{array}{l} F\left( {u, v} \right) = c\left( u \right)c\left( v \right)\sum\limits_{i = 0}^{M - 1} {\sum\limits_{j = 0}^{N - 1} {f\left( {i, j} \right) \times } } \\ \;\;\;\;\;\;\;\;\;\;{\rm{cos}}\left[ {\frac{{\left( {i + 0.5} \right){\rm{ \mathsf{ π} }}}}{M}u} \right]{\rm{cos}}\left[ {\frac{{\left( {j + 0.5} \right){\rm{ \mathsf{ π} }}}}{N}v} \right] \end{array} $ | (7) |
式中:F(u, v)为DCT系数;c(u)和c(v)为补偿系数,定义为
| $ c\left( u \right) = \left\{ \begin{array}{l} \sqrt {\frac{1}{M}} \;\;\;\;\;\;u = 0\\ \sqrt {\frac{2}{M}} \;\;\;\;\;\;u \ne 0 \end{array} \right. $ | (8) |
| $ c\left( v \right) = \left\{ \begin{array}{l} \sqrt {\frac{1}{N}} \;\;\;\;\;\;v = 0\\ \sqrt {\frac{2}{N}} \;\;\;\;\;\;v \ne 0 \end{array} \right. $ | (9) |
对应的反变换为
| $ \begin{array}{l} f\left( {x, y} \right) = \sum\limits_{i = 0}^{M - 1} {\sum\limits_{j = 0}^{N - 1} {c\left( u \right)c\left( v \right)F\left( {u, v} \right) \times } } \\ \;\;\;\;\;\;\;\;\;\;{\rm{ cos}}\left[ {\frac{{\left( {i + 0.5} \right){\rm{ \mathsf{ π} }}}}{M}u} \right]{\rm{cos}}\left[ {\frac{{\left( {j + 0.5} \right){\rm{ \mathsf{ π} }}}}{N}v} \right] \end{array} $ | (10) |
通过DCT变换可获得DCT字典。据DCT字典本身特性,常用于表征地震信号的局部奇异部分。
1.5.2 Shearlet字典Shearlet变换是基于具有合成膨胀的仿射系统构建的新型多尺度几何变换,用于对图像等高维数据进行更为稀疏的表示。相比于Curvelet变换,Shearlet变换具有更简单的数学结构及更突出的稀疏表示能力[18]。
在二维情况下,Shearlet函数系统ψa, s, t(x)有如下定义:
(1)
其中:a、s、t分别表示尺度参数、剪切参数和平移参数;
(2)
| $ \hat \psi \left( {\mathit{\pmb{\xi}}} \right) = {\hat \psi _1}\left( {{\xi _1}} \right){\hat \psi _2}\left( {\frac{{{\xi _2}}}{{{\xi _1}}}} \right) $ |
其中
(3)
| $ {{\hat \psi }_1} \in {{\mathit{\pmb{C}}}^\infty }\left( {\mathit{\pmb{R}}} \right)\;\;\;\;\;{\rm{supp}}{{\hat \psi }_1} \subset \left[ { - 2, - \frac{1}{2}} \right] \cup \left[ {\frac{1}{2}, 2} \right] $ |
(4)
在满足上述定义的前提下,对函数f(x)的连续Shearlet正变换可表示为
| $ {\rm{S}}{{\rm{H}}_f}\left( {a, s, t} \right) = \left\langle {f, {\psi _{a, s, t}}} \right\rangle $ | (11) |
其中〈·〉表示内积。
通过对Shearlet函数ψa, s, t中三个参数的调整,也即对函数进行伸缩、旋转、平移,可生成Shearlet字典,它具有很好的方向性和各向异性,可用于表示地震信号中的平滑和线性部分。
2 数值实验 2.1 评价参数为了对重建结果进行定量描述,本文引入两个评价参数,其定义如下:
(1) 信噪比
| $ {R_{S/N}} = 10{\rm{lg}}\frac{{\left\| {\mathit{\pmb{X}}} \right\|_2^2}}{{\left\| {\hat {\mathit{\pmb{X}}} - {\mathit{\pmb{X}}}} \right\|_2^2}} $ | (12) |
(2) 峰值信噪比
| $ R_{{\rm{S/N}}}^{\rm{P}} = 10{\rm{lg}}\frac{{{\rm{ma}}{{\rm{x}}^2}\left( {\mathit{\pmb{X}}} \right)}}{{{E_{{\rm{MSE}}}}}} $ | (13) |
式中EMSE表示均方差,计算公式为
| $ {E_{{\rm{MSE}}}} = \frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\left\| {{\mathit{\pmb{X}}}\left( {i, j} \right) - \hat {\mathit{\pmb{X}}}\left( {i, j} \right)} \right\|} } _2^2 $ | (14) |
测量矩阵与稀疏字典的不相干性,也即地震数据重建中的随机采样是一个十分重要的条件。因此,选取随机采样中的Jitter采样方式生成的缺失地震数据进行重建实验。为了验证重建效果,首先针对合成地震记录进行实验。图 1a为含有512道、每道包含512个采样点的原始合成地震记录,时间采样率为2ms;图 1b为通过Jitter采样形成的缺失程度为50%的采样矩阵;图 1c为利用采样矩阵生成的缺失地震记录(RS/N=3.0103dB,RS/NP=9.5186dB)。

|
图 1 合成地震记录 (a)原始记录;(b)缺失50%的采样矩阵;(c)缺失地震记录 |
实验所用稀疏字典通过Shearlet变换生成,采用FPOCS算法求解。利用Jitter采样形成的欠完整地震数据的缺失程度分别为10%、30%、50%、70%和90%。
图 2为上述各缺失地震数据重建结果及(原始数据与重建结果之间的)差值剖面对比图。可见随着缺失程度的增加,重建结果的精度逐渐下降。当缺失程度超过70%时,重建结果中同相轴的连续性变得更差,重建剖面的能量逐渐减少,已不能得到良好恢复结果。
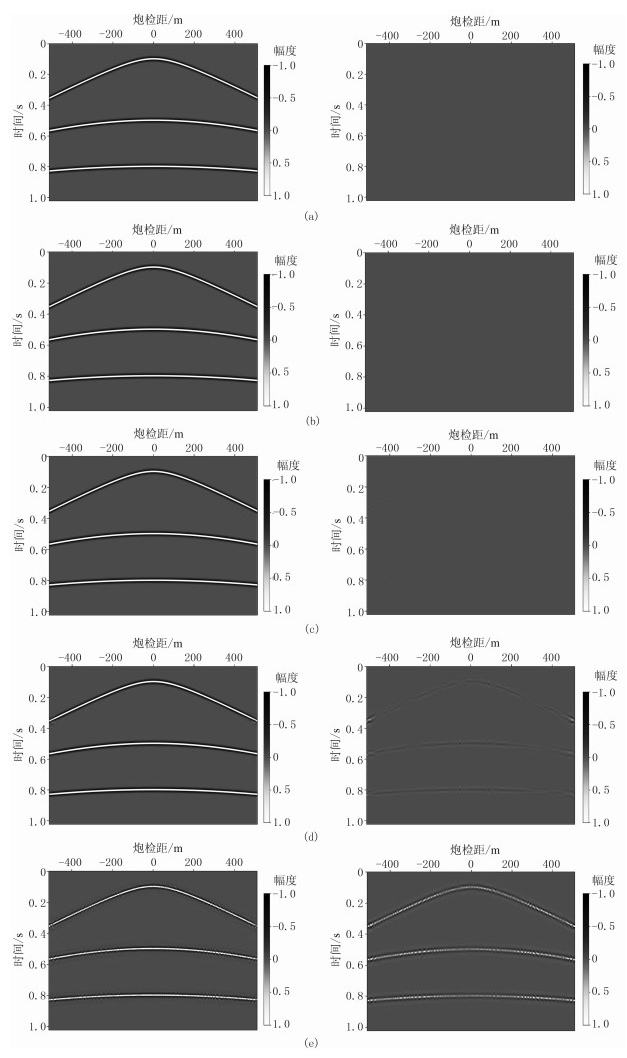
|
图 2 Jitter采样生成的不同缺失程度数据的Shearlet变换重建结果(左)及其差值剖面(右)对比 (a)缺失10%;(b)缺失30%;(c)缺失50%;(d)缺失70%;(e)缺失90% |
分别采用Curvelet+DCT字典组合、单独Shearlet字典、Shearlet+Curvelet字典组合、Shearlet +DCT字典组合对缺失50%的数据进行重建,重建结果及差值剖面如图 3所示。
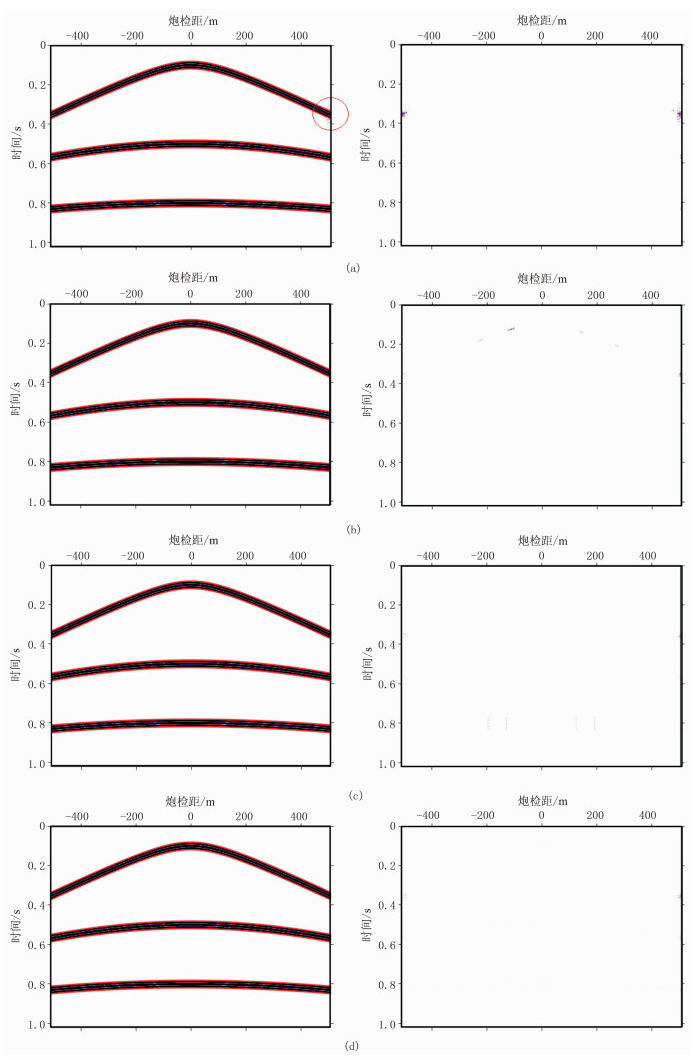
|
图 3 四种字典组合方式重建结果(左)及差值剖面(右) (a)Curvelet+DCT字典组合;(b)单独Shearlet字典;(c)Shearlet+Curvelet字典组合;(d)Shearlet+DCT字典组合 |
从图 3可见,Curvelet+DCT字典组合在重建结果中引入了少量噪声,而其他三种字典(组合)方式所得结果均未引入噪声;四种字典组合差值剖面上残留能量均较少,其中Shearlet+DCT字典组合方式最少,这充分表明了MCA方法的有效性。
从表 1的评价参数对比可知,相对于Curvelet+DCT字典组合,其他三种字典组合重建结果在RS/N和RS/NP上均有大幅度提升,这缘于Shearlet变换在方向性、稀疏性上均优于Curvelet变换。
|
|
表 1 四种字典组合重建结果评价参数 |
不同的拉格朗日乘子数值对恢复重建的效果不同。从图 4中可看出选取拉格朗日乘子为0.95时,高于0.90时重建后的信噪比。同样,当迭代次数增加时,重建后信噪比也会有所提高;但并不是迭代次数越多越好,迭代次数的增加也意味着重建时间的加长。在本次测试处理中,当迭代次数达到150时,就能取得很好重建效果。
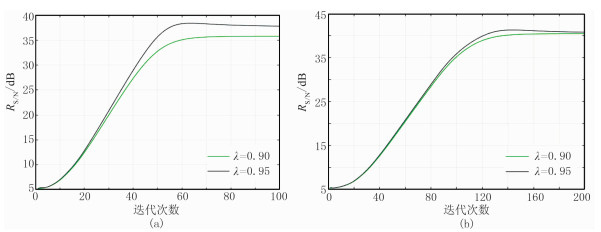
|
图 4 拉格朗日乘子及迭代次数与重建信号信噪比 (a)迭代次数为100; (b)迭代次数为200 |
与此同时,对Shearlet字典分块的选取也做了相应的对比试算。分别测试了分块为1、2、4、8时的情形:当分块为1时,恢复重建耗时为16s;分块为2时需38s;分块为4和8时,重建耗时分别为104s和3014s。可见Shearlet字典分块数越大则耗时越长,但重建效果就越好。在实际处理中需在满足重建精度情况下,选择适宜的字典分块数目。通过本文试算对比,建议选取的字典分块数目为4。
2.3 实际数据实验进一步针对实际地震数据进行测试以验证重建效果。图 5a为原始陆上地震记录,共有430道,每道包含512个采样点,空间采样间隔为12.5m;图 5b是通过Jitter采样生成的缺失程度为50%的采样矩阵;图 5c为应用采样矩阵之后生成的缺失地震记录(RS/N=2.9772dB,RS/NP=12.3500dB)。
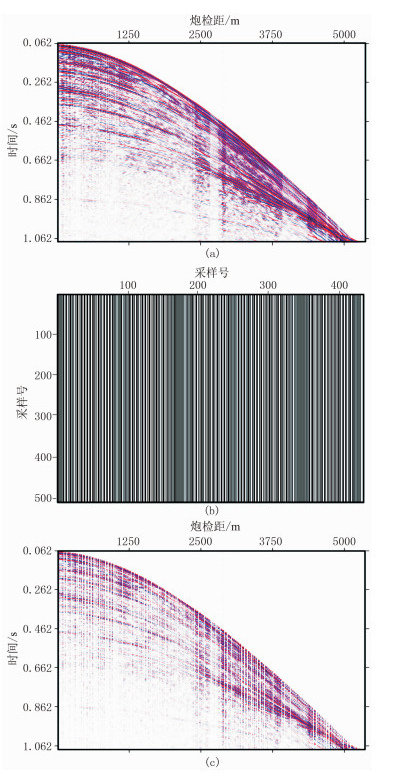
|
图 5 实际地震记录 (a)完整合成记录;(b)缺失50%的采样矩阵;(c)缺失地震记录 |
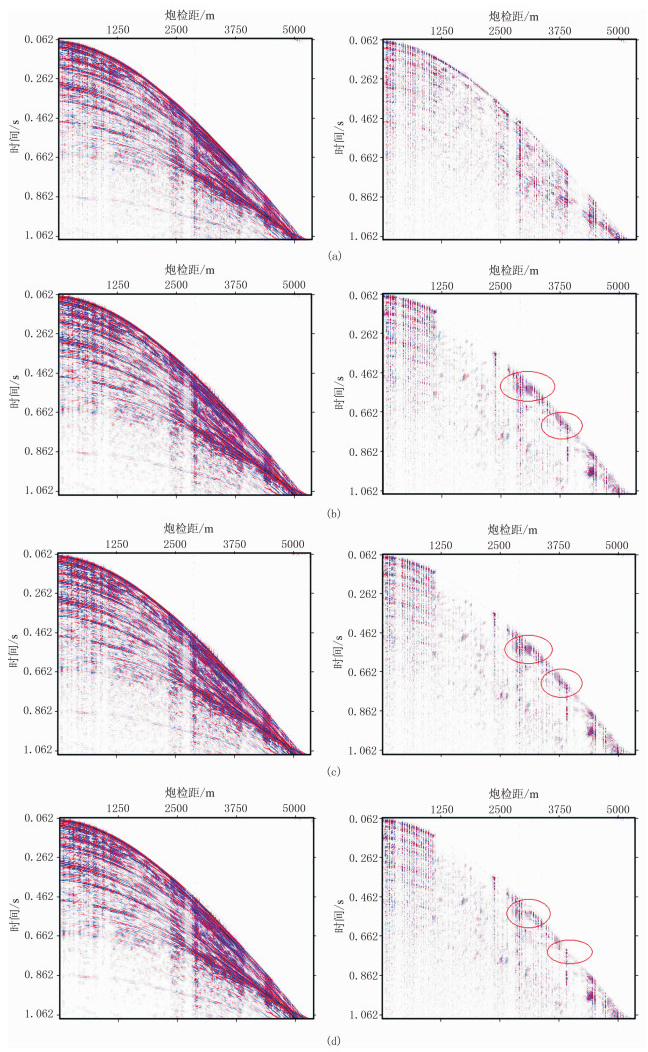
依然选用四种字典组合方式分别进行地震数据重建,重建结果及差值剖面如图 6所示,对应的评价参数如表 2所示。
|
图 6 四种字典组合重建结果(左)及差值剖面(右) (a)Curvelet+DCT字典组合;(b)Shearlet字典;(c)Shearlet+Curvelet字典组合;(d)Shearlet+DCT字典组合 |
|
|
表 2 四种字典组合重建结果评价参数 |
从图 6可见,相比于Curvelet+DCT字典组合,其他三种字典组合差值剖面上的残留能量均有所减少,其中Shearlet+DCT字典组合残留能量最少。从表 2中的评价参数对比可知,相比于Curvelet+DCT字典组合,其他三种字典组合重建结果在RS/N和RS/NP上均有提升,其中Shearlet+DCT字典组合的评价参数最优。
3 结论在MCA框架下,本文提出一种基于Shearlet+ DCT字典组合的地震数据重建方法:首先分别选取DCT字典和Shearlet字典稀疏表示地震数据中的局部奇异部分和平滑线状部分;再通过加入指数阈值模型和指数阈值函数的块坐标松弛算法重建各个分量;最后合并各个分量得到最终重建结果。合成地震数据和真实地震数据的对比分析表明,Shearlet字典与DCT字典组合的重建精度高于单一Shearlet字典、Shearlet+Curvelet字典、Curvelet+DCT字典组合,证明了Shearlet变换比Curvelet变换具有更强的稀疏表达能力;同时也验证了方法的有效性和优越性。
重建算法效率的提升以及学习型字典的加入将是下一步研究方向。
| [1] |
Candès E J, Romberg J, Tao T. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [2] |
Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [3] |
温睿, 刘国昌, 冉扬. 压缩感知地震数据重建中的三个关键因素分析[J]. 石油地球物理勘探, 2018, 53(4): 682-693. WEN Rui, LIU Guochang and RAN Yang, RAN Yang. Three key factors in seismic data reconstruction based on compressive sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 682-693. |
| [4] |
Zwartjes P, Gisolf A. Fourier reconstruction with sparse inversion[J]. Geophysical Prospecting, 2007, 5(2): 199-221. |
| [5] |
Herrmann F J, Hennenfent G. Non-parametric seismic data recovery with curvelet frames[J]. Geophysical Journal International, 2008, 173(1): 233-248. DOI:10.1111/j.1365-246X.2007.03698.x |
| [6] |
Hennenfent G, Herrmann F J. Simply denoise:Wave-field reconstruction via jittered under sampling[J]. Geophysics, 2008, 73(3): V19-V28. DOI:10.1190/1.2841038 |
| [7] |
陈祖斌, 王丽芝, 宋扬, 等. 基于压缩感知的小波域地震数据实时压缩与高精度重建[J]. 石油地球物理勘探, 2018, 53(4): 674-681, 693. CHEN Zubin, WANG Lizhi, SONG Yang, et al. Seismic data real-time compression and high-precision reconstruction in the wavelet domain based on the compressed sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 674-681, 693. |
| [8] |
Wu R S, Geng Y, Ye L.Preliminary study on Dreamlet based compressive sensing data recovery[C].SEG Technical Program Expanded Abstracts, 2013, 32: 3585-3590.
|
| [9] |
Guo K, Kutyniok G, Labate D.Sparse multidimensional representations using anisotropic dilation and shear operators[C]. International Conference on the Interaction Between Wavelets and Splines, 2005.
|
| [10] |
Labate D, Lim W Q, Kutyniok G, et al. Sparse multidimensional representation using shearlets[J]. Optics & Photonics, 2005, 5914: 254-262. |
| [11] |
张良, 韩立国, 刘争光, 等. 基于压缩感知和Contourlet变换的地震数据重建方法[J]. 石油物探, 2017, 56(6): 804-811. ZHANG Liang, HAN Liguo, LIU Zhengguang, et al. Seismic data reconstruction based on compressed sensing and Contourlet transform[J]. Geophysical Prospecting for Petroleum, 2017, 56(6): 804-811. DOI:10.3969/j.issn.1000-1441.2017.06.005 |
| [12] |
王新全, 耿瑜, Wu Ru-Shan, 等. 基于压缩感知的Drea-mlet域数据重构方法及应用[J]. 石油地球物理勘探, 2015, 53(3): 399-404. WANG Xinquan, GENG Yu, WU Ru-Shan, et al. Seismic data reconstruction in Dreamlet domain based on compressive sensing[J]. Oil Geophysical Prospecting, 2015, 53(3): 399-404. |
| [13] |
郭念民, 李海山, 冯雪梅, 等. 非抽样离散小波叠前地震数据重建方法[J]. 石油地球物理勘探, 2014, 49(3): 508-516. GUO Nianmin, LI Haishan, FENG Xuemei, et al. Pre-stack seismic data reconstruction based on the undecimated wavelet transform[J]. Oil Geophysical Prospecting, 2014, 49(3): 508-516. |
| [14] |
Liang J W, Ma J W, Zhang X Q. Seismic data restoration via data-driven tightframe[J]. Geophysics, 2014, 79(3): V65-V74. DOI:10.1190/geo2013-0252.1 |
| [15] |
Starck J L, Elad M, Donoho D L. Redundant multiscale transforms and their application for morphological component separation[J]. Advances in Imaging & Electron Physics, 2004, 132(4): 287-348. |
| [16] |
李海山, 吴国忱, 印兴耀. 形态分量分析在地震数据重建中的应用[J]. 石油地球物理勘探, 2012, 47(2): 236-243. LI Haishan, WU Guochen, YIN Xingyao. Morphological component analysis in seismic data reconstruction[J]. Oil Geophysical Prospecting, 2012, 47(2): 236-243. |
| [17] |
周亚同, 刘志峰, 张志伟. 形态分量分析框架下基于DCT与曲波字典组合的地震信号重建[J]. 石油物探, 2015, 54(5): 560-568. ZHOU Yatong, LIU Zhifeng, ZHANG Zhiwei. Seismic signal reconstruction under the morphological component analysis framework combined with discrete cosine transform (DCT) and curvelet dictionary[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 560-568. DOI:10.3969/j.issn.1000-1441.2015.05.009 |
| [18] |
刘成明, 王德利, 王通, 等. 基于Shearlet变换的地震随机噪声压制[J]. 石油学报, 2014, 35(4): 692-699. LIU Chengming, WANG Deli, WANG Tong, et al. Random seismic noise attenuation based on the Shearlet transform[J]. Acta Petrolei Sinica, 2014, 35(4): 692-699. |
| [19] |
张良, 韩立国, 许德鑫, 等. 基于压缩感知技术的Shearlet变换重建地震数据[J]. 石油地球物理勘探, 2017, 52(2): 220-225. ZHANG Liang, HAN Liguo, XU Dexin, et al. Seismic data reconstruction with Shearlet transform based on compressed sensing technology[J]. Oil Geophysical Prospecting, 2017, 52(2): 220-225. |
| [20] |
舒国旭, 吕公河, 吕尧, 等. 基于压缩感知的地震数据重建[J]. 石油物探, 2018, 57(4): 549-554. SHU Guoxu, LYU Gonghe, LYU Yao, et al. Seismic data reconstruction based on compressive sensing[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 549-554. DOI:10.3969/j.issn.1000-1441.2018.04.008 |
| [21] |
Sardy S, Bruce A G, Tseng P. Block coordinate relaxation methods for nonparametric wavelet denoising[J]. Journal of Computational and Graphical Statistics, 2000, 9(2): 361-379. |
| [22] |
Yang P, Fomel S. Seislet-based morphological component analysis using scale-dependent exponential shrinkage[J]. Journal of Applied Geophysics, 2015, 118: 66-74. DOI:10.1016/j.jappgeo.2015.04.003 |



 张凯, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
张凯, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: