② 中国地质大学(武汉)数学与物理学院, 湖北武汉 430074
② School of Mathematics and Physic, China University of Geosciences(Wuhan), Wuhan 430074, China
在应用科学和工程领域,观测的数据集往往是高维的,提取高维数据的低秩结构尤为重要[1]。主成分分析(Principal Component Analysis, PCA)作为一种经典的低秩矩阵逼近方法被广泛应用。对于被独立同分布的高斯噪声污染的观测数据,经典PCA往往能够给出低秩矩阵逼近问题的最优解,然而对于被高度污染的数据(如有色噪声)却难以准确估计[2]。
为了解决数据被高度污染的低秩矩阵逼近问题,Candes等[3-5]提出鲁棒主成分分析(Robust Principal Component Analysis, RPCA)。该方法在经典PCA的基础上,将原来求解噪声矩阵Frobenius范数极小化的数学模型,拓展到求解低秩成分矩阵的秩和噪声矩阵的L0范数极小化的数学模型。基于合理的数学模型,RPCA迅速成为图像处理和数据挖掘领域的研究热点。针对RPCA数学模型的优化问题,许多学者进行了研究。史加荣等[6]采用迭代阈值算法(Iterative thresholding, IT)求解其提出的数学模型。该算法具有迭代形式简单且收敛的优点,但是由于收敛速度慢及难以选取步长,所以应用范围有限。Lin等[2]采用加速近端梯度算法(Accelerated proximal gradient, APG)求解RPCA的数学模型。与IT算法相比,APG算法迭代次数大大降低。Lin等[2]提出精确拉格朗日乘子(Exact augmented Lagrange multipliers, EALM)法和不精确拉格朗日乘子(Inexact augmented Lagrange multipliers, IALM)法。实践证明,EALM和IALM法具有更高的计算效率和精度[6],因而逐渐成为求解RPCA数学模型的主流算法。本文采用EALM求解RPCA数学模型。
重磁场是由具有不同密度和磁性的地质体的共同响应,即不同尺度、不同幅值异常的叠加。如何从混叠重磁场中分离出目标地质体引起的异常,是重磁数据处理的重点之一。
位场的识别与分离方法包括解析延拓、滑动平均、趋势分析、匹配滤波、插值切割以及近年发展起来的小波分析、最小曲率等[7-8]。Spector等[9]推导了航磁异常的能谱公式,提出利用能谱分析粗略估计块状体埋深的方法,并在1975年提出匹配滤波法分离重磁场;程方道等[10]提出插值切割法分离磁异常;Mickus等[11]首次将最小曲率法应用于美国某地区的布格重力异常分离;王万银等[12-13]研究了位场数据最小曲率扩边和补空方法;随着小波分析法的提出,Fedu等[14]、侯遵泽等[15]和杨文采等[16]提出一种基于离散小波变换的重磁位场分离方法。
现有的位场分离方法往往会出现参数难选择、分离效果差、虚假异常等情况,这不仅会造成主观上地质认识的错误,还给后续反演解释带来偏差。因此,精度高、自适应性强、应用简单的位场分离方法是最佳选择。朱丹等[17]提出基于奇异谱分析的位场分离方法,该方法先将位场数据表示成Hankel矩阵(原始数据是一维的情况)或块Hankel矩阵(原始数据是二维的情况),然后利用PCA或EOF(经验正交函数分解,empirical orthogonal functions)实现数据降维,从而达到区域场与局部场分离的目的。
本文RPCA是信号处理领域的一种新方法。利用RPCA实现Hankel矩阵或块Hankel矩阵的降维,RPCA可有效处理低秩矩阵逼近问题,其特点是参数设置简单、结果稳健。本文主要研究RPCA在位场分离中的应用,介绍经典PCA和RPCA的数学模型,并从位场的低秩性和稀疏性的角度分析位场分离问题;利用EALM算法求解RPCA数学模型,并提出针对一维信号的RPCA处理方法;通过理论模型展示分离效果及参数的选取方式,并将本文方法应用于实际数据处理。
1 PCA和RPCA的数学模型及EALM求解方法假设有一高维的数据嵌套在低维线性子空间中,那么PCA和RPCA的目标就是高效且准确地提取这个低维子空间。
1.1 数学模型假定已知一混叠低秩和高秩成分的观测矩阵D∈Rm×n,为了提取D的低秩成分,将D分解成矩阵A和E,这里A是低秩矩阵,E是服从独立同高斯分布的矩阵。那么通过PCA估计A和E可归结为求解最优化问题
| $ \mathop {\min }\limits_{\mathit{\boldsymbol{A}},\mathit{\boldsymbol{E}}} {\left\| \mathit{\boldsymbol{E}} \right\|_{\rm{F}}}\;\;\;\;\;\;{\rm{rank}}\left( \mathit{\boldsymbol{A}} \right) \le r,\mathit{\boldsymbol{D}} = \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{E}} $ | (1) |
式中‖·‖是Frobenius范数,其定义为
| $ {\left\| \cdot \right\|_{\rm{F}}} = \sqrt {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {a_{i,j}^2} } } $ | (2) |
可利用奇异值分解D=UΣVT计算上述数学模型,确定r个主奇异值以及对应的左奇异向量。这r个主奇异值反映了信号的主要特征,并通过这r个主奇异值和奇异向量可以恢复出低秩矩阵A。
然而,若E是非独立同高斯分布矩阵,PCA方法不再适用。此时,将原数学模型修改为双目标极小的数学模型
| $ \mathop {\min }\limits_{\mathit{\boldsymbol{A}},\mathit{\boldsymbol{E}}} \left[ {{\mathop{\rm rank}\nolimits} (\mathit{\boldsymbol{A}}),{{\left\| \mathit{\boldsymbol{E}} \right\|}_0}} \right]\quad \mathit{\boldsymbol{D}} = \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{E}} $ | (3) |
式中‖E‖0是0范数,表示E中非零元素的个数。
从式(3)可以看出,与PCA只考虑‖E‖F极小不同,RPCA的数学模型要求E尽量稀疏、同时又保证了A的低秩性。
对于式(3)的双目标极小问题,可以引入惩罚函数进行求解
| $ \mathop {\min }\limits_{\mathit{\boldsymbol{A}},\mathit{\boldsymbol{E}}} \left[ {{\mathop{\rm rank}\nolimits} \left( \mathit{\boldsymbol{A}} \right) + \lambda {{\left\| \mathit{\boldsymbol{E}} \right\|}_0}} \right]\quad \mathit{\boldsymbol{D}} = \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{E}} $ | (4) |
式中λ是权系数。
由于上述数学模型是一个非凸的优化问题,为便于求解,需要将模型中的目标函数进行松弛处理[6]
| $ \mathop {\min }\limits_{\mathit{\boldsymbol{A}},\mathit{\boldsymbol{E}}} \left[ {{{\left\| \mathit{\boldsymbol{A}} \right\|}_ * } + \lambda {{\left\| \mathit{\boldsymbol{E}} \right\|}_{1,1}}} \right]\quad \mathit{\boldsymbol{D}} = \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{E}} $ | (5) |
式中‖·‖1, 1和‖·‖*分别表示(1, 1)范数和核范数,分别定义为
| $ \|\boldsymbol{E}\|_{1,1}=\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n}\left|a_{i, j}\right| $ | (6) |
| $ \begin{array}{l} {\left\| \mathit{\boldsymbol{A}} \right\|_*} = \max \left[ {{\mathop{\rm trace}\nolimits} \left( {{\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{AV}}} \right):} \right.\\ \;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{U}} = {\mathit{\boldsymbol{I}}_m},{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{I}}_n}} \right] \end{array} $ | (7) |
式中trace(·)表示求矩阵的迹。
1.2 EALM算法在介绍EALM算法之前,先引入两类优化问题及其最优解[2]。
令Q=(q1, q2, …, qn)为m×n维实矩阵,则优化问题
| $ \mathop {\min }\limits_\mathit{\boldsymbol{P}} \left( {\varepsilon {{\left\| \mathit{\boldsymbol{P}} \right\|}_{1,1}} + \frac{{\left\| {\mathit{\boldsymbol{P}} - \mathit{\boldsymbol{Q}}} \right\|_{\rm{F}}^2}}{2}} \right) $ | (8) |
的最优解为P*=Sε(Q), Sε(Q)是关于参数ε、Q的函数,表示Q的第(i, j)元素经max(|qi, j|-ε, 0)×sgn(qi, j)变换得到新的矩阵P*的第(i,j)元素,其中参数ε>0,且Sε(Q)=εS1(Q/ε)。
对于优化问题
| $ \mathop {\min }\limits_\mathit{\boldsymbol{P}} \left( {\varepsilon {{\left\| \mathit{\boldsymbol{P}} \right\|}_ * } + \frac{{\left\| {\mathit{\boldsymbol{P}} - \mathit{\boldsymbol{Q}}} \right\|_{\rm{F}}^2}}{2}} \right) $ | (9) |
有闭形式解P*=Dε(Q),其中Dε(Q)=USε(Σ)VT,UΣVT是矩阵Q的奇异值分解,并且Dε(Q)=εD1(Q/ε)。
下面使用EALM求解式(5)。构造增广拉格朗日函数
| $ \begin{array}{l} L\left( {\mathit{\boldsymbol{A}},\mathit{\boldsymbol{E}},\mathit{\boldsymbol{Y}},\mu } \right) = {\left\| \mathit{\boldsymbol{A}} \right\|_ * } + \lambda {\left\| \mathit{\boldsymbol{E}} \right\|_{1,1}} + \\ \;\;\;\;\;\;\left\langle {\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{A}} - \mathit{\boldsymbol{E}}} \right\rangle + \frac{\mu }{2}\left\| {\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{A}} - \mathit{\boldsymbol{E}}} \right\|_{\rm{F}}^2 \end{array} $ | (10) |
交替迭代A、E和μ,直到满足收敛条件或达到最大迭代次数为止,其计算流程如下。
(1) 输入观测矩阵D∈Rm×n和权系数λ。
(2) 计算Y0*=sgn(D)/J[sgn(D)],其中J(·)=max(‖·‖2, λ-1‖·‖∞),并令μ0>0, ρ>1,k=0。sgn(D)表示对矩阵D的每个元素求符号函数,其结果仍为一矩阵;‖·‖∞表示无穷范数。
(3) 解优化问题
(4) 数据初始化Ak+10=Ak*, Ek+10=Ek*, j=0。
(5) 解优化问题
| $ \boldsymbol{A}_{k+1}^{(j+1)}=\boldsymbol{D}_{\mu_{k}^{-1}}\left(\boldsymbol{D}-\boldsymbol{E}_{k+1}^{(j)}+\mu_{k}^{-1} \boldsymbol{Y}_{k}^{*}\right) $ |
(6) 解优化问题
| $ \mathit{\boldsymbol{E}}_{k + 1}^{(j + 1)} = {S_{\lambda \mu _k^{ - 1}}}\left( {\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{A}}_{k + 1}^{(j + 1)} + \mu _k^{ - 1}\mathit{\boldsymbol{Y}}_k^*} \right) $ |
(7) 若Ak+1(j+1)、Ek+1(j+1)不收敛,则j=j+1,并返回步骤(5);若满足收敛条件,则
| $ \boldsymbol{A}_{k}^{*}=\boldsymbol{A}_{k+1}^{(j+1)} $ |
| $ \boldsymbol{E}_{k}^{*}=\boldsymbol{E}_{k+1}^{(j+1)} $ |
(8) 计算Yk+1*=Yk*+μk(D-Ak+1*-Ek+1*),μk+1=ρμk。
(9) 若Ak+1*、Ek+1*和Yk+1*不收敛,则k=k+1,并返回步骤(3);若满足收敛条件,则Ak+1*和Ek+1*为式(10)的最优解。
参数ρ和μ0一般只决定算法的收敛速度,不影响Ak+1*和Ek+1*,本文所有实验和应用取ρ=6,μ0=0.5/‖D‖2。
1.3 位场数据的延滞矩阵构建秩的概念是针对矩阵而言的,对于重磁勘探一维观测数据,把它表示成空间延滞矩阵,即对一维数据Hankel矩阵化,对于二维观测数据,则构建块Hankel矩阵。对数据进行重排列的原因是延滞矩阵具有低秩结构[18]。
假设一维数据向量x=[x1, x2, …, xn]T,其中n是点数,以窗口M将x排列成延滞矩阵X
| $ \overline{\boldsymbol{X}}=\left[\begin{array}{cccc}{x_{1}} & {x_{2}} & {\cdots} & {x_{n-M+1}} \\ {x_{2}} & {x_{3}} & {\cdots} & {x_{n-M+2}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {x_{M}} & {x_{M+1}} & {\cdots} & {x_{n}}\end{array}\right] $ | (11) |
若有二维矩阵X=[xi, j]∈Rp×q,其中xi, j表示矩阵X的第i行第j列的元素。利用X的第l列构建Hankel矩阵
| $ \boldsymbol{H}_{l}=\left[\begin{array}{cccc}{x_{1, l}} & {x_{2, l}} & {x_{3, l}} & {\cdots} \\ {x_{2, l}} & {x_{3, l}} & {x_{4, l}} & {\cdots} \\ {x_{3, l}} & {x_{4, l}} & {x_{5, l}} & {\cdots} \\ {\vdots} & {\vdots} & {\vdots}\end{array}\right] $ | (12) |
其中,需要合适的M使Hl为一方阵(p是奇数时,M=(p+1)/2)或逼近方阵(p是偶数时,M=p/2)。利用Hl构建延滞矩阵X
| $ \overline{\boldsymbol{X}}=\left[\begin{array}{cccc}{\boldsymbol{H}_{1}} & {\boldsymbol{H}_{2}} & {\boldsymbol{H}_{3}} & {\cdots} \\ {\boldsymbol{H}_{2}} & {\boldsymbol{H}_{3}} & {\boldsymbol{H}_{4}} & {\cdots} \\ {\boldsymbol{H}_{3}} & {\boldsymbol{H}_{4}} & {\boldsymbol{H}_{5}} & {\cdots} \\ {\vdots} & {\vdots} & {\vdots}\end{array}\right] $ | (13) |
这里X即块Hankel矩阵。
1.4 实现步骤RPCA的位场分离方法包括下列3个步骤。
(1) 原始数据的重新排列。若数据是一维的,利用式(11)构建延滞矩阵X;若数据是二维,利用式(12)和式(13)构建延滞矩阵X。
(2) 利用RPCA实现矩阵降秩。选取合适的权参数构建双目标优化模型,并利用EALM算法求解低秩矩阵A和稀疏矩阵E。
(3) 数据重构。步骤(2)中得到的低秩矩阵A和稀疏矩阵E是近似Hankel矩阵或近似块Hankel矩阵的结构,因此需要将其恢复成严格的Hankel矩阵或块Hankel矩阵。对于一维数据,采用逆对角线平均的方法;对于二维数据,先求式(13)的逆对角线上的Hankel矩阵的平均,再求各Hankel矩阵的逆对角线平均。最后,将Hankel矩阵或块Hankel矩阵恢复成数据向量或矩阵。
2 区域场的低秩性与局部场的稀疏性矩阵秩定义为该矩阵中线性无关的行数或列数。考虑矩阵A∈Rm×m是一个方阵,其秩是矩阵A的非零特征值的个数。当A不是方阵时,即矩阵A∈Rm×n,其中m≠n,其奇异值分解A=UΣVT,且Σ=diag(σ1, σ2, …, σr, 0, …, 0),其中σi是奇异值,那么矩阵A的秩是非零奇异值的个数。若rank(A)≪min(m, n),那么称矩阵A是低秩的。
稀疏性描述的是矩阵中非零元素的个数,大多数元素为零的向量或者矩阵称为稀疏向量或稀疏矩阵[1]。考虑矩阵E∈Rm×n,若‖E‖0≪mn, 那么称矩阵E是稀疏的。实际情况中,区域场具有低秩性,局部场具有稀疏性,即位场的分离问题符合RPCA的数学模型。
下面解释区域场的低秩特征。通常能够利用数据间的相关性说明矩阵秩的大小,因为矩阵不同列之间的相关性差异往往能够反映矩阵秩的差异。考虑一种极端的情况,当矩阵中每一列都是线性无关时,该矩阵为满秩矩阵,若其中某些列是线性相关时,经过初等变换,那么可以使其中部分列变换成零向量,这时该矩阵是低秩的。
区域场通常变化平缓,其相邻观测点之间具有较强的相关性。由此,区域场的延滞矩阵的相邻列之间的相关性更强,矩阵具有更低秩的特征。统计学上采用自相关系数描述这种自相关性
| $ r(\tau)=\frac{\operatorname{Expt}\left[\left(x_{t}-\overline{x}\right)\left(x_{t+\tau}-\overline{x}\right)\right]}{\sigma^{2}} $ | (14) |
式中:xt和xt+τ分别表示t、t+τ时刻的随机过程;x和σ分别是xt的期望和方差;Expt(·)为期望函数。r(τ)是值域在[-1, 1]的关于延迟τ的函数,其值越接近于1,表示xt与xt+τ的正相关性越强;其值越接近于-1,表示其负相关性越强;其值越接近于0,表示其相关性弱或无相关性。
通过理论模型对比进一步说明区域场的低秩性。将由浅部规模较小场源引起的小尺度异常视为局部场(图 1a),将由深部规模较大场源引起的大尺度异常视为区域场(图 1b)。对比区域场、局部场和高斯白噪声的自相关系数(图 2)可以看出,区域场自相关性强,局部场次之,噪声不具有自相关性。因此区域场通过滑动窗口构成的延滞矩阵不同列之间具有较强的相关性,局部场的延滞矩阵不同列之间具有较弱的相关性,而噪声的延滞矩阵不同列之间不具有相关性。因此,从图 3可以看出,区域场延滞矩阵比局部场延滞矩阵的非零奇异值少,噪声延滞矩阵的奇异值几乎全大于0。这说明区域场延滞矩阵的秩低于局部场,噪声延滞矩阵是满秩的。
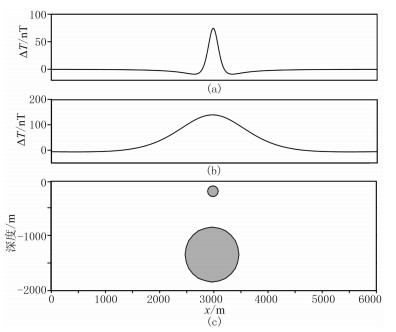
|
图 1 磁场模拟 (a)局部场;(b)区域场;(c)模型 |
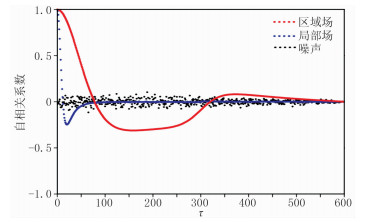
|
图 2 区域场、局部场和噪声的自相关系数 |
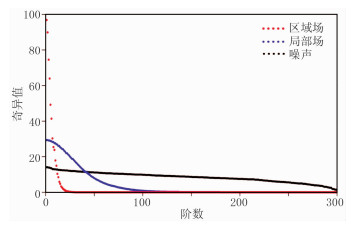
|
图 3 区域场、局部场和噪声的奇异值 |
与低秩性相比,稀疏性相对容易理解。实际应用中,向量或矩阵中的元素通常不会严格等于0,因此利用接近于0的元素或明显大于0的元素个数描述矩阵的稀疏性。深部规模大的场源引起的异常往往是大尺度的,一般会覆盖整条剖面或测区,因此异常值明显大于0的观测点个数较多,具有非稀疏性或较弱的稀疏性。对于浅部小规模场源,即使具有较大的磁化强度和剩余密度,随着观测点远离场源,它引起的异常会迅速衰减,因此仅很小的范围内位场数据数值的绝对值明显大于0。相比于区域场,局部场的稀疏性更强,并且两者稀疏性的差异通常是显著的。
3 RPCA数学模型的地球物理意义前面的分析说明尺度较大的异常具有低秩的结构,尺度较小的异常具有稀疏的结构,即区域场是低秩的,局部场是稀疏的。从区域场的逼近程度理解位场分离问题,在分离位场时往往会出现区域场的欠拟合和过拟合问题。欠拟合现象实质就是分离得到的区域场不够低秩而局部场过分稀疏;过拟合现象的实质是分离得到的区域场过于低秩导致局部场不够稀疏。利用传统位场分离方法(如匹配滤波或小波分析等)分离位场数据时,往往存在稳定性较差的问题,即参数选择的微小改变使分离结果变化显著。例如,估计对数功率谱低频线性段的斜率时,极小的估计误差就会带来深部场源似深度估计的巨大误差,这容易导致位场分离结果的欠拟合或过拟合。小波分析的应用难点在于选择哪一阶或哪几阶细节叠加构成局部场或区域场。然而,RPCA的数学模型要求E尽量稀疏的同时又保证了A的低秩性,这使系统具有更强的鲁棒性,即分离结果更稳定并且更容易避免欠拟合或过拟合现象。因为当分离的局部场过分稀疏(欠拟合)时,区域场低秩的结构被破坏并导致区域场的核范数增加;而当分离的区域场过分低秩(过拟合)时,局部场稀疏的结构被破坏并导致局部场的(1, 1)范数增加。因此,RPCA数学模型的地球物理意义在于:在保证分离区域场尽可能低秩的前提下局部场尽可能的稀疏,并且,当区域场的低秩性结构和局部场的稀疏性结构被破坏时,其对应的核范数和(1, 1)范数会快速增加。因此,采用RPCA分离位场很容易达成一种相对稳态,这种稳态体现在权系数变化时,分离结果几乎不变。处于这种稳态时的分离效果最佳。
4 权系数的选择式(3)是RPCA的数学模型,一个双目标函数极小的优化问题。由于这个问题难以求解,故将‖E‖0作为惩罚项代入rank(A)极小的目标函数。很显然,权系数λ的选取对结果是有影响的:当λ过小时,目标函数更侧重于rank(A)的极小而出现过拟合现象;当λ过大时,目标函数更侧重于‖E‖0的极小而出现欠拟合现象。因此,只有选择合理的λ才能避免出现欠拟合或过拟合现象。Candes等[5]建议λ的取值为
建立如图 4a所示的理论位场数据,并采用不同λ值分离磁异常(图 4b和图 4c)。图 4d为选取不同λ时场分离结果的均方根误差,可见当λ取值为0.0035~0.0060时,均方根误差呈下降趋势。这一过程中产生较大的均方根误差,其原因是λ的取值过小造成过拟合。当λ取值为0.0070~0.0200时,均方根误差相对稳定,在该范围内得到的分离结果相似且均方根误差最小。当λ取值0.0200~0.0500时,均方根误差上升,其原因是λ的取值过大造成欠拟合。总的来看,对于该模型,当λ的取值范围在0.0050~0.0500时,随着λ的增大,均方根误差呈降低—平稳—升高的趋势,拟合程度呈现过拟合—拟合—欠拟合的趋势。这验证了前文关于λ对分离结果影响的推论。当然,就目前信号处理的发展来看,还没有哪种方法能完全解决欠拟合和过拟合的问题,RPCA法也是一样。然而可以发现,λ在过大或过小的区间内取值时,得到的结果变化较大,而当λ在最佳的区间内取值时,得到的结果是稳健的,这也验证了前文提到的“稳态”。对于实际应用,λ最佳的取值区间是宽松的,从而更易确定λ的值。Candes等[3]建议λ取值

|
图 4 权系数与分离误差的关系 (a)理论总磁异常场; (b)理论区域场和分离的区域场; (c)理论局部场和分离的局部场; (d)选取不同λ分离的均方根误差 |
匹配滤波和小波分析是位场分离中的常用方法。匹配滤波是一种地质意义明确的位场分离方法,其基本原理是埋深不同的两种场源在对数功率谱曲线上表现出不同梯度的线性下降特征,利用这种特征的差异构制滤波器,能够分离上下叠加的地质体的场[7, 19]。小波分析能够将重磁场精细地分解到不同尺度的细节上,这些不同尺度的细节反映不同尺度和深度的场源,常被用于位场的分解和分析[15-16, 20-21]。本文通过理论模型计算对RPCA与这两种方法进行对比。
5.1 RPCA与匹配滤波法的对比通过理论模型1(图 5d)对比RPCA与匹配滤波分离法。模型正演设定256个观测点,分别对总场(图 5a)、理论区域场(图 5b)和局部场(图 5c)进行离散傅里叶变换并求取其对数功率谱。图 6是非负频率对数功率谱,每条曲线共129个离散对数功率点。根据Spector等[9]提出的方法,分别在对数功率谱的低频段和中高频段的近似线性下降部分取切线,并通过两条切线的斜率及在纵轴上的截距构建区域场和局部场滤波器,最终得到的分离结果如图 7所示。与理论场相比,匹配滤波分离的局部场多余了一部分低频成分而区域场缺失了一部分低频成分(图 7a和图 7b中蓝色虚线部分),说明分离结果与理论值不吻合。
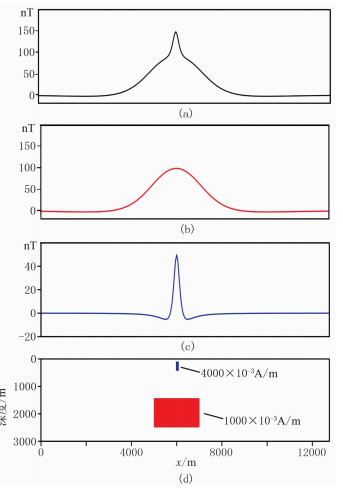
|
图 5 理论模型1及磁异常 (a)总磁场; (b)区域场; (c)异常场; (d)理论模型1 |

|
图 6 理论模型1的磁场总场、区域场和局部场的对数功率谱 |

|
图 7 理论模型1的磁场匹配滤波和RPCA法分离结果 (a)区域场;(b)局部场 |
分离效果较差的原因主要有以下几点:①区域场频谱的能量过于集中于低频段,导致只能利用很少的频率点判断切线位置。②由于局部场在低频段同样具有较强能量,并且位场具有频率叠加性,因此局部场的低频数据叠加到总场的低频段,导致总场低频段能量高于实际区域场的能量,使得估计的切线斜率大于实际值。③匹配滤波法稳定性较差,当低频段切线的首、尾端点位置选取变化较小时,其计算的斜率值变化大,导致分离结果变化大。
与匹配滤波相比,RPCA的参数估计更为简单。利用RPCA分离位场时,只需要估计权系数,又由于权系数的取值区间宽松,且当其位于最佳区间时分离结果十分稳定,因此容易选取合适的权系数λ。利用RPCA法分离图 5中理论场,当λ取值为0.03~0.10时,分离结果稳定。因此选取中间值即0.06时的分离结果(图 7红色虚线)与匹配滤波法分离结果进行对比,发现RPCA分离效果更优。
5.2 RPCA与小波分析对比通过小波分析法将模型1引起的总场异常分成5阶细节(图 8a)。可以看出,随着分解的阶数增加,细节尺度逐渐加大。将小波细节1~5阶叠加构成局部场,把4阶小波逼近作为区域场,得到分离结果如图 8b和图 8c。小波分析法的优势在于尺度不变性[15-16],因此应用相对简单,缺点主要是分解的细节没有明确的地球物理意义,难以判断哪几阶细节由局部场引起,哪阶逼近由区域场引起。从理论模型1的分离效果来看,RPCA要优于小波分析。
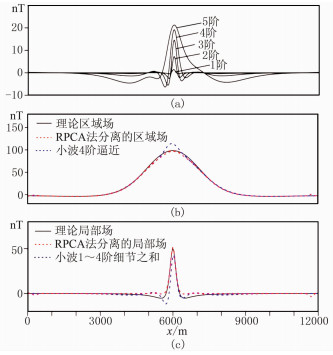
|
图 8 理论模型1的小波分析和RPCA分离结果 (a)总场的小波分解结果;(b)区域场对比;(c)局部场对比 |
为了对比RPCA与小波分析法在复杂模型情况下的分离效果,建立如图 9f所示模型。总场由三部分构成,分别是深部模型的响应、浅部模型的响应和高幅值随机噪声。调节λ,发现λ在0.1200~0.2000时,分离结果稳定。选取λ为0.1700分离总场,得到的噪点如图 9e所示。对剩余场继续分离,当权系数在0.0200~0.0400变化时,分离结果是稳定的,因此选取权系数0.0300继续分离剩余场,得到结果如图 9b和图 9d所示。利用小波分析分离总场,分别采用位场小波基、Daubechies小波簇、Coiflets小波簇、Symlets小波簇、Discrete Meyer小波基、Biorthogonal小波簇等15种小波基、Reverse Biorthogonal小波簇分离总场[22],不同小波基的分离结果差异较大,其中Symlets小波基分离的区域场误差最小(均方误差为5.160nT),分离的区域场如图 9c中蓝色虚线所示。对于高幅值随机噪点,小波分析法无法分离。可以看出,RPCA法的分离效果(均方根误差为3.289nT)优于小波分析法。
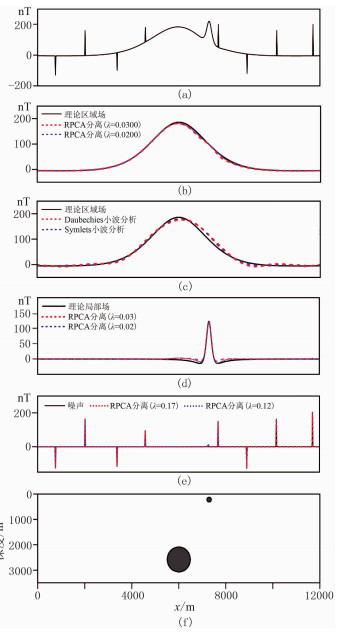
|
图 9 理论模型及RPCA和小波分析法的分离结果 (a)理论总场;(b)理论区域场和RPCA法分离的区域场;(c)理论区域场和小波分析法分离的区域场;(d)理论局部场和RPCA分离的局部场;(e)噪声和RPCA分离的噪声;(f)理论模型 |
建立三维地质模型2(图 10),其中浅部场源包括不同形状、不同尺度的4个地质体,深部地质体是一“L”形柱体。此模型的正演重、磁场见图 11。
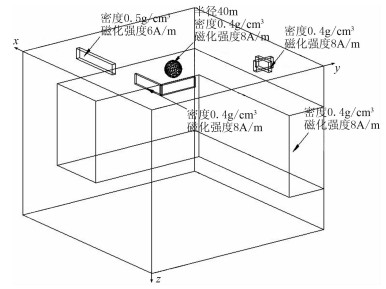
|
图 10 模型2示意图 |

|
图 11 模型2重(a)、磁(b)异常场正演结果 |
深部地质体正演区域重、磁异常分别见图 12a、图 12c,浅部地质体正演的局部重、磁异常如图 12b、图 12d所示。采用RPCA算法分离重磁场,当λ取值在0.0020附近变化时,所得的重力分离结果稳定,当λ取值在0.0030附近变化时,所得的重力分离结果稳定。小波分析和匹配滤波的参数选择原则与实验1一样,图 12i~图 12p为两种方法选择不同参数得到的最优结果。

|
图 12 模型2重、磁场异常图 (a)~(d)分别为理论计算的区域重力异常、局部重力异常、区域磁异常和局部磁异常;(e)~(h)分别为RPCA法分离的区域重力异常、局部重力异常、区域磁异常和局部磁异常;(i)~(l)分别为小波分析法分离的区域重力异常、局部重力异常、区域磁异常和局部磁异常;(m)~(p)分别为匹配滤波法分离的区域重力异常、局部重力异常、区域磁异常和局部磁异常 |
重力场的分离中,RPCA、小波分析、匹配滤波的均方根误差分别是0.016、0.020、0.028mGal。其中RPCA的分离误差最小,小波分析残留了较多深部地质体引起的异常(幅值约为0.05mGal),匹配滤波分离的局部场的异常幅值远小于实际局部场异常的幅值。磁场的分离中,RPCA、小波分析、匹配滤波的均方根误差分别是45.24、60.25、46.94nT,其中RPCA的分离误差略小于匹配滤波,但小波分析和匹配滤波分离的局部场残留了部分深部地质体引起的异常(幅值分别是120nT和110nT)。可见复杂模型的重磁场分离中,RPCA的误差相对较小。
6 RPCA应用实例卫宁北山—香山矿集区位于宁夏西部,大地构造位于北祁连走廊过渡带,东段位于阿拉善地块南缘、鄂尔多斯地块西缘的转换交界处[23],是宁夏金属矿产勘查重要地区之一。卫宁北山位于矿集区的北部,经多年勘查工作,发现多处以金、铅、银等为主的金属矿床,如金场子金矿、照璧山铁矿、大通沟铜矿等[24]。为此在该地区开展重磁勘探,目的是研究隐伏中酸性岩体的空间侵位特征。
研究区的基底层由早古生代次深海斜坡相陆源碎屑—泥质沉积为主的浊积岩系构成。刘志坚[25]推断在卫宁北山西部的单梁山西段(二人山—金场子北)及其东部一带可能存在隐伏的中酸性岩体,与出露地表的闪长玢岩脉很可能为同源、同期形成。
由于区内出露主要以沉积岩为主,因此位场地球物理方法是寻找深部隐伏岩体的有效方法。宋新华等[23]指出,区内基底具有一定磁性,沉积地层(石炭—奥陶系)岩石标本多为无磁性或弱磁性,密度约为2.68g/cm3;岩浆岩体具有磁性,密度为2.60g/cm3。结合物性特征可知,区内岩浆岩体相对围岩具有低密、高磁的物性特征,由此推断局部低重、高磁异常主要由隐伏岩浆岩体引起。
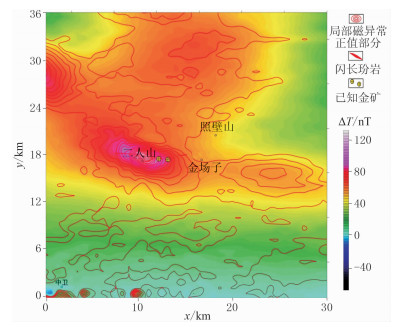
研究区布格重力异常和化极磁异常[26]分别如图 13和图 14所示。可见区内布格重力异常为-20~35mGal,呈南低北高趋势;区内化极磁异常为-60~120nT,北部分布大面积正磁异常。纬度37.55°以北的磁异常均大于20nT,其中以二人山地区磁异常最强,磁异常极大值为120nT;二人山北西部磁异常明显,极大值约为90nT;二人山东部、北部磁异常较弱,极大值约为50nT。结合物性资料推断,布格重力异常的区域性变化与致密基底起伏有关,基底的隆起会引起布格重力的升高,隐伏岩浆岩体会引起局部低重异常。化极磁异常主要由磁性基底和岩浆岩体引起,其中磁性基底的磁性较弱且埋深较大,主要引起幅值较低且变化平缓的磁异常,岩浆岩体磁性较强且埋深较浅,主要引起幅值较高且变化快的磁异常。因此,本次研究重点是从布格重力异常和化极磁异常中提取出局部低重、高磁异常,具有局部低重、高磁异常组合特征的区域即是隐伏岩浆岩体的远景区。
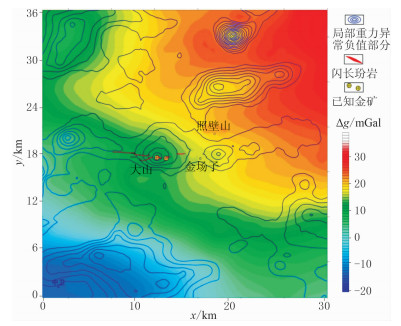
|
图 13 研究区布格重力异常叠加剩余重力异常图 底图是布格重力异常;等值线是利用RPCA法 分离的局部重力异常负值部分 |
|
图 14 研究区化极磁异常叠加剩余磁异常图 底图是化极磁异常;等值线是利用RPCA法 分离的局部磁异常正值部分 |
利用RPCA法提取局部低重、高磁异常。首先利用RPCA法分离布格重力异常,得到区域重力异常和局部重力异常。当λ取约0.0020时,分离得到的区域重力异常和局部重力异常稳定,其中局部重力异常负值部分如图 13所示。然后利用RPCA法分离化极磁异常,得到区域磁异常和局部磁异常。当λ约为0.0040时,分离的区域磁异常和局部磁异常稳定,其中局部磁异常正值部分如图 14所示。最后,将分离的局部低重异常和局部高磁异常叠合(图 15),得到7个局部低重高磁异常叠合区(A1~A7),推断为隐伏岩体可能赋存的区域。从叠合图可以看出,二人山地区已知出露的闪长玢岩岩脉与分离的局部低重高磁异常对应关系很好,其中局部低重、高磁异常向西仍有延伸(A7区),预测该区为隐伏岩浆岩体分布区。此外,A1~A6区也具有局部低重、高磁异常的组合特征,地表未见岩浆岩体或岩脉出露,将其解释为隐伏岩浆岩体区。

|
图 15 局部低重、高磁异常叠合图及岩浆岩预测区域 蓝色是局部重力异常负值部分; 红色是局部磁异常正值部分 |
本文主要研究鲁棒主成分分析在位场分离中的应用。以模型数据为基础,讨论了位场信号的低秩性和稀疏性特征,从低秩性和稀疏性的角度论述了RPCA在位场分离问题中的地球物理意义,并结合理论模型提出适用于位场分离的参数选取方法。
区域场具有低秩性和局部场具有稀疏性是利用RPCA法实现位场区域场与局部场分离的基础。从RPCA数学模型出发,该方法同时要求分离出来的区域场低秩且局部场稀疏,因此对分离出来的场具有更强的约束力,进而分离的结果更准确。由于核范数和(1, 1)范数的共同约束,采用RPCA分离位场很容易达成一种相对稳态,而这一系列的相似分离结果对应位场分离的最佳结果。因此,与传统位场分离方法相比,RPCA法的精度更高,并且在一定程度上更容易避免欠拟合或过拟合现象。同时对于稀疏且大幅值的噪声,RPCA法能够有效分离。
最后,将RPCA法用于宁夏卫宁北山地区的隐伏岩浆岩体预测,将分离得到的局部低重、高磁组合异常作为判断岩浆岩发育区的标志,预测出7个火成岩发育区。
本方法的不足之处是需要对原数据进行变换得到延滞矩阵,即对一维数据Hankel矩阵化及求两类优化问题最优解需要占用一定的内存,计算速度也没有频率域快。但是随着工作站、并行机等硬件的普及算法的改进,这些问题最终可以得到解决。
| [1] |
张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2013.
|
| [2] |
Lin Z C, Chen M M, Wu L Q, et al.The augmented large range multiplier method for exact recovery of corrupted low-rank matrices[C].https://arxiv.org/PS_cache/arxiv/pdf/1009/1009.5055v1.pdf, 2010.
|
| [3] |
Candes E J, Recht B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2009, 9(6): 717-772. DOI:10.1007/s10208-009-9045-5 |
| [4] |
Candes E J, Tao T. The power of convex relation:Near-optimal matrix completion[J]. IEEE Transaction on Information Theory, 2010, 56(5): 2053-2080. DOI:10.1109/TIT.2010.2044061 |
| [5] |
Candes E J, Li X D, Ma Y, et al. Robust principal component analysis?[J]. Journal of the ACM, 2011, 58(3): 1-37. |
| [6] |
史加荣, 郑秀云, 魏宗田, 等. 低秩矩阵恢复算法综述[J]. 计算机应用研究, 2013, 30(6): 1601-1605. SHI Jiarong, ZHENG Xiuyun, WEI Zongtian, et al. Survey on algorithms of low-rank matrix recovery[J]. Application Research of Computers, 2013, 30(6): 1601-1605. DOI:10.3969/j.issn.1001-3695.2013.06.001 |
| [7] |
杨宇山, 李媛媛, 刘天佑. 高阶统计量在地震弱信号及"磁亮点"识别中的应用[J]. 石油地球物理勘探, 2005, 40(1): 103-107. YANG Yushan, LI Yuanyuan, LIU Tianyou. Application of high-order statistics to identify weak seismic signal and "magnetic bright spot"[J]. Oil Geophysical Prospecting, 2005, 40(1): 103-107. DOI:10.3321/j.issn:1000-7210.2005.01.024 |
| [8] |
马龙, 孟军海, 付强, 等. 独立分量分析在重磁数据处理中的应用[J]. 石油地球物理勘探, 2017, 52(6): 1344-1353. MA Long, MENG Junhai, FU Qiang, et al. Application of independent component analysis in gravity and magnetic data processing[J]. Oil Geophysical Prospecting, 2017, 52(6): 1344-1353. |
| [9] |
Spector A, Grant F S. Statistical model for interpreting aeromagnetic data[J]. Geophysics, 1970, 35(2): 293-302. DOI:10.1190/1.1440092 |
| [10] |
程方道, 刘东甲, 姚汝信. 划分重力区域场与局部场的研究[J]. 物化探计算技术, 1987, 9(1): 1-9. CHENG Fangdao, LIU Dongjia, YAO Ruxin. A study on the identification of regional and local gravity fields[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1987, 9(1): 1-9. |
| [11] |
Mickus K L, Aiken C L V, Kennedy W D. Regional-residual gravity anomaly separation using the minimum-curvature technique[J]. Geophysics, 1991, 56(2): 279-283. DOI:10.1190/1.1443041 |
| [12] |
王万银, 邱之云, 刘金兰, 等. 位场数据处理中的最小曲率扩边和补空方法研究[J]. 地球物理学进展, 2009, 24(4): 1327-1338. WANG Wanyin, QIU Zhiyun, LIU Jinlan, et al. The research to the extending edge and interpolation based on the minimum curvature method in potential field data processing[J]. Progress in Geophysics, 2009, 24(4): 1327-1338. DOI:10.3969/j.issn.1004-2903.2009.04.022 |
| [13] |
纪晓琳, 王万银, 邱之云. 最小曲率位场分离方法研究[J]. 地球物理学报, 2015, 58(3): 1042-1058. JI Xiaolin, WANG Wanyin, QIU Zhiyun. The research to the minimum curvature technique for potential field data separation[J]. Chinese Journal of Geophysics, 2015, 58(3): 1042-1058. |
| [14] |
Fedu M, Quarta T. Wavelet analysis for the regional-residual and local separation of potential field anomalies[J]. Geophysical Prospecting, 1998, 46(5): 507-525. DOI:10.1046/j.1365-2478.1998.00105.x |
| [15] |
侯遵泽, 杨文采. 中国重力异常的小波变换与多尺度分析[J]. 地球物理学报, 1997, 40(1): 85-95. HOU Zunze, YANG Wencai. Wavelet transform and multi-scale analysis on gravity anomalies of China[J]. Chinese Journal of Geophysics, 1997, 40(1): 85-95. DOI:10.3321/j.issn:0001-5733.1997.01.010 |
| [16] |
杨文采, 施志群, 侯遵泽, 等. 离散小波变换与重力异常多重分解[J]. 地球物理学报, 2001, 44(4): 534-541. YANG Wencai, SHI Zhiqun, HOU Zunze, et al. Discrete wavelet transform for multiple decomposition of gravity anomalies[J]. Chinese Journal of Geophysics, 2001, 44(4): 534-541. DOI:10.3321/j.issn:0001-5733.2001.04.012 |
| [17] |
朱丹, 刘天佑, 李宏伟. 基于奇异谱分析的位场分离方法[J]. 地球物理学报, 2018, 61(9): 3800-3811. ZHU Dan, LIU Tianyou, LI Hongwei. Separation of potential field based on singular spectrum analysis[J]. Chinese Journal of Geophysics, 2018, 61(9): 3800-3811. |
| [18] |
Broomhead D S, King G P. Extracting qualitative dynamics from experimental data[J]. Physica D:Nonli-near Phenomena, 1986, 20(2): 217-236. |
| [19] |
刘天佑, 崔宁, 蔡鑫, 等. 重磁异常宽度幅值特征滤波[J]. 地球物理学报, 1996, 31(2): 225-231. LIU Tianyou, CUI Ning, CAI Xin, et al. Characteristic filtering for the width and amplitude of gravimetric-magnetic anomaly[J]. Chinese Journal of Geophysics, 1996, 31(2): 225-231. |
| [20] |
刘天佑, 吴昭才, 詹应林, 等. 磁异常小波多尺度分解及危机矿山的深部找矿:以大冶铁矿为例[J]. 地球科学, 2007, 32(1): 135-140. LIU Tianyou, WU Zhaocai, ZHAN Yinglin, et al. Wavelet multi scale decomposition of magnetic ano-maly and its application in searching for deep buried minerals in crisis mines:a case study from Daye iron mines[J]. Earth Science, 2007, 32(1): 135-140. DOI:10.3321/j.issn:1000-2383.2007.01.021 |
| [21] |
刘天佑, 盛秋红, 杨宇山. 复小波频谱分析在地震数据处理中的应用[J]. 石油地球物理勘探, 2007, 42(增刊1): 72-75. LIU Tianyou, SHENG Qiuhong, YANG Yushan. Application of frequency spectrum analysis of complex wavelet to seismic data processing[J]. Oil Geophysical Prospecting, 2007, 42(S1): 72-75. |
| [22] |
邓文彬, 尚海滨, 许闯. 小波基选取对重力异常多尺度分解的影响[J]. 测绘科学, 2018, 43(4): 30-37. DENG Wenbin, SHANG Haibin, XU Chuang. Effect of wavelet bases on multi-scale decomposition for gravity anomaly[J]. Science of Surveying and Mapping, 2018, 43(4): 30-37. |
| [23] |
宋新华, 尹秉喜, 闫红, 等. 航磁资料在卫宁北山寻找多金属矿中的应用[J]. 物探与化探, 2010, 34(3): 289-293. SONG Xinhua, YIN Bingxi, YAN Hong, et al. The relationship between the aeromagnetic weak anomalies and the polymetallic ore deposits (ore spots) in the Beishan mountain, Weining[J]. Geophysical and Geochemical Exploration, 2010, 34(3): 289-293. |
| [24] |
艾宁.宁夏卫宁北山金场子金矿矿床地质与地球化学研究[D].陕西西安: 西北大学, 2014. AI Ning.Studies on the Geochemical and Geological Characteristics of Weiningbeishan Jingchangzi Gold Deposit[D].Northwest University, Xi'an, Shaanxi, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10697-1014364637.htm |
| [25] |
刘志坚.宁夏卫宁北山金、铅、银多金属矿成矿地质特征[D].四川成都: 成都理工大学, 2013. LIU Zhijian.Metallogenic Characteristics of Weiningbeishan Au-Pb-Ag Polymetallic Deposit in Ningxia Province[D].Chengdu University of Technology, Chengdu, Sichuan, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10616-1013288653.htm |
| [26] |
张琪, 张英堂, 李志宁, 等. 改进的低纬度化极稳定算法[J]. 石油地球物理勘探, 2018, 53(3): 606-616. ZHANG Qi, ZHANG Yingtang, LI Zhining, et al. An improved stable algorithm of the reduction-to-the-pole at low latitudes[J]. Oil Geophysical Prospecting, 2018, 53(3): 606-616. |



 刘天佑, 湖北省武汉市洪山区鲁磨路388号中国地质大学地球物理与空间信息学院, 430074。Email:
刘天佑, 湖北省武汉市洪山区鲁磨路388号中国地质大学地球物理与空间信息学院, 430074。Email: