磁梯度张量(Magnetic gradient tensor,MGT)探测技术及其数据解释与应用可视为磁法勘探领域的一项突破[1]。相较于磁总场强度和磁场矢量,磁梯度张量作为磁场矢量三正交方向上的空间变化率,对测量点的空间取向和旋转噪声不敏感,梯度测量与背景匀强场环境无关。磁梯度张量技术可提取关于目标体更丰富的姿态信息和磁源信息,分辨率高且抗干扰能力强,对复杂环境的适应性较强[2-3]。利用磁梯度张量数据可实现航磁探测、矿产勘探与土壤黑色金属搜索、探寻未爆弹、排雷、潜艇侦查或水下金属目标定位及反演识别等[4-6],应用前景十分广阔。
当观测距离超过目标体尺度的2.5倍时,磁性目标可简化为磁偶极子[7]。在实测过程中,对多点根据磁偶极子场源理论进行目标定位时,测量结果如果相对稳定,则表明此时目标体可以当做磁偶极子。Nara等[8]提出基于欧拉反褶积的磁偶极子单点定位算法,通过计算张量矩阵逆与磁场矢量的乘积来估算磁性目标的位置。然而,实际应用中很难对背景地磁场与目标体的磁异常场进行分离,因而对目标体的定位精度受到限制。若想在地磁背景场中有效提取磁异常场源信息,可利用不同测点的场数据构建线性方程组,求解位置矢量,即多点定位[9-10],但是定位精度会受到航线选择的限制,且对系统姿态及位置的精度要求很高。
为在单一测量点处实现磁异常目标体的精确定位,本文对磁偶极子张量场和矢量场均满足的欧拉反褶积方程求导,进而构建一、二阶张量矩阵与位置矢量的关系方程,消除背景磁场,利用张量衍生不变关系得到目标位置信息的限定方程;同时提出二阶张量系统的概念以及测量方法,以此对磁性目标进行单点定位。由于差分测量二阶张量数据对传感器输出误差十分敏感,故需配套磁梯度张量系统校正技术以提升张量数据的解释精度。目前已有较为成熟的校正方法,如李青竹等[11-12]提出的平面十字形磁梯度张量系统的两步线性校正和基于椭球拟合的磁梯度张量系统集成校正方法、尹刚等[13]提出的磁梯度张量系统非线性校正方法等,均能较准确地估计系统误差参数,使单点定位方法可实现较高的目标定位精度。
1 磁梯度张量要素与张量不变量磁梯度张量为磁场分量在正交方向上的空间变化率,共有9个元素,其中无源静态磁场中某点磁场矢量旋度和散度为零[14],故张量矩阵对称且无迹,可表示为
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {{B_x}}\\ {{B_y}}\\ {{B_z}} \end{array}} \right]\left[ {\frac{\partial }{{\partial x}}\;\frac{\partial }{{\partial y}}\;\frac{\partial }{{\partial z}}} \right] = \left[ {\begin{array}{*{20}{c}} {{B_{xx}}}&{{B_{xy}}}&{{B_{xz}}}\\ {{B_{xy}}}&{{B_{yy}}}&{{B_{yz}}}\\ {{B_{xz}}}&{{B_{yz}}}&{ - {B_{xx}} - {B_{yy}}} \end{array}} \right] $ | (1) |
式中:Bx、By、Bz为磁场矢量的三轴分量;Bij(i, j=x, y, z)表示磁梯度张量分量,共5个独立分量,一般由差分磁梯度张量系统测得,如由四个磁通门传感器组成的平面十字形结构张量系统[11-13]。张量运算时不随坐标系旋转而改变的量,称为张量不变量。一些基本不变量[15]如下
| $ \left\{ \begin{array}{l} {I_0} = {\rm{tr}}\left( \mathit{\boldsymbol{G}} \right) = {B_{xx}} + {B_{yy}} + {B_{zz}} = {\lambda _1} + {\lambda _2} + {\lambda _3} = 0\\ {I_1} = {B_{xx}}{B_{yy}} + {B_{yy}}{B_{zz}} + {B_{xx}}{B_{zz}} - \left( {B_{xy}^2 + B_{yz}^2 + B_{xz}^2} \right)\\ \;\;\;\; = {\lambda _1}{\lambda _2} + {\lambda _2}{\lambda _3} + {\lambda _1}{\lambda _3}\\ {I_2} = \det \left( \mathit{\boldsymbol{G}} \right) = {B_{xx}}{B_{yy}}{B_{zz}} + 2{B_{xy}}{B_{xz}}{B_{yz}} - \\ \;\;\;\;\;\;\left( {B_{xz}^2{B_{yy}} + B_{yz}^2{B_{xx}} + B_{xy}^2{B_{zz}}} \right) = {\lambda _1}{\lambda _2}{\lambda _3} \end{array} \right. $ | (2) |
式中:tr(·)代表求矩阵的迹;det(·)表示求行列式的值;λ1、λ2和λ3为G的特征值,满足特征方程λ3-I0λ2+I1λ-I2=0。
背景地磁场梯度一般很小,磁梯度张量测量场可认为仅由磁异常体产生。当目标距离测量点大于2.5倍的目标长度时,磁性目标可简化为磁偶极子,可由6个未知量描述,即位置矢量r=(x, y, z)T和磁矩矢量m=(mx, my, mz)T。设M=‖m‖=(mx2+my2+mz2)1/2为磁矩模,r=‖r‖=(rx2+ry2+rz2)1/2为位置矢量模,则磁矩矢量为m的磁偶极子在r处产生的磁场矢量和磁梯度张量5个独立分量分别为
| $ \begin{array}{l} \mathit{\boldsymbol{B}} = \frac{\mu }{{4{\rm{ \mathsf{ π} }}}}\left[ {\frac{{3\left( {\mathit{\boldsymbol{m}} \cdot \mathit{\boldsymbol{r}}} \right)\mathit{\boldsymbol{r}}}}{{{r^5}}} - \frac{\mathit{\boldsymbol{m}}}{{{r^3}}}} \right]\\ \;\;\;\; = \frac{\mu }{{4{\rm{ \mathsf{ π} }}{r^5}}}\left[ {\begin{array}{*{20}{c}} {3{x^2} - {r^2}}&{3xy}&{3xz}\\ {3xy}&{3{y^2} - {r^2}}&{3yz}\\ {3xz}&{3yz}&{3{z^2} - {r^2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{m_x}}\\ {{m_y}}\\ {{m_z}} \end{array}} \right] \end{array} $ | (3) |
| $ \begin{array}{l} {\left[ {{B_{xx}}\;{B_{xy}}\;{B_{xz}}\;{B_{yy}}\;{B_{yz}}} \right]^{\rm{T}}} = \frac{\mu }{{4{\rm{ \mathsf{ π} }}{r^7}}} \times \\ \left[ {\begin{array}{*{20}{c}} {9x{r^2} - 15{x^3}}&{3y{r^2} - 15{x^2}y}&{3z{r^2} - 15{x^2}z}\\ {3y{r^2} - 15{x^2}y}&{3x{r^2} - 15x{y^2}}&{ - 15xyz}\\ {3z{r^2} - 15{x^2}z}&{ - 15xyz}&{3x{r^2} - 15x{z^2}}\\ {3x{r^2} - 15x{y^2}}&{9y{r^2} - 15{y^3}}&{3z{r^2} - 15{y^2}z}\\ { - 15xyz}&{3z{r^2} - 15{y^2}z}&{3y{r^2} - 15y{z^2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{m_x}}\\ {{m_y}}\\ {{m_z}} \end{array}} \right] \end{array} $ | (4) |
式中μ为介质磁导率,在空气中μ≈μ0,μ0=4π×10-7N·A-2为真空磁导率。
2 磁偶极子场张量衍生不变关系 2.1 特征值分析特征值λ1、λ2、λ3及特征方程系数I0、I1、I2与场源磁偶极矩有关。若m、r已知,联立式(2)和式(4),可推导张量系统测量点处磁梯度张量矩阵的特征值
| $ \left\{ {\begin{array}{*{20}{l}} {{\lambda _1} = \frac{{3{\mu _0}\mathit{\boldsymbol{m}} \cdot \mathit{\boldsymbol{r}}}}{{8{\rm{ \mathsf{ π} }}{r^5}}}\left[ { - \sqrt {5 + 4\frac{{{M^2}{r^2}}}{{{{(\mathit{\boldsymbol{m}} \cdot \mathit{\boldsymbol{r}})}^2}}}} - 1} \right]}\\ {{\lambda _2} = \frac{{3{\mu _0}\mathit{\boldsymbol{m}} \cdot \mathit{\boldsymbol{r}}}}{{8{\rm{ \mathsf{ π} }}{r^5}}}\left[ {\sqrt {5 + 4\frac{{{M^2}{r^2}}}{{{{(\mathit{\boldsymbol{m}} \cdot \mathit{\boldsymbol{r}})}^2}}}} - 1} \right]}\\ {{\lambda _3} = \frac{{3{\mu _0}}}{{4{\rm{ \mathsf{ π} }}{r^5}}}\mathit{\boldsymbol{m}} \cdot \mathit{\boldsymbol{r}}} \end{array}} \right. $ | (5) |
式中:|λ1|≥|λ3|、|λ2|≥|λ3|且λ2≥λ3≥λ1。令
| $ \left\{ \begin{array}{l} {\eta _1} = {B_{xz}}B_{xx}^2 + {B_{xz}}B_{yz}^2 + B_{xz}^3 + {B_{xx}}{B_{xy}}{B_{yz}} + \\ \;\;\;\;\;\;{B_{xy}}{B_{yz}}{B_{yy}} + {B_{xx}}{B_{yy}}{B_{xz}}\\ {\eta _2} = {B_{yz}}B_{yy}^2 + {B_{yz}}B_{xz}^2 + B_{yz}^3 + {B_{xx}}{B_{xy}}{B_{xz}} + \\ \;\;\;\;\;\;{B_{xy}}{B_{xz}}{B_{yy}} + {B_{xx}}{B_{yy}}{B_{yz}}\\ {\eta _3} = {B_{xy}}B_{xz}^2 - {B_{xy}}B_{yz}^2 + {B_{xz}}{B_{yy}}{B_{yz}} - {B_{xx}}{B_{xz}}{B_{yz}} \end{array} \right. $ | (6) |
根据G的对称性与无迹性,可推导张量矩阵特征值λ1、λ2、λ3对应的特征向量
| $ {\mathit{\boldsymbol{v}}_i} = \left[ {\begin{array}{*{20}{c}} { - {B_{yz}}\lambda _i^2 + \left( {{B_{xy}}{B_{xz}} - {B_{xx}}{B_{yz}}} \right){\lambda _i} + {\eta _2}}\\ {{B_{xz}}\lambda _i^2 - \left( {{B_{xy}}{B_{yz}} - {B_{xz}}{B_{yy}}} \right){\lambda _i} - {\eta _1}}\\ {{\eta _3}} \end{array}} \right] $ | (7) |
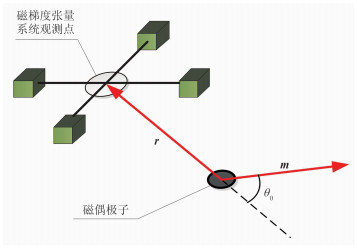
磁偶极子场源相对固定,当张量系统姿态变换时,同一测量点各姿态下不同的张量测量数据必然对应于恒定的磁矩矢量m和位置矢量r,因此m与r间的夹角θ0是不变的,将这个衍生不变关系称为磁矩夹角不变关系,如图 1所示。假设该点处特征值λ1、λ2、λ3由实际张量系统测量并求解得到,则通过矢量的点积运算,联立式(5)特征值解算式,可得到θ0的表达式
|
图 1 磁矩矢量与位置矢量夹角不变关系 |
| $ \cos {\theta _0} = \frac{{\mathit{\boldsymbol{m}} \cdot \mathit{\boldsymbol{r}}}}{{\left\| \mathit{\boldsymbol{m}} \right\| \cdot \left\| \mathit{\boldsymbol{r}} \right\|}} = \frac{{{\lambda _3}}}{{\sqrt { - \lambda _3^2 - {\lambda _1}{\lambda _2}} }} = \frac{{{\lambda _3}}}{u} $ | (8) |
式中u为归一化磁源强度(normalized source strength, NSS)。
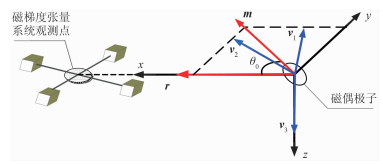
2.2.2 特征向量空间不变关系磁梯度张量系统空间姿态方向可以是任意的,选择空间坐标系以磁偶极子为原点,r矢量方向为x轴正向,m与r的平面为坐标系xoy平面,则磁矩矢量与位置矢量的夹角不变关系可用如图 2所示的空间直角坐标系表示。
|
图 2 特征向量空间不变关系在直角坐标系中的表示 |
根据文献[16]给出的偶极子位置表示方法,即磁矩矢量为m=(Mcosθ0, Msinθ0, 0)T,位置矢量可表示为r=(r, 0, 0)T。联立式(4)~式(8),可推导出特征值λ1、λ2、λ3及其对应的特征向量v1、v2、v3
| $ \left\{ \begin{array}{l} {\lambda _1} = \frac{{3{\mu _0}M}}{{8{\rm{ \mathsf{ π} }}{r^5}}}\left( { - \sqrt {5{{\cos }^2}\theta + 4} - \cos {\theta _0}} \right)\\ {\lambda _2} = \frac{{3{\mu _0}M}}{{8{\rm{ \mathsf{ π} }}{r^5}}}\left( {\sqrt {5{{\cos }^2}\theta + 4} - \cos {\theta _0}} \right)\\ {\lambda _3} = \frac{{3{\mu _0}M}}{{8{\rm{ \mathsf{ π} }}{r^5}}}\cos {\theta _0} \end{array} \right. $ | (9) |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{v}}_1} = {\left[ {\begin{array}{*{20}{c}} {\frac{{3{\mu _0}M}}{{4{\rm{ \mathsf{ π} }}{r^4}}}\sin {\theta _0}}&{{\lambda _1} + \frac{{3{\mu _0}M}}{{2{\rm{ \mathsf{ π} }}{r^4}}}\cos {\theta _0}}&0 \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{v}}_2} = {\left[ {\begin{array}{*{20}{c}} {\frac{{3{\mu _0}M}}{{4{\rm{ \mathsf{ π} }}{r^4}}}\sin {\theta _0}}&{{\lambda _2} + \frac{{3{\mu _0}M}}{{2{\rm{ \mathsf{ π} }}{r^4}}}\cos {\theta _0}}&0 \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{v}}_3} = {\left[ {\begin{array}{*{20}{c}} 0&0&1 \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (10) |
由式(10)可知,在建立的空间直角坐标系中,特征向量v3垂直于矢量m、r所在平面xoy,而特征向量v1、v2则与矢量m、r所在的平面xoy共面(图 2)。由于该空间坐标系没有对磁偶极子的磁矩信息、张量系统测量姿态施加任何约束,而只与坐标系的选择有关,因此可衍生为一般性结论:绝对值最小的特征值λ3对应的特征向量v3垂直于磁偶极子的磁矩矢量m和位置矢量r所在平面;最大和最小的两个特征值λ1、λ2对应的特征向量v1、v2与磁偶极子的磁矩矢量m和位置矢量r所在平面共面。将上述两个衍生不变关系称为特征向量空间不变关系。
以上的张量衍生不变关系均与系统姿态无关,而仅与目标源磁矩矢量和位置矢量有关,故必然能为单点定位提供关于目标位置信息的限定条件。
3 二阶张量欧拉反褶积定位方法 3.1 二阶磁梯度张量矩阵与系统磁梯度张量矩阵G各分量是磁矢量分量对于三轴坐标的一阶偏导数,因此又称为一阶磁梯度张量。通过求解磁矢量在三轴方向上的二阶偏导数,可得到二阶磁梯度张量矩阵GⅡ,共由27个元素组成
| $ \begin{array}{l} {\mathit{\boldsymbol{G}}_{{\rm{II}}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {B_{xx}}}}{{\partial x}}}&{\frac{{\partial {B_{xy}}}}{{\partial x}}}&{\frac{{\partial {B_{xz}}}}{{\partial x}}}&{\frac{{\partial {B_{xx}}}}{{\partial y}}}&{\frac{{\partial {B_{xy}}}}{{\partial y}}}&{\frac{{\partial {B_{xz}}}}{{\partial y}}}&{\frac{{\partial {B_{xx}}}}{{\partial z}}}&{\frac{{\partial {B_{xy}}}}{{\partial z}}}&{\frac{{\partial {B_{xz}}}}{{\partial z}}}\\ {\frac{{\partial {B_{yx}}}}{{\partial x}}}&{\frac{{\partial {B_{yy}}}}{{\partial x}}}&{\frac{{\partial {B_{yz}}}}{{\partial x}}}&{\frac{{\partial {B_{yx}}}}{{\partial y}}}&{\frac{{\partial {B_{yy}}}}{{\partial y}}}&{\frac{{\partial {B_{yz}}}}{{\partial y}}}&{\frac{{\partial {B_{yx}}}}{{\partial z}}}&{\frac{{\partial {B_{yy}}}}{{\partial z}}}&{\frac{{\partial {B_{yz}}}}{{\partial z}}}\\ {\frac{{\partial {B_{zx}}}}{{\partial x}}}&{\frac{{\partial {B_{zy}}}}{{\partial x}}}&{\frac{{\partial {B_{zz}}}}{{\partial x}}}&{\frac{{\partial {B_{zx}}}}{{\partial y}}}&{\frac{{\partial {B_{zy}}}}{{\partial y}}}&{\frac{{\partial {B_{zz}}}}{{\partial y}}}&{\frac{{\partial {B_{zx}}}}{{\partial z}}}&{\frac{{\partial {B_{zy}}}}{{\partial z}}}&{\frac{{\partial {B_{zz}}}}{{\partial z}}} \end{array}} \right]\\ \;\;\;\;\; = \left[ {\begin{array}{*{20}{c}} {{B_{xxx}}}&{{B_{xyx}}}&{{B_{xzx}}}&{{B_{xxy}}}&{{B_{xyy}}}&{{B_{xzy}}}&{{B_{xxz}}}&{{B_{xyz}}}&{{B_{xzz}}}\\ {{B_{yxx}}}&{{B_{yyx}}}&{{B_{yzx}}}&{{B_{yxy}}}&{{B_{yyy}}}&{{B_{yzy}}}&{{B_{yxz}}}&{{B_{yyz}}}&{{B_{yzz}}}\\ {{B_{zxx}}}&{{B_{zyx}}}&{{B_{zzx}}}&{{B_{zxy}}}&{{B_{zyy}}}&{{B_{zzy}}}&{{B_{zxz}}}&{{B_{zyz}}}&{{B_{zzz}}} \end{array}} \right] \end{array} $ | (11) |
二阶张量较一阶张量可提取出更浅表的附加磁源信息,具有更强的磁源分辨能力。在无源静态磁场中,GⅡ的27个元素中仅有7个相互独立,例如一组独立元素为Bxxx、Bxyx、Bxzx、Byxy、Byyy、Byzy、Bzzz。以平面十字形磁梯度张量系统为原型,将其扩展为二阶张量系统,能够差分测量出磁矢量分量的二阶偏导数。设计的该二阶系统结构如图 3所示。

|
图 3 平面十字形二阶磁梯度张量系统结构示意图 图中d为基线距离 |
由图 3可知,在原有平面十字形结构基础上,在中心o点处添增加了一个传感器5。该系统能够测量得到二阶张量矩阵27个元素中的6个和一阶张量矩阵G
| $ \left\{ \begin{array}{l} {B_{xxx}} = \frac{{4B_x^{(1)} + 4B_x^{(3)} - 8B_x^{(5)}}}{{{d^2}}}\\ {B_{xyx}} = \frac{{4B_y^{(1)} + 4B_y^{(3)} - 8B_y^{(5)}}}{{{d^2}}}\\ {B_{xzx}} = \frac{{4B_z^{(1)} + 4B_z^{(3)} - 8B_z^{(5)}}}{{{d^2}}}\\ {B_{yxy}} = \frac{{4B_x^{(2)} + 4B_x^{(4)} - 8B_x^{(5)}}}{{{d^2}}}\\ {B_{yyy}} = \frac{{4B_y^{(2)} + 4B_y^{(4)} - 8B_y^{(5)}}}{{{d^2}}}\\ {B_{yzy}} = \frac{{4B_z^{(2)} + 4B_z^{(4)} - 8B_z^{(5)}}}{{{d^2}}} \end{array} \right. $ | (12) |
| $ \begin{array}{l} \mathit{\boldsymbol{G}} = \frac{1}{d} \times \\ \left[ {\begin{array}{*{20}{c}} {B_x^{\left( 1 \right)} - B_x^{\left( 3 \right)}}&{B_y^{\left( 1 \right)} - B_y^{\left( 3 \right)}}&{B_z^{\left( 1 \right)} - B_z^{\left( 3 \right)}}\\ {B_x^{\left( 2 \right)} - B_x^{\left( 4 \right)}}&{B_y^{\left( 2 \right)} - B_y^{\left( 4 \right)}}&{B_z^{\left( 2 \right)} - B_z^{\left( 4 \right)}}\\ {B_z^{\left( 1 \right)} - B_z^{\left( 3 \right)}}&{B_z^{\left( 2 \right)} - B_z^{\left( 4 \right)}}&{B_x^{\left( 3 \right)} + B_y^{\left( 4 \right)} - \left( {B_x^{\left( 1 \right)} + B_y^{\left( 2 \right)}} \right)} \end{array}} \right] \end{array} $ | (13) |
式中:Bi(p)(p=1, 2, 3, 4, 5; i=x, y, z)为传感器p的磁场分量读数。式(12)中的6个二阶张量元素的准确测量是本文实现目标单点精确定位的关键。
3.2 三维欧拉反褶积公式利用欧拉反褶积法可以获得场源位置信息。若n阶齐次方程f(x, y, z)满足[17]
| $ x \frac{\partial f}{\partial x}+y \frac{\partial f}{\partial y}+z \frac{\partial f}{\partial z}=n f $ | (14) |
该方程称为欧拉方程。设地质异常体的坐标为(x0, y0, z0),则在测量点(x, y, z)处的位场函数
| $ f(x, y, z)=\frac{C}{r^{N}} $ | (15) |
式中:C为与测量点坐标无关的常数;场源到测量点的距离
| $ \begin{array}{*{20}{c}} {\left( {x - {x_0}} \right)\frac{{\partial f}}{{\partial x}} + \left( {y - {y_0}} \right)\frac{{\partial f}}{{\partial y}} + \left( {z - {z_0}} \right)\frac{{\partial f}}{{\partial z}}}\\ { = - Nf\left( {x - {x_0},y - {y_0},z - {z_0}} \right)} \end{array} $ | (16) |
当空间坐标系中磁异常场源中心位置坐标为(0, 0, 0),则磁异常场源位置矢量r=(-x, -y, -z)T,该场源产生的磁场矢量三分量为
| $ B_{i}(x, y, z)=f(x-0, y-0, z-0) $ | (17) |
式(17)满足式(16)的位场欧拉方程形式
| $ \left\{ {\begin{array}{*{20}{l}} {x\frac{{\partial {B_x}}}{{\partial x}} + y\frac{{\partial {B_x}}}{{\partial y}} + z\frac{{\partial {B_x}}}{{\partial z}} = - N{B_x}(x,y,z)}\\ {x\frac{{\partial {B_y}}}{{\partial x}} + y\frac{{\partial {B_y}}}{{\partial y}} + z\frac{{\partial {B_y}}}{{\partial z}} = - N{B_y}(x,y,z)}\\ {x\frac{{\partial {B_z}}}{{\partial x}} + y\frac{{\partial {B_z}}}{{\partial y}} + z\frac{{\partial {B_z}}}{{\partial z}} = - N{B_z}(x,y,z)} \end{array}} \right. $ | (18) |
式(18)可写为矩阵形式
| $ \left[\begin{array}{ccc}{B_{x x}} & {B_{x y}} & {B_{x z}} \\ {B_{y x}} & {B_{y y}} & {B_{y z}} \\ {B_{z x}} & {B_{z y}} & {B_{z z}}\end{array}\right]\left[\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right]=-N\left[\begin{array}{c}{B_{x}} \\ {B_{y}} \\ {B_{z}}\end{array}\right] $ | (19) |
式(19)即为三维欧拉反褶积公式。Nara定位法[8]推导了磁偶极子梯度差,得到了式(19)中N=3的特例。当位场中仅存在磁异常场,对于给定待测场源的构造指数N,测得点(x, y, z)处张量矩阵的9个元素及磁场矢量的3个元素,就能反解出场源位置矢量r=(-x, -y, -z)T。然而,实际位场不会仅仅包括磁异常场。由于此处磁场矢量(Bx、Bx、Bz)仅由场源产生,而张量系统测得的磁场矢量为磁异常场与背景磁场的矢量叠加,故Nara法对实测数据的定位精度必然受到影响。
3.3 磁性目标位置的二阶张量欧拉反褶积求解为了从叠加场中有效分离出磁性体异常场,对式(18)中各等式两边分别对x、y、z求偏导
| $ \left\{ {\begin{array}{*{20}{l}} {x{B_{xxx}} + y{B_{xyx}} + z{B_{xzx}} = - \left( {N + 1} \right){B_{xx}}}\\ {x{B_{yxy}} + y{B_{yyy}} + z{B_{yxy}} = - \left( {N + 1} \right){B_{yy}}}\\ {x{B_{zxz}} + y{B_{zyz}} + z{B_{zzz}} = - \left( {N + 1} \right){B_{zz}}} \end{array}} \right. $ | (20) |
磁偶极子的构造指数为3,用于磁性目标定位的式(20)可写为矩阵乘积的形式
| $ \left[ {\begin{array}{*{20}{c}} {{B_{xxx}}}&{{B_{xyx}}}&{{B_{xzx}}}\\ {{B_{yxy}}}&{{B_{yyy}}}&{{B_{yzy}}}\\ {{B_{zxz}}}&{{B_{zyz}}}&{{B_{zzz}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x\\ y\\ z \end{array}} \right] = - 4\left[ {\begin{array}{*{20}{c}} {{B_{xx}}}\\ {{B_{yy}}}\\ {{B_{zz}}} \end{array}} \right] $ | (21) |
本文定义上式为二阶张量欧拉反褶积公式,描述了磁偶极子在测量点处产生的一阶、二阶张量与其位置矢量之间的关系。基于3.1节中的二阶张量系统可测得式(21)中二阶张量矩阵的前6个元素和一阶张量分量Bxx、Byy、Bzz。然而,位置矢量未知数为3,则已知的两个方程构成的线性方程组是欠定的。
由张量衍生不变关系可知,磁偶极子场源下张量矩阵G的绝对值最小特征值λ3对应的特征向量v3垂直于磁偶极子磁矩矢量m和位置矢量r所在平面,有
| $ {\mathit{\boldsymbol{v}}_3} \cdot \mathit{\boldsymbol{r}} = \left[ {\begin{array}{*{20}{l}} {{v_{3x}}}&{{v_{3y}}}&{{v_{3z}}} \end{array}} \right]{\left[ {\begin{array}{*{20}{l}} x&y&z \end{array}} \right]^{\rm{T}}} = 0 $ | (22) |
则式(22)可拓展为
| $ \left[ {\begin{array}{*{20}{c}} {{B_{xxx}}}&{{B_{xyx}}}&{{B_{xzx}}}\\ {{B_{yxy}}}&{{B_{yyy}}}&{{B_{yzy}}}\\ {{v_{3x}}}&{{v_{3y}}}&{{v_{3z}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} x\\ y\\ z \end{array}} \right] = - 4\left[ {\begin{array}{*{20}{c}} {{B_{xx}}}\\ {{B_{yy}}}\\ 0 \end{array}} \right] \Rightarrow {\mathit{\boldsymbol{G}}_\mathit{\boldsymbol{v}}}\mathit{\boldsymbol{r}} = - 4{\mathit{\boldsymbol{g}}_\mathit{\boldsymbol{v}}} $ | (23) |
式中Gv、gv均可通过二阶张量系统测量后求解得到,据此可解得磁偶极子的位置矢量
| $ \boldsymbol{r}=-4 \boldsymbol{G}_{v}^{-1} \boldsymbol{g}_{v} $ | (24) |
再利用式(4)可解得磁矩矢量m。该方法仅需利用单一测量点的一阶、二阶张量数据便能实现磁偶极子的单点定位。
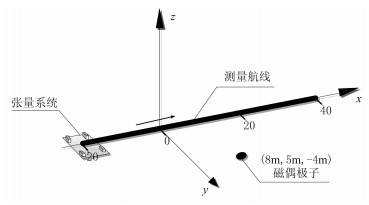
4 仿真分析将磁偶极子置于真空空间(8m, 5m, -4m)处,磁矩模为8000A·m-2,磁偶极子磁偏角为30°,磁倾角为40°。假设地磁背景场为匀强磁场,地磁总场强度(Total magnetic intensity,TMI)为55000nT,磁倾角为60°,磁偏角为-7°(西偏)。模拟搭建一个二阶平面十字形磁梯度张量系统[11]进行测量,基线距离d设为0.4m。单航线测量从(-20m, 0, 0)到(40m, 0, 0),测量试验如图 4。
|
图 4 磁偶极子场源张量系统单航线测量试验示意图 |
航线运动过程保持系统姿态不变,采样间隔为1m。在测量航线上各测量点处测得的磁场矢量三分量值如图 5所示。可见在庞大的地磁场背景下,由磁偶极子产生的部分磁场矢量分量场基本被淹没,磁异常场难以有效分离。由文献[11]知,磁传感器实际输出可表示为

|
图 5 单航线测量中磁场分量 |
| $ \begin{array}{l} {\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} {\cos \gamma }&{\sin \gamma }&0\\ { - \sin \gamma }&{\cos \gamma }&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \beta }&0&{ - \sin \beta }\\ 0&1&0\\ {\sin \beta }&0&{\cos \beta } \end{array}} \right] \times \\ \;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \alpha }&{\sin \alpha }\\ 0&{ - \sin \alpha }&{\cos \alpha } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{c_x}}&0&0\\ 0&{{c_y}}&0\\ 0&0&{{c_z}} \end{array}} \right] \times \\ \;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \varphi }&{\sin \theta \cos \varphi }&{\sin \varphi }\\ 0&{\cos \psi }&{\sin \psi }\\ 0&0&1 \end{array}} \right]{\mathit{\boldsymbol{B}}_2} + \left[ {\begin{array}{*{20}{c}} {{i_x}}\\ {{i_y}}\\ {{i_z}} \end{array}} \right] + \mathit{\boldsymbol{w}} \end{array} $ | (25) |
式中:B1为传感器实际输出;ix、iy、iz为零位偏差;cx、cy、cz为灵敏度标度因子;φ、θ、ψ为非正交角;α、β、γ为非对准误差角;w为测量噪声;B2为理想输出。利用图 3中的5个传感器的位置仿真出该点处的航线测量数据,共三组作对比。
① 理想组:误差为零、测量噪声为零;
② 实际组:随机预设各传感器的12个误差参数,并加入均值为0、方差为1nT的高斯噪声,预设参数值列于表 1中;
|
|
表 1 预设5个传感器系统误差与非对准误差 |
③ 校正组:使用两步线性校正方法[11]对②中预设误差后的各传感器的12种误差参数进行估计,并以此对实际组中的测量值进行校正。
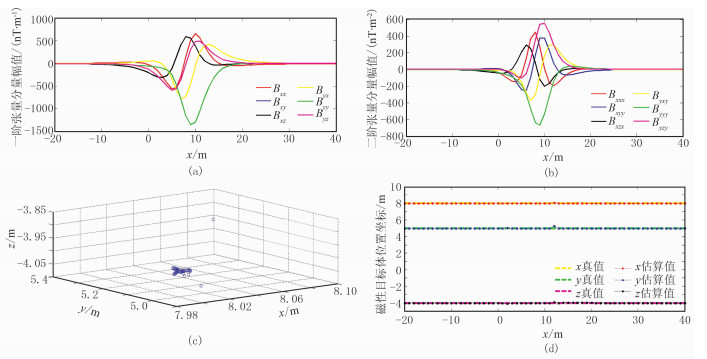
由式(1)可知G为对称矩阵,但式(13)中Bxy与Byx测量值存在差异,可视其为两个独立分量,此时G中共有6个独立分量。利用本文方法对航线上所有测量点的①、②、③组测量数据分别计算磁偶极子位置坐标,则该测量航线三组测量数据下该二阶张量系统测得的各测量点的一阶张量的6个独立分量、二阶张量的6个独立分量、估计得到的磁性目标空间位置图、磁性目标位置的坐标分别如图 6、图 7和图 8所示。
|
图 6 各传感器不加误差、噪声时的单航线张量测量结果及目标定位结果 (a)一阶张量测量的6个独立分量;(b)二阶张量测量的6个独立分量;(c)估计的磁性目标三维空间位置;(d)估计的磁性目标位置坐标 |

|
图 7 各传感器加入误差、测量噪声时的单航线张量测量结果及目标定位结果 (a)一阶张量测量的6个独立分量;(b)二阶张量测量的6个独立分量;(c)估计的磁性目标三维空间位置;(d)估计的磁性目标位置坐标 |
|
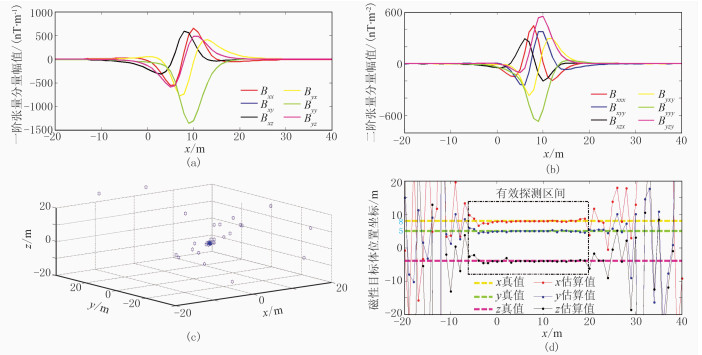
图 8 各传感器进行两步线性校正后的单航线张量测量结果及目标定位结果 (a)一阶张量测量的6个独立分量;(b)二阶张量测量的6个独立分量;(c)估计的磁性目标三维空间位置;(d)估计的磁性目标位置坐标 |
参考文献[11]中的仿真结果,在相同测量工况的12个误差参数的预设条件下,都引入了均值为0、方差为1nT的高斯噪声,由第③步中估计的各个传感器的误差接近于0。由三组测量数据的定位结果可知:①当未加入噪声和误差时,该方法对磁偶极子场源的位置估计误差接近0,且在航线上所有点位均能实现有效探测并估计出准确的场源坐标;②各传感器引入12个误差和预设噪声时,在该航线上无法有效探测到磁源目标;③加入均值为0、方差为1nT的高斯噪声后,该二阶张量系统在(-5m, 0, 0)~(20m, 0, 0)范围内基本实现了有效探测及精确定位,超出该范围的点无法被有效探测。
5 实验验证为验证方法对实际目标体的定位准确性及张量系统校正对定位精度的提升能力,设计如下实验。
① 搭建一个一阶平面十字形磁梯度张量系统(图 9),基线距离d为0.5m。二阶张量系统在中心点o处增加传感器5。为最大限度避免结构误差,在单航线测量中可利用同轴其他传感器对传感器5读数进行间接测量,从而获得二阶张量数据。间接测量示意图见图 10。

|
图 9 平面十字形磁梯度张量系统示意图 |

|
图 10 传感器5的间接测量示意图 |
② 使用标量质子磁强计选择地磁场稳定的某测区,面积为2.1m×2.1m。系统置于滑动台架上,测量平面高0.65m。测得该测区内平均TMI标量为53911.48nT。尽管台架尽量选择无磁材质,但局部连接处仍存在磁干扰。为尽量避免磁干扰影响定位精度,利用椭球拟合集成补偿方法[12]对测区内的张量系统进行校正参数估计,得到一组适用于该区域的系统各传感器误差补偿参数(集成误差补偿系数F和集成零偏向量Iw)和对准参数(旋转矩阵T),见表 2。该方法属于间接校正法,不需要估计传感器具体参数便可实现磁干扰环境下的磁梯度张量系统集成校正,对测量环境的硬、软磁干扰具有良好的补偿效果,同时可有效消除传感器系统误差和非对准误差。磁传感器输出补偿公式[12]为
|
|
表 2 预先估计的磁梯度张量系统误差补偿参数与旋转矩阵 |
| $ \boldsymbol{B}_{\mathrm{c}}=\boldsymbol{T} \boldsymbol{F}\left(\boldsymbol{B}_{\mathrm{r}}-\boldsymbol{I}_{\mathrm{w}}\right) $ | (26) |
式中:Bc为理想传感器输出;Br为待补偿的实际传感器输出。
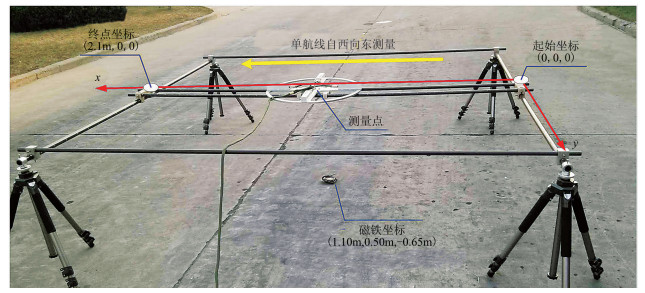
③ 以测量平面xoy建立空间直角坐标系,x轴向东为正,z轴向上为正。以一小型磁铁为探测目标,张量系统单航线测量方向自西向东,起始坐标为(0, 0, 0),终点坐标为(2.1m, 0, 0),目标磁铁坐标为(1.10m, 0.50m, -0.65m),采样间隔为0.05m,则该航线共有43个测量点,传感器5的读数间接等效于第6至第43测点的传感器4读数和第34至38测点的传感器2读数。该单航线测量实验装置示意图见图 11。
|
图 11 单航线磁性目标定位实验装置示意图 |
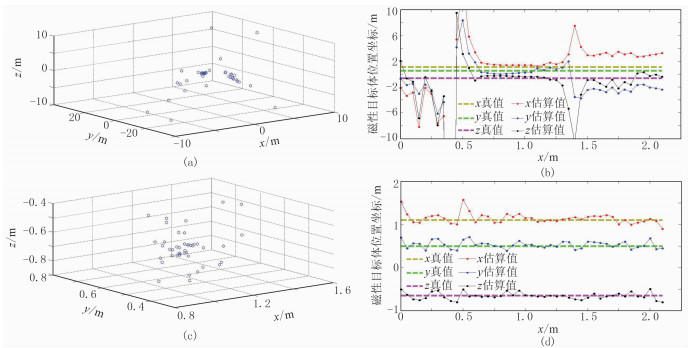
由于探测距离远大于磁铁尺度的2.5倍,因此将其视为磁偶极子,并进行目标单点定位计算。首先,将步骤③中全部原始数据直接进行磁铁位置坐标演算;然后利用表 2中参数对步骤③中全部测量数据进行校正处理,再演算磁铁坐标。校正前、后估计的磁铁位置如图 12所示。将校正前、后估算坐标的精度使用均方根误差(Root mean square error, RMSE)[19]进行量化
|
图 12 经椭球拟合集成校正前、后对磁铁的定位结果 (a)校正前目标3D空间位置;(b)校正前目标位置坐标;(c)校正后目标3D空间位置;(d)校正后目标位置坐标 为便于展示大部分数据点,图b中仅仅展示了误差小于10m的点,实际计算结果最大误差达到436m |
| $ {E_{{\rm{RMS}}}} = \sqrt {\frac{1}{X}\sum\limits_{i = 1}^X {{{\left| {{\mathit{\boldsymbol{X}}^{\rm{r}}} - \mathit{\boldsymbol{X}}_i^{\rm{e}}} \right|}^2}} } $ | (27) |
式中:Xie为第i个测量点的坐标估计值;Xr为真实坐标;X为测量点数。
实验结果表明,在该实验工况下,校正后的系统对磁铁坐标的估计精度可控制在均方根误差10cm以内(表 3)。当背景场更稳定、系统校正精度更高时,理论上能实现磁性目标厘米级别以上的精确定位。系统误差校正技术的应用对提升张量数据解释精度尤为关键。
|
|
表 3 系统校正前、后磁铁目标的坐标估计精度对比 |
(1) 推导的张量衍生不变关系表明:磁偶极子磁矩矢量与测量点的位置矢量夹角是恒定的,且仅与该点处张量矩阵特征值有关;磁偶极子场源的张量矩阵中间特征值对应的特征向量垂直于磁矩矢量与位置矢量,最大、最小特征值对应的特征向量与磁矩矢量和位置矢量共面。
(2) 提出了平面十字形二阶张量系统概念与测量方法,对三维欧拉反褶积公式求导后,利用一阶、二阶张量与张量衍生不变关系可求解磁源位置矢量。
(3) 相比Nara定位法,本文方法能将磁异常信息与背景地磁场有效分离,坐标估计值唯一,在有效探测范围内能实现测区中任意点对磁性目标的单点定位。
(4) 仿真和实验结果均表明:针对小尺度磁铁的定位实验中,在该实验工况下,经误差校正后的磁梯度张量系统的定位精度控制在均方根误差10cm以内。
基于二阶磁张量欧拉反褶积的磁源单点定位方法同样适用于其他结构类型的二阶磁梯度张量系统,且在实测中利用误差校正技术极大地提升了磁性目标的定位精度,表明误差校正对于提升张量数据解释精度的重要性。高精度目标单点定位技术与张量系统误差校正技术的结合,为后期针对磁异常体的反演识别、三维重塑等更深层次张量数据解释提供了理论基础与经验参考。
| [1] |
Schmidt P W, Clark D A. The magnetic gradient tensor:Its properties and uses in source characterization[J]. The Leading Edge, 2006, 25(1): 75-78. DOI:10.1190/1.2164759 |
| [2] |
张昌达. 航空磁力梯度张量测量——航空磁测技术的最新进展[J]. 工程地球物理学报, 2006, 3(5): 354-361. ZHANG Changda. Airborne tensor magnetic gradio-metry:the latest progress of airborne magnetometric technology[J]. Chinese Journal of Engineering Geophysics, 2006, 3(5): 354-361. DOI:10.3969/j.issn.1672-7940.2006.05.005 |
| [3] |
Li Q Z, Li Z N, Zhang Y T, et al. Artificial vector calibration method for differencing magnetic gradient tensor systems[J]. Sensors, 2018, 18(2): 361. DOI:10.3390/s18020361 |
| [4] |
张琪, 张英堂, 李志宁, 等. 改进的低纬度化极稳定算法[J]. 石油地球物理勘探, 2018, 53(3): 606-616. ZHANG Qi, ZHANG Yingtang, LI Zhining, et al. An improved stable algorithm of the reduction-to-the-pole at low latitudes[J]. Oil Geophysical Prospecting, 2018, 53(3): 606-616. |
| [5] |
尹刚, 张英堂, 米松林, 等. 基于倾斜角和Helbig方法的多磁源目标反演技术[J]. 上海交通大学学报, 2017, 51(5): 577-584. YIN Gang, ZHANG Yingtang, MI Songlin, et al. Multiple magnetic targets inversion technique based on tilt angle and Helbig method[J]. Journal of Shanghai Jiaotong University, 2017, 51(5): 577-584. |
| [6] |
王清振, 张金淼, 姜秀娣, 等. 利用梯度结构张量检测盐丘与断层[J]. 石油地球物理勘探, 2018, 53(4): 826-831. WANG Qingzhen, ZHANG Jinmiao, JIANG Xiudi, et al. Salt dome and fault detection based on the gradient-structure tensor[J]. Oil Geophysical Prospecting, 2018, 53(4): 826-831. |
| [7] |
张朝阳, 肖昌汉, 高俊吉, 等. 磁性物体磁偶极子模型适用性的试验研究[J]. 应用基础与工程科学学报, 2010, 18(5): 862-868. ZHANG Zhaoyang, XIAO Changhan, GAO Junji, et al. Experiment research of magnetic dipole model applicability for a magnetic object[J]. Journal of Basic Science and Engineering, 2010, 18(5): 862-868. DOI:10.3969/j.issn.1005-0930.2010.05.016 |
| [8] |
Nara T, Suzuki S, Ando S. A closed-form formula for magnetic dipole localization by measurement of its magnetic field and spatial gradients[J]. IEEE Tran-sactions on Magnetics, 2006, 42(10): 3291-3293. DOI:10.1109/TMAG.2006.879151 |
| [9] |
迟铖, 任建存, 吕俊伟, 等. 基于磁梯度张量的目标多测量点线性定位方法[J]. 探测与控制学报, 2017, 39(5): 58-62, 70. CHI Cheng, REN Jiancun, LYU Junwei, et al. Linear localization method based on magnetic gradient tensor of multipoint[J]. Journal of Detection & Control, 2017, 39(5): 58-62, 70. |
| [10] |
刘继昊, 李夕海, 曾小牛. 基于两点磁梯度张量的磁性目标在线定位方法[J]. 地球物理学报, 2017, 60(10): 3995-4004. LIU Jihao, LI Xihai, ZENG Xiaoniu. Online magnetic target location method based on the magnetic gradient tensor of two points[J]. Chinese Journal of Geophy-sics, 2017, 60(10): 3995-4004. DOI:10.6038/cjg20171026 |
| [11] |
李青竹, 李志宁, 张英堂, 等. 平面十字磁梯度张量系统的两步线性校正[J]. 仪器仪表学报, 2017, 38(9): 2232-2242. LI Qingzhu, LI Zhining, ZHANG Yingtang, et al. Two-step linear calibration of planar cross magnetic gradient tensor system[J]. Chinese Journal of Scientific Instrument, 2017, 38(9): 2232-2242. DOI:10.3969/j.issn.0254-3087.2017.09.018 |
| [12] |
李青竹, 李志宁, 张英堂, 等. 基于椭球拟合的磁梯度张量系统集成校正[J]. 中国惯性技术学报, 2018, 26(2): 187-195. LI Qingzhu, LI Zhining, ZHANG Yingtang, et al. Integrated calibration of magnetic gradient tensor system based on ellipsoid fitting[J]. Journal of Chinese Inertial Technology, 2018, 26(2): 187-195. |
| [13] |
尹刚, 张林, 谢艳, 等. 磁梯度张量系统的非线性校正方法[J]. 仪器仪表学报, 2018, 39(4): 35-43. YIN Gang, ZHANG Lin, XIE Yan, et al. Nonlinear calibration method of magnetic gradient tensor system[J]. Chinese Journal of Scientific Instrument, 2018, 39(4): 35-43. |
| [14] |
Salam M A.Static magnetic field//Electromagnetic Field Theories for Engineering[M].Springer, Singapore, 2014, 141-185.
|
| [15] |
Pedersen L B, Rasmussen T M. The gradient tensor of potential field anomalies:Some implications on data collection and data processing of maps[J]. Geophy-sics, 1990, 55(12): 1558-1566. |
| [16] |
吕俊伟, 迟铖, 于振涛, 等. 磁梯度张量不变量的椭圆误差消除方法研究[J]. 物理学报, 2015, 64(19): 60-67. LYU Junwei, CHI Cheng, YU Zhentao, et al. Research on the asphericity error elimination of the invariant of magnetic gradient tensor[J]. Acta Physica Sinica, 2015, 64(19): 60-67. |
| [17] |
鲁宝亮, 范美宁, 张原庆. 欧拉反褶积中构造指数的计算与优化选取[J]. 地球物理学进展, 2009, 24(3): 1027-1031. LU Baoliang, FAN Meining, ZHANG Yuanqing. The calculation and optimization of structure index in Euler deconvolution[J]. Progress in Geophysics, 2009, 24(3): 1027-1031. DOI:10.3969/j.issn.1004-2903.2009.03.029 |
| [18] |
王明, 骆遥, 罗锋, 等. 欧拉反褶积在重磁位场中应用与发展[J]. 物探与化探, 2012, 36(5): 834-841. WANG Ming, LUO Yao, LUO Feng, et al. The application and development of Euler deconvolution in gravity and magnetic field[J]. Geophysical & Geochemical Exploration, 2012, 36(5): 834-841. |
| [19] |
Chai T, Draxler R R. Root mean square error (RMSE) or mean absolute error (MAE)?-Arguments against avoiding RMSE in the literature[J]. Geoscientific Mo-del Development, 2014, 7(3): 1247-1250. DOI:10.5194/gmd-7-1247-2014 |



 李志宁, 河北省石家庄市新华区和平西路97号, 050003。Email:
李志宁, 河北省石家庄市新华区和平西路97号, 050003。Email: