② 河北省电磁场与电器可靠性重点实验室, 天津 300130;
③ 中国科学院电工研究所, 北京 100190;
④ 中国科学院大学, 北京 100049
② Hebei Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability, Hebei University of Technology, Tianjin 300130, China;
③ Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing 100190, China;
④ University of Chinese Academy of Sciences, Beijing 100049, China
随钻电磁波电阻率测井是电法测井的重要内容之一[1-5]。探测深度是衡量随钻电磁波电阻率测井仪器性能的关键指标之一。测井仪器的探测深度与源距、频率和地层电导率密切相关。提高源距是增大探测深度的有效方法。然而,在电法测井领域,长源距测井方法在实现过程中遇到了很大的挑战。接收线圈开路感应电动势随着源距的增大衰减严重,妨碍了进一步增大源距从而提高探测深度的目标。本文借鉴磁谐振耦合原理[6-8],对发射线圈和接收线圈进行同频谐振, 增大接收线圈的电压幅值,从而增大源距。
因为测井仪器是在地下探测,处于具有一定电导率的地层环境中。为了验证谐振方法的正确性,实验室验证阶段需要模拟地层电导率,通常利用刻度环实现。对于传统的随钻电磁波电阻率测井方法来说,采用线圈开路形式,相关的刻度方法研究已比较成熟。杨健弟[9]分析了单发单收线圈系单元开路时刻度环感抗对刻度值的影响;仵杰等[10]讨论了单发单收线圈系开路时刻度环大小选择、最佳刻度点和刻度电阻确定等问题;袁吉祥等[11]基于几何因子原理从线圈系和电子线路两个角度阐述了仪器刻度的原理和方法;魏宝君等[12]对单发双收线圈系在真空中的刻度方法进行了研究。这些刻度方法都是针对单发单收或单发双收结构。
为了保证谐振后增大线圈电压幅度而不改变幅度比,本文提出的谐振方法采用双发单收结构。两个发射线圈分别导通时,为了更加准确地描述在一定电导率地层中的谐振响应特性,文中深入分析了线圈源距、刻度环位置和刻度环电阻等参数的关系,提出刻度环参数的动态选择方法。本文主要围绕双发单收谐振线圈系刻度方法展开研究,由以下三部分组成。
(1) 讨论单发双收线圈系采用同频谐振的局限性,提出双发单收谐振线圈系结构。基于DOLL几何因子理论阐述了双发单收谐振型线圈系的测量原理和刻度原理。
(2) 提出了刻度环参数动态选择方法,通过数值模拟研究双发单收谐振型线圈系参数、刻度环参数和模拟地层电导率之间的变化关系。
(3) 搭建实验平台,对双发单收谐振型线圈系的刻度环参数动态选择方法进行验证,并对均匀地层中接收线圈开路和谐振响应特性进行了对比分析。
1 谐振型线圈系原理 1.1 单发双收线圈系随钻电磁波电阻率测井仪器由单个或多个线圈系单元组成。传统线圈系单元由一个发射线圈T和两个接收线圈R1、R2组成(图 1)。

|
图 1 单发双收线圈系 |
测量接收线圈开路感应电动势幅度。设R1记录的电压幅值为UR1,R2记录的电压幅值为UR2,则开路幅度比为
| $ E_{\mathrm{ATT0}}=\frac{U_{\mathrm{R}_{1}}}{U_{\mathrm{R}_{2}}} $ | (1) |
如果接收线圈R1和R2同频谐振,接收线圈R1的电压幅值被放大Q1倍,而接收线圈R2电压幅值被放大Q2倍,则谐振幅度比为
| $ E_{\mathrm{ATT1}}=\frac{Q_{1} U_{\mathrm{R}_{1}}}{Q_{2} U_{\mathrm{R}_{2}}} $ | (2) |
谐振的目的是提高接收线圈电压幅度,而不是改变幅度比。理想情况下,若R1与R2完全相同,谐振状态完全相同,则Q1=Q2,EATT0=EATT1。可以发现,此时谐振的作用仅提高了接收线圈电压幅值,并没有改变幅度比。
但是,如果两个接收线圈参数或线圈回路的谐振状态发生变化,导致两个接收线圈的电压放大倍数不同,即Q1≠Q2,则会导致EATT0≠EATT1,使测量结果偏离正确值。所以,谐振方法应用于单发双收线圈系具有一定的局限性。
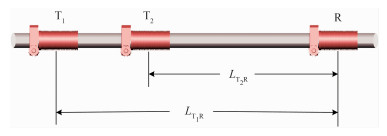
1.2 双发单收线圈系为了解决上述单发双收线圈系谐振时存在的问题,本文提出采用双发单收谐振型线圈系结构,如图 2所示。双发单收谐振型线圈系由发射线圈T1、T2和接收线圈R组成,T1和T2线圈匝数分别为nT1和nT2。T1和T2依次轮流导通,发射电流分别为I1和I2。T1导通、T2断开时,接收线圈R的感应电压为UT1;T2导通、T1断开时,接收线圈R感应电压为UT2。
|
图 2 双发单收线圈系 |
根据UT1和UT2,可得幅度比为
| $ E_{\mathrm{ATT}}=\frac{U_{\mathrm{T}_{1}}}{U_{\mathrm{T}_{2}}} $ | (3) |
本文研究均匀地层特性。只有在测量相同电导率地层时,通过测得的感应电压UT1和UT2得到的幅度比才是正确的,通过幅度比反演的地层电导率也才是可靠的。
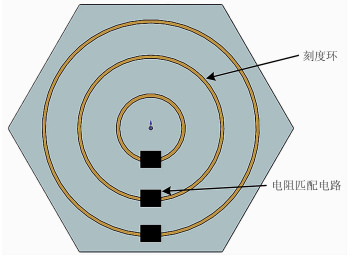
1.3 刻度原理随钻电磁波电阻率测井通过接收线圈的感应电压幅度反映地层介质的电性特征。实验室应用刻度环模拟地层电导率,如图 3所示。一般情况下,刻度环是根据要刻度系统的参数,选取一个半径为r的金属导线环匹配相应的刻度电阻。刻度环的参数与地层电导率是相对应的。通过调整刻度环的位置和r以及刻度环电阻模拟不同的地层电导率。电流依次经过T1和T2时在空间形成磁场,通过刻度环耦合到R,在R上形成响应信号。
|
图 3 刻度环示意图 |
几何因子是研究仪器响应信号时引入的、只与子午面上的面积元有关的参数。基于DOLL几何因子理论[13-16],线圈系的微分几何因子为
| $ g=\frac{\frac{r^{3}}{2} \sum\limits_{j=0}^{l} \frac{n_{\mathrm{T}_{j}}}{\left(Z_{\mathrm{T}_{j}}^{2}+r^{2}\right)^{\frac{3}{2}}} \sum\limits_{k=0}^{m} \frac{n_{\mathrm{R}_{k}}}{\left[\left(L_{\mathrm{TR}}-Z_{\mathrm{T}}\right)^{2}+r^{2}\right) ]^{\frac{3}{2}}}}{\sum\limits_{j, k=0}^{l, m} \frac{n_{\mathrm{T}_{j}} n_{\mathrm{R}_{k}}}{L_{T_{j}, R_{k}}}} $ | (4) |
式中:ZT为两个发射线圈中点到刻度环的距离;nTj为发射线圈匝数;nRk为接收线圈匝数;l为发射线圈个数; m为接收线圈个数。
半径为r的金属导线环内接入一个电阻为q的电阻,称为刻度环。刻度环可等效于一个电导率为σ、截面积为drdz、半径为r的圆环。令环的电导等于1/q,得到
| $ \sigma \mathrm{d} r \mathrm{d} z=\frac{2 {\rm{ \mathsf{ π} }} r}{q} $ | (5) |
单元环的σ和drdz虽然是未知的,但他们的乘积σdrdz却可以由电阻唯一确定。而为了构造一个视电导率值σa,所需要的正是这个乘积
| $ \sigma_{\mathrm{a}}=g_{\sigma} \mathrm{d} r \mathrm{d} z=\frac{2 {\rm{ \mathsf{ π} }} r g}{q} $ | (6) |
将g代入上式,得到
| $ \sigma_{a}=\frac{\frac{{\rm{ \mathsf{ π} }} r^{4}}{q} \sum\limits_{j=0}^{l} \frac{n_{\mathrm{T}_{j}}}{\left(Z_{\mathrm{T}}^{2}+r^{2}\right)^{\frac{3}{2}}} \sum\limits_{k=0}^{m} \frac{n_{\mathrm{R}_{k}}}{\left[\left(L_{\mathrm{TR}}-Z_{\mathrm{T}}\right)^{2}+r^{2}\right]^{\frac{3}{2}}}}{\sum\limits_{j, k=0}^{l, m} \frac{n_{\mathrm{T}_{j}} n_{\mathrm{R}_{k}}}{L_{\mathrm{T}_{j}, \mathrm{R}_{k}}}} $ | (7) |
双发单收谐振型线圈系的刻度方法与传统的电磁波测井仪器不同。传统的电磁波测井仪器刻度时,最基本的单元是一个发射线圈和一个接收线圈,线圈系固定后,源距不会发生变化,所表征的地层电导率不变。而对于双发单收线圈系,发射线圈T1和T2分别导通时,两个发射线圈与接收线圈的源距不同。由图 2可以看出,当T1导通时,源距为LT1R,式(4)中LTR=LT1R;当T2导通时,源距为LT2R,即LTR=LT2R。
根据式(7),刻度环电阻一定时,由于两个发射线圈相对于接收线圈的源距不同,刻度环在同一位置时,与发射和接收线圈的距离不同,所模拟的地层电导率不同。为了获得同一个地层电导率参数下的测量结果,本文针对双发单收线圈系提出了一种根据线圈系参数和地层电导率对刻度环参数进行动态调整的方法。
对双发单收谐振型线圈系寻找合适的刻度环位置ZT和刻度环电阻参数组合是非常必要的。下面分别讨论给定地层电导率、源距不同时刻度环位置和刻度环电阻的变化关系以及给定源距、地层电导率不同时刻度环位置和刻度环电阻的变化关系。通过对刻度环参数的分析得出合适的参数组合。
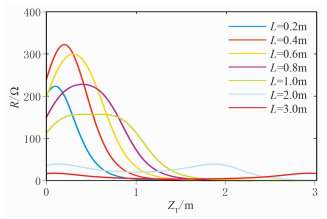
2.1 源距不同时刻度环参数的选择方法针对于特定电导率环境下,对不同源距时刻度环电阻与刻度环位置的变化关系进行分析。令发射线圈T1导通,源距L= LTR=LT1R。选取刻度环半径r=0.5m,T1线圈匝数nT1=38,T2线圈匝数nT2=38,接收线圈R匝数nR=6,给定目标视电导率σa=0.01S/m。L分别选择0.2、0.4、0.6、0.8、1.0、2.0、3.0m时,改变刻度环与发射线圈T1的距离ZT,分析刻度环电阻R与ZT之间的关系,作为发射线圈T1的实验依据,如图 4所示。该方法同样适用于发射线圈T2的位置选择。
|
图 4 变源距时刻度环电阻R与刻度环位置曲线图 |
由图 4可以看出,当源距L较小时,曲线较为陡峭。在这种情况下,为了保持相同的电导率均质环境,若ZT发生较小变化,则需要对刻度环电阻R进行较大幅度的调整。当L=1.0m时,刻度环处于发射线圈和接收线圈之间,出现了较长距离的平稳区,这区间ZT的变化几乎不会对R产生影响;当源距较大时(L>1.0m),曲线没有出现特别陡峭区,整体呈现出波浪形态势。由图 4可见,当L≤1.0m时,无论ZT取值如何,R的值都较大;当L>1.0m时,相同刻度环位置所对应的R值显著降低。
根据上述分析,选择L为1.0m可以出现较长的平稳区,在此区域可以降低ZT的微小差异所引起的视电导率误差,刻度环R大小合适,有利于电阻匹配。
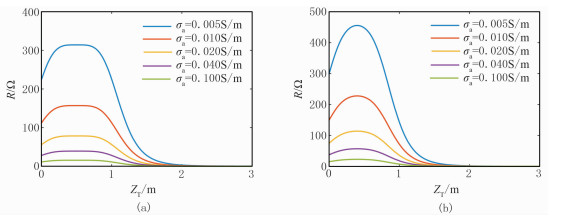
2.2 电导率不同时刻度环参数的选择方法分别选取固定源距L=1.0m和L=0.8m,发射线圈、接收线圈匝数以及刻度环半径不变。当σa取不同值时,R与ZT的关系如图 5所示。
|
图 5 变电导率时刻度环R与ZT的关系曲线 (a)L=1.0m;(b)L=0.8m |
从图 5可以看出,对于相同L,不同σa会使相同ZT位置对应的R发生改变。σa越小,对应的刻度环R越大。从图 5a可以看出,L=1.0m时在发射线圈和接收线圈之间出现了平稳区,但是相对平稳度不同。σa越大,相对平稳度越高。从图 5b可以看出,L=0.8m时,σa越小则相同ZT对应的刻度环R分辨度越好,即R的微小差异不会对σa产生很大的误差。因此在相同的ZT位置应选择刻度环电阻分辨度较好的参数。
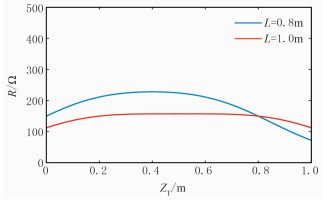
根据上述分析,为了兼顾相对平稳度与刻度环电阻分辨度,得到较为直观的变化关系,利于参数选择,固定源距L分别为1.0m和0.8m,σa=0.01S/m,得到发射线圈与接收线圈内部的刻度环电阻R与刻度环位置ZT的变化关系曲线如图 6所示。
|
图 6 特定源距组合刻度环参数 |
图 6中曲线较平稳,且有一定的电阻分辨度。因此,在此源距组合下参数选择较为稳定,可选取此组数据作为双发单收谐振型线圈系开路与谐振实验的参数,如表 1所示。
|
|
表 1 开路与谐振实验参数 |
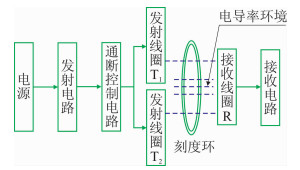
电磁波电阻率测井实验系统由电源、发射电路、通断控制电路、发射线圈、接收线圈电路和刻度环组成,如图 7所示。
|
图 7 实验平台模块示意图 |
发射电路提供场源信号,实现将产生的发射信号进行功率放大,并且在发射线圈产生一定的电流,促使在线圈上激励足够强度的电磁场。功率部分由隔离驱动电路、逆变全桥电路、输出滤波电路等组成。采用集成运算放大器与分立三极管构成的E类功率放大器。
接收电路由放大调制电路、主控制电路组成。前级放大调制电路实现对高频信号的降频和放大;主控制电路包括双路高精度模数转换器(ADC)、数字信号处理器(DSP)、双路直接数字式频率合成器(DDS)等,ADC两路同步采样,确保了幅度比和相位差的精准测量。接收电路采用TMS320F28335型数字信号处理器作为主控芯片,主要完成对ADC的控制、数字信号处理、以及对发射机的控制和驱动[19-20]。
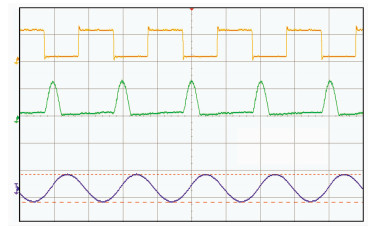
3.2 实验分析根据刻度环参数选择分析,选取发射线圈T1和接收线圈R的源距LT1R=1.0m,发射线圈T2和接收线圈R的源距为LT2R=0.8m,发射线圈T1和T2的匝数均为38,接收线圈R的匝数为6,两个发射线圈T1和T2同频谐振,分别对接收线圈开路和谐振时进行实验验证。根据表 1选取合适的ZT和R,使σa=0.01S/m,发射电路的参数如图 8所示。
|
图 8 发射电路参数 黄色曲线:驱动信号;绿色曲线:开关管电压;紫色曲线:罗氏线圈测量的接收电压 图中驱动信号的频率为990kHz, 幅值为970mV;发射线圈电流为1.02A |
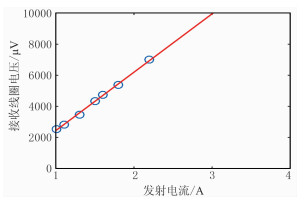
尽管模拟的是同一特定电导率地层,但是经数据采样发现,发射线圈谐振点的微小差别使得发射电路的负载产生了变化,进而使得发射电流也产生了变化,不同的发射电流在空间形成的磁场强度不同,因此在接收线圈处耦合形成的感应电动势就存在差别。在线性均匀介质中,发射电流与接收感应电动势应成线性关系。本实验系统选取了如图 9所示的一组发射线圈电流与接收线圈感应电动势变化关系。通过线性调整使T1与T2的电流相同,接收线圈感应电动势可以表征同一地层参数。
|
图 9 发射电流与接收感应电动势关系 |
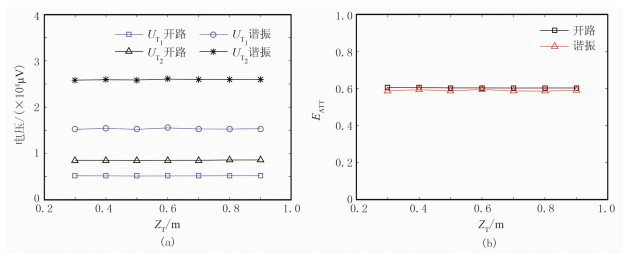
分别对接收线圈开路以及同频谐振,经过数据采样和线性调整可以得到如表 2所示结果,图 10分别是接收线圈开路和谐振时得到的电压幅值和幅度比。
|
|
表 2 开路和谐振时幅值及幅值比 |
|
图 10 接收线圈开路与谐振响应 (a)电压幅度; (b)电压幅度比 |
双发单收线圈系在某一时刻相当于单发单收线圈系。与单发单收线圈系不同的是,后期的数据处理是用两个接收线圈的幅度比来反映地层电性。
从图 10a可以看出,当双发单收谐振型线圈系源距固定时,选取合适的刻度环R和ZT参数组合,使接收线圈在开路和谐振时都能够得到基本相同的感应电动势幅值,说明选取合适的刻度环参数能够模拟相同电导率均质地层。接收线圈谐振后测得的感应电动势幅值比开路时明显提高,说明谐振方法对增大幅值有显著作用。从图 10b可以看出,接收线圈开路和谐振后的电压幅度比基本不变,可见其能够表征同一地层电导率。对比图 10a与图 10b可以发现,接收线圈谐振仅仅增大了感应电动势幅值,而幅度比基本不变。
4 结论(1) 基于DOLL几何因子理论,对双发单收谐振型线圈系结构进行刻度环参数选择分析,分别研究了变源距时和变电导率时刻度环参数的变化规律。结果表明,选择合适的刻度环参数可以获得较长距离的平稳区,刻度环位置的微小误差几乎不会对地层视电导率产生影响;也可以得到较好的电阻分辨度,电阻的微小差异不会导致视电导率产生很大的误差。因此刻度环参数的选择应兼顾相对平稳度与刻度环电阻分辨度。
(2) 根据刻度环参数规律分析,选定合适的参数组合,对接收线圈进行开路及同频谐振实验。当改变刻度环位置和电阻时,接收线圈幅值不变,表明该参数组合可以正确模拟在不同源距下相同电导率的线性均质地层,也证明了基于理论和规律分析选择参数的正确性。
(3) 通过动态调整刻度环,双发单收谐振型线圈系在大幅度增大幅值的情况下,得到了均匀地层幅度比,与开路时基本吻合,验证了双发单收型线圈系结构的合理性,证明了谐振方法的有效性,为增大源距、提高探测深度提供了可能。
| [1] |
张妙瑜, 郭宝龙, 仵杰, 等. 一种新共面线圈系对薄层的响应特征分析[J]. 石油地球物理勘探, 2018, 53(3): 578-586. ZHANG Miaoyu, GUO Baolong, WU Jie, et al. Response characteristics of a new coplanar coil system in thin beds[J]. Oil Geophysical Prospecting, 2018, 53(3): 578-586. |
| [2] |
马哲, 李军, 王朝阳, 等. 随钻感应电阻率测井仪器测量原理与应用[J]. 测井技术, 2004, 28(2): 155-157. MA Zhe, LI Jun, WANG Chaoyang, et al. Principle of tool resistivity induction MWD and its in-situ application[J]. Well Logging Technology, 2004, 28(2): 155-157. DOI:10.3969/j.issn.1004-1338.2004.02.018 |
| [3] |
杨震, 刘庆成, 岳步江, 等. 随钻电磁波电阻率测井仪器响应影响因素数值模拟[J]. 测井技术, 2011, 35(4): 325-330. YANG Zhen, LIU Qingcheng, YUE Bujiang, et al. Numerical simulation on influence factors of electromagnetic wave resistivity logging while drilling response[J]. Well Logging Technology, 2011, 35(4): 325-330. DOI:10.3969/j.issn.1004-1338.2011.04.006 |
| [4] |
Zhang Y, Xu L, Cao Z.Optimization of the electromagnetic wave resistivity tool in logging while drilling[C].IEEE International Conference on Imaging Systems and Techniques, 2014, 160-163. https://www.researchgate.net/publication/271482766_Optimization_of_the_Electromagnetic_Wave_Resistivity_tool_in_Logging_While_Drilling
|
| [5] |
Li M, Yue X, Hong D, et al. Simulation and analysis of the symmetrical measurements of a triaxial induction tool[J]. IEEE Geoscience & Remote Sensing Letters, 2015, 12(1): 122-124. |
| [6] |
张波, 疏许健, 黄润鸿. 感应和谐振无线电能传输技术的发展[J]. 电工技术学报, 2017, 32(18): 3-17. ZHANG Bo, SHU Xujian, HUANG Runhong. The development of inductive and resonant wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 3-17. |
| [7] |
Kazmierkowski M P, Moradewicz A J.Contactless energy transfer (CET) systems: a review[C].IEEE International Power Electronics and Motion Control Conference, 2012, 4-6. https://www.researchgate.net/publication/261419257_Contactless_energy_transfer_CET_systems_-_A_review
|
| [8] |
范兴明, 莫小勇, 张鑫. 磁耦合谐振无线电能传输的研究现状及应用[J]. 电工技术学报, 2013, 28(12): 75-82, 99. FAN Xingming, MO Xiaoyong, ZHANG Xin. Research status and application of wireless power transfer via coupled magnetic resonances[J]. Transactions of China Electrotechnical Society, 2013, 28(12): 75-82, 99. DOI:10.3969/j.issn.1000-6753.2013.12.010 |
| [9] |
杨健弟. 双感应测井刻度方法及测量误差分析[J]. 测井技术, 2002, 26(3): 247-251. YANG Jiandi. Calibration method for dual induction log and analysis of its measuring errors[J]. Well Logging Technology, 2002, 26(3): 247-251. DOI:10.3969/j.issn.1004-1338.2002.03.017 |
| [10] |
仵杰, 刘春雅, 张甜甜, 等. 阵列感应测井仪刻度系数特性研究[J]. 测井技术, 2006, 30(5): 400-403. WU Jie, LIU Chunya, ZHANG Tiantian, et al. A study of calibration coefficient characteristics of array induction logging tool[J]. Well Logging Technology, 2006, 30(5): 100-403. |
| [11] |
袁吉祥, 吴少威, 贺红民, 等. 感应测井仪器的刻度原理及方法[J]. 石油仪器, 2011, 25(1): 42-45, 103. YUAN Jixiang, WU Shaowei, HE Hongmin, et al. Scale principle and method of induction logging instrument[J]. Petroleum Instruments, 2011, 25(1): 42-45, 103. DOI:10.3969/j.issn.1004-9134.2011.01.014 |
| [12] |
魏宝君. 一种新型随钻电阻率测井仪器的响应和刻度[J]. 地球物理学报, 2007, 50(2): 632-641. WEI Bojun. Response and calibration of a new logging-while drilling resistivity tool[J]. Chinese Journal of Geophysics, 2007, 50(2): 632-641. DOI:10.3321/j.issn:0001-5733.2007.02.039 |
| [13] |
魏宝君, 王颖, 王甜甜. 电磁波电阻率仪器的基本理论及其在随钻测量中的应用[J]. 地球物理学进展, 2009, 24(2): 774-781. WEI Baojun, WANG Ying, WANG Tiantian. The ba-sic theory of electromagnetic wave resistivity instrument and its application to measurement of while-drilling[J]. Progress in Geophysics, 2009, 24(2): 774-781. DOI:10.3969/j.issn.1004-2903.2009.02.057 |
| [14] |
张庚骥. 电法测井[M]. 北京: 石油工业出版社, 1996.
|
| [15] |
陈爱新. 随钻电磁波测井环境影响分析[J]. 石油地球物理勘探, 2006, 41(5): 601-605. CHEN Aixin. Analysis of environment influence in electromagnetic logging while drilling[J]. Oil Geophy-sical Prospecting, 2006, 41(5): 601-605. DOI:10.3321/j.issn:1000-7210.2006.05.022 |
| [16] |
冯启宁, 鞠晓东, 柯式镇, 等. 测井仪器原理[M]. 北京: 石油工业出版社, 2010.
|
| [17] |
杨震, 岳步江, 刘庆成, 等. 随钻电磁波电阻率仪器吊零刻度原理及试验[J]. 石油仪器, 2012, 26(5): 23-25, 28. YANG Zhen, YUE Bujiang, LIU Qingcheng, et al. The principle and test of the zero scale of the electromagnetic wave resistivity instrument while drilling[J]. Petroleum Instruments, 2012, 26(5): 23-25, 28. DOI:10.3969/j.issn.1004-9134.2012.05.010 |
| [18] |
仵杰, 龚厚生, 陈草堂. 双感应测井趋肤效应校正和刻度系数计算研究[J]. 测井技术, 2001, 25(4): 261-265, 319. WU Jie, GONG Housheng, CHEN Caotang. On correcting skin effect and calculating scale coefficient in dual induction logging[J]. Well Logging Technology, 2001, 25(4): 261-265, 319. DOI:10.3969/j.issn.1004-1338.2001.04.004 |
| [19] |
陆承达, 董浩斌, 王家豪, 等. 一种电磁随钻信号接收仪器的设计[J]. 工程地球物理学报, 2015, 12(4): 423-427. LU Chengda, DONG Haobin, WANG Jiahao, et al. A design of EM-MWD signal receiver circuit based on STM32[J]. Chinese Journal of Engineering Geophy-sics, 2015, 12(4): 423-427. DOI:10.3969/j.issn.1672-7940.2015.04.001 |
| [20] |
Hou H, Hu Y, Huang D.The filter circuit design and simulation of array induction logging tools[C].IEEE International Conference on Computer Science and Information Processing, 2012, 829-832.
|



 张超, 北京市海淀区中关村北二条6号中国科学院电工研究所, 100190, Email:
张超, 北京市海淀区中关村北二条6号中国科学院电工研究所, 100190, Email: