② 油气藏地质及开发工程国家重点实验室, 四川成都 610059;
③ 中海油研究总院, 北京 100028
② State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu University of Technology, Chengdu, Shichuan 610059, China;
③ CNOOC Research Institute, Beijing 100028, China
断裂的精确刻画是地震资料解释中的一大难题,1995年Bahorich等[1]提出了地震相干数据体的计算方法,使断裂的自动解释成为可能;地震相干技术自20世纪90年代中期Amoco公司成功地应用于地震资料断裂解释以来,取得了长足的进展。1998年Marfurt等[2]提出了基于相似性计算的第二代相干体算法,比第一代互相关算法具有更高的断裂刻画能力。1999年Gersztenkorn等[3]提出了基于本征结构的第三代相干算法,较第一、二代算法具有横向分辨率高、抗噪性强的优点。诸多学者仍在不断改进、发展新的相干算法,王西文等[4]结合时频分析方法(小波变换)与相干算法,使分辨率比传统相干算法更高。
1999年Partyka等[5]提出了谱分解方法,将全频带的地震数据体分解为不同频率的数据体,以突出地震数据中一些不同尺度的地质体。2009年Zeng等[6]发现某些单频地震数据体比常规的全频带数据体对地质体的边界、范围的刻画更加清晰,细节更加丰富,为频率域的断裂解释提供了新的思路。但是受时频分析算法分辨率的影响,结果往往出现一些误差,因此,只有利用高时频分辨率算法在时频域的断裂刻画,才能得到更为准确的结果。
2011年Daubechies等[7]在小波变换的基础上提出了同步挤压变换方法,在时频域内对小波变换后的时频谱值挤压和重排,信号的瞬时频率更加接近真实频率,提高了信号时频分析的时频聚焦能力。2017年Yu等[8]拓展短时傅里叶变换(STFT)窗函数,提出了改进短时傅里叶变换,分辨率更为集中。但是,它仍受到海森堡不确定性原理的制约以及原因不明的交叉项影响。据此,在同步挤压算法的启发下,将改进短时傅里叶变换(GSTFT)与同步挤压变换算法进行结合,发展了同步挤压改进短时傅里叶变换(SSTFT)。
参考前人研究成果,本文结合同步挤压改进短时傅里叶变换与相干算法,利用同步挤压改进短时傅里叶变换的高时频聚焦能力,对南海某工区的三维地震数据体进行频谱分解,得到不同频率的单频数据体;然后应用多道倾角导向相干技术计算单频数据体。结果表明,该方法可精细刻画微小断裂或裂缝发育区,验证了该方法的准确性及实用性。
1 技术与原理 1.1 短时傅里叶变换傅里叶变换是一项实用且强大的时频分析工具,但对地震等非平稳信号开展时频分析时,仅利用傅里叶变换达不到理想的分辨率。短时傅里叶变换是在傅里叶变换的基础上使用窗函数截断非平稳信号,此时可以将窗函数内的信号看作平稳信号,再对该信号做傅里叶变换。以此类推,对全部截断的信号分别做傅里叶变换,可以得到二维时频谱图[9-15]。
假设信号x(t)属于实数域平方可积函数空间,则其短时傅里叶变换表达式为
| $ {\text{STFT}}\left( {t, f} \right) = \int_{-\infty }^\infty {x\left( t \right)g\left( {t-\tau } \right)\exp \left( {-{\text{i}}2\pi ft} \right){\text{d}}t} $ | (1) |
式中:f为频率;τ为时窗中心;i为虚数单位;g(t-τ)为窗函数。当短时傅里叶变换的窗函数确定后,分辨率也随之确定,即短时傅里叶变换的分辨率是唯一的。
将式(1)离散化可得到离散短时傅里叶变换
| $ {\text{STF}}{{\text{T}}_x}\left( {t, f} \right) = \sum\limits_{t =-\infty }^\infty {x\left( t \right)g\left( {t-\tau } \right){{\text{e}}^{-{\text{i}}ft}}} $ | (2) |
由于传统的短时傅里叶变换分辨率由窗函数确定,因此它的分辨率固定,无法满足地震数据高分辨率处理的要求。改进短时傅里叶变换窗函数得到新的短时傅里叶变换公式,由式(1)分别对信号和窗函数求复共轭,得到
| $ \begin{array}{l} {\rm{STFT}}\left( {t, f} \right) = \int_{- \infty }^\infty {x\left( t \right){{\left[{g\left( {t-\tau } \right){{\rm{e}}^{-{\rm{i}}ft}}} \right]}^*}{\rm{d}}t} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \int_{ - \infty }^\infty {x\left( t \right){{\left[{{g_\omega }\left( t \right)} \right]}^*}{\rm{d}}t} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {\hat x\left( \xi \right){{\left[{{{\hat g}_\omega }\left( \xi \right)} \right]}^*}{\rm{d}}\xi } \end{array} $ | (3) |
式中:上标*表示复共轭;
| $ {\hat g_\omega }\left( \xi \right) = \int_{-\infty }^\infty {g\left( {t-r} \right){{\rm{e}}^{{\rm{i}}ft}}{{\rm{e}}^{-{\rm{i}}\xi t}}{\rm{d}}t} $ | (4) |
令t-r=r′,则
| $ \begin{array}{l} {{\hat g}_w}\left( \xi \right) = \int_{-\infty }^\infty {g\left( {r'} \right){{\rm{e}}^{{\rm{i}}f\left( {r + r'} \right)}}{{\rm{e}}^{-{\rm{i}}\xi \left( {r + r'} \right)}}{\rm{d}}r'} \\ \;\;\;\;\;\;\;\;\;\; = {{\rm{e}}^{{\rm{i}}fr-{\rm{i}}\xi r}}\int_{ - \infty }^\infty {g\left( {r'} \right){{\rm{e}}^{{\rm{i}}fr' - {\rm{i}}\xi r'}}{\rm{d}}r'} \\ \;\;\;\;\;\;\;\;\;\; = {{\rm{e}}^{{\rm{i}}fr - {\rm{i}}\xi r}}\hat g\left( {f - \xi } \right) \end{array} $ | (5) |
式中:r为τ在频率域的表示,r′为时窗长度;
| $ \begin{array}{l} {\rm{STFT}}\left( {t, f} \right) = \frac{1}{{2\pi }}\int_{- \infty }^\infty {\hat x\left( \xi \right){{\left[{{{\rm{e}}^{{\rm{i}}ft-{\rm{i}}\xi t}}\hat g\left( {f-\xi } \right)} \right]}^*}{\rm{d}}\xi } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {{\rm{e}}^{ -{\rm{i}}ft}}\frac{1}{{2\pi }}\int_{ -\infty }^\infty {\hat x\left( \xi \right)\hat g\left( {f -\xi } \right){{\rm{e}}^{{\rm{i}}f\xi t}}{\rm{d}}\xi } \end{array} $ | (6) |
改进短时傅里叶变换为
| $ {\rm{GSTFT}}\left( {t, f} \right) = \frac{1}{{2\pi }}\int_{-\infty }^\infty {\hat x\left( \xi \right)\hat g\left( {f-\xi } \right){{\rm{e}}^{{\rm{i}}\xi t}}{\rm{d}}\xi } $ | (7) |
根据式(7),对GSTFT的时间t求导,则
| $ \begin{array}{l} {\partial _t}{\rm{GSTFT}}\left( {t, f} \right) = {\partial _t}\left[{A\hat g\left( {f-{f_0}} \right){{\rm{e}}^{{\rm{i}}{f_0}t}}} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {\rm{GSTFT}}\left( {t, f} \right){\rm{i}}{f_0} \end{array} $ | (8) |
可得信号的瞬时频率
| $ {f_0}\left( {t, f} \right) =-{\rm{i}}\frac{{{\partial _t}{\rm{GSTFT}}\left( {t, f} \right)}}{{{\rm{GSTFT}}\left( {t, f} \right)}} $ | (9) |
根据式(9),可得同步挤压改进短时傅里叶变换
| $ {\rm{SSTFT}}\left( {t, \eta } \right) = \int_{- \infty }^\infty {{\rm{GSTFT}}\left( {t, f} \right)\delta \left[{\eta-{f_0}\left( {t, f} \right)} \right]{\rm{d}}f} $ | (10) |
式中:η为同步挤压改进短时傅里叶变换后的时频谱频率;δ为同步压缩算子。
由式(10)可知,将某一时间点所对应的频谱值累加到某一瞬时频率上,可提高信号的时频分辨率。经合成的理论信号分析结果验证,SSTFT具有高时频聚焦能力。
1.4 多道倾角导向相干技术实际地质体都存在一定的倾角和方位角,而传统的相干技术是沿着地震网格方向计算相干值。因此,传统的相干算法不能很好地处理地震信号的方向特征[16],相干算法的计算路径无法与地层倾角保持一致。基于此,如果不考虑地层的倾角,相干体结果的精度将会受到严重影响,甚至会是错误的(通常会造成断裂模糊、尖灭点不清楚等现象)[17-19]。多道倾角导向相干技术是利用多条地震道的信息计算某一点的相干值,并且在倾角估算时采用多窗口方法,使该技术对断裂的刻画更加清晰[20]。
2 应用效果 2.1 时频效果分析首先利用线性调频信号检验算法的可靠性。合成信号是由两个线性调频信号叠加而成
| $ \begin{array}{l} x\left( t \right) = \cos \left[{2\pi \left( {10 + \frac{t}{{6.2}}} \right)\frac{t}{{256}}} \right] + \\ \;\;\;\;\;\;\;\;\;\cos \left[{2\pi \left( {91-\frac{t}{{6.2}}} \right)\frac{t}{{256}}} \right]\;\;\;\;\;\;\;\;\;\;\;0 \le t \le 256 \end{array} $ | (11) |
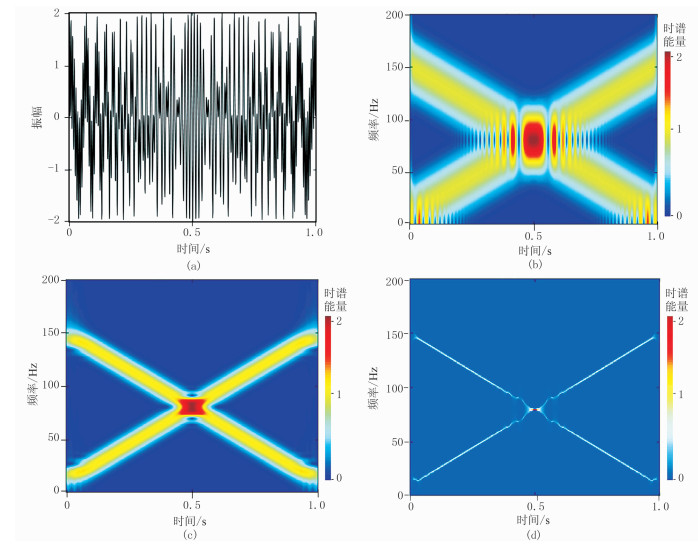
图 1a为原始合成信号,图 1b是对图 1a信号作短时傅里叶变换得到的时频谱。由图可见,短时傅里叶变换的时频分辨率不高,同时,由于短时傅里叶固定时窗,导致时频谱末端拉伸。图 1c是对图 1a信号作改进短时傅里叶变换得到的时频谱,发现改进短时傅里叶变换的时频分辨率较高,但仍然无法摆脱海森堡不确定性原理的限制以及原因不明的交叉项的干扰。由此可见,改进短时傅里叶变换与短时傅里叶变换同样存在对信号分析时频分辨率不佳的局限。图 1d是对图 1a信号作同步挤压改进短时傅里叶变换得到的时频谱,对比图 1d与图 1b、图 1c可知,同步挤压改进短时傅里叶变换具有最高的时频分辨率,能清晰地刻画信号的瞬时频率,并且克服了短时傅里叶变换固定时窗的局限。
|
图 1 合成信号及不同算法得到的时频谱 (a)原始合成信号;(b)STFT;(c)GSTFT;(d)SSTFT |
实际采集的地震数据存在大量噪声,即使进行降噪处理,但仍然无法完全消除噪声,因此,要求对地震数据时频处理的方法具有一定的抗噪性。对图 1a合成信号添加随机噪声,分别采用STFT、GSTFT、SSTFT算法处理,得到的时频谱如图 2所示。
|
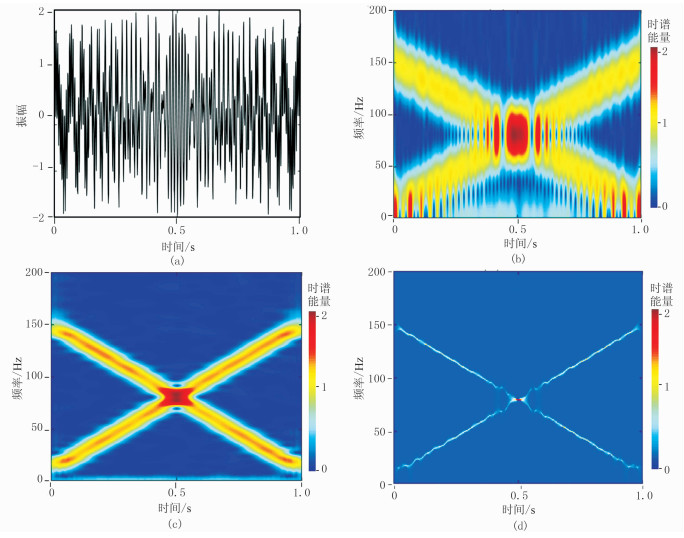
图 2 加噪信号及不同算法得到的时频谱 (a)原始加噪信号;(b)STFT;(c)GSTFT;(d)SSTFT |
图 2a为原始加噪信号。图 2b是对图 2a作短时傅里叶变换得到的时频谱,可见短时傅里叶变换受噪声影响很大,有效信息被噪声淹没,无法清晰地看出信号的时频分布。图 2c是对图 2a加噪信号作改进短时傅里叶变换得到的时频谱,时频分辨率较短时傅里叶变换得到了很大的提高,受噪声的影响非常小。由此可见,改进短时傅里叶变换具有更高的抗噪能力。图 2d是对图 2a加噪信号作同步挤压改进短时傅里叶变换得到的时频谱,有效信息几乎不受噪声的影响,具有一定的抗噪性,在含噪的信号中仍然可以得到分辨率很高的时频分析结果。
2.3 多道倾角导向相干技术应用南海海上某工区处于油气开发阶段,需要精细刻画小断裂及裂缝发育区。但前期处理的地震资料分辨率低,无法识别小断裂及裂缝发育区。为了满足不同级别断裂的识别需求,本文采用同步挤压改进短时傅里叶变换方法对地震资料进行分频处理。在分频处理时,频率的选择尤为重要。为此提取井旁地震道作时频变换处理,确定地震资料的优势频带范围。采用短时傅里叶变换和同步挤压改进短时傅里叶变换得到井旁地震道的时频谱如图 3所示。
|
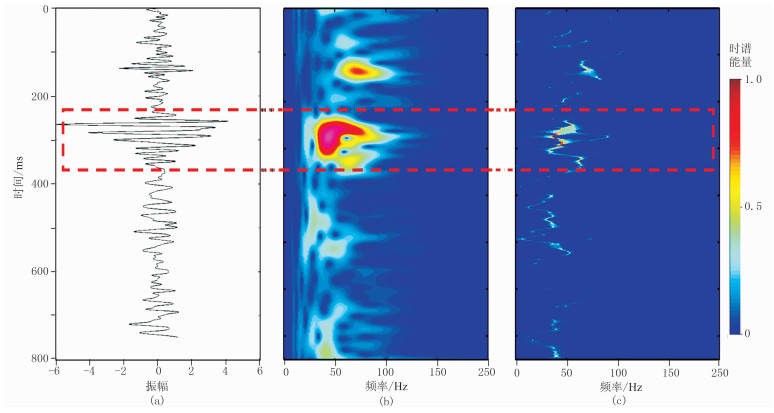
图 3 井旁地震道及不同算法得到的时频谱 (a)井旁地震道;(b)STFT;(c)SSTFT |
由图 3红色虚线框内图像可知优势频带为25~63Hz。在优势频带范围内,采用同步挤压改进短时傅里叶变换对原始三维地震资料作分频处理,分别得到25、30、40、60Hz的单频数据体,然后利用多道倾角导向相干技术进行相干计算,得到单频相干数据体。
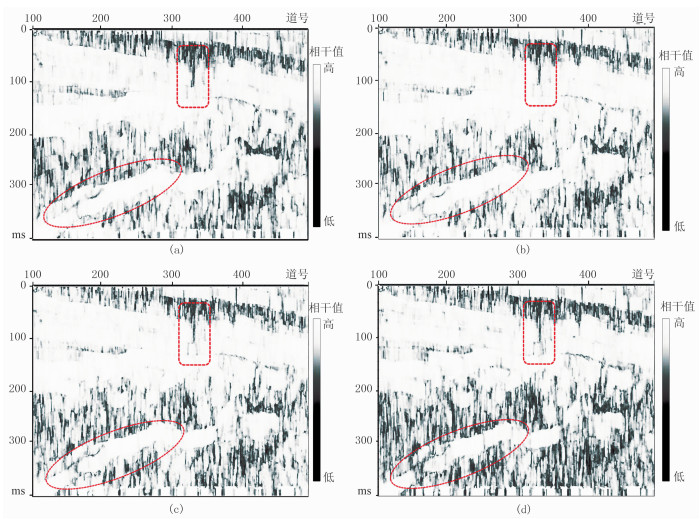
对比25、30、40、60Hz四个频率的相干属性剖面(图 4)可见,随着频率的增加,相干属性剖面中所反映出的地质信息也会随着改变。25Hz的低频相干剖面中,可识别较大尺度断裂;30Hz与40Hz的中频剖面中,不仅可见断裂整体展布特征,还可识别某些中尺度的断裂(图 4b、图 4c红色虚线框内);而60Hz的高频剖面中,则可见小断裂及裂缝发育区(图 4d红色虚线框内)。
|
图 4 单频相干属性剖面 (a)25Hz;(b)30Hz;(c)40Hz;(d)60Hz |
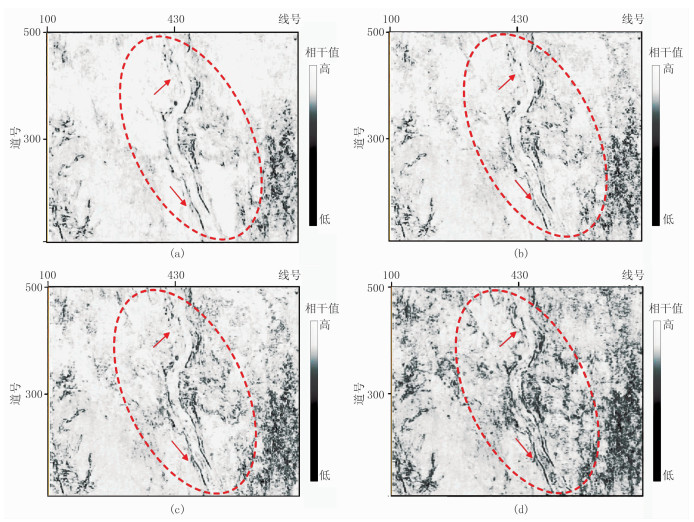
对单频相干数据体提取沿层切片,得到结果如图 5所示。图 5a为低频相干切片,可以用于刻画较大断裂;图 5b、图 5c为中频相干切片,可用于识别中尺度的断裂,如红色虚线框红色箭头所示的中尺度断裂在低频相干切片中显示不清晰,因此,中频相干切片对由大断裂所控制的中尺度断裂信息更为敏感;而高频相干切片中所反映的信息更为丰富,如图 5d红色虚线框红色箭头所示,它不仅可以凸显微小断裂,还可以识别伴生裂缝发育区。
|
图 5 单频相干属性沿层切片 (a)25Hz;(b)30Hz;(c)40Hz;(d)60Hz |
运用基于同步挤压改进短时傅里叶变换分频多道倾角导向相干技术处理南海某工区地震数据体,结果表明,得到的单频数据体可以反映与原始数据体不同的地质体边缘信息;在此基础上计算得到的单频相干属性可以识别不同级别的断裂。该方法不仅具有同步挤压改进短时傅里叶变换的高时频分辨率的优势,而且还有多道倾角导向相干技术准确识别断裂的优点。
| [1] |
Bahorich M, Farmer S.3D seismic discontinuity for faults and stratigraphic features: the coherence cube[C]. SEG Technical Program Expanded Abstracts, 1995, 14: 1053-1058.
|
| [2] |
Marfurt K J, Kirlin R L, Famrer S L, et al. 3-D seismic attributes using a semblance-based coherency algoritmh[J]. Geophysics, 1998, 63(4): 1150-1165. DOI:10.1190/1.1444415 |
| [3] |
Gersztenkorn A, Marfurt K J. Eigenstructure-based coherence computation as an aid to 3-D structural and srtatigraphic mapping[J]. Geophysics, 1999, 64(5): 1468-1479. DOI:10.1190/1.1444651 |
| [4] |
王西文, 杨孔庆, 刘全新, 等. 基于小波变换的地震相干体算法的应用[J]. 石油地球物理勘探, 2002, 37(4): 328-331. WANG Xiwen, YANG Kongqing, LIU Quanxin, et al. Research on algorithm of seismic coherent cube based on wavelet transftorm[J]. Oil Geophysical Prospecting, 2002, 37(4): 328-331. DOI:10.3321/j.issn:1000-7210.2002.04.005 |
| [5] |
Partyka G, Gridley J, Lopez J. Interpretational applications of spectral decomposition in reservoir characterization[J]. The Leading Edge, 1999, 18(3): 353-360. DOI:10.1190/1.1438295 |
| [6] |
Zeng H, John A.Frequency-dependent seismic strati-graphy[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 1097-1101.
|
| [7] |
Daubechies I, Lu J, Wu H T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 243-261. |
| [8] |
Yu G, Yu M, Xu C. Synchroextracting transform[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10): 8042-8054. DOI:10.1109/TIE.2017.2696503 |
| [9] |
韩磊, 张宏, 王劲松, 等. 分频相干技术在复杂断裂解释中的应用[J]. 复杂油气藏, 2016, 9(4): 16-21. HAN Lei, ZHANG Hong, WANG Jinsong, et al. Discrete frequency coherency technology for interpreting complicated faults and its application[J]. Complex Hydrocarbon Reservoirs, 2016, 9(4): 16-21. |
| [10] |
冯连勇, 黎莉, 裴勇. 胜利油田岩性油藏勘探中的地震技术[J]. 石油地球物理勘探, 2006, 41(2): 211-215. FENG Lianyong, LI Li, PEI Yong. Seismic technology in lithologic reservoir prospecting of Shengli oilfield[J]. Oil Geophysical Prospecting, 2006, 41(2): 211-215. DOI:10.3321/j.issn:1000-7210.2006.02.019 |
| [11] |
刘传虎. 地震相干分析技术在裂缝油气藏预测中的应用[J]. 石油地球物理勘探, 2001, 36(2): 238-244. LIU Chuanhu. Application of seismic coherent analysis technology to prediction of fractured reservoir[J]. Oil Geophysical Prospecting, 2001, 36(2): 238-244. DOI:10.3321/j.issn:1000-7210.2001.02.015 |
| [12] |
许海涛, 毕建军, 唐红光, 等. 数学形态学在地震相干属性提取中的应用[J]. 石油地球物理勘探, 2010, 45(4): 482-484. XU Haitao, BI Jianjun, TANG Hongguang, et al. Application of mathematical morphology in extraction of seismic coherent attributes[J]. Oil Geophysical Prospecting, 2010, 45(4): 482-484. |
| [13] |
常旭, 刘伊克, 王辉, 等. 地震相干偏移与数据自参照偏移的关系[J]. 地球物理学报, 2009, 52(11): 2840-2845. CHANG Xu, LIU Yike, WANG Hui, et al. Seismic interferometric migration and data-referenced-only migration[J]. Chinese Journal of Geophysics, 2009, 52(11): 2840-2845. |
| [14] |
王萍, 宋书君, 王新征, 等. 岩性油藏配套解释技术[J]. 石油地球物理勘探, 2003, 38(5): 557-560. WANG Ping, SONG Shujun, WANG Xinzheng, et al. Complete sets of interpretation technology for litho-logic reservoir[J]. Oil Geophysical Prospecting, 2003, 38(5): 557-560. DOI:10.3321/j.issn:1000-7210.2003.05.019 |
| [15] |
蔡涵鹏, 胡光岷, 贺振华, 等. 基于非线性变时窗相干算法的不连续性检测方法[J]. 石油地球物理勘探, 2016, 51(2): 371-375. CAI Hanpeng, HU Guangmin, HE Zhenhua, et al. Subtle discontinuity detection with nonlinear variable-time window coherency algorithm[J]. Oil Geophysical Prospecting, 2016, 51(2): 371-375. |
| [16] |
问雪, 陈雪芳, 陈胜红, 等. 利用结构导向平滑方法解释断层[J]. 石油地球物理勘探, 2017, 52(1): 146-151. WEN Xue, CHEN Xuefang, CHEN Shenghong, et al. Fault interpretation based on structure-orientedsmoothing method[J]. Oil Geophysical Prospecting, 2017, 52(1): 146-151. |
| [17] |
尹川, 杜向东, 赵汝敏, 等. 小波分频倾角相干在复杂断裂解释中的应用[J]. 石油地球物理勘探, 2015, 50(2): 346-350. YIN Chuan, DU Xiangdong, ZHAO Rumin, et al. Dip-steering similarity based on wavelet decomposition in complex fault interpretation[J]. Oil Geophysical Prospecting, 2015, 50(2): 346-350. |
| [18] |
刘财, 邓馨卉, 郭智奇, 等. 基于岩石物理的页岩储层各向异性表征[J]. 石油地球物理勘探, 2018, 53(2): 339-346. LIU Cai, DENG Xinhui, GUO Zhiqi, et al. Shale reservoir anisotropic characterization based on rock physics[J]. Oil Geophysical Prospecting, 2018, 53(2): 339-346. |
| [19] |
李军, 张军华, 龚明平, 等. 基于魔方矩阵的断层检测方法[J]. 石油地球物理勘探, 2018, 53(3): 552-557. LI Jun, ZHANG Junhua, GONG Mingping, et al. Fault detection based on magic matrix[J]. Oil Geophysical Prospecting, 2018, 53(3): 552-557. |
| [20] |
王清振, 张金淼, 姜秀娣, 等. 利用梯度结构张量检测盐丘与断层[J]. 石油地球物理勘探, 2018, 53(4): 826-831. WANG Qingzhen, ZHANG Jinmiao, JIANG Xiudi, et al. Salt dome and fault detection based on the gradient-structure tensor[J]. Oil Geophysical Prospecting, 2018, 53(4): 826-831. |



 严海滔, 四川省成都市二仙桥东三路1号成都理工大学地球物理学院, 610059。Email:
严海滔, 四川省成都市二仙桥东三路1号成都理工大学地球物理学院, 610059。Email: