可靠的油气检测可降低勘探风险与投入成本,对油气勘探具有重要意义。现有的叠后油气检测方法一般是利用地震数据的振幅和频率信息,如基于“低频阴影”[1-3]、基于特定优势频率段[4-5]和基于品质因子Q吸收属性[6-7]的油气检测方法等。这些技术虽然可提高油气勘探成功率,但随着勘探主体逐渐变为隐蔽的岩性油气藏,仅依靠振幅和频率信息的常规油气检测方法在实际应用中逐渐显露出局限性,即多解性严重。
双相介质模型是研究地下介质的一种重要模型,它是由岩石固体骨架和岩石孔隙中所填充的流体组成[8-9]。Biot双相介质模型假设固体骨架与孔隙流体之间是相互耦合和相互影响的,同时该模型揭示了慢纵波的存在。波在穿过双相介质后,受到介质衰减和频散的影响[10],不但会改变子波的频率,出现高频衰减和低频增强现象,而且子波相位也会发生改变[11],这一特性为利用地震资料直接寻找油气提供了理论基础。然而,现有的叠后油气检测方法一般是利用子波的振幅和频率信息,而子波相位的变化特征很少得到应用[12],其主要原因是现阶段对储层引起的相位响应特征还不够清楚,而且缺乏从地震数据中有效提取时变子波相位信息的技术手段。尽管近些年学者们不断提出高分辨率的谱分解方法[13-16],但仍然没有提取和利用相位信息的有效方法。针对该问题,本文提出了一种基于稀疏反演复谱分解技术的流体流度与时频相位融合油气检测方法,即引入相位信息作为振幅和频率信息的补充。该方法可以充分利用动力学特征检测油气,这样不仅能较好地弥补传统方法的不足,而且可与其他相关方法相互补充验证,降低油气检测的多解性和不确定性。
首先,本文实现了基于稀疏反演技术的地震复谱分解,一方面可以有效地求取时变子波的相位信息用于油气检测,另一方面可提高时频分辨率。其次,在与频率相关的反射系数低频渐近分析理论[17]基础上,推导了基于稀疏反演复谱分解技术的储层流体流度计算方法。反射地震数据中的低频信息包含了与储层及流体有关的丰富信息[18],利用从地震数据的低频信息计算得到的储层流体流度对含油气储层具有很好的成像能力[19]。然后,利用黏弹介质模型对衰减有关的子波相位变化机制进行研究,进而为利用相位信息开展油气检测提供理论依据。最后,将时频相位信息和流体流度属性有机结合,形成充分利用地震动力学特征的多信息融合油气检测方法,这样可以降低油气检测的多解性和不确定性。合成数据和渤海某探区的实际资料处理结果表明,本文提出的基于稀疏反演复谱分解技术的流体流度与时频相位融合的油气检测方法显著提高了油气与水的区分能力,降低了仅利用振幅和频率信息进行储层油气检测的多解性和不确定性,且具有较高的分辨率。
1 地震复谱分解方法 1.1 地震复谱分解方法的实现根据Bonar等[20]的复谱分解方法的思想,可以将地震复谱分解的数学模型写成矩阵与向量相乘的形式
| $ \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{n}} = \left( {{\mathit{\boldsymbol{W}}_1}\;\;{\mathit{\boldsymbol{W}}_2}\;\; \cdots \;\;{\mathit{\boldsymbol{W}}_N}} \right)\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_1}} \\ {{\mathit{\boldsymbol{r}}_2}} \\ \vdots \\ {{\mathit{\boldsymbol{r}}_N}} \end{array}} \right) + \mathit{\boldsymbol{n}} = \mathit{\boldsymbol{b}} $ | (1) |
式中:b代表地震信号;Wi表示以频率fi为主频的与频率相关的复子波卷积矩阵,i=1, 2, …, N,N代表参与计算的频率个数;ri表示与Wi相对应的与频率相关的复反射系数;A表示复子波卷积矩阵库;x表示与频率相关的复反射系数矩阵;n表示随机噪声。
在求解线性反演问题(式(1))后,得到与频率相关的复反射系数矩阵x,将其转置运算变为(r1 r2 … rN)的形式,即可以看作是通过反演得到的时频谱。在地球物理反演中,式(1)通常是一个欠定问题,为了降低解的不确定性并获得稀疏的时频谱,需要对x执行稀疏约束,进而将线性反演问题转化为基追踪去噪问题进行求解[21],即
| $ \mathop {\min }\limits_{\mathit{\boldsymbol{x}} \in {\mathit{\boldsymbol{C}}^n}} {\left\| \mathit{\boldsymbol{x}} \right\|_1} + \frac{1}{{2\mu }}\left\| {\mathit{\boldsymbol{Ax}}-\mathit{\boldsymbol{b}}} \right\|_2^2 $ | (2) |
式中:权重参数μ>0,用于最小化过程中控制式(2)中前后两项的相对权重;‖·‖22表示L2范数的平方;C代表复数集,n为维数;‖·‖1表示L1范数。
通过求解无约束基追踪去噪问题(式(2))得到时频谱x后,对时频谱x进一步运算便可得到地震信号的时频能量谱Fdom和时频相位谱φ
| $ \left\{ \begin{gathered} {\mathit{\boldsymbol{F}}_{{\text{dom}}}} = {\left| \mathit{\boldsymbol{x}} \right|^2} \hfill \\ \mathit{\boldsymbol{\varphi }} = {\tan ^{-1}}\left( \mathit{\boldsymbol{x}} \right) \hfill \\ \end{gathered} \right. $ | (3) |
近年来,学者们开发了各种先进的快速算法来求解基追踪去噪问题,其中交替方向算法是一种高效且鲁棒的重构算法,具有更好的数值计算性能[22]。因此,本文采用交替方向优化算法求解式(2)实现地震复谱分解。
当应用交替方向优化算法求解无约束基追踪去噪问题时,首先引入辅助变量υ∈Cm(m为维数),然后将式(2)转换为以下等效形式
| $ \mathop {\min }\limits_{\mathit{\boldsymbol{x}} \in {\mathit{\boldsymbol{C}}^n}, \mathit{\boldsymbol{\upsilon }} \in {\mathit{\boldsymbol{C}}^m}} \left\{ {{{\left\| \mathit{\boldsymbol{x}} \right\|}_1} + \frac{1}{{2\mu }}\left\| \mathit{\boldsymbol{\upsilon }} \right\|_2^2:\mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{\upsilon }} = \mathit{\boldsymbol{b}}} \right\} $ | (4) |
式(4)的增广拉格朗日子问题为
| $ \begin{gathered} \mathop {\min }\limits_{\mathit{\boldsymbol{x}} \in {\mathit{\boldsymbol{C}}^n}, \mathit{\boldsymbol{\upsilon }} \in {\mathit{\boldsymbol{C}}^m}} \left\{ {{{\left\| \mathit{\boldsymbol{x}} \right\|}_1} + \frac{1}{{2\mu }}\left\| \mathit{\boldsymbol{\upsilon }} \right\|_2^2- \operatorname{Re} \left[{{\mathit{\boldsymbol{y}}^{\text{H}}}\left( {\mathit{\boldsymbol{Ax}} + } \right.} \right.} \right. \hfill \\ \left. {\left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{\upsilon }}-\mathit{\boldsymbol{b}}} \right)} \right] + \frac{\beta }{2}\left\| {\mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{\upsilon }} -\mathit{\boldsymbol{b}}} \right\|_2^2} \right\} \hfill \\ \end{gathered} $ | (5) |
式中:y∈Cm是拉格朗日乘子;Re(·)表示取复数的实部;H表示共轭转置;惩罚参数β>0。如果给定(x(k),y(k))(k为迭代次数), 则可以通过采用交替最小化问题(式(5))的方法来获得(υ(k+1), x(k+1), y(k+1))。因此,求解式(2)的交替方向算法迭代公式为
| $ \left\{ \begin{gathered} {\mathit{\boldsymbol{\upsilon }}^{\left( {k + 1} \right)}} = \frac{{\mu \beta }}{{1 + \mu \beta }}\left[{\frac{{{\mathit{\boldsymbol{y}}^{\left( k \right)}}}}{\beta }-\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}^{\left( k \right)}}-\mathit{\boldsymbol{b}}} \right)} \right] \hfill \\ {\mathit{\boldsymbol{x}}^{\left( {k + 1} \right)}} = {\text{Shrink}}\left( {{\mathit{\boldsymbol{x}}^{\left( k \right)}} -\tau {\mathit{\boldsymbol{g}}^{\left( k \right)}}, \frac{\tau }{\beta }} \right) \hfill \\ {\mathit{\boldsymbol{y}}^{\left( {k + 1} \right)}} = {\mathit{\boldsymbol{y}}^{\left( k \right)}} -\gamma \beta \left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}^{\left( {k + 1} \right)}} + {\mathit{\boldsymbol{\upsilon }}^{\left( {k + 1} \right)}} -\mathit{\boldsymbol{b}}} \right) \hfill \\ \end{gathered} \right. $ | (6) |
式中:近端参数τ大于零;Shrink(·, ·)表示一维收缩算子;γ为大于零的常数;
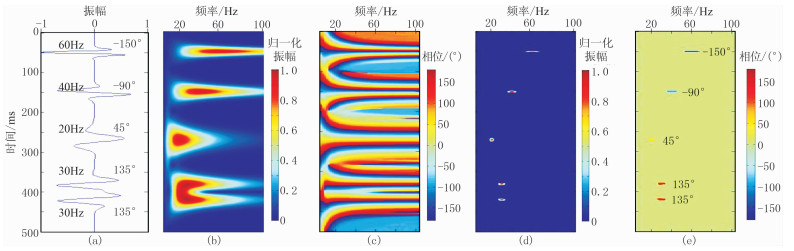
图 1a展示的一道地震信号是由不同频率和相位Ricker子波(已在图中标注)合成的,用于测试不同的谱分解方法。图 1b显示了通过连续小波变换(CWT)方法获得的时频能量谱,代表常规谱分解方法的分辨率水平。图 1c显示了通过CWT方法获得的时频相位谱,从中难以提取有效的子波相位信息。图 1d和图 1e分别为基于地震复谱分解方法获得的时频能量谱和时频相位谱。地震复谱分解方法得到的两种时频分布都具有很高的分辨率,并且可以准确提取子波相位信息,所求结果与合成地震信号真实情况一致。
|
图 1 地震复谱分解方法与常规谱分解方法关于时频分辨率的比较 (a)合成地震信号;(b)CWT时频能量谱;(c)CWT时频相位谱;(d)地震复谱分解时频能量谱;(e)地震复谱分解时频相位谱 |
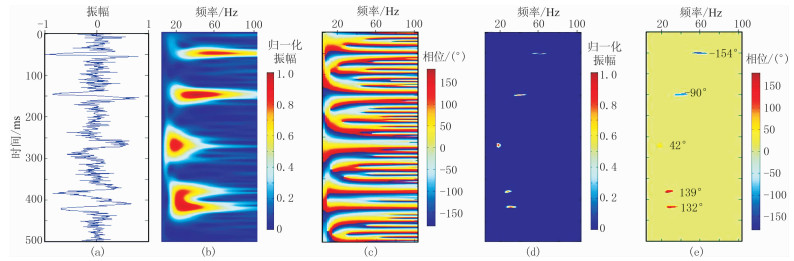
为了进一步检验地震复谱分解方法对噪声干扰的适应程度,同时也为了方便问题的说明,对图 1a所示的无噪地震信号加入信噪比SNR=2的噪声进行试算。图 2a展示的是信噪比为2的含噪声信号;图 2b和图 2c分别展示的是CWT方法获得的时频能量谱和时频相位谱;图 2d和图 2e分别为基于地震复谱分解方法获得的时频能量谱和时频相位谱。对比可以看出,在含噪声数据地震复谱分解的时频能量谱中无噪声能量,随机噪声得到了压制,而且从含噪声数据中提取的子波相位信息误差较小,与原始信号匹配较好。这主要是因为基于稀疏反演的地震复谱分解方法在迭代求解过程中可以通过设定一个容差参数来降低噪声对时频谱的影响,具有较好的噪声衰减能力。通过测试可知,地震复谱分解方法具有较好的抗噪能力,表现出较好的可靠性、有效性和稳定性。
|
图 2 地震复谱分解方法与常规谱分解方法关于抗噪能力的比较 (a)合成含噪声地震信号;(b)CWT时频能量谱;(c)CWT时频相位谱;(d)地震复谱分解时频能量谱;(e)地震复谱分解时频相位谱 |
本文提出的流体流度与时频相位融合的油气检测方法充分利用地震数据动力学特征中的振幅、频率和相位信息,其中流体流度油气检测方法是对现有油气检测方法的一种改进,时频相位油气检测方法则是增加了对相位信息的利用。下面将分别阐述储层流体流度的计算方法、利用相位信息进行油气检测的理论依据及地震多属性融合方法。
2.1 基于储层流体流度的油气检测方法地震低频信息对油气检测具有重要作用,因为其中包含了丰富的油气信息,对储层含油气性更为敏感[18]。Silin等[17]对Biot模型双相介质分界面的地震反射进行了低频渐近分析,得到了低频域流体饱和双相介质的与频率相关的地震反射系数渐近表达式。本文涉及的储层流体流度属性计算公式就是基于低频渐近分析理论推导得到的。Batzle等[23]证实了储层流体流度大小变化可导致含油气储层的速度频散变化,因此储层流体流度属性可用于地震油气检测。
低频域中流体饱和双相介质地震反射系数的渐近表达式为[17]
| $ R = {R_0} + {R_1}\left( {1 + {\text{i}}} \right)\sqrt {\frac{{\kappa {\rho _{\text{f}}}}}{\eta }\omega } $ | (7) |
式中:R0和R1分别是岩石和孔隙流体的力学特性的无量纲函数;i是虚数单位;κ表示储层的渗透率;η表示孔隙流体的黏滞系数;ω表示地震信号的角频率;ρf表示储层的流体密度。
在渗流力学中,将储层的渗透率与孔隙流体的黏滞系数的商定义为储层的流体流度Fm,即
| $ \frac{{{\text{d}}R}}{{{\text{d}}\omega }} = C\sqrt {{F_{\text{m}}}} $ | (8) |
式中,参数
进一步推导式(8)可获得储层流体流度的计算公式
| $ {F_{\text{m}}} = \frac{1}{{{C^2}}}{\left( {\frac{{{\text{d}}R}}{{{\text{d}}\omega }}} \right)^2} $ | (9) |
对地震数据进行谱分解后,其单频瞬时频谱幅度或能量可以准确地表征相同频率的地震反射幅度或能量。因此,在实际应用中,使用频率ω的瞬时频谱幅度a(ω)代替相同频率的地震反射系数R,可得储层流体流度的近似计算公式
| $ {F_{\text{m}}} \approx \frac{1}{{{C^2}}}{\left[{\frac{{{\text{d}}a\left( \omega \right)}}{{{\text{d}}\omega }}} \right]^2} $ | (10) |
实际应用中,本文所涉及的储层流体流度的计算步骤如下:首先,利用Silin等[17]提出的确定优势频率的参考方法确定计算流体流度的优势频率ω;然后,使用高分辨率地震复谱分解方法计算式(10)中的瞬时频谱幅度a(ω);最后,根据测井数据拟合估算参数C。在勘探阶段无井或少井情况下,因为参数C相当于一个比例系数,所以仍然可以在不需要井的条件下,直接计算
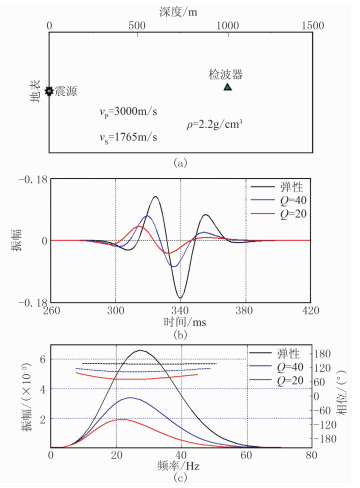
地震波在双相介质中传播时会产生衰减,并且这种衰减会引起子波频率和相位的改变。由于双相介质中的波诱导流体流动机制导致流体压力松弛,因而发展了与双相介质模型等效的黏弹介质模型,借用描述黏弹介质特性的概念描述双相介质中波的衰减和频散效应是可行的[26-27]。因此,本文采用黏弹介质模型模拟双相介质中波的衰减和频散,建立与双相介质模型等效的黏弹介质模型,并基于该黏弹介质模型正演(图 3),研究与衰减有关的子波相位变化机制。
|
图 3 黏弹介质模型的正演记录及其振幅谱、相位谱 (a)模型及观测系统;(b)弹性介质、黏弹介质正演地震记录;(c)振幅谱和相位谱 |
从图 3可见,衰减不仅会引起振幅变化,还会引起相位变化,而且衰减程度不同引起的相位变化也不同,即衰减程度越大,相位变化也越大。通常含烃储层相对于非含烃储层具有更明显的衰减,因此通过相位信息检测油气藏是可能的,这也为利用相位信息进行油气检测提供了理论依据。
2.3 地震多属性加权融合显示地震多属性加权融合显示方法将反映地下储层某一特征的不同类型地震属性按照不同的加权因子,采用代数运算的方式实现融合显示,这样可以实现不同地震属性间的加强和互补,降低多解性,提高预测的可信度。本文使用两种属性融合,采用正、余弦加权因子,即
| $ Y\left( i \right) = \cos \alpha \cdot {y_1}\left( i \right) + \sin \alpha \cdot {y_2}\left( i \right) $ | (11) |
式中:Y表示融合后的地震属性;y1代表第一个地震属性,加权因子为cosα;y2代表第二个地震属性,加权因子为sinα。在实际应用中,调整加权因子,将流体流度和时频相位属性采用正、余弦加权因子融合显示,实时扫描融合后的结果,选取储层含油气检测结果与实钻井情况及地质规律吻合度较高的加权因子,并取该权值下融合显示的属性结果作为最终的流体检测结果评价下一步的油气勘探潜力区。
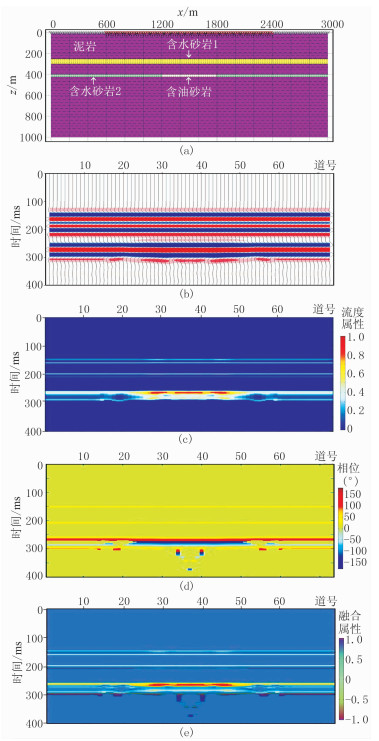
3 应用 3.1 合成数据为了验证流体流度与时频相位融合的油气检测方法的有效性,建立了如图 4所示黏弹层状介质模型。图 4b为图 4a模型的合成地震剖面,分别使用基于复谱分解技术的储层流体流度计算方法和时频相位计算方法处理,得到的高分辨率储层流体流度属性剖面(红色表示强能量异常)和时频相位谱剖面分别如图 4c和图 4d所示。
|
图 4 流体流度与时频相位融合的油气检测方法的理论合成数据验证 (a)黏弹层状介质模型;(b)合成的叠后地震剖面;(c)流体流度属性剖面;(d)时频相位谱剖面;(e)流体流度与时频相位谱的融合剖面 |
由图 4c、4d和图 4e可见,对于理论模型来说,流体流度剖面、时频相位谱剖面及融合剖面对应的异常显示与模型含油气性吻合程度好,有效地区分了模型含油和含水储层的响应,而且异常响应的分布范围与理论模型的油气聚集的横向、纵向范围一致,具有较高的分辨率。因此,根据理论模型的试算可知,利用流体流度与时频相位融合的油气检测方法对储层含油气性进行检测是可行的。
3.2 实际数据利用本文方法处理渤海某探区的实际地震数据(图 5),进一步验证基于稀疏反演复谱分解技术的流体流度与时频相位融合油气检测方法在实际应用中的效果。
|
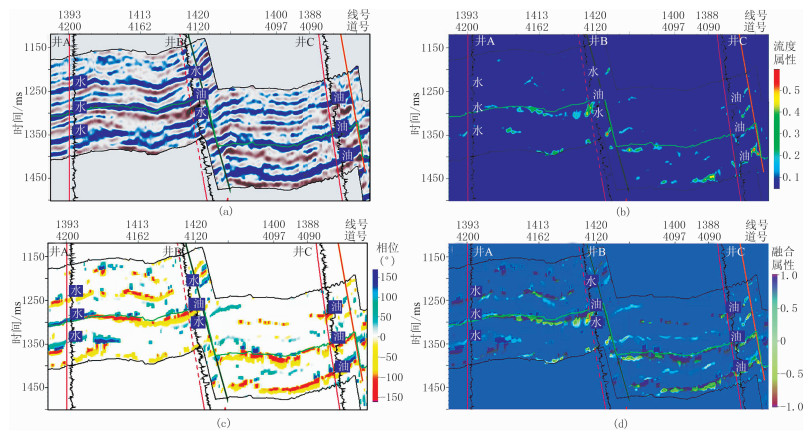
图 5 流体流度与时频相位融合的油气检测方法的实际数据验证 (a)过井A、井B和井C的实际叠后地震剖面;(b)流体流度属性剖面;(c)时频相位谱剖面;(d)对应的流体流度与时频相位谱的融合剖面 |
由图 5b和图 5c可见,单独使用流体流度油气检测方法或时频相位谱油气检测方法对储层含油气性进行预测,均不能很好地区分某些储层位置的含油和含水储层的响应,如图 5b中A井标注的第三套目标储层是水层,而在流体流度属性剖面上却显示为强能量异常,图 5c中A井标注的第一套目标储层是水层,而在时频相位谱剖面上却显示为含油气特征。而图 5d可见含油气的储层位置在剖面中均显示为明显的异常,检测结果与钻井结果完全吻合。同时,我们对研究区内的5口验证井在目的层段的含油气性预测吻合率进行了统计,预测总吻合率约为85%(表 1),表明了基于稀疏反演复谱分解技术的流体流度与时频相位融合油气检测方法对含油气储层具有较高的识别能力,可以降低油气检测的多解性和不确定性。
|
|
表 1 验证井的含油气性预测吻合率统计 |
本文首先实现了基于交替方向算法的高分辨率地震复谱分解方法,获得了高分辨率的时频能量谱和时频相位谱。然后,分别研究了基于稀疏反演复谱分解方法的流体流度油气检测方法和时频相位谱油气检测方法。最后,将流体流度属性和时频相位谱信息相融合,形成了利用动力学特征中的振幅、频率和相位信息的多信息融合油气检测方法。合成数据和实际数据处理结果表明,基于稀疏反演复谱分解技术的流体流度与时频相位融合油气检测方法对含油气储层具有良好的识别能力,降低了仅利用振幅和频率信息进行储层油气检测的多解性和不确定性,且具有较高的分辨率,为地震油气检测提供了一种新思路和新途径。
感谢中海油研究总院韩利在时频相位研究过程中提供的帮助。
| [1] |
Goloshubin G M, Korneev V A and Vingalov V M.Seismic low-frequency effects from oil-saturated re-servoir zones[C]. SEG Technical Program Expanded Abstracts, 2002, 21: 1813-1816.
|
| [2] |
Castagna J P, Sun S, Siegfried R W. Instantaneous spectral analysis: Detection of low-frequency shadows associated with hydrocarbons[J]. The Leading Edge, 2003, 22(2): 120-127. DOI:10.1190/1.1559038 |
| [3] |
Dan E. The low-frequency gas shadow on seismic sections[J]. The Leading Edge, 2004, 23(8): 772. DOI:10.1190/1.1786898 |
| [4] |
Chen G L, Finn C, Neelamani R, et al.Spectral decomposition response to reservoir fluids from a deepwater reservoir[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 1665-1669.
|
| [5] |
Liu E, Chapman M, Loizou N, et al.Applications of spectral decomposition for AVO analyses in the west of Shetland[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 279-283.
|
| [6] |
Quan Y L, Harris J M. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 1997, 62(3): 895-905. DOI:10.1190/1.1444197 |
| [7] |
郝亚炬, 黄捍东, 文晓涛, 等. 广义S域Q值估计方法及其在油气检测中的应用[J]. 石油地球物理勘探, 2017, 52(5): 1059-1066. HAO Yaju, HUANG Handong, WEN Xiaotao, et al. Q estimation in the generalized S domain and its application in the hydrocarbon detection[J]. Oil Geophysical Prospecting, 2017, 52(5): 1059-1066. |
| [8] |
Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid, Ⅰ: Low-frequency range[J]. The Journal of the Acoustical Society of America, 1956a, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [9] |
Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid, Ⅱ: Higher frequency range[J]. The Journal of the Acoustical Society of America, 1956b, 28(2): 179-191. DOI:10.1121/1.1908241 |
| [10] |
张固澜, 贺振华, 王熙明, 等. 地震波频散效应与反Q滤波相位补偿[J]. 地球物理学报, 2014, 57(5): 1655-1663. ZHANG Gulan, HE Zhenhua, WANG Ximing, et al. Seismic wave dispersion effects and inverse Q-filter phase compensation[J]. Chinese Journal of Geophy-sics, 2014, 57(5): 1655-1663. |
| [11] |
Han L, Liu C C and Yuan S Y.Can we use wavelet phase change due to attenuation for hydrocarbon detection?[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 2962-2966.
|
| [12] |
杨培杰, 罗红梅, 王金铎. 地震数据分相位重构方法[J]. 石油地球物理勘探, 2019, 54(3): 594-599. YANG Peijie, LUO Hongmei, and WANG Jinduo. Seismic data phase reconstruction[J]. Oil Geophysical Prospecting, 2019, 54(3): 594-599. |
| [13] |
陈学华, 贺振华, 黄德济. 基于广义S变换的地震资料高效时频谱分解[J]. 石油地球物理勘探, 2008, 43(5): 530-534. CHEN Xuehua, HE Zhenhua, HUANG Deji. High-efficient time-frequency spectrum decomposition of seismic data based on generalized S transform[J]. Oil Geophysical Prospecting, 2008, 43(5): 530-534. DOI:10.3321/j.issn:1000-7210.2008.05.008 |
| [14] |
Wang Y H. Seismic time-frequency spectral decomposition by matching pursuit[J]. Geophysics, 2007, 72(1): V13-V20. |
| [15] |
Han J J, Mirko V D B. Empirical mode decomposition for seismic time-frequency analysis[J]. Geophy-sics, 2013, 78(2): O9-O19. |
| [16] |
Han L, Sacchi M D, Han L G. Spectral decomposition and de-noising via time-frequency and space-wavenumber reassignment[J]. Geophysical Prospecting, 2014, 62(2): 244-257. DOI:10.1111/1365-2478.12088 |
| [17] |
Silin D B, Goloshubin G M. An asymptotic model of seismic reflection from a permeable layer[J]. Transport in Porous Media, 2010, 83(1): 233-256. DOI:10.1007/s11242-010-9533-8 |
| [18] |
Goloshubin G M, Van S C, Korneev V A, et al. Reservoir imaging using low frequencies of seismic reflections[J]. The Leading Edge, 2006, 25(5): 527-531. DOI:10.1190/1.2202652 |
| [19] |
Zhang S Q, Li C, Yan T, et al.Calculation method of reservoir fluid mobility and its application based on seismic complex spectral decomposition[C]. SEG Technical Program Expanded Abstracts, 2016, 35: 2981-2985.
|
| [20] |
Bonar D C and Sacchi M D.Complex spectral decomposition via inversion strategies[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 1408-1412.
|
| [21] |
Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 33-61. |
| [22] |
Yang J F, Zhang Y. Alternating direction algo-rithms for L1-problems in compressive sensing[J]. SIAM Journal on Scientific Computing, 2011, 33(1): 250-278. |
| [23] |
Batzle M L, Han D H, Hofmann R. Fluid mobility and frequency-dependent seismic velocity-direct mea-surements[J]. Geophysics, 2006, 71(1): N1-N9. |
| [24] |
Chen X H, He Z H, Zhu S X, et al. Seismic low-frequency-based calculation of reservoir fluid mobility and its applications[J]. Applied Geophysics, 2012, 9(3): 326-332. DOI:10.1007/s11770-012-0340-6 |
| [25] |
Chen X H, He Z H, Pei X G, et al. Numerical simulation of frequency-dependent seismic response and gas reservoir delineation in turbidites: A case study from China[J]. Journal of Applied Geophysics, 2013, 94(7): 22-30. |
| [26] |
Borcherdt R D. Viscoelastic Waves in Layered Media[M]. Cambridge University Press, 2009.
|
| [27] |
兰慧田.裂缝性孔隙介质波场模拟与频变AVO储层参数反演[D].吉林长春: 吉林大学, 2014. LAN Huitian.Wave Field Modeling in Fractured Po-rous Media and Frequency-dependent AVO Reservoir Parameters Inversion[D]. Jilin University, Changchun, Jilin, 2014. |



 张生强, 天津市滨海新区海川路2121号中海石油(中国)有限公司天津分公司渤海石油研究院, 300459。Email:
张生强, 天津市滨海新区海川路2121号中海石油(中国)有限公司天津分公司渤海石油研究院, 300459。Email: