随着地震数据采集技术的不断进步,宽方位、宽频带、高密度(“两宽一高”)采集技术得到普及,数据的信噪比、分辨率和保真度得到全面提高。一方面,数据成像品质明显改善,使常规解释技术的应用效果同时得到改善;更重要的是,保方位角偏移技术得到了应用和推广,生成的保方位角道集(也叫蜗牛道集或螺旋道集)保存了方位角信息,使各向异性研究步入了新阶段。
炮检距向量片(Offset vector tile,OVT)偏移技术是一种保方位角偏移技术。OVT的概念最早由Vermeer[1]在1998年提出;随后Vermeer[2]、Calvert等[3]和段文胜等[4]应用OVT偏移技术,生成了OVG(Offset vector gather)数据[5]。OVG数据包含了两个大地坐标、时间、炮检距和方位角信息,因此被称为五维数据,可用于裂隙检测。
Koren等[6-7]提出的局部角度域(Local angle domain,LAD)分解成像技术是一种更前沿的保方位角偏移技术,该方法是宽(全)方位数据的处理方法,实现了包括入射和散射射线对的法线倾角和方位角、入射射线和散射射线的张开角和张开方位四个角度的成像,生成的角度域共成像点道集简称ADCIG(Angle-domain common-image gathers)。
OVG和ADCIG都是保留了观测方位信息的多维(大于四维)数据,在各向异性研究方面具有很大的应用潜力[8-10]。因为LAD分解成像技术目前尚未得到大范围的普及推广,而OVT偏移技术在一些主流商业软件均得到开发,致使大量的OVG数据来到解释人员的手中。如何将五维数据所含的丰富地质信息挖掘出来,解决复杂的地质问题,是地震资料解释人员不得不面临的新考验。
早在20世纪90年代,就已经有利用具有方位信息的叠前道集进行裂缝预测的方法,如Li[11]利用正交二维地震测线道集的同相轴变化对裂缝进行描述,Feng等[12]实现了利用含有方位角信息的叠前道集属性进行裂缝检测。Sena[13]和Winkler[14]指出,在各向异性介质中,纵波速度随方位角的变化呈周期性,变化关系具有椭圆特征。Grimm等[15]利用速度随方位角椭圆变化进行天然裂缝气藏检测;Fuck等[16]利用AVO梯度拟合椭圆进行垂直裂缝描述。随着宽方位(乃至全方位)数据的广泛应用,利用方位信息进行裂缝检测的方法不断进步。Canning等[17]应用ADCIG数据进行AVAZ反演,以对裂缝储层进行表征;Nicolaevich等[18]使用ADCIG数据利用AVAZ反演技术预测碳酸盐岩储层中的裂缝分布。
在计算各向异性强度和裂缝走向时,以上利用具有方位信息的道集进行裂缝预测的方法使用的都是椭圆拟合法,这对于只发育一个方向裂缝的情况是可行的,但当有多个方位的裂缝同时发育时,应用椭圆拟合法就会得到弱各向异性甚至无各向异性的计算结果。
本文以OVG数据为基础,提出了一种全新的道集显示方法,并在此基础上,利用数据的高密度优势,提出了方位统计法绘制玫瑰图、计算各向异性强度。方位统计法可克服椭圆拟合法无法描述多方位裂缝发育的瓶颈,提高裂缝的解释精度。
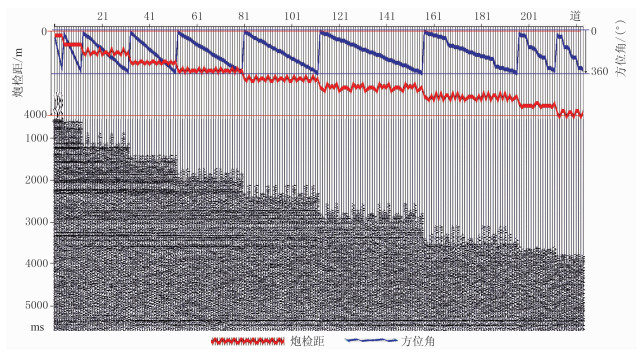
1 方法研究 1.1 炮检距—方位角域规则化及五维数据可视化 1.1.1 数据全方位化处理经过OVT偏移后的OVG数据保留了炮检距信息(图 1中红色曲线)和观测方位信息(图 1中蓝色曲线)。由图中可见,不同炮检距的共炮检距道集道数不同,不同方位角的共方位角道集道数也不同,因此解释人员无法在对等的情况下进行数据的分析对比,不利于各向异性分析和描述。数据全方位化的作用就是改变OVG数据的分布方式,使其能够方便进行不同方位的对比分析、可视化显示、道集内任意炮检距、方位角道集的抽取及分析。各向异性预测的基本思路是对比相同炮检距的数据属性在不同方位之间的差别,所以为了保证不同方位之间数据具有可比性,首先需要剔除大于最大非纵距的数据(图 2中蓝点),保留炮检距小于最大非纵距的数据(图 2中红点),将数据处理成全方位数据(图 3a)。
|
图 1 经过OVT域偏移后的OVG道集 |

|
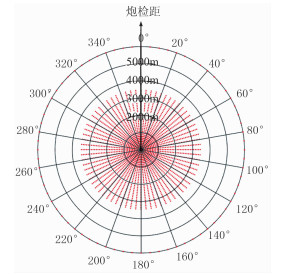
图 2 OVG数据在炮检距—方位角域的分布 红色为保留的数据点,蓝色为剔除的数据点 |

|
图 3 矩形数据规则化方法示意图(a)及加权系数μ的计算说明(b) |
在分方位数据处理中常用的是按照角度分扇区进行数据拆分,进而生成几个方位的叠后数据体用于地震解释。这种常规的拆分方法存在在小炮检距数据采样不足、远近道采样不均匀、抗噪性差的缺点,降低了AVO分析的保真度。
为了克服上述不足,实现不同方位角、不同炮检距的道集的道数相等,提高共方位数据规则化前、后的一致性,本文提出了炮检距—方位角域数据矩形规则化方法(图 3),其计算公式为
| $ {Y_{i, j}} = \sum\limits_{a, b} {{\mu _{i, j, r, \alpha }}{X_{r, \alpha }}} $ | (1) |
式中:X为初始道(图 3a);Y为规则化后的地震道(图 4);r、α分别为原始地震道的炮检距和方位角;i、j分别代表规则化后方位角和炮检距序号;μ为加权系数,是距离的函数;a、b为矩形参数(图 3b),控制μ的取值分布;μ的表达式为
|
图 4 炮检距—方位角域矩形规则化后的数据分布 |
| $ {\mu _{i, j, r, \alpha }} = \frac{{\frac{1}{{{l_k}}}}}{{\sum {\frac{1}{{{l_k}}}} }} $ | (2) |
式中lk是每一道(矩形框中的红点)到矩形框中心点的距离(图 3b)。
规则化后数据(图 4)的方位角间隔和炮检距间隔的疏密程度由原始数据的疏密程度而定,原则上以规则化后数据的数据量与原数据量变化不大为宜。
矩形数据规则化处理后,同方位不同炮检距的地震道是由相同采样数的地震道计算得到,保证了内插前后的一致性。
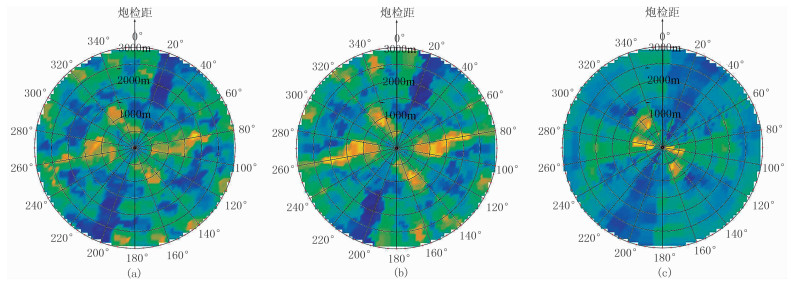
图 5为OVG道集振幅切片与不同方法规则化后道集振幅切片的对比。与扇形规则化处理结果(图 5c)相比,矩形数据规则化处理后(图 5b)振幅切片与规则化处理前(图 5a)一致性更好,并在一定程度上提高了信噪比。
|
图 5 全方位道集振幅切片 (a)原始OVG道集;(b)矩形规则化后道集;(c)扇形规则化后道集 |
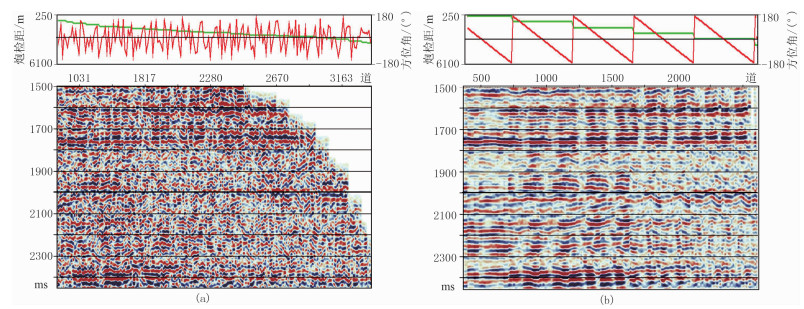
图 6为规则化前、后道集的对比,规则化后任意抽取的共炮检距道集道数都相同,共方位角道集亦然。OVT偏移后的道集按照炮检距检索,受各向异性影响,道集的同相性很差(图 6a);规则化后,数据经过炮检距—方位角域检索和存储,道集同相轴的振幅和反射时间是随方位角的变化呈周期性(图 6b),更有利于各向异性特征描述。
|
图 6 规则化前(a)、后(b)道集对比 红色为方位角曲线,绿色为炮检距曲线 |
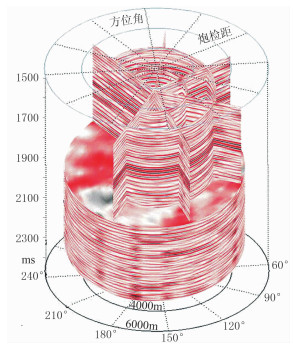
规则化后的数据按炮检距—方位角域进行格式存储,即可实现五维数据可视化(图 7)。
|
图 7 共成像点道集柱状显示 |
郝守玲等[19]对裂缝介质的纵波方位各向异性特征进行了物理模型试验研究,模型中裂缝介质是高速层,当观测方位与裂缝走向平行时(夹角为0°),反射波振幅和速度最大;随着测线方位与裂缝走向之间夹角的增大,反射波的振幅和速度逐渐减小,当夹角为90°时达到最小。
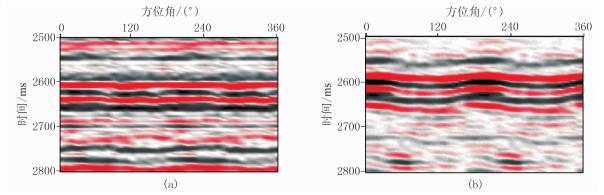
图 8为从裂缝发育区规则化后数据中抽取的不同炮检距的共炮检距道集,可见在大炮检距(4000m)的共炮检距道集上,同相轴随着方位角的变化而呈周期性波动,在裂缝走向方向(方位角为20°或200°)具有同相轴上凸和(或)强振幅的特征,在垂直于裂缝走向方向(方位角为110°)具有同相轴下凹和(或)弱振幅特征。
|
图 8 炮检距为50m(a)和4000m(b)的共炮检距道集 |
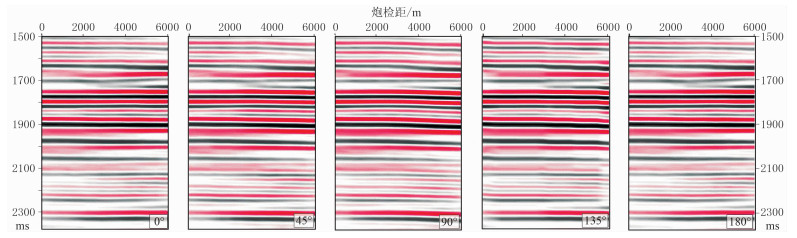
图 9为不同方位角的共方位角道集,可见平行于裂缝走向(方位角为0°)的道集同相轴平直,而垂直于裂缝走向(方位角为90°)的道集大炮检距时同相轴有明显下拉现象。
|
图 9 不同方位角的共方位角道集 |
从道集同相轴上提取的反射时间属性(图 10a),可以直观地看到反射时间大小的分布,小反射时间(绿色)的展布方向即为裂缝走向。同样地,在道集同相轴振幅属性切片(图 10b)上可以看到振幅在炮检距—方位角域的展布特征,强振幅异常(红色)的分布具有明显的方向性,其延伸方位与反射时间属性切片(图 10a)的低值延展方向基本一致,都约为40°(220°),同样反映了该点的裂缝走向。

|
图 10 柱状道集上沿同相轴提取的属性 (a)反射时间;(b)振幅 |
利用P波进行裂缝检测是裂缝性储层描述中的重要工作,国内外学者做了大量的研究[20],其中多是利用地震属性值随观测方位角的变化识别裂缝。Daley等[21]证实了地震波在各向异性介质中是以椭球体形状向外传播的。Ruger[22]推导了HTI介质纵波反射系数的近似式,证明了AVO梯度在HTI介质中随着观测方位与裂缝夹角大小的变化呈椭圆变化;Vladimir等[23]提出地震波的速度随方位角的变化可用椭圆来表示。地震属性随着方位角的变化可以写成椭圆方程
| $ F\left( \varphi \right) = A + B\sin 2\varphi $ | (3) |
式中:F为振幅、旅行时或速度的幅值;A为各向同性振幅、旅行时或速度;B为振幅、旅行时或速度随反射角的变化量;φ为观测方位与裂缝的夹角。当φ=0°时,即为裂缝走向,F(0°)=A+B,代表最大响应值;当φ=90°时,即垂直裂缝走向,F(0°)=A-B,代表最小响应值。
图 11分析了利用不同炮检距的振幅进行椭圆拟合预测裂缝的多解性。图 11a的道集振幅切片上黄绿色为强振幅,显示该点同时发育有30°和140°两组走向的裂缝,如果应用椭圆拟合法进行裂缝预测,小炮检距拟合的裂缝走向为北西向(图 11b);而中炮检距拟合无裂缝发育(图 11c);利用大炮检距拟合预测的裂缝走向为北东向(图 11d)。

|
图 11 椭圆拟合方法的多解性分析 (a)振幅切片;(b)小炮检距拟合;(c)中炮检距拟合;(d)大炮检距拟合 |
由图 11可知,椭圆拟合法的结果受炮检距影响,且无论怎样选择炮检距,也只能拟合出一个椭圆。Vasconcelos等[24]应用宽方位、多波多分量地震数据,应用椭圆拟合法对储层的两个方位的裂缝进行了表征。而只应用P波预测两组以上裂缝尚未见到先例。由上文分析可知,当同时发育多组裂缝时,P波地震拟合椭圆的离心率反而会变小,预测的各向异性强度随之减小,导致大量的优质裂缝储层被忽略。所以椭圆拟合法预测裂缝存在多解性。
Thomsen[25]给出了弱各向异性参数的定义
| $ \beta = \frac{1}{2}\left[{\frac{{F\left( {{0^ \circ }} \right)}}{{F\left( {{{90}^ \circ }} \right)}}-1} \right] = \frac{B}{{A -B}} $ | (4) |
在弱各向异性条件下,
| $ \beta \approx \frac{B}{A} $ | (5) |
由前文可知,振幅、速度等随着观测方位而变化,可以理解为振幅、速度等都是方位角的函数,则式(5)中的A、B可以写为
| $ \left\{ \begin{gathered} A = \frac{1}{{2\pi }}\int_0^{2\pi } {F\left( \varphi \right){\text{d}}\varphi } = \frac{1}{{2\pi }}\int_0^{2\pi } {\left( {A + B\cos 2\varphi } \right){\text{d}}\varphi } \hfill \\ B = \frac{1}{4}\int_0^{2\pi } {\left| {F\left( \varphi \right)-A} \right|{\text{d}}\varphi } = \frac{1}{4}\int_0^{2\pi } {\left| {B\cos 2\varphi } \right|{\text{d}}\varphi } \hfill \\ \end{gathered} \right. $ | (6) |
对方位角φ进行离散后,则各向异性强度可表示为
| $ \beta \approx \frac{\pi }{{2N}}\sum\limits_{i = 1}^N {\frac{{\left| {F\left( i \right)-\overline {F\left( i \right)} } \right|}}{{\overline {F\left( i \right)} }}} $ | (7) |
式中:N为方位角离散个数;
| $ \overline {F\left( i \right)} = \frac{1}{M}\sum\limits_{j = 1}^M {{F_{i, j}}} $ | (8) |
其中M为炮检距离散个数。M、N的大小由炮检距—方位角域内插时确定。当数据采集的覆盖次数很大时,方位角和炮检距的间隔应该小一些,否则M、N较大。
与椭圆拟合法相比,方位离散统计法对方位角进行离散,充分考虑了每组裂缝导致的方位属性值的偏离程度,多组裂缝发育时,各向异性强度值的计算结果会增大,更符合裂缝发育的实际情况,减少了裂缝预测的多解性。
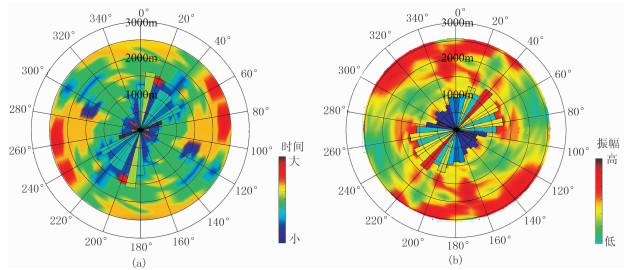
图 12为在柱状道集同相轴反射时间和振幅属性上利用方位统计法绘制的玫瑰图,式(7)即为玫瑰图的花瓣长度。可见同一点不同属性绘制的玫瑰图指示的裂缝走向是一致的。
|
图 12 道集属性切片及其对应的玫瑰图 (a)反射时间;(b)振幅 |
由式(7)计算的各向异性强度(图 13b)与相干体属性(图 13a)对比可见,方位离散方法获得的各向异性强度属性在大断层发育地区,展布特征与相干体一致;在无大断层发育的区域,各向异性强度属性比相干体属性能预测到更多的微断层和裂缝(如粉色箭头所示)。

|
图 13 相干属性(a)与各向异性强度(b)对比 |
图 14a为中国南方碳酸盐岩储层裂缝测井解释玫瑰图,发育两组斜交的裂缝。通过提取该井点目的层规则化后柱状道集的沿层振幅切片并绘制玫瑰图(图 14b),可见预测玫瑰图指示的裂缝走向与测井解释的结果一致。

|
图 14 裂缝测井解释结果(a)与对应的柱道集目的层振幅属性切片(b)的对比 |
南方A页岩气区的开采以水平井体积压裂方式为主,水平井钻探过程中,需尽量避开断层、裂缝发育位置,以防发生井漏、卡钻、轨迹出层等工程风险,保证优质页岩钻遇率,有效提高单井产能,所以裂缝的预测至关重要。
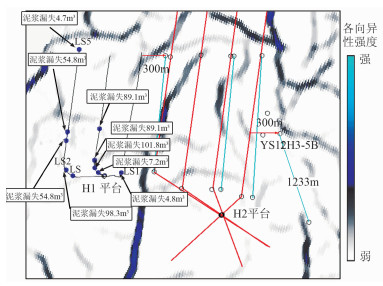
该区2015年实施了“两宽一高”地震采集并进行了OVT偏移处理。首先应用OVG数据计算了目标区的各向异性强度和方位数据体,并应用蚂蚁追踪技术对各向异性强度数据体进行了纵向增强,提取了龙马溪—五峰组的沿层切片,得到了目的层裂缝发育平面图(图 15)。图中H1为已钻井,对比可见,泥浆的漏失量与图中的裂缝发育强度呈正比,泥浆漏失量大的井段位于强各向异性区(图中深灰色),泥浆漏失量小的井段位于弱各向异性区(图中淡灰色或者白色区)。H2为设计井,红色折线为最初设计的水平井轨迹,天蓝色直线为依据各向异性强度预测结果调整后的轨迹,避开了较大的裂缝,为压裂方案制定提供了指导意见。
|
图 15 各向异性强度预测结果与钻井泥浆漏失量的叠合显示 黑色曲线为已钻H1水平井轨迹;红色折线为最初设计的H2水平井轨迹;天蓝色直线为依据各向异性强度预测结果调整后的H2水平井轨迹 |
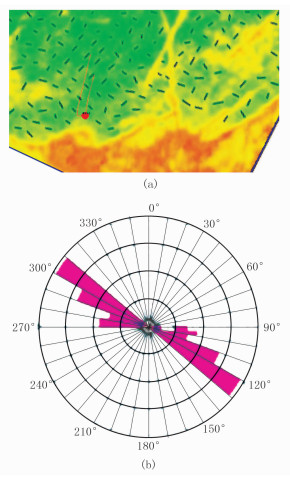
图 16a为利用各向异性方位体数据提取的沿层最大主应力方向,图中可以看出,P1井预测的最大主应力方向主要为北西向,与诱导缝的测井解释结果(图 16b)吻合,与微地震对应井段的压裂检测结果也吻合。从预测结果看,P1井的井底处最大主应力方向变成了北东向,而微地震监测的井底处也为北东向,进一步证明了方位统计法预测裂缝方位的精度。
|
图 16 P1井地应力预测结果(a)及诱导缝测井解释玫瑰图(b)的对比 |
“两宽一高”采集、保方位角偏移的地震数据使地震解释技术由三维延伸到了五维。
五维数据可视化本身即是解释过程,方位角—炮检距域规则化技术即是可视化显示及方位统计法各向异性表征的关键基础,也是提高数据信噪比的有效手段,而矩形数据规则化又是方位角—炮检距域数据内插的点睛之笔,是数据内插在不改变数据信息分布的基础上确保了数据在方位角域(各向异性)和炮检距域(AVO)的保真度。
以方位角—炮检距域数据规则化为基础的方位统计法是充分发挥高密度数据优势的一种方法,其计算的各向异性强度和绘制的玫瑰图克服了椭圆拟合法的缺陷,解决了多方位裂缝同时发育难以预测的技术瓶颈,提高了裂缝储层的预测精度。
随着多维数据解释技术的不断发展,其所包含的地质信息会不断被发掘出来,会有越来越多的地质难题被攻克。
| [1] |
Vermeer G J O. Creating image gathers in the ab-sence of proper common-offset gathers[J]. Exploration Geophysics, 1998, 29(4): 636-642. |
| [2] |
Vermeer G J O.Reciprocal offset-vector tiles in va-rious acquisition geometries[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 61-65.
|
| [3] |
Calvert A, Jenner E, Jefferson R, et al.Preserving azimuthal velocity information: experiences with cross-spread noise attenuation and offset vector tile Pre-STM[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 207-211.
|
| [4] |
段文胜, 李飞, 王彦春, 等. 面向宽方位地震处理的炮检距向量片技术[J]. 石油地球物理勘探, 2013, 48(2): 206-213. DUAN Wensheng, LI Fei, WANG Yanchun, et al. Offset vector tile for wide-azimuth seismic processing[J]. Oil Geophysical Prospecting, 2013, 48(2): 206-213. |
| [5] |
Stein J A, Wojslaw R, Langston T, et al. Wide-azimuth land processing: Fracture detection using offset vector tile technology[J]. The Leading Edge, 2010, 29(11): 1328-1337. DOI:10.1190/1.3517303 |
| [6] |
Koren Z, Ravve I. Full-azimuth subsurface angle domain wavefield decomposition and imaging, Part Ⅰ: Directional and reflection image gathers[J]. Geophy-sics, 2011, 76(1): S1-S13. |
| [7] |
Ravve I, Koren Z. Full-azimuth subsurface angle domain wavefield decomposition and imaging, Part 2: Local angle domain[J]. Geophysics, 2011, 76(2): S51-S64. DOI:10.1190/1.3549742 |
| [8] |
詹仕凡, 陈茂山, 李磊, 等. OVT域宽方位叠前地震属性分析方法[J]. 石油地球物理勘探, 2015, 50(5): 956-966. ZHAN Shifan, CHEN Maoshan, LI Lei, et al. OVT-domain wide-azimuth prestack seismic attribute analysis[J]. Oil Geophysical Prospecting, 2015, 50(5): 956-966. |
| [9] |
丁吉丰, 裴江云, 包燚. "两宽一高"资料处理技术在大庆油田的应用[J]. 石油地球物理勘探, 2017, 52(增刊1): 10-16. DING Jifeng, PEI Jiangyun, BAO Yi. Broadband, wide-azimuth and high-density (BWH) seismic data processing technology in Daqing Oilfield[J]. Oil Geophysical Prospecting, 2017, 52(S1): 10-16. |
| [10] |
孟阳, 许颖玉, 李静叶, 等. OVT域地震资料属性分析技术在断裂精细识别中的应用[J]. 石油地球物理勘探, 2018, 53(增刊2): 289-294. MENG Yang, XU Yingyu, LI Jingye, et al. Fault identification with OVT-domain seismic attribute analysis[J]. Oil Geophysical Prospecting, 2018, 53(S2): 289-294. |
| [11] |
Li X Y. Fracture detection using azimuthal variation of P-wave moveout from orthogonal seismic survey lines[J]. Geophysics, 1999, 64(4): 1193-1201. DOI:10.1190/1.1444626 |
| [12] |
Feng S, Toksoz M N. Scattering characteristics in he-terogeneous fractured reservoirs from waveform estimation[J]. SEG Technical Program Expanded Abstracts, 1998, 17: 1636-1639. |
| [13] |
Sena A G. Seismic travel time equations for azimutha-lly anisotropic and isotropic media: Estimation of interval elastic properties[J]. Geophysics, 1991, 56(12): 2090-2101. DOI:10.1190/1.1443021 |
| [14] |
Winkler K W.Laboratory observations of azimuthal velocity variations caused by borehole stress concentrations[C]. SEG Technical Program Expanded Abstracts, 1994, 13: 1133-1135.
|
| [15] |
Grimm R E, Lynn H B, Bates C R, et al. Detection and analysis of naturally fractured gas reservoirs: Multi-azimuth seismic surveys in the Wind River basin, Wyo-ming[J]. Geophysics, 1999, 64(4): 1277-1292. DOI:10.1190/1.1444634 |
| [16] |
Fuck R F, Tsvankin I.Seismic signatures of two or-thogonal sets of vertical microcorrugated fractures[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 146-149.
|
| [17] |
Canning A, Malkin A. Azimuthal AVA analysis using full-azimuth 3D angle gathers[J]. SEG Technical Program Expanded Abstracts, 2009, 28: 256-259. |
| [18] |
Nicolaevich I A, Viktorovich S I, Vasilyevich G A, et al. Applying full-azimuth angle domain prestack migration and AVAZ inversion to study fractures in carbonate reservoirs in the Russian Middle Volga region[J]. First Break, 2013, 31(2): 79-83. |
| [19] |
郝守玲, 赵群. 裂缝介质对P波方位各向异性的影响——物理模型研究[J]. 勘探地球物理进展, 2004, 27(3): 189-194. HAO Shouling, ZHAO Qun. The effect of fractured medium on P wave azimuthal anisotropy: A physical model study[J]. Progress in Exploration Geophysics, 2004, 27(3): 189-194. |
| [20] |
Hall S A, Kendall J M. Fracture characterization at Valhall: Application of P-wave amplitude variation with offset and azimuth (AVOA) analysis to a 3D ocean-bottom data set[J]. Geophysics, 2003, 68(4): 1150-1160. DOI:10.1190/1.1598107 |
| [21] |
Daley P F, Hron E. Reflection and transmission coe-fficients for seismic waves in ellipsoidally anisotropic media[J]. Geophysics, 1979, 44(1): 27-38. DOI:10.1190/1.1440920 |
| [22] |
Ruger A. Variation of P-wave reflectivity with offset and azimuth in anisotropic media[J]. Geophysics, 1998, 63(3): 935-947. DOI:10.1190/1.1444405 |
| [23] |
Vladimir G, Tsvankin I. 3-D description of normal moveout in anisotropic inhomogeneous media[J]. Geophysics, 1998, 63(3): 1079-1092. DOI:10.1190/1.1444386 |
| [24] |
Vasconcelos I and Grechka V.Seismic characterization of multiple fracture sets at Rulison Field, Colorado[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 1717-1721.
|
| [25] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |



 王霞, 河北省涿州市华阳东路东方地球物理公司科技园区研究院地质研究中心, 072751。Email:
王霞, 河北省涿州市华阳东路东方地球物理公司科技园区研究院地质研究中心, 072751。Email: