天然裂缝型油气藏近年来在勘探和生产中引起了较大的关注。天然裂缝控制储层的渗透率,决定油气的分布以及采收率,因此描述波在裂缝介质中的传播特征对于识别裂缝以及提高采收率具有重要意义。
叠前方位反演是目前最常用的识别裂缝方向、估计裂缝密度以及预测流体分布的方法[1-3],其中的反射系数方程由准静态等效裂缝模型所得,以HTI介质反射系数公式[4]、傅里叶级数展开[5]为代表。现阶段最常用、最直观的裂缝介质等效理论模型分别为线性滑移模型[6]、Hudson[7]刚度扰动硬币型裂缝模型和Thomson[8]各向异性参数裂缝模型,通过忽略裂缝微观结构以及孔缝间的流体交换模拟岩石弹性模量。上述方法在甚高频率下模拟的饱和岩石弹性模量适用于超声频带。对于低频,一般先求得干燥裂缝介质的等效模量,然后利用各向异性Gassmann方程进行流体替换[9]。虽然人们探讨了单组、两组及多组裂缝等效模型及裂缝间的相互影响[10-13],但仍不能准确地描述波在裂缝介质中的传播特征。
波在介质中传播时发生的频散和衰减是表征裂缝介质弹性特征的重要属性。除介质本身固有的衰减机制外,波在介质中传播时引起的孔隙间、缝隙间以及孔缝间的流体流动也是一种重要的衰减模式。常规准静态裂缝模型只适用于弛豫和非弛豫状态,因而裂缝介质的多尺度、全频带衰减特征研究成为近年的研究热点。Chapman等[14-15]假定每个硬币型裂缝都与固定数量的球形孔隙相连,提出微观到介观尺度频变裂缝裂隙模型。基于White周期层状等效模型[16],Brajanovski等[17-18]将裂缝等效为无限长平面薄层,借助等效传播矩阵的求解方法,得到了裂缝的法向频变弹性模量,进一步结合层状介质的Backus平均理论,分别得到高、低频极限裂缝介质的频变弹性模量。Galvin等[19-21]将裂缝的影响视为各向同性背景介质中的扰动,将裂缝视为薄硬币形状,利用多重散射定理,给出了随机裂缝介质的法向频变弹性模量。Brajanovski模型和Galvin模型的衰减在低频范围与频率成正比,在高频范围与频率的平方根成正比,与Johnson[22]的认识一致。Gurevich等[23]将Brajanovski模型和Galvin模型统一,给出了全频带裂缝介质弹性模量的统一表达式;Guo等[24]进一步将其拓展到有限厚度平面裂缝模型。另外,借助Krzikalla等[25]提出的频变张量近似式,Galvin等[26]进一步分析了硬币型裂缝VTI介质的相速度频散和衰减,Yang等[27]和Kong等[28]研究了平面裂缝介质模型的相速度频散、衰减以及黏弹性AVO响应。
本文利用离散积分方法给出了硬币型裂缝法向弹性模量的数值模拟过程,并结合线性滑移理论,分别得到了高、低频弹性模量,进一步分析了油、气、水饱和情况下的频散、衰减以及黏弹性反射响应。
1 硬币型裂缝孔隙弹性理论对于硬币型裂缝介质的频变性质,Galvin等[21]提出了数值模拟的Fredholm方程
| $ B(x)+\frac{1}{\pi} \int_{0}^{\infty} R(x, y) T(y) B(y) \mathrm{d} y=-p_{0} S(x) $ | (1) |
式中:x、y为积分变量;S(x)=(2/π)[sin(ax)-axcos(ax)]/x2; R(x, y)=sin[a(x-y)]/(x-y)-sin[a(x+y)]/(x+y), a为硬币型裂缝长度;B为待求函数;p0为流体压力;T(y)为中间函数
| $ \begin{array}{l} T(y) = M\left\{ {\frac{{{{\left( {2\alpha g{y^2} - k_2^2} \right)}^2}}}{{2gyHk_2^2(g - 1)\sqrt {{y^2} - k_2^2} }} - } \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{{2yag\sqrt {{y^2} - k_2^2} \left[ {(\alpha g - 2)k_2^2 + 2\alpha g{y^2}} \right]}}{{2gyHk_2^2(g - 1)\sqrt {{y^2} - k_2^2} }}} \right\} \end{array} $ | (2) |
式中:M=1/[(α-ϕ)/Kg+ϕ/Kf], 其中α=1-K/Kg, K为干岩石的体积模量,g=μ/(K+4μ/3), Kg为固体颗粒的体积模量,ϕ为孔隙度,μ为干岩石的剪切模量,Kf为流体的体积模量;k22=iωηH/[κM(K+4μ/3)],其中H=K+4μ/3+α2M,k2为慢纵波的波数,i为虚数单位,ω为角频率,η为流体黏度,κ为渗透率。
硬币型裂缝介质在垂直方向的频变弹性模量p33与B的关系为[21]
| $ {p_{33}} = \frac{{\rho {\omega ^2}}}{{k_1^2{{\left[ {1 - \frac{{2{\rm{i}}\varepsilon (H - \alpha M)}}{{{a^3}{k_1}\mu H(1 - g)}}\mathop {\lim }\limits_{x \to 0} \frac{{B(x)}}{x}} \right]}^2}}} $ | (3) |
式中:ρ为介质密度;ε为裂缝密度;k1为快纵波的波数。
式(1)、式(3)即为Galvin等[21]的硬币型裂缝数值模拟表达式,利用常规积分方法求解难度较大。为此,下面深入分析数值求解方法。
2 数值求解方法首先求解式(1)得到B的表达式,然后求取
由文献[20]可知,除了直接由式(1)求解B外,还可以使用方程
| $ \theta (\zeta ) + \frac{1}{{\rm{ \mathsf{ π} }}}\int_0^a \mathit{\Gamma } (\zeta ,\xi )\theta (\xi ){\rm{d}}\xi = - {p_0}\zeta $ | (4) |
求取。式中:θ(ζ)为待求函数;Γ(ζ,ξ)为核函数,满足
| $ \mathit{\Gamma }(\zeta ,\xi ) = {\rm{ \mathsf{ π} }}\sqrt {\zeta \xi } \int_0^\infty y T(y){J_{\frac{1}{2}}}(\zeta y){J_{\frac{1}{2}}}(\xi y){\rm{d}}y $ | (5) |
式中J为Bessel函数。θ(ζ)与B(x)的关系为
| $ B(x)=\frac{2}{\pi} \int_{0}^{a} \theta(\zeta) \sin (\xi x) \mathrm{d} \xi $ | (6) |
利用式(4)~式(6)也可以计算B,但相比式(1),式(4)~式(6)在形式上更复杂。在实际求解中,发现式(6)可以避免奇异点的影响,而且求取极限的步骤可以合并,进而基于Gauss-Lobatto离散积分,通过数值求解得到频变弹性模量。
首先,取Bessel函数的高阶项
| $ {J_{\frac{1}{2}}}(x) = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}x}}} \sin x $ |
对核函数Г化简
| $ \mathit{\Gamma }(\zeta ,\xi ) = 2\int_0^\infty T (y)\sin (\zeta y)\sin (\xi y){\rm{d}}y $ | (7) |
对于区间[0, a]的积分函数f(x)可以离散为
| $ \int_{0}^{a} f(x) \mathrm{d} x \approx \sum\limits_{j=1}^{n} A_{f} f\left(x_{j}\right) $ | (8) |
式中:xj∈[0, a]为求积节点;Aj为求积系数。式(1)可以离散为
| $ \theta (x) + \frac{1}{\pi }\sum\limits_{j = 1}^n {{A_j}} \mathit{\Gamma }\left( {x,{x_j}} \right)\theta \left( {{x_j}} \right) = F(x) $ | (9) |
令x=x1, …, xn, 并记θi=θ(xi), Γij=Γ(xi, xj), Fi=F(xi), 则式(9)可写为
| $ {\theta _i} + \frac{1}{\pi }\sum\limits_{j = 1}^n {{A_j}} {\mathit{\Gamma }_{ij}}{\theta _j} = {F_i} $ | (10) |
将上式表示为矩阵形式
| $ \left[ {\begin{array}{*{20}{c}} {{\theta _1}}\\ {{\theta _2}}\\ \vdots \\ {{\theta _n}} \end{array}} \right] + \frac{1}{{\rm{ \mathsf{ π} }}}\left[ {\begin{array}{*{20}{c}} {{A_1}{\mathit{\Gamma }_{11}}}&{{A_2}{\mathit{\Gamma }_{12}}}& \cdots &{{A_n}{\mathit{\Gamma }_{1n}}}\\ {{A_1}{\mathit{\Gamma }_{21}}}&{{A_2}{\mathit{\Gamma }_{22}}}& \cdots &{{A_n}{\mathit{\Gamma }_{2n}}}\\ \vdots & \vdots &{}& \vdots \\ {{A_1}{\mathit{\Gamma }_{n1}}}&{{A_2}{\mathit{\Gamma }_{n2}}}& \cdots &{{A_n}{\mathit{\Gamma }_{nn}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\theta _1}}\\ {{\theta _2}}\\ \vdots \\ {{\theta _n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_1}}\\ {{F_2}}\\ \vdots \\ {{F_n}} \end{array}} \right] $ | (11) |
可以看出,求解式(11)可以得到每一个节点的θi值。需要注意,Г函数是T(y)sin(ζy)sin(ξy)在区间(0,∞)积分的震荡函数,当积分变量y的值较大后积分函数快速衰减。图 1为当频率为10、100、10000Hz时积分函数随lgy的变化曲线。由图可见,当积分变量y>104后,积分函数趋于0,因此为加快计算速度,积分区间一般取(0,104)。
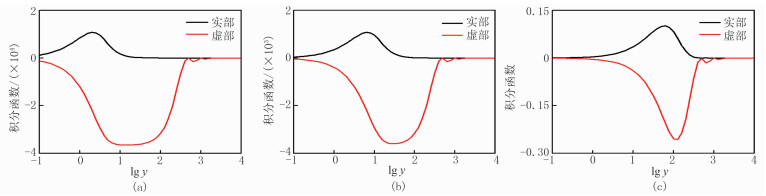
|
图 1 当频率为10(a)、100(b)、10000Hz(c)时积分函数随lgy的变化曲线 |
进一步
| $ \lim\limits _{x \rightarrow 0} \frac{B(x)}{x}=\lim\limits_{x \rightarrow 0} \frac{\int_{0}^{a} \theta(\xi) \sin (\xi x) \mathrm{d} \xi}{x}=\int_{0}^{a} \xi \theta(\xi) \mathrm{d} \xi $ | (12) |
上式将求极限问题转变为求积分。利用Gauss-Lobatto方法对上式离散化
| $ \int_{0}^{a} x \theta(x) \mathrm{d} x \approx \sum\limits_{j=1}^{n} A_{j} x_{j} \theta\left(x_{j}\right) $ | (13) |
只要将式(11)得到的每一个节点处的θ(xj)值乘以对应的节点值和积分系数,最后求和就可以得到极限值。
3 硬币型裂缝介质频变弹性张量Galvin等[21]只给出裂缝法向的弹性模量,其他方向的弹性模量可以通过Krzikalla等[25]推导的频变弹性模量关系得到
| $ p_{i j}(\omega)=C_{i j}^{\operatorname{high}}-\frac{\left[p_{33}(\omega)-C_{33}^{\mathrm{high}}\right]\left(C_{i j}^{\mathrm{high}}-C_{i j}^{\mathrm{low}}\right)}{C_{33}^{\mathrm{low}}-C_{33}^{\mathrm{high}}} $ | (14) |
式中Cij为刚度系数,下标i, j=1, …, 6,上标“high”代表高频,“low”代表低频。可见,除了已知法向弹性模量p33,还需知道高、低频极限条件的其他各个弹性参数。
3.1 低频极限研究低频条件的流体充填孔隙介质的等效弹性模量时,一般利用Gassmann方程[29]对干岩石骨架进行流体置换分析。
对于干岩石的描述,Galvin和Hudson裂缝模型给出的结果相同。干硬币型裂缝的法向弱度ΔN和切向弱度ΔT分别为[30]
| $ \Delta_{\mathrm{N}}=\frac{4 \varepsilon}{3 g(1-g)} $ | (15) |
| $ \Delta_{\mathrm{T}}=\frac{16 \varepsilon}{3(3-2 g)} $ | (16) |
结合线性滑移模型,将干岩石和裂缝参数代入Gassmann方程,可以得到其他弹性参数
| $ \left\{ \begin{array}{l} C_{11}^{{\rm{low}}} = \left( {\lambda + 2\mu } \right)\left[ {1 - \frac{{{\lambda ^2}\Delta_{\rm{N}}}}{{{{\left( {\lambda + 2\mu } \right)}^2}}}} \right] + \\ \;\;\;\;\;\;\;\;\;\frac{{{{\left( {{K_{\rm{g}}} - K + \frac{{\lambda {\Delta _{\rm{N}}}K}}{{\lambda + 2\mu }}} \right)}^2}}}{{\frac{{{K_{\rm{g}}}\phi \left( {{K_{\rm{g}}} - {K_{\rm{f}}}} \right)}}{{{K_{\rm{f}}}}} + {K_{\rm{g}}} - K\left( {1 - \frac{{{\Delta _{\rm{N}}}K}}{{\lambda + 2\mu }}} \right)}}\\ C_{13}^{{\rm{low}}} = \lambda \left( {1 - {\Delta _{\rm{N}}}} \right) + \\ \;\;\;\;\;\;\;\;\;\frac{{\left( {{K_{\rm{g}}} - K + {\Delta _{\rm{N}}}K} \right)\left( {{K_{\rm{g}}} - K + \frac{{\lambda {\Delta _{\rm{N}}}K}}{{\lambda + 2\mu }}} \right)}}{{\frac{{{K_{\rm{g}}}\phi \left( {{K_{\rm{g}}} - {K_{\rm{f}}}} \right)}}{{{K_{\rm{f}}}}} + \left( {{K_{\rm{g}}} - K + \frac{{{\Delta _{\rm{N}}}K}}{{\lambda + 2\mu }}} \right)}}\\ C_{33}^{{\rm{low}}} = H\left[ {1 - \frac{{4\varepsilon {{\left( {H - \alpha M} \right)}^2}}}{{3\mu H\left( {1 - g} \right)}}} \right]\\ C_{44}^{{\rm{low}}} = \mu \left( {1 - {\Delta _{\rm{T}}}} \right)\\ C_{66}^{{\rm{low}}} = \mu \end{array} \right. $ | (17) |
式中λ、μ为干岩石的拉梅参数。
3.2 高频极限当波在介质中传播时,会引起应力变化。在高频条件下惯性占据主导,因此流体没有足够的时间在孔隙和缝隙间流动使介质中的应力达到平衡状态,此时流体流动产生的影响可以忽略,可将裂缝和孔隙视为独立存在、互不影响。岩石的高频弹性模量可模拟为饱和背景岩石与饱和裂缝弹性模量的叠加,流体饱和裂缝法向弱度ΔN由Hudson模型模拟[30]
| $ \Delta_{\mathrm{N}}=\frac{4 \varepsilon}{3 g(1-g)\left[1+\frac{1}{\pi g(1-g)}\left(\frac{K_{\mathrm{f}}+\frac{4}{3} \mu_{\mathrm{f}}}{\mu}\right)\left(\frac{a}{c}\right)\right]} $ | (18) |
式中:μf为流体的剪切模量(近似为零);c为裂缝厚度。
饱和裂缝的切向弱度等于干岩石裂缝的切向弱度ΔT(式16)。
将饱和背景岩石与饱和裂缝的弹性模量叠加,得到裂缝介质的高频模量
| $ \left\{ \begin{array}{l} C_{11}^{{\rm{high}}} = H - \frac{{{{\left( {H - 2\mu } \right)}^2}}}{H}{\Delta _{\rm{N}}}\\ C_{33}^{{\rm{high}}} = H\left( {1 - {\Delta _{\rm{N}}}} \right)\\ C_{13}^{{\rm{high}}} = C_{33}^{{\rm{high}}}\left( {1 - 2\frac{\mu }{H}} \right)\\ C_{44}^{{\rm{high}}} = \mu \left( {1 - {\Delta _{\rm{T}}}} \right)\\ C_{66}^{{\rm{high}}} = \mu \end{array} \right. $ | (19) |
VTI介质中复相速度VP的频散表达式为[31]
| $ \begin{array}{l} {V_{\rm{P}}}\left( {\theta ,\omega } \right) = \frac{1}{{\sqrt {2\rho } }} \times \\ \sqrt {\left( {{p_{11}} + {p_{44}}} \right){{\sin }^2}\theta + \left( {{p_{33}} + {p_{44}}} \right){{\cos }^2}\theta + D} \end{array} $ | (20) |
其中
| $ \begin{array}{l} D = \left\{ {{{\left[ {\left( {{p_{11}} - {p_{44}}} \right){{\sin }^2}\theta - \left( {{p_{33}} - {p_{44}}} \right){{\cos }^2}\theta } \right]}^2}} \right.\\ \;\;\;\;\;\; + {\left( {{p_{13}} + {p_{44}}} \right)^2}\sin 2\theta {\} ^{\frac{1}{2}}} \end{array} $ |
黏弹性VTI介质纵、横波反射、透射系数满足下式[32]
| $ \left[ {\begin{array}{*{20}{c}} {{\beta _{{\rm{P1}}}}}&{{\beta _{{\rm{S1}}}}}&{ - {\beta _{{\rm{P2}}}}}&{ - {\beta _{{\rm{S2}}}}}\\ {{\gamma _{{\rm{P1}}}}}&{{\gamma _{{\rm{S1}}}}}&{{\gamma _{{\rm{P2}}}}}&{{\gamma _{{\rm{S2}}}}}\\ {{Z_{{\rm{P1}}}}}&{{Z_{{\rm{S1}}}}}&{ - {Z_{{\rm{P2}}}}}&{ - {Z_{{\rm{S2}}}}}\\ {{W_{{\rm{P1}}}}}&{{W_{{\rm{S1}}}}}&{{W_{{\rm{P2}}}}}&{{W_{{\rm{S2}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{R_{{\rm{PP}}}}}\\ {{R_{{\rm{PS}}}}}\\ {{T_{{\rm{PP}}}}}\\ {{T_{{\rm{PS}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {\beta _{{\rm{P1}}}}}\\ {{\gamma _{{\rm{P1}}}}}\\ { - {Z_{{\rm{P1}}}}}\\ {{W_{{\rm{P1}}}}} \end{array}} \right] $ | (21) |
式中:R为反射系数;T为透射系数;下标P代表纵波,S代表横波,1代表界面上方,2代表界面下方。其中
| $ \beta = {\left[ {\frac{{{p_{44}}s_x^2 + {p_{33}}s_z^2 - \rho }}{{{p_{11}}s_x^2 + {p_{33}}s_z^2 + {p_{44}}\left( {s_x^2 + s_z^2} \right) - 2\rho }}} \right]^{\frac{1}{2}}} $ | (22) |
| $ \gamma = \pm {\left[ {\frac{{{p_{11}}s_x^2 + {p_{44}}s_z^2 - \rho }}{{{p_{11}}s_x^2 + {p_{33}}s_z^2 + {p_{44}}\left( {s_x^2 + s_z^2} \right) - 2\rho }}} \right]^{\frac{1}{2}}} $ | (23) |
| $ W=p_{55}\left(\gamma_{S_{x}}+\beta s_{z}\right) $ | (24) |
| $ Z=\beta p_{13} s_{x}+\gamma p_{33} s_{z} $ | (25) |
| $ s_{z}=\frac{\left(K_{1} \mp \sqrt{K_{1}^{2}-4 K_{2} K_{3}}\right)^{\frac{1}{2}}}{\sqrt{2}} $ | (26) |
式中sz为垂直方向的慢度,和水平方向慢度sx及刚度的关系为
| $ K_{1}=\frac{\rho}{p_{44}}+\frac{\rho}{p_{33}}+\left[\frac{p_{13}}{p_{33} p_{44}}\left(p_{13}+p_{55}\right)-\frac{p_{11}}{p_{44}}\right] s_{x}^{2} $ | (27) |
| $ K_{2}=\frac{p_{11} s_{x}^{2}-\rho}{p_{33}} $ | (28) |
| $ K_{3}=s_{x}^{2}-\frac{\rho}{p_{55}} $ | (29) |
首先利用离散积分法模拟硬币型裂缝介质饱含水的法向频变弹性模量,VTI裂缝介质参数如表 1所示,流体参数如表 2所示,其频散与衰减如图 2所示。
|
|
表 1 VTI裂缝介质参数 |
|
|
表 2 流体参数 |
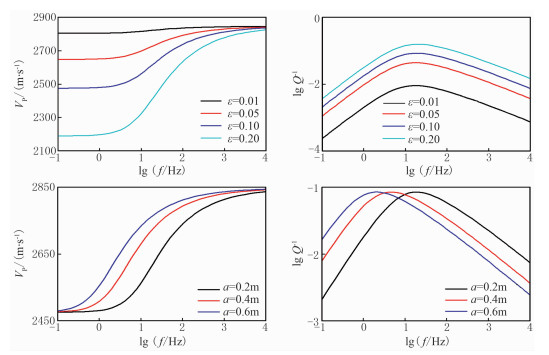
|
图 2 不同裂缝密度(上)、裂缝长度(下)的硬币型裂缝的频散(左)与衰减(右) |
由图可见:①在弛豫状态,由于波长远大于裂缝尺度,由波动引起的应力变化在很短时间达到平衡,速度几乎不变;在非弛豫状态,应力变化加快,流体的惯性逐渐成为主导,速度趋于稳定;在过渡状态,因为岩石中的流体流动减弱,整体柔度减小,对应刚度增加,因而随频率增加,速度不断变大(图 2左)。②当裂缝密度增加时,岩石柔度增加,速度变小,对应的衰减整体变大,但衰减峰值频率基本不变(图 2右)。③如果裂缝密度不变,裂缝长度由小变大,速度与衰减曲线的趋势基本不变,只是整体左移。
图 3为不同频率的含水介质速度和衰减随入射角的变化,图 4为不同入射角的含水介质频散和衰减。由图可见:在垂直于裂缝方向(θ=0°)速度和衰减变化最大,在平行裂缝方向(θ=90°)趋于定值;随入射角变大,各向异性程度减小,速度的频散趋势减缓,衰减峰值也逐渐减小。

|
图 3 不同频率的含水介质速度(左)和衰减(右)随入射角的变化 |
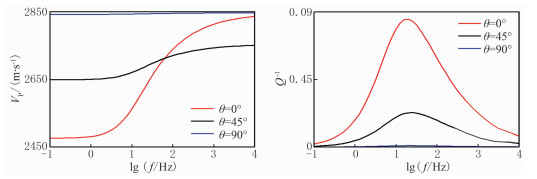
|
图 4 不同入射角的含水介质频散(左)和衰减(右) |
图 5为含气介质的速度与能量随入射角和频率的变化。由图可见:由于含气介质的密度较含水介质小,速度整体变小(图 5左);由于气体黏度较低,当频率较高时,在短时间内通过流体交换达到平衡,因而弛豫和非弛豫之间的过渡区向高频移动,振幅峰值也向高频移动(图 5右)。
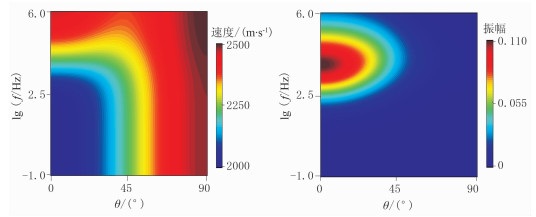
|
图 5 含气介质的速度(左)与能量(右)随入射角和频率的变化 |
图 6为含油介质的速度与能量随入射角和频率的变化。由图可见:速度变化与饱水介质相似(图 6左);由于油的黏度较高,在较低频带就达到非弛豫状态,因而峰值频率向低频移动(图 6右)。

|
图 6 含油介质的速度(左)与能量(右)随入射角和频率的变化 |
图 7为含水、含油、含气介质频变反射系数与流度。由图可见:①由于上层波阻抗大于裂缝介质,垂直反射系数为负,因此在弛豫与非弛豫过渡区,随频率增加,裂缝刚度增加、岩石的波阻抗增加,导致反射系数幅值减小(图 7左)。②当裂缝介质饱含气时,在入射角较小范围,反射系数幅值明显大于含水、含油(图 7下左)。③流度的峰值频率与能量的峰值频率相对应,即含油时峰值流度最大(图 7中右),含气时峰值流度最小(图 7下右);随入射角增大,各向异性程度减弱,整体幅值减小。
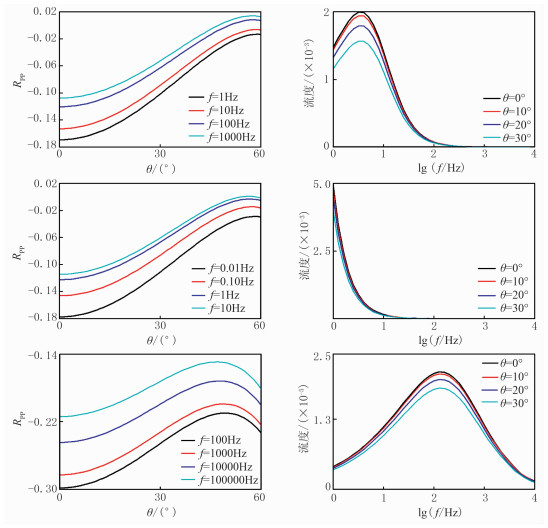
|
图 7 含水(上)、含油(中)、含气(下)介质频变反射系数(左)与流度(右) 裂缝介质上覆高速、高密度各向同性介质层,密度为2700kg/m3,纵、横波速度分别为3000、1600m/s |
本文通过岩石物理分析,研究了VTI硬币型裂缝介质频散、衰减规律的数值模拟方法,并分析了不同流体饱和介质的频散、衰减现象,得到以下认识:
(1) 通过离散积分和高阶近似方法,将第二类Fredholm积分方程与多重散射方程的远场极限值求解相统一,为数值模拟硬币型裂缝模型的法向频变弹性模量提供快速、准确的方法;结合线性滑移理论和Hudson裂缝模型,得到了频变弹性模量的解析式。
(2) 分析VTI介质相速度与黏弹性反射、透射系数方程可知,裂缝长度决定弛豫向非弛豫过渡区的频带,裂缝密度影响衰减峰值;当裂缝介质中饱含不同流体时,流体的黏度成为决定弛豫向非弛豫过渡的又一因素,饱气时反射系数幅值大于饱油、饱水时,流度的变化趋势与衰减的变化趋势相似。
| [1] |
吴国忱, 赵小龙, 罗辑, 等. 基于扰动弹性阻抗的裂缝参数反演方法[J]. 石油地球物理勘探, 2017, 52(2): 340-349. WU Guochen, ZHAO Xiaolong, LUO Ji, et al. Fracture parameter inversion based on perturbation elastic impedence[J]. Oil Geophysical Prospecting, 2017, 52(2): 340-349. |
| [2] |
龚明平, 张军华, 王延光, 等. 分方位地震勘探研究现状及进展[J]. 石油地球物理勘探, 2018, 53(3): 642-658. GONG Mingping, ZHANG Junhua, WANG Yanguang, et al. Current situation and recent progress in different azimuths seismic exploration[J]. Oil Geophysical Prospecting, 2018, 53(3): 642-658. |
| [3] |
薛姣, 顾汉明, 蔡成国. 准静态孔缝介质广义裂隙弱度研究[J]. 石油地球物理勘探, 2015, 50(6): 1146-1153. XUE Jiao, GU Hanming, CAI Chengguo. General fracture weakness for quasi-static porous fractured media[J]. Oil Geophysical Prospecting, 2015, 50(6): 1146-1153. |
| [4] |
Rüger A. P wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry[J]. Geophysics, 1997, 62(3): 713-722. DOI:10.1190/1.1444181 |
| [5] |
Downton J E, Roure B. Interpreting azimuthal Fourier coefficients for anisotropic and fracture parameters[J]. Interpretation, 2015, 3(3): ST9-ST27. |
| [6] |
Schoenberg M. Elastic wave behavior across linear slip interfaces[J]. Journal of the Acoustical Society of America, 1980, 68(5): 1516-1521. DOI:10.1121/1.385077 |
| [7] |
Hudson J A. Overall properties of cracked solid[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1980, 88(2): 371-384. DOI:10.1017/S0305004100057674 |
| [8] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [9] |
Mavko G, Mukerji T, Dvorkin J. The Rock Physics Handbook[M]. New York: Cambridge University Press, 2009.
|
| [10] |
Far M E, Sayers C M, Thomsen L, et al. Seismic cha-racterization of naturally fractured reservoirs using amplitude versus offset and azimuth analysis[J]. Geophysical Prospecting, 2013, 61(2): 427-447. DOI:10.1111/1365-2478.12011 |
| [11] |
Far M E, Thomsen L, Sayers C M. Seismic characteri-zation of reservoirs with asymmetric fractures[J]. Geophysics, 2013, 78(2): N1-N10. |
| [12] |
Grechka V, Kachanov M. Seismic characterization of multiple fracture sets: Does orthotropy suffice?[J]. Geophysics, 2006, 71(3): D93-D105. DOI:10.1190/1.2196872 |
| [13] |
Grechka V, Kachanov M. Effective elasticity of rocks with closely spaced and intersecting cracks[J]. Geophysics, 2006, 71(3): D85-D91. DOI:10.1190/1.2197489 |
| [14] |
Chapman M. Frequency dependent anisotropy due to mesoscale fractures in the presence of equant porosity[J]. Geophysical Prospecting, 2010, 51(5): 369-379. |
| [15] |
Chapman M, Liu E, Li X. The influence of fluid sensitive dispersion and attenuation on AVO analysis[J]. Geophysical Journal of the Royal Astronomical Society, 2010, 167(1): 89-105. |
| [16] |
吴建鲁, 吴国忱. 一维频率域中观尺度虚岩石物理方法[J]. 石油地球物理勘探, 2018, 53(1): 105-112. WU Jianlu, WU Guochen. A method of 1D mesoscopic digital rock physics in the frequency domain[J]. Oil Geophysical Prospecting, 2018, 53(1): 105-112. |
| [17] |
Brajanovski M, Gurevich B, Schoenberg M. A model for P wave attenuation and dispersion in a porous medium permeated by aligned fractures[J]. Geophysical Journal of the Royal Astronomical Society, 2005, 163(1): 372-384. DOI:10.1111/j.1365-246X.2005.02722.x |
| [18] |
Brajanovski M, Müller T M, Gurevich B. Characteristic frequencies of seismic attenuation due to wave-induced fluid flow in fractured porous media[J]. Geophysical Journal of the Royal Astronomical Society, 2006, 166(2): 574-578. DOI:10.1111/j.1365-246X.2006.03068.x |
| [19] |
Galvin R J, Gurevich B. Interaction of an elastic wave with a circular crack in a fluid-saturated porous medium[J]. Applied Physics Letters, 2006, 88(6). DOI:10.1063/1.2165178 |
| [20] |
Galvin R J, Gurevich B. Effective properties of a poroelastic medium containing a distribution of aligned cracks[J]. Journal of Geophysical Research Solid Earth, 2009, 114(7). DOI:10.1029/2008JB006032 |
| [21] |
Galvin R J, Gurevich B. Scattering of a longitudinal wave by a circular crack in a fluid-saturated porous medium[J]. International Journal of Solids & Structures, 2007, 44(22-23): 7389-7398. |
| [22] |
Johnson D L. Theory of frequency dependent acoustics in patchy-saturated porous media[J]. Journal of the Acoustical Society of America, 2001, 110(2): 682-694. DOI:10.1121/1.1381021 |
| [23] |
Gurevich B, Brajanovski M, Galvin R J, et al. P-wave dispersion and attenuation in fractured and porous reservoirs poroelasticity approach[J]. Geophysical Prospecting, 2010, 57(2): 225-237. |
| [24] |
Guo J, Germán R J, Barbosa N D, et al. Seismic dispersion and attenuation in saturated porous rocks with aligned fractures of finite thickness: Theory and numerical simulations-Part 1: P-wave perpendicular to the fracture plane[J]. Geophysics, 2018, 83(1): 1-44. |
| [25] |
Krzikalla F, Müller T M. Anisotropic P-SV-wave dispersion and attenuation due to inter-layer flow in thinly layered porous rocks[J]. Geophysics, 2011, 76(3): WA135-WA145. DOI:10.1190/1.3555077 |
| [26] |
Galvin R J, Gurevich B. Frequency-dependent aniso-tropy of porous rocks with aligned fractures[J]. Geophysical Prospecting, 2015, 63(1): 141-150. DOI:10.1111/1365-2478.12177 |
| [27] |
Yang X, Cao S, Guo Q, et al. Frequency-dependent amplitude versus offset variations in porous rocks with aligned fractures[J]. Pure & Applied Geophy-sics, 2017, 174(3): 1-17. |
| [28] |
Kong L, Gurevich B, Zhang Y, et al. Effect of fracture fill on frequency-dependent anisotropy of fractured porous rocks[J]. Geophysical Prospecting, 2017, 65(6): 1649-1661. DOI:10.1111/1365-2478.12505 |
| [29] |
Gassman F. Abiat the elasticity of porous media[J]. Zurich Quarterly Natare Research, 1951, 96(1): 1-23. |
| [30] |
Bakulin A, Tsvankin I, Grechka V. Estimation of fracture parameters from reflection seismic data-Part Ⅰ: HTI model due to a single fracture set[J]. Geophy-sics, 2000, 65(6): 1788-1802. |
| [31] |
Rüger A.Reflection Coefficients and Azimuthal AVO Analysis in Anisotropic Media[D]. Colorado School of Mines, 1996.
|
| [32] |
Carcione J M. Reflection and transmission of qP-qS plane waves at a plane boundary between viscoelastic transversely isotropic media[J]. Geophysical Journal International, 1997, 129(3): 669-680. DOI:10.1111/j.1365-246X.1997.tb04502.x |



 张繁昌, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
张繁昌, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: