② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China
微地震监测技术是水力压裂过程中了解压裂效果的一种非常重要的手段,通过对微地震事件的定位、能量大小估计以及震源机制研究等可了解裂缝发育的区域和几何形状等信息[1-2]。震源机制解对于分析震源区裂缝发育特点、应力状态以及裂缝破裂机制等具有重要作用,利用震源机制分析岩石破裂面的张裂和剪切滑动等属性,获得破裂面的方向和倾角等参数,为解释水力压裂产生的缝网和计算有效压裂体积提供依据[3]。受井中接收器数量的限制以及井中监测张角小且方位单一等因素的影响,井中微地震监测信号的震源定位和震源机理分析结果有时不够准确[4]。地面微地震监测凭借其观测范围大、覆盖次数高以及不影响油田正常生产活动等优势,近年来得到广泛应用,尤其在压裂井附近缺少监测井的情况下,地面微地震监测是更好的选择。前人研究了水力压裂微地震震源机制反演:Vavryuk[5]研究了张裂源震源机制反演方法;Urbancic等[6]利用记录到的微地震信息,通过震源机制反演获得微地震事件的破裂类型;杨心超等[7-8]根据水力压裂过程中的P波初动极性获得了震源机制解;翟鸿宇等[9]分析了地层吸收衰减因子的变化对微地震震源机制反演分辨率的影响。水力压裂诱发的微地震以及火山和地热区域的微地震事件中很多为非双力偶(非DC)类型[10]。Foulger等[11]分析便携式地震记录仪记录的密集网格数据得到加利福尼亚长谷破火山口的多个微地震矩张量,利用P波、S波极性和振幅比等信息反演各种非DC机制,这些非DC可以简单地解释为剪切和拉张断裂的组合。有多种产生非DC分量的原因,如:地热以及火山活动区观测的正各向同性部分(ISO)和补偿线性矢量偶极成分(CLVD)分量通常与高压流体引起的张裂纹有关;矿山中的洞穴垮塌等导致非DC分量为负,说明震源机制中存在压缩成分。此外,单力偶也可以产生非DC分量,如滑坡、火山喷发等[12]。反演和解释非DC分量难度较大,这是由于非DC分量可能由模拟误差引起,除了速度模型误差、地震定位误差以外,接收器的稀疏分布以及数据噪声、简化的震源模型也会产生非DC分量[13]。因此需要认真分析非DC分量,研究目标区非DC分量的不确定性,在反演前首先测试非DC分量对接收器分布、地震特征以及数据质量等的敏感性,以便获得更可信的结果[14]。
本文首先介绍利用P波初动振幅信息反演水力压裂裂缝震源机制解的方法原理,然后通过理论模型记录测试、分析方法的应用效果。
1 矩张量理论分析 1.1 源张量与矩张量采用断面法向矢量n=(n1, n2, n3)T及位错方向矢量v=(v1, v2, v3)T表示源张量[15]
| $ \mathit{\boldsymbol{D}} = \frac{P}{2}\left[ {\begin{array}{*{20}{c}} {2{n_1}{v_1}}&{{n_1}{v_2} + {n_2}{v_1}}&{{n_1}{v_3} + {n_3}{v_1}}\\ {{n_1}{v_2} + {n_2}{v_1}}&{2{n_2}{v_2}}&{{n_2}{v_3} + {n_3}{v_2}}\\ {{n_1}{v_3} + {n_3}{v_1}}&{{n_2}{v_3} + {n_3}{v_2}}&{2{n_3}{v_3}} \end{array}} \right] $ | (1) |
式中P为源强度。
由剪张源模型(图 1)可知

|
图 1 剪张源模型 ϕ为走向角、η为倾角、θ为滑动角、α为张裂角 |
| $ \left\{\begin{array}{l}{n_{1}=-\sin \eta \sin \phi} \\ {n_{2}=\sin \eta \cos \phi} \\ {n_{3}=-\cos \eta}\end{array}\right. $ | (2) |
| $ \left\{\begin{array}{l}{v_{1}=(\cos \theta \cos \phi+\cos \eta \sin \theta \sin \phi) \cos \alpha-\sin \eta \sin \phi \sin \alpha} \\ {v_{2}=(\cos \theta \sin \phi-\cos \eta \sin \theta \cos \phi) \cos \alpha+\sin \eta \cos \phi \sin \alpha} \\ {v_{3}=-\sin \theta \sin \eta \cos \alpha-\cos \eta \sin \alpha}\end{array}\right. $ | (3) |
走向角ϕ、倾角η、滑动角θ和张裂角α(图 1)通常是空间位置和时间的函数,为了简化起见,在研究剪张错动的点源近似时可视为常量。走向角、倾角和滑动角描述了断面法向和断面位错矢量的切向,张裂角描述了位错矢量偏离断面的程度。张裂角α∈[-90°,90°],即:当α>0°时为剪张源,对于纯张裂源,α=90°;当α<0°时,为压裂源,对于纯压裂源,α=-90°;对于纯剪切源,α=0°。
微地震震源机制可用矩张量的形式表示[16]
| $ \boldsymbol{M}=M_{0}\left[\begin{array}{lll}{M_{11}} & {M_{12}} & {M_{13}} \\ {M_{21}} & {M_{22}} & {M_{23}} \\ {M_{31}} & {M_{32}} & {M_{33}}\end{array}\right] $ | (4) |
式中:M为对称矩阵,满足Mij=Mji,其中独立元素有6个,Mij表示沿着±i方向大小相等并且在j方向相距无限小的力偶(i、j=1,2,3);M0为地震矩幅度。
对于各向同性介质而言,矩张量分量Mij和源张量分量Dij满足
| $ M_{i j}=\lambda D_{k k} \delta_{i j}+2 \mu D_{i j} $ | (5) |
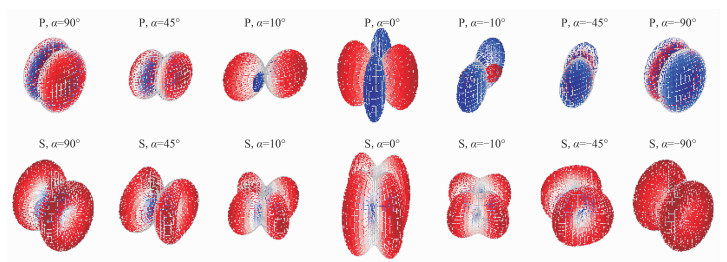
式中:λ和μ为震源区介质的拉梅常数;Dkk表示下标相同的源张量分量;δ为克罗内克函数,当i=j时,δij=1,当i≠j时,δij=0。辐射花样可观测破裂面的几何分布和破裂机制类型,本质上是对沙滩球显示的拓展。图 2为不同张裂角震源的纵、横波辐射花样图。
|
图 2 不同张裂角震源的纵、横波辐射花样图 ϕ=45°, η=50°, θ=-40° |
对微地震震源矩张量M采用特征值分解法分解为双力偶部分MDC、补偿线性矢量偶极成分MCLVD和各向同性部分MISO[17]
| $ \boldsymbol{M}=\boldsymbol{M}^{\mathrm{ISO}}+\boldsymbol{M}^{\mathrm{CLVD}}+\boldsymbol{M}^{\mathrm{DC}} $ | (6) |
其中
| $ \boldsymbol{M}^{\mathrm{ISO}}=\frac{1}{3} \operatorname{tr}(\boldsymbol{M})\left[\begin{array}{ccc}{1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {0} & {1}\end{array}\right] $ |
| $ \boldsymbol{M}^{\mathrm{CLVD}}=|\varepsilon| M_{\max }^{*}\left[\begin{array}{ccc}{-1} & {0} & {0} \\ {0} & {-1} & {0} \\ {0} & {0} & {2}\end{array}\right] $ |
| $ {\mathit{\boldsymbol{M}}^{{\rm{DC}}}} = (1 - 2|\varepsilon |)M_{\max }^ * \left[ {\begin{array}{*{20}{c}} { - 1}&0&0\\ 0&0&0\\ 0&0&1 \end{array}} \right] $ |
式中Mmax*、Mmin*分别为矩张量偏量部分M*的最大、最小特征值。MCLVD可以概念性地理解为圆柱轴向扩展、周围收缩给予补偿,以维持总体积的特定震源类型。对于可能存在的负MCLVD,表示轴向收缩被周围的扩张所抵消。MISO和MCLVD分量合称为非DC成分,MCLVD和MDC合称为矩张量偏量部分M*。首先求取M*的特征值M*,比较特征值的绝对值的相对大小,取绝对值最小的|M*|min和最大的|M*|max,则参数ε=-Mmin*/|M*|max。对于纯CLVD源,ε=±0.5;对于纯DC源,ε=0;对于膨胀源,ε>0;对于收缩源,ε<0[18]。
各分量所占的比例满足
| $ \left\{ {\begin{array}{*{20}{l}} {{H_{{\rm{ISO}}}} = \frac{1}{3}\frac{{{\mathop{\rm tr}\nolimits} (\mathit{\boldsymbol{M}})}}{{\left| {{M_{{\rm{max}}}}} \right|}}}\\ {{H_{{\rm{ClVD}}}} = - 2\varepsilon \left( {1 - \left| {{H_{{\rm{ISO}}}}} \right|} \right)}\\ {{H_{{\rm{DC}}}} = 1 - \left| {{H_{{\rm{ISO}}}}} \right| - \left| {{H_{{\rm{CLVD}}}}} \right|} \end{array}} \right. $ | (7) |
式中Mmax为M的最大特征值。在各向同性介质中,非DC分量决定源的类型,即:当非DC分量都为正值时,源是张裂源(裂纹张开);当非DC分量都为负值时,源是压缩源(裂纹闭合);DC分量总是正的;当为纯剪切源时DC分量占比为100%。
1.3 矩张量图示Hudson等[19]定义了一种震源类型的图解表示法,可实现各种破裂模式的概念化和可视化,可以研究矩张量中剪切组分和张性组分的分布情况。首先对矩张量进行正则化分解,然后计算其特征值Mj,并按大小排序
| $ M_{1} \geqslant M_{2} \geqslant M_{3} $ | (8) |
则ISO组分M及其对应的偏差Mj′分别为
| $ \overline{M}=\left(M_{1}+M_{2}+M_{3}\right) / 3 $ | (9) |
| $ M_{j}^{\prime}=M_{j}-\overline{M} \quad j=1,2,3 $ | (10) |
通过下列参数化运算,可以计算张性组分k和剪切组分T
| $ k = \left\{ {\begin{array}{*{20}{l}} {\frac{{\bar M}}{{|\bar M| - M_2^\prime }}}&{M_3^\prime \ge 0}\\ {\frac{{\bar M}}{{|\bar M| + M_1^\prime }}}&{M_3^\prime < 0} \end{array}} \right. $ | (11) |
| $ T = \left\{ {\begin{array}{*{20}{c}} {\frac{{ - 2M_3^\prime }}{{M_2^\prime }}}&{M_3^\prime > 0}\\ 0&{M_3^\prime = 0}\\ {\frac{{2M_3^\prime }}{{M_1^\prime }}}&{M_3^\prime < 0} \end{array}} \right. $ | (12) |
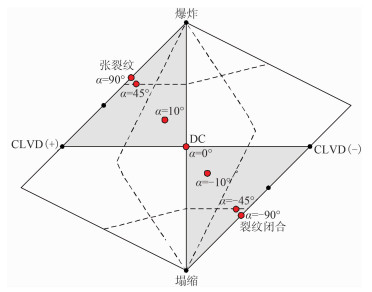
从而将矩张量的6个独立元素简化为Hudson图中的点(T,k)[20](图 3)。
|
图 3 不同张裂角(α=90°、45°、10°、0°、-10°、-45°、-90°)震源的Hudson图 横坐标表示剪切组分T值,纵坐标表示张性组分k值,两者的取值范围均为-1~1。各向同性爆炸型震源(ISO)中的膨胀震源(E)和压缩震源(I)的T-k坐标分别为(0,1)和(0,-1);纯剪切源的坐标为(0,0),位于图的中心位置;两类错动方向相反的补偿线性偶极子震源(CLVD+与CLVD-)的T-k坐标分别为(-1,0)和(1,0) |
微地震震源矩张量反演方法很多,包括采用极性、振幅以及全波形或集中考虑特定的体波相位(如P波和S波)的反演方法等。根据输入数据的质量和数量,可获得全张量或者部分张量,如果限制反演为偏量部分能够减少未知参数的数目,从而增强反演问题的稳定性[21-22]。
矩张量反演利用点源在均匀弹性介质中P波和S波的质点运动方程计算格林函数。P波和S波在x点、t时刻的振幅分别满足
| $ A_{i}^{\mathrm{P}}(x, t)=\frac{1}{4 \pi r \rho V_{\mathrm{P}}^{3}} \gamma_{i} \gamma_{j} \gamma_{k} M_{j k} $ | (13) |
| $ A_i^{\rm{S}}(x,t) = \frac{1}{{4{\rm{ \mathsf{ π} }}r\rho V_{\rm{S}}^3}}\left[ {\left( {{\delta _{ij}} - {\gamma _i}{\gamma _j}} \right){\gamma _k}{M_{jk}}} \right] $ | (14) |
式中:i为分量号;r为源到接收器的距离;ρ为密度;VP为P波速度;VS为S波速度;γi、γj和γk为从源到接收器的方位余弦;Mjk为矩张量分量;δij为克罗内克函数。
忽略震源时间函数时求解式(13)、式(14)的问题简化为
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Gm}} $ |
式中:d为包含N个振幅的矢量;G为格林矩阵,表征震源和接收器之间的振幅变化;m为地震矩矢量,包含矩张量的6个独立参数。上式的矩阵形式为
| $ \left[ {\begin{array}{*{20}{c}} {u_1^{\left( 1 \right)}}\\ {u_2^{\left( 1 \right)}}\\ {u_3^{\left( 1 \right)}}\\ \vdots \\ {u_1^{\left( N \right)}}\\ {u_2^{\left( N \right)}}\\ {u_3^{\left( N \right)}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {G_{11}^{\left( 1 \right)}}&{G_{12}^{\left( 1 \right)}}&{G_{13}^{\left( 1 \right)}}&{G_{14}^{\left( 1 \right)}}&{G_{15}^{\left( 1 \right)}}&{G_{16}^{\left( 1 \right)}}\\ {G_{21}^{\left( 1 \right)}}&{G_{22}^{\left( 1 \right)}}&{G_{23}^{\left( 1 \right)}}&{G_{24}^{\left( 1 \right)}}&{G_{25}^{\left( 1 \right)}}&{G_{26}^{\left( 1 \right)}}\\ {G_{31}^{\left( 1 \right)}}&{G_{32}^{\left( 1 \right)}}&{G_{33}^{\left( 1 \right)}}&{G_{34}^{\left( 1 \right)}}&{G_{35}^{\left( 1 \right)}}&{G_{36}^{\left( 1 \right)}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {G_{11}^{\left( N \right)}}&{G_{12}^{\left( N \right)}}&{G_{13}^{\left( N \right)}}&{G_{14}^{\left( N \right)}}&{G_{15}^{\left( N \right)}}&{G_{16}^{\left( N \right)}}\\ {G_{21}^{\left( N \right)}}&{G_{22}^{\left( N \right)}}&{G_{23}^{\left( N \right)}}&{G_{24}^{\left( N \right)}}&{G_{25}^{\left( N \right)}}&{G_{26}^{\left( N \right)}}\\ {G_{31}^{\left( N \right)}}&{G_{32}^{\left( N \right)}}&{G_{33}^{\left( N \right)}}&{G_{34}^{\left( N \right)}}&{G_{35}^{\left( N \right)}}&{G_{36}^{\left( N \right)}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{M_{11}}}\\ {{M_{22}}}\\ {{M_{33}}}\\ {{M_{23}}}\\ {{M_{13}}}\\ {{M_{12}}} \end{array}} \right] $ | (15) |
通过
| $ \boldsymbol{m}=\boldsymbol{G}^{-1} \boldsymbol{d} $ |
计算矩张量。上式为超定方程,求解需要更多的观测数据。为此,采用G-g代替G-1进行反演
| $ \boldsymbol{G}^{-\mathrm{g}}=\left[\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G}\right]^{-1} \boldsymbol{G}^{\mathrm{T}} $ | (16) |
由于实际地震数据中含有噪声,因此需要6个以上的振幅值准确求解m。在获得m后,需要稳定性分析以证明解的可靠性。反演的稳定性依赖于很多方面,如接收器的分布以及信号的信噪比等。如果要计算剪张源的角度参数,可以通过非线性反演方法获得,或者先求出Mij,再计算各个角度参数。针对震源机制的反演问题,Li等[23]和Tan等[24]研究了高频波形匹配和非线性反演方法。
实际矩张量和反演矩张量的误差为
| $ E=\left[\frac{1}{9} \sum\limits_{i=1}^{3} \sum\limits_{j=1}^{3}\left(\hat{M}_{i j}-M_{i j}\right)\right]^{1 / 2} $ | (17) |
式中Mij和
矩张量反演的置信度取决于多种因素。信噪比的局限性造成的输入信号振幅的不确定性、信号初动估计不准与定位不准导致的不确定性以及对穿过界面的反射(透射)损失考虑不周全、射线路径聚焦效应考虑不当、地震衰减与各向异性解释不当等都会影响矩张量反演结果。辐射花样的震源球采样对矩张量反演结果影响很大,测井资料由于井的数据观测范围有限和不规则方向孔径使矩张量反演结果不稳定。在没有先验约束条件时,利用单观测井数据通常不足以唯一地确定矩张量;当有3口观测井数据时单独使用P波或P波与S波联合反演可以获得全部矩张量;当有2口观测井数据时则须采用P波与S波联合反演才可获得全部矩张量[25]。地面监测能够在各个方向提供良好的震源球覆盖,单分量地面接收器可获得纵波振幅和初动,若没有横波信息约束,也会影响矩张量反演的稳定性。
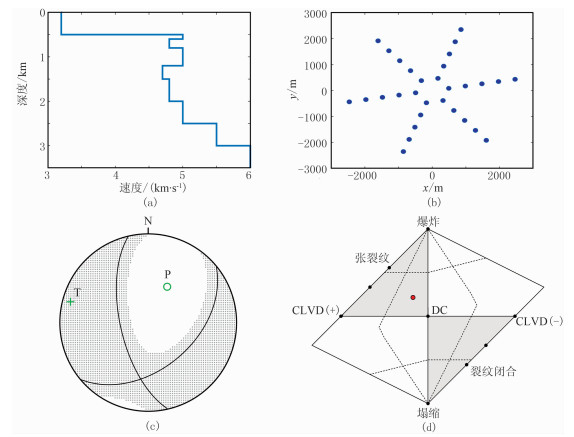
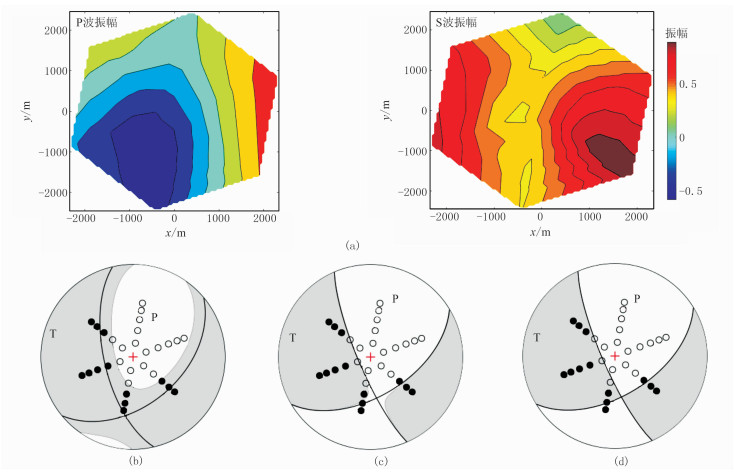
3.1 数据误差对反演结果的影响设定速度模型(图 4a)的观测系统台站为星形排列(图 4b),震源位于地下2600m处,选取相应震源机制(图 4c),获得的MDC、MISO和MCLVD的百分比分别为61.34%、21.48%和17.18%(图 4d)。图 5为理论模型矩张量反演结果。由图可见:基于振幅信息的偏量解在源中没有体积变化,因此不包含MISO,仅包含MCLVD和MDC(图 5c);基于振幅信息的MDC解在源中没有体积变化和MCLVD成分,因此仅包含MDC成分(图 5d)。
|
图 4 理论模型的Hudson图
(a)速度模型;(b)星形排列接收器;(c)震源机制;(d)Hudson图 ϕ=45°,η=50°,θ=-40°,α=10°。压缩象限的中心为P轴,扩张象限的中心为T轴,下同 |
|
图 5 理论模型矩张量反演结果
(a)振幅分布;(b)基于振幅信息的全矩张量解;(c)基于振幅信息的偏量解;(d)基于振幅信息的DC解 ○表示负极性,●表示正极性,下同 |
本文的反演结果由振幅信息获得,可根据反演结果绘制沙滩球,沙滩球使用纵波初动表征的震源机制图。震源机制反演可得到一组节面,其中一个为断面,另一个为辅助面。对于纯剪切源(DC)来说,这两个面是等价的,还需要借助其他辅助信息(如应力或地质信息等)确定具体节面类型。对于地面微地震监测数据处理,可以采用P波振幅信息反演震源机制。地面微地震监测具有较高的覆盖次数、较宽的方位角以及较大炮检距等特点,因此利用P波振幅信息可以得到稳定的震源机制解,文中采用全张量反演、偏量解和DC解反演方法。为了测试不同参数误差的影响,采用Monte-Carlo测试方法,对于不同误差均进行100次随机试验,采用MISO分量和MCLVD分量百分比分布图以及矩张量Hudson图与钻石图展示反演结果。根据输入数据的质量和数量,可获得全张量或者部分张量,如果限制反演为偏量部分可减少未知参数的数目、增强反演的稳定性。
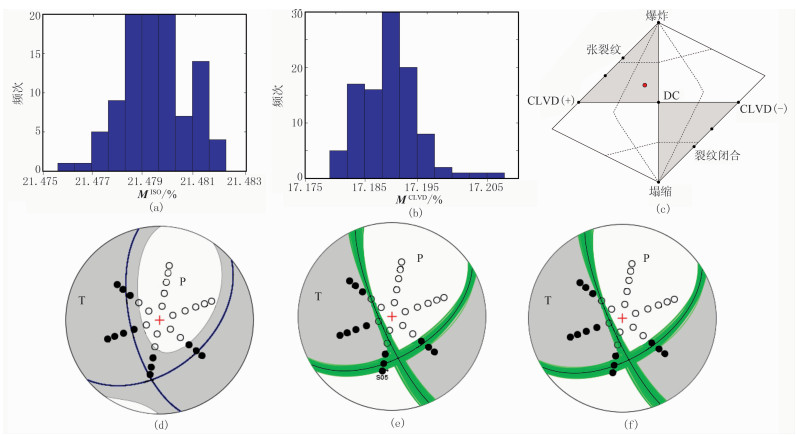
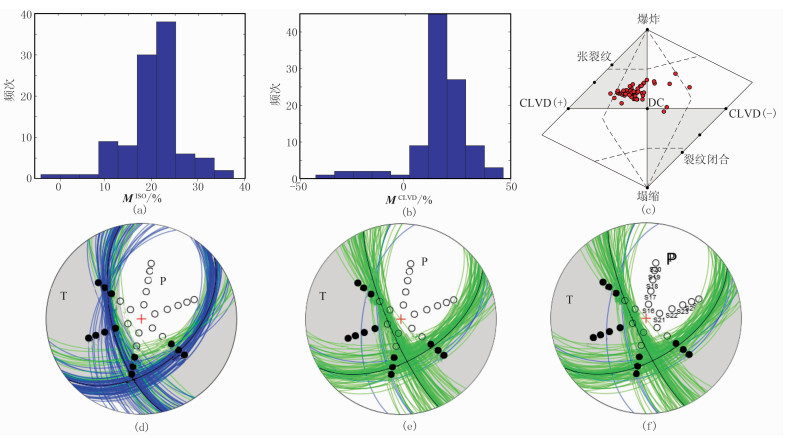
受环境干扰影响,地面微地震监测资料信噪比低,考虑随机噪声对振幅的影响,首先分析极性误差和振幅误差的影响。图 6是振幅误差为20%时的全矩张量反演结果,图 7是极性误差为5%时的全矩张量反演结果。对比两图可见,振幅误差导致反演结果偏差较小(图 6),极性误差导致反演结果偏差较大(图 7)。采用P波振幅反演结果的MISO反演误差相对较小,而全矩张量反演的MCLVD误差相对较大,观测误差主要影响MCLVD的结果。原因为:矩张量分解为MISO和MCLVD时,MCLVD由计算最小特征值/最大特征值的比值获得,MCLVD对反演矩张量的精度更敏感;MISO和矩张量特征值之间满足线性关系,因此相对于MCLVD,MISO对振幅误差不敏感。
|
图 6 振幅误差为20%时的全矩张量反演结果
(a)MISO百分比;(b)MCLVD百分比;(c)Hudson图;(d)全矩张量解;(e)偏量解;(f)DC解 蓝色、绿色分别对应反演结果为正断层、走滑断层 |
|
图 7 极性误差为5%时的全矩张量反演结果
(a)MISO百分比;(b)MCLVD百分比;(c)Hudson图;(d)全矩张量解;(e)偏量解;(f)DC解 蓝色、绿色和红色分别对应反演结果为正断层、走滑断层和逆断层 |
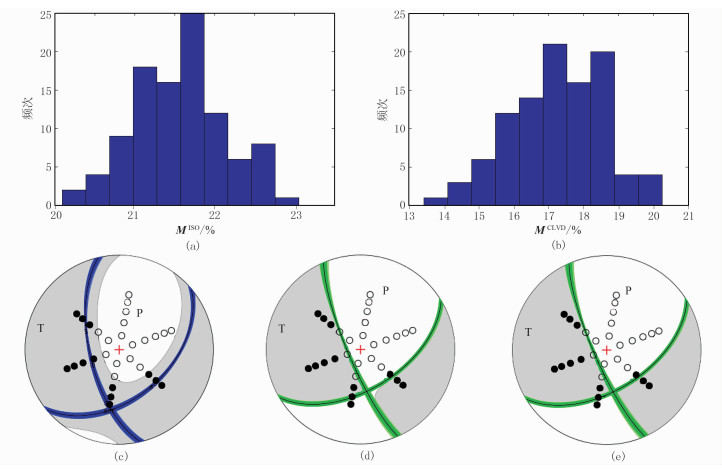
研究表明,模型参数的正确性、震源—接收器的几何分布以及定位精度等影响反演结果的可靠性,接收器的分布和选择影响反演结果的稳定性。图 8为接收器20%重采样时的全矩张量反演结果。由图可见,将数据随机舍去20%,实现20%重采样,观测系统对非DC分量的反演结果非常重要,合适的观测系统可增加地震矩张量DC和非DC分量分析的可信性。
|
图 8 接收器20%重采样时的全矩张量反演结果
(a)MISO百分比;(b)MCLVD百分比;(c)全矩张量解;(d)偏量解;(e)DC解 蓝色、绿色分别对应反演结果为正断层、走滑断层 |
图 9为定位误差小于30m时的全矩张量反演结果。由图可见,当存在定位误差时,理论计算结果和反演结果的均方根误差较小,非DC分量也受影响,采用P波时误差较大,非DC分量易被虚假的DC分量所掩盖。

|
图 9 定位误差小于30m时的全矩张量反演结果 (a)MISO百分比;(b)MCLVD百分比 |
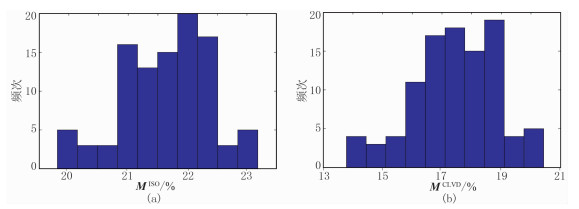
图 10为速度参数误差小于10%时的全矩张量反演结果。由图可见,当速度参数误差较大时,采用P波振幅时非DC分量的误差较大。
|
图 10 速度参数误差小于10%时的全矩张量反演结果 (a)MISO百分比;(b)MCLVD百分比 |
不同震源类型的辐射花样间存在差异,因此有限的震源球覆盖导致反演多解性。图 11为不同震源类型在振幅误差为20%及极性误差为5%时的全矩张量反演结果。由图可知,张裂角α=90°时受到极性和振幅误差的影响较大,节面分布较杂乱(图 11b、图 11e),与前文的结果类似,相对于MCLVD的结果而言,MISO的误差更小。

|
图 11 不同震源类型在振幅误差为20%及极性误差为5%时的全矩张量反演结果 (a)Hudson图(α=0°);(b)Hudson图(α=90°);(c)Hudson图(α=10°);(d)全矩张量解(α=0°);(e)全矩张量解(α=90°);(f)全矩张量解(α=10°)蓝色、绿色和红色线分别对应反演结果为正断层、走滑断层和逆断层 |
本文研究了利用P波初动振幅信息反演水力压裂裂缝震源机制解的方法原理,并通过理论模型记录测试、分析了方法的应用效果。基于P波辐射花样进行微地震震源机制反演,避免了传统P波初动极性反演方法的不确定性,可以得到更可靠的压裂裂缝解释结果。获得以下认识:
(1) 矩张量反演的置信度取决于多种因素,振幅误差导致反演结果偏差较小,极性误差导致反演结果偏差较大。相对于CLVD分量,采用全矩张量反演时ISO分量对误差不敏感,这是由于在矩张量分解时,ISO分量是矩张量特征值的线性函数,而CLVD分量是其非线性函数。
(2) 观测系统对于非DC分量的反演结果非常重要,合适的观测系统可增加地震矩张量DC和非DC分量分析的可信度。当模型误差较大时,采用P波振幅反演时非DC分量的误差较大。
(3) 辐射花样能够观测破裂面的几何分布和破裂机制类型,不同震源类型的辐射花样间存在差异,因此有限的震源球覆盖导致反演多解性。
本文利用P波初至振幅信息反演震源机制全矩张量,由于地面资料信噪比低、数据量大、观测范围大,只利用P波资料反演可以得到相对稳定的震源机制解,若利用P波、S波振幅信息联合反演可进一步提高反演的稳定性,同时在一定程度上能消除传播路径、近地表效应和仪器响应等因素对反演结果的影响。
| [1] |
赵邦六, 董世泰, 曾忠. 井中地震技术的昨天、今天和明天——井中地震技术发展及应用展望[J]. 石油地球物理勘探, 2017, 52(5): 1112-1123. ZHAO Bangliu, DONG Shitai, ZENG Zhong. Borehole seismic development, status quo and future:Application prospect of borehole seismic[J]. Oil Geophysical Prospecting, 2017, 52(5): 1112-1123. |
| [2] |
张云银, 刘海宁, 李红梅, 等. 应用微地震监测数据估算储层压裂改造体积[J]. 石油地球物理勘探, 2017, 52(2): 309-314. ZHANG Yunyin, LIU Haining, LI Hongmei, et al. Reservoir fracturing volume estimation with micro-seismic monitoring data[J]. Oil Geophysical Prospecting, 2017, 52(2): 309-314. |
| [3] |
方兵, 孙成禹, 唐杰, 等. 微地震信号频率特性分析[J]. 石油地球物理勘探, 2015, 50(3): 411-417. FANG Bing, SUN Chengyu, TANG Jie, et al. Analysis of frequency characteristics of micro-seismic signals[J]. Oil Geophysical Prospecting, 2015, 50(3): 411-417. |
| [4] |
唐杰, 王浩, 温雷, 等. 剪张型微地震震源机制与振幅分布特征[J]. 石油地球物理勘探, 2018, 53(3): 502-510. TANG Jie, WANG Hao, WEN Lei, et al. Focal me-chanism of shear-tensile microseismic and amplitude distribution characteristics[J]. Oil Geophysical Prospecting, 2018, 53(3): 502-510. |
| [5] |
Vavryuk V. Inversion for parameters of tensile earthquakes[J]. Journal of Geophysical Research, 2001, 106(8): 16339-16355. |
| [6] |
Urbancic T, Baig A.How microseismic data from over a decade of cyclic steaming stimulations can yield insight into a heavy oil reservoir?[C]. 75th EAGE Conference & Exhibition-Workshops, 2013.
|
| [7] |
杨心超, 朱海波, 崔树果, 等. P波初动震源机制解在水力压裂微地震监测中的应用[J]. 石油物探, 2015, 54(1): 43-50. YANG Xinchao, ZHU Haibo, CUI Shuguo, et al. Application of P-wave first-motion focal mechanism solutions in microseismic monitoring for hydraulic fracturing[J]. Geophysical Prospecting for Petroleum, 2015, 54(1): 43-50. DOI:10.3969/j.issn.1000-1441.2015.01.006 |
| [8] |
杨心超, 朱海波, 李宏, 等. 基于P波辐射花样的压裂微地震震源机制反演方法研究及应用[J]. 石油物探, 2016, 55(5): 640-648. YANG Xinchao, ZHU Haibo, LI Hong, et al. Microseismic focal mechanism inversion based on P-wave radiation pattern and its application[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 640-648. DOI:10.3969/j.issn.1000-1441.2016.05.002 |
| [9] |
翟鸿宇, 常旭, 王一博. 含衰减地层微地震震源机制反演及其反演分辨率[J]. 地球物理学报, 2016, 59(8): 3025-3036. ZHAI Hongyu, CHANG Xu, WANG Yibo. Inversion for microseismic focal mechanisms in attenuated strata and its resolution[J]. Chinese Journal of Geophy-sics, 2016, 59(8): 3025-3036. |
| [10] |
Vavryuk V. Inversion for the composite moment tensor[J]. Bulletin of the Seismological Society of Ame-rica, 2015, 105(6): 3024-3035. DOI:10.1785/0120150163 |
| [11] |
Foulger G R, Julian B R, Hill D P, et al. Non-double-couple microearthquakes at Long Valley caldera, California, provide evidence for hydraulic fracturing[J]. Journal of Volcanology and Geothermal Research, 2004, 132(1): 45-71. DOI:10.1016/S0377-0273(03)00420-7 |
| [12] |
Pesicek J D, Cieślik K, Lambert M. Dense surface seismic data confirm non-double-couple source mechanisms induced by hydraulic fracturing[J]. Geophy-sics, 2016, 81(6): 207-217. |
| [13] |
Lizurek G. Full moment tensor inversion as a practical tool in case of discrimination of tectonic and anthropogenic seismicity in Poland[J]. Pure and Applied Geophysics, 2016, 174(1): 197-212. |
| [14] |
Kuang W, Zoback M, Zhang J. Estimating geomecha-nical parameters from microseismic plane focal me-chanisms recorded during multistage hydraulic fracturing[J]. Geophysics, 2017, 82(1): 1-11. |
| [15] |
Jost M L, Herrmann R H. A student's guide to and review of moment tensors[J]. Seismological Research Letters, 1989, 60(2): 37-57. DOI:10.1785/gssrl.60.2.37 |
| [16] |
Stierle E, Vavryčuk V, ŠílenÝ J, et al. Resolution of non-double-couple components in the seismic moment tensor using regional networks-1:A synthetic case study[J]. Geophysical Journal International, 2014, 196(3): 1869-1877. DOI:10.1093/gji/ggt502 |
| [17] |
Stierle E, Vavryuk V, Kwiatek G, et al. Seismic moment tensors of acoustic emissions during laboratory rock deformation experiments:sensitivity to attenuation and anisotropy[J]. Geophysical Journal International, 2016, 205(1): 38-50. DOI:10.1093/gji/ggw009 |
| [18] |
Knopoff L, Randall M J. The compensated linear-vector dipole:A possible mechanism for deep earthquakes[J]. Journal of Geophysical Research, 1970, 75(26): 1957-1963. |
| [19] |
Hudson J, Pearce R, Roberts R. Source type plot for inversion of the moment tensor[J]. Journal of Geophysical Research, 1989, 94(1): 765-774. |
| [20] |
Grechka V, Li Z, Howell B, et al. Single-well moment tensor inversion of tensile microseismic events[J]. Geophysics, 2016, 81(6): 219-229. DOI:10.1190/geo2016-0186.1 |
| [21] |
刁瑞, 吴国忱, 尚新民, 等. 地面微地震有源噪声自动识别与匹配压制方法[J]. 石油地球物理勘探, 2018, 53(2): 311-319. DIAO Rui, WU Guochen, Shang Xinmin, et al. Microseismic active noise automatic identification and ma-tching denoising[J]. Oil Geophysical Prospecting, 2018, 53(2): 311-319. |
| [22] |
余洋洋, 梁春涛, 康亮, 等. 微地震地面监测系统的优化设计[J]. 石油地球物理勘探, 2017, 52(5): 974-983. YU Yangyang, LIANG Chuntao, KANG Liang, et al. Design optimization of surface-based microseismic monitoring system for hydraulic fracturing[J]. Oil Geophysical Prospecting, 2017, 52(5): 974-983. |
| [23] |
Li J L, Zhang H J, Kuleli H S, et al. Focal mechanism determination using high-frequency waveform ma-tching and its application to small magnitude induced earthquakes[J]. Geophysical Journal International, 2011, 184(3): 1261-1274. DOI:10.1111/j.1365-246X.2010.04903.x |
| [24] |
Tan Y Y, Zhang H J, Li J L, et al. Focal mechanism determination for induced seismicity using the neighbourhood algorithm[J]. Geophysical Journal International, 2018, 214(3): 1715-1731. DOI:10.1093/gji/ggy224 |
| [25] |
唐杰, 方兵, 孙成禹, 等. 压裂诱发的微地震震源机制及信号传播特性研究[J]. 石油地球物理勘探, 2015, 50(4): 643-649. TANG Jie, FANG Bing, SUN Chengyu, et al. Study on focal mechanism of micro-seismic induced by hydrofracture and signal propagation characteristics[J]. Oil Geophysical Prospecting, 2015, 50(4): 643-649. |



 唐杰, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
唐杰, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: