现今地震勘探已不仅仅关注构造形态的准确性,更力求得到可靠的岩性、物性等信息,这就要求偏移成像技术在得到足够高的成像精度的同时还具有一定振幅保真能力。叠前深度偏移成像技术已由最初的Kirchhoff算法发展到单程波偏移算法和逆时偏移算法。其中的单程波算法对复杂构造具有一定成像能力,且运算效率较高等特点,因此近年来有较快发展。
自Stoffa等[1]提出裂步傅里叶法(Split-step Fourier,SSF)和Ristow等[2]提出傅里叶有限差分法(Fourier finite-difference,FFD)这两种对横向速度变化介质有一定适应能力的偏移算法之后,频率—波数域单程波偏移算法逐渐受到关注。朱遂伟等[3]采用模拟退火算法全局优化FFD算法,提高了对陡倾地层的成像精度。梅金顺等[4]通过引入ω循环型边界条件,结合正则化方法,克服了FFD算法的边界效应并加快收敛速度。黄建平等[5]和朱峰等[6]通过推导黏声VTI介质中的FFD波场延拓算子,进一步扩大了FFD算法的适用范围。另外,de Hoop等[7]和Le Rousseau等[8]通过对相位屏理论的研究,提出了广义屏偏移算子(Generalized screen propagator,GSP),它也能准确描述地震波在陡倾地层或复杂构造中的传播情形。此后,Shin等[9]将广义屏算子应用于TTI介质构造成像,Kim等[10]将该偏移算子引入弹性介质多波多分量地震勘探,均拓展了广义屏算子的实际应用范围。
另一方面,随着勘探目标从过去的构造油气藏转向更加隐蔽的岩性、地层油气藏,甚至是致密油气或页岩气领域,地震波的振幅信息在地震资料精细解释和储层预测工作中也越来越重要,使波动方程叠前深度偏移方法也向振幅保真的方向发展,力求能更精确地定量描述储层岩性、物性、流体性质等。张关泉[11]通过分别推导上、下行波波动方程,得出在非均匀介质中符合地震波传播动力学的上、下行波耦合方程组。张宇[12]根据从双程波方程中分裂得出的上、下行单程波方程组,在波场延拓中求解真振幅共炮集波动方程。在此基础上,刘定进等[13-14]分别对傅里叶有限差分算子和广义屏算子进行真振幅推导,并且修改边界条件,从而得到保幅的叠前偏移结果。吕彬等[15]探讨了保幅型SSF叠前深度偏移方法的理论及应用;崔兴福等[16]实现了非均匀介质中波动方程混合法保幅偏移;叶月明等[17]通过合成平面波的方法显著提高了单程波偏移算法的计算效率。
波场延拓和成像条件是偏移成像的两个部分,二者需相互匹配才能得到准确的地质构造图像。对于真振幅的偏移成像,不仅需要在波场延拓时保持能量的稳定,还需要在保幅的成像条件下进行,这样才能保留更完整的岩性、物性以及流体性质等储层信息。目前对保幅的成像条件研究较少,在常用的成像条件互相关和反褶积中,仅反褶积成像条件具备部分保幅能力。但由于它为除法运算,所以存在成像不稳定的现象。针对反褶积成像的不稳定性,学者们利用不同的方法提高了该算法的实用性。如Guitton等[18-19]通过对算式中分母项添加阻尼因子以确保结果的稳定,而叶月明等[20]则采用平滑算法来保持计算稳定。
本文从成像精度和保幅能力两个方面对常规保幅高阶广义屏算法进行改进:首先利用粒子群优化算法对广义屏算子中近似展开式的常系数项做最优化求解,提高广义屏算法的成像角度(精度);再利用高斯窗函数反褶积成像条件进行成像,有效提高了偏移成像的保幅效果。
1 高阶广义屏保幅偏移算法根据张关泉[11]和张宇[12]的推导,二维保幅单程声波方程为
| $ \left(\frac{\partial}{\partial z}+\Lambda-\Gamma\right) p_{\mathrm{U}}(\omega, x, z)=0 $ | (1) |
| $ \left(\frac{\partial}{\partial z}-\Lambda-\Gamma\right) p_{\mathrm{D}}(\omega, x, z)=0 $ | (2) |
式中:pU、pD分别为上行、下行波场;ω为圆频率;Λ和Γ在频率—波数域中的表达式分别为
| $ \Lambda=\exp \left(\mathrm{i} \Delta z \frac{\omega}{v} \sqrt{1-\frac{v^{2}}{\omega^{2}} k_{x}^{2}}\right)=\exp \left(\mathrm{i} \Delta z k_{z}\right) $ |
| $ \Gamma=\exp \left(\Delta z \frac{v^{\prime}}{2 v} \frac{1}{1-\frac{v^{2}}{\omega^{2}} k_{x}^{2}}\right) $ |
式中:kx为(沿x方向的)水平波数;kz为(沿z方向的)垂直波数。
在保幅单程波方程中,地震波既能保持其运动学特征,又能保留其动力学特征。对Λ的求解情况决定构造形态的准确性;对Γ的求解情况决定地震波振幅的保真效果。目前对Λ和Γ的求解均是对其中的变量进行泰勒展开近似计算,其具体表达式[14, 21-22]分别为
| $ \begin{array}{*{20}{c}} {{k_z} = \frac{\omega }{v}\sqrt {1 - \frac{{{v^2}}}{{{\omega ^2}}}k_x^2} = \frac{\omega }{v} - \frac{\omega }{{{v_0}}} + \sqrt {\frac{{{\omega ^2}}}{{v_0^2}} - k_x^2} + }\\ {\omega \sum\limits_{j = 1}^n {{a_j}} {{\left( {\frac{1}{{{v^2}}} - \frac{1}{{v_0^2}}} \right)}^j}\left[ {{{\left( {\frac{\omega }{{\sqrt {\frac{{{\omega ^2}}}{{v_0^2}} - k_x^2} }}} \right)}^{2j - 1}} - v_0^{2j - 1}} \right]} \end{array} $ | (3) |
| $ \begin{array}{l} \frac{{{v^\prime }}}{{2v}}\frac{1}{{1 - \frac{{{v^2}}}{{{\omega ^2}}}k_x^2}} = \frac{{v_0^\prime }}{{2{v_0}}}\frac{1}{{1 - \frac{{{v^2}}}{{{\omega ^2}}}k_x^2}} + \\ \;\;\;\;\left( {\frac{{{v^\prime }}}{{2v}} - \frac{{v_0^\prime }}{{2{v_0}}}} \right) + \sum\limits_{j = 1}^n {\left[ {\frac{{{v^\prime }}}{{2v}}{{\left( {\frac{{{v^2}}}{{{\omega ^2}}}} \right)}^j} - \frac{{v_0^\prime }}{{2{v_0}}}{{\left( {\frac{{v_0^2}}{{{\omega ^2}}}} \right)}^j}} \right]} k_x^{2j} \end{array} $ | (4) |
式中:v0为参考速度;
由式(3)可知,在波场延拓中的垂直波数算子kz是根据泰勒公式展开近似得到,则其精确程度取决于泰勒公式的近似精度。对kz的泰勒近似计算是将其视为1-x(0<x<1)的形式进行的,其展开式可简单表示为
| $ \sqrt{1-x}=1-\frac{1}{2} x-\frac{1}{8} x^{2}-\frac{1}{16} x^{3}-\frac{5}{128} x^{4}-\cdots $ | (5) |
将该多项式系数项设为待定系数做重新拟合逼近,其展开式可表示为如下形式
| $ \sqrt{1-x}=1+a_{1} x+a_{2} x^{2}+a_{3} x^{3}+a_{4} x^{4}+\cdots $ | (6) |
式中aj为待定系数。
根据函数最佳平方逼近理论,求解多元函数方程的最优值,即可写为
| $ I\left(a_{1}, a_{2}, \cdots, a_{n}\right)=\int_{0}^{1}[f(x)-\varphi(x)]^{2} \mathrm{d} x $ | (7) |
其中
| $ f(x)=\sqrt{1-x} $ |
| $ \varphi(x)=1+a_{1} x+a_{2} x^{2}+a_{3} x^{3}+a_{4} x^{4}+\cdots $ |
由于垂直波数算子kz具有实际物理意义,表示在波场延拓中随延拓深度的递增而反复迭代运算得到的波场值,所以求取全局最优解才能得到更准确的波场值,也即取得更好逼近效果。
2.2 粒子群优化算法原理粒子群优化算法(Particle Swarm Optimization, PSO)是一种原理简单易懂、算法易于实现的智能寻优算法,自Kennedy等[23-24]提出后便广泛应用于众多领域。目前在地球物理相关领域的应用大多为反演和数据处理方面,而在成像偏移上涉及较少。
其基本原理简述为:在第k次迭代时,m维的第i个粒子具有速度vi(t)和位置xi(t),而该粒子下一时刻的速度vi(t+1)和位置xi(t+1)将由该粒子当前的速度和位置、当前最优位置Pi(t)和全局最优位置Pg(t)共同决定,通过反复迭代最终得到全局最优解。用公式表述为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{v}}_i}(t + 1) = \omega {\mathit{\boldsymbol{v}}_i}(t) + {c_1}{r_1}\left[ {{\mathit{\boldsymbol{P}}_i}(t) - {\mathit{\boldsymbol{x}}_i}(t)} \right] + }\\ {{c_2}{r_2}\left[ {{\mathit{\boldsymbol{P}}_g}(t) - {\mathit{\boldsymbol{x}}_i}(t)} \right]} \end{array} $ | (8) |
| $ {\mathit{\boldsymbol{x}}_i}\left( {t + 1} \right) = {\mathit{\boldsymbol{x}}_i}\left( t \right) + {\mathit{\boldsymbol{v}}_i}\left( {t + 1} \right) $ | (9) |
式中:ω为惯性权值,调节算法收敛速度;c1和c2为学习因子,用于控制算法不陷入局部极值;r1和r2为取值在[0, 1]区间的随机数。
2.3 PSO-GSP应用计算将粒子群优化算法应用于高阶广义屏偏移算子的计算流程如下:
(1) 设置相关参数,如确定求解的维度m,粒子个数n(即求解待定常系数),以及每个粒子初始化位置和飞行速度等;
(2) 调整惯性权值,计算每个粒子的历史最好位置和历史全局最好位置;
(3) 根据式(7)做全局最优化求解;
(4) 判断是否为全局最优值,若不是则返回(2);
(5) 将求得的待定常系数代入式(3)中进行计算。
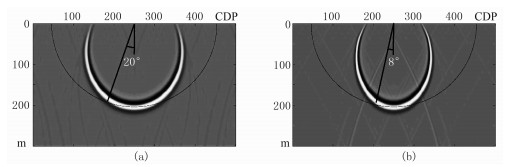
为了直观验证PSO-GSP算法对成像角度的提高,现将四阶PSO-GSP与常规四阶GSP以及常用的两种单程波偏移算法(SSF和FFD)在脉冲试验中进行对比分析,如图 1~图 4所示。从单程波偏移算子的推导中可知,波场延拓过程中均会参考v0用以计算,v0即同一深度中所有点所对应实际速度v的最小值。当v0远小于实际速度v时,即地层横向速度变化剧烈时,速度扰动的增大就会影响波场传递的结果,使地震波无法以严格的球形传播规律向下传播,成像角度便会大幅度减小,以至于成像结果不准确,而不同的偏移算法对地震波保持球形传播的能力有所不同。那么,在脉冲试验的均匀介质中,分别选取v0=v/2和v0=v/3,检验四种单程波偏移算法对角度成像的优劣。
|
图 1 v0=v/2 (a)和v0=v/3 (b)时的SSF脉冲响应 |

|
图 2 v0=v/2 (a)和v0=v/3 (b)时的FFD脉冲响应 |

|
图 3 v0=v/2 (a)和v0=v/3 (b)时的四阶GSP脉冲响应 |

|
图 4 v0=v/2 (a)和v0=v/3 (b)时的四阶PSO-GSP脉冲响应 |
由图 1~图 4可知,对于不同的v0,SSF的成像角度均最小,四阶GSP适中,FFD和PSO-GSP成像角度均较高;对比FFD、四阶GSP和PSO-GSP发现,当v0= v/2时,PSO-GSP优于FFD和四阶GSP,当v0= v/3时,四阶GSP成像角度较小,其余两者成像角度相当,但FFD算法可看到明显的背景噪声,这对偏移成像质量有影响。由此可见,四阶PSO-GSP算法对横向速度变化较为剧烈的地层成像效果更好;在地层相对平缓的地区,与FFD的成像效果相当。
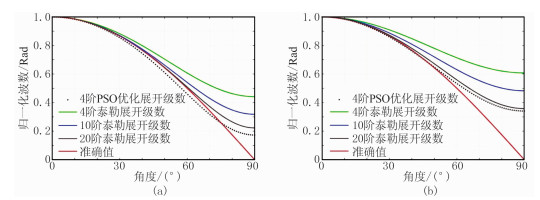
为进一步量化四阶PSO-GSP算法在成像精度上的提高幅度,对四阶PSO-GSP与各阶GSP分别在不同程度的陡倾地层中成像精度随入射角度增加的变化情况进行对比分析。如图 5a所示,以v0= v/2模拟横向速度变化剧烈的地层情况,随着入射角的增大,四阶GSP在入射角大于30°后便逐渐偏离准确成像值;而四阶PSO-GSP在入射角度小于60°时的成像精度与10阶GSP相当,在小于80°时的成像精度也能保持与20阶GSP相似。以v0=v/3模拟更为陡倾的地层情况(图 5b),可见各种算法的成像误差都有所增大,四阶GSP在入射角度大于20°后误差即大幅增加;但PSO-GSP依然保持与20阶GSP相当的成像精度,在入射角大于60°后误差才逐渐增加。因此,在相同的近似展开阶数情况下,PSO-GSP的成像精度相较于GSP大幅提升,对陡倾地层的成像能力更强。
|
图 5 当v0=v/2(a)和v0=v/3 (b)时四阶PSO-GSP与各阶GSP随入射角度变化曲线图 |
地震资料偏移成像的过程,不仅需对波场外推以获得地震波在不同深度点的波场值,还需要合适的成像条件对所求取的上、下行波场进行相关成像,得到直观的地下构造特征。而根据式(4),在保幅的波场延拓条件下,对成像条件的要求也随之变高。成像条件不仅需要提供准确的相位信息,更要在保幅波场延拓计算中使振幅保真,得到真实且完整的地下岩性、物性以及流体性质等储层信息。
目前,应用最为广泛与普遍的成像条件有两种,分别为互相关和反褶积,其公式如下
| $ R_{\mathrm{cor}}(x, z)=\frac{1}{2 \pi} \int p_{\mathrm{U}}(\omega, x, z) p_{\mathrm{D}}^{*}(\omega, x, z) \mathrm{d} \omega $ | (10) |
| $ {R_{{\rm{dec\_ \mathsf{ σ} }}}}(x,z) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int {\frac{{{p_{\rm{U}}}(\omega ,x,z)p_{\rm{D}}^*(\omega ,x,z)}}{{{p_{\rm{D}}}(\omega ,x,z)p_{\rm{D}}^*(\omega ,x,z) + \sigma }}} {\rm{d}}\omega $ | (11) |
式中σ表示阻尼因子。
这两种成像条件均有各自的优缺点:①互相关成像条件只有乘法运算,算法相对稳定,但其只能保证成像中相位正确,无法满足振幅保真的需求;②反褶积成像条件加入除法运算,具有一定的振幅保真能力,但当分母项趋近于零值时,会出现成像不稳定现象;为了避免除法运算的不稳定性,需额外加入阻尼因子σ,但却带来了阻尼因子选取的问题,且大幅提高了成像过程中的人为因素,进而导致振幅的失真或不可控的噪声干扰。
为了既保证在成像过程中的振幅保真,又避免成像条件的不稳定或干扰,叶月明等[20]首次提出了寻找一种窗函数平滑反褶积成像中的分母项,消除成像的奇异值影响。本文利用高斯窗函数对反褶积成像中的分母项进行平滑,其表达式如下
| $ G(x)=\frac{1}{\lambda \sqrt{2 \pi}} \mathrm{e}^{-\frac{x^{2}}{2 \lambda^{2}}} $ | (12) |
式中λ为平滑参数,即高斯窗的长度。该参数类似高斯分布函数的均方差,值越大表示高斯窗中的散点越多,则参与平滑运算的点数也变多,那么相对应的成像效果就会越好,其稳定性就会越高,当然计算量也会随之增加,所以对于平滑参数λ的选取需根据实际情况而定。
利用高斯窗函数对反褶积成像条件中的分母项进行平滑,就相当于褶积滤波的过程,即将高斯窗函数当做是滤波器,反褶积的分母项当作是信号输入,则平滑处理的表达式如下
| $ \begin{array}{*{20}{l}} {{f_{\rm{G}}}\left[ {{p_{\rm{D}}}(\omega ,x,z)p_{\rm{D}}^*(\omega ,x,z)} \right]}\\ {\quad = \int G (x - \xi ){p_{\rm{D}}}(\omega ,\xi ,z)p_{\rm{D}}^*(\omega ,\xi ,z){\rm{d}}\xi } \end{array} $ | (13) |
将高斯窗函数平滑后的下行波场值代入式(11)中,即可得到基于高斯窗函数平滑的反褶积成像条件
| $ {R_{{\rm{ gauss }}}}(x,z) = \frac{1}{{2\pi }}\int {\frac{{{p_{\rm{U}}}(\omega ,x,z)p_{\rm{D}}^*(\omega ,x,z)}}{{{f_{\rm{G}}}\left[ {{p_{\rm{D}}}(\omega ,x,z)p_{\rm{D}}^*(\omega ,x,z)} \right]}}} {\rm{d}}\omega $ | (14) |
以中点放炮、双边接收的简单水平层模型为例(图 6a),对比以上三种成像条件的结果:①互相关(图 6b)和反褶积(图 6c)的成像结果随着地震波入射角的增大在水平层两端的同相轴不同程度地出现拉伸、变粗现象,而高斯窗函数反褶积(图 6d)的成像结果在不同角度入射时可保持同相轴形态的稳定;②提取水平反射层附近的最大振幅值(图 6e)发现,三种成像条件的结果有相同规律,即随入射角增大而振幅值增大,当入射角超过可成像角度后振幅值迅速衰减。其中,高斯窗函数反褶积在可成像角度范围内的振幅值最稳定,保持相近振幅值,且在超出可成像角度范围后具有与互相关相近的振幅衰减速率,而反褶积的振幅衰减较慢,这是导致成像结果中有背景干扰噪声的主要原因。对比该水平层模型三种成像条件结果可知,高斯窗函数在振幅保真方面优于另两种传统成像条件。

|
图 6 水平层模型及其成像结果 (a)水平层模型;(b)互相关成像;(c)反褶积成像(σ=0.01);(d)高斯窗函数反褶积成像;(e)峰值振幅曲线 |
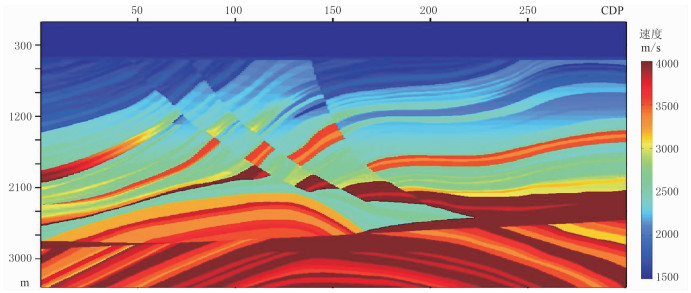
利用Marmousi模型(图 7)分别检验高斯窗函数对偏移成像的保幅效果及粒子群优化算法相对于传统广义屏算子的成像精度对比。该模型的横向采样点数为300,横向采样间隔dx=12.5m,纵向采样点数为560,纵向采样间隔dz=6m。用于偏移的炮集记录共240个,120道接收,炮间距为25m,道间距为12.5m,记录时间长度为3.5s,时间采样间隔为4ms。
|
图 7 Marmousi速度模型 |
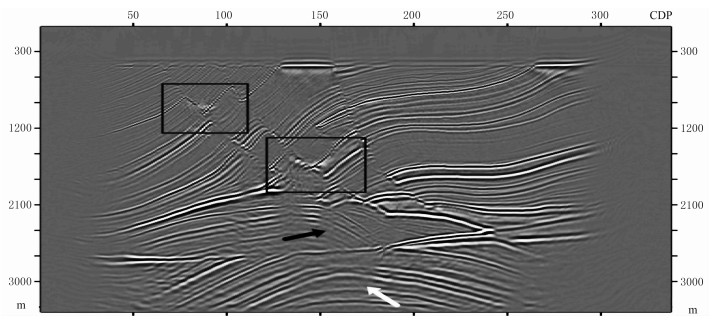
首先,应用互相关、反褶积和高斯窗函数反褶积三种不同的成像条件,对基于四阶PSO-GSP波场延拓算子偏移得到波场值进行成像,得到的剖面分别如图 8~图 10所示。图 8显示互相关成像条件的浅层成像效果较好,能量较强,但深层能量明显减弱(白色箭头所指);此外,位于约2200m处的中部背斜构造的内幕细节构造成像差,难以分辨(黑色箭头所指)。图 9是利用反褶积成像条件进行成像后的结果,选取的阻尼因子σ=0.01,图中振幅保真较互相关成像条件有所改善,但地层倾角较大时成像干扰较严重(黑色方框所指),且陡倾地层以下成像较为模糊;另外,中部背斜构造内幕的细节特征依然模糊,无太大改善。图 10是采用高斯窗函数反褶积成像条件得到的成像结果,选取的平滑参数λ=150,与前两种方法对比,高斯窗函数反褶积成像条件的振幅保真效果较好,3000m处的古地层构造清晰可见,在地层倾角较大处也能准确描绘同相轴。在设置平滑参数后,整幅图的噪声干扰明显减弱,位于约2200m处的中部背斜构造的内幕反射特征清晰可辨,同相轴的描绘与模型基本一致。上述对比分析结果充分说明高斯窗函数具有良好保幅和抗干扰能力。

|
图 8 基于保幅四阶PSO-GSP算子利用互相关成像条件的成像剖面 |

|
图 9 基于保幅四阶PSO-GSP算子利用阻尼反褶积成像条件的成像剖面(阻尼因子σ=0.01) |
|
图 10 基于保幅四阶PSO-GSP算子利用高斯窗函数反褶积成像条件的成像剖面(平滑参数λ=150) |
其次,将四阶PSO-GSP在Marmousi模型中的成像效果与四阶GSP、单程波偏移中最常见的SSF和FFD对比,主要从成像精度和抗噪能力等方面探讨分析。对SSF、FFD、四阶GSP三种单程波偏移算子均选用与四阶PSO-GSP(图 10)一致的平滑参数(λ=150)的高斯窗反褶积成像条件进行成像,所得Marmousi成像剖面如图 11~图 13所示。

|
图 11 基于SSF真振幅偏移剖面 |

|
图 12 基于FFD真振幅偏移剖面 |

|
图 13 基于四阶GSP真振幅偏移剖面 |
图 11为SSF偏移剖面,由于SSF对强横向速度变化的介质适应性较差,导致其对Marmousi模型中部的陡倾地层绕射波无法归位,尽管浅部及两侧的地层构造能较好地成像,基本无法分辨断面,位于陡倾地层下方的深部断层由于浅层构造归位不准确,导致深层构造形态十分模糊(白色箭头所指)。图 12为FFD偏移剖面,相较于SSF的成像结果,FFD算子的断面归位清晰,地层层状特征明显,但对陡倾地层的成像出现假象(黑色方框所指),且整幅剖面依然在成像平滑后有噪声,这或许是由图 2所示的FFD在大角度时波形恢复有假象造成;另外在2200m处中部背斜地层内部的细节构造也能成像(黑色箭头所指),但存在干扰。图 13为四阶GSP偏移剖面,该算法的成像效果与FFD较为相似,地层和构造特征基本一致,且对陡倾地层的成像均有部分归位不完全的现象,但其噪声干扰明显减少。四阶PSO-GSP偏移剖面(图 10))与FFD和四阶GSP偏移剖面相比,可见其对陡倾地层(黑色方框所指)的成像效果最佳,断点分明,绕射波基本完全归位。
5 实际资料分析选取一条二维地震数据进行偏移成像处理。该实际资料取自中国南海某区块的数据,在进行叠前偏移之前,对该资料炮集记录做了一些常规的地震资料预处理,包括定义观测系统、线性干扰压制、预测反褶积、叠加速度分析以及压制海上多次波(拉东变换和SRME)等。在获得了较为准确的层速度(图 14)之后,分别利用SSF、FFD、四阶GSP和四阶PSO-GSP对其进行偏移成像。

|
图 14 海上实际数据层速度模型 |
该实际地震资料速度模型尺寸为5250m×4250m,纵向采样间隔dz=6m,横向采样间隔dx=25m。采集炮集记录共计742炮,每炮360道接收,炮检距和道间距均为25m,接收时长为5s,时间采样间隔为2ms。基于以上四种单程波波场延拓算子偏移得到的成像剖面如图 15~图 18所示,其成像条件均为高斯窗函数的反褶积成像条件。
|
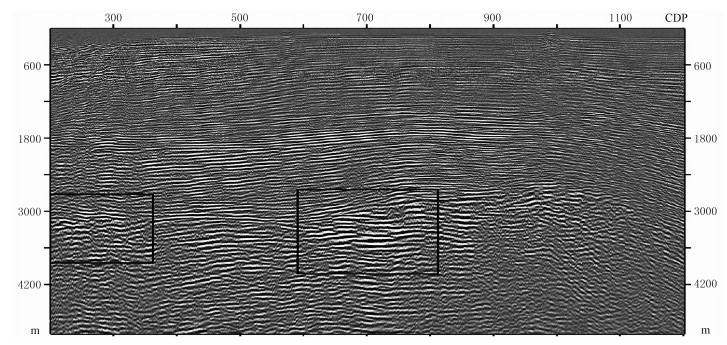
图 15 基于SSF真振幅偏移剖面 |
|
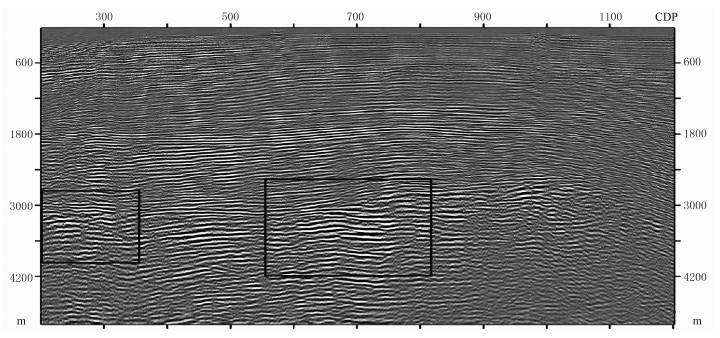
图 16 基于FFD真振幅偏移剖面 |
|
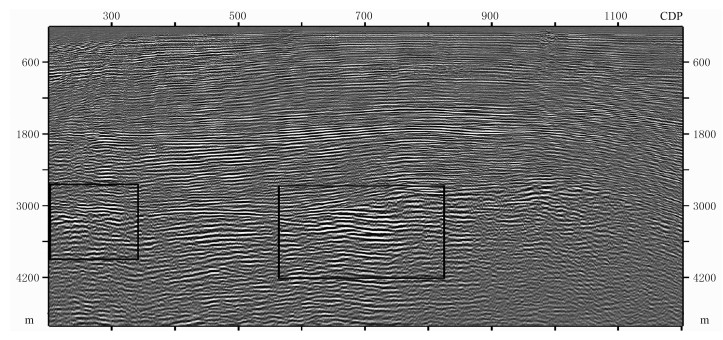
图 17 基于四阶GSP真振幅偏移剖面 |
|
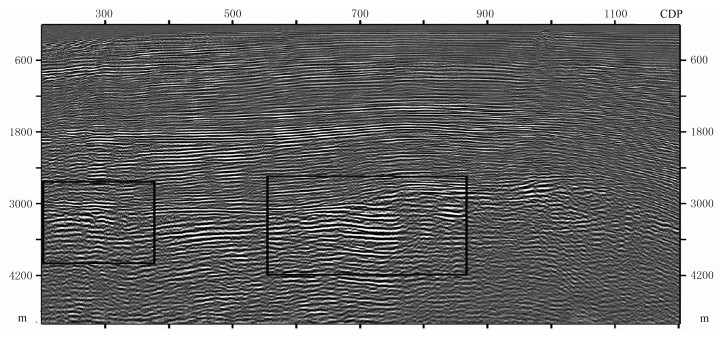
图 18 基于四阶PSO-GSP真振幅偏移剖面 |
由于该实际资料横向太长,图 15~图 18只截取其中第200~第1200个CDP共计1001个采样点做对比分析。对比四幅图发现,由于该海上资料浅层沉积较平整,四种偏移算子的成像结果差别甚微;但对于深部的背斜,四种偏移算子的成像剖面有所差异,如图 15的黑色方框所示,SSF偏移得到的地层同相轴的连续性很差,受到的干扰很严重,与图 16和图 17相比,其地层倾角也不一致,SSF剖面中地层为水平但不连续;而FFD和四阶GSP的偏移剖面中地层有一定倾角且连续性较好,这两种方法对此实际资料的成像能力相当。图 18为四阶PSO-GSP偏移剖面,在黑色方框内分辨率比FFD和四阶GSP更高,连续性更强。放大四种算法剖面的中部基岩黑色方框处(图 19)可发现,四阶PSO-GSP红色方框内的同相轴连续性更好,FFD次之,其余两种算法同相轴连续性较差;而竖直红线右侧部分,四阶PSO-GSP算法更能保持地层能量信息,优于其余三种算法。

|
图 19 各真振幅偏移剖面的局部放大 (a)SSF;(b)FFD;(c)四阶GSP;(d)四阶PSO-GSP |
本文从成像精度和保幅能力两个方面对传统保幅高阶广义屏叠前深度偏移算法进行改进。在成像精度方面,利用粒子群优化算法对高阶广义屏算子中垂直波数的常系数项进行全局最优化求解,进一步提高了高阶广义屏算法的成像角度;在保幅能力方面,利用高斯窗反褶积成像条件对保幅波场延拓的高阶广义屏算法的振幅保真效果进一步加强。通过脉冲试验和Marmousi模型对四种算法的对比分析,基于粒子群优化和保幅成像条件的高阶广义屏算法相较于其他三种传统单程波保幅偏移算法不仅有更高的成像精度、能够更好地适应陡倾地层的成像,还能有效提高地震波振幅保真效果,为下一步解释提供有力依据。通过对实际资料的应用效果分析,证明基于粒子群优化和保幅成像条件的高阶广义屏算法能有效提高保幅单程波偏移的成像质量,具有实际应用价值。
| [1] |
Stoffa P L, Fokkema J T, de Luma Freire R M, et al. Split-step Fourier migration[J]. Geophysics, 1990, 55(4): 410-421. DOI:10.1190/1.1442850 |
| [2] |
Ristow D, Rǘhl T. Fourier finite-difference migration[J]. Geophysics, 1994, 59(12): 1882-1893. DOI:10.1190/1.1443575 |
| [3] |
朱遂伟, 张金海, 姚振兴. 基于多参量的模拟退火全局优化傅里叶有限差分算子[J]. 地球物理学报, 2008, 51(6): 1844-1850. ZHU Suiwei, ZHANG Jinhai, YAO Zhenxing. Globally optimized Fourier finite-difference operator using simulated annealing algorithm based on multi-parameter[J]. Chinese Journal of Geophysics, 2008, 51(6): 1844-1850. DOI:10.3321/j.issn:0001-5733.2008.06.026 |
| [4] |
梅金顺, 王润秋, 于志龙, 等. 基于ω循环型预条件共轭梯度法正则化的偏移成像[J]. 石油地球物理勘探, 2014, 49(5): 892-898. MEI Jinshun, WANG Runqiu, YU Zhilong, et al. Re-gularization migration imaging based on the ω-circulant preconditioner conjugate gradient methods[J]. Oil Geophysical Prospecting, 2014, 49(5): 892-898. |
| [5] |
黄建平, 朱峰, 李振春, 等. VTI介质FFD叠前深度偏移成像方法[J]. 石油地球物理勘探, 2017, 52(3): 491-501. HUANG Jianping, ZHU Feng, LI Zhenchun, et al. FFD prestack depth migration for VTI media[J]. Oil Geophysical Prospecting, 2017, 52(3): 491-501. |
| [6] |
朱峰, 黄建平, 李振春. 黏声VTI介质傅里叶有限差分叠前深度偏移[J]. 石油地球物理勘探, 2017, 52(5): 956-966. ZHU Feng, HUANG Janping, LI Zhenchun. FFD prestack depth migration for visco-acoustic VTI me-dium[J]. Oil Geophysical Prospecting, 2017, 52(5): 956-966. |
| [7] |
de Hoop M V, Le Rousseau J H, Wu R S. Generalization of the phase-screen approximation for the scattering of acoustic waves[J]. Wave Motion, 2000, 31(1): 43-70. DOI:10.1016/S0165-2125(99)00026-8 |
| [8] |
Le Rousseau J H, de Hoop M V. Modeling and imaging with the scalar generalized-screen algorithms in isotropic media[J]. Geophysics, 2001, 66(5): 1551-1568. DOI:10.1190/1.1487101 |
| [9] |
Shin S, Byun J, Seol S J. Imaging tilted transversely isotropic media with a generalized screen propagator[J]. Exploration Geophysics, 2015, 46(4): 349-358. DOI:10.1071/EG14113 |
| [10] |
Kim B Y, Seol S J, Lee H Y, et al. Prestack elastic generalized-screen migration for multicomponent data[J]. Journal of Applied Geophysics, 2016, 126(3): 116-127. |
| [11] |
张关泉. 波动方程的上行波和下行波的耦合方程组[J]. 应用数学学报, 1993, 16(2): 251-263. ZHANG Guanquan. System of coupled equations for upcoming and downgoing wave[J]. Acta Mathematicae Applicatae Sinica, 1993, 16(2): 251-263. |
| [12] |
张宇. 振幅保真的单程波方程偏移理论[J]. 地球物理学报, 2006, 49(5): 1410-1430. ZHANG Yu. The theory of true amplitude one-way wave equation migration[J]. Chinese Journal of Geophysics, 2006, 49(5): 1410-1430. DOI:10.3321/j.issn:0001-5733.2006.05.021 |
| [13] |
刘定进, 印兴耀. 傅里叶有限差分法保幅叠前深度偏移方法[J]. 地球物理学报, 2007, 50(1): 268-276. LIU Dingjin, YIN Xingyao. A method of Fourier finite-difference preserved-amplitude prestack depth migration[J]. Chinese Journal of Geophysics, 2007, 50(1): 268-276. DOI:10.3321/j.issn:0001-5733.2007.01.033 |
| [14] |
刘定进, 杨瑞娟, 罗申玥, 等. 稳定的保幅高阶广义屏地震偏移成像方法研究[J]. 地球物理学报, 2012, 55(7): 2402-2411. LIU Dingjin, YANG Ruijuan, LUO Shenyue, et al. The method of preserved-amplitude seismic migration imaging with stable generalized high order screen[J]. Chinese Journal of Geophysics, 2012, 55(7): 2402-2411. |
| [15] |
吕彬, 王宇超, 李斐. 保幅型裂步傅里叶叠前深度偏移方法探讨[J]. 岩性油气藏, 2007, 19(3): 101-105. LYU Bin, WANG Yuchao, LI Fei. Research and application of amplitude preserved split step Fourier prestack depth migration[J]. Lithologic Reservoirs, 2007, 19(3): 101-105. DOI:10.3969/j.issn.1673-8926.2007.03.018 |
| [16] |
崔兴福, 张关泉, 吴雅丽. 三维非均匀介质中真振幅地震偏移算子研究[J]. 地球物理学报, 2004, 47(3): 509-513. CUI Xingfu, ZHANG Guanquan, WU Yali. True am-plitude seismic migration operator in 3-D heteroge-neous medium[J]. Chinese Journal of Geophysics, 2004, 47(3): 509-513. DOI:10.3321/j.issn:0001-5733.2004.03.022 |
| [17] |
叶月明, 庄锡进, 胡冰, 等. 基于单程波方程的合成平面波保幅偏移[J]. 石油地球物理勘探, 2013, 48(5): 711-716. YE Yueming, ZHUANG Xijin, HU Bing, et al. Synthesized plane wave preserved amplitude prestack depth migration based one-way wave equation[J]. Oil Geophysical Prospecting, 2013, 48(5): 711-716. |
| [18] |
Guitton A, Valenciano A, Bevc D.Robust imaging condition for shot-profile migration[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 2519-2522.
|
| [19] |
Guitton A, Valenciano A, Bevc D, et al. Smoothing i-maging condition for shot-profile migration[J]. Geophysics, 2007, 72(3): 149-154. DOI:10.1190/1.2712113 |
| [20] |
叶月明, 李振春, 仝兆岐, 等. 基于稳定成像条件的保幅叠前深度偏移[J]. 石油地球物理勘探, 2009, 44(1): 28-32. YE Yueming, LI Zhenchun, TONG Zhaoqi, et al. Amplitude-preserved prestack depth migration based on stable imaging condition[J]. Oil Geophysical Prospecting, 2009, 44(1): 28-32. DOI:10.3321/j.issn:1000-7210.2009.01.006 |
| [21] |
Ferguson R J, Margrave G F. Planned seismic imaging using explicit one-way operators[J]. Geophysics, 2005, 70(5): S101-S109. DOI:10.1190/1.2073885 |
| [22] |
Chen J B. On the selection of reference velocities for split-step Fourier and generalized-screen migration methods[J]. Geophysics, 2010, 75(6): S249-S257. DOI:10.1190/1.3517745 |
| [23] |
Kennedy J, Eberhart R C.Particle Swarm optimization[C]. Proceedings of IEEE International Conference on Neural Networks, 1995, 1942-1948.
|
| [24] |
Kennedy J, Eberhart R C. Swarm Intelligence[M]. San Francisco: Morgan Kaufmann Publication, 2001: 134-142.
|



 何润, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email:
何润, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email: