射线束偏移是一种灵活、高效且精度较高的深度域成像方法。它克服了传统基于射线的Kirchhoff偏移方法的某些缺陷,如高斯束偏移使用复值的初始束参数解决了常规射线追踪振幅在焦散区奇异性问题[1-3];高斯束偏移在局部平面波假设前提下使每条高斯束独立传播,实现了多波至成像[4-5],并能对陡倾构造成像。
在高斯束理论研究的基础上[6-8],Hill[9-10]先后提出叠后和叠前高斯束偏移算法。后来,Hill的成果被拓展到共炮点道集[11-12]、各向异性介质[13-14]以及弹性介质[15-17]。国内学者在高斯束偏移方面也做了大量研究,如李瑞忠等[18]利用局部倾斜叠加法实现了高斯束叠后偏移;李振春等[19]、岳玉波等[20-21]实现了角度域、炮域和复杂地表条件的保幅高斯束深度偏移。此外,黄建平等[22-25]、韩冰凯等[26]、吴娟等[27]和代福材等[28]也针对高斯束偏移技术进行了深入研究并发表了相应著述。
经过几十年的快速发展,高斯束偏移在理论上已经得到很好的证实,并作为Kirchhoff偏移的一种替代方法逐渐应用于实际地震数据处理。射线束偏移中一个重要步骤就是对叠前数据局部倾斜叠加后形成, τ-p域道集上的同相轴进行选择,该同相轴最终贡献于最后的成像。尽管高斯束偏移克服了Kirchhoff偏移的一些缺点,但传统的高斯束偏移在成像原理上与Kirchhoff类似,也是将所有反射能量投影到旅行时椭圆等时线上,这就意味着将, τ-p域道集上的所有点(同相轴)进行偏移,不仅增大了计算量,而且还会产生一些画弧噪声和偏移假象,尤其是在偏移叠加效果不好的复杂构造区域。
针对这个问题,很多学者做了有益的研究。Gao等[29]发展了快速束偏移方法,显著提高了偏移效率,但该方法在处理过程中会造成有效信号能量的缺失,很难解决复杂构造的精确成像问题。Vetle等[30]详细介绍了控制束偏移方法的优势,该方法是由CGG Veritas开发的高斯束偏移增强版,但未给出其具体原理和实现方法。Sherwood等[31]和Ting等[32]对控制束偏移方法进行了大量的研究和实际应用分析。Hu等[33]将慢度信息与高斯束偏移方法结合实现了一种慢度驱动的高斯束叠前深度偏移方法,该方法虽在某种程度能压制一些相干噪声,但它仅在共炮点域计算了检波点的水平慢度信息,忽略了对共检波点域炮点慢度信息的使用。为充分利用叠前地震数据炮点和检波点慢度信息,Yang等[34-35]提出一种基于优化策略的数据驱动的高斯束偏移方法,可有效地压制传统高斯束偏移所产生的噪声,且具实用性。
本文基于控制束偏移的思想,结合叠前数据的炮点和检波点水平慢度信息,并设计一个偏移质量控制因子进行偏移同相轴的选取,对偏移中引起的噪声(画弧和相干噪声等)和假象进行压制从而提高成像质量。具体实现上,首先对局部共炮点和共检波点道集进行局部倾斜叠加,并利用相干分析在, τ-p域拾取炮点和束中心位置水平慢度信息;然后设计一个偏移质量控制因子对同相轴进行筛选(去除非一次反射同相轴);最后采用经典高斯束偏移的算法进行成像。三个理论模型数据试验和实际资料应用证明了本文方法的可行性、有效性以及适用性,并且对比了本文方法和传统高斯束方法在Mar-mousi模型上的计算效率。
1 方法原理 1.1 射线参数拾取最常用的提取水平射线参数信息的方法有三种:平面波分解[36],多道互相关和相干分析[37]。Chopra等[38]指出,即使在噪声严重的数据中,相干性分析依然是一种稳健并能提供高分辨率同相轴连续性剖面的方法。所以,本文采用相干性分析在, τ-p域道集来估计水平射线参数信息,除了使用实值道集以外,还利用数据的解析道集计算相干系数,其公式可写为
| $ \sigma \left( {\tau , {\mathit{\boldsymbol{x}}_0}, p} \right) = \frac{{\sum\limits_{j = - n}^n {\left\{ {{{\left[ {\sum\limits_{i = 1}^k u \left( {\tau + j\Delta t - p\left( {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_0}} \right), {\mathit{\boldsymbol{x}}_i}} \right)} \right]}^2} + {{\left[ {\sum\limits_{i = 1}^k {{u_{\rm{H}}}} \left( {\tau + j\Delta t - p\left( {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_0}} \right), {\mathit{\boldsymbol{x}}_i}} \right)} \right]}^2}} \right\}} }}{{2nk\sum\limits_{j = - n}^n {\sum\limits_{i = 1}^k {\left\{ {{u^2}\left[ {\tau + j\Delta t - p\left( {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_0}} \right), {\mathit{\boldsymbol{x}}_i}} \right] + u_{\rm{H}}^2\left[ {\tau + j\Delta t - p\left( {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_0}} \right), {\mathit{\boldsymbol{x}}_i}} \right]} \right\}} } }} $ | (1) |
式中:, τ表示截距时间;p表示水平慢度或射线参数;x0为中心道的坐标,xi表示第i个局部道集的坐标;n表示一个时窗宽度半径;u(t, xi)和uH(t, xi)分别表示地震数据及其希尔伯特变换后数据;Δt为采样间隔。随着时窗宽度的增大,虽然相干性计算越稳定,但是局部同相轴监测的分辨率会越来越低,所以本文使用的时窗宽度为1。
本文使用炮点水平射线参数(ps)、检波点水平射线参数(pr)及反射时间(t)三个参数表征地震数据中的一个局部同相轴。根据炮检点互换原理,需拾取相同的同相轴,即在共检波点域道集的, τ-p域和共炮点域道集的, τ-p域上分别拾取具有相同反射时间的ps和pr。图 1是使用相干分析拾取上述三个参数(x或z方向分量)的简单示例,红叉指示局部最大值位置,即相干能量最强的参数位置。

|
图 1 射线参数拾取 |
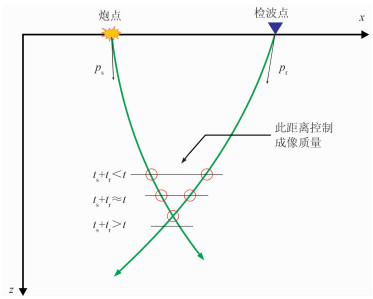
实际中有许多因素影响射线束偏移成像质量,本文假设速度模型和拾取的射线参数等都是准确的,唯一考虑的因素是成像的聚焦程度,所以使用两条射线的距离作为偏移质量控制因子,如图 2所示。在射线束偏移中,射线末端交点所估计的偏移位置,在该深度上炮点旅行时和检波点旅行时之和ts+tr等于反射时间t。如果两个射线末端点之间的距离太大,那么这个结果不能用于叠加成像。由于射线束偏移不是点对点成像,而是使用一个偏移“波形”代替这个成像点。所以,为了不损失有效信号能量,本文设置一个距离范围对偏移的同相轴进行选择,即成像距离在这个范围内的同相轴。控制因子的表达式可写为
| $ \begin{array}{c}{t-\alpha \Delta t<t_{\mathrm{s}}+t_{\mathrm{r}}<t+\alpha \Delta t} \\ {\left|\boldsymbol{d}_{\mathrm{s}}-\boldsymbol{d}_{\mathrm{r}}\right|<\beta \Delta x}\end{array} $ | (2) |
式中:ts、tr和t分别表示炮点、检波点射线旅行时和反射时间;Δt表示时间间隔;Δx表示速度模型水平间隔;ds和dr分别表示两条射线末端位置坐标;α和β是两个可控参数,通过设置这两个参数控制时间和距离大小范围。
|
图 2 偏移质量控制因子 |
本文将α的值设为4、β的值设为6,已知反射时间t,利用拾取的炮点射线参数ps和检波点射线参数pr发射射线得到两条射线交点位置附近的炮点射线旅行时ts和检波点射线旅行时tr,以及两条射线末端位置坐标ds和dr,最后判断两条射线的旅行时之和以及末端坐标位置之差是否满足式(2),据此筛选待成像的炮点和检波点射线参数。
1.3 高斯束偏移公式根据Clearbout[39-40]提出的互相关成像原理,反射界面存在于地下这样一些点上,在这些点上,下行波的波前到达或产生与上行波的波前到达或产生在时间上是一致的。互相关成像公式可写为
| $ I(\boldsymbol{x})=\int \mathrm{d} \omega D^{*}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}, \omega\right) U\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}, \omega\right) $ | (3) |
式中:ω为角频率;xs表示炮点坐标;D(x, xs, ω)表示下行波场;U(x, xs, ω)表示上行波场;上标*表示复数共轭。
上行波场可由地表接收的地震波场向下延拓得到,据Hill[10]的研究可知
| $ U\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) = - \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int {\frac{{\partial {G^*}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{r}}}, \omega } \right)}}{{\partial {z_{\rm{r}}}}}} U\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right)d{x_{\rm{r}}} $ | (4) |
式中:xr表示检波点坐标;G(x, xs, ω)表示从xr到x的格林函数;U(xr, xs, ω)表示地表接收到的地震记录。
下行波场可近似表示为格林函数,即D(x, xs, ω)≈G(x, xs, ω),则共炮域的叠前偏移成像公式表示为
| $ \begin{array}{l} \mathit{\boldsymbol{I}}(\mathit{\boldsymbol{x}}) = - \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int {\rm{d}} \omega \int {\rm{d}} {x_{\rm{s}}}{G^*}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) \times \\ \;\;\;\;\;\;\;\;\int {\rm{d}} {x_{\rm{r}}}\frac{{\partial {G^*}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{r}}}, \omega } \right)}}{{\partial {\mathit{z}_{\rm{r}}}}}U\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) \end{array} $ | (5) |
在高斯束偏移中,格林函数由一系列从不同角度出射的高斯束的叠加积分求得
| $ \begin{array}{*{20}{c}} {G\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) = \frac{{\rm{i}}}{{{\rm{2 \mathsf{ π} }}}}\int {\frac{{d{p_{{\rm{s}}x}}}}{{{p_{{\rm{s}}z}}}}} {u_{GB}}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right)}\\ { = \frac{{\rm{i}}}{{{\rm{2 \mathsf{ π} }}}}\int {\frac{{d{p_{{\rm{s}}x}}}}{{{p_{{\rm{s}}z}}}}} A\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\exp \left[ {{\rm{i}}\omega T\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right]} \end{array} $ | (6) |
式中:uGB(x, xs, ω)表示频率域高斯束函数;A(x, xs)和T(x, xs)分别表示高斯束的复值振幅和旅行时间;psx和psz分别表示水平慢度和垂直慢度。
为了使接收到的地震波场与高斯束表示的波场相匹配,需要进行加窗处理,根据Hill[10]给出的高斯窗函数
| $ 1 \approx \frac{{\Delta L}}{{\sqrt {2{\rm{ \mathsf{ π} }}} {w_0}}}{\left| {\frac{\omega }{{{\omega _r}}}} \right|^{1/2}}\sum\limits_L {\exp } \left[ { - \left| {\frac{\omega }{{{\omega _{\rm{r}}}}}} \right|\frac{{{{\left( {{x_{\rm{r}}} - L} \right)}^2}}}{{2w_0^2}}} \right] $ | (7) |
式中:w0为初始束宽;ωr为参考角频率;L为束中心位置;ΔL表示束中心间隔。将式(6)、式(7)代入式(5),并引入相位校正因子,消除检波点和束中心位置不一致的影响,得到
| $ \begin{array}{l} \mathit{\boldsymbol{I}}(\mathit{\boldsymbol{x}}) = - \frac{{{\rm{i}}\Delta L{\omega _{\rm{r}}}}}{{8{{\rm{ \mathsf{ π} }}^3}\sqrt {2{\rm{ \mathsf{ π} }}} {w_0}}}\sum\limits_{{x_{\rm{s}}}} {\sum\limits_L {\int {\frac{{{\rm{d}}{p_{{\rm{s}}\mathit{x}}}}}{{{p_{{\rm{s}}\mathit{z}}}}}} } } \int {\rm{d}} {p_{{\rm{r}}\mathit{x}}}{A^*}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) \times \\ \;\;\;\;\;\;\;\;\int {\rm{d}} \omega \exp \left[ { - {\rm{i}}\omega T\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right]{D_{\rm{s}}}\left( {L, {p_{{\rm{r}}\mathit{x}}}, \omega } \right) \end{array} $ | (8) |
式中:A(xr, xs)=A(x, xr)A(x, xs)、T(xr, xs)=T(x, xr)+T(x, xs),均为复值;Ds(L, prx, ω)表示地震记录的局部倾斜叠加,其表达式为
| $ \begin{array}{l} {D_{\rm{s}}}\left( {L, {p_{{\rm{r}}x}}, \omega } \right) = {\left| {\frac{\omega }{{{\omega _{\rm{r}}}}}} \right|^{3/2}}\int {\rm{d}} {x_{\rm{r}}}U\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) \times \\ \;\;\;\;\;\exp \left[ {{\rm{i}}\omega {p_{{\rm{r}}\mathit{x}}}\left( {{x_{\rm{r}}} - L} \right) - \left| {\frac{\omega }{{{\omega _{\rm{r}}}}}} \right|\frac{{{{\left( {{x_{\rm{r}}} - L} \right)}^2}}}{{2w_0^2}}} \right] \end{array} $ | (9) |
根据Hale的成像方法[41-42],对式(8)进行化简,最终的成像公式为
| $ \begin{array}{l} \mathit{\boldsymbol{I}}(\mathit{\boldsymbol{x}}) = \frac{{{\rm{i}}\Delta L{\omega _{\rm{r}}}}}{{8{{\rm{ \mathsf{ π} }}^3}\sqrt {{\rm{2 \mathsf{ π} }}} {w_0}}}\sum\limits_{{x_{\rm{s}}}} {\sum\limits_L {\int {\frac{{{\rm{d}}{p_{{\rm{s}}x}}}}{{{p_{{\rm{s}}\mathit{z}}}}}} } } \int {\rm{d}} {p_{{\rm{r}}x}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\left[ {{A_{\rm{r}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)D\left( {L, {p_{{\rm{r}}x}}, t} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;{A_{\rm{i}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){D^{\rm{H}}}\left( {L, {p_{{\rm{r}}x}}, t} \right)] \end{array} $ | (10) |
式中:D(L, prx, t)为时间域的局部倾斜叠加道集;DH(L, prx, t)为其对应的希尔伯特变换道集。
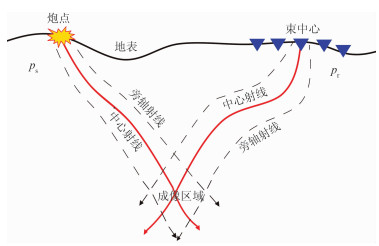
综上所述,本文数据驱动的控制束偏移原理和算法实现流程分别如图 3和图 4所示。
|
图 3 数据驱动的控制束偏移原理 |

|
图 4 数据驱动的控制束偏移实现流程 |
为了说明本文方法的正确性、适用性以及计算效率,分别使用三个理论模型和某工区的实际资料对本文算法效果进行验证,并且对比了本文方法与传统高斯束偏移方法在Marmousi模型上的计算效率。
第一个理论模型是简单的三层层状模型,其单炮记录如图 5a所示。对比使用传统高斯束偏移(图 5b)和使用本文控制束偏移(图 5c)成像结果,在后者中未见画弧(图 5b红色箭头所示)等噪声。

|
图 5 层状模型的偏移成像 (a)单炮记录;(b)传统高斯束偏移;(c)本文控制束偏移 |
第二个理论模型是洼陷模型(图 6a)。模型尺寸为640m×375m,水平网格间距为15m,垂向网格间距为8m。正演记录由二阶有限差分计算得到。观测系统为中间激发、两边接收,共121炮,炮间距为30m,每炮接收道数为121,道间距为30m。每道采样点数为750,采样间隔为4ms,其单炮记录如图 6b所示。图 6c和图 6d是对第61炮记录分别使用传统高斯束偏移和本文控制束偏移的结果。图 6e和图 6f是对所有炮记录分别使用传统高斯束和本文控制束偏移结果。在图 6c和图 6e中可发现主要包括广角反射叠加噪声和画弧噪声等(红色箭头)大量偏移噪声。使用本文控制束偏移方法进行成像,这些噪声可被很好地压制,得到较清晰的偏移剖面(图 6d和图 6f)。

|
图 6 洼陷模型的偏移成像 (a)速度模型;(b)第61炮记录;(c)图b的传统高斯束偏移结果;(d)图b的控制束偏移结果;(e)全部炮的传统高斯束偏移结果;(f)全部炮的控制束偏移结果 |
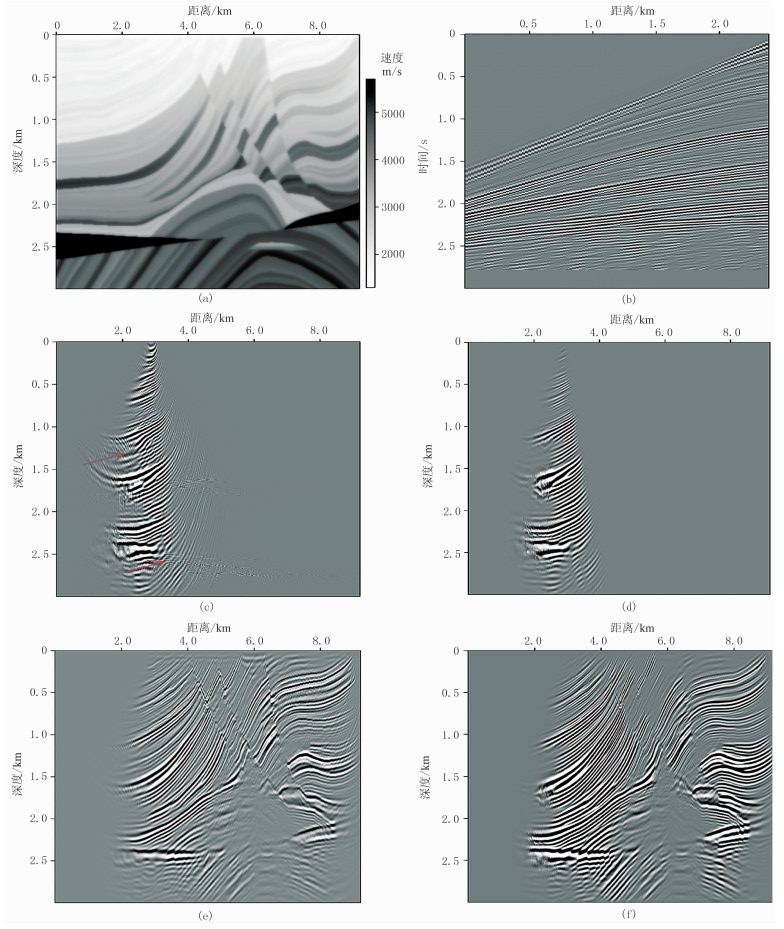
使用Marmousi模型分析本文方法对复杂构造的成像效果。图 7a是Marmousi速度模型,图 7b是该模型的第一炮地震记录。图 7c和图 7d分别是该单炮的传统高斯束偏移结果和本文的控制束偏移结果,从两图对比可以看出在本文方法成像结果中偏移噪声和一些假象得到了很好的压制(红色箭头)。图 7e和图 7f是所有炮偏移的结果,由图可见,本文方法可以有效地压制传统高斯束偏移中所产生的噪声和偏移假象。然而,由于成像中舍弃了一些弱能量信号,在大倾角断面成像方面,控制束成像结果能量较弱,表明控制束偏移方法目前还有一定的局限性。
|
图 7 Marmousi模型的偏移成像 (a)速度模型;(b)第1炮记录;(c)图b的传统高斯束偏移;(d)图b的控制束偏移;(e)全部炮的传统高斯束偏移;(f)全部炮的控制束偏移 |
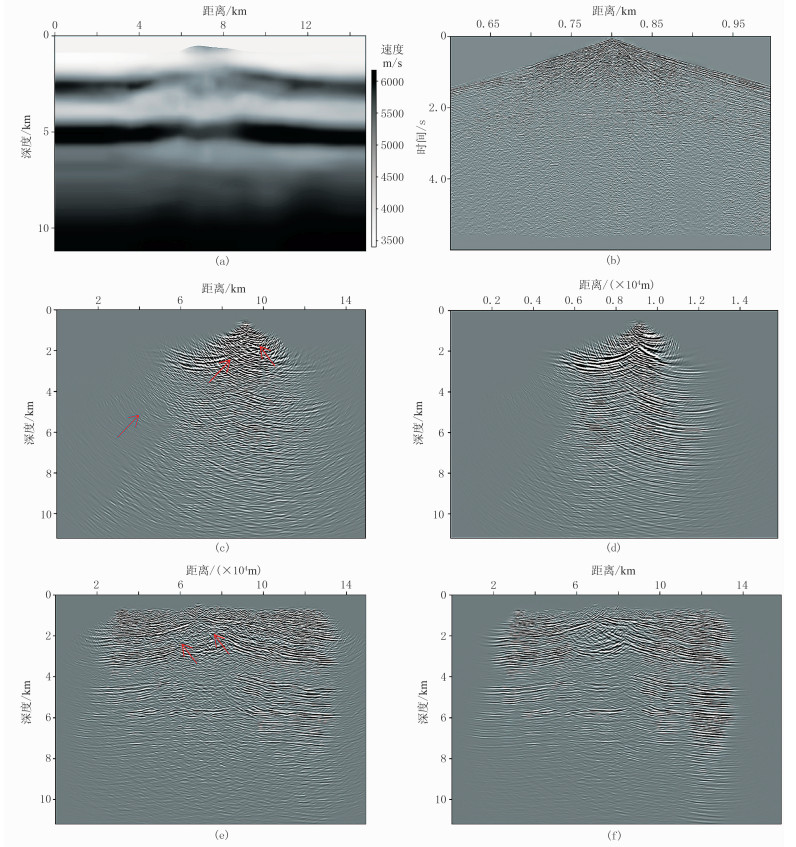
为了检验本文方法对实际资料的适用性及有效性,选用采集于M山地起伏地表的地震数据进行偏移成像。图 8a是通过速度建模得到的该工区的速度模型。图 8b是某一炮的地震记录,可以看出信噪比较低。图 8c和8d分别是该单炮的传统高斯束偏移结果和本文的控制束偏移结果,图 8d中没有图 8c中出现的偏移噪声和假象,并且图 8d中的有效反射能量(红色箭头)更加明显。图 8e和图 8f是所有炮的偏移结果,图 8f相比于图 8e具有更高的信噪比和更强的同相轴连续性。
|
图 8 实际资料的偏移成像 (a)速度模型;(b)单炮记录;(c)图b的传统高斯束偏移;(d)图b的控制束偏移;(e)全部炮的传统高斯束偏移;(f)全部炮的控制束偏移 |
本文充分利用炮点和检波点的水平慢度信息并设计一个偏移质量控制因子,在传统高斯束偏移的基础上,发展了一种数据驱动的控制束偏移算法流程。从共检波点和共炮点的, τ-p域道集拾取水平慢度信息,利用相干分析提高了拾取精度;通过偏移质量控制因子对偏移同相轴进行筛选。这些做法不仅可压制传统高斯束偏移所产生的噪声和偏移假象,且可提高计算效率。
模型试验和实际资料应用结果表明,本文数据驱动的控制束偏移算法能有效压制低信噪比地震数据成像噪声,提高复杂山地低信噪比数据的深度域成像质量,特别是能显著改善干扰严重的浅层的成像效果。
炮点和检波点道集优势同相轴提取是本文算法的关键之一,后续将深入研究基于压缩感知技术的稀疏平面波数据分解方法,以进一步提高数据分解和提取精度。
感谢科罗拉多矿业学院CWP提供的SU软件平台支持。
| [1] |
Cerveny V, Popov M M, Psencik I. Computation of wave fields in inhomogeneous media-Gaussian beam approach[J]. Geophysical Journal International, 1982, 70(1): 109-128. DOI:10.1111/j.1365-246X.1982.tb06394.x |
| [2] |
Popov M M. A new method of computation of wave fields using Gaussian beams[J]. Wave Motion, 1982, 4(1): 85-97. DOI:10.1016/0165-2125(82)90016-6 |
| [3] |
Bleistein N.Mathematics of Modeling, Migration and Inversion with Gaussian Beams[R]. Lecture Notes, 2009.
|
| [4] |
Etgen J, Gray S H, Zhang Y. An overview of depth imaging in exploration geophysics[J]. Geophysics, 2009, 74(6): WCA5-WCA17. DOI:10.1190/1.3223188 |
| [5] |
Liu J, Palacharla G. Multiarrival Kirchhoff beam migration[J]. Geophysics, 2011, 76(5): WB109-WB118. DOI:10.1190/geo2010-0403.1 |
| [6] |
Cerveny V. Synthetic body wave seismograms for la-terally varying layered structures by the Gaussian beam method[J]. Geophysical Journal International, 1983, 73(2): 389-426. DOI:10.1111/j.1365-246X.1983.tb03322.x |
| [7] |
Cerveny V, Psencik I. Gaussian beams and paraxial ray approximation in three-dimensional elastic inhomogeneous media[J]. Journal of Geophysics, 1983, 53: 1-15. |
| [8] |
Katchalov A P, Popov M M. Gaussian beam me-thods and theoretical seismograms[J]. Geophysical Journal International, 1988, 93(3): 465-475. DOI:10.1111/j.1365-246X.1988.tb03874.x |
| [9] |
Hill N R. Gaussian beam migration[J]. Geophysics, 1990, 55(11): 1416-1428. DOI:10.1190/1.1442788 |
| [10] |
Hill N R. Prestack Gaussian beam depth migration[J]. Geophysics, 2001, 66(4): 1240-1250. DOI:10.1190/1.1487071 |
| [11] |
Nowack R L, Sen M K, Stoffa P L.Gaussian beam mi-gration for sparse common-shot and common-receiver data[C]. SEG Technical Program Expanded Abstracts, 2003, 22: 1114-1117. https://www.researchgate.net/publication/255585869_Gaussian_Beam_Migration_for_Sparse_Common-Shot_and_Common-Receiver_Data
|
| [12] |
Gray S H. Gaussian beam migration of common-shot records[J]. Geophysics, 2005, 70(4): S71-S77. DOI:10.1190/1.1988186 |
| [13] |
Zhu T, Gray S H, Wang D. Prestack Gaussian beam depth migration in anisotropic media[J]. Geophysics, 2007, 72(3): S133-S138. DOI:10.1190/1.2711423 |
| [14] |
Protasov M. 2-D Gaussian beam imaging of multicomponent seismic data in anisotropic media[J]. Geophy-sics Journal International, 2015, 203(3): 2021-2031. DOI:10.1093/gji/ggv408 |
| [15] |
Protasov M, Tcheverda V A. True amplitude elastic Gaussian beam imaging of multicomponent walkaway vertical seismic profiling data[J]. Geophysical Prospecting, 2012, 60(6): 1030-1042. DOI:10.1111/j.1365-2478.2012.01068.x |
| [16] |
Huang J P, Duan X Y, Yuan M L, et al.Elastic Gaus-sian beam migration method for rugged tomography[C]. Extended Abstracts of 75th EAGE Conference & Exhibition, 2013, Tu P06.
|
| [17] |
Yang J D, Huang J P, Wang X, et al.Common-shot elastic Gaussian beam depth migration[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 2159-2164.
|
| [18] |
李瑞忠, 杨长春, 陈辉国. 高斯束方法及其应用[J]. 地球物理学进展, 2006, 21(3): 739-745. LI Ruizhong, YANG Changchun, CHEN Huiguo. The Gaussian beam method and its application[J]. Progress in Geophysics, 2006, 21(3): 739-745. DOI:10.3969/j.issn.1004-2903.2006.03.009 |
| [19] |
李振春, 岳玉波, 郭朝斌, 等. 高斯波束共角度保幅深度偏移[J]. 石油地球物理勘探, 2010, 45(3): 360-365. LI Zhenchun, YUE Yubo, GUO Chaobin, et al. Gaus-sian beam common angle preserved-amplitude migration[J]. Oil Geophysical Prospecting, 2010, 45(3): 360-365. |
| [20] |
岳玉波, 李振春, 刘伟, 等. 保幅炮域高斯波束偏移[J]. 中国石油大学学报(自然科学版), 2011, 35(1): 52-55. YUE Yubo, LI Zhenchun, LIU Wei, et al. Preserved amplitude shot domain Gaussian beam migration[J]. Journal of China University of Petroleum (Edition of Natural Science), 2011, 35(1): 52-55. DOI:10.3969/j.issn.1673-5005.2011.01.009 |
| [21] |
岳玉波.复杂介质高斯束偏移成像方法研究[D].山东青岛: 中国石油大学(华东), 2010. http://cdmd.cnki.com.cn/article/cdmd-10425-1011286385.htm
|
| [22] |
黄建平, 张晴, 张凯, 等. 格林函数高斯束逆时偏移[J]. 石油地球物理勘探, 2014, 49(1): 101-106. HUANG Jianping, ZHANG Qing, ZHANG Kai, et al. Reverse time migration with Gaussian beams based on the Green function[J]. Oil Geophysical Prospecting, 2014, 49(1): 101-106. |
| [23] |
黄建平, 袁茂林, 段新意, 等. 一种解耦的起伏地表弹性波高斯束偏移方法[J]. 石油地球物理勘探, 2015, 50(3): 460-468. HUANG Jianping, YUAN Maolin, DUAN Xinyi, et al. Decoupled elastic Gaussian beam migration for rugged topography[J]. Oil Geophysical Prospecting, 2015, 50(3): 460-468. |
| [24] |
黄建平, 袁茂林, 李振春, 等. 双复杂条件下弹性波非倾斜叠加精确束偏移方法研究[J]. 石油物探, 2015, 54(1): 56-63. HUANG Jianping, YUAN Maolin, LI Zhenchun, et al. An accurate elastic beam migration method without slant stack for complex surface and subsurface geological conditions[J]. Geophysical Prospecting for Petroleum, 2015, 54(1): 56-63. DOI:10.3969/j.issn.1000-1441.2015.01.008 |
| [25] |
黄建平, 吴建文, 杨继东, 等. 一种τ-p域二维控制束成像方法[J]. 石油地球物理勘探, 2016, 51(2): 342-349. HUANG Jianping, WU Jianwen, YANG Jidong, et al. A 2D control beam migration in the τ-p domain[J]. Oil Geophysical Prospecting, 2016, 51(2): 342-349. |
| [26] |
韩冰凯, 顾汉明, 刘少勇. TI介质带限射线束传播及偏移方法[J]. 石油地球物理勘探, 2018, 53(2): 297-303, 310. HAN Bingkai, GU Hanming, LIU Shaoyong. Band-limited beam propagation and migration in TI media[J]. Oil Geophysical Prospecting, 2018, 53(2): 297-303, 310. |
| [27] |
吴娟, 白敏, 张华. 基于高斯束偏移的鬼波压制[J]. 石油地球物理勘探, 2018, 53(3): 443-448. WU Juan, BAI Min, ZHANG Hua. Deghosting with Gauss beam migration[J]. Oil Geophysical Prospecting, 2018, 53(3): 443-448. |
| [28] |
代福材, 黄建平, 李振春, 等. 角度域黏声介质高斯束叠前深度偏移方法[J]. 石油地球物理勘探, 2017, 52(2): 283-293. Dai Fucai, Huang Jianping, Li Zhenchun, et al. Angle domain prestack Gaussian beam migration for visco-acoustic media[J]. Oil Geophysical Prospecting, 2017, 52(2): 283-293. |
| [29] |
Gao F, Zhang P, Wang B, et al.Fast-beam migration-A step toward interactive imaging[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 2470-2474.
|
| [30] |
Vetle V, Graham R, Roger T. Controlled beam migration:a versatile structural imaging tool[J]. First Break, 2008, 26(9): 109-113. |
| [31] |
Sherwood J, Sherwood K, Tieman H, et al.3D beam prestack migration with examples from arround theworld[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 438-442.
|
| [32] |
Ting C and Wang D L.Controlled beam migration application in Gulf of Mexico[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 368-372.
|
| [33] |
Hu C, Stoffa P L. Slowness-driven Gaussian beam prestack depth migration for low-fold seismic data[J]. Geophysics, 2009, 74(6): WCA35-WCA45. DOI:10.1190/1.3250268 |
| [34] |
Yang J D, Zhu H J, Huang J P, et al.Study of data-driven optimization strategy for beam migration[C]. SEG Technical Program Expanded Abstracts, 2016, 35: 4316-4320.
|
| [35] |
Yang J D, Zhu H J. A practical data-driven optimization strategy for Gaussian beam migration[J]. Geophysics, 2017, 83(1): S81-S92. |
| [36] |
Fomel S. Applications of plane-wave destruction filters[J]. Geophysics, 2002, 67(6): 1946-1960. DOI:10.1190/1.1527095 |
| [37] |
Stoffa P L, Buhl P, Diebold J B, et al. Direct mapping of seismic data to the domain of intercept time and ray parameter-a plane wave decomposition[J]. Geophy-sics, 1981, 46(3): 255-267. |
| [38] |
Chopra S and Pickford S.Adding the Coherence Di-mension to 3D Seismic data[R]. CSEG Recorder, 2001, 15: 5-8.
|
| [39] |
Claerbout J F. Coarse grid calculations of waves in inhomogeneous media with applications to delineation of complicated seismic structure[J]. Geophysics, 1970, 35(3): 407-418. DOI:10.1190/1.1440103 |
| [40] |
Claerbout J F. Fundamentals of Geophysical Data Processing[M]. McGraw-Hill, 1976.
|
| [41] |
Hale D.Computational Aspects of Gaussian Beam Migration[R]. Colorado School of Mines Center for Wave Phenomena Report, 1992, 139.
|
| [42] |
Hale D.Migration by Kirchhoff, Slant Stack, and Gaussian Beam Methods[R]. Colorado School of Mines Center for Wave Phenomena Report, 1992, 121.
|



 吕考考, 北京市海淀区学院路20号中国石油勘探开发研究院油气地球物理研究所, 100083。Email:
吕考考, 北京市海淀区学院路20号中国石油勘探开发研究院油气地球物理研究所, 100083。Email: