② 东华理工大学地球物理与测控技术学院, 江西南昌 330013
② Department of Geophysics, School of Geophysics and Measurement-control Technology, East China University of Technology, Nanchang, Jiangxi 330013, China
室内实验和野外实践发现自然界的地层和岩石呈现出各向异性性质[1-3]。常规各向异性介质,在增加一定的假设条件后,可以近似成特定的各向异性介质[4-6],如:三斜各向异性介质、单斜各向异性介质、正交各向异性介质、椭圆各向异性介质和横向各向同性介质等[7-9]。
地震波旅行时计算结果在合成地震记录、速度层析成像、震源定位、克希霍夫叠前深度偏移等方面均具有广泛应用价值[10-11]。当介质存在各向异性时,地震速度层析成像不仅可以运用于近地表速度建模,还可以用于裂缝探测、储层预测等[12]。计算地震旅行时的主要方法可分为有限差分法、有限单元法和射线追踪法,其中求解程函方程(Eikonal equation)有限差分法计算效率高、更易于编程实现。Vidale[13]和Van Trier等[14]提出了几种有限差分旅行时计算方法,但目前较为流行的是快速推进法[15-19]和快速扫描法,这两种流行算法排序理念不同:快速推进法使用堆排序算法,在运算中对旅行时进行排序,利用严格的因果关系强制执行对旅行时做合理排序,这样后求解的旅行时对先前的结果没有影响;快速扫描法[20-27]使用Gauss-Seidel迭代,将计算后得到的值马上代入迭代循环中,如果方程存在严格的因果关系,则可以保证在有限次迭代后达到收敛。这两种方法可以得到相同精度的旅行时,后者具有较高的计算效率,但是选择哪一种方法更优,则需要根据求解的方程确定。另外还有一些其他形式的程函方程求解方法[28-32]。
Zhao[20]将快速扫描算法运用于各向同性介质旅行时计算,Zhang等[21]和Qian等[22]对算法进行了一系列的改进,包括适应各向异性介质的快速扫描算法和高阶快速扫描算法;Fomel等[23]提出了一种基于因式分解程函方程的快速扫描算法,对各向同性的程函方程进行乘法因式分解,提高了旅行时的计算精度;Qian等[24]提出了基于静态凸Hamilton-Jacobi方程的快速扫描算法,并推导了椭圆各向异性介质程函方程。Luo等[25]针对椭圆各向异性介质提出了加法和乘法因式分解形式的快速扫描算法,并对比了两种分解形式的计算精度;Waheed等[26-27]推导了各向异性声波近似方程的因式分解形式,并利用快速扫描算法求解。
相比各向同性介质,各向异性介质程函方程较为复杂,快速扫描法的效率相对较低。特别是当模型较大时,提高算法的效率更具有实用价值。本文对椭圆各向异性程函方程进行因式分解,以压制震源奇异性产生的旅行时误差,提高旅行时计算的精度;根据地震波旅行时计算的因果关系,提出源点快速扫描方式,以去除不必要的计算过程,提高旅行时计算的效率;同时,结合迎风差分格式,通过添加差分方向判定因子,使算法的计算更加合理和有效;最后,应用数值模型验证了算法可靠性和高效性。
1 方法原理 1.1 椭圆各向异性介质程函方程各向同性介质的程函方程为
| $ \left\{ \begin{array}{l} \left| {\nabla T\left( \mathit{\boldsymbol{x}} \right)} \right| = s\left( \mathit{\boldsymbol{x}} \right)\;\;\;\;\;x \in \mathit{\boldsymbol{ \boldsymbol{\varOmega} \backslash }}\left\{ {{\mathit{\boldsymbol{x}}_0}} \right\}\\ T\left( {{\mathit{\boldsymbol{x}}_0}} \right) = 0 \end{array} \right. $ | (1) |
式中:s(x)=1/v(x),为速度的倒数,即慢度;T为旅行时;Ω∈RN为N维的有界开集,二维情况下N=2;x=(x, y)为计算点坐标,x0=(x0, y0)为源点坐标。在点震源情况下,椭圆各向异性介质的程函方程为
| $ \left\{ \begin{array}{l} H\left[ {\mathit{\boldsymbol{x}},\nabla T\left( \mathit{\boldsymbol{x}} \right)} \right] = \sqrt {\nabla T\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{x}} \right)\nabla {T^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = 1\;\;\;\;\;\;\;\;\;\;\;\;\;x \in \mathit{\boldsymbol{ \boldsymbol{\varOmega} \backslash }}\left\{ {{\mathit{\boldsymbol{x}}_0}} \right\}\\ T\left( {{\mathit{\boldsymbol{x}}_0}} \right) = 0 \end{array} \right. $ | (2) |
式中:
| $ \left\{\begin{array}{l}{\sqrt{a(\boldsymbol{x}) T_{x}^{2}-2 c(\boldsymbol{x}) T_{x} T_{y}+b(\boldsymbol{x}) T_{y}^{2}}=1} \\ {T\left(\boldsymbol{x}_{0}\right)=0}\end{array}\right. $ | (3) |
式中:Tx和Ty分别为旅行时在x、y方向的导数;系数a(x)、b(x)、c(x)分别代表横向、纵向和倾斜方向的各向异性强度,且满足a(x)>0,b(x)>0,c2(x)-a(x)b(x)<0。各向异性对称正定矩阵为
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {a\left( \mathit{\boldsymbol{x}} \right)}&{ - c\left( \mathit{\boldsymbol{x}} \right)}\\ { - c\left( \mathit{\boldsymbol{x}} \right)}&{b\left( \mathit{\boldsymbol{x}} \right)} \end{array}} \right] $ | (4) |
指示各向异性程度的系数为
| $ \eta = \sqrt {\frac{{{\lambda _{\max }}\left( \mathit{\boldsymbol{M}} \right)}}{{{\lambda _{\min }}\left( \mathit{\boldsymbol{M}} \right)}}} $ | (5) |
式中λmax和λmin分别表示矩阵M最大、最小特征值。
1.2 乘法因式分解常规求解程函方程计算旅行时的有限差分方法存在源奇异性问题[24],求解因式分解形式的程函方程能得到更高精度的旅行时结果。
对式(3)中的旅行时T进行乘法分解,即
| $ T=T_{0} \tau $ | (6) |
式中:T0为假设模型为均匀介质时的旅行时值;τ为扰动值,代表波场传播过程中波前曲率的变化,是需要求取的参数。T的导数可表示为
| $ \nabla T=\nabla T_{0} \tau+T_{0} \nabla \tau $ | (7) |
式(3)的乘法因式分解形式为
| $ \begin{array}{l} \left\{ {{\tau ^2}\left( {aT_{0x}^2 - 2c{T_{0x}}{T_{0y}} + bT_{0y}^2} \right) + } \right.\\ \;\;\;\;2{T_0}\tau \left[ {a{T_{0x}}{\tau _x} - c\left( {{T_{0x}}{\tau _y} + {T_{0y}}{\tau _x}} \right) + b{T_{0y}}{\tau _y}} \right] + \\ \;\;\;\;{\left. {T_0^2\left( {a\tau _x^2 - 2c{\tau _x}{\tau _y} + b\tau _y^2} \right)} \right\}^{\frac{1}{2}}} = 1 \end{array} $ | (8) |
式中:T0x、T0y分别为T0在x和y方向上的偏导数;τx和τy同理。其中T0的定义为
| $ \begin{array}{*{20}{l}} {{T_0}(x,y) = }\\ {\sqrt {\frac{{{b_0}{{\left( {x - {x_0}} \right)}^2} + 2{c_0}\left( {x - {x_0}} \right)\left( {y - {y_0}} \right) + {a_0}{{\left( {y - {y_0}} \right)}^2}}}{{{a_0}{b_0} - c_0^2}}} } \end{array} $ | (9) |
式中a0、b0、c0为源点的系数。
1.3 加法因式分解加法因式分解比乘法因式分解更为简单。将T进行加法分解,有
| $ T=T_{0}+\tau $ | (10) |
则
| $ \nabla T = \nabla {T_0} + {\nabla _\tau } $ | (11) |
式(3)的加法分解形式为
| $ \begin{array}{l} \left[ {aT_{0x}^2 - 2c{T_{0x}}{T_{0y}} + bT_{0y}^2 + } \right.\\ \;\;\;\;\;\;\;2{\tau _x}\left( {a{T_{0x}} - c{T_{0y}}} \right) + 2{\tau _y}\left( {b{T_{0y}} - c{T_{0x}}} \right) + \\ \;\;\;\;\;\;\;{\left. {a\tau _x^2 - 2c{\tau _x}{\tau _y} + b\tau _y^2} \right]^{\frac{1}{2}}} = 1 \end{array} $ | (12) |
加法因式分解的T0(x,y)与乘法形式的一致,都由式(9)计算得到。
由于加法因式分解计算效果不如乘法分解,故本文应用乘法因式分解方法。
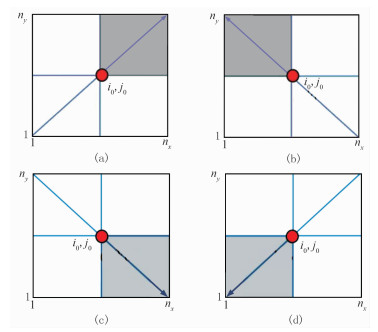
2 源点快速扫描算法 2.1 常规快速扫描算法的扫描方式常规快速扫描算法直接对计算域进行全局扫描。假设震源点位于计算区域中心(i0,j0)(红点处),若x方向共有nx个点、y方向共有ny个点,以T(i,j)表示计算点(i,j)的旅行时,则常规快速扫描算法的扫描方式如图 1所示。
|
图 1 常规快速扫描法的四种扫描方式 (a)i=(1,2,…,nx),j=(1,2,…,ny);(b)i=(nx,nx-1,…, 1),j=(1,2,…,ny);(c)i=(1,2,…,nx),j=(ny,ny-1,…, 1);(d)i=(nx,nx-1,…, 1),j=(ny,ny-1,…,1)。nx、ny分别为x、y方向网格点总数 |
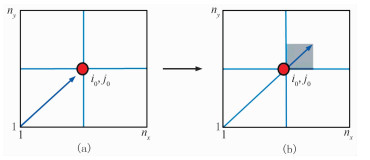
以图 1a为例,扫描未抵达源点前,由于方程没有源点信息作为初始条件,无法计算得到有效旅行时。当扫描经过源点后,才能得到有效的旅行时信息(图 2)。因此,图中只有对灰色区域(i=(i0,i0+1,…,nx),j=(j0,j0+1,…,ny))的扫描有效,对其余白色区域的扫描是无效的。
|
图 2 扫描方式分析 (a)扫描未抵达源点前;(b)扫描经过源点后 |
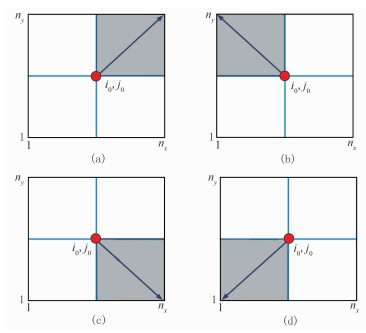
常规快速扫描算法的扫描方式存在大量无效扫描,为解决该问题,提出了一种源点快速扫描方法。将扫描的起始点移至震源点处,可以减少大量的无效扫描过程。源点快速扫描算法的扫描方式如图 3所示。
|
图 3 源点扫描法的四种扫描方式 (a)i=(i0,i0+1,…,nx),j=(j0,j0+1,…,ny);(b)i=(i0,i0-1,…,1),j=(j0,j0+1,…,ny);(c)i=(i0,i0+1,…,nx),j=(j0,j0-1,…,1);(d)i=(i0,i0-1,…,1),j=(j0,j0-1,…,1)。i0和j0分别为源点的x、y方向网格序号 |
源点快速扫描算法相对于常规快速扫描算法省去了从端点处开始至源点的扫描部分,直接将源点作为起始点开始扫描,扫描过程更简洁有效。
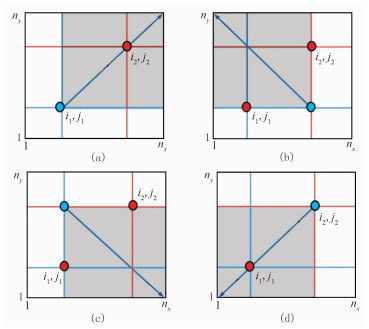
2.3 多个震源的源点快速扫描算法当存在多个震源时,选取所有震源中x和y方向上的坐标序号最大值和最小值组成新的起始扫描点。设有O1(i1,j1)、O2(i2,j2)、…、On(in,jn)共n个源点,则x和y方向上的坐标序号最大和最小值为imin=min(i1,i2,…,in);imax=max(i1,i2,…,in);jmin=min(j1,j2,…,jn);jmax=max(j1,j2,…,jn)。当存在多个震源点时,为覆盖所有震源点,扫描的起始位置不再固定为某个点。图 4以两个震源点O1(i1,j1)、O2(i2,j2)为例。
|
图 4 多震源源点扫描法的四种扫描方式 (a)i=(imin,imin+1,…,nx),j=(jmin,jmin+1,…,ny);(b)i=(imax,imax-1,…,1),j=(jmin,jmin+1,…,ny);(c)i=(imin,imin+1,…,nx),j=(jmax,jmax-1,…,1);(d)i=(imax,imax-1,…,1),j=(jmax,jmax-1,…,1) |
多个震源情况下的快速扫描算法对扫描速率的提升依赖于震源的分布情况。当多个震源集中分布时,源点快速扫描算法可以节省更多的计算时间。
3 数值算法实现过程 3.1 差分方向判定因子本文主要讨论二维情况下的源点快速扫描法,离散化网格如图 5所示。
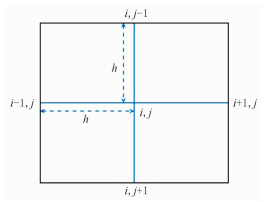
|
图 5 离散化网格 h表示网格步长 |
差分方向判定因子Sx和Sy的定义为
| $ {S_x} = \left\{ {\begin{array}{*{20}{c}} 1&{{T_{i + 1}} \le {T_{i - 1}}}\\ { - 1}&{{T_{i + 1}} > {T_{i - 1}}} \end{array}} \right. $ | (13) |
| $ {S_y} = \left\{ {\begin{array}{*{20}{c}} 1&{{T_{j + 1}} \le {T_{j - 1}}}\\ { - 1}&{{T_{j + 1}} > {T_{j - 1}}} \end{array}} \right. $ | (14) |
式(8)中的T0x、T0y和τx、τy离散化形式为
| $ \left\{ {\begin{array}{*{20}{l}} {{T_{0x}} = \frac{{{S_x}\left( {{T_{0i,j}} - {T_{0i + {S_x},j}}} \right)}}{h}}\\ {{T_{0y}} = \frac{{{S_y}\left( {{T_{0i,j}} - {T_{0i,j + {S_y}}}} \right)}}{h}} \end{array}} \right. $ | (15) |
| $ \left\{ \begin{array}{l} {\tau _x} = \frac{{{S_x}\left( {{\tau _{i,j}} - {\tau _{i + {S_x},j}}} \right)}}{h}\\ {\tau _y} = \frac{{{S_y}\left( {{\tau _{i,j}} - {\tau _{i,j + {S_y}}}} \right)}}{h} \end{array} \right. $ | (16) |
将T0x、T0y和τx、τy离散化形式代入式(8),得到乘法因式分解形式程函方程的离散形式为
| $ \begin{array}{l} 1 = \left\{ {\tau _{i,j}^2\left( {aT_{0x}^2 - 2c{T_{0x}}{T_{0y}} + bT_{0y}^2} \right) + } \right.\\ \;\;\;\;\;\frac{{2{T_0}}}{h}{\tau _{i,j}}\left[ {a{T_{0x}}{S_x}\left( {{\tau _{i,j}} - {\tau _{i + {S_x},j}}} \right) - } \right.\\ \;\;\;\;\;c\left( {{T_{0x}}{S_y}\left( {{\tau _{i,j}} - {\tau _{i,j + {S_y}}}} \right) + {T_{0y}}{S_x}\left( {{\tau _{i,j}} - {\tau _{i + {S_x},j}}} \right)} \right) + \\ \;\;\;\;\;\left. {b{T_{0y}}{S_y}\left( {{\tau _{i,j}} - {\tau _{i,j + {S_y}}}} \right)} \right] + \frac{{T_0^2}}{{{h^2}}}\left[ {a{{\left( {{\tau _{i,j}} - {\tau _{i + {S_x},j}}} \right)}^2} - } \right.\\ \;\;\;\;\;2c{S_x}{S_y}\left( {{\tau _{i,j}} - {\tau _{i + {S_x},j}}} \right)\left( {{\tau _{i,j}} - {\tau _{i,j + {S_y}}}} \right) + \\ \;\;\;\;\;{\left. {\left. {b{{\left( {{\tau _{i,j}} - {\tau _{i,j + {S_y}}}} \right)}^2}} \right]} \right\}^{\frac{1}{2}}} \end{array} $ | (17) |
上式去根号后,可以简化为一元二次方程形式
| $ a^{*} \tau_{i, j}^{2}+b^{*} \tau_{i, j}+c^{*}=0 $ | (18) |
式中
| $ \begin{array}{l} {a^*} = \left( {aT_{0x}^2 - 2c{T_{0x}}{T_{0y}} + bT_{0y}^2} \right) + \\ \;\;\;\;\;\;\;\frac{{2{T_0}}}{h}\left[ {{S_x}\left( {a{T_{0x}} - c{T_{0y}}} \right) + {S_y}\left( {b{T_{0y}} - c{T_{0x}}} \right)} \right] + \\ \;\;\;\;\;\;\;\frac{{T_0^2}}{{{h^2}}}\left( {a - 2c{S_x}{S_y} + b} \right) \end{array} $ | (19) |
| $ \begin{array}{l} {b^*} = \frac{{2{T_0}}}{h}\left[ {{S_x}{\tau _{i + {S_x},j}}\left( {c{T_{0y}} - a{T_{0x}}} \right) + } \right.\\ \;\;\;\left. {{S_y}{\tau _{i,j + {S_y}}}\left( {c{T_{0x}} - b{T_{0y}}} \right)} \right] - \\ \;\;\;\frac{{2T_0^2}}{{{h^2}}}\left[ {a{\tau _{i + {S_x},j}} - c{S_x}{S_y}\left( {{\tau _{i + {S_x},j}} + {\tau _{i,j + {S_y}}}} \right) + b{\tau _{i,j + {S_y}}}} \right] \end{array} $ | (20) |
| $ {c^ * } = \frac{{T_0^2}}{{{h^2}}}\left( {a\tau _{i + {S_x},j}^2 - 2c{S_x}{S_y}{\tau _{i + {S_x},j}}{\tau _{i,j + {S_y}}} + b\tau _{i,j + {S_y}}^2} \right) - 1 $ | (21) |
求解式(18)可得到扰动量τi,j,再进一步利用式(6)可得到旅行时Ti,j。加法因式分解形式程函方程的离散化与乘法形式相似,在此不再赘述。
3.3 因果性判定条件式(18)的解可能存在三种情况,分别为:无根、有两个相同根和有两个不同根。利用因果条件,可对解的正确性进行判断。
若式(18)有根(不管两个根相同与否),由于程函方程属于Hamilton-Jacobi方程,而在Hamilton-Jacobi系统下,方程的解应同时满足
| $ \left\{ \begin{array}{l} \frac{{\partial \tau }}{{\partial x}}\frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial {p_x}}} \ge 0\\ \frac{{\partial \tau }}{{\partial y}}\frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial {p_y}}} \ge 0 \end{array} \right. $ | (22) |
式中:H表示Hamilton量;px和py为对应x和y方向上慢度导数。椭圆各向异性介质程函方程式(3)的因果条件为
| $ \left\{ {\begin{array}{*{20}{l}} {a\frac{{\partial T}}{{\partial x}} - c\frac{{\partial T}}{{\partial y}} \ge 0}\\ {b\frac{{\partial T}}{{\partial y}} - c\frac{{\partial T}}{{\partial x}} \ge 0} \end{array}} \right. $ | (23) |
离散化因果判定条件为
| $ \left\{ \begin{array}{l} \frac{{{S_x}}}{h}\left[ {{S_x}a\left( {{T_{i,j}} - {T_{i + {S_x},j}}} \right) - {S_y}c\left( {{T_{i,j}} - {T_{i,j + {S_y}}}} \right)} \right] \ge 0\\ \frac{{{S_y}}}{h}\left[ {{S_y}b\left( {{T_{i,j}} - {T_{i,j + {S_y}}}} \right) - {S_x}c\left( {{T_{i,j}} - {T_{i + {S_x},j}}} \right)} \right] \ge 0 \end{array} \right. $ | (24) |
当方程无根时,需要考虑波单独沿x轴和y轴传播的情况。
对于乘法因式分解方法,当
| $ {\tau ^{x * }} = \frac{{{T_0}{\tau _{i + {S_x},j}} + {h_x}\sqrt {\frac{b}{{ab - {c^2}}}} }}{{{T_0} + {h_x}\left| {{T_{0x}}} \right|}} $ | (25) |
当
| $ {\tau ^{y*}} = \frac{{{T_0}{\tau _{i,j + {S_y}}} + {h_y}\sqrt {\frac{a}{{ab - {c^2}}}} }}{{{T_0} + {h_y}\left| {{T_{0y}}} \right|}} $ | (26) |
加法因式分解方法的计算公式分别为
| $ {\tau ^{x*}} = {\tau _{i + {S_x},j}} + {h_x}\sqrt {\frac{b}{{ab - {c^2}}}} - {h_x}\left| {{T_{0y}}} \right| $ | (27) |
| $ \tau^{y *}=\tau_{i, j+S_{y}}+h_{y} \sqrt{\frac{a}{a b-c^{2}}}-h_{y}\left|T_{0 y}\right| $ | (28) |
(1) 将计算区域的所有τ值都设定为一个较大值τmax(τmax大于计算区域最终计算出的最大τ值)。
(2) 设定震源点处τ0值,乘法分解形式设定为τ0=1,加法分解形式设定为τ0=0。
(3) 利用式(9)计算T0,迭代过程中T0保持不变。
(4) 通过式(6)或式(10)计算旅行时T的初始值。
3.4.2 旅行时计算(1) 定义τ*为中间变量,求解式(18),当方程存在两个解,分别为τ1*和τ2*。若τ1*和τ2*都符合因果条件式(24),则τ*=min(τ1*, τ2*);若仅τ1*符合因果条件,则τ*=τ1*;若仅τ2*符合因果条件,则τ*=τ2*。
(2) 若τ1*和τ2*都不符合因果条件,则利用式(25)和式(26)计算τx*和τy*的值。若τx*和τy*满足Ti, j=T0i, jτx*≥Ti+Sx, j, Ti, j=T0i, jτy*≥Ti, j+Sy则τ*=min(τx*, τy*);若仅Ti, j=T0i, jτx*≥Ti+Sx, j,则τ*=τx*;若仅Ti, j=T0i, jτy*≥Ti, j+Sy,则τ*=τy*。
(3) 最终,τnew=min(τ*,τmax), Ti, jnew=T0i, jτnew迭代计算的扫描方式应用源点快速扫描算法的扫描方式。
3.4.3 终止条件设定趋近于0的阈值δ,当迭代循环满足|Tnew-Told|≤δ时,终止迭代。
4 数值模拟 4.1 旅行时计算过程分析将旅行时扫描过程分解,对比常规快速扫描算法和源点快速扫描算法在不同扫描阶段的区别。测试模型选择具有解析解的各向异性介质模型[25]。
各向异性模型的参数设置为:网格数为500×500,网格间距为2m,源点位置为(500m,500m),阈值δ=1×10-9,设置较大值τmax=10000s,各向异性参数为:a=b=c=exp(2m)。旅行时解析解为:Tana=1-exp(-m)。其中
图 6中,利用常规快速扫描算法进行了全局扫描,每次扫描后,全局的旅行时都会向最终结果靠近一些,扫描完成后得到稳定的旅行时结果。图 7中,源点快速扫描算法以源点作为起始点开始扫描,每次只扫描计算区域中有效的一部分,完成扫描过程后,同样能得到稳定的旅行时场结果。

|
图 6 常规快速扫描算法的扫描过程分解 (a)i=(1,2,…,nx),j=(1,2,…,ny);(b)i=(nx,nx-1,…,1),j=(1,2,…,ny);(c)i=(1,2,…,nx),j=(ny,ny-1,…,1);(d)i=(nx,nx-1,…,1),j=(ny,ny-1,…,1) |
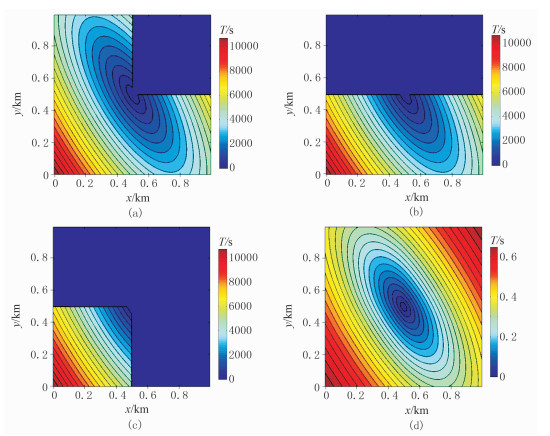
|
图 7 源点快速扫描算法的扫描过程分解 (a)i=(i0,i0+1,…,nx),j=(j0,j0+1,…,ny);(b)i=(i0,i0-1,…,1),j=(j0,j0+1,…,ny);(c)i=(i0,i0+1,…,nx),j=(j0,j0-1,…,1);(d)i=(i0,i0-1,…,1),j=(j0,j0-1,…,1) |
令T1为解析解旅行时,T2为常规快速扫描算法旅行时,T3为源点快速扫描算法旅行时,T2、T3与T1的对比如图 8所示。由图可知,两种方法数值解接近一致(红色与蓝色等值线几乎重合),且在在旅行时变化平缓区域的精度较高,在旅行时变化剧烈的区域则存在一定误差。
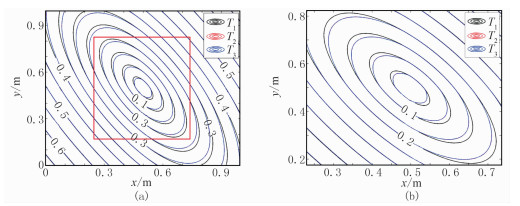
|
图 8 均匀各向异性模型两种方法计算的旅行时与理论旅行时等值线(单位:s)对比(a)及其局部放大显示(b) |
计算T3与T2的平均绝对误差
| $ {T_{{\rm{error}}}} = \frac{1}{{{n_x} \times {n_y}}}\sum\limits_{i = 1}^{{n_x}} {\sum\limits_{j = 1}^{{n_y}} {\left| {{T_{3i,j}} - {T_{2i,j}}} \right|} } $ | (29) |
由上式得到Terror=3.2458×10-5s,说明源点快速扫描算法与常规快速扫描算法的计算结果基本一致。
4.3 计算效率分析 4.3.1 单震源计算效率对比应用不同网格数各向异性模型比较常规快速扫描算法和源点快速扫描算法的计算效率。模型网格数分别设置为200×200、400×400、800×800、1600×1600、3200×3200。网格间距固定为1m,阈值δ=1×10-9,源点位置固定为(nx/2,ny/2)。两种算法各测试5次,取均值后,记录CPU平均计算时间如图 9所示。图中源点快速扫描算法运行时间(蓝色实线)整体上要小于常规快速扫描算法运行时间(红色实线),显然源点快速扫描算法的计算效率要高于常规快速扫描算法。
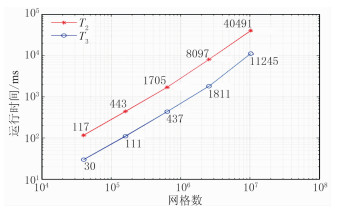
|
图 9 两种算法的运行时间比较 |
若固定模型网格数为1000×1000,其他参数设定不变,仅改变震源位置,测试震源位置分布对源点快速扫描算法计算效率的影响。源点位置设定为:O1(10,10);O2(100,100);O3(300,300);O4(500,500);O5(300,800);O6(100,900);O7(10,990)。不同震源位置两种旅行时计算方法运行耗时如图 10所示。可以看出,源点位置的改变对源点快速扫描算法的计算效率没有影响,证明单个点源情况下,无论点源位置如何分布,源点快速扫描算法对计算效率的提升都是等效的。
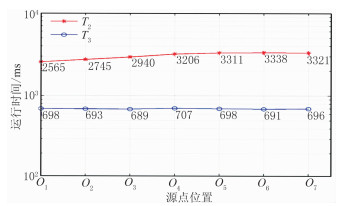
|
图 10 不同源点位置对算法计算速度的影响分析 |
应用各向同性介质模型中,测试多个震源时,源点快速扫描算法的计算效率。
设均匀各向同性介质模型速度为1km/s,网格数为1000×1000,网格间距为1m,阈值δ=1×10-9。设置四种不同的震源分布:分布Ⅰ,四个震源分别位于(600,600)、(400,600)、(600,400)、(400,400),代表震源分布集中;分布Ⅱ,四个震源分别位于(700,700)、(300,700)、(700,300)、(300,300),代表震源分布较集中;分布Ⅲ,四个震源分别位于(800,800)、(200,800)、(800,200)、(200,200),代表震源分布较分散;分布Ⅳ,四个震源分别位于(900,900)、(100,900)、(900,100)、(100,100),代表震源分布分散。
图 11为四个震源不同分布时源点快速扫描算法的旅行时计算结果,图 12为四种震源不同分布时源点快速扫描算法运行时间对比。随着震源点的分布越来越分散,源点快速扫描算法的运行时间逐渐向常规快速扫描算法的运行时间靠近。震源分布越集中,源点快速扫描算法的计算效率提高越明显。
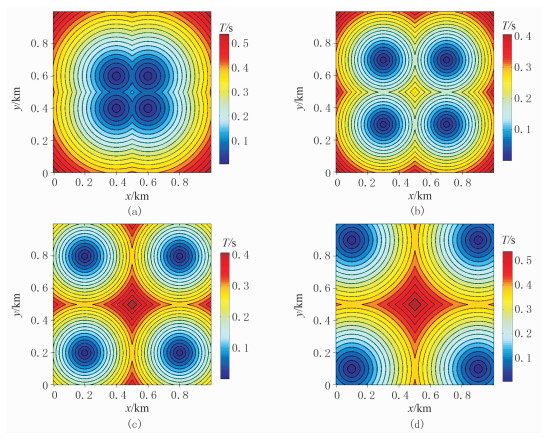
|
图 11 均匀各向同性介质四种震源不同分布时源点快速扫描算法的旅行时计算结果 (a)分布Ⅰ;(b)分布Ⅱ;(c)分布Ⅲ;(d)分布Ⅳ |
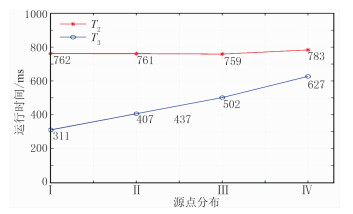
|
图 12 均匀各向同性介质四种震源不同分布时源点快速扫描算法与常规快速扫描算法的运行时间对比 |
常规的快速扫描算法直接对计算区域进行全局扫描,运算过程中存在大量无效扫描。本文提出的源点快速扫描算法将扫描的起始点移至源点处,使算法的扫描过程更高效。通过求解因式分解形式的椭圆各向异性程函方程,利用源点快速扫描算法实现了各向异性介质中的旅行时计算。数值模拟结果表明:
(1) 计算参数相同的前提条件下,源点快速扫描算法和常规快速扫描算法的计算精度一致;
(2) 单震源情况下,源点快速扫描算法的计算效率明显高于常规快速扫描算法,且源点的位置不影响算法的计算效率;
(3) 多震源情况下,震源分布越集中,源点快速扫描算法计算效率提升越大。
(4) 源点快速扫描算法适用于各向同性和各向异性介质的旅行时计算。
| [1] |
Stoep D M. Velocity anisotropy measurements in wells[J]. Geophysics, 1966, 31(5): 900-916. DOI:10.1190/1.1439822 |
| [2] |
Crampin S. Suggestions for a consistent terminology for seismic anisotropy[J]. Geophysical Prospecting, 1989, 37(7): 753-770. DOI:10.1111/j.1365-2478.1989.tb02232.x |
| [3] |
Fomel S. On anelliptic approximations for qP velocities in VTI media[J]. Geophysical Prospecting, 2004, 52(3): 247-259. DOI:10.1111/j.1365-2478.2004.00413.x |
| [4] |
Alkhalifah T, Fomel S. The basic components of residual migration in VTI media using anisotropy continuation[J]. Journal of Petroleum Exploration and Production Technology, 2011, 1(1): 17-22. DOI:10.1007/s13202-011-0006-6 |
| [5] |
黄国娇, 孙江兵, 白超英, 等. 三维TI介质中多波旅行时层析成像[J]. 石油地球物理勘探, 2018, 53(1): 63-72. HUANG Guojiao, SUN Jiangbing, BAI Chaoying, et al. Seismic multi-wave traveltime tomography in 3D TI media[J]. Oil Geophysical Prospecting, 2018, 53(1): 63-72. |
| [6] |
刘财, 邓馨卉, 郭智奇, 等. 基于岩石物理的页岩储层各向异性表征[J]. 石油地球物理勘探, 2018, 53(2): 339-346. LIU Cai, DENG Xinhui, GUO Zhiqi, et al. Shale reservoir anisotropic characterization based on rock physics[J]. Oil Geophysical Prospecting, 2018, 53(2): 339-346. |
| [7] |
胡书华, 王宇超, 刘文卿, 等. 复杂TTI介质稳定的纯qP波波场模拟方法[J]. 石油地球物理勘探, 2018, 53(2): 280-287. HU Shuhua, WANG Yuchao, LIU Wenqing, et al. Pure quasi-P wave stable simulation in complex TTI media[J]. Oil Geophysical Prospecting, 2018, 53(2): 280-287. |
| [8] |
程玖兵, 康玮, 王腾飞. 各向异性介质qP波传播描述Ⅰ:伪纯模式波动方程[J]. 地球物理学报, 2013, 56(10): 3474-3486. CHENG Jiubing, KANG Wei, WANG Tengfei. Description of qP-wave propagation in anisotropic media, Part Ⅰ:Pseudo-pure-mode wave equations[J]. Chinese Journal of Geophysics, 2013, 56(10): 3474-3486. DOI:10.6038/cjg20131022 |
| [9] |
程玖兵, 陈茂根, 王腾飞, 等. 各向异性介质qP波传播描述Ⅱ:分离纯模式标量波[J]. 地球物理学报, 2014, 57(10): 3389-3401. CHENG Jiubing, CHEN Maogen, WANG Tengfei, et al. Description of qP-wave propagation in anisotropic media, Part Ⅱ:Separation of pure-mode scalar waves[J]. Chinese Journal of Geophysics, 2014, 57(10): 3389-3401. DOI:10.6038/cjg20141025 |
| [10] |
Huang G, Zhou B, Li H, et al. 2D seismic reflection tomography in strongly anisotropic media[J]. Journal of Geophysics and Engineering, 2014, 11(6): 1-8. |
| [11] |
Huang G, Zhou B, Li H, et al. Seismic traveltime inversion based on tomographic equation without integral terms[J]. Computers & Geosciences, 2017, 104: 29-34. |
| [12] |
Taillandier C, Noble M, Chauris H, et al. First-arrival traveltime tomography based on the adjoint-state method[J]. Geophysics, 2009, 74(6): WCB1-WCB10. DOI:10.1190/1.3250266 |
| [13] |
Vidale J E. Finite-difference calculation of travel times[J]. Bulletin of the Seismological Society of America, 1988, 78(6): 2062-2076. |
| [14] |
Van Trier J, Symes W W. Upwind finite-difference calculation of traveltimes[J]. Geophysics, 1991, 56(6): 812-821. DOI:10.1190/1.1443099 |
| [15] |
Qin F, Luo Y, Olsen K B, et al. Finite-difference solution of the eikonal equation along expanding wave-fronts[J]. Geophysics, 1992, 57(3): 478-487. DOI:10.1190/1.1443263 |
| [16] |
Sethian J A, Popovici A M. 3-D traveltime computation using the fast marching method[J]. Geophysics, 1999, 64(2): 516-523. DOI:10.1190/1.1444558 |
| [17] |
谢春, 刘玉柱, 董良国, 等. 伴随状态法初至波旅行时层析[J]. 石油地球物理勘探, 2014, 49(5): 877-883. XIE Chun, LIU Yuzhu, DONG Liangguo, et al. First arrival traveltime tomography based on the adjoint state method[J]. Oil Geophysical Prospecting, 2014, 49(5): 877-883. |
| [18] |
黄兴国, 孙建国, 孙章庆, 等. 基于复程函方程和改进的快速推进法的复旅行时计算方法[J]. 石油地球物理勘探, 2016, 51(6): 1109-1118. HUANG Xingguo, SUN Jianguo, SUN Zhangqing, et al. Complex traveltime calculation method based on complex function equation and improved fast mar-ching method[J]. Oil Geophysical Prospecting, 2016, 51(6): 1109-1118. |
| [19] |
孙章庆, 孙建国, 韩复兴. 三维起伏地表条件下地震波旅行时计算的不等距迎风差分法[J]. 地球物理学报, 2012, 55(7): 2441-2449. SUN Zhangqing, SUN Jianguo, HAN Fuxing. Traveltime computation using the upwind finite difference method with nonuniform grid spacing in a 3D undulating surface condition[J]. Chinese Journal of Geophysics, 2012, 55(7): 2441-2449. |
| [20] |
Zhao H. A fast sweeping method for Eikonal equations[J]. Mathematics of Computation, 2004, 74(250): 603-627. DOI:10.1090/S0025-5718-04-01678-3 |
| [21] |
Zhang Y, Zhao H, Qian J, et al. High order fast swee-ping methods for static Hamilton-Jacobi equations[J]. Journal of Scientific Computing, 2006, 29(1): 25-56. DOI:10.1007/s10915-005-9014-3 |
| [22] |
Qian J, Zhang Y, Zhao H, et al. Fast sweeping methods for eikonal equations on triangular meshes[J]. SIAM Journal on Numerical Analysis, 2007, 45(1): 83-107. |
| [23] |
Fomel S, Luo S, Zhao H, et al. Fast sweeping method for the factored eikonal equation[J]. Journal of Computational Physics, 2009, 228(17): 6440-6455. DOI:10.1016/j.jcp.2009.05.029 |
| [24] |
Qian J, Zhang Y, Zhao H, et al. A fast sweeping method for static convex Hamilton-Jacobi equations[J]. Journal of Scientific Computing, 2007, 31(1): 237-271. |
| [25] |
Luo S, Qian J. Fast sweeping methods for factored anisotropic eikonal equations:Multiplicative and additive factors[J]. Journal of Scientific Computing, 2012, 52(2): 360-382. DOI:10.1007/s10915-011-9550-y |
| [26] |
Waheed U B, Yarman C E, Flagg G, et al. An iterative, fast-sweeping-based eikonal solver for 3D tilted anisotropic media[J]. Geophysics, 2015, 80(3): C49-C58. DOI:10.1190/geo2014-0375.1 |
| [27] |
Waheed U B, Alkhalifah T. A fast sweeping algorithm for accurate solution of the tilted transversely isotro-pic eikonal equation using factorization[J]. Geophy-sics, 2017, 82(6): WB1-WB8. |
| [28] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [29] |
Alkhalifah T. An acoustic wave equation for orthorhombic anisotropy[J]. Geophysics, 2003, 68(4): 1169-1172. DOI:10.1190/1.1598109 |
| [30] |
Bakulin A, Grechka V, Tsvankin I, et al. Estimation of fracture parameters from reflection seismic data-Part Ⅰ:HTI model due to a single fracture set[J]. Geophysics, 2000, 65(6): 1788-1802. DOI:10.1190/1.1444863 |
| [31] |
Sethian J A, Vladimirsky A. Ordered upwind methods for static Hamilton-Jacobi equations:Theory and algorithms[J]. SIAM Journal on Numerical Analysis, 2003, 41(1): 325-363. DOI:10.1137/S0036142901392742 |
| [32] |
Tsai Y R, Cheng L, Osher S, et al. Fast sweeping algorithms for a class of Hamilton-Jacobi equations[J]. SIAM Journal on Numerical Analysis, 2003, 41(2): 673-694. DOI:10.1137/S0036142901396533 |



 黄光南, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院地球物理系, 330013。Email:
黄光南, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院地球物理系, 330013。Email: