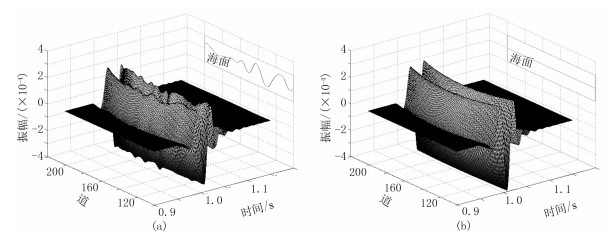
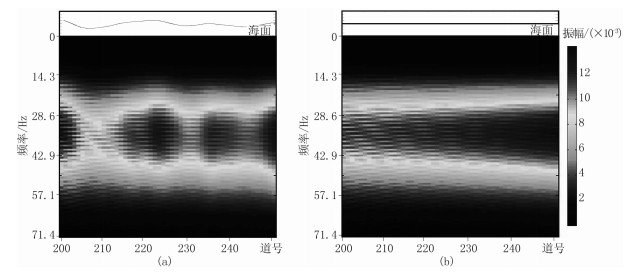
近年来,随着海上时移地震的兴起,随机时变的起伏海面对反射地震响应的影响逐渐得到重视[1-2]。Laws等[3]分析时移地震成像观测结果后认为:起伏海面造成的成像误差不可忽略;随后,系统地讨论了北大西洋起伏海面对地震数据的影响,指出即使在适度平静的海面之下,原始地震数据的振幅在某些频段的误差达1~3dB,相位误差达10°~20°,叠后地震数据的均方根误差达5%~10%。
为了研究起伏海面对地震波传播的影响,人们普遍使海面“冻结”到某一个时刻上——“冻结”海面模型。有多种常用的求解不规则边界的偏微分方程的方法,包括有限元法、谱元法、Kirchoff近似法、有限差分法等[4];Robertsson等[5]同时采用谱元法、Kirchoff近似法、有限差分法进行起伏海面地震波数值模拟,并对比、分析了三种方法的优缺点;Ego-rov等[6]采用Kirchoff近似法模拟起伏海面数据并与实际地震数据对比。上述研究的区域和建模所用的海浪谱主要来自北海和北大西洋等海域。起伏海面条件下的反射地震响应主要与海面的起伏形态有关,而海面起伏形态一般受当地的重力加速度、水深、海风和潮汐等因素影响,故在不同的海域,海面起伏呈不同特征。
为了更真实地模拟起伏海面的影响,本文利用兼顾精度与计算效率的有限差分法,采用基于鬼点外推的不等距差分格式,利用中国的海浪谱建立起伏海面模型,以此研究中国海域内起伏海面条件下的反射地震响应。
1 基本原理 1.1 差分离散格式在不规则边界处求解声波方程时,大部分边界点与网格点并不重合,而是落在两个网格点之间。这种没有落在网格点上的边界点称之为非正则内点。不等距差分是有限差分的一种网格剖分格式,其算子包含了起伏边界处的高程信息,算子形态灵活、网格起伏整洁而光滑。
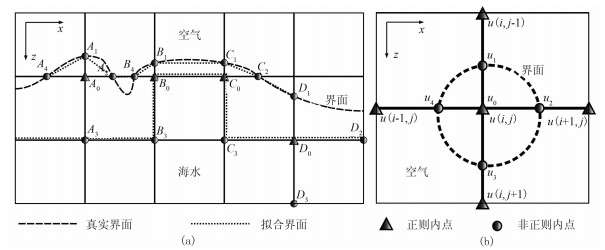
图 1为以A0、B0、C0、D0为中心的不同形态的不等距差分算子(时间二阶、空间二阶)及其结构。由图可见:以D0为中心的算子只需在计算z方向波场二阶导数时采用不等距差分格式;以A0、B0、C0为中心的算子需要在计算x和z方向波场二阶导数时同时采用不等距差分格式(图 1a)。对于声波方程
|
图 1 以A0、B0、C0、D0为中心的不同形态的不等距差分算子(时间二阶、空间二阶)(a)及其结构(b) |
| $ \frac{\partial^{2} u}{\partial t^{2}}=v^{2}\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial z^{2}}\right) $ | (1) |
在x方向, 不等距(式(2)上)和均匀网格(式(2)下)差分离散格式的波场二阶导数分别为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\partial ^2}u}}{{\partial {x^2}}} = \frac{2}{{{h^2}}}\left[ {\frac{{{u_2} - {u_0}}}{{{\theta _2}\left( {{\theta _2} + {\theta _4}} \right)}} + \frac{{{u_4} - {u_0}}}{{{\theta _2}\left( {{\theta _2} + {\theta _4}} \right)}}} \right]}\\ {\frac{{{\partial ^2}u}}{{\partial {x^2}}} = \frac{1}{{{h^2}}}[u(i + 1, j) - 2u(i, j) + u(i - 1, j)]} \end{array}} \right. $ | (2) |
式中:h为网格间距;
可见,不等距差分离散格式二阶导数中包含了真实界面的高程信息,均匀网格离散格式二阶导数中不包含高程信息。则不等距差分的离散格式(时间二阶、空间二阶)为
| $ \begin{array}{*{20}{c}} u\left( i,j,2 \right)=2u\left( i,j,1 \right)-u\left( i,j,0 \right)+\\ {\frac{2}{{{h^2}}}\left[ {\frac{{{u_1}}}{{{\theta _1}\left( {{\theta _1} + {\theta _3}} \right)}} + \frac{{{u_2}}}{{{\theta _2}\left( {{\theta _2} + {\theta _4}} \right)}} + \frac{{{u_3}}}{{{\theta _3}\left( {{\theta _1} + {\theta _3}} \right)}} + } \right.}\\ {\frac{{{u_4}}}{{{\theta _4}\left( {{\theta _2} + {\theta _4}} \right)}} - \left( {\frac{1}{{{\theta _1}{\theta _3}}} + \frac{1}{{{\theta _2}{\theta _4}}}} \right){u_0}] + }\\ {s(t)\delta \left( {i - {i_0}} \right)\delta \left( {j - {j_0}} \right)} \end{array} $ | (3) |
式中u(i, j, 0)、u(i, j1)、u(i, j2)分别为上一时刻、此时刻、下一时刻空间的波场值。对于不等距差分算子,当u1、u2、u3、u4为正则内点时,那么θ1、θ2、θ3、θ4等于1,此时不等距差分算子转化为均匀网格差分算子(时间二阶、空间二阶)。
对于起伏海面这种小尺度不规则边界的波动方程的求解,若采用均匀网格有限差分离散格式,则拟合出的实际界面为由点A3、B3、B0、C0、C3、D0连接的阶梯状起伏界面;若在起伏海面附近采用不等距差分离散格式,则拟合的实际反射界面为由点A4、A1、A2、B4、B1、C1、C2、D1连接的一条较光滑的折线(图 1a)。与均匀网格有限差分相比,不等距差分能更加真实地拟合复杂边界形态。因此,在起伏界面附近,采用不等距差分格式,在远离不规则边界的计算区域,采用均匀网格差分格式。
1.2 非正则内点处波场计算不等距差分法的关键是计算非正则内点处的波场,使其满足自由边界条件。在计算非正则内点处的波场值时,鬼点外推法是一种有效方法。Zhang等[7]利用鬼点外推的不等距差分法实现了复杂起伏地表条件下的最小二乘逆时偏移。
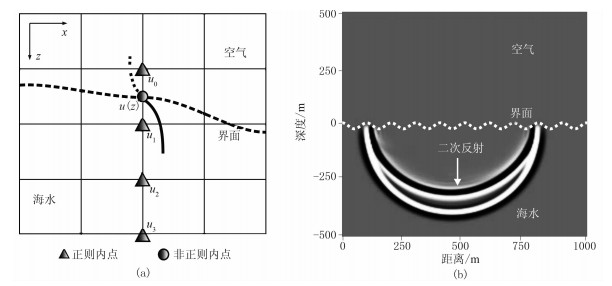
根据流体力学理论,海面和海面以上的波场值为0。为了使地震波场满足自由边界条件,在不等距差分格式中,往往假设非正则内点uz或海面以上的点u0的波场值不为0,称uz或u0这类点为鬼点。以z方向为例,鬼点外推法的主要思想是假设鬼点的波场值不为0,以此求解在海面附近的波场二阶导数(图 2a)。根据不规则边界运算区域内的u1、u2、u3等点的波场值及其一阶导数,通过多项式外推法计算鬼点的波场值。在数值模拟过程中,鬼点的波场值仅仅用于计算波场二阶导数,而与波场的空间分布无关。由鬼点外推法的波场快照(图 2b)可见,基于鬼点外推法的不等距差分格式的模拟结果符合物理规律。
|
图 2 鬼点外推示意图(a)与波场快照(t=0.3s)(b) |
构建z方向的多项式
| $ u(z)=a z^{3}+b z^{2}+c z+d $ | (4) |
求取非正则内点的波场值。式中:a、b、c、d为与正则内点u1、u2、u3的波场值和一阶导数有关的系数;u(z)为非正则内点的波场值。
2 算例利用不等距差分的离散格式和波场外推方法进行数值模拟,通过分析模拟结果阐述中国海域内起伏海面对地震数据的影响。
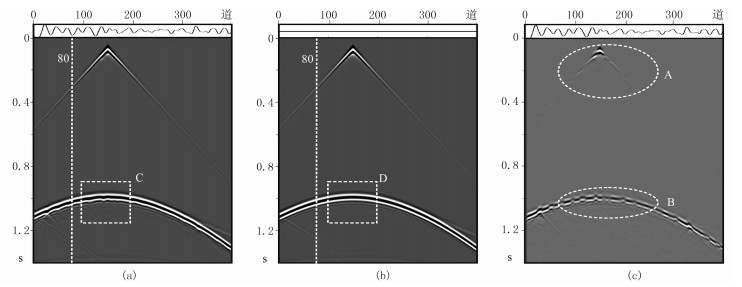
2.1 基于起伏海面的层状速度模型建立层状速度模型(图 3),采用文圣常等[8]提出的海浪谱计算模型建立了有效波高为2m的适度平静海面起伏模型(见附录A的图 A1)。由不同海面模型地震记录发现:①与平静海面模型地震记录(图 4b)相比,起伏海面模型地震记录的同相轴存在“抖动”的现象(图 4a),二次反射的“抖动”更明显,这是由于一次反射经过起伏海面的不规则反射造成的。②起伏海面模型与平静海面模型地震记录存在差别(图 4c),这种差别是由海面起伏造成的,具体表现为:对于直达波(图 4c的A区域),误差主要分布在炮检距较小的位置,随着炮检距增大,误差逐渐减小;对于反射波(图 4c的B区域),误差均匀分布,且误差大小与海面起伏形态有关。造成上述误差分布的原因为:在炮检距较大处,地震波的入射和反射方向几乎平行于海面,直达波和鬼波发生相对规则的干涉,起伏海面影响较小;对于反射波,地震波的入射方向几乎垂直于海面,一次反射和鬼波发生不规则干涉,起伏海面影响较大。
|
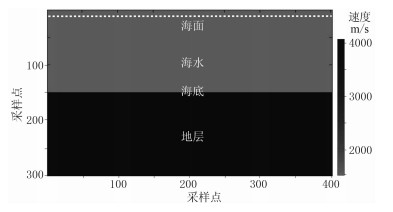
图 3 层状速度模型 模型横向有401个采样点,纵向有301个采样点,空间中正则内点采样间距为5m,非正则内点的采样间距主要与海面高程有关,介于0~5m。拖缆位于水下10m处,震源位于横向第150个采样点处,主频为30Hz,采用PML吸收边界条件 |
|
图 4 不同海面模型地震记录 (a)起伏海面模型;(b)平静海面模型;(c)图a与图b数据之差 |
通过对比发现:在时间和空间方向上,平静海面模型地震反射同相轴光滑且能量均匀(图 5b),起伏海面模型地震反射同相轴粗糙且能量不均匀(图 5a),这是由于规则的一次反射与经过起伏海面产生的不规则二次反射相互干涉所致。在起伏海面环境下,由于存在地震数据的“抖动”和能量不均匀分布现象,往往造成压制鬼波效果不理想、成像信噪比和分辨率低、地下照明不均匀等问题。频谱分析结果表明:与平静海面模型的地震数据频谱(图 6b)相比,起伏海面模型地震数据频谱的频带宽窄和能量分布发生变化(图 6a),这种变化与海面起伏形态有关。
2.2 单道直达波、反射波分析
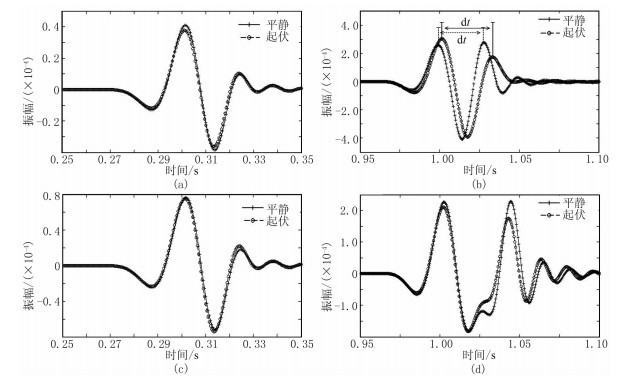
抽取第80道直达波和反射波数据(图 7)直观地分析起伏海面对观测地震数据的影响。由图 7a、图 7c可见:起伏海面的直达波振幅与平静海面差别较小,且这种差别与拖缆深度无关;起伏海面的直达波走时与平静海面几乎相同。原因为:对于直达波的虚反射来说,声波波长远大于海面的起伏高度,且入射方向平行于海面,由起伏海面产生的向其他方向的散射能量主要集中于镜反射方向[9],故虚反射影响较小,因此虚反射与直达波发生干涉后对直达波的影响较小。由图 7b、图 7d可见:起伏海面的振幅、走时与平静海面差别较大,且这种差别与拖缆深度有关,这是造成起伏海面条件下鬼波压制效果不理想的主要因素之一。原因为:起伏海面改变了虚反射的路径,因此虚反射和一次反射的互相干涉改变了一次反射的波形;随着拖缆深度增加,虚反射和一次反射的走时时差增大,造成一次反射和虚反射的互相干涉减弱。综上所述,随着拖缆深度的不同,一次反射和不规则的虚反射产生了不同的干涉,导致起伏海面对地震数据的影响程度不同。
|
图 7 第80道地震数据 (a)拖缆深度为10m的直达波;(b)拖缆深度为10m的反射波;(c)拖缆深度为20m的直达波;(d)拖缆深度为20m的反射波 |
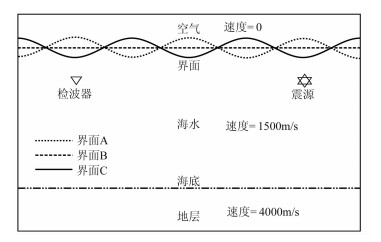
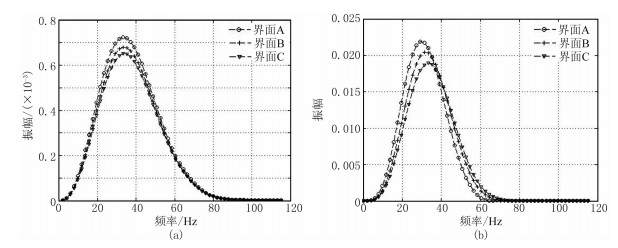
为了验证起伏海面对地震波频谱的影响,利用正弦函数建立海面速度模型(图 8),对单道地震记录的直达波和反射波分别进行振幅谱(图 9)、相位谱(图 10)分析。由图 9可见,振幅谱的影响主要体现在不同频率地震波的振幅差异,表现为:①波峰地震记录的直达波能量较大,频带变宽;波谷地震记录的直达波能量较小,频带变窄(图 9a)。②当目标检波器上方为波峰时,反射波频谱面积增大,总能量增大,即相对于平静海面,频谱低频能量增大,高频能量减小,向低频移动;当目标检波器上方为波谷时,反射波频谱面积减小,总能量减小,即相对于平静海面,频谱低频能量减小,高频能量增大,向高频移动(图 9b)。
|
图 8 海面起伏呈正弦函数的速度模型 检波器分别置于A、B、C三个海面的波峰、水平点、波谷 |
|
图 9 直达波(a)、反射波(b)振幅谱分析 |
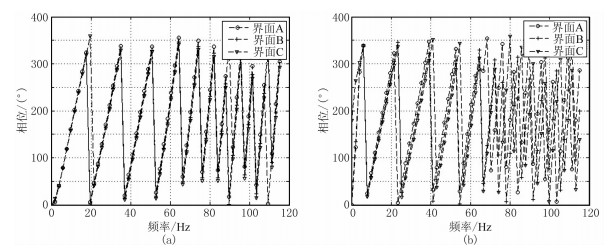
相位谱的影响主要体现在不同频率地震波的走时差异。由图 10可见:起伏海面对直达波的相位谱影响较小,只在高频部分有一定影响(图 10a);无论低、高频成分,起伏海面对反射波的相位谱影响较大(图 10b)。
|
图 10 直达波(a)、反射波(b)相位谱分析 |
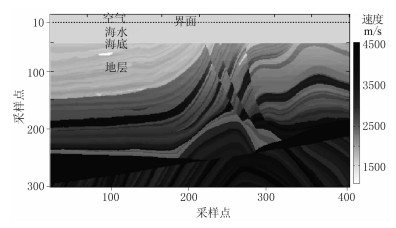
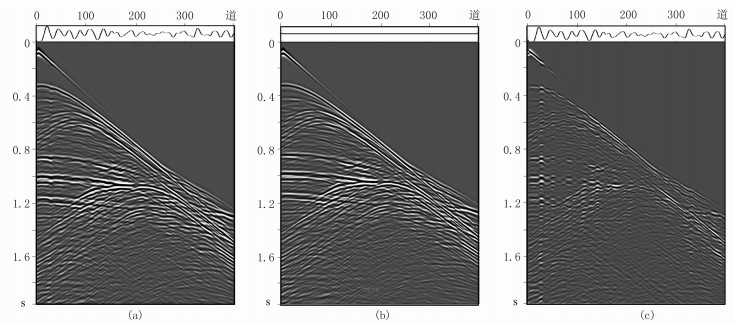
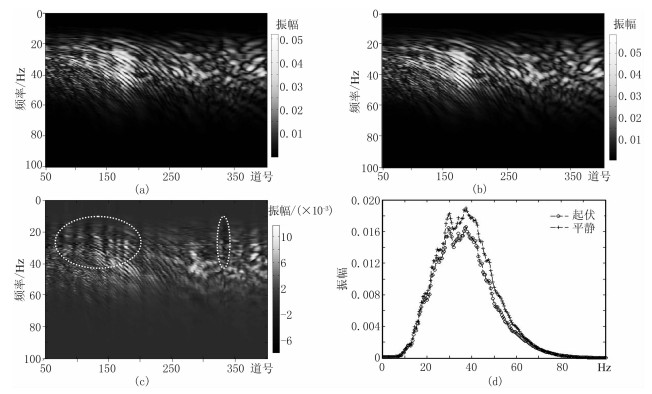
建立Marmousi速度模型(图 11),图 12为Marmousi模型地震记录。由图可见:由起伏海面产生的同相轴抖动现象在所有时刻都存在,且与海面的起伏形态相关(图 12a)。图 13为Marmousi模型地震记录振幅谱分析。由图可见:与平静海面地震数据相比,起伏海面地震数据在某些地震道的低频段(图 13c的椭圆区域)能量较大,这种分布与海面起伏形态具有一定相关性,在其他区域能量较小;与平静海面地震数据相比,起伏海面地震数据的高频能量损失大于低频能量,致使频带变窄(图 13d),意味着地震子波分辨率降低,因此对拖缆资料的宽频处理和鬼波压制提出了新的挑战[10-15]。
|
图 11 Marmousi速度模型 横向有401个采样点,纵向有301个采样点,空间采样间距为5m,拖缆位于水下10m处,震源位于横向第5个采样点处,主频为30Hz,采用PML吸收边界条件 |
|
图 12 Marmousi模型地震记录 (a)起伏海面;(b)平静海面;(c)图a与图b数据之差 |
|
图 13 Marmousi模型地震记录振幅谱分析 (a)起伏海面;(b)平静海面;(c)图a与图b数据之差;(d)图a与图b数据的平均功率谱 |
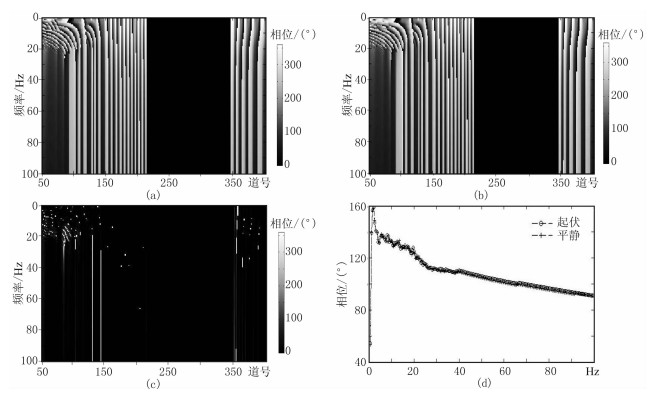
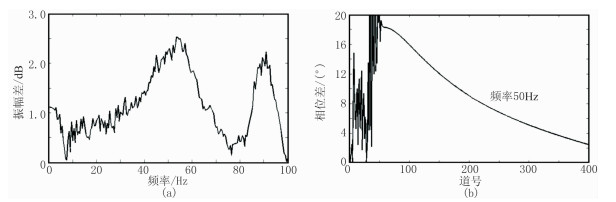
图 14为Marmousi模型地震记录相位谱分析。由图 14c可见,相位谱差异主要分布于较小炮检距道。原因为:当炮检距较小时,地震波近似垂直入射于海面,对地震波走时的影响较大;当炮检距较大时,射向海面的地震波入射角较大,对地震波走时的影响较小。由图 14d可见,起伏海面对地震数据的平均相位谱也有一定影响。图 15为起伏海面与平静海面地震数据的振幅差和相位差。由图可见:在有效波高为2m的条件下,起伏海面在某些频段引起的振幅差可达1.0~2.5dB(图 15a),在频率为50Hz时相位差可达20°(图 15b)。
|
图 14 Marmousi模型地震记录相位谱分析 (a)起伏海面;(b)平静海面;(c)图a与图b数据之差;(d)图a与图b数据的平均相位谱 |
|
图 15 起伏海面与平静海面地震数据的振幅差(a)和相位差(b) |
采用文圣常等[8]提出的海浪谱计算模型建立了有效波高为2m的适度平静海面起伏模型,通过对简单的层状模型和Marmousi模型的数值模拟,得到以下认识:
(1) 受起伏海面影响,鬼波与一次反射发生不规则的干涉而产生不同的反射地震响应。
(2) 由起伏海面产生的地震反射同相轴“抖动”现象在所有时刻都存在,且与海面的起伏形态相关。
(3) 由于二次反射的不均匀照明及其与一次反射的不规则干涉,造成地震反射能量的空间分布不均匀现象,影响直达波和反射波的走时、波形、振幅、频谱、相位和带宽等,造成鬼波压制效果不佳、成像信噪比低、分辨率低、局部反演结果不收敛等一系列实际问题。
附录A 基于海浪谱的起伏海面建模针对起伏海面的建模与仿真问题,人们常用海浪谱模拟海面的起伏形态。早在20世纪40年代,人们就把海面的起伏看成由不同频率、不同振幅、不同相位的波动的叠加结果。海面起伏是一个时变过程,具有一定的随机性。Pierson等[16]用随机过程分析海浪(谱分析法)。在某一点
| $ \eta (t) = \sum\limits_{n = 1}^\infty {{a_n}} \cos \left( {{\omega _n}t + {\varepsilon _n}} \right) $ | (A-1) |
式中:η(t)为质点在t时刻的振动幅度;an、ωn分别为振幅和频率;εn为在0~2π内随机分布的初始相位。海浪的能量由
| $ S(\omega)=\frac{1}{\Delta \omega} \sum\limits_{\omega}^{\omega+\Delta \omega} \frac{1}{2} a_{n}^{2} $ | (A-2) |
表示。S(ω)可以看成角频率为ω的海浪的能量,由S(ω)和ω构成的描述海水能量分布的谱线即为海浪谱。某个区域的海浪谱通常是在海浪的不同形成时期和不同海洋环境下,经过多次观测、拟合得到的经验性结果;在不同的海区,气候、风力、潮汐、水深、当地的重力加速度和海水的多种物性参数等都会对海面的起伏形态产生一定的影响,因此,不同海域的海浪谱一般不同。
Neumann于20世纪50年代根据经验提出了Neumann谱[17]
| $ S(\omega ) = c\frac{{\rm{ \mathit{ π} }}}{4}\frac{1}{{{\omega ^6}}}\exp \left( { - \frac{{2{g^2}}}{{{w^2}{\omega ^2}}}} \right) $ | (A-3) |
式中:c=3.05;g为当地的重力加速度;w为高于海面7.5m处的风速。
Pierson等[18]对北大西洋充分成长型海浪进行观测,并提出PM谱
| $ S(\omega)=a \frac{g^{2}}{\omega^{5}} \exp \left(-\frac{\beta g^{4}}{w^{4} \omega^{4}}\right) $ | (A-4) |
式中:a=0.0081;β=0.74;g为重力加速度;w为高于海面19.5m处的风速。
中国研究者通过对渤海资料的观测,提出了一种符合中国海域的海浪谱,并与JONSWAP谱进行对比[19-20]。文圣常等[8]在广泛研究中国海域资料的基础上,对前人提出的谱进行改进和简化,提出了一种新海浪谱
| $ \left\{ {\begin{array}{*{20}{c}} {S(\omega ) = 0.0111{H^2}TP\exp \left[ { - 95\left( {\ln \frac{P}{{1.522 - 0.245P + 0.00292{P^2}}}} \right){{(0.177\omega - 1)}^{\frac{{12}}{5}}}} \right]\quad 0 \le \omega \le 6.58\frac{1}{T}}\\ {S(\omega ) = 20.8\frac{{{H^3}}}{{{T^3}}}\left( {1.522 - 0.245P + 0.00292{P^2}} \right)\frac{1}{{{\omega ^4}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\omega > 6.58\frac{1}{T}} \end{array}} \right. $ | (A-5) |
式中:H为有效波高;T为有效周期;
| $ \omega^{2}(k)=g k $ | (A-6) |
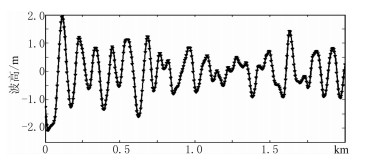
把海浪谱写成波数域的形式,将波数域的海浪谱乘以一组高斯分布的随机复数,然后对其进行傅里叶逆变换,便得到不同海况下的随机起伏海面模型(图 A1)。
|
图 A1 海面起伏模型 有效波高为2m,道间距为5m |
| [1] |
Cecconello E, Asgedom E G, Orji O C, et al. Modeling scattering effects from time-varying sea surface based on acoustic reciprocity[J]. Geophysics, 2017, 83(2): T49-T68. |
| [2] |
Kragh E, Laws R. Rough seas and statistical deconvolution[J]. Geophysical Prospecting, 2006, 54(4): 475-485. DOI:10.1111/j.1365-2478.2006.00549.x |
| [3] |
Laws R, Kragh E. Rough sea wavelet and time-lapse seismic[J]. Geophysical Prospecting, 2002, 50(2): 195-208. DOI:10.1046/j.1365-2478.2002.00311.x |
| [4] |
孙建国. 复杂地表条件下地球物理场数值模拟方法评述[J]. 世界地质, 2007, 26(3): 345-362. SUN Jianguo. Methods for numerical modeling of geophysical fields under complex topographical conditions:a critical review[J]. Global Geology, 2007, 26(3): 345-362. DOI:10.3969/j.issn.1004-5589.2007.03.015 |
| [5] |
Robertsson J O A, Laws R, Chapman C, et al. Modelling of scattering of seismic waves from a corrugated rough sea surface:a comparison of three methods[J]. Geophysical Journal International, 2006, 167(1): 70-76. DOI:10.1111/j.1365-246X.2006.03115.x |
| [6] |
Egorov A, Glubokovskikh S, Bona A, et al.Influence of rough sea surface on sea surface reflections: deep towed high-resolution marine seismic case study[C]. SEG Technical Program Expanded Abstracts, 2015, 34, Document ID: SEG-2015-5897880.
|
| [7] |
Zhang D, Schuster G T, Zhan G.Multi-source least-squares reverse time migration with topography[C]. SEG Technical Program Expanded Abstracts, 2013, 32, Document ID: SEG-2013-0270.
|
| [8] |
文圣常, 张大错, 郭佩芳, 等. 改进的理论风浪频谱[J]. 海洋学报, 1990, 12(3): 271-283. |
| [9] |
周建波, 朴胜春, 黄益旺, 等. 波浪起伏对噪声场空间特性的影响[J]. 哈尔滨工程大学学报, 2017, 38(7): 1056-1064. ZHOU Jianbo, PIAO Shengchun, HUANG Yiwang, et al. Effect of wave fluctuation on the spatial characteristics of noise field[J]. Journal of Harbin Engineering University, 2017, 38(7): 1056-1064. |
| [10] |
张威, 韩立国, 李洪建. 基于起伏海水表面的拖缆鬼波压制方法[J]. 石油物探, 2017, 56(4): 500-506. ZHANG Wei, HAN Liguo, LI Hongjian. Deghosting method based on a variable sea surface for conventional streamer seismic data[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 500-506. DOI:10.3969/j.issn.1000-1441.2017.04.005 |
| [11] |
吴志强. 海洋宽频带地震勘探技术新进展[J]. 石油地球物理勘探, 2014, 49(3): 421-430. WU Zhiqiang. New advances in marine broadband seismic exploration[J]. Oil Geophysical Prospecting, 2014, 49(3): 421-430. |
| [12] |
公亭, 王兆磊, 顾小弟, 等. 宽频地震资料处理配套技术[J]. 石油地球物理勘探, 2016, 51(3): 457-466. GONG Ting, WANG Zhaolei, GU Xiaodi, et al. Broadband seismic data matching processing[J]. Oil Geophysical Prospecting, 2016, 51(3): 457-466. |
| [13] |
丁在宇, 杨勇, 王一鸣, 等. 浅海拖缆地震数据处理中关键技术的应用与效果[J]. 石油地球物理勘探, 2017, 52(增刊2): 56-63. DING Zaiyu, YANG Yong, WANG Yiming, et al. Key processing techniques for shallow water tow-streamer seismic data[J]. Oil Geophysical Prospecting, 2017, 52(S2): 56-63. |
| [14] |
王建花, 王艳冬, 刘国昌. 基于波场延拓和反演的变深度缆地震数据鬼波压制方法[J]. 石油地球物理勘探, 2017, 52(5): 885-893. WANG Jianhua, WANG Yandong, LIU Guochang. A deghosting method on variable-depth streamer data based on wavefield extrapolation and inversion[J]. Oil Geophysical Prospecting, 2017, 52(5): 885-893. |
| [15] |
李振勇, 姜浩, 李东升. 海洋地震数据处理技术探讨[J]. 石油地球物理勘探, 2007, 42((增刊1): 8-13. LI Zhenyong, JIANG Hao, LI Dongsheng. Discussion on marine seismic data processing technique[J]. Oil Geophysical Prospecting, 2007, 42(S1): 8-13. |
| [16] |
Pierson W J, Neumann G, James R W. Practical Me-thods for Observing and Forecasting Ocean Waves by Means of Wave Spectra and Statistics[M]. U.S Navy Hydrographic Office, 2012.
|
| [17] |
文圣常. 海浪理论与计算原理[M]. 北京: 科学出版社, 1984.
|
| [18] |
Pierson W J, Moskowitz L. A proposed spectral form for fully developed wind seas based on the similarity theory of SA Kitaigorodskii[J]. Journal of Geophysical Research, 1964, 69(24): 5181-5190. DOI:10.1029/JZ069i024p05181 |
| [19] |
Wen S C, Zhang D C, Chen B H, et al. Theoretical wind wave frequency spectra in deep water-Ⅰ:Form of spectrum[J]. Acta Oceanologica Sinica, 1988, 7(1): 1-16. |
| [20] |
Wen S C, Chen B H, Guo P F, et al. Theoretical wind wave frequency spectra in deep water-Ⅱ:Comparison and verification of spectra[J]. Acta Oceanologica Sinica, 1988, 7(2): 159-169. |



 孙建国, 吉林省长春市西民主大街938号地球探测科学与技术学院, 130026。Email:
孙建国, 吉林省长春市西民主大街938号地球探测科学与技术学院, 130026。Email: