② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Laboratory for Marine Mineral Resource, Qing-dao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China
近年来,共反射面元(CRS)叠加在地震数据低信噪比地区已逐步成为NMO/DMO叠加的备选方法。CRS叠加方法[1]通过计算反射段(二维)或反射面(三维)上的、时空域的叠加算子获得高信噪比和高质量的零炮检距地震剖面。CRS叠加在实现地震成像时,不需要提供宏观速度模型,仅需知道近地表速度,成像结果的信噪比更高。在二维情况下,经典的CRS叠加算子取决于3个运动学波场属性[2],即法向射线在地面的出射角α、法向入射点(Normal Incident Point,NIP)波波前曲率半径RNIP和法向(Normal,N)波波前曲率半径RN。拓展到三维,叠加算子由8个参数确定[3-4],即零炮检距射线出射的倾角和方位角、NIP波波前曲率矩阵和N波波前曲率矩阵(均为2×2的对称矩阵)。在中国,不少学者在CRS叠加理论与实践方面做了深入的研究[5-10]。CRS叠加效果由波场运动学属性参数确定,因此参数的选择成为实现CRS叠加的关键。同时在数据中进行参数搜索时,需要相干分析技术的支持,涉及到最优化问题。前人应用线性搜索进行参数选择,但效率较低。
本文采用粒子群(PSO)算法实现对初始二维CRS叠加参数的选择。与常规CRS叠加方法相比,在不影响叠加效果的基础上,提高了参数搜索的效率,大大缩短了计算时间。
1 CRS方法原理及实现策略CRS叠加的本质,是对一个反射段上相邻CMP道集构成的CRS叠加面进行动校正叠加,可以大幅度提高叠加次数,提高信噪比[11-12]。
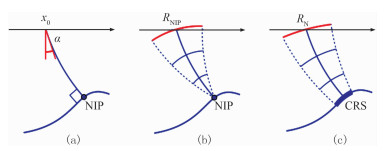
CRS算子由三个波场属性组成,其物理意义如图 1所示。
|
图 1 特征波示意图 (a)法向射线;(b)NIP波;(c)N波 |
图 1a表示从地下反射界面出发的法向射线在地面以α角度出射;图 1b表示把点震源放在图中NIP点上,波前的初始曲率半径为0,这种波称为法向入射点波;图 1c中表示了地下反射界面上一部分弧段激发产生的波前,其初始曲率半径与地层局部曲率半径一致,这种波称为法向波。
CRS叠加方法的理论基础是几何地震学,并利用了多次覆盖数据。下面给出用三参数表示的二维CRS叠加算子。二维CRS叠加旅行时近似公式为
| $ \begin{aligned} t^{2}\left(x_{\mathrm{m}}\right)=&\left[t_{0}+\frac{2 \sin \alpha}{v_{0}}\left(x_{\mathrm{m}}-x_{0}\right)\right]^{2}+\\ & \frac{2 t_{0} \cos ^{2} \alpha}{v_{0}}\left[\frac{\left(x_{\mathrm{m}}-x_{0}\right)^{2}}{R_{\mathrm{N}}}+\frac{h^{2}}{R_{\mathrm{NIP}}}\right] \end{aligned} $ | (1) |
式中:v0为近地表速度;h为半炮检距;t0为零炮检距双程旅行时;x0和xm分别为中心和相邻CDP的横向坐标;RNIP为法向入射点波在地面处的波前曲率半径;RN为法向波在地面处的波前曲率半径[13]。
与常规CMP叠加不同的是,CRS叠加涉及三个参数的搜索,计算量较大。实用的策略是首先在简化的道集中如共中心点(CMP)道集或零炮检距道集进行分步搜索得到三参数的初值,然后在CRS道集中利用三参数初值做CRS叠加。如果需要进一步提高叠加效果,可以利用局部优化算法(如下山单纯形、POWELL算法等)优化三参数,再进行CRS叠加。
2 粒子群算法及应用地球物理数据的处理、解释通常需要求解逆问题。很多数学方法可用于地球物理数据反演,其中粒子群算法(Particle Swarm Optimization,PSO)由Eberhart等[14]在1995年提出,模拟鸟类或鱼类在食物搜索中的社会行为,近年来在地震勘探领域有了更深层次的应用[15-16]。
PSO法开始于一组随机分布的粒子,首先在整个搜索空间计算特定问题的目标函数最大值,搜索每个粒子的最优解,并记为该粒子当前的个体极值;然后比较所有粒子的个体极值,找到一个最优的个体极值,作为粒子群当前的全局最优解;比较当前粒子群中的所有粒子的个体极值和粒子群当前全局最优解,调整每个粒子的变化速度和位置。即在每次迭代中,基于相应的函数值更新粒子位置,实现每个粒子的个体认知加权到整个粒子群。
PSO定义了一个M维空间中的粒子群,每个粒子记忆其以前最佳位置和速度。在每次迭代中,粒子的速度根据该粒子的最佳位置和全局的最佳位置进行调整。新的速度用于计算粒子的新位置。由个体以前的最佳位置确定速度调整被称为“认知”,同时受整个粒子群影响,即粒子具有社会行为。
假设第k次迭代的第i个粒子的当前位置和速度分别为mi(k)和vi(k),该粒子到目前为止的最佳位置为mi1。此外,考虑到在第k次迭代之前粒子群所获得的最佳位置是mg,那么在第k+1次迭代中第i个粒子的速度和位置分别为
| $ \begin{array}{l} \mathit{\boldsymbol{v}}_i^{(k + 1)} = \mathit{\boldsymbol{v}}_i^{(k)} + b \times r\left[ {\mathit{\boldsymbol{m}}_i^1 - \mathit{\boldsymbol{m}}_i^{(k)}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;c \times r\left[ {{\mathit{\boldsymbol{m}}^{\rm{g}}} - \mathit{\boldsymbol{m}}_i^{(k)}} \right] \end{array} $ | (2) |
| $ \boldsymbol{m}_{i}^{(k+1)}=\boldsymbol{m}_{i}^{(k)}+a \boldsymbol{v}_{i}^{(k+1)} $ | (3) |
式中:b和c为常数,分别表示粒子的认知和社会行为的学习效率;常数a是Clerc等[17]引入的一个收缩因子,随着迭代次数的增加逐渐降低速度的影响,减小a值可使搜索逐渐集中到局部极值上;r为在开放区间(0,1)中均匀分布的随机数。对于所有的粒子,初始速度vi(0)=0。
首先,从预设的参数搜索空间中随机选择一组粒子,并将每个粒子的速度初始化为零。随后,根据式(2)和式(3)更新粒子的速度和位置,同时规定每个粒子的位置不超过指定参数空间的边界。以下为PSO算法的基本实现步骤:
(1) 设置最大迭代次数和粒子个数;
(2) 设置每个粒子的初始位置和速度;
(3) 计算每个粒子的适应度函数;
(4) 搜索每个粒子的最佳位置(局部最优解);
(5) 计算每个局部最优解的适应度函数;
(6) 确定每个粒子的历史最佳位置和目前的全局最优解;
(7) 满足精度要求或达到最大迭代次数吗?
(8) 否,更新每个粒子的速度和位置,返回步骤(3);是,输出结果,结束。
粒子群算法仅由一个算子控制,即速度更新。在CRS叠加中,对每一特定粒子,首先利用CRS叠加时距公式计算其对应的CRS叠加曲面,进而在地震数据中计算叠加能量或相干值,以此确定适应度函数的值。一般而言,优化算法需要对控制参数进行仔细的调整,这极大地影响了优化方法的行为。将PSO算法引入CRS参数搜索中,相应的计算步骤如下:
(1) 设置最大迭代次数;
(2) 在搜索空间中初始化CRS三参数的位置;
(3) 在搜索空间中确定CRS三参数的当前位置;
(4) 利用CRS三参数求取地震数据相干值,以此为准则计算每个粒子的适应度函数值;
(5) 根据最佳适应度找到全局最优位置;
(6) 如果新CRS参数值能够得到更高的地震数据相干值,重复步骤(3)~步骤(5);
(7) 终止条件是达到最大的迭代次数或参数的全局最优位置满足最小门槛。
3 模型试算及实例分析用图 2所示的凹陷模型评价基于PSO算法的CRS叠加的抗干扰能力。

|
图 2 凹陷模型 |
模型尺寸为9600m×3000m,离散成640×750个矩形网格。横向网格间距为15m,纵向网格间距为4m。起始炮点位于地表 1000m,结束炮点位于8600m,炮点间隔为60m。使用双边排列接收,最小炮检距为100m,最大炮检距为3000m,接收点间隔为30m。使用有限差分进行波动方程正演,选用主频为30Hz的Ricker子波作为震源,时间采样间隔为4ms。
图 3b~图 3e是由基于PSO优化后的CRS叠加得到的叠加剖面、相干剖面及各参数剖面。其深层的反射也清晰可见,叠加效果较好。该模型试算的结果证明了PSO算法在CRS叠加中的适用性和正确性。

|
图 3 凹陷模型基于PSO的CRS叠加处理结果 (a)叠加剖面;(b)相干剖面;(c)α剖面;(d)RNIP剖面;(e)RN剖面 |
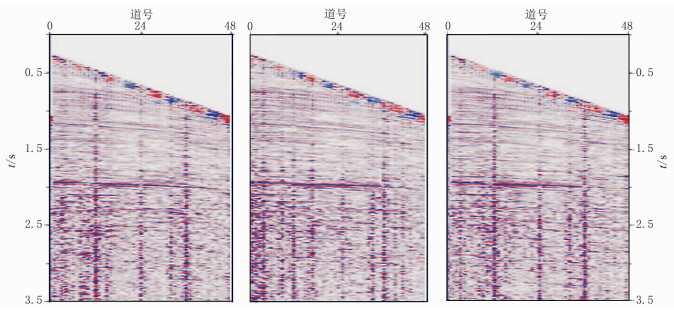
选取海上一条二维测线的实际资料进行处理。图 4为该测线3个CMP道集,已经做过前期的一些处理,如消除直达波、去噪、振幅补偿等。可以看出,由于道集覆盖次数较低,信噪比不高尤其是深层信噪比较低。图 5为常规叠加剖面与本文基于PSO优化的CRS叠加剖面对比,可见基于PSO优化的CRS叠加结果信噪比远高于常规叠加剖面。中深部存在陡倾地层,基于PSO优化的CRS叠加对其进行了清晰的成像,同相轴更为丰富,连续性也得到提高,深部的弱同相轴也隐约可见。该实际资料的处理结果证明了PSO全局优化方法在CRS参数搜索中的可行性和实用性。
|
图 4 海上实际数据三个CMP道集 |

|
图 5 海上实际数据数据的常规叠加(a)与本文的CRS叠加(b)剖面对比 |
在渤海实际二维数据的测试中,使用的机群有28个节点,每个节点8个CPU并共享16G内存。对于约6GB、2000个CMP道集的地震数据量,基于PSO全局优化算法的CRS叠加, 在运行过程中,每个进程占用1.02G内存,总计算时间约为5h。而基于三步法的常规CRS叠加,在第一步CMP叠加和第二步零炮检距叠加时占用内存较少,计算较快,但在第三步CRS叠加时依然占用1.02G内存,总计算时间约为15h。
在取得相同CRS叠加效果的前提下,运用PSO全局优化算法实现的一步法CRS叠加,计算时间约为常规三步法的1/3,计算效率大为提高,在大数据量尤其是三维数据的情况下更能体现计算效率的优势。
4 结束语本文将PSO算法引入CRS叠加的参数搜索,模型数据和实际数据处理结果说明,在不影响叠加效果的基础上,提高了参数搜索的效率,缩短了计算时间。更为重要的是,PSO全局优化算法不依赖初值选取,使得CRS实现流程大大简化。
如何更好地优化PSO算法的参数选取、提高CRS参数搜索效率,以及将本文的CRS叠加方法拓展到三维,有待进一步研究。
| [1] |
Hubral P. Computing true amplitude reflections in a laterally inhomeogeneous Earth[J]. Geophysics, 1983, 48(8): 1052-1062. |
| [2] |
Tygel M, Schleicher J, Hubral P. A unified ap-proach to 3-D seismic reflection imaging, Part Ⅱ:Theory[J]. Geophysics, 1996, 61(3): 759-775. DOI:10.1190/1.1444002 |
| [3] |
Höcht G.Traveltime Approximations for 2D and 3D Media and Kinematic Wavefield Attributes[D]. University of Karlsruhe, 2002.
|
| [4] |
Müller N.Determination of Interval Velocities by Inversion of Kinematic 3D Wavefield Attributes[D]. University of Karlsruhe, 2007.
|
| [5] |
韩立国.CRS叠加成像的属性参数反演与应用[C].中国地球物理学会第十七届年会论文集, 2001. http: //cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGDW200110001052.htm
|
| [6] |
李振春, 姚云霞, 马在田, 等. 基于参数多级优化的共反射面叠加方法及其应用[J]. 石油地球物理勘探, 2003, 38(2): 156-161. LI Zhenchun, YAO Yunxia, MA Zaitian, et al. Common reflection surface stack method based on multi-level optimization of parameters and its application[J]. Oil Geophysical Prospecting, 2003, 38(2): 156-161. DOI:10.3321/j.issn:1000-7210.2003.02.011 |
| [7] |
王征, 杨锴, 董水利, 等. 应用叠前时间偏移/反偏移与CRS-OIS叠加削弱倾角歧视影响[J]. 石油地球物理勘探, 2015, 50(5): 839-847. WANG Zheng, YANG Kai, DONG Shuili, et al. Dip discrimination reduction with CRS-OIS[J]. Oil Geophysical Prospecting, 2015, 50(5): 839-847. |
| [8] |
倪瑶, 杨锴. 基于GPU计算平台实现三维输出道方式的共反射面元(3D-CRS-OIS)叠加[J]. 石油地球物理勘探, 2013, 48(1): 49-57. NI Yao, Yang Kai. 3D common reflection surface stack algorithm based GPU with the output imaging scheme(3D-CRS-OIS)[J]. Oil Geophysical Prospecting, 2013, 48(1): 49-57. |
| [9] |
覃天, 段云卿, 赵勇. 共反射面元叠加波场属性参数的应用[J]. 石油地球物理勘探, 2006, 41(5): 530-533. QIN Tian, DUAN Yunqing, ZHAO Yong. Application of attribute parameter of common reflection surface(CRS) stack wave field[J]. Oil Geophysical Prospecting, 2006, 41(5): 530-533. DOI:10.3321/j.issn:1000-7210.2006.05.009 |
| [10] |
张金淼, 陈宝书, 汪小将, 等. 等旅行时面共反射面元叠加的应用研究[J]. 石油地球物理勘探, 2011, 46(6): 881-889. ZHANG Jinmiao, CHEN Baoshu, WANG Xiaojiang, et al. Application of 2D DORS-OIS to 2D real data acquired in deep water of South China Sea[J]. Oil Geophysical Prospecting, 2011, 46(6): 881-889. |
| [11] |
Bruno P P. High-resolution seismic imaging in complex environments:A comparison among common-reflection-surface stack, common-midpoint stack, and prestack depth migration at the Ilva-Bagnoli brownfield site, Campi Flegrei, Italy[J]. Geophysics, 2015, 80(6): B203-B214. DOI:10.1190/geo2014-0488.1 |
| [12] |
Walda J and Gajewski D.Common-reflection-surface stack improvement by differential evolution and conflicting dip processing[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 3842-3847.
|
| [13] |
Santos L T, Schleicher J.Fast estimation of CRS parameters using local slopes[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 3735-3739.
|
| [14] |
Eberhart R, Kennedy J.A new optimizer using particle swarm theory[C]. Proceeding of the IEEE 6th International Symposium on Micro Machine and Human Science, 1995.
|
| [15] |
蔡伟, 宋先海, 袁士川, 等. 利用粒子群优化算法快速、稳定反演瑞雷波频散曲线[J]. 石油地球物理勘探, 2018, 53(1): 25-34. CAI Wei, SONG Xianhai, YUAN Shichuan, et al. Fast and stable Rayleigh-wave dispersion-curve inversion based on particle swarm optimization[J]. Oil Geophysical Prospecting, 2018, 53(1): 25-34. |
| [16] |
谢玮, 王彦春, 刘建军, 等. 基于粒子群优化最小二乘支持向量机的非线性AVO反演[J]. 石油地球物理勘探, 2016, 51(6): 1187-1194. XIE Wei, WANG Yanchun, LIU Jianjun, et al. Non-linear AVO inversion based on PSO-LSSVM[J]. Oil Geophysical Prospecting, 2016, 51(6): 1187-1194. |
| [17] |
Clerc M.The swarm and the queen: towards a deterministic and adaptive particle swarm optimization[C]. Proceedings of the IEEE Congress of Evolutionary Computation, 1999, 1951-1957.
|



 贾延睿, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
贾延睿, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: