② 东华理工大学地球物理与测控技术学院, 江西南昌 33001;
③ 江西省基础地理信息中心, 江西南昌 330209
② School of Geophysics and Measurement-control Technology, East China University of Technology, Nanchang, Jiangxi 330013, China;
③ Jiangxi Fundamental Geographic Information Center, Nanchang, Jiangxi 330209, China
地震信号随机噪声衰减是地震数据处理领域的热点和难点问题。从观测数据中有效去除随机噪声干扰、提高信号信噪比和分辨率,是正、反演计算和地质解释的前提。目前,学者们提出了大量的地震信号随机噪声压制方法,比如基于滤波理论的方法[1-2]、基于小波域变换方法[3-6]、基于矩阵理论的变换方法[7-10]、基于信号分解理论方法[11-16]等。近年来,由于在处理非平稳及非线性数据上具有很高的信噪比,基于信号分解的经验模态分解(Empirical Mode Decomposition,EMD)方法[17]已成为信号分解领域研究的热点。
学者们在EMD方法基础上,进一步提出两种经典的改进方法,即集合经验模态分解(Ensemble EMD,EEMD)[18]和完备集合经验模态分解(Complete EEMD,CEEMD)[19]。其中,EEMD避免了EMD方法中的模态混叠,而CEEMD改善了EEMD方法中因辅助噪声造成的噪声污染。但是,CEEMD方法中依然采用递归迭代式筛选分解过程,非平稳地震信号极值点插值和包络计算过程耗时过长,在处理多维度和多尺度地震数据时存在一定限制。为了解决这些问题,以进一步提升信号分解的精度,本文提出全新的非线性、非递归的完全自适应时序序列分解算法——基于变分模态分解(Variational Modal Decomposition,VMD)的地震信号分解方法,并应用于二维和三维地震数据随机噪声压制中。
1 基本原理VMD的基本思路是:在EMD的固有模态函数(Intrinsic Mode Function,IMF)分量基础上,引入更严格的频率域带宽先验约束(Band-Limited Intrinsic Mode Function,BIMF)信号,又称带限分量,解决EMD中模态混叠和高频率信号丢失问题。IMF被定义为在信号极值点个数和过零点个数相等或相差一个时,任一时刻点由局部极值点所确定包络均值为零的信号。
VMD基本原理是:在IMF信号分量基础上,通过引入调幅—调频(AM-FM)信号
| $ u_{k}(t)=A_{k}(t) \cos \varphi_{k}(t) $ | (1) |
式中:Ak(t)和φk(t)分别为uk(t)的瞬时幅值和瞬时相位。φk(t)为非减函数,即瞬时角频率
| $ \omega_{k}(t)=\frac{\mathrm{d} \varphi_{k}(t)}{\mathrm{d} t} \geqslant 0 $ | (2) |
与φk(t)相比,Ak(t)和ωk(t)的变化较为缓慢,即在短时范围内可认为是一个幅值和频率不变的谐波信号。将满足上述条件的BIMF赋予具体的物理意义,即VMD将输入信号自适应分解成有限个BIMF分量之和,分解过程满足每个带限BIMF分量的估计聚集带宽之和为最小。与传统EMD方法不同,在获取BIMF分量时,VMD方法的递归迭代筛选模式将信号的分解过程转换至变分问题的求解,在寻找变分模型最优解的过程中完成信号的自适应分解。
2 地震随机噪声压制 2.1 地震信号的域表示线性地震数据可表示为
| $ d(t, x)=w\left(t-\frac{x}{c}\right) $ | (3) |
式中:t和x为时间和炮检距轴;w为地震子波函数,如Ricker子波;c为波在介质中的传播速度。将同相轴数据沿t(时间轴)作傅里叶变换,将t-x域转换到f-x域,得到原始数据的f-x频谱
| $ D(f, x)=\hat{w}(f) \mathrm{e}^{\mathrm{i} 2 \pi f \frac{x}{c}} $ | (4) |
将式(4)进行离散化,即可得到D(f-x)的离散表示
| $ D_{f}(m) \equiv D(f, m \Delta x) \quad m=1,2, \cdots, M $ | (5) |
式中:Δx表示沿x轴方向的道间距;m为地震采样道数,M为总道数。统计相邻两道可表示为
| $ D_{f}(m) \equiv \mathrm{e}^{\mathrm{i} 2 \pi f \frac{\Delta x}{c}} D_{f}(m-1) \quad m=1,2, \cdots, M $ | (6) |
式(6)是一阶递归微分方程,对应每一个频率切片Df(m)信号,由一个复调和谐波函数(调幅—调频)组成。因此,通过在t-x域中的无噪声线性数据中找到递归系数ei2πfΔx/c,使其在f-x域中完全可预测。类似地,t-x域中N个线性事件的叠加相当于f-x域中的N个复数谐波的叠加。
2.2 VMD框架求解基于上述地震数据域分析,在频率域中估计BIMF分量频率带宽目标函数[20]
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\}} \left\{ {\sum\limits_{k = 1}^K {\left\| {{\partial _t}\left\{ {\left[ {\delta (t) + \frac{{\rm{i}}}{{{\rm{ \mathsf{ π} }}t}}} \right]*{u_k}(t){{\rm{e}}^{ - {\rm{i}}{\omega _k}t}}} \right\}} \right\|_2^2} } \right\},}\\ {且满足\;\sum\limits_{k = 1}^K {{u_k}} = F} \end{array} $ | (7) |
式中:min(·)表示函数最小化;ωk为对应模态的瞬时频率;K为预设分解尺度个数;uk即为VMD分解后具备带限性质的BIMF分量;δ(·)为Dirac冲击函数;*为卷积符号;F为原始的频率域实值信号。
通过将VMD方法的变分优化框架(式(7))拓展至复数空间,而复数空间正弦信号的傅里叶频谱是单边的,因此式(7)改写为
| $ \mathop {\min }\limits_{\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\}} \left\{ {\sum\limits_{k = 1}^K {\left\| {{\partial _x}\left[ {{u_k}(x)} \right]{{\rm{e}}^{ - {\rm{i}}{\omega _k}x}}} \right\|_2^2} } \right\},且满足\;\sum\limits_{k = 1}^K {{u_k}} = F $ | (8) |
为求解式(8)中变分问题,采用增广Lagrange函数[14]计算其最优解。通过引入二次惩罚因子α和拉格朗日乘法算子λ,将约束性变分问题转换为非约束性变分形式
| $ \begin{array}{*{20}{c}} {L\left( {\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\},\lambda } \right): = \alpha \sum\limits_{k = 1}^K {\left\| {{\partial _x}\left[ {{u_k}(x)} \right]{{\rm{e}}^{ - {\rm{i}}{\omega _k}x}}} \right\|_2^2} + }\\ {\left\| {F - \sum\limits_{k = 1}^K {{u_k}} (x)} \right\|_2^2 + \left\langle {\lambda ,F - \sum\limits_{k = 1}^K {{u_k}} (x)} \right\rangle } \end{array} $ | (9) |
式中:L(·)表示目标函数;“:”是一个函数的标记;〈·, ·〉表示內积;二次惩罚因子α是控制数据保真度的均衡参数,用于平衡变分正则项和二次约束项,在含噪声情形时可保证信号重构精度;λ可以保证模型约束条件的严格性。
采用交替方向乘子算法(Alternate Direction Method of Multipliers,ADMM)[22]求解式(9),具体步骤如下:
(1) 初始化uk(1)、ωk(1)、λ(1),n=0;
(2) n=n+1,执行主循环;
(3) For k=1:K-1,执行第一个内循环更新uk
| $ u_k^{(n + 1)} \leftarrow \arg \mathop {\min }\limits_{{u_k}} L\left( {\left\{ {u_{i < k}^{(n + 1)}} \right\},\left\{ {u_{i \ge k}^{(n)}} \right\},\left\{ {\omega _i^{(n)}} \right\},{\lambda ^{(n)}}} \right) $ | (10) |
式中arg min表示函数L(·)达到最小时ukn+1的值。
(4) k=K,结束第一个内循环;
(5) For k=1:K-1,执行第二个内循环更新ωk
| $ \omega _k^{(n + 1)} \leftarrow \arg \mathop {\min }\limits_{{\omega _k}} L\left( {\left\{ {u_i^{(n + 1)}} \right\},\left\{ {\omega _{i < k}^{(n + 1)}} \right\},\left\{ {\omega _{i \ge k}^{(n)}} \right\},{\lambda ^{(n)}}} \right) $ | (11) |
(6) k=K,结束第二个内循环;
(7) 对于所有ωk>0, k∈[1, K],双重对偶上升,更新λ
| $ \lambda^{(n+1)} \leftarrow \lambda^{(n)}+\tau\left(f-\sum\limits_{k=1}^{K} u_{k}^{(n+1)}\right) $ | (12) |
式中τ表示噪声容限参数。在噪声压制任务中(而不是信号的重构),更新参数τ=0以得到更好的去噪效果;
(8) 给定判定精度ε>0, k∈[1, K],重复步骤(2)~(7),直至满足迭代停止条件
| $ \sum\limits_{k=1}^{K} \frac{\left\|u_{k}^{(n+1)}-u_{k}^{(n)}\right\|_{2}^{2}}{\left\|u_{k}^{(n)}\right\|_{2}^{2}}<\varepsilon $ | (13) |
(9) 结束迭代,即得到K个带限BIMF分量。
从上述步骤可知,ADMM的求解过程包含VMD的模态和频率中心更新。其中,ωk的更新由对应模态的能量谱重新得到,uk模态更新对应于1/βω2的Wiener滤波器结构(β为白噪声方差,1/ω2表示信号的能量谱为低通形式)。参数α控制着Wiener滤波器的宽度,本文称为保真度均衡参数。增大α值,Wiener滤波器宽度变窄,可以滤除更多的噪声,但也使得BIMF分量包含更少的真实信号峰值信息,同时算法趋于发散不收敛的几率增加,反之亦然。式(7)的增广Lagrange函数形式与Tikhonov正则一致,具有保真项和正则项。其中,VMD方法中分解的带限BIMF分量具有明显的稀疏特性,因而正则项可用稀疏先验。α与正则参数类似,用于控制保真项和正则项的权重,使BIMF模态分量的更新公式(式(10)~式(12))具备Wiener滤波特性,这正是VMD方法具有较强抗噪性能的关键因素。
2.3 基于VMD的二维地震信号去噪方法根据上述理论,基于VMD方法的二维地震信号随机噪声压制处理算法流程如下:
(1) 选择一个时间窗口将原始含噪地震信号d(x, t)作傅里叶变换至f-x域;
(2) 对每一个频率切片数据进行复数VMD分解;
(3) 将VMD分解得到的BIMF分量组合得到滤波后的信号;
(4) 将信号作傅里叶逆变换回t-x域;
(5) 对下一个时间窗口重复以上操作,地震记录全部处理完毕后,即得到最终的二维地震去噪结果。
2.4 基于VMD的三维地震信号去噪方法在三维地震数据中,平面波可表示为
| $ d(t,\mathit{\boldsymbol{x}}) = w\left( {t - \frac{{\langle \mathit{\boldsymbol{x}},\mathit{\boldsymbol{n}}\rangle }}{c}} \right) $ | (14) |
式中:x=(m, h)为中心点和炮检距坐标;n为波的传播单位方向。三维地震模型的频率切片Df是由沿n方向的一个f-m-h域复谐波模式组成。将d(t, x)沿时间轴上作傅里叶变换得到f-m-h谱,每个频率切片数据即为Df。相应地t-m-h域中p个平面波的叠加与f-m-h域中p个复谐波叠加等效。本文将二维VMD拓展到复值,拓展后的目标优化函数为
| $ \mathop {\min }\limits_{\left\{ {{u_k}} \right\},\left\{ {{v_k}} \right\}} \left\{ {\sum\limits_{k = 1}^K {\left\| {\nabla \left[ {{u_k}(\mathit{\boldsymbol{x}}){{\rm{e}}^{ - {\rm{i}}\left( {{\mathit{\boldsymbol{v}}_k},\mathit{\boldsymbol{x}}} \right)}}} \right]} \right\|_2^2} } \right\},且满足\;\sum\limits_{k = 1}^K {{u_k}} = F $ | (15) |
式中vk为二维平面的波数向量。与一维VMD求解类似,通过引入二次惩罚和拉格朗日乘数(增广Lagrange)重建约束变分框架,由ADMM优化求解,二维VMD的三维地震随机噪声压制算法步骤如下:
(1) 选择一个时间窗口将原始含噪地震信号d(m, h, t)作傅里叶变换至f-m-h域;
(2) 对每一个频率切片数据进行二维复数VMD分解;
(3) 组合VMD分解的BIMF分量得到滤波后的信号;
(4) 将信号作傅里叶逆变换回t-m-h域;
(5) 对下一个时间窗口重复以上操作;
(6) 地震记录全部处理完毕后,即得到最终的三维地震去噪结果。
3 算例 3.1 VMD参数优选VMD变分模型目标函数是非凸的,算法的收敛性与参数的设置有密切联系,有三个重要参数,即带限BIMF分量个数K、ωk和α。其中,K依据BIMF分量瞬时频率均值的极大值点确定;ωk采用匹配追踪算法(Matching Pursuits,MP)[23]确定;α与原始信号的噪声水平有关,用来控制保真项和正则项的权重,本文采用“L”曲线法则确定α。为验证VMD方法的有效性,本文将三个不同中心频率余弦信号累加构成合成信号s(t)
| $ \left\{ \begin{array}{l} {s_i}(t) = \cos \left( {2{\rm{ \mathsf{ π} }}{f_i}t} \right)\;\;\;\;{f_i} = 2,24,288(i = 1,2,3)\\ s(t) = \sum\limits_{i = 1}^3 {{s_i}} (t) \end{array} \right. $ | (16) |
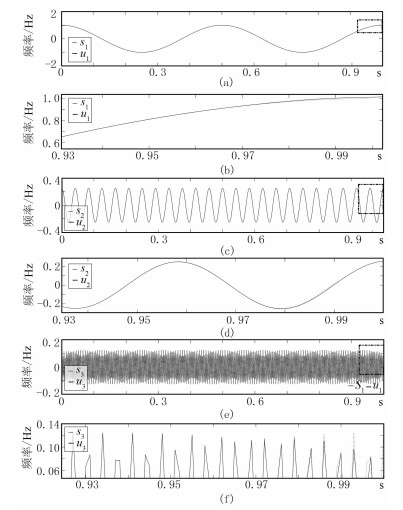
图 1a、图 1c、图 1e显示了合成信号s(t)经VMD分解得到的3个BIMF分量信号,图 1b、图 1d、图 1f分别为上述相应的BIMF分量信号局部放大结果。从分解结果可以看出,各个BIMF分量信号与原始组分信号几乎一致,仅在信号两端点处出现微小误差。
|
图 1 各组分信号及VMD分解BIMF分量 (a)、(c)、(e)为各组分信号及VMD分解对应BIMF分量;(b)、(d)、(f)为相应点线矩形框内的局部放大信号。si、ui为各信号分量 |
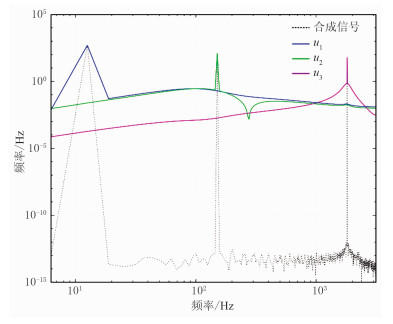
图 2为原始合成信号的频谱分布与VMD分解后的3个BIMF分量信号的频谱图(双对数坐标),每个重构BIMF模态分量的频谱都有一个最高峰值,对应其中心频率,与原始信号的期望中心频率2、24、288Hz高度一致(非等间距横坐标),VMD分解得到的3个BIMF分量均能成功捕捉对应中心频率。
|
图 2 VMD分解各模态频谱分布 |
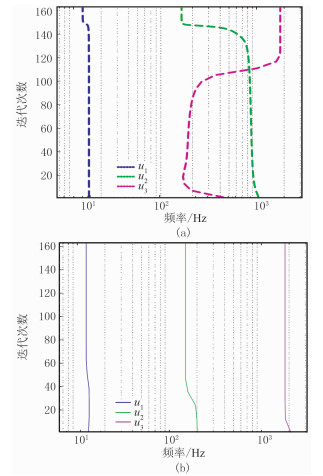
图 3为分解各模态信号的频率中心随迭代次数的变化曲线(半对数坐标)。由图可见,图 3a迭代更新过程较慢,在150次后才找到最优的中心频率,而图 3b经3次迭代即可获得最佳频率中心分布。
|
图 3 VMD分解各模态频率中心变化 (a)0值初始化ωk; (b)匹配追踪初始化ωk |
图 4是一组由四个线性事件组成的合成地震数据、加噪数据及其对应的f-x频谱图、f-k频谱图。对图 4b中第40个采样点切片含噪数据作VMD分解,结果如图 5所示。设置参数α=2000,K=4,以匹配追踪算法初始化ωk分解得到四个近似谐波信号,各个BIMF分量的频谱与原始信号的频谱峰值高度一致。
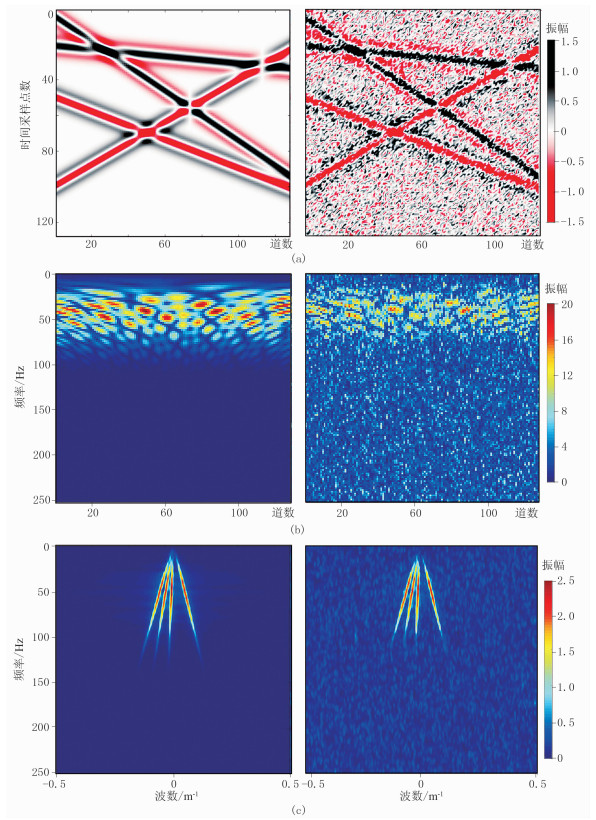
|
图 4 合成地震数据(左)及加噪数据(右)频谱对比 (a)原始数据;(b)f-x域;(c)f-k域 |
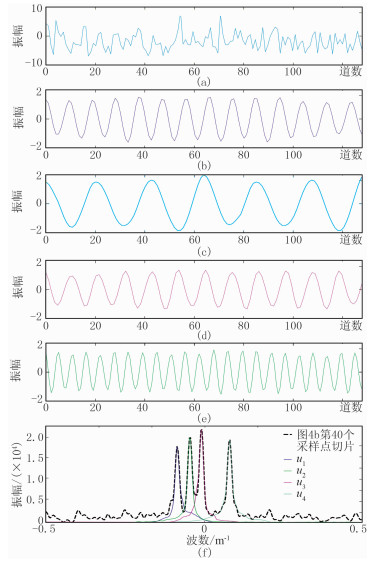
|
图 5 含噪f-x谱第40个采样点切片数据作VMD分解 (a)图 4b右图中第40个采样点切片数据;(b~e)由图a信号VMD分解得到的u1~u4BIMF分量;(f)图a~图e信号的波数谱 |
本文采用信噪比(SNR)、局部相似度(Local Similarity,LS)[24]、结构相似度(Structural Simila-rity Index,SSIM)[25]评价算法的有效性。局部相似度定义为
| $ \mathrm{LS}=\sqrt{c_{1}^{\mathrm{T}} c_{2}} $ | (17) |
式中:T表示转置;c1、c2通过最小二乘问题最小化得到
| $ {c_1} = \arg \mathop {\min }\limits_{{c_1}} \left\| {\mathit{\boldsymbol{a}} - \mathit{\boldsymbol{B}}{c_1}} \right\|_2^2 $ | (18) |
| $ {c_2} = \arg \mathop {\min }\limits_{{c_2}} \left\| {\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{A}}{c_2}} \right\|_2^2 $ | (19) |
式中:a和b为矩阵;A、B分别为a、b构成的对角算子。LS值变化范围为[0, 1],LS值越大表示去噪结果与噪声剖面的局部相似程度越高,有效能量泄漏越严重,算法的幅值保持能力越差。
结构相似度定义为
| $ \operatorname{SSIM}(x, y)=\frac{\left(2 \mu_{x} \mu_{y}+C_{1}\right)\left(2 \sigma_{x y}+C_{2}\right)}{\left(\mu_{x}^{2}+\mu_{y}^{2}+C_{1}\right)\left(\sigma_{x}^{2}+\sigma_{y}^{2}+C_{2}\right)} $ | (20) |
式中:μx、μy分别表示图像x、y的均值;σx、σy分别表示图像x、y的标准差;σx、σy分别表示图像x、y的方差;σxy代表图像x和y的协方差;C1、C2为常数,C1=(k1L)2,C2=(k2L)2,L为像素动态范围,一般k1=0.01、k2=0.03、L=255;SSIM值变化范围为[0, 1],值越大表示两个图像的结构相似程度越高,去噪性能越强。
图 6表示一个含有多层倾斜地层、一个不整合面、一条断层和多套正弦起伏形态地层组成的理论合成地震记录Sigmoid模型[26],含256道,每道有256个时间采样。为验证VMD方法的有效性,本文将VMD与Curvelet(曲波)、NLM(非局部均值)、BM 3D(三维块匹配)、CEEMD四种方法进行对比。
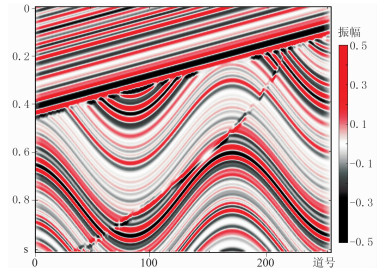
|
图 6 合成地震记录Sigmoid模型 |
在本实验中,VMD方法中K=4,α=2000,ωk初始化采用匹配追踪方法,时间轴窗口长度取64个采样点,空间轴窗口长度取64道,时间轴和空间轴的滑动步长重叠度均设置为50%;CEEMD方法集总次数I取100;Curvelet、NLM和BM3D三种方法采用工具包中的默认参数。算法运行平台参数为MATLAB 2017a Parallel Pool×8、Win 10×64、i7-7700K CPU 4.2GHz。
图 7a~图 7f左图为地震数据加噪后用不同方法去噪的结果,右图为相应的噪声剖面局部相似度。由图可知,五种方法均达到一定的去噪效果,但Curvelet方法去噪结果有一定的变形,在正弦状起伏的强反射同相轴周围发生明显伪影现象,断层现象不明显,弱反射同相轴连续性差,对应的局部相似度图表明有效能量泄漏明显(图 7b);NLM去噪结果中仍保留有肉眼可视的噪声信息,对应的局部相似度图表明线性和双曲线有效能量均出现泄漏,对原图像的结构信息保护不够,这与NLM算法中在计算图像块相似性时只考虑块的平移特性有关(图 7c);相对Curvelet和NLM方法,CEEMD方法在SNR数值上有些提升,但去噪结果中仍保留部分噪声信息,断层部分尚可辨识,对应的局部相似度图在正弦状起伏的强反射同相轴有些许能量损失(图 7d);BM 3D方法的去噪效果较好,但也可见部分低能量有效信号被当做噪声被去除(图 7e);VMD的去噪结果中SNR提升最为明显,优于其余四种方法,合成模型中的倾斜、正弦状起伏地层以及断层位置都得到了很好的保留,噪声得到有效压制,视觉表现上与原始无噪模型最为接近。对比局部相似度图可知,VMD方法有效能量泄漏程度最轻微,保真度性能最好(图 7f)。
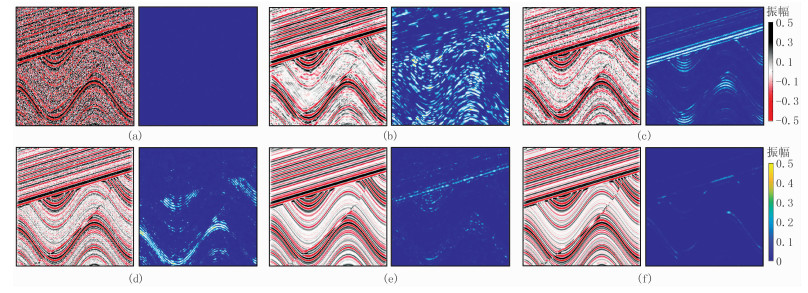
|
图 7 Sigmoid模型五种方法去噪结果(左)及相应的局部相似度(右) (a)20%高斯白噪声加噪数据(SNR=-2.82dB);(b)Curvelet去噪(SNR=7.77dB);(c)NLM去噪(SNR=8.36dB);(d)CEEMD去噪(SNR=9.41dB);(e)BM 3D去噪(SNR=11.42dB);(f)VMD去噪(SNR=14.73dB) |
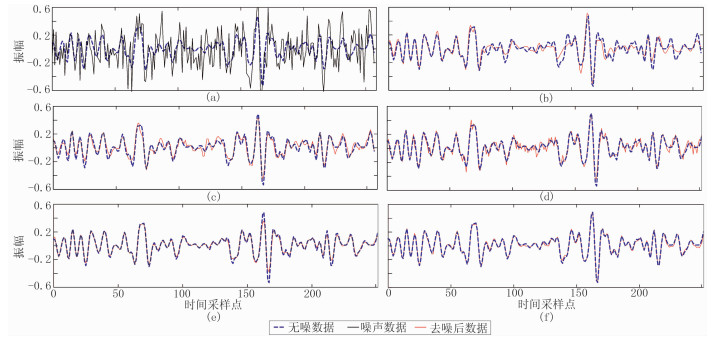
图 8给出了五种方法的第175道信号去噪结果对比,可以看出VMD去噪结果与无噪信号最为接近。因此,VMD方法在去除强噪声的同时,可最大程度的减少有效地震能量的损失。
|
图 8 Sigmoid模型五种方法第175道去噪结果对比 (a)含噪信号;(b)Curvelet去噪;(c)NLM去噪;(d)CEEMD去噪;(e)BM 3D去噪;(f)VMD去噪 |
Curvelet、NLM、BM 3D、CEEMD和VMD五种方法处理耗时分别为0.724、11.291、181.039、2.207和2.513s,Curvelet去噪处理效率最高,BM3D处理效率最低。
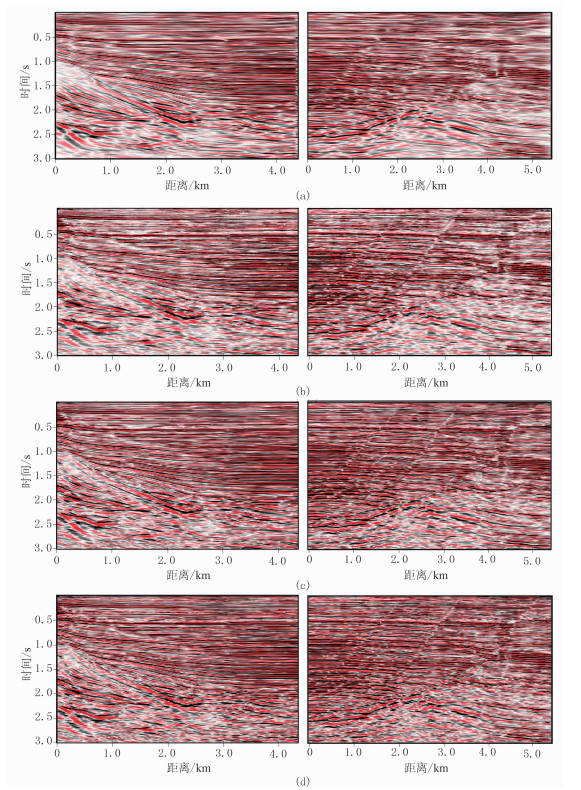
3.3 三维地震去噪实例处理效率是考虑算法是否适用的重要指标,在三维甚至五维地震资料的随机噪声压制处理中,尤其需考虑计算耗时。本文将Curvelet 3D、NLM 3D、BM 4D和二维VMD(VMD 2D)四种方法运用于三维实际含噪地震数据处理。取某地随机噪声分布较多的三维叠后实际资料,数据尺度为221×271×752(依次表示x、y和时间三个方向的采样点数),采样间隔分别为20m和4ms。取实际数据x、y方向的第100个切片,如图 9所示。
|
图 10 三维实际资料去噪结果 (a)Curvelet 3D;(b)NLM 3D;(c)BM 4D;(d)VMD 2D |
|
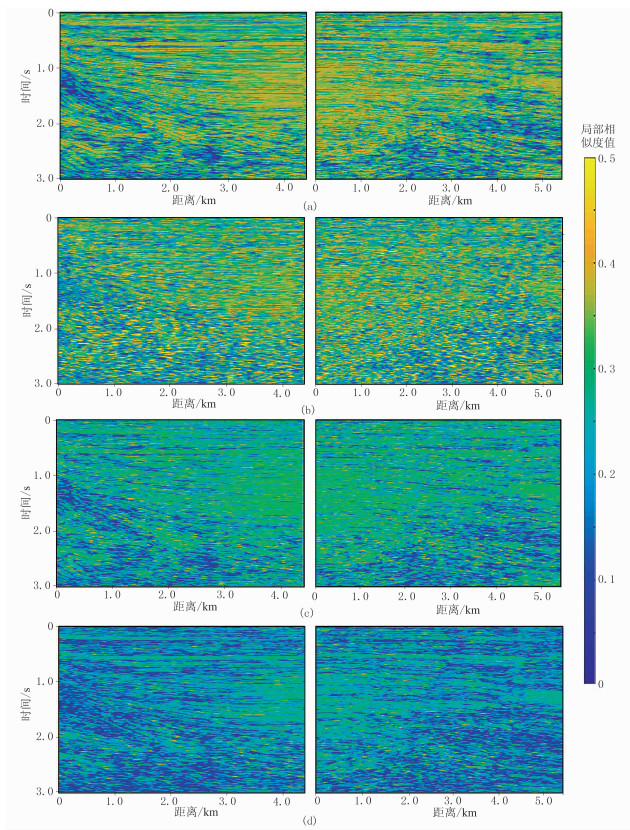
图 11 三维实际资料去噪后噪声剖面的局部相似度 (a)Curvelet 3D;(b)NLM 3D;(c)BM 4D;(d)VMD 2D |
图 10为四种方法去噪结果,图 11为相应的噪声剖面局部相似度图,去噪结果与噪声剖面的局部相似程度越高,表明有效能量泄漏越严重。对比各图可知,Curvelet 3D方法去噪结果过于平滑,同相轴边缘细节信息模糊,较难辨别,对应局部相似度表现较多的有效能量损失;NLM 3D方法去噪结果中局部块状细节消失,可见部分噪声依然分布于去噪结果中,对应局部相似度出现较多的局部高异常区域;BM 4D方法的去噪效果有所改善,剖面视觉效果较好,局部相似度表现为有效信息损失少;本文二维VMD 2D方法的去噪结果最优,剖面上同相轴细节、断裂走向清晰,局部相似度呈低能均匀分布,有效同相轴信息丢失最少。
Sigmoid模型和实际资料的去噪结果数值统计如表 1所示,可见Curvelet方法的SNR数值提升最小,但时间效率最高;CEEMD方法处理耗时最长;与CEEMD递归式模态分解方法不同,VMD在变分框架约束下一次性求解得到所有带限BIMF分量,在SNR和SSIM指标上均达最优,去噪结果与原始无噪信号在细节上最为接近。由于在匹配追踪优化下快速定位到频率中心,VMD方法时间效率高于NLM、CEEMD和BM 3D方法。三维实际地震资料的去噪结果LS同样验证其有效性。因此,VMD方法具备优异的噪声压制、幅值保持性能的同时,还有具有较高的计算效率,可以满足实时处理要求。
|
|
表 1 去噪结果统计 |
本文在EMD信号分解理论基础上,提出了在频率域内复数VMD方法。通过将信号分解过程转移到变分框架内,引入增广Lagrange函数迭代求解各分量的频率中心及带宽参数,生成窄带约束模态分量,使VMD方法在噪声压制和有效能量保持间寻求最优平衡。实验结果表明,在二维地震数据的随机噪声压制处理方面,与CEEMD、Curvelet、NLM和BM 3D方法相比,VMD方法在SNR、SSIM和视觉效果方面均保持最优趋势,处理后同相轴细节变得清晰连续,微弱信号被有效保留;在三维地震数据的随机噪声压制处理方面,与Curvelet 3D、NLM 3D和BM 4D方法相比,VMD方法具备优异的噪声压制性能且计算效率高。
| [1] |
Chen K, Sacchi M D. Robust f-x projection filtering for simultaneous random and erratic seismic noise attenuation[J]. Geophysical Prospecting, 2017, 65(3): 650-668. DOI:10.1111/1365-2478.12429 |
| [2] |
李宇, 韩立国, 叶林, 等. 基于F-K域和Curvelet-中值滤波联合去噪的混采数据分离方法[J]. 世界地质, 2017, 36(2): 609-615. LI Yu, HAN Liguo, YE Lin, et al. Blended acquisition data separation method based on F-K domain and Curvelet-median filter joint denoising[J]. Global Geo-logy, 2017, 36(2): 609-615. DOI:10.3969/j.issn.1004-5589.2017.02.028 |
| [3] |
Mao J, Gao J, Chen W. On the denoising method of prestack seismic data in wavelet domain[J]. Chinese Journal of Geophysics, 2006, 25(1): 1155-1163. |
| [4] |
勾福岩, 刘财, 刘洋, 等. 基于OC-Seislet变换的海洋涌浪噪声衰减方法[J]. 吉林大学学报(地球科学版), 2015, 45(3): 962-970. GOU Fuyan, LIU Cai, LIU Yang, et al. Swell noise attenuation methods based on OC-Seislet transform[J]. Journal of Jilin University (Earth Science Edition), 2015, 45(3): 962-970. |
| [5] |
张华, 陈小宏, 李红星, 等. 曲波变换三维地震数据去噪技术[J]. 石油地球物理勘探, 2017, 52(2): 226-232. ZHANG Hua, CHEN Xiaohong, LI Hongxing, et al. 3D seismic data de-noising approach based on Curvelet transform[J]. Oil Geophysical Prospecting, 2017, 52(2): 226-232. |
| [6] |
张岩, 任伟建, 唐国维. 利用多道相似组稀疏表示方法压制随机噪声[J]. 石油地球物理勘探, 2017, 52(3): 442-450. ZHANG Yan, REN Weijian, TANG Guowei. Random noise suppression based on sparse representation of multi-trace similarity group[J]. Oil Geophysical Prospecting, 2017, 52(3): 442-450. |
| [7] |
邵婕, 孙成禹, 唐杰, 等. 基于字典训练的小波域稀疏表示微地震去噪方法[J]. 石油地球物理勘探, 2016, 51(2): 254-260. SHAO Jie, SUN Chengyu, TANG Jie, et al. Micro-seismic data denoising based on sparse representations over learned dictionary in the wavelet domain[J]. Oil Geophysical Prospecting, 2016, 51(2): 254-260. |
| [8] |
张恒磊, 胡哲, 胡祥云, 等. 基于反射波各向异性特征的保真去噪方法[J]. 石油地球物理勘探, 2017, 52(2): 233-241. ZHANG Henglei, HU Zhe, HU Xiangyun, et al. Seismic fidelity denoising with reflection anisotropy[J]. Oil Geophysical Prospecting, 2017, 52(2): 233-241. |
| [9] |
Liu W, Cao S, Chen Y, et al. An effective approach to attenuate random noise based on compressive sensing and curvelet transform[J]. Journal of Geophysics & Engineering, 2016, 13(2): 135-145. |
| [10] |
Cheng J, Sacchi M D. Separation and reconstruction of simultaneous source data via iterative rank reduction[J]. Geophysics, 2015, 80(4): 57-66. |
| [11] |
Zhang D, Zhou Y, Chen H, et al. Hybrid rank-sparsity constraint model for simultaneous reconstruction and denoising of 3D seismic data[J]. Geophysics, 2017, 82(5): V351-V367. DOI:10.1190/geo2016-0557.1 |
| [12] |
Zhou Y T, Shi C J, Chen H M, et al. Spike-like blending noise attenuation using structural low-rank decomposition[J]. IEEE Geoscience & Remote Sensing Letters, 2017, 14(9): 1633-1637. |
| [13] |
Chen Y K, Zhou Y T, Chen W, et al. Empirical low-rank approximation for seismic noise attenuation[J]. IEEE Transactions on Geoscience & Remote Sensing, 2017, 55(8): 4696-4711. |
| [14] |
颜中辉, 栾锡武, 王赟, 等. 基于经验模态分解的分数维地震随机噪声衰减方法[J]. 地球物理学报, 2017, 60(7): 2845-2857. YAN Zhonghui, LUAN Xiwu, WANG Yun, et al. Seismic random noise attenuation based on empirical mode decomposition of fractal dimension[J]. Chinese Journal of Geophysics, 2017, 60(7): 2845-2857. |
| [15] |
Chen W, Chen Y, Liu W. Ground roll attenuation using improved complete ensemble empirical mode de-composition[J]. Journal of Seismic Exploration, 2016, 25(5): 485-495. |
| [16] |
Chen W, Xie J Y, Zu S H, et al. Multiple-reflection noise attenuation using adaptive randomized-order empirical mode decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(1): 18-22. DOI:10.1109/LGRS.2016.2622918 |
| [17] |
Huang N E, Zheng S, Long S R, et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C].Proceedings Mathematical Physical & EngineeringSciences, 1998, 454(1971): 903-995.
|
| [18] |
Wu Z, Huang N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. |
| [19] |
Torres M E, Colominas M A, Schlotthauer G, et al.A complete ensemble empirical mode decomposition with adaptive noise[C].IEEE international Conference on Acoustics, Speech and Signal Processing (ICASSP), 2011: 4144-4147.
|
| [20] |
Dragomiretskiy K.Variational Methods in Signal Decomposition and Image Processing[D].UCLA, University of California, Los Angeles, 2015.
|
| [21] |
Hestenes M R. Multiplier and gradient methods[J]. Journal of Optimization Theory & Applications, 1969, 4(5): 303-320. |
| [22] |
Powell M J D. A method for nonlinear constraints in minimization problems[J]. Optimization, 1969, 5(6): 283-298. |
| [23] |
Mallat S G, Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [24] |
Fomel S. Local seismic attributes[J]. Geophysics, 2007, 72(3): A29-A33. DOI:10.1190/1.2437573 |
| [25] |
Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment:from error visibility to structural simila-rity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
| [26] |
Claerbout J, Black J L, Biondi B. Basic Earth Imaging[M]. Stanford University, 2001.
|



 方江雄, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email:
方江雄, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email: