海水鸣震是海洋地震资料处理中最大的噪声干扰。海底电缆(OBC)水、陆检资料合并处理的最大优点就是能够有效去除海水鸣震干扰[1-6]。由同一位置处水检和陆检记录相同的海水鸣震,其相位相反,通过适当的合并与组合,既能够去除海水鸣震,还能够去除接收点虚反射[7-14]。水、陆检资料合并处理要求陆检与对应的水检数据振幅和能量匹配,即海水鸣震同相轴具有相同的幅度[15-18]。对强海水鸣震干扰,简单合并处理不能有效去除。基于Backus海水鸣震逆滤波器的方法,可有效去除强海水鸣震干扰[19-20]。海水深度、海水速度和海底反射系数是Backus海水鸣震逆滤波器的重要参数[21-24]。因此,估算海水深度是海上OBC资料处理消除鸣震干扰技术的关键。
确定海水深度常用方法是基于上、下行波场数据互相关方法。上、下行波场数据互相关函数最大值所对应的延迟时间就是地震波场在海水中的双程旅行时间,在垂直入射情况下,海水双程旅行时间对应的深度就是海水深度。因此,使用共检波点道集近炮检距水、陆检数据可以估算海水深度[20]。但大量的自相关和互相关计算非常费时。实际水、陆检资料中,存在各种噪声,且有效带宽不同,低频和高频噪声分布也不同,特别是陆检数据包含着较强的低频面波。另外,叠前资料包含振幅较强的干扰波,互相关也包含噪声成分,因此计算的海水深度存在较大误差。高少武等[25-26]提出了基于功率谱的海水深度估算方法,功率谱是二阶统计量,对平稳高斯噪声有一定的压制效果,但不能压制非高斯噪声。
基于高阶统计量的互双谱能抑制高斯和非高斯噪声[27-29],因此提出了利用数据分段互双谱直接计算海水深度的方法。该方法通过对水、陆检数据分段,计算分段的上、下行波场数据及其功率谱;再计算分段的上行波场数据自双谱和上、下行波场数据互双谱;然后计算各段数据的功率谱、自双谱、互双谱的平均谱;最后计算水、陆检数据的相干互双谱和互相关谱,由互相关谱确定海水深度。将本文方法计算的海水深度用于水、陆检数据合并处理,不但能消除海水鸣震多次波干扰,而且保留了陆检数据低频成分和水检数据高频成分,有效拓宽了OBC资料有效带宽,提高了地震资料信噪比和分辨率。实际数据处理结果验证了方法的有效性和实用性。
1 方法原理水中检波器记录压力波场,构成水检数据;陆地检波器记录垂直位移速度,构成陆检数据。将共检波点道集水、陆检数据分段为
| $ \left\{ {\begin{array}{*{20}{l}} {{h_{j,1}}(n) = {H_j}(n)}\\ {{g_{j,1}}(n) = {G_j}(n)}\\ {{h_{j,i}}(n) = {H_j}\left[ {(i - 1)\left( {{N_{\rm{L}}} - {N_{\rm{Q}}}} \right) + n} \right]}\\ {{g_{j,i}}(n) = {G_j}\left[ {(i - 1)\left( {{N_{\rm{L}}} - {N_{\rm{Q}}}} \right) + n} \right]} \end{array}} \right. $ | (1) |
式中:hj,i(n)和gj,i(n)分别是共检波点道集第j道第i段水、陆检数据;Hj(n)和Gj(n)分别是共检波点道集第j道水、陆检数据;i=1、2、…、IL,IL为数据段数;j=1、2、…、JL,JL为共检波点道集数据道数;n=1、2、…、NL,NL为每段样点数;NQ为段间重叠数据样点数。IL、NL、NQ与每道总样点数NN满足
| $ \left\{ {\begin{array}{*{20}{l}} {{I_{\rm{L}}} = {\mathop{\rm INT}\nolimits} \left( {\frac{{{N_{\rm{N}}}}}{{{N_{\rm{L}}}}}} \right) + 1}\\ {{N_{\rm{Q}}} = {\mathop{\rm INT}\nolimits} \left( {\frac{{{N_{\rm{L}}}{I_{\rm{L}}} - {N_{\rm{N}}}}}{{{I_{\rm{L}}} - 1}}} \right) + 1} \end{array}} \right. $ | (2) |
式中INT(·)为取整函数,且NL<NN。
基于压力波场和位移速度波场的波动方程,上行波场数据是水检与陆检数据之和,下行波场数据是水检与陆检数据之差[1-2]。上、下行波场分段数据可表示为
| $ u_{j, i}(n)=h_{j, i}(n)+g_{j, i}(n) $ | (3) |
| $ d_{j, i}(n)=h_{j, i}(n)-g_{j, i}(n) $ | (4) |
利用上、下行波场分段数据的傅里叶变换Uj,i(k)和Dj,i(k)计算上、下行波场数据的分段功率谱
| $ P_{j, i}(k)=U_{j, i}(k) U_{j, i}^{*}(k) $ | (5) |
| $ Q_{j, i}(k)=D_{j, i}(k) D_{j, i}^{*}(k) $ | (6) |
式中:上标“*”表示复共轭运算;k=1、2、…、NK,NK为傅里叶变换正半支长度。上、下行波场平均功率谱分别为
| $ P(k) = \sum\limits_{j = 1}^{{J_{\rm{L}}}} {\sum\limits_{i = 1}^{{I_{\rm{L}}}} {{P_{j,i}}} } (k) $ | (7) |
| $ Q(k) = \sum\limits_{j = 1}^{{J_{\rm{L}}}} {\sum\limits_{i = 1}^{{I_{\rm{L}}}} {{Q_{j,i}}} } (k) $ | (8) |
计算分段数据的上行波场自双谱和上、下行波场互双谱
| $ {A_{j,i}}\left( {{k_1},{k_2}} \right) =\\ \left\{ {\begin{array}{*{20}{c}} {{U_{j,i}}\left( {{k_1}} \right){U_{j,i}}\left( {{k_2}} \right)U_{j,i}^*\left( {{k_1} + {k_2} - 1} \right)}&{2 \le {k_1} + {k_2} \le {N_{\rm{K}}} + 1}\\ {{U_{j,i}}\left( {{k_1}} \right){U_{j,i}}\left( {{k_2}} \right)U_{j,i}^*\left( {{k_1} + {k_2} - 1 - {N_{\rm{K}}}} \right)}&{{N_{\rm{K}}} + 1 < {k_1} + {k_2} \le 2{N_{\rm{K}}}} \end{array}} \right. $ | (9) |
| $ {B_{j,i}}\left( {{k_1},{k_2}} \right) =\\ \left\{ {\begin{array}{*{20}{c}} {{D_{j,i}}\left( {{k_1}} \right){U_{j,i}}\left( {{k_2}} \right)U_{j,i}^*\left( {{k_1} + {k_2} - 1} \right)}&{2 \le {k_1} + {k_2} \le {N_{\rm{K}}} + 1}\\ {{D_{j,i}}\left( {{k_1}} \right){U_{j,i}}\left( {{k_2}} \right)U_{j,i}^*\left( {{k_1} + {k_2} - 1 - {N_{\rm{K}}}} \right)}&{{N_{\rm{K}}} + 1 < {k_1} + {k_2} \le 2{N_{\rm{K}}}} \end{array}} \right. $ | (10) |
式中k1、k2=1、2、…、NK。上行波场的平均自双谱和上、下行波场的平均互双谱分别为
| $ A\left( {{k_1},{k_2}} \right) = \sum\limits_{j = 1}^{{J_{\rm{L}}}} {\sum\limits_{i = 1}^{{I_{\rm{L}}}} {{A_{j,i}}} } \left( {{k_1},{k_2}} \right) $ | (11) |
| $ B\left( {{k_1},{k_2}} \right) = \sum\limits_{j = 1}^{{J_{\rm{L}}}} {\sum\limits_{i = 1}^{{I_{\rm{L}}}} {{B_{j,i}}} } \left( {{k_1},{k_2}} \right) $ | (12) |
则水、陆检数据的相干互双谱为
| $ C\left(k_{1}, k_{2}\right)=\frac{B\left(k_{1}, k_{2}\right)}{A\left(k_{1}, k_{2}\right)} $ | (13) |
水、陆检数据互相关谱为
| $ R(k)=\sqrt{\frac{P(k)}{Q(k)}} \sum\limits_{l=1}^{N_{\mathrm{K}}} C(k, l) $ | (14) |
互相关谱逆傅里叶变换就是互相关函数r(n),其中n=1、2、…、NR,NR是互相关函数长度。
确定互相关函数最大值位置
| $ m=\max\limits _{m \in\left[1, N_{\mathrm{R}}\right]}\left[r(1), r(2), \cdots, r\left(N_{\mathrm{R}}\right)\right] $ | (15) |
由m可计算海水双程旅行时间τ
| $ \tau=m \Delta t $ | (16) |
式中Δt为时间采样间隔。则海水深度为
| $ H=\frac{1}{2} v \tau $ | (17) |
式中v为海水速度。
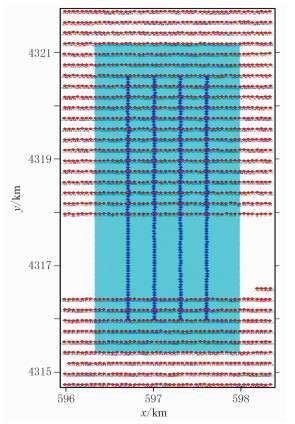
2 数据试算利用实际海上采集的OBC数据在水、陆检合并处理前反演海水深度。图 1是实际现场OBC数据采集时的观测系统。图 2是原始陆检、水检炮集数据,其中炮点位于(597.8410km,4319.5667km),接收线为图 1左边第1条线,共92个接收点。水检与陆检数据差异很大,水检数据包含较强的海水鸣震干扰。
|
图 1 OBC野外采集观测系统 红色圆点为炮点;蓝色圆点为接收点 |
|
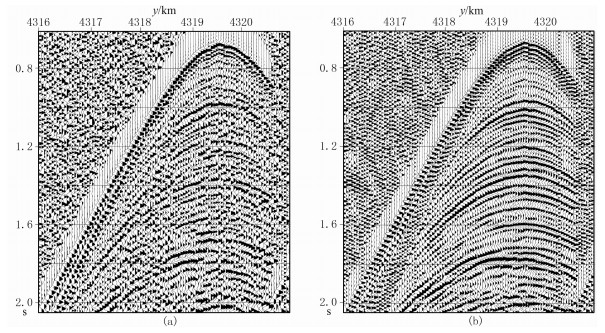
图 2 原始陆检(a)、水检(b)炮集数据 |
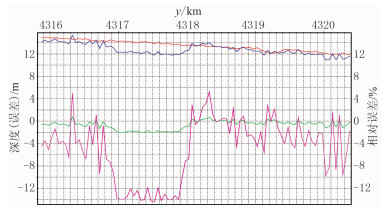
直接使用原始采集的水、陆检数据根据观测系统进行参数估算和合并处理。图 3是计算与实测海水深度对比(测线为图 1左边第1条接收线),绝对平均误差小于1.5m,平均相对误差小于10%,而较大误差是由于覆盖次数低引起的(即图 1缺炮部位)。
|
图 3 反演与实测海水深度对比 红色:实测;蓝色:反演;绿色:绝对误差;品红色:相对误差 |
使用本方法估计的海水深度,配合其他方法估算的标定因子和海底反射系数,进行合并处理,得到合并处理数据(图 4)。图 5为双检合并前、后的振幅谱对比,水检数据在频率60Hz附近包含较强的海水鸣震干扰,造成较强的频率凹陷;陆检数据没有明显的频率凹陷;合并数据明显补偿了水检数据频率凹陷,且吸收了陆检数据低频成分。图 6为双检合并前、后自相关函数对比,水检和陆检数据自相关函数旁瓣能量强,表现出较强的海水鸣震干扰,同时水检数据自相关函数的震荡也很强,表明包含较强的干扰,而合并后数据,明显消除了自相关函数旁瓣强能量和水检数据自相关函数的强震荡。

|
图 4 水、陆检合并后炮集数据 |

|
图 5 水、陆检数据合并前、后的振幅谱对比 蓝色:陆检;红色:水检;绿色:合并 |

|
图 6 自相关函数对比 (a)陆检;(b)水检;(c)合并 |
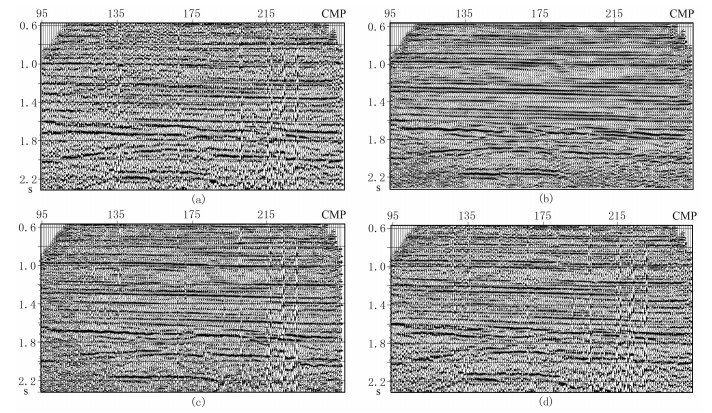
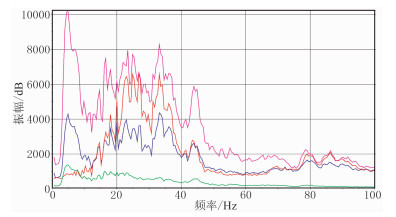
图 7为双检合并前后叠加剖面对比,其中常规剖面是使用现有合并技术的处理结果。图 8是图 7数据的频谱对比,常规处理振幅明显高于水检和陆检数据,且低频能量明显高于中频能量,说明常规方法水检和陆检数据合并处理并不合理;本文方法合合并后低频和中频能量一致,且位于水检和陆检数据能量之间。从叠加数据的频谱上,看不到水、陆检数据明显的频率凹陷,这是因为海底起伏,接收点位置深度不同,因而每一道数据频率凹陷位置处频率不同,叠加数据上频率凹陷互相补偿,不会产生明显频率凹陷。由合并前、后的双检记录、频谱和自相关函数可以看出,合并后数据有效压制了海水鸣震干扰,提高了OBC数据的信噪比,既保留了陆检数据低频成分,也保留了水检数据高频成分,因此拓宽了数据有效带宽,提高了OBC数据分辨率。
|
图 7 叠加数据对比 (a)陆检;(b)水检;(c)本文方法合并;(d)常规方法合并 |
|
图 8 叠加数据频谱对比 绿色:陆检;红色:水检;蓝色:本文方法合并;品红色:常规方法合并 |
总之,利用本方法反演的海水深度,用于双检数据合并能有效消除水层产生的干扰、提高OBC数据信噪比。
3 结论(1) 水检与陆检数据分段互双谱和相干互双谱的引入,使海水深度估算更加稳健和精确,是海底电缆水、陆检合并处理中一种有效的海水深度反演方法。
(2) 使用本文方法获得的海水深度进行水、陆检合并处理,能有效压制海底电缆水、陆检数据海水鸣震干扰,保留了陆检数据低频成分和水检数据高频成分,拓宽了海底电缆数据有效频带,提高了OBC数据信噪比和分辨率。
| [1] |
Barr F J and Sanders J I.Attenuation of water column reverberations using pressure and velocity detectors in a water-bottom cable[C].SEG Technical Program Expanded Abstracts, 1989, 8: 653-656.
|
| [2] |
Barr F J. Dual-sensor OBC technology[J]. The Lea-ding Edge, 1997, 16(1): 45-51. DOI:10.1190/1.1437427 |
| [3] |
Dragoset B, Barr F J.Ocean-bottom cable dual-sensor scaling[C].SEG Technical Program Expanded Abstracts, 1994, 13: 857-860.
|
| [4] |
高少武, 钱忠平, 马玉宁, 等. OBC水陆检数据合并处理技术[J]. 石油地球物理勘探, 2018, 53(4): 703-709. GAO Shaowu, QIAN Zhongping, MA Yuning, et al. OBC dual-sensor data combination processing[J]. Oil Geophysical Prospecting, 2018, 53(4): 703-709. |
| [5] |
高少武, 赵波, 罗国安, 等.一种水陆检波器地震数据合并处理的方法及装置[P].中国, ZL201510556940.3, 2015-09-02.
|
| [6] |
高少武, 赵波, 钱忠平, 等.一种水陆检波器地震数据合并处理的方法及装置[P].中国, 201710565184.X, 2017-7-12.
|
| [7] |
梁鸿贤, 秦宁, 高丽董. 海底电缆双检资料正演模拟及特征分析[J]. 地球物理学进展, 2017, 32(4): 1798-1802. LIANG Hongxian, QIN Ning, GAO Lidong. Numerical simulation and feature analysis of OBC dual sensor data[J]. Progress in Geophysics, 2017, 32(4): 1798-1802. |
| [8] |
赫建伟, 邓勇, 邓盾, 等. 基于非高斯性最大化的起伏海面环境下双检信号波场分离[J]. 石油地球物理勘探, 2018, 53(4): 694-702. HE Jianwei, DENG Yong, DENG Dun, et al. Dual-sensor signal wavefield separation based on non-Gaussianity maximum under undulation sea surface[J]. Oil Geophysical Prospecting, 2018, 53(4): 694-702. |
| [9] |
Max D, Ramesh N.OBC multiple suppression with the Texas two-step[C].SEG Technical Program Expanded Abstracts, 2005, 24: 2123-2126.
|
| [10] |
Soubaras R.Ocean bottom hydrophone and geophone processing[C].SEG Technical Program Expanded Abstracts, 1996, 15: 24-27.
|
| [11] |
Vaughn B, Dennis C.Dual-sensor summation of noisy ocean-bottom data[C].SEG Technical Program Expanded Abstracts, 1996, 15: 28-31.
|
| [12] |
王振华, 夏庆龙, 田立新, 等. 消除海底电缆双检地震资料中的鸣震干扰[J]. 石油地球物理勘探, 2008, 43(6): 626-635. WANG Zhenhua, XIA Qinglong, TIAN Lixin, et al. Elimination of singing interference in OBC dual-geophone seismic data[J]. Oil Geophysical Prospecting, 2008, 43(6): 626-635. DOI:10.3321/j.issn:1000-7210.2008.06.003 |
| [13] |
张保庆.海底双检地震数据质量品质影响因素分析及关键处理技术研究[D].北京: 中国石油大学(北京), 2016. ZHANG Baoqing.Quality Influence Factor Analysis of Ocean Bottom Dual-Sensor Seismic Data and Key Processing Technical Research[D].China University of Petroleum (Beijing), Beijing, 2016. |
| [14] |
张兴岩.海底四分量地震资料处理方法研究[D].北京: 中国矿业大学, 2017. ZHANG Xingyan.Research of 4C-OBC Seismic Data Processing Technology[D].China University of Mining & Technology, Beijing, 2017. |
| [15] |
高少武, 黄燕.一种水陆检波器地震数据标定因子反演的方法[P].中国, ZL201310736942.1, 2013-11-29.
|
| [16] |
高少武, 祝宽海.一种水陆检波器地震数据匹配的方法[P].中国, ZL201310531139.4, 2013-10-31.
|
| [17] |
高少武, 赵波, 高轩, 等. OBC水陆检数据匹配技术[J]. 石油地球物理勘探, 2015, 50(1): 29-32. GAO Shaowu, ZHAO Bo, GAO Xuan, et al. A method for OBC dual-sensor data matching[J]. Oil Geophysical Prospecting, 2015, 50(1): 29-32. |
| [18] |
高轩, 弓小平, 高少武, 等. OBC水陆检数据标定因子估算方法[J]. 石油地球物理勘探, 2016, 51(1): 49-53. GAO Xuan, GONG Xiaoping, GAO Shaowu, et al. Scale factor estimation for OBC dual-sensor seismic data[J]. Oil Geophysical Prospecting, 2016, 51(1): 49-53. |
| [19] |
Backus M M. Water reverberations-their nature and elimination[J]. Geophysics, 1959, 24(2): 233-261. DOI:10.1190/1.1438579 |
| [20] |
Paffenholz J, Barr F J.An improved method for deriving water-bottom reflectivities for processing dual-sensor ocean-bottom cable data[C].SEG Technical Program Expanded Abstracts, 1995, 14: 987-990.
|
| [21] |
董崇志, 宋海斌, 王东晓, 等. 海水物性对地震反射系数的相对贡献[J]. 地球物理学报, 2013, 56(6): 2123-2132. DONG Chongzhi, SONG Haibin, WANG Dongxiao, et al. Relative contribution of seawater physical property to seismic reflection coefficient[J]. Chinese Journal of Geophysics, 2013, 56(6): 2123-2132. |
| [22] |
高少武, 赵波, 罗国安, 等.一种水陆检波器数据海底反射系数反演的方法[P].中国, ZL201410379202.1, 2014-08-04.
|
| [23] |
龚旭东, 周滨, 高梦晗, 等. 检波点水深误差对OBC双检资料合并处理的影响与对策[J]. 石油物探, 2014, 53(3): 324-329. GONG Xudong, ZHOU Bin, GAO Menghan, et al. The influence and strategy of water depth error at receivers on dual-sensor summing processing[J]. Geophysical Prospecting for Petroleum, 2014, 53(3): 324-329. DOI:10.3969/j.issn.1000-1441.2014.03.010 |
| [24] |
高少武, 钱忠平, 马玉宁, 等. 基于延迟波场特征法的海底反射系数估算技术[J]. 石油物探, 2018, 57(3): 389-394. GAO Shaowu, QIAN Zhongping, MA Yuning, et al. Estimating ocean bottom reflection coefficient using delayed wavefield charactistic method[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 389-394. DOI:10.3969/j.issn.1000-1441.2018.03.008 |
| [25] |
高少武, 赵波, 钱忠平等.水陆检波器数据海水深度反演方法和装置[P].中国, ZL201410377324.7, 2014-08-01.
|
| [26] |
高少武, 钱忠平, 黄少卿等.OBC水陆检数据海水深度估算方法[J].中国石油学会2017年物探技术研讨会论文集, 2017, 983-987. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-SYDQ201704001248.htm
|
| [27] |
张贤达. 时间序列分析——高阶统计量方法[M]. 北京: 清华大学出版社, 1996. ZHANG Xianda. Time Series Analysis:Method for Higher-order Statistics[M]. Beijing: Tsinghua University Press, 1996. |
| [28] |
高少武, 赵波, 钱忠平, 等.一种确定海水深度的方法及装置[P].中国, 201510963991.8, 2015-12-21.
|
| [29] |
Yung S K, Ikelle L T. An example of seismic time picking by third-order bicoherence[J]. Geophysics, 1997, 62(6): 1947-1951. DOI:10.1190/1.1444295 |



 高少武, 河北省涿州市华阳东路东方地球物理公司科技园物探技术研究中心, 072750。Email:
高少武, 河北省涿州市华阳东路东方地球物理公司科技园物探技术研究中心, 072750。Email: