② 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266061;
③ 中国石油化工股份有限公司胜利油田分公司, 山东东营 257100
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266061, China;
③ Shengli Oilfield Branch Co., SINOPEC, Dongying, Shandong 257100, China
地震资料的随机噪声通常源于仪器、环境及信号采集时的诸多因素,降低了地震资料的信噪比和分辨率[1]。压制随机噪声的主要目的是分离有效信号与噪声及保持有效信号的波形[2]。根据有效信号和噪声在视速度、频率等方面的差异,相继出现了F-X反褶积、Radon变换、小波分析、模态分解等去噪方法[3-6]。近年来,小波变换以优越的时频聚焦特性迅速从数学、信号处理拓展到各个领域,但其在一维信号的优良特性并不适用于高维,对方向的不敏感使信号表征存在局限[7-8]。
随着多尺度几何分析方法的不断发展、成熟,逐渐用于地震勘探领域,为高保真去噪提供了丰富的数学基础及新思路。多尺度几何分析也称多分辨率分析[9],最早由Rosenfeld等提出,具有多分辨率、局部化、多方向性及各向异性等特征,可更好地表征信号的局部特征,并实现信号的稀疏表示,在去噪和压缩方面具有明显优势。近年来相继出现了Ridgelet[10]、Curvelet[11]、Contourlet[12]、Shearlet[13]等变换的多尺度几何分析方法,其中Shearlet变换以优越的多分辨率特性在中国发展迅速,已广泛用于图像处理领域,并取得了良好效果[14-17]。同样,Shearlet变换的多分辨率、多方向性等特性在地震数据去噪中也获得较好的应用效果[18-20]。
Shearlet变换通过对变换系数设定阈值约束分离信噪,其中阈值函数至关重要。目前常用的阈值函数对多尺度、多方向的Shearlet变换局限性很大,会造成噪声压制不彻底或损失有效信号等问题。为此,本文将信噪比与阈值函数有机关联,在不同尺度下基于信噪比约束自适应求取阈值,实现自适应去噪。在保证有效信号不受损失的情况下,恢复被噪声掩盖的弱信号,有效地改善去噪效果。
1 方法原理 1.1 Shearlet变换Shearlet变换[21]是通过特定形式的合成膨胀仿射系统构造的一种多尺度几何分析工具,是小波变换的高维扩展,具有接近最优的非线性误差逼近性能,数学结构严谨,计算复杂度低。Shearlet变换由拉普拉斯金字塔变换和方向滤波器组构成。设
| $ \boldsymbol{A}=\left(\begin{array}{ll}{a} & {0} \\ {0} & {\sqrt{a}}\end{array}\right) $ |
| $ \boldsymbol{B}=\left(\begin{array}{cc}{1} & {-s} \\ {0} & {1}\end{array}\right) $ |
式中:A为尺度矩阵,根据抛物尺度准则划分尺度,其中a>0为尺度参数;B为剪切矩阵,进行方向剖分,其中s(整数)为剪切参数。令j、l、k分别代表尺度、方向和系数位置序号,则由j、l、k定义的实数域连续可积函数为
| $ \psi_{j, l, k}(x)=|\operatorname{det} \boldsymbol{A}|^{j/2} \psi\left(\boldsymbol{B}^{l} \boldsymbol{A}^{j} x-k\right) $ | (1) |
x为自变量。若使ψ满足Parseval框架,则信号函数f∈L2(R2)的连续Shearlet变换为
| $ \mathrm{SH}_{f}(j, k, l)=\left\langle f, \psi_{j, l, k}\right\rangle $ | (2) |
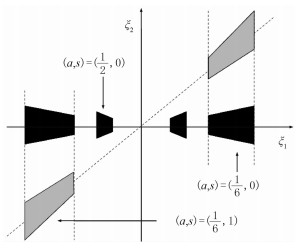
通过对参量j、l、k的控制实现不同尺度、不同方向的剖分,该过程相当于由平移、伸缩、旋转后的基函数逼近信号函数。在频域中,每一对Shearlet基函数都有一对楔形支撑区间,随尺度因子变小而变窄(图 1)。
|
图 1 Shearlet基函数频域支撑区间(据文献[8]修改) |
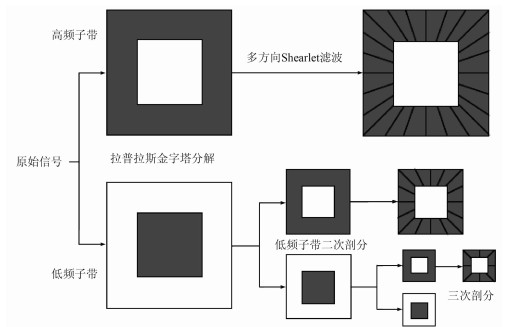
根据Shearlet变换的多尺度、多方向性特点,地震数据经过Shearlet变换会得到一系列不同尺度、不同方向的Shearlet系数。若Shearlet基函数的方向越逼近有效信号,则Shearlet系数越大;若基函数的方向与信号方向偏差越大,则Shearlet系数越小。由于随机噪声不具有方向性,所以经Shearlet变换后所得系数较小。利用阈值函数去掉较小的Shearlet系数,保留较大的部分,就能压制随机噪声,再进行Shearlet反变换得到去噪后的记录。获得Shearlet系数的流程(图 2)为:①利用拉普拉斯金字塔变换多尺度剖分信号,得到低、高频子带;②进行多方向分解,并在高频子带的伪极坐标进行傅里叶变换;③用Meyer函数滤波步骤②得到的结果;④对低频子带循环进行步骤①~③;⑤在笛卡尔坐标系对滤波数据进行快速傅里叶反变换,得到Shearlet变换系数。
|
图 2 Shearlet变换流程 |
在阈值类去噪方法中,阈值选取和阈值函数设计直接影响去噪效果。传统的阈值选取方法是对所有变换域系数使用统一阈值,但对Shearlet变换而言,各尺度、各方向的有效信号和噪声均存在差异,因此全局硬阈值存在一定局限性[22-23]。局部阈值则根据一定范围内的系数分布情况确定。本文在局部阈值的基础上改进贝叶斯阈值,形成一种适用于Shearlet变换的自适应阈值函数。
贝叶斯阈值是Chang等[24]利用小波系数的广义高斯分布提出的一种具有自适应性的阈值函数,其公式为
| $ T=\frac{\sigma_\text{n}^{2}}{\sigma_\text{s}} $ | (3) |
式中:T为阈值;σn2为噪声方差;σs为信号标准差。在式(3)引入一个与各尺度记录信噪比相关的权值系数λ,形成新的阈值函数
| $ T_{\lambda}=\lambda \frac{\sigma_\text{n}^{2}}{\sigma_\text{s}} $ | (4) |
式中σn由中值估计法得到
| $ \sigma_{\mathrm{n}}(j, l)=\frac{f_{\mathrm{Median}}(|S(j, l, k)|)}{0.6745} $ | (5) |
fMedian代表求取中值,σn和σs满足σd2=σs2+σn2,且
| $ \sigma_{\mathrm{s}}(j, l)=\sqrt{\max \left[\sigma_{\mathrm{d}}^{2}(j, l)-\sigma_{\mathrm{n}}^{2}(j, l), 0\right]} $ | (6) |
| $ \sigma_{\mathrm{d}}^{2}(j, l)=\frac{1}{n} \sum\limits_{k=1}^{n} S^{2}(j, l, k) $ | (7) |
σd为Shearlet系数的均方根;S(j, l, k)为Shearlet系数;n为某尺度、某方向Shearlet系数的个数。式(4)由不同尺度、不同方向的σn、σs及λj共同确定,λj与信噪比相关
| $ \lambda_{j}=\frac{1}{\operatorname{SNR}(j)} $ | (8) |
SNR(j)为不同尺度Shearlet系数单独构成的地震信噪比,由相邻地震道互相关求得
| $ \operatorname{SNR}(j)=\frac{N \sum\limits_{i=1}^{N-1} Q_{i,i+1}}{(N-1) \sum\limits_{i=1}^{N} Q_{i, i}(0)-N \sum\limits_{i=1}^{N-1} Q_{i, i+1}} $ | (9) |
式中:Qi, i+1为第i道和第i+1道互相关函数最大值;Qi, i(0)为第i道自相关函数最大值;N为道数。
确定阈值后即可调节Shearlet系数
| $ S_{\mathrm{new}}=\left\{\begin{array}{ll}{S} & {|S| \geqslant T_{\lambda}} \\ {0} & {|S|<T_{\lambda}}\end{array}\right. $ | (10) |
式中S、Snew分别为阈值处理前、后的Shearlet系数。自适应阈值函数方法通过将信噪比作为阈值设定的因素,即不同信噪比的权值系数不同,可以自适应求取不同尺度阈值,最大限度地改善去噪效果,避免有效信号损失。
2 模型试算与实际资料应用 2.1 模型试算为测试Shearlet变换自适应阈值方法(下称本文方法)的去噪效果,首先进行模拟数据试算。图 3展示了模拟单炮记录去噪效果。由图可见:采用全局硬阈值方式的Curvelet变换方法虽然去除了大部分高斯随机噪声,但仍有部分残留,效果不佳(图 3c);Shearlet变换全局阈值方法去噪效果较明显,基本压制了高斯随机噪声(图 3d);本文方法去噪结果的信噪比进一步提高(图 3e)。

|
图 3 模拟单炮记录去噪效果 (a)模拟单炮记录;(b)图a数据加入高斯噪声;(c)Curvelet变换全局阈值;(d)Shearlet变换全局阈值;(e)本文方法模拟单炮记录共128道,2000个采样点,采样率为1ms。为了更好地呈现去噪效果,进行了顶切处理 |
表 1展示了不同方法去噪前、后信噪比,可以看出本文方法的去噪效果更好。图 4为不同方法去噪前、后的残差剖面。由图可见:采用Curvelet变换全局阈值(图 4a)、Shearlet变换全局阈值(图 4b)去噪方法在深度较大的位置(红圈区域)造成有效信号损失,信号的保真度较低;采用本文方法去噪的残差剖面上不存在有效信号(图 4c),去噪结果(图 3e)与模拟单炮记录(图 3a)基本一致。
|
|
表 1 不同方法去噪前、后信噪比 |
2.2 实际资料应用
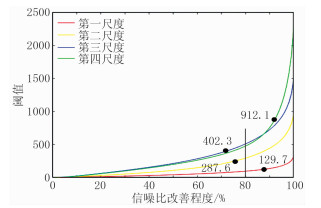
为进一步检验本文方法的有效性,选取A区陆地三维地震资料测试随机噪声压制效果。该区的偏移地震数据虽经过初步处理,但仍含有较强随机噪声,致使目标层局部有效弱信号被噪声淹没。图 5为Inline 100629剖面Shearlet变换不同尺度的地震记录。由图可见,不同尺度的有效信号与噪声分布存在差异(即信噪比不同),因此采用传统的阈值方法去噪存在局限性。截取Inline 100629剖面中深部区域(图 6a的黑框区域)进行去噪,图 6为实际地震记录去噪效果。由图可见:经各种方法去噪后随机噪声得到有效压制、信噪比得到提高,其中Shearlet变换全局阈值(图 6d)较Curvelet变换全局阈值(图 6c)的去噪效果好,局部弱信号得到恢复(红圈区域),但部分有效信号仍受噪声干扰,去噪效果不佳;经本文方法去噪后,弱信号更清晰、连续,明显提高了信噪比(图 6e)。图 7为Shearlet变换信噪比改善程度—阈值曲线。由图可见:传统全局硬阈值求取方法采用黑色竖线与各尺度曲线交点处的值作为阈值,没有考虑各尺度的信噪特征;图中4条曲线的标注点对应的纵坐标数值为本文方法确定的阈值。

|
图 5 Inline 100629剖面Shearlet变换不同尺度的地震记录 (a)第一尺度;(b)第二尺度;(c)第三尺度;(d)第四尺度 |

|
图 6 实际地震记录去噪效果 (a)Inline 100629剖面原始记录;(b)图a方框所选数据;(c)Curvelet变换全局阈值;(d)Shearlet变换全局阈值;(e)本文方法 |
|
图 7 Shearlet变换信噪比改善程度—阈值曲线 |
本文方法通过求取各尺度分量的信噪比,并将其作为约束条件,获得符合多尺度、多分辨率特征的阈值,去噪记录保真度更高。
为了更好地体现本文方法的自适应性,图 8给出了Inline 100629剖面不同方法去噪前、后的残差剖面。由图可见:采用Curvelet变换全局阈值(图 8a)、Shearlet变换全局阈值(图 8b)去噪方法虽然有效地压制了噪声,但由于受各尺度阈值设定的单一性限制,去噪程度基本一致;本文方法处理的残差剖面中出现较明显的弱能量区(红圈区域),这是由于目标层有效信号区域的初始信噪比较高(红圈区域中与有效信号混在一起的随机噪声已得到初步压制)所致,意味着采用本文方法的去噪效果不明显,充分体现了去噪的自适应特点。

|
图 8 Inline 100629剖面不同方法去噪前、后的残差剖面 (a)Cunelet变换全局阈值;(b)Shearlet变换全局阈值;(c)本文方法 |
表 2为不同区域去噪前、后信噪比。由表可见,原始剖面中信噪比不同的区域使用本文方法去噪后信噪比基本相同,这也说明自适应阈值函数通过计算局部信噪比约束去噪效果,可避免有效信号的损失,使剖面质量明显提高。
|
|
表 2 不同区域去噪前、后信噪比 |
Shearlet变换作为一种多尺度几何分析新方法,较小波变换等传统信号分析方法具有更多优良特性,且运算效率高。另外,针对地震数据去噪过程中传统全局阈值方法的局限性,本文通过改进自适应阈值函数压制随机噪声,在模型试算与实际资料应用中取得了满意的去噪效果,验证了方法的可行性和有效性。
尚需指出,目前Shearlet变换自适应阈值方法仅利用了Shearlet变换的多方向、多分辨率特性,其优良的稀疏特性同样值得进一步探索并用于地震数据处理领域,如尝试将Shearlet变换稀疏性与压缩感知理论结合,以期得到更好的去噪或拓频方法等。
在模型试算与实际地震资料处理中使用了中国石油集团东方地球物理公司提供的GeoEast软件,在此表示感谢。
| [1] |
李庆忠. 走向精确勘探的道路[M]. 北京: 石油工业出版社, 1993.
|
| [2] |
孔德辉, 彭真明, 江阳.基于广义全变差法的地震信号Shearlet域随机噪声衰减[C].中国石油学会2015年物探技术研讨会论文集, 2015.
|
| [3] |
康冶, 于承业, 贾卧, 等. f-x域去噪方法研究[J]. 石油地球物理勘探, 2003, 38(2): 136-138. KANG Ye, YU Chengye, JIA Wo, et al. A study on noise-suppression method in f-x domain[J]. Oil Geophysical Prospecting, 2003, 38(2): 136-138. DOI:10.3321/j.issn:1000-7210.2003.02.007 |
| [4] |
张军华, 陆基孟. 小波变换方法在地震资料去噪和提高分辨率中的应用[J]. 石油大学学报(自然科学版), 1997, 21(1): 18-21. ZHANG Junhua, LU Jimeng. Application of wavelet transform in removing noise and improving resolution of seismic data[J]. Journal of the University of Petroleum (Edition of Natural Science), 1997, 21(1): 18-21. |
| [5] |
张军华, 吕宁, 田连玉, 等. 地震资料去噪方法综合评述[J]. 石油地球物理勘探, 2005, 49(增刊): 121-127. |
| [6] |
蔡希玲, 吕英梅. 地震数据时频分析与分频处理[J]. 勘探地球物理进展, 2005, 28(4): 265-270. CAI Xiling, LYU Yingmei. Time-frequency analysis and frequency-divisional processing of seismic data[J]. Progress in Exploration Geophysics, 2005, 28(4): 265-270. |
| [7] |
Zheng H C, Yu D G, Peng W, et al. A novel fusion algorithm of visible image and infrared image based on NSCT[J]. Advanced Materials Research, 2012, 424-425(1): 223-226. |
| [8] |
张华, 陈小宏, 李红星, 等. 曲波变换三维地震数据去噪技术[J]. 石油地球物理勘探, 2017, 52(2): 226-232. ZHANG Hua, CHEN Xiaohong, LI Hongxing, et al. 3D seismic data de-noising approach based on Curvelet transform[J]. Oil Geophysical Prospecting, 2017, 52(2): 226-232. |
| [9] |
谢成芳.地震属性多分辨融合方法及应用研究[D].四川成都: 电子科技大学, 2015. XIE Chengfang.Research on Seismic Attributes Fusion Method based on Multi-resolution Analysis and its Application[D].University of Electronic Science and Technology of China, Chengdu, Sichuan, 2015. |
| [10] |
金丹, 程建远, 王保利, 等. 基于Curvelet变换的地震资料弱信号识别及去噪方法[J]. 煤炭学报, 2016, 41(2): 332-337. JIN Dan, CHENG Jianyuan, WANG Baoli, et al. Seismic weak signal identification and noise elimination based on curvelet domain[J]. Journal of China Coal Society, 2016, 41(2): 332-337. |
| [11] |
王建花, 王守东, 刘燕峰. 基于Contourlet系数相关性的地震噪声压制方法[J]. 中国海上油气, 2016, 28(1): 35-40. WANG Jianhua, WANG Shoudong, LIU Yanfeng. Seismic noise suppression method based on correlation of Contourlet coefficients[J]. China Offshore Oil and Gas, 2016, 28(1): 35-40. |
| [12] |
Xu K, Liu S H, Ai Y H. Application of Shearlet transform to classification of surface defects for metals[J]. Image and Vision Computing, 2015, 35(3): 23-30. |
| [13] |
Guo F M. Study on multi-focus images fusion via shearlet transformation[J]. Recent Patents on Computer Science, 2017, 10(1): 89-95. |
| [14] |
邓承志. Shearlet变换与图像处理应用[J]. 南昌工程学院学报, 2011, 30(6): 1-6. DENG Chengzhi. Shearlet transform and its applications in image processing[J]. Journal of Nanchang Institute of Technology, 2011, 30(6): 1-6. DOI:10.3969/j.issn.1006-4869.2011.06.002 |
| [15] |
朱华生, 徐晨光. Shearlet变换域自适应图像去噪算法[J]. 激光与红外, 2012, 42(7): 811-814. ZHU Huasheng, XU Chenguang. Adaptive image denoising algorithm based on Shearlet transform[J]. Laser & Infrared, 2012, 42(7): 811-814. |
| [16] |
胡海智, 孙辉, 邓承志, 等. 基于Shearlet变换的图像去噪算法[J]. 计算机应用, 2010, 30(6): 1562-1564. HU Haizhi, SUN Hui, DENG Chengzhi, et al. Image denoising algorithm based on Shearlet transform[J]. Journal of Computer Applications, 2010, 30(6): 1562-1564. |
| [17] |
屈勇, 曹俊兴, 朱海东, 等. 一种改进的全变分地震图像去噪技术[J]. 石油学报, 2011, 32(5): 815-819. QU Yong, CAO Junxing, ZHU Haidong, et al. An improved total variation technique for seismic image denoising[J]. Acta Petrolei Sinica, 2011, 32(5): 815-819. |
| [18] |
Du S C, Liu C P, Huang D L. A shearlet-based separation method of 3D engineering surface using high definition metrology[J]. Precision Engineering, 2015, 40(1): 55-73. |
| [19] |
刘成明, 王德利, 王通, 等. 基于Shearlet变换的地震随机噪声压制[J]. 石油学报, 2014, 35(4): 692-699. LIU Chengming, WANG Deli, WANG Tong, et al. Random seismic noise attenuation based on the Shearlet transform[J]. Acta Petrolei Sinica, 2014, 35(4): 692-699. |
| [20] |
张良, 韩立国, 许德鑫, 等. 基于压缩感知技术的Shearlet变换重建地震数据[J]. 石油地球物理勘探, 2017, 52(2): 220-225. ZHANG Liang, HAN Liguo, XU Dexin, et al. Seismicdata reconstruction with Shearlet transform based on compressed sensing technology[J]. Oil Geophysical Prospecting, 2017, 52(2): 220-225. |
| [21] |
Guo K, Labate D, Lim W. Edge analysis and identification using the continuous shearlet transform[J]. Applied & Computational Harmonic Analysis, 2009, 27(1): 24-46. |
| [22] |
曹静杰, 杨志权, 杨勇, 等. 一种基于曲波变换的自适应地震随机噪声消除方法[J]. 石油物探, 2018, 57(1): 72-78. CAO Jingjie, YANG Zhiquan, YANG Yong, et al. An adaptive seismic random noise elimination method based on Curvelet transform[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 72-78. DOI:10.3969/j.issn.1000-1441.2018.01.010 |
| [23] |
程浩, 陈刚, 王恩德, 等. 基于Shearlet变换的自适应阈值地震数据去噪方法[J]. 石油学报, 2018, 39(1): 82-91. CHENG Hao, CHEN Gang, WANG Ende, et al. Seismic data de-noising method of adaptive threshold based on Shearlet transform[J]. Acta Petrolei Sinica, 2018, 39(1): 82-91. |
| [24] |
Chang S G, Yu B, Vetterli M. Spatially adaptive wavelet thresholding with context modeling for image denoising[J]. IEEE Trans Image Process, 2000, 9(9): 1522-1531. DOI:10.1109/83.862630 |



 童思友, 山东省青岛市松岭路238号中国海洋大学海洋地球科学学院, 266100。Email:
童思友, 山东省青岛市松岭路238号中国海洋大学海洋地球科学学院, 266100。Email:
