② 中国石油西南油气田分公司, 四川成都 610051;
③ 胜利油田分公司物探研究院, 山东东营 257000;
④ 四川职业技术学院电子电气工程系, 四川遂宁 629000
② Southwest Oil & Gas Field Company, PetroChina, Chengdu, Sichuan 610051, China;
③ Research Institute of Geophysics, Shengli Oilfield Branch Co., SINOPEC, Dongying, Shandong 257000, China;
④ Department of Electrical and Electronic Engineering, Sichuan Vocational and Technical College, Suining, Sichuan 629000, China
稀疏脉冲反褶积是目前较为常用的提高地震资料分辨率的方法,其目的是利用带限的地震记录反演地下反射系数,从而得到高分辨率的地震数据[1-2]。稀疏脉冲反褶积的原理是在传统的最小二乘反褶积的基础上,加上一个稀疏先验约束项,通过求解L2范数与L1范数之和形式的目标函数得到高分辨率的反演结果[3-4]。
基追踪[5]方法利用Nesterov[6-8]提出的近端梯度的概念,使用二次函数近似表示目标函数,最终利用梯度法求解。该方法具有结构简单、实现容易、计算效率高等特点,是主流求解方法。
FISTA算法是Beck等[9]提出的基追踪方法,用于求解具有复合结构函数的最值
| $ \min \limits_{\boldsymbol{x} \in \boldsymbol{Q}}F(\boldsymbol{x})=f(\boldsymbol{x})+\varphi(\boldsymbol{x}) $ | (1) |
式中:F(x)为具有复合结构的目标函数,x为反射系数向量;f(x)为具有Lipschitz连续梯度的凸函数;φ(x)为在可行域Q上不可微的凸函数。根据Nesterov[6-8]提出的近端梯度法,式(1)对应的近端算子可以写作
| $ p_{L}(\boldsymbol{y})=\mathop {\arg \;\;{\text{min}}}\limits_{x \in \boldsymbol{R}} \left[\frac{1}{2}\left\|\boldsymbol{x}-\boldsymbol{y}+\frac{1}{L} \nabla f(\boldsymbol{y})\right\|_{2}^{2}+\varphi(\boldsymbol{x})\right] $ | (2) |
式中x, y∈R,y为x的近似值。由式(2)可以看出,Nesterov[6-8]采用二次函数近似式(1)的f(x),通过求解式(2)迭代求解式(1)。式(2)的常数L即为内部梯度的步长,它决定了FISTA算法的收敛度。通常无法准确给出L,FISTA算法采用线性搜索方法寻找最佳L[10]。然而,线性搜索只能使L朝着增大的方向搜索,严重影响了FISTA算法的收敛性。线性搜索算法的主要缺点为:①当L的初始估计值L0大于实际值时,整个迭代过程的L偏大,无法快速收敛[11];②当函数f(x)的局部曲率在初始迭代点附近较大,但在最优点附近减小时,如果L一直偏大,很可能导致“周波跳跃”而无法收敛。
针对上述问题前人进行了研究[12-16],但效果不好。为此,本文提出了一种改进的自适应步长FISTA方法,在没有外部参数调整的情况下仍能够求解,并利用实验验证了方法的可靠性。
1 FISTA方法原理时间域矩阵形式的稀疏脉冲反褶积的目标函数为[17]
| $ \|\boldsymbol{W x}-\boldsymbol{S}\|_{2}^{2}+\lambda\|\boldsymbol{x}\|_{1} $ | (3) |
式中:S为地震记录向量;W为由地震子波组成的矩阵;λ为正则化参数变量。式(3)前半部分为最小二乘约束项,代表通过褶积模型生成的地震记录与实际地震记录的相似程度,后半部分为数据的稀疏先验项。
根据前文所述,式(3)可以利用FISTA算法求解,其求解过程如图 1所示。由于采用线性搜索的方法,常数L只能沿着增大的方向变化,因此L的初始值决定了算法的收敛度,从而造成FISTA算法的不可控性。
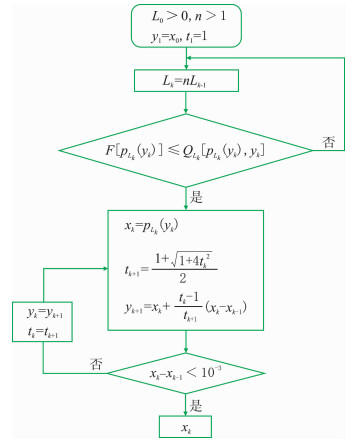
|
图 1 FISTA计算流程图
QL(x, y)=f(y)+〈x-y, ▽f(y)〉+ |
当常数L不变时,辅助序列tk+1与L无关,可以直接由下式确定[18]
| $ t_{k+1}^{2}-t_{k+1}=t_{k}^{2} $ | (4) |
为了能够满足理论上的收敛性,构造一个新的辅助序列,该辅助序列不仅只由tk和tk+1决定,还与前、后两次迭代的常数Lk和Lk+1有关,即
| $ t_{k+1}^{2}-t_{k+1}=\frac{L_{k+1}}{L_{k}} t_{k}^{2} $ | (5) |
由此,结合FISTA算法和式(5)可以得到一种自适应步长的改进算法(下文简称改进算法),算法流程如图 2所示。改进算法在不同模型下均可取得满意的计算效果。通过对比FISTA算法流程(图 1)和改进算法流程(图 2)可知,在每次迭代中,当L不满足F[pLk(yk)]≤QLk[pLk(yk), yk]时:①图 1通过Lk=nLk-1线性增大常数L,而在下一次迭代中直接使用Lk。②图 2则在每次迭代中,仍通过Lk=bLk-1线性增大常数L,但是在下一次迭代前,先通过Lk=aLk-1收缩L,然后利用收缩后的Lk进行后续迭代;与此同时,在每一次迭代过程中,利用前、后两次迭代常数L的信息更新辅助序列tk,使其在理论上可收敛。
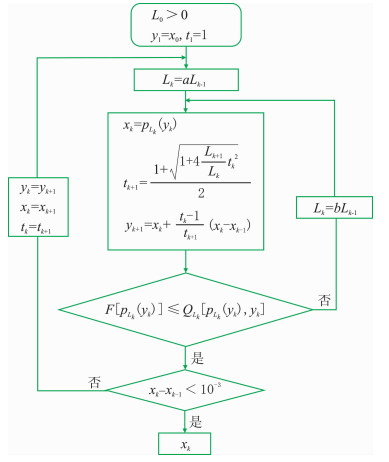
|
图 2 自适应步长FISTA方法流程图 其中0 < a < 1, b>1。a为收缩因子,在每一次迭代前收缩常数L,b为放大因子,在每一次迭代中放大常数L。参数a,b的取值对计算结果影响较小,经实验得a=0.7、b=2.0 |
为了验证改进算法的稀疏脉冲反褶积效果,首先合成一个理论模型(图 3),分别利用FISTA算法和改进算法对理论模型进行稀疏脉冲反褶积。分两种情况进行计算:①初始输入常数L值过大,L=10L0(图 4);②初始输入常数L值过小,L=0.3L0(图 5)。整个过程中取a=0.7、b=2.0。
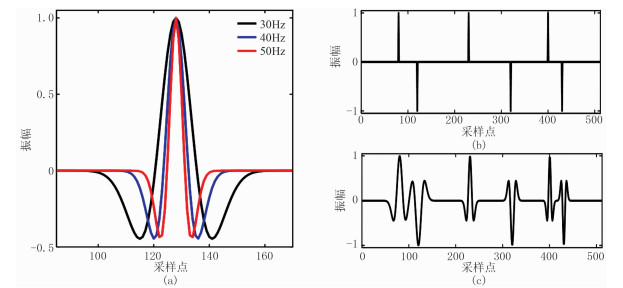
|
图 3 理论模型
(a)地震子波;(b)反射系数;(c)合成地震记录 图a由30、40、50Hz三个频率成分的零相位Ricker子波叠加,图b包含512个采样点、6个反射点 |
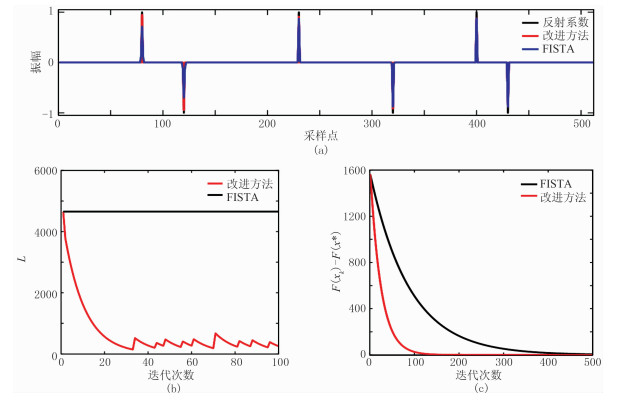
|
图 4 初始L过大时反褶积结果 (a)反褶积结果对比;(b)常数L估计值曲线;(c)收敛度曲线 F(xk)-F(x*)表示当前迭代次数下的xk与真实值x*对应目标函数值之差,代表收敛度,图 5同 |
|
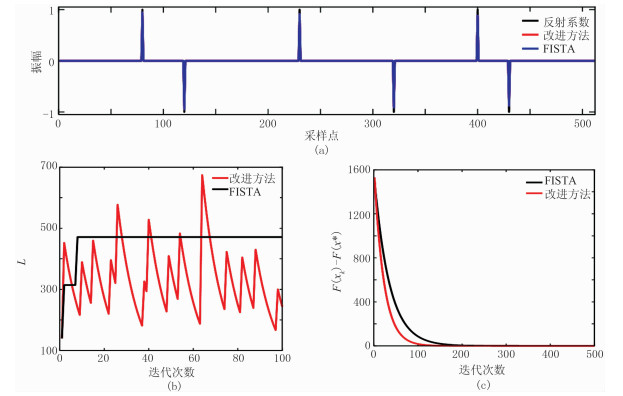
图 5 初始L过小时反褶积结果 (a)反褶积结果对比;(b)常数L估计值曲线;(c)收敛度曲线 |
由图 4可见:当初始L过大时,改进算法反褶积效果优于传统基于FISTA算法(图 4a);当初始L过大时,传统方法无法调整L的大小,改进算法能够自适应地调整L(图 4b);在相同迭代次数的情况下,由于常数L的调整使改进算法收敛度远远高于传统方法(图 4c)。由图 5可见:当初始L过小时,改进算法与传统方法计算过程大致相同,因此改进算法的计算效果与传统算法的差异不大(图 5a);改进算法在相同迭代次数下,收敛度略高于传统算法(图 5b、图 5c)。
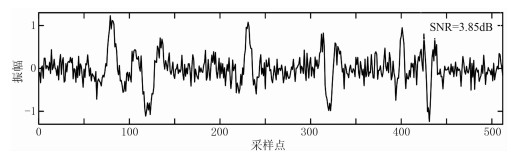
采用带随机噪声的数据进一步测试算法效果。在理论合成地震记录(图 3c)中加入随机噪声,得到了一个低信噪比理论模型(图 6),对该资料分别使用过大和过小L值进行反演,获得不同方法反褶积结果(图 7)。可见,基于传统FISTA的稀疏脉冲反褶积方法在低信噪比情况下无法得到准确的反褶积结果,由改进算法能得到较准确的反褶积结果。上述分析进一步证明了改进方法具有更好的收敛性,能在不同信噪比下得到理想的反演结果,较常规FISTA算法具有更好的抗噪能力。
|
图 6 含噪声理论模型 |

|
图 7 不同方法反褶积结果(SNR=3.85dB) (a)初始L过大;(b)初始L过小 |
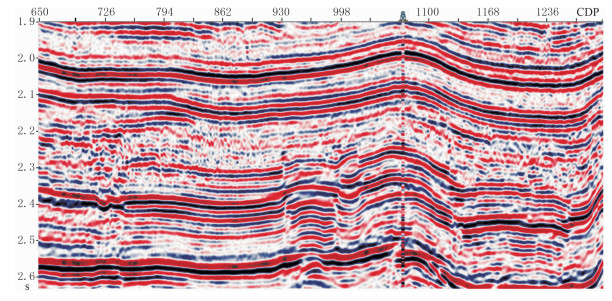
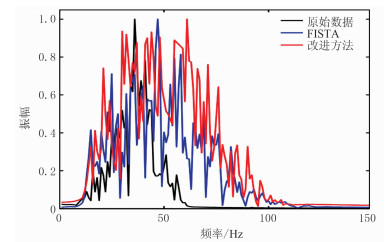
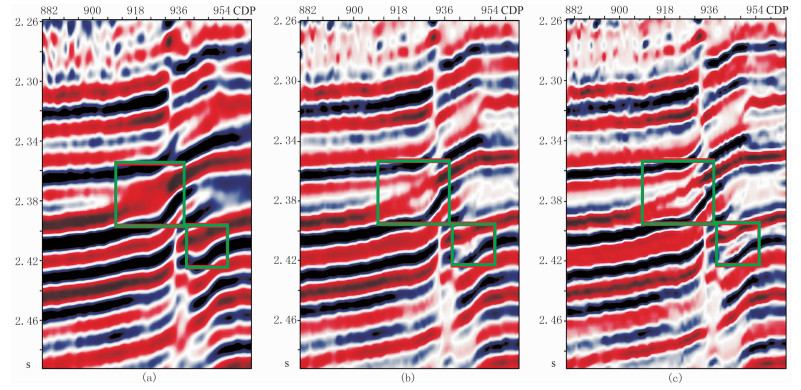
选取吐哈盆地雁木西北部地震资料测试改进算法的适用性[19-20]。图 8为雁木西T3井区Line 299测线地震剖面,可见地震分辨率较低,无法满足精细解释的需求。为此,分别采用基于传统FISTA算法的稀疏脉冲反褶积以及改进算法对图 8数据进行高分辨率处理。由处理结果可见:在相同的时间段内,改进算法反褶积结果(图 9b)的同相轴数目较FISTA算法(图 9a)多;经过基于FISTA算法的稀疏脉冲反褶积以及改进算法处理的地震资料的分辨率都得到提升,但是后者的频带更宽(图 10)、细节刻画更清楚(图 11c),利于高精度构造解释。
|
图 8 雁木西T3井区Line 299测线地震剖面 |

|
图 9 反褶积剖面 (a)FISTA;(b)改进算法 |
|
图 10 图 9数据的频谱 |
|
图 11 图 9的局部放大 (a)原始地震记录;(b)传统FISTA处理结果;(c)改进方法处理结果 |
本文提出了一种基于自适应步长FISTA算法的稀疏脉冲反褶积方法,该方法在FISTA算法的基础上,通过在每一次迭代之前适当减小常数L,然后利用线性搜索的方式寻找最优的常数L,以达到自适应调整L的目的。为了使算法达到理论收敛,通过结合前、后两次的L,对传统FISTA算法的辅助序列进行修改,最终使整套算法在理论上得以收敛。理论模型与实际地震资料的处理、分析结果表明,改进方法具有更好的收敛性,能在不同信噪比下得到理想的反演结果,较常规FISTA算法具有更强的抗噪能力。
| [1] |
张繁昌, 刘杰, 印兴耀, 等. 修正柯西约束地震盲反褶积方法[J]. 石油地球物理勘探, 2008, 43(4): 391-398. ZHANG Fanchang, LIU Jie, YIN Xingyao, et al. Mo-dified Cauchy-constrained seismic blind deconvolution[J]. Oil Geophysical Prospecting, 2008, 43(4): 391-398. DOI:10.3321/j.issn:1000-7210.2008.04.006 |
| [2] |
宋维琪, 吴彩端. 利用压缩感知方法提高地震资料分辨率[J]. 石油地球物理勘探, 2017, 52(2): 214-219. SONG Weiqi, WU Caiduan. Seismic data resolution improvement based on compressed sensing[J]. Oil Geophysical Prospecting, 2017, 52(2): 214-219. |
| [3] |
王宇, 韩立国, 周家雄, 等. L1-L2范数联合约束稀疏脉冲反演的应用[J]. 地球科学——中国地质大学学报, 2009, 34(5): 835-840. WANG Yu, HAN Liguo, ZHOU Jiaxiong, et al. A-pplication of combined norm constrained sparseness spike inverse[J]. Earth Science:Journal of China University of Geosciences, 2009, 34(5): 835-840. |
| [4] |
曹静杰. 基于广义高斯分布和非凸Lp范数正则化的地震稀疏盲反褶积[J]. 石油地球物理勘探, 2016, 51(3): 428-433. CAO Jingjie. Seismic sparse blind deconvolution based on generalized Gaussian distribution and non-convex Lp norm regularization[J]. Oil Geophysical Prospecting, 2016, 51(3): 428-433. |
| [5] |
Chen S S, Donoho D L, Saunders M A. Atomic Decomposition by Basis Pursuit[M]. Society for Industrial and Applied Mathematics, 1998.
|
| [6] |
Nesterov Y. A method of solving a convex progra-mming problem with convergence rate O(1/k2)[J]. Soviet Mathematics Doklady, 1983, 27(2): 372-376. |
| [7] |
Nesterov Y. Introductory Lectures on Convex Optimization[M]. Kluwer Academic Publishers, 2014.
|
| [8] |
Nesterov Y. Gradient methods for minimizing com-posite objective function[J]. Core Discussion Papers, 2007, 140(1): 125-161. |
| [9] |
Beck A, Teboulle M. A fast iterative shrinkage-thre-sholding algorithm for linear inverse problems[J]. Siam Journal on Imaging Sciences, 2009, 2(1): 183-202. DOI:10.1137/080716542 |
| [10] |
Civicioglu P. Backtracking search optimization algo-rithm for numerical optimization problems[J]. Applied Mathematics & Computation, 2013, 219(15): 8121-8144. |
| [11] |
Deimling K. Nonlinear Functional Analysis[M]. Springer-Verlag, 1980.
|
| [12] |
Becker S R, Candès E J, Grant M C. Templates for convex cone problems with applications to sparse signal recovery[J]. Mathematical Programming Computation, 2011, 3(3): 165-218. DOI:10.1007/s12532-011-0029-5 |
| [13] |
Zhang Z, Saligrama V.Rapid: Rapidly accelerated proxi-mal gradient algorithms for convex minimization[C].IEEE International Conference on Acoustics, Speech and Signal Processing, 2015, doi: 10.1109/ICASSP.2015.7178681.
|
| [14] |
Levy S, Fullagar P K. Reconstruction of a sparse spike train from a portion of its spectrum and application to high-resolution deconvolution[J]. Geophysics, 1981, 46(46): 1235-1243. |
| [15] |
Mehrotra S. On the implementation of a primal-dual interior point method[J]. Siam Journal on Optimization, 1992, 2(4): 575-601. DOI:10.1137/0802028 |
| [16] |
Parikh N, Boyd S. Proximal algorithms[J]. Foundations & Trends in Optimization, 2013, 1(3): 121-231. |
| [17] |
Chambolle A, Dossal C. On the convergence of the iterates of the "fast iterative shrinkage thresholding algorithm"[J]. Journal of Optimization Theory and Applications, 2015, 166(3): 968-982. DOI:10.1007/s10957-015-0746-4 |
| [18] |
Levitin E S, Polyak B T. Constrained minimization methods[J]. USSR Computational Mathematics & Mathematical Physics, 1966, 6(5): 1-50. |
| [19] |
蔡志东, 刘聪伟, 王勇, 等. 井地联合地震数据反褶积[J]. 石油地球物理勘探, 2017, 52(1): 8-12. CAI Zhidong, LIU Congwei, WANG Yong, et al. Seismic data deconvolution with VSP operator[J]. Oil Geophysical Prospecting, 2017, 52(1): 8-12. |
| [20] |
吕铁良, 王永刚, 谢万学, 等. 稀疏脉冲反演技术在井间地震反演中的应用[J]. 石油物探, 2007, 46(1): 58-63. LYU Tieliang, WANG Yonggang, XIE Wanxue, et al. Application of sparse pulse inversion in crosswell seismic data[J]. Geophysical Prospecting for Petroleum, 2007, 46(1): 58-63. |



 潘树林, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院, 610500。Email:
潘树林, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院, 610500。Email: