② 黄河勘测规划设计研究院有限公司, 河南郑州 45000;
③ 中国能源建设集团新疆电力设计院有限公司, 新疆乌鲁木齐 830001
地震信号中混入随机噪声时,会大大降低地震资料的信噪比,严重影响对有效信号的检测和准确估计。研究表明,由于在各个时刻具有不确定性,决定了随机噪声呈现在零点处自相关函数值最大,而在其他点处自相关函数值迅速衰减的特点。对于理想高斯白噪声,其自相关函数值在零点处应表现为一个尖脉冲;而对于其他一般信号,由于存在固有的关联度,其自相关函数值的变化规律明显不同于随机噪声[1]。
现有的地震信号去噪方法已相当成熟,主要包括Wiener滤波[2]、谱减法[3]、小波变换[4-5]等传统的(去噪)算法及其改进方法。
KSVD(K Singular Value Decomposition)字典稀疏去噪法属于基本压缩感知理论[6-7]的改进算法,该方法通过大量样本信号训练获得过完备冗余字典,能更自适应地以稀疏基表征[8-9]信号,从而更精确地重构信号,实现去噪目的。尽管KSVD字典[10-11]稀疏去噪可使信号中大部分随机噪声得到有效抑制或消除,但在信号的各个波峰和波谷处总会残留一些毛刺[12]。
经验模态分解(Empirical Mode Decomposition,EMD)可对信号局部时变特征做自适应时频分解[13-14],非常适用于非平稳、非线性信号分析,但它存在模态混叠和端点效应问题[15]。
完备总体经验模态分解(Complete Ensemble Empirical Mode Decomposition,CEEMD)[16]弥补了EMD存在的缺陷,在分解信号的每一阶段添加一种特定白噪声,同时计算唯一的残差以获取每个符合定义的固有模态分量(IMF),这是一个完备的分解过程。CEEMD提供的模态分离效果明显好于EMD,同时对原始信号的重构更为精确,且计算效率相对更高[17]。
本文针对传统地震信号的随机噪声去除方法的不足及KSVD字典稀疏去噪后信号中总会残留毛刺的问题,提出一种CEEMD与KSVD字典训练相结合的去噪方法,以期能够在实际地震资料中更好地消除随机噪声的影响。
1 理论基础 1.1 CEEMD基本原理总体经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)在一定程度上解决了EMD的模态混叠效应,提高了EMD的分解质量;同时也造成了新问题,如加入不同高斯白噪声会导致分解出的IMF不是唯一解,与IMF的原始定义不能很好吻合,这样就失去它所代表的物理含义。EEMD算法的完备性不强,对处理后结果做累加难以完美重构原来信号;同时受到加总平均[12]的影响,在很大程度上,噪声添加越多分解结果越好,但其计算成本也会相应地增加。
Torres等[18]于2011年提出了一种噪声自动适应的完备总体经验模态分解(CEEMD),该算法与EEMD相同点在于也利用了噪声进行辅助分析,但具体实现过程与EEMD区别很大。此算法不仅解决了模态混叠问题,同时提高了原信号重构的精度、提升了计算效率也降低了成本,总体上明显优于EMD、EEMD方法。其具体步骤描述如下。
(1) 将不同的白噪声分别与原来信号合成T个混合信号,应用EMD对其处理,计算集合平均并将其作为原来信号的第一个固有模态函数IMF1
| $ \operatorname{IMF}_{1}(t)=\frac{1}{T} \sum\limits_{i=1}^{T} F_{1}\left[x(t)+\varepsilon_{0} \omega^{i}(t)\right] $ | (1) |
式中:Fj(·)为EMD处理后获取的第j阶模态;ωi为i个高斯白噪声;εk为每一阶段白噪声加入的比例大小;x(t)为初始信号。
(2) 令r0(t)=x(t),对k=1、…、K计算第k阶残差rk(t)
| $ r_{k}(t)=r_{k-1}(t)-\operatorname{IMF}_{k}(t) $ | (2) |
(3) 对rk(t)+εkFk[ωi(t)]做EMD处理,获取对应的IMF1;计算总体平均并将其作为IMFk+1
| $ \operatorname{IMF}_{k+1}(t)=\frac{1}{T} \sum\limits_{i=1}^{T} F_{1}\left[r_{k}+\varepsilon_{k} F_{k}\left(\omega^{i}\right)\right] $ | (3) |
(4) 重复步骤(2)和步骤(3),直到残差信号不能分解为止,得到最终残差
| $ r_{K+1}(t)=x(t)-\sum\limits_{k=1}^{K} \operatorname{IMF}_{k}(t) $ | (4) |
KSVD算法[19]主要包括字典更新和稀疏编码两个步骤,获取字典的同时也获得稀疏系数矩阵。
在稀疏编码过程中,常用的稀疏分解方法为正交匹配追踪算法(Orthogonal Matching Pursuit,OMP)。字典更新的常用方法有MOD(Method of Optimal Directions)和KSVD,两者差异之处在于字典更新原子时所用更新机制不同:MOD是对字典中所有原子进行更新,而KSVD只针对字典中某个原子进行。
在字典[20]更新过程中,KSVD学习字典使用了奇异值分解更新字典原子,与固定基字典相比,训练的字典具有更能反映信号特征的优点。KSVD算法具体流程(图 1)如下。
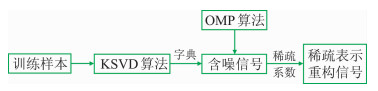
|
图 1 KSVD稀疏去噪方法框图 |
参数初始化:给定训练样本X=[x1, x2, …, xN],初始超完备字典D,正则化参数λ和迭代次数J。
(1) 稀疏编码阶段:固定字典D,用OMP算法对每个训练样本做稀疏分解,得到稀疏分解系数矩阵A={αi}i=1N,其中
| $ \alpha_{i}=\arg \min \left\|x_{i}-D \alpha_{i}\right\|_{2}^{2}+\lambda\left\|\alpha_{i}\right\|_{1} $ | (5) |
(2) 字典更新阶段:固定稀疏系数矩阵A,逐列更新字典D中的原子:①假定当前正在更新的字典原子为dk,记Ik={i|αi(k)≠0, 1≤i≤N},其中αi(k)为αi中的第k个元素,Ik表示全部训练样本中用到原子dk的索引集;②计算残差矩阵Ek=X-
(3) 达到迭代次数J即结束,否则返回步骤(1)。
经过上述步骤(1)~步骤(3),即可得到学习后的KSVD字典,在整个KSVD运算中,每次字典更新时都能保证总误差单调下降,因此该算法具有较好收敛特性。此外,KSVD算法还具有一定的去噪功能。
2 CEEMD与KSVD联合去噪方法CEEMD去噪方法盲目舍弃高频IMF模态分量有可能导致高频有效信号损失或高频噪声压制不完全。KSVD字典稀疏去噪尽管去除了大部分噪声,但弱随机噪声尚存在于局部信号中,尤其在信号各个波峰和波谷处尚残留一些较明显毛刺。鉴于此,本文将CEEMD与KSVD相结合,通过互补方式弥补上述方法存在的两点不足。
CEEMD-KSVD联合去噪具体实现步骤(图 2,其中“过渡模态”是指介于噪声主导模态与信号主导模态之间的模态)如下:
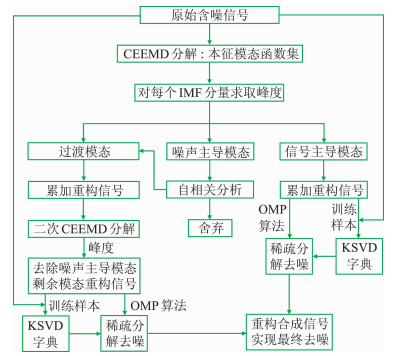
|
图 2 本文去噪方法流程框图 |
(1) 采用CEEMD对观测含噪信号y模态分解获得本征模态函数集。
(2) 求取每个IMF分量的峰度,识别噪声主导模态,过渡模态和信号主导模态。
(3) 噪声主导模态分量:直接舍弃。
(4) 过渡模态分量:①对过渡模态分量累加合成新信号x,并对其二次CEEMD分解;②利用各个模态分量求取的峰度,舍弃噪声主导模态;③对步骤②中的剩余IMF分量累加合成新信号x1,并与观测信号y作为训练样本,获得KSVD学习字典;④利用上步字典及OMP算法对信号x1稀疏去噪获得去噪结果y1。
(5) 信号主导模态分量:①各个信号主导模态累加重构得到新信号z;②将信号z和y作为训练样本,获取KSVD学习字典;③利用学习字典及OMP算法对信号z稀疏去噪得到y2。
(6) 将步骤(4)和步骤(5)中的去噪结果y1和y2重构合并,得到最终去噪结果。
峰度又称峰态系数,是用于表征数据的概率密度分布曲线在平均值处峰值高低的特征数[21]。对于服从高斯分布的随机噪声信号,其峰度F接近0;对于服从超高斯分布的随机噪声信号,其峰度大于0;反之,服从亚高斯分布的随机噪声信号,其峰度小于0。
下文中峰度评判标准:噪声主导模态是|F|≤0.1,过渡模态是0.1<|F|≤1.0,信号主导模态是|F|>1.0。
3 模型试算设计如图 3所示的褶积模型,该模型共有三层,上下两层为水平层,中间层为倾斜层,并与上覆层斜交。横向共有25道,纵向上有300个采样点,采样频率为500Hz,雷克子波主频为25Hz,模型中加入两种不同比例高斯白噪声,分别采用五种方法对含噪模拟地震数据进行去噪,通过分析验证五种方法去噪效果。

|
图 3 无噪模拟地震记录 |
特别说明:本文所使用的剖面数据的字块为8×8,字典原子的维数是64×256;由于过渡模态部分合成信号的随机噪声较强,使用的迭代次数为20,信号主导模态部分合成信号的随机噪声相对弱小,为提高计算效率,使用的迭代次数为10;同时分割子块尺寸和字典维数不变时,迭代次数越多,字典就会变得越稀疏,计算效率也就越高;反之迭代次数不变时,子块尺寸和字典维数越大,计算效率越低。本文加入的高斯白噪声频谱范围分布广泛,包含地震频带(图 4)。
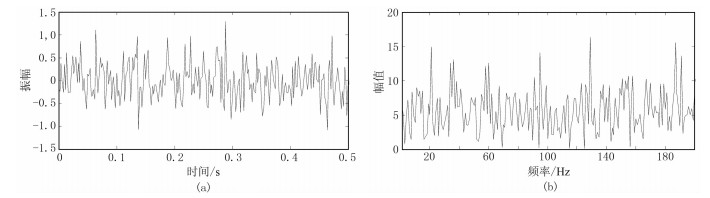
|
图 4 高斯白噪声(a)及其频谱特征(b) |
加入较高比例的高斯白噪声构成信噪比为0.88的加噪模拟地震记录(图 5a),图 5b~图 5f为五种方法的去噪结果。从图中可看到:F-X域去噪和CEEMD分频去噪效果最差;小波软阈值去噪效果也不太理想;KSVD稀疏去噪效果较好,但尚存一些毛刺现象;本文方法基本保存了原始信号的有效信息,去噪效果最好。表 1为五种方法去噪结果评价指标对比。从各方法去噪结果及其评价指标的对比得知,五种方法中后两种去噪效果较好,尤其本文方法相比其他方法去噪后信噪比最高,有效信息损失最少,是一种有效保幅的去噪方法。信噪比计算公式如下
|
|
表 1 五种方法去噪结果评价指标对比 |
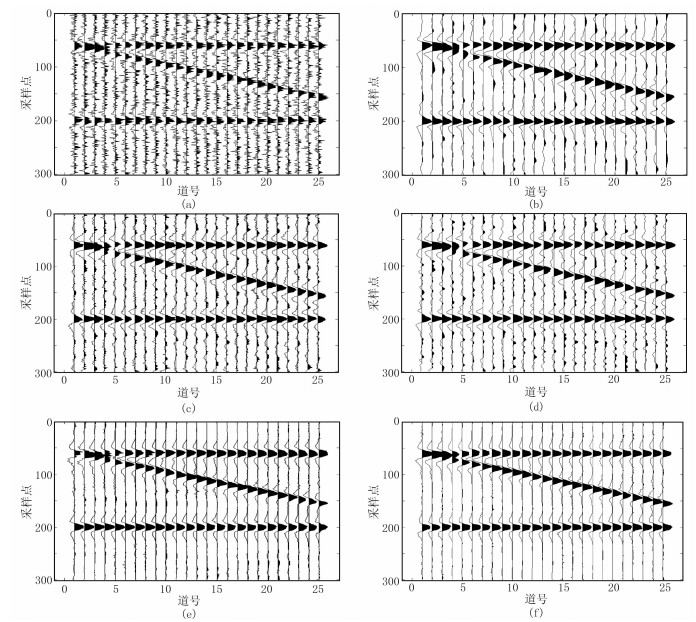
|
图 5 含较高比例噪声模拟地震记录五种方法去噪效果对比 (a)加噪模拟地震记录;(b)小波软阈值;(c)F-X域;(d)CEEMD分频;(e)KSVD稀疏;(f)本文方法 |
| $ R_{\mathrm{S} / \mathrm{N}}=10 \cdot \lg \frac{S^{2}}{\left(S_{1}-S\right)^{2}} $ | (6) |
式中:S1为去噪后的数据;S为无噪数据;RS/N为去噪后信噪比。
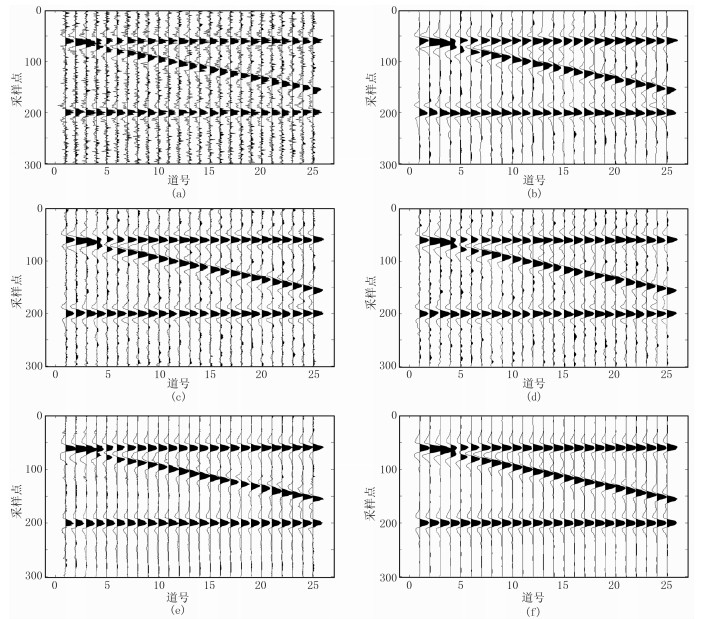
3.2 信噪比RS/N=3.13加入较低比例的高斯白噪声构成信噪比为3.13的加噪模拟地震记录(图 6a),图 6b~图 6f为五种方法的去噪结果。从图中可知:五种方法都能将大部分噪声压制,但F-X域去噪和CEEMD分频去噪有明显的噪声残余;小波软阈值去噪没有毛刺现象,但在局部改变了信号的幅值;KSVD稀疏去噪效果较好,与本文方法去噪效果相差无几,但是仔细观察仍存在轻微的毛刺现象。表 2为五种方法去噪结果评价指标对比。因此,综合对比五种方法的去噪结果及其评价指标可看出:对高信噪比资料,后三种方法去噪效果均较好,尤其KSVD稀疏去噪与本文方法去噪效果只有些许差别。
|
图 6 含较低比例噪声模拟地震记录五种方法去噪效果对比 (a)加噪模拟地震记录;(b)小波软阈值;(c)F-X域;(d)CEEMD分频;(e)KSVD稀疏;(f)本文方法 |
|
|
表 2 五种方法去噪结果评价指标对比 |
通过上述分析可得到以下认识:F-X域去噪和CEEMD分频去噪不管是在高信噪比还是低信噪比资料中尽管能压制一定程度的噪声,但都未获取理想去噪结果;小波软阈值去噪和KSVD稀疏去噪效果质量与信噪比呈线性关系,信噪比越高,效果越好;本文方法实用性强,在不同信噪比资料中都能获取较好的去噪效果。
4 实际地震资料应用为了进一步测试本文去噪方法对实际地震资料的处理,将其应用于实际地震资料。
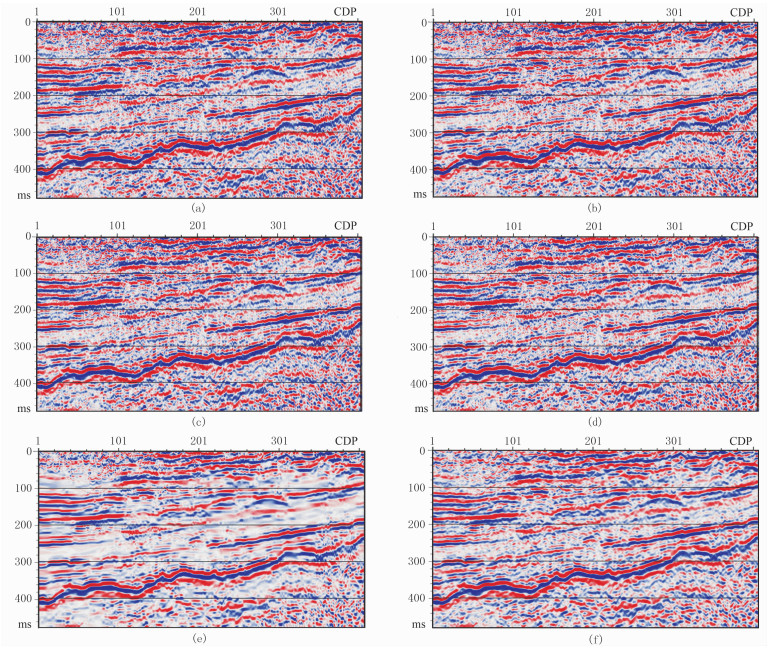
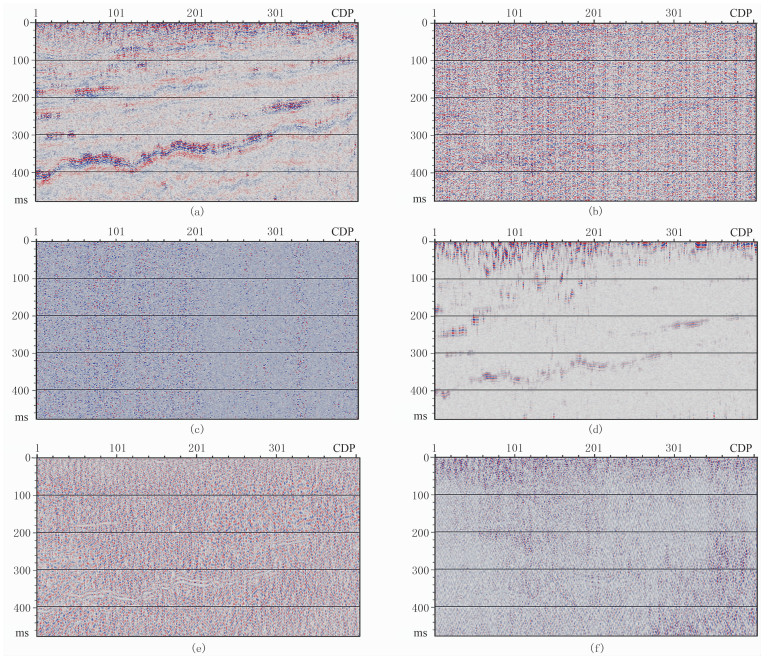
图 7a为某一工区的叠后地震记录,该地震记录的CDP数目为250,采样点个数为500,采样时间为2ms,从图中可见地震剖面上由于存在大量的随机噪声致使剖面同相轴不连续或错断,剖面显示不清晰,对地质解释带来诸多不便。为了消除随机噪声的影响,分别利用上述五种方法进行去噪处理,对比这五种方法去噪后的成果剖面(图 7b~图 7f)可知:F-X域去噪与CEEMD分频去噪效果最差,去噪后还存在许多噪声残留;小波软阈值去噪方法除掉了大量随机噪声,仍存有少许随机噪声,去噪效果一般;KSVD稀疏去噪与本文方法去噪效果相比前三种较好,但KSVD稀疏去噪在一些细节(弱幅度有效信号)上不如本文方法,由图 7d和图 7e可知,本文方法充分压制了随机噪声,同相轴相对更加连续,有效信息得以保留,地震剖面清晰度提高。图 8为各种去噪方法获得的残差剖面图。由残差剖面可知,F-X域、KSVD稀疏、小波等去噪法都或多或少地去除了部分有效信号,尤其F-X域去噪损失有效信号最严重;CEEMD分频去噪,当舍弃模态IMF1时,去除的基本上是随机噪声,但是去除IMF1 +IMF2时,导致一部分有效信号的丢失,而本文方法去噪不仅随机噪声得以完全压制,同时又不伤害有用信号,取得了很好的去噪效果。
|
图 7 针对实际资料五种方法去噪效果对比 (a)原始地震剖面;(b)F-X域;(c)小波软阈值;(d)CEEMD分频;(e)KSVD稀疏;(f)本文方法 |
|
图 8 五类去噪方法对应的残差剖面 (a)F-X域;(b)小波软阈值;(c)CEEMD分频(去除IMF1);(d)CEEMD分频(去除IMF1+IMF2);(e)KSVD稀疏;(f)本文方法 |
(1) 本文研究表明:F-X域去噪方法能去除部分随机噪声,但会导致假同相轴、有效波波形畸变;由于阈值很难精准选取,小波去噪方法在去除大量噪声的同时也丢失了部分有效信号;CEEMD去噪方法因盲目舍弃IMF分量可能造成高频有效信息缺失;KSVD稀疏去噪总有残留毛刺,且当资料信噪比较低时,去噪效果也随之变差;本文提出的CEEMD-KSVD联合去噪方法的去噪效果优于其他四种方法,能显著提高地震资料品质。
(2) 随机噪声的频率大多较高,CEEMD分频去噪方法通过舍弃前若干个模态,主要用于去除高频部分的随机噪声,KSVD稀疏去噪方法是以随机噪声与信号在整个定义域上稀疏分解系数分布差异较大为基础,两种方法都立足于随机噪声的特性。因此,本文去噪方法更适用于随机噪声的压制,对于其他类型噪声,其适用性有待测试。
| [1] |
王婷.EMD算法研究及其在信号去噪中的应用[D].黑龙江哈尔滨: 哈尔滨工程大学, 2010. WANG Ting.Research on EMD Algorithm and Its Application in Signal Denoising[D].Harbin Engineering University, Harbin, Heilongjiang, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10217-1011020271.htm |
| [2] |
Chen J, Benesty J, Huang Y, et al. New insights into the noise reduction Wiener filter[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2006, 14(4): 1218-1234. DOI:10.1109/TSA.2005.860851 |
| [3] |
Boll S. Suppression of acoustic noise in speech using spectral subtraction[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1979, 27(2): 113-120. DOI:10.1109/TASSP.1979.1163209 |
| [4] |
DonohoDL. De-noisingbysoft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613-627. DOI:10.1109/18.382009 |
| [5] |
薛雅娟, 曹俊兴. 聚合经验模态分解和小波变换相结合的地震信号衰减分析[J]. 石油地球物理勘探, 2006, 51(6): 1148-1155. XUE Yajuan, CAO Junxing. Seismic attenuation ana-lysis using the EEMD and CWT[J]. Oil Geophysical Prospecting, 2006, 51(6): 1148-1155. |
| [6] |
宋维琪, 吴彩端. 利用压缩感知方法提高地震资料分率[J]. 石油地球物理勘探, 2017, 52(2): 214-219. SONG Weiqing, WU Caiduan. Seismic data resolution improvement based on compressed sensing[J]. Oil Geophysical Prospecting, 2017, 52(2): 214-219. |
| [7] |
温睿, 刘国昌, 冉扬. 压缩感知地震数据重建中的三个关键因素分析[J]. 石油地球物理勘探, 2018, 53(4): 682-693. WEN Rui, LIU Guochang, RAN Yang. Three key factors in seismic data reconstruction based on compressive sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 682-693. |
| [8] |
Elad M. Sparse and Redundant Representations:from Theory to Applications in Signal and Image Processing[M]. Springer, 2010: 23-35.
|
| [9] |
杨荣根, 任明武, 杨静宇. 基于稀疏表示的人脸识别方法[J]. 计算机科学, 2010, 37(9): 267-269. YANG Ronggen, REN Mingwu, YANG Jingyu. Sparse representation based face recognition algorithm[J]. Computer Science, 2010, 37(9): 267-269. DOI:10.3969/j.issn.1002-137X.2010.09.066 |
| [10] |
Rubinstein R, Zibulevsky M, Elad M. Double sparsity:Learning sparse dictionaries for sparse signal approximation[J]. IEEE Transactions on Signal Processing, 2009, 58(3): 1553-1564. |
| [11] |
刘平, 刘晓曼, 朱永贵. 基于K-SVD宇典学习的核磁共振图像重建方法[J]. 中国传媒大学学报(自然科学版), 2013, 20(4): 34-39. LIU Ping, LIU Xiaoman, ZHU Yonggui. MR image reconstruction based on K-SVD dictionary learning[J]. Journal of Communication University of China (Science and Technology), 2013, 20(4): 34-39. DOI:10.3969/j.issn.1673-4793.2013.04.005 |
| [12] |
甘振业, 陈浩, 杨鸿武. 结合EEMD与K-SVD字典训练的语音增强算法[J]. 清华大学学报(自然科学版), 2017, 57(3): 286-292. GAN Zhenye, CHEN Hao, YANG Hongwu. Speech enhancement algorithm that combines EEMD and K-SVD dictionary trainning[J]. Journal of Tsinghua University (Science and Technology), 2017, 57(3): 286-292. |
| [13] |
Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London.Series A:Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [14] |
Huang N E, Shen Z, Long S R. A new view of nonli-near water waves:The Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31(1): 417-457. |
| [15] |
Yeh J R, Shieh J S, Huang N E. Complementary ensemble empirical mode decomposition:a novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156. |
| [16] |
张猛, 王华忠, 隋志强, 等. 基于经验模态分解和小波变换的地震瞬时频率提取方法及应用[J]. 石油地球物理勘探, 2016, 51(3): 565-571. ZHANG Meng, WANG Huazhong, SUI Zhiqiang, et al. Seismic instantaneous frequency extraction based on empirical mode decomposition and wavelet transform[J]. Oil Geophysical Prospecting, 2016, 51(3): 565-571. |
| [17] |
曹思远, 邴萍萍, 路交通, 等. 利用改进希尔伯特-黄变换进行地震资料时频分析[J]. 石油地球物理勘探, 2013, 48(2): 246-254. CAO Siyuan, BING Pingping, LU Jiaotong, et al. Seismic data time-frequency analysis by the improved Hilbert-Huang transform[J]. Oil Geophysical Prospecting, 2013, 48(2): 246-254. |
| [18] |
Torres M E, Colominas M A, Schlotthauer G, et al.A complete ensemble empirical mode decomposition with adaptive noise[C].IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP), IEEE, 2011, 4144-4147.
|
| [19] |
张广智, 常德宽, 王一惠, 等. 基于稀疏冗余表示的三维地震数据随机噪声压制[J]. 石油地球物理勘探, 2015, 50(4): 600-606. ZHANG Guangzhi, CHANG Dekuan, WANG Yihui, et al. Random noise suppression of 3D seismic data based on sparse redundancy representation[J]. Oil Geophysical Prospecting, 2015, 50(4): 600-606. |
| [20] |
邵婕, 孙成禹, 唐杰, 等. 基于字典训练的小波域稀疏表示微地震去噪方法[J]. 石油地球物理勘探, 2016, 51(2): 254-260. SHAO Jie, SUN Chengyu, TANG Jie, et al. Micro-seismic data denoising based on sparse representations over learned dictionary in the wavelet domain[J]. Oil Geophysical Prospecting, 2016, 51(2): 251-260. |
| [21] |
刘陈希.基于EMD-ICA的地震资料去噪方法研究[D].山东青岛: 中国石油大学(华东), 2017. LIU Chenxi.Denoising Research of Seismic data Based on EMD-ICA Method[D].China University of Petroleum (East China), Qingdao, Shandong, 2017. |



 杨涛, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
杨涛, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: