② 长江大学地球科学学院, 湖北武汉 430100;
③ 油气资源与勘探技术教育部重点实验室(长江大学), 湖北武汉 430100;
④ 长江大学地球物理与石油资源学院, 湖北武汉 430100
② School of Geosciences, Yangtze University, Wuhan, Hubei 430100, China;
③ Key Laboratory of Exploration Technology for Oil and Gas Resources, Ministry of Education, Yangtze University, Wuhan, Hubei 430100, China;
④ School of Geophysics and Petroleum Resources, Yangtze University, Wuhan, Hubei 430100, China
在大地电磁测深(MT)二维正演数值模拟中,有限差分法(FDM)和有限元法(FEM)是主要的计算方法[1]。FEM的核心基础是变分原理和加权余量法,Coggon[2]最先实现FEM的电磁正演模拟,随后William等[3]、Rijo[4]、Wannamaker等[5]和Franke等[6]分别采用矩形元、三角元、混合元和非结构化三角剖分等实现了FEM的MT二维正演模拟。陈乐寿等[7-8]、胡建德等[9-10]先期实现了有限元MT二维正演模拟;徐世浙等[11-13]深入研究了FEM及其网格剖分;陈小斌等[14-15]提出了有限元直接迭代算法,取得了很好的效果。FDM的原理是将连续微分方程及边界条件用含有限个未知数的离散差分方程近似代替,差分方程的解就是微分方程边值问题的数值解。Madden等[16]率先采用交错网格FDM进行三维大地电磁正演;随后Mackie等[17-20]围绕交错采样的FDM进行了大量研究;谭捍东等[21]在此基础上引入了双共轭稳定梯度法,提高了正演的精度和效率;肖骑彬等[22]对不同网格精度、系统方程、边界条件以及预条件线性算子等进行对比,提出了FDM的MT正演的最优方案。
FDM和FEM各有优缺点。前者运算简便易行、迭代收敛稳定、计算速度快,但仅适用于地下介质形状规则的情况;后者不要求规则的网格剖分,适用于复杂结构的问题,但其存储量大,求解速度慢,算法的实用性差。为了解决这一难题,不少学者研究了多种新型的正演方法,如无网格法[23-24]、多重网格法[25-26]等,取得了一定的效果。四叉树(Quadtree)和八叉树(Octree)方法[27]是一类适应能力强且高效的网格剖分方法。四叉树是一种树状数据结构,将平面模型的外接矩形等分成四个小的矩形, 然后递归划分,直至达到精度要求。四叉树数据结构在计算机领域用于研究图像分割、遥感图像处理和地理信息系统,Yerry等[28-29]首先将四叉树数据结构应用于网格生成,随后四叉树网格的数值模拟被广泛应用于流体力学领域[30]。Haber等[31]、Lior等[32]将八叉树数据结构应用于可控源电磁法的数值模拟,但是用于MT正演的研究很少。
本文将四叉树网格剖分应用于MT二维FDM正演,推导出四叉树网格的差分公式,并对其计算结果进行了验证。
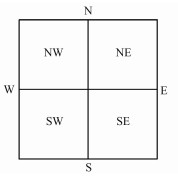
1 地电模型的四叉树网格剖分大地电磁场是从高空垂直入射到地面的平面电磁波,在地球空间中广泛存在,其外边界为无穷远,实际正演模拟时需取足够大的矩形区域。这个矩形区域对应四叉树的根节点。四叉树网格将大地电磁场的计算区域按如图 1所示的四个象限(NE, NW, SW, SE)进行递归分割,逐步分解成一系列矩形区域,直至整个区域的各个部分达到预定的最高分辨率,所分解的最小矩形区域即是一个具有单一属性(电性参数)的矩形单元,对应四叉树数据结构中的叶节点,每一个叶节点与实际模型中的某一矩形区域对应。
|
图 1 四叉树网格剖分示意图 |
四叉树编码分为显式四叉树和线性四叉树。显式四叉树通过父节点和子节点之间设立指针的方式建立整个树结构,又称为有指针四叉树。显式四叉树节点不仅要记录节点所对应的矩形区域的信息,还要记录一个父节点和四个子节点的指针,整个四叉树不仅要记录叶节点还要记录非叶节点,所以占用储存空间较多。线性四叉树只记录从根节点到叶节点的路径以及叶节点的属性,占用储存空间小。但是显式四叉树由于使用指针连接各节点,所以其邻域查询更快捷[33]。在正演计算建立差分方程时要频繁地查询各矩形单元的邻域,所以本文选择使用显式四叉树法。
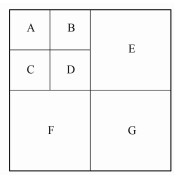
显式四叉树的邻域查询采用最近公共祖先方法,这种方法不考虑节点的位置坐标,只需要四叉树的树结构。下面以图 2中节点D邻域的查询为例介绍显式四叉树的邻域查询方法。对矩形单元D的四个节点建立差分方程时,需要获取与单元D相邻的六个单元A、B、C、E、F、G的信息,就要通过四叉树查询这六个叶节点。对于节点D,沿四叉树向上查询的到其父节点,该父节点含A、B、C、D四个子节点,且A、B、C均为叶节点,故A、B、C都为D节点的邻域,且他们的层级(距离根节点的层数)相同。在节点D的父节点再查询上一级父节点,该节点包含E、F、G三个叶节点和节点D的父节点,故节点E、F、G即为节点D的邻域,且层级比D低1。若节点E为非叶节点,则需要向下查询节点E的子节点,直至找到与节点D相邻的某个叶节点。
|
图 2 四叉树网格邻域查找示意图 |
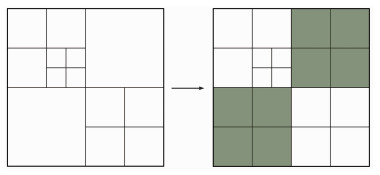
在查询邻域时,要检查节点的邻域与节点的层级差。如图 3所示,左图中存在相邻单元层级差大于1,要对层级较小的单元进行二次划分,从而得到右图所示更光滑的网格,以限制离散误差[34]。
|
图 3 网格的光滑处理 |
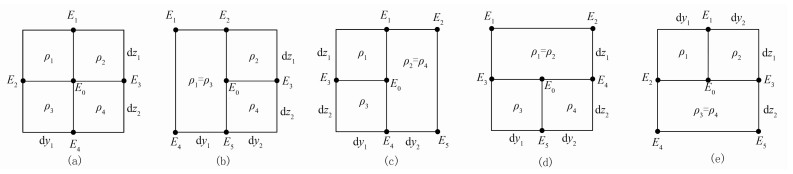
在四叉树网格剖分中,网格节点除边界点外,可以分为如图 4所示的五种节点,其中类型a网格节点与常规的有限差分相同,采用五点中心差分即可;其他四种节点呈T形,需要另行推导差分公式。下面用待定系数法[35]推导各种节点的差分公式。
|
图 4 五种节点类型 图a~图e分别对应类型a~e的网格 |
取二维构造的走向方向为x,由Helmholtz方程可以推导出二维情况下MT响应所满足的偏微分方程为
TE模式
| $ \frac{{{\partial ^2}{E_x}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{E_y}}}{{\partial {z^2}}} + {\rm{i}}\omega \mu \sigma {E_x} = 0 $ | (1) |
TM模式
| $ \frac{\partial }{{\partial y}}\left( {\rho \frac{{\partial {H_x}}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\rho \frac{{\partial {H_x}}}{{\partial z}}} \right) + {\rm{i}}\omega \mu {H_x} = 0 $ | (2) |
式(1)和式(2)中:E表示电场;H表示磁场;ω表示角频率;μ表示磁导率;σ表示电导率。为简洁方便,下文推导中均略去Ex和Hx中的下标x,分别记为E和H。图 4中的类型a~e各点的差分公式系数TE模式和TM模式分别记为a0、a1、…、a4、b0、b1、…、b5、c0、c1、…、c5、d0、d1、…、d5、e0、e1、…、e5和a’0、a’1、…、a’4、b’0、b’1、…、b′5、c’0、c’1、…、c’5、d’0、d’1、…、d’5、e’0、e’1、…、e’5。下文分别描述TE和TM模式下的差分公式系数的求解公式。
2.1 TE模式对图 4中类型a, 可以离散为五点差分公式
| $ E = {a_0}{E_0} + {a_1}{E_1} + {a_2}{E_2} + {a_3}{E_3} + {a_4}{E_4} = 0 $ | (3) |
分别对图 4a中的电场分量E1~E4在E0处泰勒展开
| $ \left\{ \begin{array}{l} {E_1} = {E_0} - {\rm{d}}{z_1}\frac{{\partial E}}{{\partial z}} + \frac{{{{\left( {{\rm{d}}{z_1}} \right)}^2}}}{2}\frac{{{\partial ^2}E}}{{\partial {z^2}}} + O\left[ {{{\left( {{\rm{d}}{z_1}} \right)}^2}} \right]\\ {E_2} = {E_0} - {\rm{d}}{y_1}\frac{{\partial E}}{{\partial y}} + \frac{{{{\left( {{\rm{d}}{y_1}} \right)}^2}}}{2}\frac{{{\partial ^2}E}}{{\partial {y^2}}} + O\left[ {{{\left( {{\rm{d}}{y_1}} \right)}^2}} \right]\\ {E_3} = {E_0} - {\rm{d}}{y_2}\frac{{\partial E}}{{\partial y}} + \frac{{{{\left( {{\rm{d}}{y_2}} \right)}^2}}}{2}\frac{{{\partial ^2}E}}{{\partial {y^2}}} + O\left[ {{{\left( {{\rm{d}}{y_2}} \right)}^2}} \right]\\ {E_4} = {E_0} - {\rm{d}}{z_2}\frac{{\partial E}}{{\partial z}} + \frac{{{{\left( {{\rm{d}}{z_2}} \right)}^2}}}{2}\frac{{{\partial ^2}E}}{{\partial {z^2}}} + O\left[ {{{\left( {{\rm{d}}{z_2}} \right)}^2}} \right] \end{array} \right. $ | (4) |
把式(4)代入式(3),整理得到
| $ \begin{array}{l} \left( {{a_0} + {a_1} + {a_2} + {a_3} + {a_4}} \right){E_0} + \left( {{a_3}{\rm{d}}{y_2} - {a_2}{\rm{d}}{y_1}} \right)\frac{{\partial E}}{{\partial y}} + \\ \left( {{a_4}{\rm{d}}{z_2} - {a_1}{\rm{d}}{z_1}} \right)\frac{{\partial E}}{{\partial z}} + \left[ {{a_2}\frac{{{{\left( {{\rm{d}}{y_1}} \right)}^2}}}{2} + {a_3}\frac{{{{\left( {{\rm{d}}{y_2}} \right)}^2}}}{2}} \right]\frac{{{\partial ^2}E}}{{\partial {y^2}}} + \\ \left[ {{a_1}\frac{{{{\left( {{\rm{d}}{z_1}} \right)}^2}}}{2} + {a_4}\frac{{{{\left( {{\rm{d}}{z_2}} \right)}^2}}}{2}} \right]\frac{{{\partial ^2}E}}{{\partial {z^2}}} + {a_1}O\left[ {{{\left( {{\rm{d}}{z_1}} \right)}^2}} \right] + \\ {a_2}O\left[ {{{\left( {{\rm{d}}{y_1}} \right)}^2}} \right] + {a_3}O\left[ {{{\left( {{\rm{d}}{y_2}} \right)}^2}} \right] + {a_4}O\left[ {{{\left( {{\rm{d}}{z_2}} \right)}^2}} \right] = 0 \end{array} $ | (5) |
式(5)与式(1)等价。略去高阶余项,则
| $ \left\{ \begin{array}{l} {a_0} + {a_1} + {a_2} + {a_3} + {a_4} = {\rm{i}}\omega \mu \sigma \\ {a_3}{\rm{d}}{y_2} - {a_2}{\rm{d}}{y_1} = 0\\ {a_4}{\rm{d}}{z_2} - {a_1}{\rm{d}}{z_1} = 0\\ \begin{array}{*{20}{l}} {{a_2}\frac{{{{\left( {{\rm{d}}{y_1}} \right)}^2}}}{2} + {a_3}\frac{{{{\left( {{\rm{d}}{y_2}} \right)}^2}}}{2} = 1}\\ {{a_1}\frac{{{{\left( {{\rm{d}}{z_1}} \right)}^2}}}{2} + {a_4}\frac{{{{\left( {{\rm{d}}{z_2}} \right)}^2}}}{2} = 1} \end{array} \end{array} \right. $ | (6) |
解之即可得5点差分格式(图 4中类型a)的系数
| $ \left\{ \begin{array}{l} {a_0} = {\rm{i}}\omega \mu \bar \sigma - \frac{2}{{{\rm{d}}{y_1}{\rm{d}}{y_2}}} - \frac{2}{{{\rm{d}}{z_1}{\rm{d}}{z_2}}}\\ {a_1} = \frac{2}{{{\rm{d}}{z_1}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)}}\\ {a_2} = \frac{2}{{{\rm{d}}{y_1}\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}}\\ {a_3} = \frac{2}{{{\rm{d}}{y_2}\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}}\\ {a_4} = \frac{2}{{{\rm{d}}{z_2}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)}} \end{array} \right. $ | (7) |
同样对于T型节点(类型b~e)也可以同样推导出差分公式,例如类型d可以离散为
| $ d_{0} E_{0}+d_{1} E_{1}+d_{2} E_{2}+d_{3} E_{3}+d_{4} E_{4}+d_{5} E_{5}=0 $ | (8) |
对E1~E5泰勒展开后,代入式(8)解得
| $ \left\{ \begin{array}{l} {d_0} = {\rm{i}}\omega \mu \bar \sigma - \frac{2}{{{\rm{d}}{y_1}{\rm{d}}{y_2}}} - \frac{2}{{{\rm{d}}{z_2}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)}}\\ {d_1} = \frac{{2{\rm{d}}{y_2}}}{{{\rm{d}}{z_1}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}}\\ {d_2} = \frac{{2{\rm{d}}{y_1}}}{{{\rm{d}}{z_1}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}}\\ {d_3} = \frac{2}{{{\rm{d}}{y_1}\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}} - \frac{{2{\rm{d}}{y_2}}}{{{\rm{d}}{z_1}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}}\\ \begin{array}{*{20}{l}} {{d_4} = \frac{2}{{{\rm{d}}{y_2}\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}} - \frac{{2{\rm{d}}{y_1}}}{{{\rm{d}}{z_1}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}}}\\ {{d_5} = \frac{2}{{{\rm{d}}{z_2}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)}}} \end{array} \end{array} \right. $ | (9) |
式中
| $ \overline{\sigma}=\frac{\left(\mathrm{d} y_{1}+\mathrm{d} y_{2}\right)\left(\mathrm{d} z_{1}+\mathrm{d} z_{2}\right)}{\rho_{1} \mathrm{d} y_{1} \mathrm{d} z_{1}+\rho_{2} \mathrm{d} y_{2} \mathrm{d} z_{1}+\rho_{3} \mathrm{d} y_{1} \mathrm{d} z_{2}+\rho_{4} \mathrm{d} y_{2} \mathrm{d} z_{2}} $ | (10) |
将式(2)展开为
| $ \rho\left(\frac{\partial^{2} H}{\partial y^{2}}+\frac{\partial^{2} H}{\partial z^{2}}\right)+\frac{\partial \rho}{\partial y} \frac{\partial H}{\partial y}+\frac{\partial \rho}{\partial z} \frac{\partial H}{\partial z}+\mathrm{i} \omega \mu H=0 $ | (11) |
由于只有矩形单元内的电阻率值,式(11)中的
| $ \left\{ \begin{array}{l} \rho = \frac{{{\rho _1}{\rm{d}}{y_1}{\rm{d}}{z_1} + {\rho _2}{\rm{d}}{y_2}{\rm{d}}{z_1} + {\rho _3}{\rm{d}}{y_1}{\rm{d}}{z_2} + {\rho _4}{\rm{d}}{y_2}{\rm{d}}{z_2}}}{{{\rm{d}}{y_1}{\rm{d}}{z_1} + {\rm{d}}{y_2}{\rm{d}}{z_1} + {\rm{d}}{y_1}{\rm{d}}{z_2} + {\rm{d}}{y_2}{\rm{d}}{z_2}}}\\ \frac{{\partial \rho }}{{\partial y}} = \frac{{\frac{{{\rho _2}{\rm{d}}{z_1} + {\rho _4}{\rm{d}}{z_2}}}{{{\rm{d}}{z_1} + {\rm{d}}{z_2}}} - \frac{{{\rho _1}{\rm{d}}{z_1} + {\rho _3}{\rm{d}}{z_2}}}{{{\rm{d}}{z_1} + {\rm{d}}{z_2}}}}}{{\frac{{{\rm{d}}{y_1} + {\rm{d}}{y_2}}}{2}}}\\ \frac{{\partial \rho }}{{\partial y}} = \frac{{\frac{{{\rho _3}{\rm{d}}{y_1} + {\rho _4}{\rm{d}}{y_2}}}{{{\rm{d}}{y_1} + {\rm{d}}{y_2}}} - \frac{{{\rho _1}{\rm{d}}{y_1} + {\rho _2}{\rm{d}}{y_2}}}{{{\rm{d}}{y_1} + {\rm{d}}{y_2}}}}}{{\frac{{{\rm{d}}{z_1} + {\rm{d}}{z_2}}}{2}}} \end{array} \right. $ | (12) |
差分公式推导以类型d为例说明,设其差分公式为
| $ \begin{array}{c}{d_{0}^{\prime} H_{0}+d_{1}^{\prime} H_{1}+d_{2}^{\prime} H_{2}+d_{3}^{\prime} H_{3}+} \\ {d_{4}^{\prime} H_{4}+d_{5}^{\prime} H_{5}=0}\end{array} $ | (13) |
各点处的泰勒展开为
| $ \left\{ \begin{array}{l} {H_1} = {H_0} - {\rm{d}}{y_1}\frac{{\partial H}}{{\partial y}} - {\rm{d}}{z_1}\frac{{\partial H}}{{\partial z}} + \frac{{{{\left( {{\rm{d}}{y_1}} \right)}^2}}}{2}\frac{{{\partial ^2}H}}{{\partial {y^2}}} + \\ \;\;\;\;\;\;\;\;{\rm{d}}{y_1}{\rm{d}}{z_1}\frac{{{\partial ^2}H}}{{\partial y\partial z}} + \frac{{{{\left( {{\rm{d}}{z_1}} \right)}^2}}}{2}\frac{{{\partial ^2}H}}{{\partial {z^2}}} + \\ \;\;\;\;\;\;\;\;O\left[ {\sum\limits_{i = 0}^2 {{{\left( {{\rm{d}}{z_1}} \right)}^i}} {{\left( {{\rm{d}}{y_1}} \right)}^{2 - i}}} \right]\\ {H_2} = {H_0} + {\rm{d}}{y_2}\frac{{\partial H}}{{\partial y}} - {\rm{d}}{z_1}\frac{{\partial H}}{{\partial z}} + \frac{{{{\left( {{\rm{d}}{y_2}} \right)}^2}}}{2}\frac{{{\partial ^2}H}}{{\partial {y^2}}} - \\ \;\;\;\;\;\;\;\;{\rm{d}}{y_2}{\rm{d}}{z_1}\frac{{{\partial ^2}H}}{{\partial y\partial z}} + \frac{{{{\left( {{\rm{d}}{z_1}} \right)}^2}}}{2}\frac{{{\partial ^2}H}}{{\partial {z^2}}} + \\ \;\;\;\;\;\;\;\;O\left[ {\sum\limits_{i = 0}^2 {{{\left( {{\rm{d}}{z_1}} \right)}^i}} {{\left( {{\rm{d}}{y_1}} \right)}^{2 - i}}} \right]\\ {H_3} = {H_0} - {\rm{d}}{y_1}\frac{{\partial H}}{{\partial y}} + \frac{{{{\left( {{\rm{d}}{y_1}} \right)}^2}}}{2}\frac{{{\partial ^2}H}}{{\partial {y^2}}} + O\left[ {{{\left( {{\rm{d}}{y_1}} \right)}^2}} \right]\\ {H_4} = {H_0} + {\rm{d}}{y_2}\frac{{\partial H}}{{\partial y}} + \frac{{{{\left( {{\rm{d}}{y_2}} \right)}^2}}}{2}\frac{{{\partial ^2}H}}{{\partial {y^2}}} + O\left[ {{{\left( {{\rm{d}}{y_2}} \right)}^2}} \right]\\ {H_5} = {H_0} + {\rm{d}}{z_2}\frac{{\partial H}}{{\partial z}} + \frac{{{{\left( {{\rm{d}}{z_2}} \right)}^2}}}{2}\frac{{{\partial ^2}H}}{{\partial {z^2}}} + O\left[ {{{\left( {{\rm{d}}{z_2}} \right)}^2}} \right] \end{array} \right. $ | (14) |
将式(14)代入式(13),整理得
| $ \begin{array}{l} \left( {d_0^\prime + d_1^\prime + d_2^\prime + d_3^\prime + d_4^\prime + d_5^\prime } \right){H_0} + \\ \left( {d_2^\prime {\rm{d}}{y_2} + d_4^\prime {\rm{d}}{y_2} - d_1^\prime {\rm{d}}{y_1} - d_3^\prime {\rm{d}}{y_1}} \right)\frac{{\partial H}}{{\partial y}} + \\ \left( {d_5^\prime {\rm{d}}{z_2} - d_1^\prime {\rm{d}}{z_1} - d_2^\prime {\rm{d}}{z_1}} \right)\frac{{\partial H}}{{\partial z}} + \\ \left[ {d_1^\prime \frac{{{{\left( {{\rm{d}}{y_1}} \right)}^2}}}{2} + d_2^\prime \frac{{{{\left( {{\rm{d}}{y_2}} \right)}^2}}}{2} + d_3^\prime \frac{{{{\left( {{\rm{d}}{y_1}} \right)}^2}}}{2} + } \right.\\ d_4^\prime \frac{{{{\left( {{\rm{d}}{y_2}} \right)}^2}}}{2}]\frac{{{\partial ^2}H}}{{\partial {y^2}}} + \left( {d_1^\prime {\rm{d}}{y_1}{\rm{d}}{z_1} - d_2^\prime {\rm{d}}{y_2}{\rm{d}}{z_1}} \right)\frac{{{\partial ^2}H}}{{\partial y\partial z}} + \\ \left[ {d_1^\prime \frac{{{{\left( {{\rm{d}}{z_1}} \right)}^2}}}{2} + d_2^\prime \frac{{{{\left( {{\rm{d}}{z_1}} \right)}^2}}}{2} + d_5^\prime \frac{{{{\left( {{\rm{d}}{z_2}} \right)}^2}}}{2}} \right]\frac{{{\partial ^2}H}}{{\partial {z^2}}} + \\ d_1^\prime O\left[ {\sum\limits_{i = 0}^2 {{{\left( {{\rm{d}}{z_1}} \right)}^i}} {{\left( {{\rm{d}}{y_1}} \right)}^{2 - i}}} \right] + d_2^\prime O\left[ {\sum\limits_{i = 0}^2 {{{\left( {{\rm{d}}{z_1}} \right)}^{2 - i}}} } \right] + \\ d_3^\prime O\left[ {{{\left( {{\rm{d}}{y_1}} \right)}^3}} \right] + d_4^\prime O\left[ {{{\left( {{\rm{d}}{y_2}} \right)}^3}} \right] + d_5^\prime O\left[ {{{\left( {{\rm{d}}{z_2}} \right)}^3}} \right] = 0 \end{array} $ | (15) |
式(15)与式(13)等价,可得
| $ \left\{ \begin{array}{l} d_0^\prime + d_1^\prime + d_2^\prime + d_3^\prime + d_4^\prime + d_5^\prime = {\rm{i}}\omega \mu \\ d_2^\prime {\rm{d}}{y_2} + d_4^\prime {\rm{d}}{y_2} - d_1^\prime {\rm{d}}{y_1} - d_3^\prime {\rm{d}}{y_1} = \frac{{\partial \rho }}{{\partial y}}\\ d_5^\prime {\rm{d}}{z_2} - d_1^\prime {\rm{d}}{z_1} - d_2^\prime {\rm{d}}{z_1} = \frac{{\partial \rho }}{{\partial z}}\\ d_1^\prime \frac{{{{\left( {{\rm{d}}{y_1}} \right)}^2}}}{2} + d_2^\prime \frac{{{{\left( {{\rm{d}}{y_2}} \right)}^2}}}{2} + d_3^\prime \frac{{{{\left( {{\rm{d}}{y_1}} \right)}^2}}}{2} + \\ \;\;\;\;d_4^\prime \frac{{{{\left( {{\rm{d}}{y_2}} \right)}^2}}}{2} = \rho \\ d_1^\prime {\rm{d}}{y_1}{\rm{d}}{z_1} - d_2^\prime {\rm{d}}{y_2}{\rm{d}}{z_1} = 0\\ d_1^\prime \frac{{{{\left( {{\rm{d}}{z_1}} \right)}^2}}}{2} + d_2^\prime \frac{{{{\left( {{\rm{d}}{z_1}} \right)}^2}}}{2} + d_5^\prime \frac{{{{\left( {{\rm{d}}{z_2}} \right)}^2}}}{2} = \rho \end{array} \right. $ | (16) |
由式(12)~式(16)可解得
| $ \left\{ \begin{array}{l} d_0^\prime = {\rm{i}}\omega \mu - \left( {d_1^\prime + d_2^\prime + d_3^\prime + d_4^\prime + d_5^\prime } \right)\\ d_1^\prime = \frac{{2{\rm{d}}{y_2}\left( {{\rho _1}{\rm{d}}{y_1} + {\rho _2}{\rm{d}}{y_2}} \right)}}{{{\rm{d}}{z_1}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right){{\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}^2}}}\\ d_2^\prime = \frac{{2{\rm{d}}{y_1}\left( {{\rho _1}{\rm{d}}{y_1} + {\rho _2}{\rm{d}}{y_2}} \right)}}{{{\rm{d}}{z_1}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right){{\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}^2}}}\\ d_3^\prime = \frac{{2\left( {{\rho _1}{\rm{d}}{z_1} + {\rho _3}{\rm{d}}{z_2}} \right)}}{{{\rm{d}}{y_1}\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)}} - \\ \;\;\;\;\;\;\;\frac{{2{\rm{d}}{y_2}\left( {{\rho _1}{\rm{d}}{y_1} + {\rho _2}{\rm{d}}{y_2}} \right)}}{{{\rm{d}}{z_1}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right){{\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}^2}}}\\ d_4^\prime = \frac{{2\left( {{\rho _2}{\rm{d}}{z_1} + {\rho _4}{\rm{d}}{z_2}} \right)}}{{{\rm{d}}{y_2}\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)}} - \\ \;\;\;\;\;\frac{{2{\rm{d}}{y_1}\left( {{\rho _1}{\rm{d}}{y_1} + {\rho _2}{\rm{d}}{y_2}} \right)}}{{{\rm{d}}{z_1}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right){{\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}^2}}}\\ d_5^\prime = \frac{{2\left( {{\rho _3}{\rm{d}}{y_1} + {\rho _4}{\rm{d}}{y_2}} \right)}}{{{\rm{d}}{z_2}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)\left( {{\rm{d}}{y_1} + {\rm{d}}{y_2}} \right)}} \end{array} \right. $ | (17) |
式(17)即为TM模式下节点类型d的差分方程的系数。
用上述方法可以推导出TE模式、TM模式各类节点处的差分方程,在此不赘述。由推导过程可知差分方程具有二阶精度,且节点类型a处TE、TM模式的差分方程与常规的有限差分方程一致。
通过上述差分公式可以求得各节点处TE模式下的Ex和TM模式下的Hx,此外还需根据对应的正交辅助场Hy和Ey计算阻抗ZTE、ZTM、视电阻率ρTE、ρTM和相位φTE、φTM。同样用待定系数法可以求得Hy和Ey,如对节点类型a有
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {{H_y} = \frac{{\partial {E_x}}}{{\partial z}} = - \frac{{{\rm{d}}{z_2}}}{{{\rm{d}}{z_1}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right.}}){E_1} + }\\ {\left( {\frac{1}{{{\rm{d}}{z_1}}} - \frac{1}{{{\rm{d}}{z_2}}}} \right){E_0} + \frac{{{\rm{d}}{z_1}}}{{{\rm{d}}{z_2}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)}}{E_4}} \end{array}\\ {E_y} = \frac{{\partial {H_x}}}{{\partial z}} = - \frac{{{\rm{d}}{z_2}}}{{{\rm{d}}{z_1}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)}}{H_1} + \\ \left( {\frac{1}{{{\rm{d}}{z_1}}} - \frac{1}{{{\rm{d}}{z_2}}}} \right){H_0} + \frac{{{\rm{d}}{z_1}}}{{{\rm{d}}{z_2}\left( {{\rm{d}}{z_1} + {\rm{d}}{z_2}} \right)}}{H_4} \end{array} \right. $ | (18) |
式(18)同样具有二阶精度。为提高地表阻抗的计算精度,可考虑加密阻抗计算点附近的网格。阻抗、视电阻率和相位的计算公式分别为
| $ \left\{\begin{array}{l}{Z_{\mathrm{TE}}=\frac{E_{x}}{H_{y}}} \\ {Z_{\mathrm{TM}}=\frac{E_{y}}{H_{x}}}\end{array}\right. $ | (19) |
| $ \left\{\begin{array}{l}{\rho=\frac{|Z|^{2}}{\omega \mu}} \\ {\varphi=\arctan \frac{\operatorname{Im}(Z)}{\operatorname{Re}(Z)}}\end{array}\right. $ | (20) |
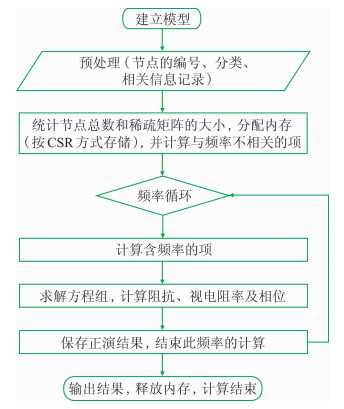
根据上述差分公式(式(9)和式(17)),按图 5所示的流程利用Fortran语言编写了四叉树有限差分法(Quadtree-FDM,简称QFDM)二维MT正演程序,并与FDM和FEM的计算结果进行对比。
|
图 5 四叉树有限差分法MT正演流程图 |
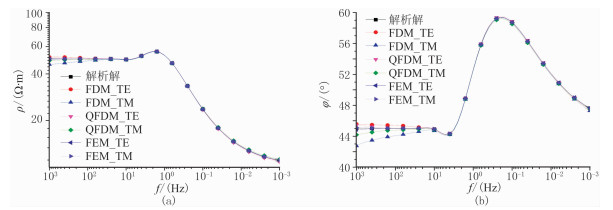
首先用一维模型进行验证。设计一个三层模型,从上至下各层电阻率分别为:ρ1=50Ω·m,ρ2= 1000Ω·m,ρ3=10Ω·m,对应各层厚度分别为:h1=2600m,h2=400m。对该模型分别用解析法、FEM、FDM和QFDM进行正演计算,其中FEM和FDM采用相同的网格剖分(共100行100列,中间部分dy和dz均为100m,共30×30个网格,网格大小按1.2倍率向四周扩展),QFDM对FDM的网格地表部分局部加密。计算结果如图 6所示,可以看出在10-3~101Hz频率范围内,几种方法计算的视电阻率值和阻抗相位值与一维解析解吻合很好;101~103Hz的高频部分,几种方法均有不同程度的误差(表 1),且频率越高误差越大,其中FEM的误差最小,QFDM其次,FDM误差最大。
|
图 6 一维模型不同方法正演结果 (a)视电阻率;(b)相位 |
|
|
表 1 一维模型不同方法计算误差统计 |
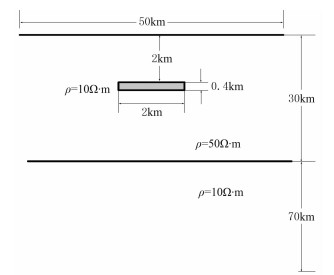
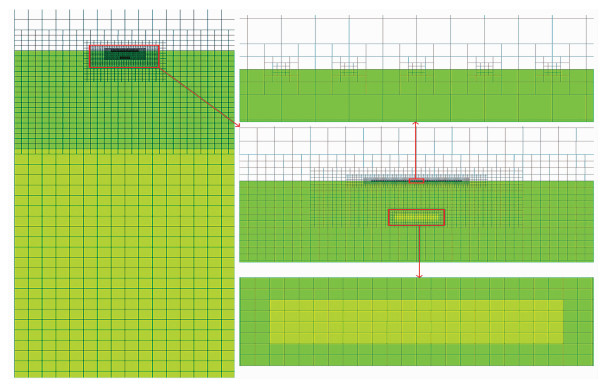
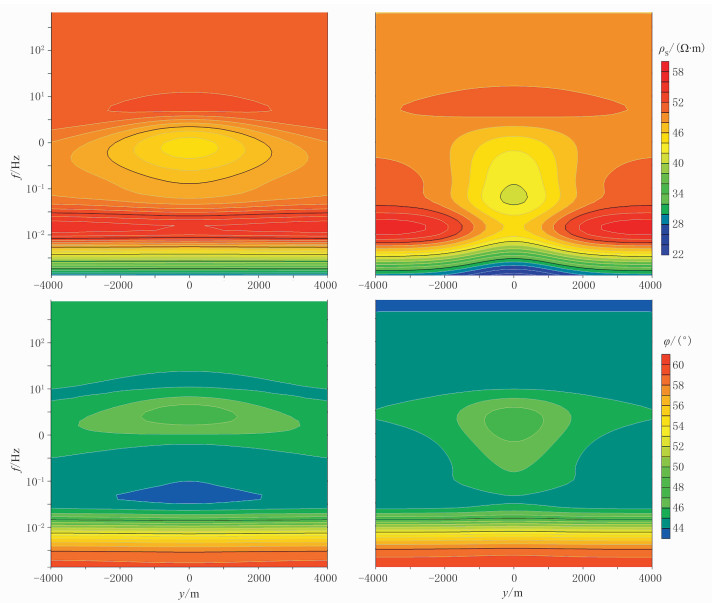
用二维理论模型分析不同剖分方法的效果。设计如图 7的理论模型:上覆地层的电阻率ρ1=50Ω·m,厚度为30km;下伏低阻层电阻率ρ2=10Ω·m,厚度为70km;在2km深处有一个二维矩形低阻异常体,沿x方向(长度)无限延伸,宽度为2km, 厚度为0.4km,电阻率为ρ3=10Ω·m。其四叉树网格剖分如图 8所示,可以看出,正演核心区域网格剖分较密,向四周逐渐变稀,在近地表和异常体边界处再次加密,符合大地电磁场分布的基本特征。图 9为用QFDM正演得到的视电阻率和相位拟断面图(绘图范围为[-4000m,4000m])。同样用FEM和FDM对相同理论模型进行正演计算。FDM采用常规的网格剖分,其加密区域与四叉树网格基本一致,最小网格大小也与QFDM一样,FEM的网格在FDM的基础上再次加密,用FEM计算结果为标准解,在y=-2000~2000m区间以100m为间隔共设41个观测点,频率范围从10-3~103Hz按对数等间隔取61个频点,正演得到共2501个数据,统计FDM和QFDM的计算效率和效果如表 2所示。从表 2可以看出,QFDM的计算量和计算时间仅约为FDM的60%,但计算精度优于FDM。
|
图 7 二维理论模型示意图 |
|
图 8 二维模型的四叉树剖分示意图 |
|
图 9 二维模型TE(左)、TM(右)模式下的视电阻率(上)和相位(下)拟断面图 |
|
|
表 2 二维模型不同方法计算效率及误差统计表 |
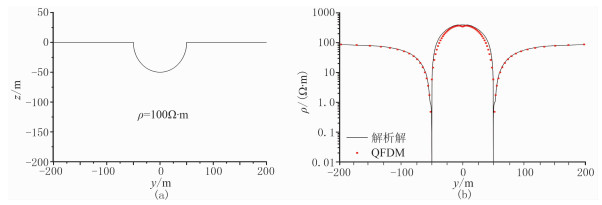
最后,利用二维半圆柱山谷模型和山脊模型验证本文算法对地形的适应性。Ward[36]给出了二维半圆柱山谷模型的解析响应。在电阻率为100Ω·m的均匀半空间中,有一个直径为100m的半圆柱状山谷(图 10a)。用QFDM计算0.01Hz、TM极化模式的视电阻率响应(图 10b)。从图中可以看出QFDM计算结果与解析解基本一致。
|
图 10 半圆柱山谷模型(a)及TM视电阻率曲线(b) |
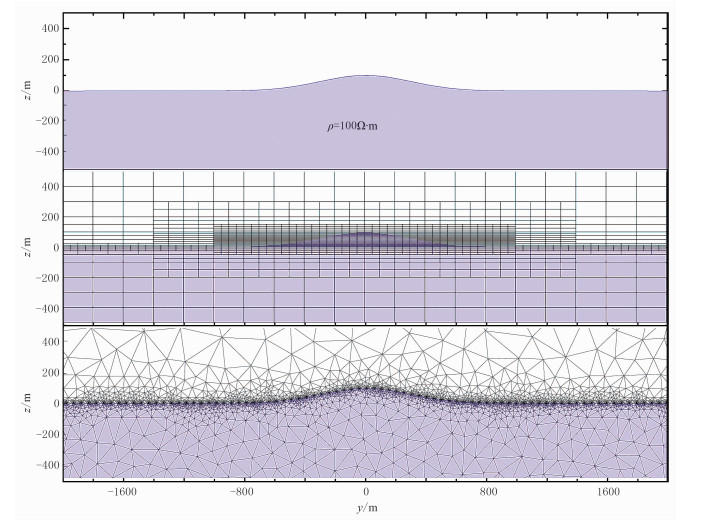
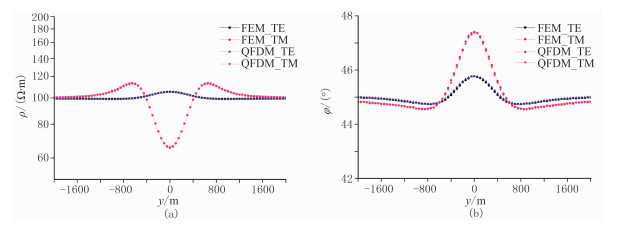
二维山脊模型如图 11上所示,电阻率ρ= 100Ω·m,求解区域(y方向)为-2000~2000m,点距为50m,共81个测点,起伏落差为100m,山脊底部宽2.4km,频率为10Hz。Wannamaker等[37]采用三角网格、线性插值FEM,徐世浙等[38]采用边界单元法、刘云等[39]采用自适应地形的四边形网格、双二次插值FEM,均在10Hz频点处对此模型做过模拟。本文用QFDM和FEM分别对该模型进行计算, 两种方法计算的网格核心区域如图 11中、图 11下所示,计算结果如图 12所示。由图可见,在10Hz频点处,QFDM与FEM的计算结果基本一致,但QFDM算法由于采用矩形单元计算,并不能完全贴合地形起伏,只能以阶梯状模拟带地形的模型,在地表曲率较大的点(如山脊两边的山脚和山脊的脊背),粗糙网格的计算结果并不平滑,TM极化对地形起伏的响应更强烈。关于这种台阶型地形,陈小斌[40]已有详细论述。若要改善这些测点的计算效果,可以加密这些测点附近的网格,再调整模型,使模型在地表与空气的接触面更加平滑。以上两个模型的正演计算表明QFDM对起伏地形的计算结果是正确的。
|
图 11 山脊模型(上)及QFDM(中)和FEM(下)网格剖分方案示意图 |
|
图 12 山脊模型10Hz正演响应视电阻率(a)和相位(b)曲线 |
QFDM相较于FDM有很多优势。主要体现在以下几个方面。
(1) QFDM由于网格剖分自由度高,能根据实际地质情况加密或抽稀网格,对复杂地质情况适应能力更强,能计算的频带也更宽。
(2) QFDM在电性突变界面加密网格可以有效减小离散误差,在地表观测点附近适当加密网格,可以提升主场和辅助场的精度,使正演结果更加精确;在精度要求相同的情况下,网格剖分合理的QFDM计算量远小于FDM。
(3) QFDM相较于FEM,在相同网格剖分的情况下计算精度略有不足,但计算效率更高。若兼顾计算效率与计算精度,采用网格略密集的QFDM是最优选择。
本文采用QFDM算法在保证计算精度的前提下,计算效率比常规FDM提高约一倍,所以该算法可望推广到三维,为三维反演提供快速算法。三维模型的剖分需采用八叉树剖分方法,将是进一步研究的内容。
| [1] |
陈理, 秦其明, 王楠, 等. 大地电磁测深正演和反演研究综述[J]. 北京大学学报(自然科学版), 2014, 50(5): 979-984. CHEN Li, QIN Qiming, WANG Nan, et al. Review of the forward modeling and inversion in magnetotelluric sounding field[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2014, 50(5): 979-984. |
| [2] |
Coggon J H. Electro magnetic and electrical modeling by the finite element method[J]. Geophysics, 1971, 36(1): 132-155. DOI:10.1190/1.1440151 |
| [3] |
William L, Ro di. A technique for improving the accuracy of finite element solution for magnetotelluric data[J]. Geophysical Journal International, 1976, 4(2): 483-506. |
| [4] |
Rijo L.Modeling of Electric and Electromagnetic Data[D].University of Utah, 1977.
|
| [5] |
Wannamaker P E, Stodt J A, Rijo L. A stable finite element solution for two-dimensional magnetotelluric modeling[J]. Geophysics, 1987, 88(1): 277-296. |
| [6] |
Franke A, Ralph B, Klaus S.2D finite element mode-ling of plane-wave diffusive time-harmonic electro-magnetic fields using adaptive unstructured grids[C].Proceeding of the 17th Workshop on Electromagnetic Induction in the Earth, Hyderabad, India, 2004.
|
| [7] |
陈乐寿. 有限元法在大地电磁场正演计算中的应用及改进[J]. 石油物探, 1981, 20(3): 84-103. CHEN Leshou. Application and improvement of finite element method in forward calculation of geo-electromagnetic field[J]. Geophysical Prospecting for Petroleum, 1981, 20(3): 84-103. |
| [8] |
陈乐寿, 孙必俊. 有限元法在大地电磁场二维正演中的改进[J]. 石油地球物理勘探, 1982, 17(3): 69-76. CHEN Leshou, SUN Bijun. Improvements on the application of finite element method to the two dimensional forward solution in the magnetotelluric method[J]. Oil Geophysical Prospecting, 1982, 17(3): 69-76. |
| [9] |
胡建德, 王光锷, 陈乐寿, 等. 大地电磁场二维正演计算中若干问题的讨论[J]. 石油地球物理勘探, 1982, 17(6): 47-55, 65. HU Jiande, WANG Guang'e, CHEN Leshou, et al. Discussion on some problems in the calculation of two dimension forward of magnetotelluric field[J]. Oil Geophysical Prospecting, 1982, 17(6): 47-55, 65. |
| [10] |
胡建德, 蔡纲. 用三角形二次插值有限元法计算二维大地电磁测深曲线[J]. 石油地球物理勘探, 1984, 19(4): 358-367. HU Jiande, CAI Gang. Calculating two dimensional geomagnetic sounding curve with triangular quadratic interpolation finite element method[J]. Oil Geophysical Prospecting, 1984, 19(4): 358-367. |
| [11] |
徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.
|
| [12] |
徐世浙, 于涛, 李予国, 等. 电导率分块连续变化的二维MT有限元模拟(Ⅰ)[J]. 高校地质学报, 1995, 1(2): 65-73. XU Shizhe, YU Tao, LI Yuguo, et al. The finite element method for modeling 2-D MT field on a geoelectrical model with continuous variation of conductivity within each block (Ⅰ)[J]. Geological Journal of China Universities, 1995, 1(2): 65-73. |
| [13] |
徐世浙, 于涛, 李予国, 等. 电导率分块连续变化的二维MT有限元模拟(Ⅱ)[J]. 高校地质学报, 1996, 2(4): 448-452. XU Shizhe, YU Tao, LI Yuguo, et al. The finite element method for modeling 2-D MT field on a geoelectrical model with continuous variation of conductivity within each block (Ⅱ)[J]. Geological Journal of China Universities, 1996, 2(4): 448-452. |
| [14] |
陈小斌. 有限元直接迭代算法[J]. 物探化探计算技术, 1999, 21(2): 165-171. CHEN Xiaobin. Direct iterative algorithm of the finite element[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1999, 21(2): 165-171. DOI:10.3969/j.issn.1001-1749.1999.02.010 |
| [15] |
陈小斌, 张翔, 胡文宝. 有限元直接迭代算法在MT二维正演计算中的应用[J]. 石油地球物理勘探, 2000, 35(4): 487-496. CHEN Xiaobin, ZHANG Xiang, HU Wenbao. Application of finite-element direct iteration algorithm to MT 2-D forward computation[J]. Oil Geophysical Prospecting, 2000, 35(4): 487-496. DOI:10.3321/j.issn:1000-7210.2000.04.011 |
| [16] |
Madden T R, Mackie R L. Three-dimensional magnetotelluric modelling and inversion[J]. Proceeding of the IEEE, 1989, 77(2): 318-333. DOI:10.1109/5.18628 |
| [17] |
Mackie R L.Three-Dimensional Magnetotlluric Mode-ling and Inversion with Applications to the California Basin and Range Province[D].Massachusetts Institute of Technology, 1991.
|
| [18] |
Mackie R L, Madden T R, Wannamaker P E. Three-dimensional magnetotelluric modeling using difference equations:Theory and comparisons to integral equation solutions[J]. Geophysics, 1993, 58(2): 215-226. DOI:10.1190/1.1443407 |
| [19] |
Mackie R L, Madden T R. Conjugate direction relaxation solutions for 3D magnetotelluric modeling[J]. Geophysics, 1993, 58(7): 1052-1057. DOI:10.1190/1.1443481 |
| [20] |
Mackie R L, Smith J T, Madden T R. Three-dimensional electromagnetic modeling using finite diffe-rence equations:The magnetotelluric example[J]. Radio Science, 1994, 29(4): 923-945. DOI:10.1029/94RS00326 |
| [21] |
谭捍东, 余钦范, Booker J, 等. 大地电磁法三维交错采样有限差分数值模拟[J]. 地球物理学报, 2003, 46(5): 1011-1020. TAN Handong, YU Qinfan, Booker J, et al. Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method[J]. Chinese Journal of Geophysics, 2003, 46(5): 1011-1020. |
| [22] |
肖骑彬, 赵国泽. 大地电磁有限差分数值解对比[J]. 地球物理学报, 2010, 53(3): 622-630. XIAO Qibin, ZHAO Guozhe. Comparison of finite difference numerical solutions in magnetotelluric mode-lling[J]. Chinese Journal of Geophysics, 2010, 53(3): 622-630. |
| [23] |
苏洲, 胡文宝. 二维大地电磁正演中的无网格算法[J]. 物探与化探, 2012, 36(6): 1024-1028, 1039. SU Zhou, HU Wenbao. Meshless algorithm in two-dimensional electromagnetic forward calculation[J]. Geophysical & Geochemical Exploration, 2012, 36(6): 1024-1028, 1039. |
| [24] |
李俊杰, 严家斌. 无网格点插值法大地电磁二维正演数值模拟[J]. 石油物探, 2014, 53(5): 617-626. LI Junjie, YAN Jiabin. Magnetotelluric two-dimensional forward numerical modeling by meshfree point interpolation method[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 617-626. DOI:10.3969/j.issn.1000-1441.2014.05.016 |
| [25] |
陈小斌.大地电磁多重网格二维反演方法的应用实践[C].中国地球物理学会第二十七届年会论文集, 2011.
|
| [26] |
杨振威, 冯磊, 赵宁, 等. 多重网格法二维Helmholtz方程解算及其在电磁法正演模拟中的应用[J]. 石油地球物理勘探, 2017, 52(1): 167-172. YANG Zhenwei, FENG Lei, ZHAO Ning, et al. Calculating 2D Helmholtz equation based on multigrid method and application in magnetotelluric modeling[J]. Oil Geophysical Prospecting, 2017, 52(1): 167-172. |
| [27] |
Doctor L J, Torborg J G. Display techniques for octree-encoded objects[J]. IEEE Computer Graphics and Applications, 2006, 1(3): 29-38. |
| [28] |
Yerry M A, Shephard M S. A modified quadtree approach to finite element mesh generation[J]. IEEE Computer Graphies and Applications, 1983, 3(1): 39-46. DOI:10.1109/MCG.1983.262997 |
| [29] |
Yerry M A, Shephard M S. Automatic three-dimen-sional mesh generation by the modified-octree technique[J]. International Journal for Numeric Methods in Engineering, 1984, 20(11): 1965-1990. DOI:10.1002/(ISSN)1097-0207 |
| [30] |
刘晓东, 周媛媛, 华祖林, 等. 四叉树网格下水动力及物质输运数值模拟研究进展[J]. 水电能源科学, 2014, 32(11): 111-114. LIU Xiaodong, ZHOU Yangyuan, HUA Zulin, et al. Advance in numerical simulation of shallow water flow and mass transport on quad-tree grids[J]. Water Resources and Power, 2014, 32(11): 111-114. |
| [31] |
Haber E, Heldmann S. An octree multigrid method for quasi-static Maxwell's equations with highly discontinuous coefficients[J]. Journal of Computational Physics, 2007, 223(2): 783-796. DOI:10.1016/j.jcp.2006.10.012 |
| [32] |
Lior H, Eldad H. A second order discretization of Maxwell's equations in the quasi-static regime on octree grids[J]. SIAM Journal on Scientific Computing, 2011, 33(5): 2805-2822. DOI:10.1137/100798508 |
| [33] |
张芩, 郭薇. 基于四叉树的邻域查询技术[J]. 系统仿真学报, 2001, 13(增刊2): 48-50. ZHANG Qin, GUO Wei. Neighbor-finding technology based on quadtree[J]. Acta Simulata Systematica Sinica, 2001, 13(S2): 48-50. |
| [34] |
刘晓东, 华祖林, 赵玉萍. 基于四叉树网格的Godunov型二维水流数值计算模式[J]. 河海大学学报(自然科学版), 2002, 30(6): 6-10. LIU Xiaodong, HUA Zulin, ZHAO Yuping. Quad-tree meshes based Godunov-type 2-D flow numerical model[J]. Journal of Hohai University, 2002, 30(6): 6-10. DOI:10.3321/j.issn:1000-1980.2002.06.002 |
| [35] |
张文生. 微分方程数值解:有限差分理论方法与数值计算[M]. 北京: 科学出版社, 2015: 111-126.
|
| [36] |
Ward S H. Electromagnetic theory for geophysical applications[J]. Mining Geophysics, 1967, 2(1): 13-196. |
| [37] |
Wannamaker P E, John A S, Luis R. Two-dimensional topographic responses in magnetotellurics modeled using finite elements[J]. Geophysics, 1986, 51(11): 2131-2144. DOI:10.1190/1.1442065 |
| [38] |
徐世浙, 王庆乙, 王军. 用边界单元法模拟二维地形对大地电磁场的影响[J]. 地球物理学报, 1992, 35(3): 380-388. XU Shizhe, WANG Qingyi, WANG Jun. Modeling 2D terrain effect on MT by the boundary element method[J]. Chinese Journal of Geophysics, 1992, 35(3): 380-388. DOI:10.3321/j.issn:0001-5733.1992.03.012 |
| [39] |
刘云, 王绪本. 大地电磁二维自适应地形有限元正演模拟[J]. 地震地质, 2010, 32(3): 382-391. LIU Yun, WANG Xuben. FEM using adaptive topo-graphy in 2-D MT forward modeling[J]. Seismology and Geology, 2010, 32(3): 382-391. DOI:10.3969/j.issn.0253-4967.2010.03.004 |
| [40] |
陈小斌. MT二维正演计算中地形影响的研究[J]. 石油物探, 2000, 39(3): 112-120. CHEN Xiaobin. On the research of the influence of terrain to MT 2D forward computation[J]. Geophysical Prospecting for Petroleum, 2000, 39(3): 112-120. DOI:10.3969/j.issn.1000-1441.2000.03.015 |



 胡华, 湖北省武汉市蔡甸区大学路111号长江大学地球科学学院, 430100。Email:
胡华, 湖北省武汉市蔡甸区大学路111号长江大学地球科学学院, 430100。Email: