② 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266061;
③ 中国石化胜利油田分公司勘探开发研究院, 山东东营 257015
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266061, China;
③ Research Institute of Exploration and Production, Shengli Oilfield Branch Co., SINOPEC, Dongying, Shandong 257015, China
重力勘探是通过探测地下介质的密度分布研究地层结构或目标体的重要地球物理手段之一。目前,重力数据反演主要包括两方面的内容。一是界面(几何参数)反演[1-3],通常假设地层密度已知,通过反演观测重力数据确定某个密度体的边界或地层界面深度,广泛应用于求取沉积层的基底深度[4]或深部不连续界面等;重力反演的另外一个内容就是地层或目标体的密度(物性参数)[5-6],通常将地下介质网格剖分成许多矩形单元,每个矩形单元的密度值设为一个常数,利用观测的重力异常值,通过反演获得密度分布,据此识别断裂带、深部岩浆体或者描绘浅部岩脉和矿体展布等。
现有的密度反演方法通常是在水平方向和垂向上剖分网格单元,假设每个单元为常密度,通过反演每个单元的密度值获得地下空间的密度分布。较为典型的方法是L2模约束反演[7],该方法通过数据项匹配和平滑约束获得具有地质意义的解,再通过密度全正或全负约束压缩解空间,但反演模型结果较发散,尤其是当正、负密度异常同时存在时,此现象更严重。为了更好地研究异常体边界,把稀疏约束、最小支撑约束等加入反演,发展了聚焦反演法[8-9],通过数学手段实现模型体积最小化。然而,上述方法均基于横向和垂向上同时进行网格剖分。若所划分网格单元数目过少,则反演结果必然不够精细;若垂向网格单元划分数目过多,反演未知量的数目和占用内存也会成倍增加,多解性问题也更严重。为此,姚长利等[10-11]研究了重磁异常快速计算和有效存储技术。
近年来,变密度方法逐渐受到学者们的关注。该方法假设密度随深度变化,地层密度的垂向变化可以表示为深度的函数,简单密度函数产生的重力异常可直接推导出相应的解析表达式[12-14],无需进行网格剖分即可计算变密度体的重力异常。鉴于变密度体重力异常解析表达精度高、耗时少等优点,低阶的密度函数形式(如二次函数、指数函数、抛物线函数、双曲线函数等)已广泛应用于密度界面的反演[15-16]。
但是,变密度迟迟未能在反演中发挥作用,原因是低阶的密度函数变化趋势相近且单调,无法描述地下复杂的密度变化,而且对应的重力异常解析表达式各不相同,这为重力反演带来诸多不便。针对上述问题,Zhang等[17]利用任意阶多项式表示地下密度异常分布,且推导了计算二维变密度体重力异常的解析表达式。近些年,二维和三维变密度体重力异常正演计算得到进一步完善和发展[18-21], 为任意不规则变密度体的重力异常正演和垂向无网格剖分的变密度反演奠定了坚实基础。
本文在变密度体重力异常正演的基础上,提出一种基于高阶多项式密度函数的重力异常反演方法,该方法无需在垂向上进行网格剖分,通过反演多项式密度函数的系数就可以确定地下物质的密度分布。理论模型测试和实际资料应用结果证明了方法的有效性。
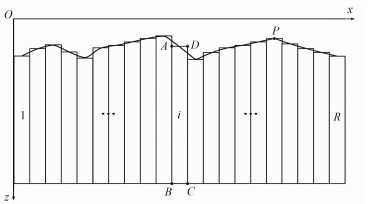
1 方法原理 1.1 变密度直立矩形二度体重力异常正演解析式与常规密度反演的网格剖分方法不同,将地下空间划分为R个横向排列的长条矩形单元(图 1),将第i个矩形单元的密度差ρi表示为随深度z变化的N阶多项式函数
| $ {\rho _i}\left( z \right) = \sum\limits_{j = 0}^N {{a_{i,j}}{z^j}} $ | (1) |
|
图 1 地下介质网格划分示意图 |
式中ai, j是第i个矩形单元多项式的系数。
如图 1所示,假设第i个矩形单元的四个顶点坐标分别为A(xi,1, zi,1), B(xi,1, zi,2), C(xi,2, zi,2)和D(xi,2, zi,1),该矩形单元的横截面用Si表示,则该单元在测点P(xp, zp)处产生的重力异常为
| $ \Delta {g_i}\left( {{x_p},{z_p}} \right) = 2G\iint_{{S_i}} {\frac{{{\rho _i}\left( z \right)\left( {z - {z_p}} \right)}}{{{{\left( {x - {x_p}} \right)}^2} + {{\left( {z - {z_p}} \right)}^2}}}{\text{d}}x{\text{d}}z} $ | (2) |
式中G是万有引力常数。将式(1)代入式(2),得
| $ \Delta {g_i}\left( {{x_p},{z_p}} \right) \\ = 2G\sum\limits_{j = 0}^N {\left[ {{a_{i,j}}\iint_{{S_i}} {\frac{{{z^j}\left( {z - {z_p}} \right)}}{{{{\left( {x - {x_p}} \right)}^2} + {{\left( {z - {z_p}} \right)}^2}}}{\text{d}}x{\text{d}}z}} \right]} \\ $ | (3) |
根据斯托克斯定理和文献[17-18, 22],可将式(3)中的面积分转换为矩形单元四条边沿逆时针方向的闭环积分,整理可得
| $ \begin{array}{l} \Delta {g_i}\left( {{x_p},{z_p}} \right) = - 2G\sum\limits_{j = 0}^N {{a_{i,j}}\sum\limits_{m = 0}^j {\left[ {\frac{1}{{j - m - 1}}C_j^m{{\left( {{z_p}} \right)}^m}} \right]} } \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{k = 1}^4 {{E_i}\left( {j,m,k} \right)} \end{array} $ | (4) |
式中:Cjm是二项式展开系数;Ei(j, m, k)代表第k条边上的线积分,表达式为
| $ \begin{array}{l} {E_i}\left( {j,m,k} \right) = \\ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \left( {{x_{i,k}} - {x_p}} \right){K_{j - m + 1}}\\ - {\left( {{z_{i,k}} - {z_p}} \right)^{j - m + 2}}{I_0}\\ 0 \end{array}&\begin{array}{l} {x_{i,k}} = {x_{i,k + 1}}\\ {x_{i,k}} \ne {x_{i,k + 1}}\;且\;{z_{i,k}} \ne {z_p}\\ {x_{i,k}} \ne {x_{i,k + 1}}\;且\;{z_{i,k}} = {z_p} \end{array} \end{array}} \right. \end{array} $ | (5) |
其中
| $ {K_l} = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{2}\ln \frac{{{{\left( {{x_{i,k + 1}} - {x_p}} \right)}^2} + {{\left( {{x_{i,k + 1}} - {z_p}} \right)}^2}}}{{{{\left( {{x_{i,k}} - {x_p}} \right)}^2} + {{\left( {{x_{i,k}} - {z_p}} \right)}^2}}}}&{l = 1}\\ {\left( {{z_{i,k + 1}} - {z_{i,k}}} \right) - \left| {{x_{i,k}} - {x_p}} \right|\left( {\arctan \frac{{{z_{i,k + 1}} - {z_p}}}{{\left| {{x_{i,k}} - {x_p}} \right|}} - \arctan \frac{{{z_{i,k}} - {z_p}}}{{\left| {{x_{i,k}} - {x_p}} \right|}}} \right)}&{l = 2}\\ {\frac{1}{{l - 1}}\left[ {{{\left( {{z_{i,k + 1}} - {z_p}} \right)}^{l - 1}}{{\left( {{z_{i,k}} - {z_p}} \right)}^{l - 1}}} \right] - {{\left( {{x_{i,k}} - {x_p}} \right)}^2}{K_{l - 2}}}&{l > 2} \end{array}} \right. $ | (6) |
| $ \begin{array}{l} {I_0} = \frac{1}{{\left| {{z_{i,k}} - {z_p}} \right|}} \times \\ \;\;\;\;\;\left( {\arctan \frac{{{x_{i,k + 1}} - {x_p}}}{{\left| {{z_{i,k + 1}} - {z_p}} \right|}} - \arctan \frac{{{x_{i,k}} - {x_p}}}{{\left| {{z_{i,k}} - {z_p}} \right|}}} \right) \end{array} $ | (7) |
式(4)为一个矩形单元在测点P处产生的重力异常,该测点测得的重力异常为所有直立矩形单元产生重力异常的叠加,即
| $ \Delta g\left( {{x_p},{z_p}} \right) = \sum\limits_{i = 1}^R {\sum\limits_{j = 0}^N {f\left( {{x_p},{z_p},i,j} \right){a_{i,j}}} } $ | (8) |
式中
假设
| $ {\mathit{\boldsymbol{F}}_{M \times \left( {N + 1} \right)R}}{\mathit{\boldsymbol{a}}_{\left( {N + 1} \right)R \times 1}} = \Delta {\mathit{\boldsymbol{g}}_{M \times 1}} $ | (9) |
式中
| $ {\mathit{\boldsymbol{F}}_{M \times \left( {N + 1} \right)R}} =\\ \left[ {\begin{array}{*{20}{c}} {f\left( {{x_1},{z_1},1,0} \right)}& \cdots &{f\left( {{x_1},{z_1},1,N} \right)}& \cdots &{f\left( {{x_1},{z_1},R,0} \right)}& \cdots &{f\left( {{x_1},{z_1},R,N} \right)}\\ {f\left( {{x_2},{z_2},1,0} \right)}& \cdots &{f\left( {{x_2},{z_2},1,N} \right)}& \cdots &{f\left( {{x_2},{z_2},R,0} \right)}& \cdots &{f\left( {{x_2},{z_2},R,N} \right)}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots \\ {f\left( {{x_M},{z_M},1,0} \right)}& \cdots &{f\left( {{x_M},{z_M},1,N} \right)}& \cdots &{f\left( {{x_M},{z_M},R,0} \right)}& \cdots &{f\left( {{x_M},{z_M},R,N} \right)} \end{array}} \right] $ | (10) |
为重力核函数矩阵;
| $ {\mathit{\boldsymbol{a}}_{\left( {N + 1} \right)R \times 1}} = {\left[ {{a_{1,0}}, \cdots ,{a_{1,N}}, \cdots ,{a_{R,0}}, \cdots ,{a_{R,N}}} \right]^{\rm{T}}} $ | (11) |
为由R个矩形单元密度函数多项式系数组成的矩阵。
与其他位场反演一样,重力反演具有很强的多解性,降低其多解性的有效方法之一就是施加各种约束。为此,结合密度差上下限约束、平滑约束、深度加权和聚焦约束等建立目标函数,以期在尽量少的先验信息和人为干预下产生符合地质规律的解。目标函数为
| $ \begin{array}{l} \psi \left( \mathit{\boldsymbol{a}} \right) = \left\| {{\mathit{\boldsymbol{W}}_d}\left( {\mathit{\boldsymbol{Fa}} - \Delta \mathit{\boldsymbol{g}}} \right)} \right\|_2^2 + {\lambda _1}\left\| {{\mathit{\boldsymbol{C}}_m}{\mathit{\boldsymbol{C}}_d}\mathit{\boldsymbol{Pa}}} \right\|_2^2 + \\ \;\;\;\;\;\;\;\;\;\;{\lambda _2}\left\| {\mathit{\boldsymbol{Ha}}} \right\|_2^2 + {\lambda _3}\left\| {\mathit{\boldsymbol{Va}}} \right\|_2^2 \end{array} $ | (12) |
式中:λ1、λ2、λ3分别为各项的权重系数;Wd=diag{1/σ1, 1/σ2, …, 1/σM}为数据权重矩阵,其中σi为第i个测点观测数据的标准偏差;第一项为数据残差项;第二项为先验模型约束项,在先验密度差模型信息未知时,该项用零模型约束;第三项为横向平滑约束项;第四项为垂向平滑约束项。式中其他参数及约束施加具体描述如下。
1.2.2 上、下限约束一般来说,密度差分布在一定区间范围内。密度差的上下限约束有利于减少反演多解性。因此构建对角分块矩阵P=diag{Pi}(i=1, 2, …, R),其中
| $ {\mathit{\boldsymbol{P}}_i} = \left[ {\begin{array}{*{20}{c}} 1&{{z_1}}& \cdots &{z_1^N}\\ 1&{{z_2}}& \cdots &{z_2^N}\\ \vdots & \vdots & \ddots & \vdots \\ 1&{{z_K}}& \cdots &{z_K^N} \end{array}} \right] $ | (13) |
这里的z1、z2、…、zK为K个不同的深度点。那么,式(12)中的Pa即可表示每个矩形单元不同深度点的密度差。令ρmin≤Pa≤ρmax,其中ρmin和ρmax分别为密度差的上、下限,从而实现对密度差绝对幅值的约束。
1.2.3 平滑约束平滑约束,即幅值相对约束,有利于产生最小结构解。与平滑相关的差分矩阵广泛应用于反演问题中。式(12)中,H为密度差横向二阶差分矩阵,具体形式为
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{P}}_1}}&{2{\mathit{\boldsymbol{P}}_2}}&{ - {\mathit{\boldsymbol{P}}_3}}&{}&{}&{}\\ {}&{ - {\mathit{\boldsymbol{P}}_2}}&{2{\mathit{\boldsymbol{P}}_3}}&{ - {\mathit{\boldsymbol{P}}_4}}&{}&{}\\ {}&{}& \ddots & \ddots & \ddots &{}\\ {}&{}&{}&{ - {\mathit{\boldsymbol{P}}_{R - 2}}}&{2{\mathit{\boldsymbol{P}}_{R - 1}}}&{ - {\mathit{\boldsymbol{P}}_R}} \end{array}} \right] $ | (14) |
式(12)中V为密度差纵向二阶差分矩阵,具体形式为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{V}} = {\rm{diag}}\left\{ {{\mathit{\boldsymbol{V}}_i}} \right\}}&{i = 1,2, \cdots ,R} \end{array} $ | (15) |
式中
| $ {\mathit{\boldsymbol{V}}_i} = \left[ {\begin{array}{*{20}{c}} 0&{ - {z_1} + 2{z_2} - {z_3}}& \cdots &{ - z_1^N + 2z_2^N - z_3^N}\\ 0&{ - {z_2} + 2{z_3} - {z_4}}& \cdots &{ - z_2^N + 2z_3^N - z_4^N}\\ \vdots & \vdots & \ddots & \vdots \\ 0&{ - {z_{K - 2}} + 2{z_{K - 1}} - {z_K}}& \cdots &{ - z_{K - 2}^N + 2z_{K - 1}^N - z_K^N} \end{array}} \right] $ |
深度加权可以减弱重力核函数随深度增加而衰减的影响。式(12)中Cd为深度加权矩阵
| $ {\mathit{\boldsymbol{C}}_d} = {\rm{diag}}\left\{ {{c_{d\left( {i,k} \right)}}} \right\}\;\;\;\;i = 1,2, \cdots ,R,k = 1,2, \cdots ,K $ | (16) |
其元素值与深度有关,表示为
| $ {c_{d\left( {i,k} \right)}} = \frac{1}{{{{\left( {{z_k} + {z_0}} \right)}^{\beta /2}}}} $ | (17) |
式中:β一般取1.5~2;z0值大小取决于目标体的中心埋深与重力异常幅值之间的关系,重力异常幅值越大,目标体埋深越浅,则z0取值越大。
1.2.5 聚焦约束平滑约束产生的结果往往较为发散,聚焦约束则可以压缩模型体积,突出异常体的边界特征。式(12)中Cm为聚焦约束矩阵,聚焦可通过多次反演改变模型空间内部的权重实现
| $ {\mathit{\boldsymbol{C}}_m} = {\rm{diag}}\left\{ {{c_{m\left( {i,k} \right)}}} \right\}\;\;\;\;i = 1,2, \cdots ,R,k = 1,2, \cdots ,K $ | (18) |
利用最小支撑泛函, Cm中的元素值表示为
| $ {c_{m\left( {i,k} \right)}} = \frac{1}{{{{\left( {\rho _{i,k}^2 + {\gamma ^2}} \right)}^{1/2}}}} $ | (19) |
式中:ρi, k表示某次反演获得的第i个长条矩形在zk深度处的密度值;γ为一个防止分母无意义的很小值。
关于多项式最大阶数的选择,一般地,多项式最高阶数越大,能够模拟的模型复杂程度越高,Jiang等[19]指出8阶多项式便可以较好地表示密度突变的情况。为兼顾计算效率,取N在8~11范围内。在利用多项式函数模拟密度变化时,多项式曲线在阶次较高时容易出现振荡现象,通过式(12)中第二项施加的先验模型约束和上下限约束可较好地解决这一问题。
由于通过反演多项式系数可间接获得地下密度分布,约束的施加需要取一系列深度点并通过多项式函数将其转换为密度值。深度取样间隔不可过大,过大则缺乏约束能力,正如同网格剖分法中单元划分过于稀疏,从而降低反演的分辨率。与网格剖分法不同的是,本文方法可适当增加约束点数而不增加反演未知参量的数量。
2 理论模型试验为了验证本文提出的密度多项式系数反演方法,设计了3个模型进行试验。研究区范围均设置为8km×3km,理论重力异常数据利用式(8)计算,并添加均值为0、标准差为0.01mGal的高斯白噪声。使用本文方法将地下等间距划分为60个长条矩形,每个矩形的纵向长度均为3km;将密度随深度变化用9阶多项式函数表示,即N=9;设置密度差值约束的上、下限分别为500kg/m3和-500kg/m3;设置权重参数λ2=λ3=0.01,初次反演时取λ1=0.01,后续迭代中取λ1=1;迭代次数一般取5~10;初次反演时Cm取为单位矩阵,即无聚焦约束,相当于仅L2模约束反演;后续迭代中Cm由式(19)不断更新,进而得到最终的反演结果。
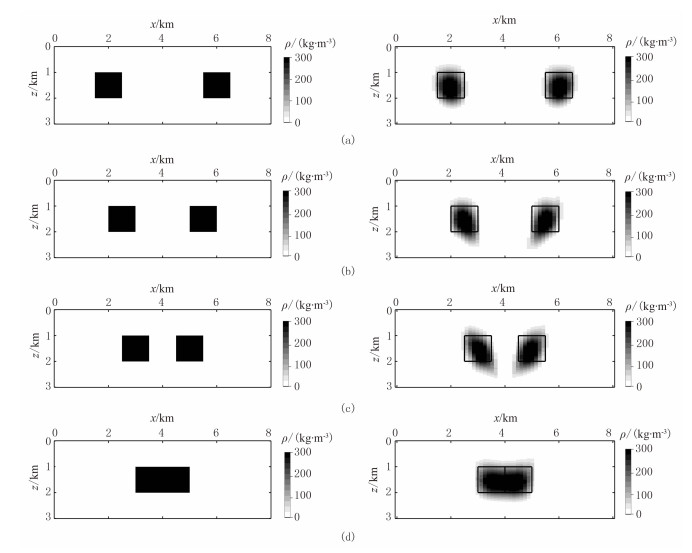
2.1 模型Ⅰ:中心埋深相同、水平间距不同的双密度体模型模型Ⅰ(图 2左)截面由两个边长为1 km的正方体组成,中心埋深均为1.5 km,两异常体密度差均为300kg/m3。为了测试算法在水平方向上分辨两异常体的能力,设置两密度体的水平间距d分别为3、2、1、0km。模拟测线沿水平方向,在0~8km等间距布设120个测点,理论重力异常如图 3所示。
|
图 2 模型Ⅰ两个异常体在不同水平间距d时的真实模型(左)及反演结果(右) (a)d=3km; (b)d=2km; (c)d=1km; (d)d=0 |
|
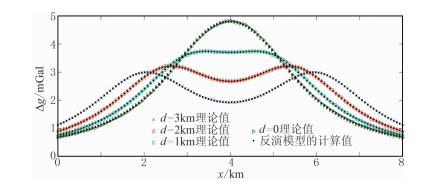
图 3 模型Ⅰ两个异常体在不同水平间距d时的重力异常理论曲线与反演值 |
图 2右显示了不同水平间距下模型的迭代反演结果。由图可见,在水平间距较大时,本文反演方法能较好地分辨两异常体(图 2a);随着水平间距减小,两密度体产生的重力异常叠加效应增强,此时,两异常体仍然能被分辨出来(图 2b和图 2c);直到两异常体合并在一起(图 2d),反演结果能正确反映异常体的规模和边界。图 3中灰色点线是不同水平间距下利用反演模型计算的重力异常值,可见与理论值吻合很好。
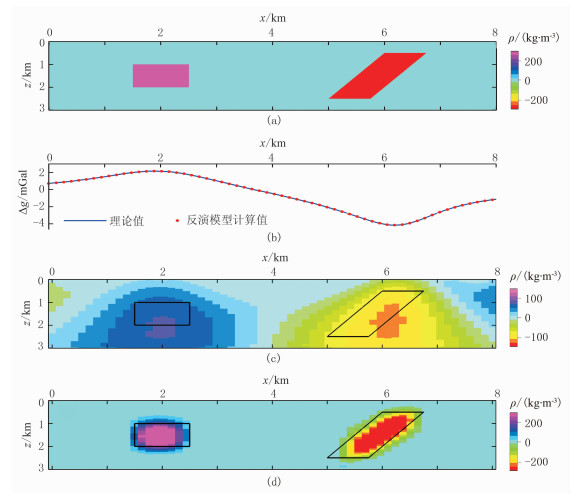
2.2 模型Ⅱ:中心埋深相同、形状不同的正负密度体模型模型Ⅱ由一个边长为1km的正方体和一倾斜的截面为平行四边形密度异常体组成(图 4a),两个异常体的中心埋深均为1.5km,两异常体密度差分别为300kg/m3和-300kg/m3。
|
图 4 模型Ⅱ正、反演结果 (a)模型示意图;(b)重力异常理论值与反演模型正演结果比较; (c)初次反演结果(仅L2模约束);(d)本文方法反演结果 |
首先,利用本文方法在无聚焦约束下进行初次反演(图 4c),可见该结果呈现出一正一负的两个密度异常区域,但异常范围较实际范围稍大,且异常幅值比实际值偏小,解较发散,倾斜异常体的倾向无法识别。另外,由于正负异常同时存在,反演结果表现为正负极性之间平缓过渡。将模型划分为60×30个常密度单元,采用L2模约束进行反演,其结果(本文未展示)与图 4c基本一致。多项式系数反演方法仅需要反演60×10=600个系数,而网格剖分法需要反演1800个密度值。采用本文方法迭代反演的结果如图 4d所示,可见反演结果的异常体位置和形状都与模型较吻合,且异常体边界更加清晰,倾向也更易识别。
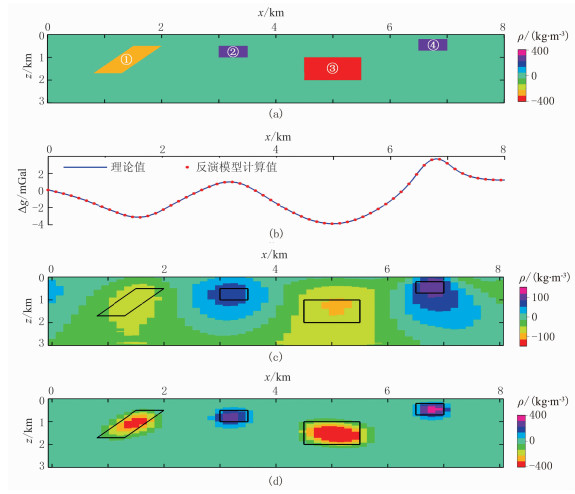
2.3 模型Ⅲ:形状、中心埋深均不同的正、负密度体模型模型Ⅲ由规模、埋深均不相同的两个正、两个负密度异常体组成(图 5a),异常体参数见表 1。该模型产生的重力异常如图 5b所示,由图可见,浅部异常体产生的重力异常更为高陡,而埋深较深的密度体产生的重力异常较为宽缓。图 5c是本文方法仅L2模约束下的初次反演结果。由图可见,与模型二模拟结果类似,密度模型较为弥散,且重力异常幅值较真实值偏小,浅部异常体产生的异常较深部异常体误差稍小一些;深度越大,异常弥散范围越大,仅能大体判断异常体的中心位置;图 5d为本文方法反演结果,可以看出浅部与深部异常体的重力异常在位置和形状上均与真实模型吻合较好,异常体规模和边界更加突出。图 5a中利用反演结果(图 5d)正演计算的重力异常值与理论重力异常值吻合较好,两者误差小于0.5%,表明了本文反演方法在复杂多源情况下是可行的。
|
图 5 模型Ⅲ正、反演结果 (a)模型示意图;(b)重力异常理论值与反演模型正演结果比较;(c)初次反演结果(仅L2模约束);(d)本文方法反演结果 |
|
|
表 1 模型Ⅲ密度异常体位置及密度差参数 |
研究区位于渤海湾盆地济阳坳陷,研究目标是该区的古潜山。渤海湾盆地历经印支期褶皱隆升、燕山期断块抬升和喜山期拉张断块改造及覆盖掩埋等三个重要的演化阶段[23]。研究区地势平坦,由地形引起的重力异常可忽略不计。东营运动之后,盆地渐趋稳定,地形逐渐夷平,浅部地层厚度基本一致,且构造运动不明显,内部密度分布均匀。因此,第四系底界面及新近系与古近系之间的界面对重力场形态的影响较小[24]。古潜山顶面是该区最主要的物性界面,也是本文主要的研究对象。该区潜山主要由下古生界碳酸盐岩和太古界变质岩组成,表现为高密度、高阻抗的特征。区内局部凹陷主要由中、新生代(部分地区含石炭、二叠系)碎屑岩组成,相对于潜山呈现低密度特征。潜山与上覆低密度体的密度差最大可达180kg/m3,这为利用重力资料研究潜山构造提供了物性基础。
图 6是过研究区的一条南北向地震剖面,从图中可以比较容易地识别地层分界面和正断层等。古近纪该区经历了断陷、断拗和拗陷等阶段,在地震剖面上可观察到左侧凹陷至凸起(潜山)的过渡带上广泛发育超覆尖灭和错断。潜山顶界面为速度和密度的突变面,由于地层的高速屏蔽效应,地震波难对潜山内部进行成像。右侧潜山的顶界面成像较为清晰,而左侧潜山右翼顶界面成像模糊。仅凭现有地震资料,两潜山之间是否存在低密度沟槽尚存在争议。

|
图 6 研究区重力测线(图 7)对应的叠后地震剖面 |
|
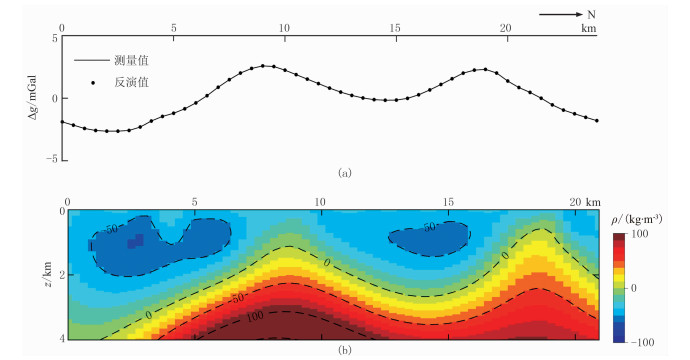
图 7 实际资料反演 (a)实测剩余重力异常值与反演结果正演曲线比较;(b)反演密度差剖面 |
由图 7a所示的经区域背景场分离后获得的剩余重力异常(实线)可见,剩余重力异常曲线可以突出潜山顶面起伏及沉积盖层的厚度变化。重力低对应基底断陷或坳陷,盖层增厚;重力高对应基底隆起,盖层减薄。重力异常曲线明显出现两个重力高值区,在约9.5km和19.0km处分别存在一重力极大值点,该重力高解释为地下潜山的响应。采用本文方法进行反演,将地下等间距划分为70个长条矩形,矩形单元的最大深度为4km,将密度随深度变化用10阶多项式函数表示,反演各长条矩形多项式密度函数的系数以获得地下密度分布。
图 7b为利用本文方法反演得到的密度差剖面,结果显示研究区存在明显的“两正两负”的密度异常区,正密度区域指示了潜山的分布位置,而负密度区域则指示了凹陷或沟槽的存在。对比发现反演的密度差剖面(图 7b)与地震剖面(图 6)有良好的对应关系:正密度体规模和边界与地震潜山成像及潜山顶界面吻合;两潜山之间的沟槽在反演结果也有体现,呈“两凸夹一凹”的特征。对比利用反演密度模型计算的重力异常(图 7a)与实测的剩余重力异常,两者相对误差小于1%。基于本文方法的重力反演结果弥补了该区现有地震资料的不足,证实了沟槽的存在。
4 结论本文提出了一种基于高阶多项式密度函数的重力异常反演方法,该方法具有以下特征:
(1) 地下复杂的密度变化可利用多项式函数表示,变密度体产生的重力异常采用解析式表达,计算效率较高;
(2) 将地下划分为竖直并排的矩形单元,只需反演各个矩形单元的多项式系数,无需在垂向上剖分网格,求解未知量相对较少,一定程度上降低了反演的多解性;
(3) 构建的目标函数灵活,可以方便地施加约束条件和其他地质、地球物理先验信息;
(4) 将随深度连续变化的密度多项式函数与多种约束相结合,既能研究异常体的空间位置和规模,又能突出异常体边界信息,得到符合地质规律的模型解。
该方法成功应用于渤海湾盆地济阳坳陷区古潜山的识别,重力反演结果证实了该区潜山与沟槽呈高低相间的展布特征。本文仅就基于高阶多项式密度函数的二维重力反演的原理方法做了详细阐述,并进行初步应用,但所述反演思路和约束策略同样适用于三维情况。
需要指出的是,由于多项式函数是连续平滑的,本文密度表示方法可能更适合描述密度连续变化的地层。在反演局部密度体时,由于多解性的存在,施加合理的约束是必要的。本文只对高阶多项式密度函数展开研究,对低阶多项式讨论较少,而低阶多项式可以模拟密度的整体趋势,不同阶次信息的结合和充分利用是下一步需要研究和完善的方向。
| [1] |
张建中. 解重力反问题的边界元法[J]. 石油地球物理勘探, 1993, 28(5): 603-613. ZHANG Jianzhong. Boundary element method for gravity inversion[J]. Oil Geophysical Prospecting, 1993, 28(5): 603-613. |
| [2] |
谷文彬, 陈清礼, 王余泉, 等. 饶阳凹陷虎8北潜山重力三维松约束反演[J]. 石油地球物理勘探, 2016, 51(6): 1219-1226. GU Wenbin, CHEN Qingli, WANG Yuquan, et al. Part-constrained 3D gravity inversion for the Hubabei buried hill in Raoyang Sag[J]. Oil Geophysical Prospecting, 2016, 51(6): 1219-1226. |
| [3] |
林宝泽, 肖锋, 王明常. 二维重力数据径向反演及应用[J]. 石油地球物理勘探, 2018, 53(2): 403-409. LIN Baoze, XIAO Feng, WANG Mingchang. 2D gra-vity data radial inversion[J]. Oil Geophysical Prospecting, 2018, 53(2): 403-409. |
| [4] |
张建中, 戴云, 钟本善. 下辽河裂谷型断陷盆地基底的重力解释方法[J]. 物探化探计算技术, 1999, 21(3): 252-256. ZHANG Jianzhong, DAI Yun, ZHONG Benshan. Gravitational method for determining the basement of Liaohe rifted basin[J]. Computing Techniques for Geophysical & Geochemical Exploration, 1999, 21(3): 252-256. DOI:10.3969/j.issn.1001-1749.1999.03.013 |
| [5] |
耿美霞, 杨庆节. 应用RBF神经网络反演二维重力密度分布[J]. 石油地球物理勘探, 2013, 48(4): 651-657. GENG Meixia, YANG Qingjie. 2-D density inversion with the RBF neural network method[J]. Oil Geophysical Prospecting, 2013, 48(4): 651-657. |
| [6] |
舒梦珵, 王彦飞. 储层重力密度反演后验约束正则化方法[J]. 地球物理学报, 2015, 58(6): 2079-2086. SHU Mengcheng, WANG Yanfei. The posterior constrained regularization method for reservoir density inversion[J]. Chinese Journal of Geophysics, 2015, 58(6): 2079-2086. |
| [7] |
Li Y G, Oldenburg D W. 3-D inversion of gravity data[J]. Geophysics, 1998, 63(1): 109-119. DOI:10.1190/1.1444302 |
| [8] |
Portniaguine O, Zhdanov M S. Focusing geophysical inversion images[J]. Geophysics, 1999, 64(3): 874-887. DOI:10.1190/1.1444596 |
| [9] |
Commer M. Three-dimensional gravity modelling and focusing inversion using rectangular meshes[J]. Geophysical Prospecting, 2011, 59(5): 966-979. |
| [10] |
姚长利, 郝天珧, 管志宁, 等. 重磁遗传算法三维反演中高速计算及有效存储方法技术[J]. 地球物理学报, 2003, 46(2): 252-258. YAO Changli, HAO Tianyao, GUAN Zhining, et al. High-speed computation and efficient storage in 3-D gravity and magnetic inversion based on genetic algorithms[J]. Chinese Journal of Geophysics, 2003, 46(2): 252-258. DOI:10.3321/j.issn:0001-5733.2003.02.020 |
| [11] |
姚长利, 郑元满, 张聿文. 重磁异常三维物性反演随机子域法方法技术[J]. 地球物理学报, 2007, 50(5): 1576-1583. YAO Changli, ZHENG Yuanman, ZHANG Yuwen. 3-D gravity and magnetic inversion for physical properties using stochastic subspaces[J]. Chinese Journal of Geo-physics, 2007, 50(5): 1576-1583. DOI:10.3321/j.issn:0001-5733.2007.05.035 |
| [12] |
Chai Y, Hinze W J. Gravity inversion of an interface above which the density contrast varies exponentially with depth[J]. Geophysics, 1988, 53(6): 837-845. DOI:10.1190/1.1442518 |
| [13] |
Chakravarthi V, Sundararajan N. Ridge-regression algorithm for gravity inversion of fault structures with variable density[J]. Geophysics, 2004, 69(6): 1394-1404. DOI:10.1190/1.1836814 |
| [14] |
Chappell A, Kusznir N. An algorithm to calculate the gravity anomaly of sedimentary basins with exponential density-depth relationships[J]. Geophysical Prospecting, 2008, 56(2): 249-258. DOI:10.1111/gpr.2008.56.issue-2 |
| [15] |
张盛, 孟小红. 约束变密度界面反演方法[J]. 地球物理学进展, 2013, 28(4): 1714-1720. ZHANG Sheng, MENG Xiaohong. Constraint interface inversion with variable density model[J]. Progress in Geophysics, 2013, 28(4): 1714-1720. |
| [16] |
商宇航, 邰振华, 秦涛. 基于双曲线密度模型的频率域界面反演[J]. 石油地球物理勘探, 2018, 53(4): 858-864. SHANG Yuhang, TAI Zhenhua, QIN Tao. Interface inversion in the frequency domain based on the hyper-bolic density model[J]. Oil Geophysical Prospecting, 2018, 53(4): 858-864. |
| [17] |
Zhang J Z, Zhong B S, Zhou X X, et al. Gravity ano-malies of 2-D bodies with variable density contrast[J]. Geophysics, 2001, 66(3): 809-813. DOI:10.1190/1.1444970 |
| [18] |
Zhou X. Analytic solution of the gravity anomaly of irregular 2D masses with density contrast varying as a 2D polynomial function[J]. Geophysics, 2010, 75(2): I11-I19. DOI:10.1190/1.3294699 |
| [19] |
Jiang L, Zhang J Z, Feng Z B. A versatile solution for the gravity anomaly of 3D prism-meshed bodies with depth-dependent density contrast[J]. Geophysics, 2017, 82(4): G77-G86. DOI:10.1190/geo2016-0394.1 |
| [20] |
Zhang J Z, Jiang L. Analytical expressions for the gravitational vector field of a 3-D rectangular prism with density varying as an arbitrary-order polynomial function[J]. Geophysical Journal International, 2017, 210(2): 1176-1190. DOI:10.1093/gji/ggx230 |
| [21] |
Jiang L, Liu J, Zhang J Z, et al. Analytic expressions for the gravity gradient tensor of 3D prisms with depth-dependent density[J]. Surveys in Geophysics, 2018, 39(3): 337-363. DOI:10.1007/s10712-017-9455-x |
| [22] |
张建中, 周熙襄, 王克斌. 密度随深度变化的二度体重力正演公式[J]. 石油地球物理勘探, 2000, 35(2): 202-207. ZHANG Jianzhong, ZHOU Xixiang, WANG Kebin. 2-D gravity forward formula showing density variation with depth[J]. Oil Geophysical Prospecting, 2000, 35(2): 202-207. DOI:10.3321/j.issn:1000-7210.2000.02.009 |
| [23] |
李丕龙, 张善文, 王永诗, 等. 断陷盆地多样性潜山成因及成藏研究——以济阳坳陷为例[J]. 石油学报, 2004, 25(3): 28-31. LI Peilong, ZHANG Shanwen, WANG Yongshi, et al. Multiplex buried-hill genesis and pool-forming in rift-ed basin[J]. Acta Petrolei Sinica, 2004, 25(3): 28-31. DOI:10.3321/j.issn:0253-2697.2004.03.005 |
| [24] |
胡加山, 胡贤根, 崔世凌. 东营凹陷典型剖面重磁电震综合解释方法研究[J]. 石油物探, 2009, 48(4): 401-406. HU Jiashan, HU Xian'gen, CUI Shiling. Gravity-magnetic-electric-seismic integrated interpretation method for typical profile of Dongying Sag[J]. Geophysical Prospecting for Petroleum, 2009, 48(4): 401-406. DOI:10.3969/j.issn.1000-1441.2009.04.013 |



 张建中, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院C415室, 266100。Email:
张建中, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院C415室, 266100。Email: