② 中国人民解放军94019部队, 新疆和田 848000
② Force Unit 94019, the Chinese People's Liberation Army, Hetian, Xinjiang 848000, China
利用地磁场异常探测地下或水下物体,一直是勘探地球物理界的研究热点。目前地磁技术研究的主要对象是地下或水下大型异常体(如潜艇),而对诸如管道、未爆弹药等小型铁磁性物体,始终缺乏成熟的技术进行探测。当前,磁梯度张量方法受到广泛关注,成为探测小型磁性目标体形状、大小、姿态等信息的新手段。
孙刃[1]较系统地分析总结了利用磁异常正反演识别目标的方法,并将其用于水下沉船、管线、未爆军火等目标的探测;吴国超[2]提出利用张量矩阵特征值和6个矩阵元素对大型地质体进行边界识别,分辨率较高,试验效果很好;王林飞等[3]利用磁梯度张量研究大型磁源体的位置与边界;李金朋等[4]研究了地下小目标体的反演及三维成像;尹刚等[5]利用张量不变量和矩阵特征值定位磁目标体;朱慧慧等[6]建立了基于磁偶极子构造法几何建模的地下管线磁异常正演模型,分析了多种磁化因素对铁管磁异常正演结果的影响,为高精度地下管线磁探测奠定了理论基础。上述方法主要针对磁性目标的二维边界识别、三维姿态反演、磁性目标定位等,是局部磁异常识别方法,而且无法避免磁测数据的正、反演,运算量大,受测量数据精度的限制较大,因而不能清晰地表现磁测目标体。谢永茂[7]提出了建立样本库,通过模板匹配识别地下磁性体,提供了一种新的磁异常体识别思路。
本文首先建立地下小型磁性目标体不同形状、不同方位条件下模型的正演数据库,分析了9个磁梯度张量矩阵属性参量,论证其作为分类属性的可行性;利用这9个矩阵属性参量融合识别磁源目标体的形状,可在一定程度上弥补磁测数据精度的不足;再将这9个属性参量用于支持向量机(Support Vector Machine,SVM)对目标进行分类;然后利用量子粒子群算法优化的支持向量机对仿真模型数据分类,推断目标体形状,取得了很好的识别效果;最后设计实验验证其实用性。
1 磁梯度张量矩阵及属性参量 1.1 磁梯度张量矩阵地磁总场包括地磁场和异常场,其中地磁场在空间上的变化很小,在小范围内可以看做一个稳定场,所以磁梯度张量可以认为是磁异常矢量在x、y、z三个方向上的变化率。梯度张量元素受地磁场倾向、偏角影响较小,通过反演能够更精确地描述场源体的磁化方向和几何形态[8]。
地磁场是矢量场,由矢量场三分量推导梯度张量矩阵G表达式为
| $ \boldsymbol{G} = \left[\begin{array}{lll}{B_{x x}} & {B_{x y}} & {B_{x z}} \\ {B_{y x}} & {B_{y y}} & {B_{y z}} \\ {B_{z x}} & {B_{z y}} & {B_{z z}}\end{array}\right] = \left[\begin{array}{ccc}{\frac{\partial^{2} U}{\partial x^{2}}} & {\frac{\partial^{2} U}{\partial x \partial y}} & {\frac{\partial^{2} U}{\partial x \partial z}} \\ {\frac{\partial^{2} U}{\partial y \partial x}} & {\frac{\partial^{2} U}{\partial^{2} y}} & {\frac{\partial^{2} U}{\partial y \partial z}} \\ {\frac{\partial^{2} U}{\partial z \partial x}} & {\frac{\partial^{2} U}{\partial z \partial y}} & {\frac{\partial^{2} U}{\partial z^{2}}}\end{array}\right] $ | (1) |
式中U为磁标势,矩阵中的9个元素即为磁场矢量B在空间三个方向分量(Bx、By、Bz)的变化率。磁法勘探中地磁场及铁磁物质产生的异常场可看作无源的静磁场[5]。由式(1)可知梯度张量矩阵是对称的,且旋度和散度均为0,因此梯度张量矩阵G的9个元素中,只有5个(Bxx、Byy、Bxy、Bxz、Byz)相互独立[9]。
1.2 特征提取作为一种机器学习方法,支持向量机需对分类对象进行特征提取,通过对特征进行分类来识别目标。每一个特征都与分类对象本身相关,且不同对象的特征之间都应该保持离散。特征的数量越多,分类越准确。为保证信息不冗余,不同的特征之间必须互不相关,或相关度很低,这些特征即可作为支持向量机分类的属性参量。从样本库中提取不同属性参量的数据构造特征向量,作为支持向量机的训练和测试样本数据。
选择磁总场模量(TMI)、矩阵特征值的最大值(ME)、两个矩阵不变量(I1、I2)作为分类的属性参量。
TMI可由磁场三分量计算
| $ \mathrm{TMI} = \sqrt{B_{x}^{2}+B_{y}^{2}+B_{z}^{2}} $ | (2) |
设A为n阶矩阵,λ为常数,X为n维非零向量。若AX = λX,则λ称为矩阵A的特征值。因为式(1)是3阶张量矩阵,因此最多只有3个特征值。其中最大特征值对磁目标体边界和形状都很敏感,识别能力较强。
矩阵不变量能够表征一个矩阵的特征,经由梯度张量矩阵计算得到的张量不变量不需要额外的处理就可以很好地描述磁场源。该矩阵的不变量蕴含着很多磁目标体的特征信息,可以作为地下磁目标体识别的分类属性参量。式(1)中矩阵的特征值即是基本不变量[10],矩阵中的其他不变量可由矩阵特征值表示。
定义λ1、λ2、λ3为张量矩阵G的特征值,则其余两个矩阵不变量为
| $ \left\{\begin{array}{l}{I_{1} = B_{x x} B_{y y}+B_{y y} B_{z z}+B_{x x} B_{z z}-B_{x y}^{2}-B_{y z}^{2}-B_{x z}^{2}} \\ \;\;\;\; { = \lambda_{1} \lambda_{2}+\lambda_{2} \lambda_{3}+\lambda_{1} \lambda_{3}} \\ {I_{2} = B_{x x}\left(B_{y y} B_{z z}-B_{y z}^{2}\right)+B_{x y}\left(B_{y z} B_{x z}-B_{x y} B_{z z}\right)+} \\ \;\;\;\; {B_{x z}\left(B_{x y} B_{y z}-B_{x z} B_{y y}\right) = \lambda_{1} \lambda_{2} \lambda_{3}}\end{array}\right. $ | (3) |
除以上4个属性参量之外,还提取了式(1)中的Bxx、Bxy、Bxz、Byy、Byz等5个独立元素作为支持向量机分类的属性参量,总共使用这9个属性参量识别目标。
2 基于量子粒子群优化的支持向量机支持向量机可用于模式分类和非线性回归,具有结构风险最小化的优势,具有很好的泛化性能。支持向量机的算法公式为
| $ f(\boldsymbol{S}) = \sum\limits_{i = 1}^{n} \partial_{i} L_{i} K\left(\boldsymbol{S}_{i}, \boldsymbol{S}\right)+b $ | (4) |
式中:Si为训练样本;Li为训练样本的标签;∂i和b为训练样本的拉格朗日乘子;K(S1, S2) =
加入松弛因子ξ(i),用于衡量实际指示值Li与支持向量机输出之间的距离,支持向量机优化的目标函数为[11]
| $ \begin{array}{l} \;\;\;\min \left( {\frac{1}{2}{{\left\| \mathit{\boldsymbol{w}} \right\|}^2}} \right) + c\sum\limits_{i = 1}^l {{\mathit{\boldsymbol{\xi }}_i}} \\ {L_i}\left( {{\mathit{\boldsymbol{w}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_i} + b} \right) \ge 1, i = 1, 2, \cdots, l \end{array} $ | (5) |
式中:w即是对目标进行分类的超平面的法向量;l为分类时特征向量的维数;c是惩罚因子。
影响SVM的因素非常多,如惩罚因子c以及核函数参数σ,对于小型样本分类精准度的影响最大[12]。因此,在应用SVM做分类预测时,这两个参数的选取尤为关键。
一般通过网格划分来寻找参数c和σ的最佳值。虽然采用网格搜索能够获得最高的分类准确率,即全局最优解,但如果要在更大范围内寻找参数c和σ的最佳值会很费时。本文应用一种通过寻找最优解来求解最佳参数的算法,即量子粒子群优化算法(Quantum Particle Swarm Optimization,QPSO)[11]。
粒子群优化算法是智能计算领域中,除蚁群算法之外的另一种基于群体智能的优化算法。该方法通过粒子在解空间的搜索来寻找最优解。相比基因等其他算法,粒子群优化算法无需交叉、变异、选择等流程,正确率比较高,全局最优值收敛速度快,参数寻优耗时短。
Sun等[13]认为粒子具有量子性,从量子力学的角度提出了一种新的粒子群优化算法模型,并经实验证明其具有更好的收敛性。粒子群优化算法[14]具体过程如下。
在有M个粒子进行寻优的J维搜索空间中,假设第i个粒子的位置为Xi = (Xi, 1,Xi, 2,…,Xi, J),这里t为进化代数;其每代最优位置为Pi = (pi, 1,pi, 2,…,pi, J),整个量子粒子群目前所搜索到的全局最优解为Pg = (pg, 1,pg, 2,…,pg, J)。通过200次迭代,选取全局最优的c和σ。
粒子i的位置为
| $ \left\{ \begin{array}{l} X_{i, j}^{(t + 1)} = p_{i, j}^{(t + 1)} \pm \beta \ln \frac{1}{u}\left| {{m_{{\rm{best}}, i}}-X_{i, j}^{(t)}} \right|\\ {m_{{\rm{best}}, i}} = \sum\limits_{j = 1}^J {\frac{{{p_{i, j}}}}{J}} \\ p_{i, j}^{(t + 1)} = rp_{i, j}^{(t)} + (1-r){p_{g, j}} \end{array} \right. $ | (6) |
式中:mbest, i是粒子i的最优位置;Xi(t)是第t代粒子i的位置;β为QPSO的收缩系数;u、r是[0, 1]的随机数。在迭代过程中,±是由区间[0, 1]的随机数u的大小决定的,大于0.5时取负,其余情况取正[14]。
最后得到进化t代之后的pi, j,即可得到最优参数c和σ。基于量子粒子群算法优化后的c和σ,可建立最优化QPSO-SVM分类模型。
3 仿真分析 3.1 仿真数据库的建立为了进行仿真验证,首先构建一个垂直磁化的磁性体进行正演。在观测面上建立以观测原点为中心的61×61个网格节点的数据平面。数据平面上每个网格节点都包含该位置的梯度张量信息,即一个由式(1)计算的3阶梯度张量矩阵。
设置8组长方体磁性体正演模型,模型中心位置均处于坐标原点,埋深均为5m,磁化率相同,姿态都为水平,但他们的形状和磁化方向不同,即构建8种不同尺寸的长方体模型。每个模型的磁化偏角范围为0°~180°,间隔设置为10°(0°与180°重合),这样得到共180种不同磁化方向组合,总共8×9×180个包含61×61个网格点的数据平面。分别计算平面上61×61个点的TMI、3个不变量和5个张量矩阵元素,这样每个平面都可以衍生出9个61维的独立属性矩阵。具体的数据结构参见图 1。
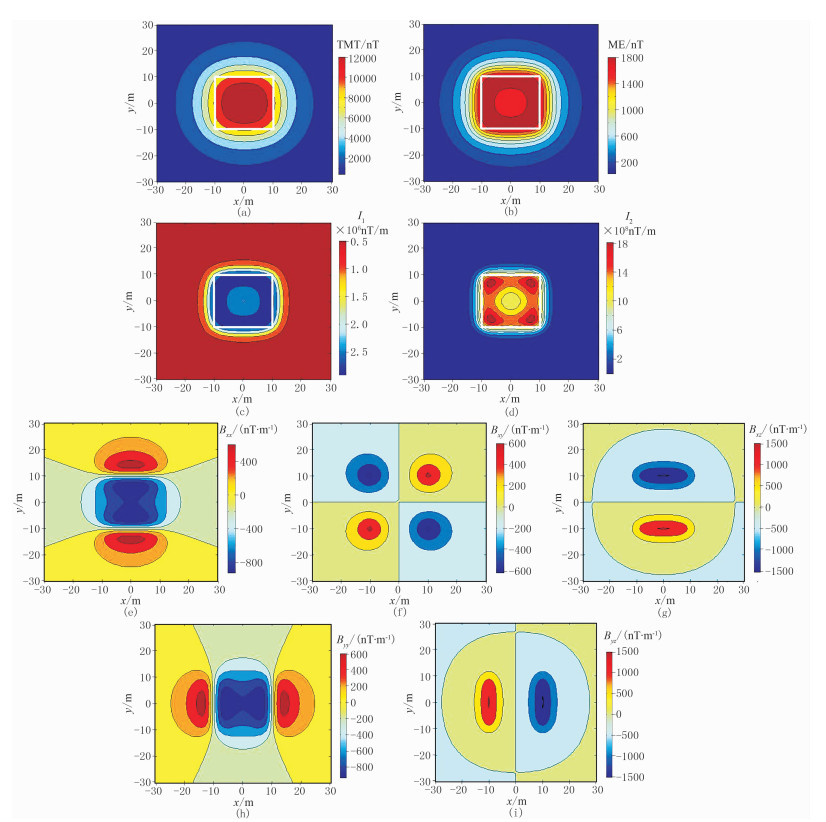
|
图 1 9个属性参量的等值线图 (a)TMI;(b)ME;(c)I1;(d)I2;(e)Bxx;(f)Bxy;(g)Bxz;(h)Byy;(i)Byz 图a~图d中白色矩形框是磁化体的轮廓 |
图 1为9个属性参量的等值线图,每幅图都代表一个属性参量的属性矩阵。图中每个像素点的数值就是矩阵中相应位置的值。
3.2 特征提取为论证9个属性参量作为支持向量机分类的属性参量的可行性,以长、宽、高均为10m、埋深为15m的正方体模型为例进行正演。设磁倾角为90°,磁偏角为0°,磁化率为0.4。
由图 1可见,TMI的等值线分布(图 1a)比较均匀,但磁化体边角特征不明显;磁性体矩阵的最大特征值ME(图 1b)和I1(图 1c)相较于其他属性参量,能更详细和清晰地描述磁性体的边界和形状特征;I2(图 1d)对边角特征更敏感,能凸显浅部源;5个矩阵独立元素(图 1e~图 1d)中,Bxx描述y轴方向的边界情况,出现了三个极值点,Bxy可描述磁性体的边角,Bxz可描述y轴方向的边界情况,出现了两个极值点,Byy可描述x轴方向的边界情况,出现了三个极值点,Byz主要描述x轴方向的边界,出现了两个极值点[15]。可见这5个矩阵独立元素也能较清晰地表现磁性体的部分特征。可以看出,这5个属性参量都与磁性体的形状有着较高的相关性,可从不同角度反映磁性体的形状特征。
图 2为所有样本的9个属性参量的分维属性图,可据此分析这9个独立属性参量对不同形状和倾角的敏感性。图中每个点线代表不同的磁偏角和磁倾角。对于倾角的敏感性,可根据每条点线的倾斜角度进行分析,因为每个点都代表不同的倾角,而这些点的排列是有规律的,因此对倾角变化敏感性强的属性参量就是可用于研究磁化体形状和姿态特征的分类。

|
图 2 9个属性参量的分维属性 (a)TMI;(b)ME;(c)I1;(d)I2;(e)Bxx;(f)Bxy;(g)Bxz;(h)Byy;(i)Byz |
不失一般性,可以认为这9个属性参量与磁源的形状、磁化方向等信息有着很高的相关性。由图 2可见,不同形状时正演结果变化明显,如基于属性参量TMI(图 2a)与属性参量I2(图 2d)可以很明显地区分出8种形态;而属性参量I1(图 2c)和Bxx(图 2e)对于磁化角度的敏感性随着磁偏角的变化明显不同,分别出现递增和递减两种变化趋势。从图 2还可以看出,分类属性值与偏角呈明显的线性关系。属性参量Bxx与Byy、Bxz与Byz形态虽然相似,但数值大小相差两个数量级。由式(1)可知,Bxx与Byy、Bxz与Byz相互独立,因此它们之间具有离散性,即各属性参量之间的数值相差很大,远远大于属性参量内部的数值差,不同参量的数值在数域上明显分别开。因此,可以参与分类。
上述分析表明,这9个属性参量对磁性体有良好的辨识能力,能够作为支持向量机分类的属性参量。每个属性参量的样本数据都可以构造一个特征向量,作为支持向量机分类的输入向量。
从样本库中调取数据,计算每个独立属性矩阵的最大特征值,分别对应9个特征向量中的某一个元素。对于这8种形状的磁化体,每种磁化体共有180个属性参量平面,即可构造出8组9×180的特征矩阵。以此作为PSO-SVM的训练样本,并随机抽选每种形状下各90组数据为训练样本,另外90组数据可作为测试样本。
3.3 识别测试在支持向量机中,8种长方体形状分别对应的输出代码为整数1~8,即类别标签设置为1~8,分类结果通过数字体现。
在仿真数据输入前,必须对数据进行归一化预处理
| $ f : p \rightarrow q = \frac{p-\min (p)}{\max (p)-\min (p)} $ | (7) |
式中p、q∈R。归一化的目的是将原始数据规一化到[0, 1]范围。结果输出后再进行反归一化,最后经过处理获得1~8的分类标签。
设置量子粒子群优化的初始搜索参数为:最大进化数量为200,种群最大数量为20。经过200次进化寻优,可以得到参数c和σ的最优解分别为77.4375和6.2357。
适应度用于评价粒子寻找最优解的能力强弱,适应度越大粒子寻优能力越强,反之适应度越小。适应度度量函数因具体情况而异。适应度的度量公式为
| $ F = \sum\limits_{d = 1}^{J} \frac{\left|p_{i, j}-p_{g, j}\right|}{m_{i, \text { best }}-p_{g, d}} $ | (8) |
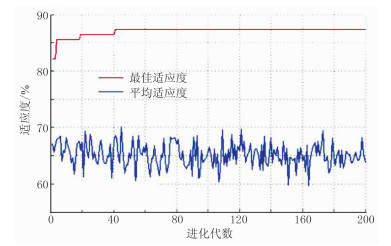
图 3为最终适应度曲线,其中最佳适应性曲线为每代粒子中的最佳适应度,平均适应度曲线为每代粒子的平均适应度,其最佳适应度最终为87.36%。
|
图 3 最终适应度曲线 |
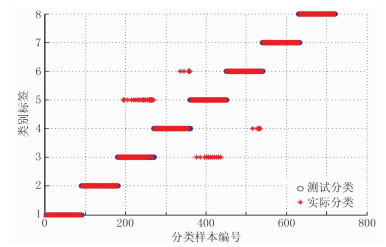
利用得到的c和σ的最优解构建基于QPSO-SVM的支持向量机。输入720个训练样本,对支持向量机进行训练,最后用测试样本进行测试,结果见图 4,识别正确率约为93%。
|
图 4 测试分类与实际分类对比图 |
为验证本文方法的可行性,采用4个磁通门传感器构建了平面十字形磁梯度张量系统。图 5为实验所使用的实验台,图 6为实测结果。

|
图 5 实验系统设计 |
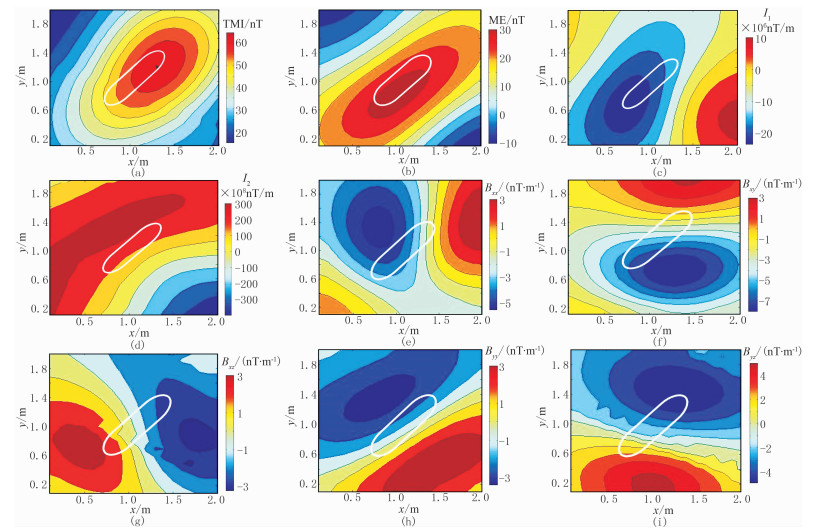
|
图 6 实测磁异常场分布 (a)TMI;(b)ME;(c)I1;(d)I2;(e)Bxx;(f)Bxy;(g)Bxz;(h)Byy;(i)Byz 图中白色曲线是目标体轮廓 |
实验采用直径分别为10、20cm、对应长度为100、70cm的两种铁圆柱和一个半径为20cm、厚度为10cm的铁圆板三种样品作为识别对象。分类标签分别设置为1、2、3。设置水平埋深为2m。搭建边长(x,y轴)为2m的水平正方形实验测量系统,x和y轴方向每隔0.1m设置一测量点,测量三种样品在同一空间位置时的正方形实验面中20×20个测量点的磁场数据,因此得到一个20×20的矩阵。对三种样品的4种姿态(与x轴分别成0°、45°、90°和135°)各采集了5组磁异常数据,并将样本数据以3:2的比例随机分成训练样本和测试样本,建立磁异常数据库。实验测量前,先测量背景场,对仪器进行校正。
以长度为1m,直径为10cm的铁质圆柱体为例分析结果。将其放置在实验台的正中位置,与实验台x轴夹角为45°,测量其地磁总场后减去背景场,即可得到异常场。由图 6可见,实测数据包含很强的干扰和噪声,主要来自大地、实验仪器和其他地下大型铁磁性物体,干扰了对目标体方位、轮廓、边缘等细节的分析。实验地点处于中纬度地区,磁倾角约为55°,磁偏角约为-9°,斜磁化使磁异常信号畸变和偏移,提高了信号分析的难度。但是根据图 6的磁异常分布仍然可以较清晰地分辨出目标的方位,也可大致辨别异常体的部分轮廓信息,且表现出与图 1理论仿真信号相似的形态特征。
图 6中属性参量TMI、I1、I2和ME均在一定程度上包含目标体的形状和姿态信息。对比图 1的仿真结果可以看出,这4个参量的分布形态虽然发生了偏移和扭曲,但是等值线的形态仍与目标体保持了一定的相似性,可反映出目标的部分轮廓。而另外的5个张量矩阵独立元素受到斜磁化影响较大,不能直观地反映目标形态,但是等值线峰值的连线却可大致反映出目标体的姿态。以上9个属性参量分布图表明,通过实测磁异常信号并不能直观地识别目标,但是实际信号与目标之间仍保持一定的相关性。因此,不失一般性地,认为这9个属性参量可以用于实际目标分类。这就是本方法的基本思想,对于不能直观反映目标信息的实测磁场,利用支持向量机对信号的特征进行分类,以达到识别目标的目的。
最后采用PSO-SVM进行分类,结果见图 7,识别正确率约为87.5%。

|
图 7 实验分类结果 |
由实验可知,本方法对小型铁磁性物体的识别取得了一定的效果。由于地磁背景场比较强,异常体或目标体的磁异常信号易被背景磁场淹没,降低了正确率。如图 7所示,识别错误主要集中在标签1和标签2,有两个标签1被识别为2,一个标签2被识别为1,这是因为这两种识别对象的形状相似度较高。因此关于细节识别有待进一步的研究。
5 结论(1) 利用矩阵最大特征值,构造模式识别的特征向量,分析并提取张量矩阵的9个属性参量联合识别磁性目标体,一定程度上弥补了磁测数据精度不足的缺点,也避免了大量磁测数据的计算。
(2) 将机器学习的方法引入地下磁性目标体的识别。利用量子粒子群改进的支持向量机识别地下小型目标体的形状,取得了较好的效果。
(3) 本文仅研究磁性异常体形状的识别,但此方法还可以识别磁目标的姿态、深度等。由实验结果可知,本文方法对磁异常信号的测量和特征分析仍有很大的研究空间。
| [1] |
孙刃.磁异常正反演技术在水下磁性目标探测中的应用研究[D].北京: 中国地质大学(北京), 2014. http://cdmd.cnki.com.cn/article/cdmd-11415-1015518014.htm
|
| [2] |
吴国超.基于磁异常的目标体定位反演方法研究[D].吉林长春: 吉林大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10183-1015599940.htm
|
| [3] |
王林飞, 郭灿灿, 薛典军, 等. 磁梯度张量解析信号分析法及其在场源位置识别中的应用[J]. 地球物理学进展, 2016, 31(3): 1164-1172. WANG Linfei, GUO Cancan, XUE Dianjun, et al. Ana-lytic signals of magnetic gradient tensor and their application to estimate source location[J]. Progress in Geophysics, 2016, 31(3): 1164-1172. |
| [4] |
李金朋, 张英堂, 范红波, 等. 基于磁梯度张量的地下小目标相关成像方法[J]. 探测与控制学报, 2016, 38(3): 75-78. LI Jinpeng, ZHANG Yingtang, FAN Hongbo, et al. Correlation imaging method of small subsurface target based on magnetic gradient tensor[J]. Journal of Detection & Control, 2016, 38(3): 75-78. |
| [5] |
尹刚, 张英堂, 李志宁, 等. 磁偶极子梯度张量的几何不变量及其应用[J]. 地球物理学报, 2016, 59(2): 749-756. YIN Gang, ZHANG Yingtang, LI Zhining, et al. Research on geometric invariant of magnetic gradient tensors for a magnetic dipole source and its application[J]. Chinese Journal of Geophysics, 2016, 59(2): 749-756. |
| [6] |
朱慧慧, 刘得军, 冯硕, 等. 基于磁偶极子构造法几何建模的铁管磁异常正演[J]. 计算机测量与控制, 2017, 25(3): 201-204. ZHU Huihui, LIU Dejun, FENG Shuo, et al. Magnetic dipole reconstruction geometry modeling for underground ferromagnetic pipe magnetic abnormal detection[J]. Computer Measurement & Control, 2017, 25(3): 201-204. |
| [7] |
谢永茂.基于模板匹配的局部磁异常识别方法[D].北京: 中国地质大学(北京), 2012. http://cdmd.cnki.com.cn/Article/CDMD-11415-1012364785.htm
|
| [8] |
张昌达. 航空磁力梯度张量测量——航空磁测技术的最新进展[J]. 工程地球物理学报, 2006, 3(5): 354-361. ZHANG Changda. Airborne tensor magnetic gradio-metry:the latest progress of airborne magnetometric technology[J]. Chinese Journal of Engineering Geophysics, 2006, 3(5): 354-361. DOI:10.3969/j.issn.1672-7940.2006.05.005 |
| [9] |
Hyoungrea R, Young S P, Hyen K J. Interpretation of magnetic gradient tensor for automatic locating a dipole source[J]. ASEG Extended Abstracts, 2012, 26. |
| [10] |
余天庆, 毛为民编著. 张量分析及应用[M]. 北京: 清华大学出版社, 2006.
|
| [11] |
张光辉, 程昱. 干扰识别的量子粒子群和支持向量机算法[J]. 中国电子科学研究院学报, 2011, 6(5): 490-493. ZHANG Guanghui, CHENG Yu. The quantum-behave particle swarm optimization support vectors machine method of jamming recognition[J]. Journal of China Academy of Electronics and Information Technology, 2011, 6(5): 490-493. DOI:10.3969/j.issn.1673-5692.2011.05.010 |
| [12] |
孙瑶琴. 改进粒子群算法优化支持向量机在故障诊断中的应用研究[J]. 计算机测量与控制, 2017, 25(3): 48-50. SUN Yaoqin. Application of improved particle swarm optimization support vector machine in fault diagnosis[J]. Computer Measurement & Control, 2017, 25(3): 48-50. |
| [13] |
Sun J, Feng B, Xu W.Particle swarm optimization withparticles having quantum behavior[C].Proceedings of the 2004 IEEE Congress on Evolutionary Computation, 2004.
|
| [14] |
李旭芳, 王士同. 基于QPSO训练支持向量机的网络入侵检测[J]. 计算机工程与设计, 2008, 29(1): 34-36. LI Xufang, WANG Shitong. Network intrusion detection method based on novel support vector machine[J]. Computer Engineering and Design, 2008, 29(1): 34-36. |
| [15] |
刘丽敏.磁通门张量的结构设计、误差分析及水下目标探测[D].吉林长春: 吉林大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10183-1012371597.htm
|



 郑建拥, 河北省石家庄市和平西路97号13号楼2楼, 050003。Email:
郑建拥, 河北省石家庄市和平西路97号13号楼2楼, 050003。Email: